Experimental investigation of non-Newtonian droplet collisions: the role of extensional viscosity

Abstract

We investigate the collision behaviour of a shear thinning non-Newtonian fluid xanthan, by binary droplet collision experiments. Droplet collisions of non-Newtonian fluids are more complex than their Newtonian counterpart as the viscosity no longer remains constant during the collision process. Despite the complex collision dynamics, we are able to present a complete regime map based on non-dimensional Weber (We) number and impact parameter (B). We compare the collision outcomes of xanthan, glycerol and a milk concentrate at similar impact conditions. These experiments reveal very rich and complex collision morphologies for shear thinning xanthan solution, strikingly different from Newtonian droplet collisions. Unlike glycerol and milk, xanthan collisions show no reflexive separation even at very high We number. Instead of breakup, we observe disc-like shapes with an oscillating behaviour of the colliding droplets. A detailed analysis reveals that this outcome is related to increased viscous energy dissipation and extensional effects.

1 Introduction

The study of droplet–droplet collision behaviour has been of considerable interest for more than a century because of its complexity as a fluid dynamics problem and because of its numerous industrial applications. Waste treatment, liquid–liquid extraction, combustion engines, surface treatment, and dense spray systems are some examples of industrial processes in which droplet collisions appear (Arkhipov et al. 1978; Ashgriz and Givi 1989; Qian and Law 1997; Willis and Orme 2003). In spray applications, the reliable prediction of the droplet collision outcome is essential to control and manipulate the droplet size distribution to achieve the desired performance, Munnannur and Reitz (2007).

The production of powders is common in chemical, pharmaceutical, food, and dairy industries. Powders are often manufactured from highly viscous liquid suspensions which are non-Newtonian in nature. Non-Newtonian droplet collisions occur, for example, during the production of powdered milk. Milk shows a shear thinning behaviour at increased milk solid concentrations, Trinh et al. (2007). A spray dryer consists of a large spray drying tower coupled with a cyclone. The highly viscous suspension is atomized with heated air through the pressure nozzle in the drying chamber. The very small droplets are dried by the hot air fed to the drying chamber. Dry product particles then leave the drying chamber at the bottom. The prediction of the collision outcomes enables the production of high quality powder with optimized characteristics suited for the intended application.

Numerous experimental (Sommerfeld and Kuschel 2016; Kuschel and Sommerfeld 2013; Kurt et al. 2007, 2009; Gotaas et al. 2007; Brenn and Kolobaric 2006; Willis and Orme 2003, 2000; Estrade et al. 1999; Qian and Law 1997; Jiang et al. 1992; Ashgriz and Poo 1990; Arkhipov et al. 1978) and numerical studies (Pan and Suga 2005; Li and Fritsching 2011; Nikolopoulos et al. 2009; Nobari and Tryggvason 1996; Focke et al. 2013) on Newtonian droplet collisions have already been performed in the last half century. The major objectives of these works consisted of investigating collision outcomes and their characteristics as well as the parameters defining the boundaries between different types of collisions for different fluids and conditions.

1.1 Newtonian and non-Newtonian collisions

Ashgriz and Poo (1990) performed binary water droplet collisions experiments for various impact conditions. The collision regimes of coalescence, reflexive, and stretching separation have been identified, and theoretical models for their occurrence have been provided. The current collision outcome boundary models are based on Ashgriz and Poo (1990) theory and extended to include viscous dissipation of energy.

The model of Jiang et al. (1992) was one of the first approaches which explicitly includes the viscosity as a parameter. The experiments for water and alkanes were limited to a small range of viscosities, from 0.4 to 3.5 mPas. They showed that the onset of reflexive separation shifts to higher Weber number (We) as the liquid viscosity-to-surface tension ratio increases. The model was later refined with the introduction of the Ohnesorge (Oh) number by Qian and Law (1997). Furthermore, Jiang et al. (1992) concluded that the extent of viscous energy dissipation occurring during the initial stage of droplet deformation is independent of the droplet viscosity. Willis and Orme (2000, 2003) conducted an experimental investigation of viscous droplet collisions in a vacuum environment to avoid aerodynamic effects during collisions. Their results showed a proportional dependence of energy dissipation on droplet viscosity, in contradiction to Jiang et al. (1992). Brenn and Kolobaric (2006) extended the model for the prediction of satellite formation after stretching separation of Brenn et al. (2001) by including the effect of viscosity. The model gave good predictions for highly viscous liquids and high We numbers, but was not able to describe low-viscous liquids such as water and alcohol. Gotaas et al. (2007) studied experimentally and numerically the influence of viscosity in a range from 0.9 to 50 mPas, analysing n-decane and mono-, di-, and triethylene glycol. In general, it was observed that the coalescence-to-separation boundaries shift to higher We number for fluids with higher viscosity. They confirmed that the results for the onset of reflexive separation for viscous fluids provided by Jiang et al. (1992) were not valid for relatively high viscosity fluids and a new empirical correlation was presented. In the study of Kurt et al. (2007), the collision behaviour for pure liquids and suspensions was explored. They identified the difficulty of working with suspensions because of instabilities appearing in the mono-dispersed droplet chain. The number of satellite droplets was found to increase with viscosity for glycerine solutions. The opposite behaviour was noticed for suspensions of solid particles. The authors claim that a higher concentration of particles may develop perturbations of the combined drop and the break-up of the ligament becomes faster. In addition, Kuschel and Sommerfeld (2013) investigated experimentally the effect of viscosity. The model of Ashgriz and Poo (1990) for the coalescence-stretching separation boundary was considered valid by Kuschel and Sommerfeld (2013) only for low capillary numbers (Ca) (< 0.577). For liquids exceeding this critical Ca number, they applied a combination of Ashgriz and Poo (1990) and Jiang et al. (1992) models. The boundary of coalescence–reflexive separation was observed only at small solid mass fractions. Sommerfeld and Kuschel (2016) experimentally extended the previous work of Kuschel and Sommerfeld (2013) considering different alcohols and an oil. The derived models are, also in this case, a combination of Ashgriz and Poo (1990) and Jiang et al. (1992) models.

While the studies on Newtonian fluids are numerous, only few are dedicated to non-Newtonian droplet collisions and mostly are based on computational investigations. Brenn (2011) mentioned the complexity of performing experiments with non-Newtonian fluids and, therefore, explains the lack of experimental investigations in the literature. There are practical experimental difficulties connected to the jet generation and control of the droplet size before impact.

Some experiments have been carried out for cases where the colliding fluid droplets are non-Newtonian, such as in the work of Motzigemba et al. (2002). Their experiments involved Newtonian and non-Newtonian liquids using Newtonian water/glycerol solutions and non-Newtonian shear thinning water/carboxymethylcellulose (CMC) solutions. CMC was chosen, because it has strong shear thinning behaviour and low elastic effects. Droplets were created by liquid flow through a circular orifice and subsequent Rayleigh break-up of the produced jet. It was found that the collision of CMC droplets produces a disc of larger diameter post-collision compared to the Newtonian droplet experiments. The increase of the collision complex diameter over time during collision was also measured for both types of fluids at different We numbers. The time for the colliding droplet to reach maximum expansion was found to be monotonously dependent on the We number. Newtonian and non-Newtonian collisions were compared, where the Newtonian viscosity was set equal to the zero shear rate viscosity of the non-Newtonian fluid. In their experiments, only the dynamics of coalescence was analysed for We numbers higher than 500. Because non-zero impact parameters were not considered, the collisions were not analysed in terms of a regime map.

In Focke and Bothe (2011), the experimental data of Motzigemba et al. (2002) were investigated using direct numerical simulations (DNS) with the volume of fluid (VOF) method. An important result of their investigation is that, for a Newtonian fluid, an effective viscosity can be chosen, which reproduces the same droplet collision dynamics as the shear thinning fluid. This viscosity is found by simulating the collisions with different Newtonian viscosities and comparing each maximum collision complex diameter with the one formed in the collision of non-Newtonian droplets. The effective viscosity was not equal to the zero shear rate viscosity. The simulated viscosity field showed that half of the energy at zero shear viscosity is dissipated in the early stages of collisions. The study was limited to collisions at B = 0 and very high We, and therefore, a systematic analysis of the viscosity variation for different impacting conditions is not presented. Focke and Bothe (2012) introduced a lamella stabilization method to demonstrate that an effective viscosity also exists in case of off-center collisions at high We. Non-Newtonian collisions lead to the formation of a thin liquid film in the center of the collision complex and a simulation can lead to reliable results only when the collision lamella remain intact. In the work of Sun et al. (2015), the collisions of non-Newtonian shear thinning and shear thickening fluid droplets were computationally investigated using the lattice Boltzmann method. The regimes of interest were only coalescence and reflexive separation for head-on collisions and the range of We number was approximately between 20 and 200. Their results show that the influence of the shear thinning viscosity on the collision dynamics is very complex and strongly dependent on the fluid rheology. For shear thickening fluid, the droplet deformation is significantly suppressed due to the increasing viscous dissipation with the extent of shear thickening. Non-Newtonian rheological effects have been considered in the field of droplet impact onto a solid surface by Bergeron et al. (2000). By adding a very low concentration of polymer to water, the droplet rebound after impact with the surface is inhibited promoting deposition. This behaviour is explained by considering non-Newtonian extensional viscosity, which provides a large resistance to drop retraction after impact.

Most of the previous research on non-Newtonian droplet collisions are focused on head-on interactions (B = 0), and so far, a complete regime map has unfortunately not been presented. Moreover, the current literature lacks a detailed experimental study and analysis on non-Newtonian droplet collisions. In our experiments, a full regime map for binary droplet collision of a shear thinning liquid is developed. Although the solute concentration of the considered liquid is low, a complete study on the collision dynamics dependent on impact conditions is presented. The collision outcome regimes of bouncing, coalescence, and separation are obtained and physically analysed. To highlight the shear thinning effect on the collision interactions, similar impact conditions are compared with a Newtonian liquid. The morphological evolution of impacting droplets of complex fluids, reported in this work, can serve as a benchmark for development of CFD methods for free-surface non-Newtonian flows.

1.2 Droplet collisional theory

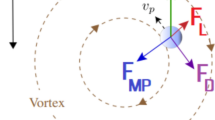
In most of the droplet–droplet collisional theories, a regime map, where the non-dimensional impact parameter and the collision Weber number are on the axes, is used to represent the droplet collision outcomes. A typical collision outcome regime map is illustrated in Fig. 1. The previous studies show that the collision of two droplets will result in one of four outcomes: bouncing, coalescence, stretching separation, or a reflexive breakup.

Fig. 1

Collision outcome regime map Qian and Law (1997)

When two spherical droplets approach each other, a gas layer is formed in between the surfaces. This layer of compressed gas can be of such high pressure that the drops are unable to make contact, resulting in deformation of both droplets and subsequent bouncing apart. If two droplets do not bounce and their surfaces make contact, they can permanently form one large droplet by coalescence, or temporarily by reflexive separation or stretching separation. These maps are not universal but specific to the droplet substance, in particular the droplet viscosity, and therefore, we need to consider at least one other dimensionless number. The definitions of the dimensionless parameters characterizing a collision of two droplets are given below.

The Weber number is the ratio between inertia forces and surface tension:

$$\begin{aligned} We=\frac{\rho _\mathrm{d}d_\mathrm{s}|v_\mathrm{rel}|^{2}}{\sigma }, \end{aligned}$$

(1)

where $\rho _\mathrm{d}$ is the droplet density, $d_\mathrm{s}$ is the diameter of the smallest droplet, $v_\mathrm{rel}$ is the relative velocity, and $\sigma$ is the surface tension. The ratio between $d_\mathrm{s}$ and the large droplet diameter $d_\mathrm{l}$ is the size ratio $\Delta$.

Fig. 2

Droplet collisional system geometry

The impact parameter B is defined, before the moment of impact, as the distance b between the two droplet centres in the plane perpendicular to the relative velocity vector (Fig. 2), normalized by the average droplet diameter:

$$\begin{aligned} \textit{B}=\frac{2b}{d_\mathrm{s}+d_\mathrm{l}}. \end{aligned}$$

(2)

When B is equal to 0, it is a head-on collision and when it is 1 a grazing collision.

The Ohnesorge number (Oh) represents the ratio of viscous forces and the combined effect of inertial forces and surface tension:

$$\begin{aligned} Oh=\frac{\mu _\mathrm{d}}{\sqrt{\rho _\mathrm{d}d_\mathrm{s}\sigma }}, \end{aligned}$$

(3)

where $\mu _\mathrm{d}$ is the droplet fluid viscosity. For a non-Newtonian fluid, either the zero shear viscosity can be used or, more appropriately, the viscosity at an estimated dominant shear rate during the collision. We will take the latter approach as we will discuss in more detail later. The collision outcome boundary models for Newtonian liquid are presented in "Appendix".

A collision theory for shear rate-dependent liquids was never fully developed because, as mentioned before, of the lack of investigations on collisions of non-Newtonian droplets.

1.3 Shear and extensional flow

Flows are broadly classified in shear and extensional flow. For example, for shear flow in the x direction with a gradient of magnitude $\dot{\gamma }$ in the y direction, the velocity gradient field is:

$$\begin{aligned} \overrightarrow{\nabla } \overrightarrow{u}= \dot{\gamma } \begin{pmatrix} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix}. \end{aligned}$$

(4)

For an incompressible Newtonian fluid, the stress tensor is given by

$$\begin{aligned} \tau = \mu \left( \overrightarrow{\nabla } \overrightarrow{u}+\overrightarrow{\nabla } \overrightarrow{u}^{T}\right) , \end{aligned}$$

(5)

with $\mu$ the shear viscosity of the fluid. Therefore, for a Newtonian fluid under shear flow, the viscous dissipation per unit volume is:

$$\begin{aligned} \tau :\overrightarrow{\nabla } \overrightarrow{u}= \mu \dot{\gamma }^{2}. \end{aligned}$$

(6)

The flow resulting from an incompressible fluid subjected to uniaxial extension with extensional rate $\dot{\varepsilon }$ in the x direction is characterized by a velocity gradient field expressed as follows:

$$\begin{aligned} \overrightarrow{\nabla } \overrightarrow{u}= \dot{\varepsilon } \begin{pmatrix} 1 &{} 0 &{} 0 \\ 0 &{} -\dfrac{1}{2} &{} 0 \\ 0 &{} 0 &{} -\dfrac{1}{2} \end{pmatrix}. \end{aligned}$$

(7)

In general, for both Newtonian and non-Newtonian fluids, the extensional viscosity is defined as $\mu _\mathrm{E}=-\dfrac{(\tau _{xx}-\tau _{yy})}{\dot{\varepsilon }}$. First of all, it is simple to show that this implies that, for a Newtonian fluid, the extensional viscosity is equal to $\mu _\mathrm{E}=3 \mu$. More generally, for non-Newtonian fluids, the so-called Trouton ratio $\mathrm{Tr}=\dfrac{\mu _\mathrm{E}}{\mu }$ is no longer 3, and the viscous dissipation per unit volume is:

$$\begin{aligned} \tau :\overrightarrow{\nabla } \overrightarrow{u}= \mu _\mathrm{E} \dot{\varepsilon }^{2}. \end{aligned}$$

(8)

Because for non-Newtonian fluids, the Trouton ratio can be significantly higher than 3, the amount of viscous dissipation in extensional flow can be higher than for an equivalent Newtonian fluid. The loss due to viscous dissipation decreases the amount of kinetic energy available for breaking the merged droplet. Therefore, more coalescence is expected in extensional flow.

2 Experimental methodology

2.1 Fluid characterization

As non-Newtonian fluid, a shear thinning xanthan solution is used in this work. Xanthan is extensively used in the industry as a food additive and viscosifying agent Palaniraj and Jayaraman (2011). A xanthan solution of 500 ppm was prepared by addition of xanthan to distilled water with careful stirring to obtain uniform mixing. The viscosity of the xanthan solution was measured with an Anton Paar MCR 302 series rheometer, using the standard strain controlled double gap rheometry at room temperature (22 $^\circ$C). The xanthan solution has a shear thinning rheology, as shown in the rheogram in Fig. 3. The viscosity profile obtained here is similar to other literature results Zhong et al. (2013), Wyatt et al. (2011). We have fitted the steady shear rheology data with the Carreau–Yasuda (CY) model Bird et al. (1977). The CY model describes the shear thinning behaviour of xanthan accurately:

$$\begin{aligned} \eta (\dot{\gamma })-\eta _{\infty }=(\eta _{0}-\eta _{\infty }) \left[ {1} +(\lambda \dot{\gamma }^{a}) \right] ^{\dfrac{(n-1)}{a}}, \end{aligned}$$

(9)

where $\eta$ is the shear rate-dependent viscosity, $\eta _{0}$ is the shear rate viscosity, $\eta _{\infty }$ is the infinite shear viscosity, $\lambda$ is the relaxation time, n is the power law index, and a is a parameter describing the rate of transition from the Newtonian plateau to the power law region. Table 1 shows the fit parameters from the CY model. The average error between the experimental and predicted viscosity values is less than ± 1$\%$ for the fit. The rheological measurements have been repeated over time, to observe any possible polymer degradation. For the typical duration of our experiments, no polymer degradation was found.

Fig. 3

Steady shear viscosity vs. shear rate for the xanthan solution, fitted with the Carreau–Yasuda (CY) model

Table 1 Rheological parameters from Carreau–Yasuda (CY) model

The surface tension of each prepared Xanthan solution was measured prior to each droplet collision experiment with a Kruss K20 Force Tensiometer. The surface tension showed a low amount of variability, with an average and standard deviation of 72.2 ± 0.3 mN/m.

2.2 Setup

Fig. 4

Schematic of the experimental setup

The experimental setup illustrated in Fig. 4 consists of a droplet generator (BUCHI, Switzerland) which produces two streams of mono-dispersed droplets. The perturbation of the streams is produced through an oscillating electrical signal at the desired frequency which causes a mechanical vibration of the structure. On exiting the nozzle, the liquid stream separates into equal size droplets. The frequency for these experiments is in the range of 500–750 Hz. The liquid is introduced into the producing unit by two 60 ml syringe pumps. The liquid then passes thought the vibration chambers and nozzles of 450 $\upmu$m.

The area before and after the collision is recorded by a Davis high-speed camera. The background of this area is a white plastic plate illuminated by a series of LEDs, to optimize the contrast of the droplets with respect to the background. A Sigma 105 mm f/2.8 EX DG Macro lens is used for the camera in front of the droplets.

Finally, to ensure that the two droplet streams collide in the same plane, the z position of the left vibration chamber can be adjusted. For this alignment procedure, a second high-speed side camera is added in the collision plane, perpendicular to the front camera. As the side camera is further away from the droplet streams, it is combined with a Nikon 200 mm f/4 AF-D macrolens to provide more magnification at a larger distance. The cameras are operated at a frequency of 4000 Hz and an exposure of 1/20000 s.

For each specific collision, the Weber number, the Ohnesorge number, and the impact parameter are determined by post-processing the pre-collision area of the recorded video. The area below the collision is used to visually determine the collision outcome. The processing procedure of the recorded frames is described in "Appendix".

3 Results

3.1 Xanthan

The lack of experimental investigations in this field is due to the extremely difficult calibration of the operating conditions to obtain streams of mono-dispersed drops stable streams. The complexity of performing droplet collision experiments resides in the difficulty of controlling the two streams. Brenn (2011) attributed the experimental complications to elastic stresses upon extensional and/or shearing motion of the liquid. For shear thinning inelastic liquids, we observed a delay of the jet droplet breakup and an unstable formation of the mono-disperse stream of droplets. A patient calibration of the syringe pump flow rate in correspondence to the vibrational frequency allowed us to achieve a remarkable number of droplet events for different impacting conditions. A large number of analysed recordings were neglected and discarded because of satellite droplet formation before impact or undesired collisions between two consecutive droplets in the same stream. In the case smaller satellites were visible in the recording before collision or if the droplet diameter difference in the stream was greater than 4$\%$, the recordings were discarded and a new optimal frequency was individuated. We observed many injecting issues in stabilizing the stream breakup using smaller nozzles diameter than 450 $\upmu$m. Because of this experimental restriction, droplet diameters of approximately 1 mm were generated.

The camera resolution was also an important factor to take into consideration. Our aim is to observe the total collisional event, pre- and post-collision, with a sufficient number of pixels per drop diameter, and therefore, we choose a suitable observation frame. With smaller droplet sizes, the process of tracking and analysis of drops would have not been accurate.

All the collision events presented in this work are with equal size droplets ($\Delta$ = 1).

Table 2 Estimated Oh numbers corresponding to low and high shear rates

When placing the outcomes of non-Newtonian fluid droplet collisions in regime maps, it is important to have an estimate for the most relevant shear rate, because the viscosity is shear rate-dependent. The work of Finotello et al. (2018) showed that the range of shear rates in which experiments with milk were performed are in between $0.8 \times 10^{3}$/s and $4.7 \times 10^{3}$/s. These were calculated according to Eq. 10, where $v_r$ is the relative velocity between the droplets at the moment of collision and d is the diameter of the droplets (Chandra and Avedisian (1991)). The diameters of the droplets in Finotello et al. (2018) experiments ranged from 620–770 $\upmu {\rm m}$ and the relative velocities from 0.5–3 m/s:

$$\begin{aligned} \dot{\gamma } = \left| \frac{\partial u_\mathrm{r}}{\partial z} \right| \sim \frac{v_\mathrm{r}}{d}. \end{aligned}$$

(10)

The relative velocities of the droplets in this study range from 0.8–3.8 m/s and the droplet diameters from 990–1200 $\upmu {\rm m}$. Equation 10 thus yields an approximation for the shear rates of the fluids of 800–3200/s . To properly consider the viscosity variations, an apparent viscosity needs to be measured for each colliding pair of drops, and therefore, a corresponding Oh number. This is not convenient when the collision events are analysed in a regime map, which is obtained for a constant Oh. We measured the Oh number for the extremes cases of experienced shear rate, see Table 2. Because, in our experiments, the difference in Oh number between the most extreme cases is not very large, we decided to represent the results in a regime map at the average Oh number equal to 0.014. An alternative approach would be to consider a different dimensionless parameter, depending on the shear rate or shear thinning exponent, for example. Since our objective is to compare also collision morphologies at similar impacting conditions, we opted for using an average Oh number.

Fig. 5

Collision regime map of 500 $\mathrm{ppm}$ Xanthan solution, Oh = 0.014. Blue stars are used for representing coalescence, green squares for stretching separation, and magenta circles for bouncing. Black diamonds indicate the collisions of the supplementary videos

The resulting collision regime map of the 500 $\mathrm{ppm}$ xanthan collision experiments can be seen in Fig. 5. The observed collision outcomes are bouncing (magenta circles), coalescence (blue stars), and stretching separation (green squares). The regimes of bouncing, coalescence, and stretching separation occur very similarly as in collisions of a Newtonian fluid. The main difference resides in the absence of the reflexive separation regime. Reflexive separation, which is typically observed in Newtonian fluid droplets for head-on collisions (B = 0), is not observed in any of the collision experiments with xanthan. Even for We larger than 200, there is only coalescence at low impact parameters. Three droplet collisions have been selected in which reflexive separation would be expected, for a Newtonian fluid, and shown in Fig. 6. As the Weber number increases, the disc diameter of the combined droplet after the initial merging increases without breakage. From the side camera views, a very thin fluid film (lamella) with a thick toroidal rim can be detected. In addition, in Focke and Bothe (2011), non-Newtonian fluids presented an enlargement of the collision complex compared to Newtonian cases. Successively, the combined droplet evolves in time until reaching an approximately spherical shape. In the side images in Fig. 6, the droplets before collision are not in focus. This is because they are out of the plane of focus which is imposed for our experiments to be at the droplet impact position. Proper alignment of the two streams needs to be, indeed, verified at the droplet impact position.

Fig. 6

Three droplet collisions for xanthan at We = 40, 99, and 211 and an impact parameter B close to zero. Note that the droplets seen in a collision example are the same, in both the side camera and front camera frame

The reader is referred to the supplementary videos for the collision dynamics of xanthan (video 1 for bouncing at We = 19 and B = 0.55, video 2 for coalescence at We = 129 and B = 0.2, and video 3 for stretching separation at We = 204 and B = 0.65).

3.2 Comparison with glycerol and milk

Table 3 Droplet collision parameters

Fig. 7

Collision regime maps of 20 $\%$ TS milk concentrate, 40 $v \%$ glycerol solution obtained by Finotello et al. (2018), together with the collision regime map of 500 $\mathrm{ppm}$ xanthan (this work). The dashed lines are the boundary models for reflexive separation [adapted from Qian and Law (1997)], the continuous lines for stretching separation [adapted from Jiang et al. (1992)]. The Estrade et al. (1999) prediction for bouncing is represented by the dashed–dotted line

The 500 $\mathrm{ppm}$ xanthan solutions have a comparable viscosity profile as that of 20$\%$ total solids’ (TS) content milk concentrate used in the collision experiments by Finotello et al. (2018). The total solids content TS is calculated with

$$\begin{aligned} \mathrm{TS}=\dfrac{\mathrm{Dry \, mass}}{\mathrm{Total\, wet \, mass}}\times 100. \end{aligned}$$

(11)

In their work, experiments were also carried out with 40 $v \%$ glycerol, which has a constant viscosity of $5 \times 10^{-3}$ Pa s, similar to that of a 20$\%$ TS milk concentrate at $4.3 \times 10^{-3}$ Pas. Trinh et al. (2007) explained that the rheology of milk concentrates is Newtonian for milk concentrates below approximately 30$\%$ TS content and non-Newtonian when the milk is more concentrated. From Eq. 10, we obtain an approximation for the shear rate of 800–3200/s. For 40 $v \%$ glycerol and 20$\%$ TS milk, the shear rates are between 800 and 4700/s . The range of Oh numbers investigated in this work is lower than the average Oh numbers corresponding to the collision experiments for the 20 $\%$ TS milk, which were 0.022, and for the 40 $v \%$ glycerol experiments, which were 0.021. However, they are still in the same range and a comparison between the collision outcomes can be made between the three different fluids. In Table 3, the physical and collision parameters of the three liquids considered in this comparison are summarized. The collision results of 20 $\%$ TS milk concentrate and 40 $v \%$ glycerol solution, as well as that of 500 ppm xanthan, are shown in Fig. 7. The regime map for xanthan is the same as in Fig. 5, but, now, includes the collision model boundaries, while We numbers larger than 100 are not shown to facilitate comparison with the other two regime maps.

Fig. 8

Collision of 40 $v\%$ glycerol, 20$\%$ TS milk, and 500 ppm xanthan droplet collisions at We $\backsim$ 40 and B $\backsim$ 0.63

Fig. 9

Collision of 40 $v\%$ glycerol, 20$\%$ TS milk, and 500 ppm xanthan droplet collisions at We $\backsim$ 40 and B $\backsim$ 0

The models that predict collision boundaries for bouncing, stretching separation, and reflexive separation are also shown in Fig. 7. The model that is used for predicting the boundary between coalescence and stretching separation, seen in Eq. 24, is developed by Jiang et al. (1992). The fitting parameters $C_1$ and $C_2$ obtained by Finotello et al. (2018) from collision experiments with milk, $C_1=3$ and $C_2=0.05$, are also used in this work. As seen in Eq. 24, the model is dependent on fluid characteristic parameters $\eta$, $\sigma$, and $\rho$, which were entered accordingly for each fluid.

The empirical model used for prediction of the bouncing collision boundary is seen in Eq. 25, and is developed by Estrade et al. (1999). In this model, $\Delta$ represents the size ratio and $\Theta$ represents the shape parameter, which was empirically found to be $\Theta = 3.351$, as obtained from ethanol collision experiments.

A combined model of Ashgriz and Poo (1990) and Qian and Law (1997) is used for predicting the boundary between the reflexive separation regime and coalescence regime. The Ashgriz and Poo (1990) model is developed for water droplet collisions, without accounting for the viscous dissipation. Qian and Law (1997) further developed this model by including a dependence on the viscosity through the Ohnesorge number. The model curve from Ashgriz and Poo (1990) is, therefore, shifted to higher Weber numbers by moving the position of the critical Weber number, the Weber number from which reflexive separation occurs at impact parameters close to zero. The model is dependent on fitting parameters $C_a$ and $C_b$. The fitting parameters derived for milk experiments are $C_a=510$ and $C_b=17.05$.

Significant differences between the collision outcomes of Xanthan, glycerol, and milk are observed.

Bouncing is present in both glycerol and xanthan for a comparable regime of Weber numbers, impact parameters, and similar Oh. Shear thinning behaviour, even if at very low concentrations, seems not to be the mechanism that leads to the absence of bouncing in milk. The collision boundary of the bouncing regime is not very well predicted by the bouncing model of Estrade et al. (1999), but it can still be used for reference as it is one of the very few models that describe the bouncing regime of droplets. Further investigation is required to include viscous energy dissipation and to define a shape parameter which better describes our experiments.

Stretching separation is present in all three fluids and can be described in a reasonable way by the adapted Jiang et al. (1992) model. Recording examples of stretching separation droplets of 20$\%$ TS milk, 40 $v\%$ glycerol, and 500 ppm xanthan are shown in Fig. 8 for comparable Weber numbers. Note that while, for xanthan, we are still in the ligament formation stage, for glycerol and milk, the collision outcomes can already be observed. The stretching morphology appears to be similar for all three fluids.

Reflexive separation is not found for any collisions of 500 ppm xanthan, even at very high Weber numbers. Instead of a breakup, we see the formation of a disc with a large radius, and oscillation of the combined drop shape due to elongation and retraction dynamics, as seen in Fig. 6. To illustrate the difference between milk and glycerol droplet collisions, Fig. 9 shows recording the examples of all three fluids at We $\sim$40 and B$\sim$0, where the 20$\%$ TS milk and 40 $v\%$ glycerol droplet collisions have a reflexive separation outcome and the 500 ppm xanthan droplets have a coalescence collision outcome. Although the spherical shape of a typical coalesced droplet is not visible in the last frame, we can definitely predict coalescence as collision outcome. One reason is related to the fact that we observe coalescence for B = 0 also at higher We number, so an onset for the reflexive separation boundary is not determined. Second, the ligament formed after collision does not breakup but instead the two tip edges retract back to each other and the droplet complex is newly compressed. The initial kinetic energy is not sufficient to separate the ligament in the early stages after collision and, because it dissipate after collision, will not be able later to breakup the droplet. As, for the stretching separation case, while xanthan is still in the process of forming a stable coalesced droplet, for glycerol and milk, the collision outcomes can already be observed.

3.3 Energy dissipation and extensional effect

We hypothesize that the absence of reflexive separation in xanthan droplets in the considered range of Weber numbers might be related to the fact that the shear viscosity is not the only relevant viscosity component, but that there is also an extensional viscosity component.

Indeed, Figs. 6 and 9 suggest that, for nearly head-on collisions, the droplets experience extensional flow rather than shear flow. At the high deformation rates investigated in our experiments, the Trouton ratio (ratio of extensional-to-shear viscosity) for xanthan solutions of comparable concentration is found to be much more than the value of 3 valid for Newtonian fluids, as shown in the works of Secor et al. (1989); Fuller et al. (1987); Khagram et al. (1985). For the 500 ppm xanthan solution, the extensional viscosity was found to be almost two orders of magnitude higher than the corresponding shear viscosity, Tr =104.9, Fuller et al. (1987). The presence of such a high extensional viscosity component might strongly influence the collision dynamics. The extensional viscosity $\mu _\mathrm{E}$ for xanthan 500 ppm corresponds, therefore, to $\mu _\mathrm{E}=\mathrm{Tr} \mu (\dot{\gamma })=0.4$ Pas.

Note that the theoretical derivations for energy dissipation assumed a Newtonian fluid, and, therefore, largely underestimated the energy dissipation for non-Newtonian fluids at low impact parameter. However, we also note that, in deriving the energy dissipation for low impact parameters, these theoretical derivations actually assumed an extensional flow. Therefore, the results for low impact parameters may still be valid for non-Newtonian fluid provided that we replace all occurrences of the shear viscosity $\mu$ by 1/3rd of the extensional viscosity. This implies that, for low impact parameters, one should take into account an effective extensional Ohnesorge number $Oh_\mathrm{E}= Oh \dfrac{\mathrm{Tr}}{3}$, with Tr the Trouton ratio. For a droplet of xanthan of 1 mm diameter, we have $Oh_{E}=0.495$. Applying the model for reflexive to coalescence boundary, we can predict an onset of the transition between the two regimes $We_\mathrm{crit} (Oh_\mathrm{E})$ of approximately 270. Therefore, we find that the extensional viscosity dominates during drop retraction and, consequently, inhibits droplet separation in the range of collision velocities examined in our work. As already mentioned, in our experiments, the maximum We number reached for head-on collision was 220 and no reflexive separation was observed. For higher We number, the streams became very unstable and the drops were exhibiting shape deformation even before collision, so that the automated detection of the diameters was negatively affected. It was, therefore, not possible to perform experiments at higher We number to verify the prediction of 270 as $We_\mathrm{crit}$ for xanthan, but we can confirm with certainty that reflexive separation does not occur before We = 220.

Fig. 10

Evolution in time of the two axial sizes of the collisional complex for milk 20% TS content, glycerol 40 $v\%$, and xanthan at We = 40 and B = 0

Fig. 11

Evolution in time of the two axial sizes of the collisional complex for xanthan with B=0 and for the cases We = 40, We = 99, and We = 210

In addition, in the work of Bergeron et al. (2000), the capillary number Ca was reformulated using the extensional, rather than the shear viscosity to demonstrate the difference between the Newtonian and non-Newtonian solutions. When a water droplet collided onto a solid surface, a retraction and rebound was observed, while the impact of a droplet of a very dilute polymer solution in water showed deposition on the surface. They attributed this behaviour to the predominance of the extensional over the shear viscosity.

The kinetic energy before impact, responsible for the droplet separation after impact, is dissipated by viscous dissipation. For Newtonian fluids such as glycerol solutions and 20$\%$ TS milk concentrate, the kinetic energy is only partially dissipated but still sufficient to lead to separation. For non-Newtonian liquids such as xanthan solutions, the extensional viscosity is typically much larger than the shear viscosity, and, therefore, might play a crucial role. In this case, the same amount of kinetic energy is not sufficient (as compared to a Newtonian fluid) to generate breakup, since more is dissipated by viscous dissipation. Focke and Bothe (2011) also reported that the extensional part of the dissipated energy is higher than the shear part for non-Newtonian binary droplet collisions.

The total amount of dissipated energy DE can be related to the viscous dissipation rate VDR (units J/s) and dissipation function $\Phi$ (units J/s/m$^3$) through a time integral and a spatial integral:

$$\begin{aligned} \mathrm{DE}(t)=\int _0^t \mathrm{VDR}(t)\mathrm{d}t, \end{aligned}$$

(12)

$$\begin{aligned} \mathrm{VDR}(t)=\int \int \int _{V_{d}} \Phi \mathrm{d}V. \end{aligned}$$

(13)

The dissipation function $\Phi$ quantifies the local volumetric viscous dissipation rate. Its volume integral, the viscous energy dissipation rate VDR, has relatively high values from the time of droplet impact to the time the two droplets reach the maximum deformation.

In extensional flow, the viscous dissipation per unit volume and unit time is $\tau :\overrightarrow{\nabla } \overrightarrow{u}=\Phi =\mu _\mathrm{E} \dot{\varepsilon }^{2}$. The extensional rate $\dot{\varepsilon }$ is of the order of the ratio of the relative velocity of the drops and the typical droplet size $\dfrac{v_\mathrm{rel}}{d}$ . The total volume of the two droplets is deformed due to extensional effects changing the spherical shape to a disc of large diameter. The time that the drops collide towards each others and reach the maximum deformation is of the order of $t_\mathrm{maxDef}=\dfrac{d}{v_\mathrm{rel}}$. The total dissipated energy is, therefore, of the order of $\mathrm{DE}(t_\mathrm{maxDef})=2\mu _\mathrm{E}\dfrac{v_\mathrm{rel}}{d} \dfrac{\pi d^{3}}{6}$. The kinetic energy of two droplets in relative motion, calculated with their reduced mass, is $\mathrm{KE}=\dfrac{1}{2} \left[ \dfrac{1}{2}\rho \dfrac{\pi d^{3}}{6} \right] v_\mathrm{rel}^{2}$. The ratio of the kinetic over the dissipated energy $\mathrm{KE/DE}$ for a collision of two droplets of xanthan 500 ppm with diameter 1 mm and relative velocity 3 m/s is reported in Table 4.

Table 4 Estimate of extensional effect for droplet collisions of Newtonian and Non-Newtonian liquids

Figure 10 shows the evolution of the normalized dimension in x- and y-directions of the colliding complex for the impact condition of We = 40 and B$\sim$0 for xanthan, glycerol 40 $v\%$, and milk 20% TS content. The $x\Delta$ and $y\Delta$ values are normalized with the corresponding initial droplet diameter. These dimensions have been obtained in Matlab by forming a bounding box around the collision complex. From this figure, we learn that the collision dynamics is very similar in the first stages, because a first disc is formed which retracts back to a cylindrical shape. The initial neck destabilization from the two tip edges is visible for glycerol already at t = 3 ms, while, for milk, 20% TS only at t = 4 ms. The consequent pinch-off of the liquid bridge between the two edges appears only for these two liquids, while, for xanthan, the internal forces move the two edges once again towards each other. In the work of Sun et al. (2015), a droplet collision of Newtonian liquid at We = 40, B = 0, and Oh = 0.0265 is compared with a shear thinning droplet collision (CY model with n = 0.4) at We = 40, B = 0, and an effective Oh = 0.0350. The time sequence of the non-Newtonian droplet collision shows similar morphologies to the one observed in our work (Fig. 10) with formation of a disc which retracts to an ellipsoidal shape. Moreover, also in their results, coalescence is preferred as a collision outcome. This confirms that reflexive separation is more difficult to occur compared to Newtonian droplet collisions.

To investigate the effect of the relative velocity on the collision complex of xanthan, three impact conditions, We = 40, We = 99, and We = 210 at B $\sim$ 0, are considered in Fig. 11. The collision morphology presents more fluctuations from the typical spherical or cylindrical shape when the We is higher. In addition, the disc formed after impact is more extended as indicated by the first peak in the normalized $y\Delta$ plot in Fig. 11.

We stress that the data from Figs. 10 and 11 should not be taken as absolute values. A small misalignment of the streams leads to a slight rotation of the collision complex, so $x\Delta$ and $y\Delta$ are not fully aligned with the symmetry axes of the impact, especially after 5 ms (see Fig. 10 and 11).

Fig. 12

Regime map for Xanthan 500 ppm with adapted collision boundary for coalescence to reflexive separation

The regime boundary model demarcating stretching separation and coalescence can well describe the transition for glycerol 40 v$\%$, milk 20$\%$ TS, and xanthan 500 ppm. This demarcation boundary is, therefore, not influenced by the extensional viscosity, in contrast to the boundary between reflexive separation and coalescence. This can be understood, because, in a stretching separation case, the impact parameter is large, meaning that the internal flows during impact are expected to be more of shearing character than of extensional character. As a consequence, the viscous dissipation during stretching separation collisions is similar to that of a Newtonian liquid with similar (effective) viscosity, and the kinetic energy is still sufficient to lead to breakup of the combined droplet.

In Fig. 12, the regime map for xanthan 500 ppm is illustrated together with the collision regime boundaries. The coalescence to reflexive separation model has been adapted taking into consideration that the critical We, $We_{\rm crit}(Oh_{\mathrm{E}})$, is dependent of the shear and extensional viscosity. The coalescence regime for near head-on collision of Xanthan 500 ppm drops would be extended until $We_\mathrm{crit} (Oh_{\mathrm{E}})$=270 where reflexive separation occur. It has to be noted that this collision transition is only predicted and needs to be verified by future experiments or simulations. Due to experimental limitations, we cannot reach We number larger than approximately 210. Note that, at high We number, the separation of droplets is characterized by fingering where the periphery of the expanding disc after impact is wrinkled and formation of very small satellites might occur, Pan et al. (2009). At even larger We number, breakup with fragmentation of the disc in satellites and splattering occur.

Although, with this work, only a qualitative description can be provided, it is the first attempt to investigate shear thinning liquid droplet collisions through a large number of highly complex experiments and to characterize them using droplet–droplet collisional theory. A systematic quantification of extensional effects remains the subject of future work.

4 Conclusions

Binary collisions between droplets of non-Newtonian shear thinning xanthan have been experimentally investigated with jet generation and break-up equipment. The difficulties of performing experiments with non-Newtonian liquids were overcome by a careful optimization of the vibration frequency and initial impact conditions. The collision dynamics for a broad range of We number $We=8.8-220$ and impact parameters $B=0.0015--0.95$ were identified and analysed. These experiments generate a benchmark for validation of numerical methods for free-surface flows with non-Newtonian fluids. The regime map, obtained in this work, can be used for modelling spray processes of non-Newtonian liquids. The different impact conditions enabled us to identify the regimes of bouncing, coalescence, and stretching separation together with the transition boundaries. For the first time, a complete We-B regime map of non-Newtonian droplet collisions is obtained.

The collision outcomes and the boundaries demarcating collisional regimes are analysed and compared with a previous investigation on viscous droplet collisions, in which 20$\%$ TS reconstituted milk concentrate and Newtonian 40 $v \%$ glycerol/water solutions were studied. These liquids have a similar viscosity in the range of shear rates experienced by the droplets at the moment of impact, so that also the Oh numbers are similar. The bouncing behaviour of 500 ppm xanthan is comparable to that of glycerol. The bouncing model by Estrade et al. (1999) is able to predict the boundary only in the region of high We numbers. The stretching separation is observed for all three liquids and can be reasonably well described by the adapted Jiang et al. (1992) collision boundary model.

The regime of reflexive separation is, however, not observed for any of the xanthan droplet collisions, even for relatively high Weber numbers of We>200. Instead, droplet coalescence is promoted. For 20$\%$ TS milk and 40 $v \%$ glycerol, reflexive separation occurs already at We approximately equal to 35. The collision dynamics of head-on interactions are temporally analysed for Newtonian and non-Newtonian counterparts. The results reveal a more complex and rich collisional evolution for our shear thinning droplets. The lack of reflexive separation in xanthan might be related to dominant extensional effects at such high deformation rates. Because the extensional viscosity in xanthan is at least an order of magnitude higher than the shear viscosity at these rates of deformation, significantly more viscous dissipation takes place during collision. Therefore, droplet coalescence is promoted instead of breaking up for low impact parameter collisions.

This research provides significant new insights in droplet collisions of shear thinning non-Newtonian fluids. In future work, droplet collisions with more complex rheologies should be studied and compared with numerical models. New phenomenological models for collision boundaries can also be developed to include such non-Newtonian effects based on our experimental findings.

Appendix

1.1 A: Models for Newtonian fluids

A model that can be applied to low-viscous liquids is the one proposed by Ashgriz and Poo (1990). In their theory, reflexive separation occurs if the effective kinetic energy is larger than 75$\%$ of the nominal surface energy of the merged droplets. For head-on collisions ($B=0$), the boundary between coalescence and reflexive separation corresponds to $We_\mathrm{c}$=19 when $\Delta$ is 1. More generally, for non-zero values of B, the model for the boundary between reflexive separation and coalescence is given by:

$$\begin{aligned} We_\mathrm{c}=3\left[ 7\left( 1+\Delta ^{3}\right) ^{2/3}-4\left( 1+\Delta ^{2}\right) \right] \frac{\Delta \left( 1+\Delta ^{3}\right) ^{2}}{\Delta ^{6}\eta _\mathrm{s}+\eta _\mathrm{l}}, \end{aligned}$$

(14)

where

$$\begin{aligned} \eta _\mathrm{s}=2(1-\xi )^{2}\left( 1-\xi ^{2}\right) ^{1/2}-1, \end{aligned}$$

(15)

$$\begin{aligned} \eta _\mathrm{l}=2(\Delta -\xi )^{2}\left( \Delta ^{2}-\xi ^{2}\right) ^{1/2}-\Delta ^{3}, \end{aligned}$$

(16)

$$\begin{aligned} \xi =\frac{1}{2}B\left( 1+\Delta \right) . \end{aligned}$$

(17)

For the boundary between stretching separation and coalescence, they found:

$$\begin{aligned} We_\mathrm{c}=\frac{4\left( 1+\Delta ^{3}\right) ^{2}\left[ 3\left( 1+\Delta \right) \left( 1-B\right) \left( \Delta ^{3}\phi _\mathrm{s}+\phi _\mathrm{l}\right) \right] ^{1/2}}{\Delta ^{2}\left[ \left( 1+\Delta ^{3}\right) -\left( 1-B^{2}\right) \left( \phi _\mathrm{s}+\Delta ^{3}\phi _\mathrm{l}\right) \right] }, \end{aligned}$$

(18)

where

$$\begin{aligned} \phi {}_\mathrm{s}={\left\{ \begin{array}{ll} 1-\frac{1}{4\Delta ^{3}}\left( 2\Delta -\tau \right) ^{2}\left( \Delta +\tau \right) &{} h>\dfrac{1}{2}d_\mathrm{s}\\ \frac{\tau ^{2}}{4\Delta ^{3}}\left( 3\Delta -\tau \right) &{} h<\dfrac{1}{2}d_\mathrm{s}, \end{array}\right. } \end{aligned}$$

(19)

$$\begin{aligned} \phi _\mathrm{l}={\left\{ \begin{array}{ll} 1-\frac{1}{4}\left( 2-\tau \right) ^{2}\left( 1+\tau \right) &{} h>\dfrac{1}{2}d_\mathrm{l}\\ \frac{\tau ^{2}}{4}\left( 3-\tau \right) &{} h<\dfrac{1}{2}d_\mathrm{l}, \end{array}\right. } \end{aligned}$$

(20)

$$\begin{aligned} h=\frac{1}{2}\left( d_\mathrm{l}+d_\mathrm{s}\right) \left( 1-B\right) , \end{aligned}$$

(21)

$$\begin{aligned} \tau =(1-B)(1+\Delta ). \end{aligned}$$

(22)

The model of Jiang et al. (1992) is valid only for relatively low-viscous liquids but takes into account that a portion of the kinetic energy dissipates because of viscous flow inside the droplets. For the critical We, demarcating the transition from coalescence to reflexive separation for head-on collisions ($B=0$), Jiang et al. (1992) proposed a direct dependence on the viscosity:

$$\begin{aligned} We_\mathrm{c}=C_{1}\frac{\mu _\mathrm{d}}{\sigma }+C_{2}, \end{aligned}$$

(23)

with $C_{1}$ in (m/s). Successively, Qian and Law (1997) modified the viscosity-to-surface tension ratio with the Oh number and used two constants, $C_{3}$ related to geometrical parameters, and $C_{4}$ to the surface tension energy of the deformed droplet. The model for the critical impact parameter demarcating the boundary between coalescence and stretching separation proposed by the same authors is:

$$\begin{aligned} B_\mathrm{c}=\frac{1}{We^{1/2}}\left[ 1+k\frac{\mu _\mathrm{d}}{\sigma }\left( \frac{\rho _\mathrm{d}d_\mathrm{s}}{\sigma }\right) \right] , \end{aligned}$$

(24)

where k is a constant. It can be noticed that Eqs. 23 and 24 contain constants which are not dimensionless, and, therefore, likely to be dependent on the system under consideration. This triggered other authors to develop theories or correlations which are presented in dimensionless form.

The criterion for bouncing, formulated by Estrade et al. (1999), is that when the droplet initial kinetic energy of deformation does not exceed the energy required to produce a certain threshold deformation. The viscous dissipation was neglected. The model predicts collision outcomes especially well at large Weber numbers:

$$\begin{aligned} We_\mathrm{c} = \frac{{\Delta \left( {1 + {\Delta ^2}} \right) \left( {4\phi ' - 12} \right) }}{{{\phi _\mathrm{l}}{{\left( {1-B^2} \right) }}}}, \end{aligned}$$

(25)

$$\begin{aligned} \phi ' = 2{\left( {\frac{3}{{{\phi ^2}}} + 1} \right) ^{ - {\textstyle {2 \over 3}}}} + {\left( {\frac{3}{{{\phi ^2}}} + 1} \right) ^{{\textstyle {1 \over 3}}}}. \end{aligned}$$

(26)

The shape parameter $\phi$ depends on the material properties of the liquid and the gas, and is determined experimentally. The value reported by Estrade et al. (1999) for ethanol droplets is $\phi$ = 3.351. Kuschel and Sommerfeld (2013) found a continuous distribution of the shape factor as a function of viscosity for both PVP K30 and saccharose. Successively, Sommerfeld and Kuschel (2016) attributed values between 3.3 and 3.8 for various alcohols.

1.2 B: Droplet image analysis

The recorded images are analysed using MATLAB R2015a and processed following two different procedures, corresponding to before and after collision. For a detailed description of the image processing, see Finotello et al. (2018). The recording is discarded if the error in the alignment of the two streams is greater than 5$\%$ of the droplet diameter.

Fig. 13

Droplet image analysis

The pre-collisional area is selected manually and the locations of all droplets are determined with the imfindcircles function, as illustrated in Fig. 13. The droplet on the left side is associated with the one on the right side with the smallest vertical distance. In Frame 2, 13, all droplets are again localized using the location of the droplet pair in the previous frame. The horizontal and vertical displacements from the previous frame are determined and velocity components are derived. The script continues with the next frames. The process for a pair stops when the circles around the two droplets are in contact or overlap. With the displacements and positions of the droplets at the moment of collision, the relative velocity and impact parameter are calculated for each pair in the recording. The distance b between the two droplet centres, is calculated according to:

$$\begin{aligned} b=\left| \frac{\Delta y \Delta v_{x} - \Delta x \Delta v_{y}}{v_\mathrm{rel}} \right| . \end{aligned}$$

(27)

With viscosity, density, and surface tension of the colliding liquid, the relevant dimensionless numbers are calculated and then stored in a matrix.

The post-collision procedure consists in the visual analysis of the recording and detection of the collision outcome for each droplet pair. The duration which a droplet travels in the region of interest, from entering the frame to the bottom, is typically 7.5 ms.