Abstract
The interaction of meandering tip vortices shed from a leading wing with a downstream wing was investigated experimentally in a water tunnel using flow visualization, particle image velocimetry measurements, and volumetric velocity measurements. Counter-rotating upstream vortices may exhibit sudden variations of the vortex core location when the wing-tip separation is within approximately twice the vortex core radius. This is caused by the formation of vortex dipoles near the wing tip. In contrast, co-rotating upstream vortices do not exhibit such sensitivity. Large spanwise displacement of the trajectory due to the image vortex is possible when the incident vortex is further inboard. For both co-rotating and counter-rotating vortices, as long as there is no direct impingement upon the wing, there is a little change in the structure of the time-averaged vortex past the wing, even though the tip vortex shed from the downstream wing may be substantially weakened or strengthened. In the absence of the downstream wing, as well as for weak interactions, the most energetic unsteady modes represent the first helical mode |m| = 1, which is estimated from the three-dimensional Proper Orthogonal Decomposition modes and has a very large wavelength, on the order of 102 times the vortex core radius, λ/a = O(102). Instantaneous vorticity measurements as well as flow visualization suggest the existence of a smaller wavelength, λ/a = 5–6, which is not among the most energetic modes. These two-orders of magnitude different wavelengths are in agreement with the previous measurements of tip vortices and also exhibit qualitative agreement with the transient energy growth analysis. The very long wavelength mode in the upstream vortex may persist during the interaction, and reveal coupling with the trailing vortex as well as increased meandering.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Streamwise vortex–wing interactions
There are many biological and engineering examples in which streamwise-oriented vortices interact with the downstream surfaces and wings. For example, it has been well known that birds are able to fly in formation for long distance flights; and it has been understood that flying in formation provides a significant improvement in aerodynamic performance (Hummel 1983, 1995). Early studies showed that more than 70% energy saving could be achieved on large-scale bird formation flight (Lissaman and Shollenberger 1970). Similarly, it was suggested that significant benefits exist for fixed-wing aircraft (Vachon et al. 2002; Wagner et al. 2002; Han and Manson 2005; Bangash et al. 2006; Inasawa et al. 2012; Kless et al. 2013). A series of simulations, wind tunnel tests, and flight tests suggested that formation flight could lead to drag reduction of up to 20%. The most common configuration of formation flight is the V-formation in which the upstream vortex and the tip vortex of the downstream wing rotate in the opposite direction. We designate this as the interaction of the “counter-rotating vortex” with the wing. The case of interaction of co-rotating vortex with a downstream wing is relevant to flight refueling (Bloy and Jouma’a 1995) as well as to canard–wing–vortex interactions (Erickson et al. 1990). In this paper, both co-rotating and counter-rotating trailing vortices have been considered. Another related application is the buffeting of aircraft fins due to the interaction with the leading-edge vortices (Mabey 1997). Flow physics of the various types of vortex–body interactions have been reviewed by Rockwell (1998).
As the distance between the vortex and wing surface becomes smaller, flow separation and unsteady effects are likely to become important (Bodstein et al. 1996). There is also the possibility of significant changes in the structure of the vortex due to the interaction with the wing. For example, in the case of the interaction of leading-edge vortices with an oscillating downstream surface, there may be an upstream effect on the vortex breakdown (Gursul and Xie 1999, 2001). These unsteady aspects could lead to structural vibrations of the wing, buffeting, and flight control problems.
More recently, the effects of an analytically defined vortex impinging upon a wing at different spanwise locations were studied by Garmann and Visbal (2015) using numerical simulations. High-fidelity simulations were performed for a flat-plate wing with an aspect ratio of six at a Reynolds number of 20,000. A q-vortex model was used to define the incoming vortex and the main parameters were selected as q = 2 and the axial velocity deficit as Δu = 0.4U∞. Their results confirmed that an increase in lift-to-drag ratio is achievable, and also revealed the unsteady aspects of the interaction. As the vortex interacts with the wing, depending on the spanwise location, it may form a dipole with the wing-tip vortex, disintegrate as a result of direct impingement, or split into two. A spiraling mode instability in the incident vortex core was found just upstream of the wing, with a relatively high Strouhal number (St = 1.1). Apparently, whether the helical mode instability developed upstream of the wing or not depended on whether the vortex experienced an adverse or favorable pressure gradient during the interaction with the wing (Barnes et al. 2016). It was suggested that the variation of the local q-parameter near the wing determines the stability of the vortex during the interaction. For upstream values of the q-parameter and axial velocity deficit, Leibovich (1984) predicts a supercritical vortex flow well upstream of the wing, in which disturbances cannot propagate upstream. However, Barnes et al. (2016) suggest that the local value of the q-parameter may fall below the critical value (q = \(\sqrt{2}\)), leading to the development of the instability. According to Leibovich and Stewartson (1983), azimuthal instabilities are excited for q < \(\sqrt{2}\). It is noted that, for the pre-defined q-vortex model in these simulations, both the upstream vortex and freestream were free of any unsteadiness. Qualitatively similar results were obtained when the incident vortex was generated by a wing rather than using a pre-defined q-vortex (Barnes et al. 2015). In this case, the simulations were performed for a streamwise distance of five chord lengths between the two wings at a Reynolds number of 30,000.
Experiments carried out at a Reynolds number of Re = 8000 (McKenna et al. 2017) showed similar results to these computational simulations. Rapid changes in the structure of the incident vortex, including an attenuation of axial vorticity and increase of streamwise velocity deficit, due to the upstream influence of the downstream wing were noted. Although the q-parameter in the undisturbed vortex well upstream was higher (q = 3.95) compared to the simulations, the swirl ratio still decreased below the critical value during the close interaction, accompanied by increased unsteadiness of the flow. The occurrence of the helical mode instability in the otherwise laminar q-vortex in the simulations might be difficult to capture in the experiments as the incident vortex is unsteady due to the meandering behavior.
1.2 Meandering of tip vortices
Large velocity fluctuations in the core due to the displacement of the trailing vortices are well known (Baker et al. 1974; Green and Acosta 1991; Devenport et al. 1996). The meandering (also called wandering) behavior of the incident vortex might have two consequences with regard to the vortex–wing interactions. First, the instantaneous location of the vortex core with respect to the downstream wing will be time-dependent. Considering the sensitivity of the interaction to the vertical offset, meandering may lead to large unsteady variations in the structure of the incident vortex and highly unsteady flow over the wing. Second, one needs to be cautious in interpreting the time-averaged interactions. For example, a decrease in the time-averaged streamwise vorticity might also be caused by increased meandering amplitude.
While the origin of vortex meandering is disputed, it is known that downstream distance from the wing, freestream turbulence level, Reynolds number, and whether the wing flow is attached or separated (Zhou et al. 2004), all affect the amplitude of meandering. In particular, the latter may be significant in the near-wake where the vortex–wing interactions take place. Zhou et al. (2004) showed that the meandering amplitude increases by one-order of magnitude between the attached and stalled wing flows. This illustrates that the roll-up process is strongly affected by the separated shear flow and cannot be neglected in the near-wake. Measurements report meandering amplitudes varying from about one-third of the core radius to about one core radius (see for example Devenport et al. 1996; Zhou et al. 2004; Bailey and Tavoularis 2008; Margaris et al. 2008; del Pino et al. 2011). There have been suggestions of vortex instabilities as the source of meandering (Jacquin et al. 2005). Antkowiak and Brancher (2004) proposed the possibility of a relationship between meandering of vortex cores and transient amplification of |m| = 1 disturbances (first helical mode). This mode has been documented in wing-tip vortices (Roy and Leweke 2005; del Pino et al. 2011; Chen et al. 2016) and leading-edge vortices (Zhang et al. 2016; Ma et al. 2017). Recently, this mode was measured and also predicted by a spatial stability analysis (Edstrand et al. 2016) in tip vortices.
1.3 Objectives
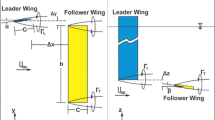
The previous advances have provided new understanding of the internal structure of the incident vortex as it interacts with the wing. One important conclusion has been the significant sensitivity of the vortex interactions to the relative location of the incident vortex with respect to the wing. The relative location naturally varies as a function of time due to the meandering of the incident vortex. This paper reports an experimental investigation on the interaction of vortices from a leading wing with a downstream wing and its own tip vortices. The main focus is on the meandering behavior of the incident vortex, its interaction with the downstream wing, and vortex instabilities. Particular attention was given to the most energetic unsteady flow modes in the incident vortex and in the interaction zone. Flow visualization, particle image velocimetry measurements, and volumetric velocity measurements were conducted in a water tunnel. Both counter-rotating and co-rotating incident vortices were considered. A schematic of the setup of the two wings is shown in Fig. 1. The angle of attack of the upstream wing can be positive or negative to obtain co- or counter-rotating vortices.
This paper is organized as follows: we begin with descriptions of the experimental setup and methods. The presentation of results and discussion begins with an overall description of the vortex–wing interactions using flow visualization and then examines in detail by means of particle image velocimetry and volumetric velocity measurements.
2 Experimental apparatus and methods
2.1 Experimental setup
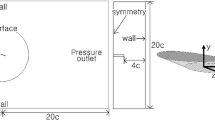
The experiments were performed in an Eidetics Model 1520 free surface closed loop water tunnel located at the University of Bath. The water tunnel has a test section of 0.381 m (width) × 0.508 m (height) × 1.524 m (length) with a maximum freestream speed of U∞ = 0.5 m/s and a turbulence intensity of less than 0.5% of the freestream velocity. The tunnel has four viewing windows: three surrounding the test section and one downstream allowing axial viewing. The height of the test section above the floor allows flow visualization from below as well as from the sides (see Fig. 2).
Both the upstream wing and the downstream wing have a cross-sectional profile of NACA0012 and a chord length of c = 60 mm. Both wings were mounted vertically. To remove free surface effects, a fixed endplate was placed below the free surface, at the root of the wing, yielding a half model. The upstream wing has a semi-span of b = 360 mm, resulting in a semi-aspect ratio of sAR = 6. The downstream wing has a semi-span of 240 mm, resulting in a semi-aspect ratio of sAR = 4. The location of the downstream wing was fixed. The upstream wing was attached to a traverse that features two translation rails for y- and z-axes (see Fig. 1) adjustment. A circular movable endplate was fixed onto the upstream wing in the (x, z) plane and sits against the large endplate to provide a good seal in full range of the spanwise separation of the wings Δy, vertical separation of the wings Δz, and angle of attack of the upstream (leading) wing αLW, with the trailing edge tip of the downstream wing being the origin of the coordinate system (see Fig. 1). The experiments were conducted at a constant streamwise separation, Δx, of 360 mm. The range of the traverse allows a Δy range of − 30 to 30 mm and a Δz range of − 42 to 24 mm. In the present study, the incidence of downstream (trailing) wing was fixed at αTW = 5°. The leading wing incidence was varied as α LW = − 10°, − 5°, 5°, 10°.
2.2 Flow visualization
Laser-induced fluorescent flow visualization in crossflow planes was performed using fluorescent dye. A laser sheet generated by a water cooled Coherent Innova70 4-W Argon-Ion continuous laser and an HD digital video camera viewing from downstream were used. For all cases, flow visualization was also performed using flood lighting, with a 1000 W halogen soft light and a 400 W UV light, and a DSLR camera viewing from both side window and downstream window.
For the crossflow visualization, the laser beam was converted into a sheet using a combination of a cylindrical and a spherical lens, illuminating the crossflow (y, z) plane 1c downstream (x/c = 1) of the trailing edge of the trailing wing. Orange and green fluorescent dyes were released from the wing tips of the leading wing and the trailing wing, respectively. The dyes were carried by the wing-tip vortices passing through the laser sheet, thus showing the tip-vortex structure which was then recorded by the digital camera through the downstream viewing window. Figure 3a presents a typical flow visualization image in the crossflow plane for αLW = 10° and αTW = 5°. In this study, the flow visualization was conducted at a Reynolds number of Re = 5000.
a Sample image of laser-induced fluorescent flow visualization; b enhanced image with background removal; c superposition of images for varying vertical locations of the incident vortex. The leading wing vortex is in orange and the trailing wing vortex is in green; blue lines link leading and trailing vortices of the same case. Re = 5000, Δy/c = 0.28
2.3 Particle image velocimetry (PIV) measurements
Particle image velocimetry measurements were carried out using a TSI 2D-PIV system incorporating a dual Nd:Yag 120 mJ laser and a 8 bit greyscale 2048 × 2048 pixel digital camera. Both wings were painted black to minimize the reflection noise. Seeding was achieved using 5 µm hollow glass particles. The arrangement of the PIV camera and laser is shown in Fig. 2. The laser was mounted on a traverse, so that it could be moved along the streamwise direction for measurements in various crossflow planes (x/c = − 2 to 0.1). The software package Insight 3G and a Hart cross-correlation algorithm were used to analyze the images. For the image processing, an interrogation window size of 24 × 24 or 32 × 32 pixels was used, thus producing velocity vectors for further processing. The effective grid size was 0.6–0.8 mm. The estimated uncertainty for velocity measurements was 2% of the freestream velocity U∞. The PIV measurements were conducted at Reynolds numbers of Re = 5000 and Re = 15,000.
2.4 Volumetric velocimetry measurements
Volumetric velocity measurements were conducted using a TSI Volumetric 3-Component Velocimetry (V3V) system. The volume of interest was illuminated using a dual ND:YAG 200 mJ pulsed laser, equipped with two cylindrical lenses. The two lenses are offset by 90 degrees to allow expansion in both the horizontal and vertical axes, generating the required laser cone. The tri-camera system, which has three 4MP CCD cameras with 28 mm lens located in a triangular fashion, was placed by the side window of the test section (Fig. 2). The seeding particles used were hollow glass beads with a mean diameter of 50 µm. The instantaneous velocity has an uncertainty of less than 3% of the freestream velocity. Experiments were conducted at a Reynolds number of Re = 15,000.
3 Results and discussion
3.1 Flow visualization
Figure 3a presents a typical flow visualization image of the leading wing vortex (αLW = 10°, co-rotating vortex, orange) and the trailing wing vortex (αTW = 5°, green) in a crossflow plane downstream of the trailing wing, x/c = 1. For the clarity of the presentation, the raw image was digitally processed to enhance the image with background removal, as shown in Fig. 3b. Subsequently, the vertical location of the upstream (leading) vortex was varied by traversing the upstream wing (Δy/c = 0.28), and flow visualization was recorded for each location. Figure 3c shows the superposition of the images for various vertical locations of the upstream vortex for a fixed spanwise location of the wing. In doing so, the leading and trailing vortices were connected by a blue line for the same case. Figure 3c suggests that, for this spanwise location of the upstream wing, the interaction of the co-rotating vortex with the downstream wing is likely to be weak. The locus of the approximate vortex centres is a nearly vertical line when the wing is traversed vertically.
Similar vertical traversing was repeated for spanwise locations of the upstream wing in the range of − 0.30 ≤ Δy/c ≤ 0.25; however, the results shown in Fig. 4 are only for the counter-rotating upstream vortices in the range of − 0.05 ≤ Δy/c ≤ 0.20 only. Only for the most outboard locations of the wing (Δy/c = 0.20), the upstream vortex remains outboard of the downstream wing; however, there is indication of an increasing interaction with the wing and its own tip vortex (the locus starts to deviate from a nearly vertical line for z > 0). This is due to the pairing of the counter-rotating upstream vortex with the tip vortex of the downstream wing. With further decrease in Δy/c (to 0.15 and 0.10), as the upstream vortex is moved up, it also moves inboard and above the wing due to the induced velocity of the vortex pair. For Δy/c ≤ 0.05, there is a discontinuity in the locus, the vortex jumping from the lower branch to the upper branch as it is moved up. The jump of the vortex, when the wing separation is small, − 0.05 ≤ Δy/c ≤ 0.05, is particularly significant. Interestingly, in the previous studies, small wingtip separations were found to provide larger benefits in the formation flight. The change in the spanwise coordinate of the upstream vortex due to the jump is around 0.4c. Given that the vortex radius (where the maximum tangential velocity is found) of the ensemble-averaged instantaneous undisturbed vortex is a = 0.11c at this Reynolds number (Re = 5000) as obtained from the PIV measurements, this jump is equivalent to nearly four times the vortex core radius. Although the jump in the location of the vortex is clear from the two branches of the locus of the vortex centres, it is difficult to judge how rapidly it takes place when the wing separation is varied. The unsteady nature of the vortices and the qualitative nature of the flow visualization are further complicated by the direct impingement of the vortex during the jump between the two branches. Nevertheless, it is clear that there is increased sensitivity of the location of the upstream vortex when the wing separation is near zero. We note that, once the upstream vortex is above the wing, it tends to move more inboard.
The previous computational (Garmann and Visbal 2015; Barnes et al. 2015, 2016) and experimental studies (McKenna et al. 2017) revealed the importance of the spanwise separation and vertical separation for some selected configurations. Our flow visualization study, although qualitative in nature, confirms that the most sensitive region is near the wing tip, which covers an area with a radius of approximately 0.2c (roughly twice the vortex core radius). In this region, the locus of upstream vortex may exhibit a discontinuity. This jump (equivalent to the vertical distance between the two branches) approaches nearly 0.4c (or four times the vortex core radius) when the upstream vortex is inboard. The locus of the upstream vortex has been found to be a useful way to visualize the vortex–wing interactions. In addition, the changes in the locus appear to be consistent with the induced velocity of the vortex pair of opposite sign that is formed by the incident vortex and the tip vortex of the downstream wing.
In contrast, for co-rotating vortices (αLW = 10°) shown in Fig. 5, the locations of the upstream vortices were much less influenced by the interaction. The locus of the vortex centres is a nearly vertical line when the upstream vortex is outboard of the downstream wing and two nearly vertical lines when the upstream vortex is inboard. Only when the leading wing is slightly outboard of the trailing wing, e.g., Δy/c = 0.05 and for small vertical separations, there is an indication of interaction between the vortices. For the most inboard location of the wing (Δy/c = − 0.15) shown in Fig. 5, the incident vortex appears to be displaced further inboard when it is above the wing. These aspects will be discussed more quantitatively with the velocity measurements. The previous computational and experimental studies did not include the cases of co-rotating vortices.
Although most of the flow visualization study was focused on the interaction with the wing and its vortex over the wing and just downstream of the wing, an increased amplitude of unsteadiness further downstream was observed in some experiments. Figure 6 shows the flow visualization viewed from downstream (top image) and from side view (bottom image) using flood lighting. The leading (upstream) vortex is in orange and the trailing (downstream) vortex is in green. Both wings have the same angle of attack of αLW = 5° (hence, co-rotating vortex interaction), and Δy/c = 0.25 (upstream wing is outboard), Δz/c = − 0.03. Videos of both views confirmed that the helical structure of the trailing vortex is rotating and convected downstream. These videos are available in the supporting media for this manuscript. The trailing vortex appears to be a helical wave with growing amplitude. The wavelength of the helical wave was measured to be between 0.54c and 0.58c in the bottom image of Fig. 6. Even more interestingly, similar wavelength, but with much smaller amplitude, is seen in the upstream vortex. We recognize the need to be careful when interpreting streak lines in unsteady flows (Gursul et al. 1990), and, nevertheless, one possible interpretation in this case is that the helical disturbance in the upstream vortex excites the downstream vortex through the interaction. The resulting image at the bottom of Fig. 6 is similar to the symmetric Crow instability. The average wavelength (0.56c) is roughly five times the vortex core radius for the upstream vortex (λ/a ≈ 5). Even though we did not investigate the details of the downstream interaction, the possible existence of helical perturbations in the upstream vortex will be discussed when we present the volumetric velocity measurements.
3.2 PIV measurements
Figure 7 presents the time-averaged vorticity patterns for co-rotating (αLW = 10°) leading vortices as they interact with the downstream wing in the crossflow plane just downstream of the trailing wing (x/c = 0.1) for various Δy and Δz combinations. It can be seen that, when the leading wing was located above the trailing wing (Δz/c = 0.33, top row), for Δy/c = − 0.33 and Δy/c = 0, secondary vortices formed due to the separation on the downstream wing, caused by the swirling velocity of the leading vortex. The tip vortex shed from the downstream wing as well as the time-averaged secondary vorticity were weak when the leading wing was moved further outboard to Δy/c = 0.33. When the leading wing was aligned vertically with the downstream wing (Δz/c = 0, middle row), again for the inboard location (Δy/c = − 0.33), an elongated secondary vorticity pattern was observed, while, for the outboard location (Δy/c = 0.33), the tip vortex of the downstream wing was completely suppressed due to the direction of the induced velocity of the upstream vortex. Similar vorticity patterns were also observed when the leading wing was located below the downstream wing (Δz/c = − 0.33). Figure 7 shows that, when the leading wing is outboard, the common feature is the suppression of the formation of the trailing vortex by the strong downwash induced by the leading wing vortex.
Figure 8 shows the vorticity field for the counter-rotating vortices (αLW = − 10°) in the same measurement plane for the same wing locations. In contrast to the co-rotating vortices, the strength of trailing wing vortices intensified due to the upwash induced by the counter-rotating leading wing vortices when the wing was outboard. When the leading wing was aligned vertically with the downstream wing (Δz/c = 0, middle row), the leading vortex appeared to be split in two, each passing over and below the wing for Δy/c = − 0.33. This is similar to the direct impingement cases observed in the previous computational simulations (Garmann and Visbal 2015; Barnes et al. 2015, 2016) and experiments (McKenna et al. 2017). Note that, for Δy/c = 0 in the middle row, a closely coupled vortex pair with elongated shape is observed. When the wing location was traversed vertically in small steps (Chen et al. 2016), similar elongated (time-averaged) vortex pairs were found in the vicinity of the wing tip. The induced velocity of the vortex pairs can be oriented at inboard, oblique, or outboard directions. Similar to the co-rotating cases, the interaction of the counter-rotating vortices reveals negligible effect on the time-averaged structure of the incident vortex when the leading wing is located below or outboard of the trailing wing.
3.3 Proper orthogonal decomposition (POD) analysis
The proper orthogonal decomposition (POD) analysis is used to capture the most energetic unsteady structures of the flow (Lumley 1970). The energy of stochastic signal is given by the sum of the eigenvalues, so that each eigenvalue taken individually represents the energy contribution of the corresponding deterministic function (Berkooz et al. 1993). In the present investigation, the method of snapshots (Sirovich 1987) was used and the POD analysis was performed on the vorticity field data using MATLAB codes developed based on the data analysis technique proposed by Chen et al. (2012). For each case, the first four most energetic modes were extracted.
Figure 9 compares the time-averaged vorticity and the dominant POD modes for αLW = 10° and Re = 5000 in the same crossflow plane as in the two previous figures (x/c = 0.1) for three cases: the upstream vortex in the absence of downstream wing (top), upstream vortex outboard of the wing, Δy/c = 0.33, Δz/c = 0.33 (middle), and upstream vortex impinging on the wing, Δy/c = − 0.33, Δz/c = 0 (bottom). For the POD analysis, rectangular frames with dashed line show the regions of the incident vortex that we focus on to analyze the unsteadiness. The energy contribution of each mode as a percentage of the total energy is also given below each mode. It is observed that, for the upstream vortex alone, the first (most energetic) mode, contributing around 26% of the total energy, exhibited a vortex pair which was centered on the time-averaged upstream vortex (Fig. 9, top), representing vertical displacements of the vortex. The fact that the most energetic mode is mostly in the vertical direction might be due to the effect of the wake oscillations in the near-wake of the airfoil. A similar vortex pair was also observed in the second mode (second most energetic), contributing nearly 8% of the total energy, which was also centered on the time-averaged vortex with its main direction perpendicular to the first mode. A linear combination of these eigenmodes provides displacements of the vortex core, which can be characterized as an azimuthal wavenumber of |m| = 1. Even though the amplitudes of the two dominant modes are not equal, the paired helical mode (with 8% of the total energy) is still significant. Therefore, these modes can be considered to be paired helical |m| = 1 modes. If vortex meandering is defined as the deviations of the location of the instantaneous vortex core from the center of the time-averaged vortex, only the |m| = 1 helical mode can represent the meandering for the wave-like disturbances. This is the only mode with nonzero radial velocity at the vortex axis. However, this mode can have different wavelengths (or frequencies). Hence, meandering can be considered due to the sum of various wavelengths of the first helical mode. The two-dimensional POD modes cannot reveal the dominant wavelength. Note that the same first helical mode was also identified in the meandering of the trailing vortices (Roy and Leweke 2005; del Pino et al. 2011; Chen et al. 2016; Edstrand et al. 2016), delta wing vortices (Zhang et al. 2016; Ma et al. 2017), afterbody vortices (Bulathsinghala et al. 2017), and inlet vortices (Wang and Gursul 2012). Higher modes are also shown in Fig. 9, where relative energy contributions of the third and fourth modes are much smaller than those of the 1st and 2nd modes.
When the upstream vortex is outboard of the wing tip (see Fig. 9 (middle) for Δy/c = 0.33 and Δz/c = 0.33), although there is a significant effect on the tip vortex shed from the downstream wing (which is almost completely suppressed), there is not much effect on the time-averaged upstream vortex itself. For this case of weak interaction, the first two dominant POD modes of the leading vortex remain similar to those of the undisturbed vortex, even though the relative energy contributions decrease. Hence, the helical mode of meandering remains essentially similar. For the case of strong interaction shown in Fig. 9 (bottom) for Δy/c = − 0.33, Δz/c = 0, all the dominant modes changed dramatically. The first helical mode of meandering is no longer identifiable. Hence, there is indication that, unless there is direct impingement and loss of coherency of the vortex, the first helical mode of meandering is still observed after the vortex has passed the wing.
The helical mode of meandering is also observed at the higher Reynolds number (Re = 15,000) and other crossflow planes along the streamwise direction, as long as direct impingement does not occur. Figure 10 presents the time-averaged vorticity patterns and the flow structures of the dominant modes in crossflow planes at various streamwise locations for αLW = 10°, Re = 15,000, and a weak interaction case (Δy/c = − 0.33, Δz/c = 0.33). For completeness, we calculated the meandering amplitude by tracking the instantaneous core location using the γ method (Graftieaux et al. 2001). In the absence of the downstream wing, we found σ = 0.027c and ensemble-averaged core radius a = 0.075c (hence, σ/a = 0.36). The first measurement plane (x/c = −2), which is slightly upstream of the wing, and the other planes further downstream show that the mean vorticity is nearly axisymmetric. For this weak interaction case, the core radius and meandering amplitude do not change much. Note that at x/c = − 0.5 (over the trailing wing) and downstream, the development of the trailing vortex as well as the secondary vorticity on the upper surface of the wing are visible. The strength, size, and relative position of the time-averaged upstream vortex were unchanged, confirming the weak interaction. However, for all values of x/c, the most energetic modes (contributing more than 40% of the total energy) exhibit a vortex pair with its main direction changing from the spanwise direction to a slightly inclined direction as the vortex interacts with the wing. The fact that the dominant direction becomes nearly horizontal may be due to the effect of the image vortex. The second most energetic mode also has a vortex dipole which is perpendicular to that of the first mode, and experiences a slight change in its orientation as the vortex interacts with the wing. As these PIV measurements at different streamwise stations were not taken simultaneously, no information could be obtained on the wavelength of the helical mode of meandering. However, this is possible with the volumetric velocity measurements discussed below.
3.4 Volumetric velocity measurements
Figure 11 presents, for two cases, the isosurfaces of the time-averaged vorticity magnitude, coloured by streamwise vorticity, for αLW = 5° (co-rotating vortices) and Re = 15,000. It is observed that, for Δy/c = − 0.25 and Δz/c = − 0.05 (Fig. 11a), the leading vortex follows the top surface of the trailing wing, and the secondary vorticity due to the flow separation outboard of the leading vortex is also captured. The side view suggests the trajectory of the upstream vortex is similar to the mean streamlines over an airfoil; hence, the vortex is likely to be subject to the acceleration. This will be discussed further with the variation of the axial velocity later on. When the co-rotating vortex is moved closer to the tip, as shown in Fig. 11b for Δy/c = 0.2, Δz/c = 0, the upstream vortex just misses the tip of the wing. It is not clear if a separate tip vortex develops from the wing in this case due to the downwash effect of the co-rotating upstream vortex. If it does, the tip vortex from the wing is expected to be very weak (see the top view).
When the strength of the co-rotating upstream vortex is increased (αLW = 10°), Fig. 12 reveals very similar vortex interactions. In Fig. 12a, the upstream vortex seems close to the wing surface, and passes the wing, following the curvature of the wing cross-section. Although the vortex remains coherent, the decrease of the mean streamwise vorticity in the core is apparent in this case. The interaction shown in Fig. 11a for the weaker vortex has the same feature. However, this observation may be due to the increased meandering of the vortex. The decrease of the streamwise vorticity is not observed when the vortex just misses the wing tip in Figs. 11b and 12b, which may be due to the smaller change in meandering. We also note that, for both co-rotating cases of αLW = 5° and 10°, the trajectory of the upstream vortex changes negligibly in the spanwise direction for all cases.
Figure 13 presents, for three cases, the isosurfaces of time-averaged vorticity magnitude, coloured by streamwise vorticity for αLW = − 5° (counter-rotating vortices). For all cases in this figure, the leading wing vortices were displaced inboard during the interaction. For Δy/c = − 0.25 and Δz/c = 0.05 (Fig. 13a), the leading wing vortex follows the top surface profile of the trailing wing, which is similar to the co-rotating case (see Figs. 11a, 12a). When the leading wing was moved lower to Δz/c = − 0.08 (slightly below the trailing wing), the leading wing vortex impinged on the leading edge of the trailing wing, as shown in Fig. 13b. The leading wing vortex was split into two parts; the top part moved inboard and the lower part moved outboard. Instantaneous flow fields suggest that the split vortex is not simply an artifact of time-averaging of the vortex travelling either above or below the wing. Rapid decrease of the streamwise vorticity due to the impingement is visible. The meandering behavior might have contributed to this rapid decrease in the mean streamwise vorticity. When the leading wing is located slightly outboard at Δy/c = 0.2 and Δz/c = − 0.05 (Fig. 13c), an intense interaction can be observed near the wing tip. The formation of a counter-rotating vortex pair results in both vortices moving upward and inboard. Similar observation of vortex dipole formation was noted by Garmann and Visbal (2015).
With stronger counter-rotating leading wing vortices for αLW = − 10°, we show four different cases in Fig. 14. In all cases, substantial deviations in the trajectory of the upstream vortex are visible. For Δy/c = − 0.42 and Δz/c = 0 (Fig. 14a), the leading wing vortex drifts inboard. In this case, due to the much stronger downwash of the upstream vortex, the tip vortex shed from the wing is very weak. It appears that the upstream vortex is displaced inboard due to the induced velocity of its image vortex, not due to the much weaker tip vortex of the opposite sign. As the leading wing moves to Δy/c = 0, Δz/c = − 0.1 (Fig. 14b), the leading wing vortex partially impinges on the trailing wing near the tip, and is displaced inboard. The vortex is closer to the wing surface, resulting in stronger flow separation as seen inboard of the vortex. The tip vortex developing on the wing is also stronger in this case. We observed dramatic changes when the upstream wing was slightly lowered to Δz/c = − 0.22. In Fig. 14c, it can be seen that the leading wing vortex goes under the trailing wing, and is displaced outboard substantially, forming a vortex pair with the trailing wing-tip vortex. (Note that, in this configuration, we were not able to capture the flow below the wing as the laser light illuminates from the top; this gives rise to the “interrupted” vortex just below the wing). The tip vortex shed from the wing is much stronger than in the other cases. Similar observations of the strengthening of the tip vortex were made by Barnes et al. (2015). When the leading wing is moved further outboard to Δy/c = 0.2, Δz/c = − 0.15 (Fig. 14d), both leading wing and trailing wing vortices bend inboard and upward due to the strong induced velocity created by the counter-rotating vortex pair.
The streamwise velocity defect found by the volumetric velocity measurements is presented in Figs. 15 and 16; these correspond to the same wing configurations whose vorticity fields have been discussed in Figs. 11 and 13, respectively. The isosurfaces are vorticity magnitudes which were coloured by the streamwise velocity defect defined by (U − U∞)/U∞. It is observed that, for all cases, the vortices upstream of the wing have lower axial velocity than the freestream velocity, corresponding to wake-like axial velocity profiles. Barnes et al. (2016) showed that, when the incident vortex is just above the wing and, therefore, subject to a favorable pressure gradient, the velocity defect remains fairly constant. On the other hand, when the incident vortex is just below the wing and subject to an adverse pressure gradient, the velocity defect increases faster. We have not investigated this aspect any further as it has been discussed extensively in the literature and is not the focus of this paper.
As the vortices convect over the wing, the axial velocity increases in the core, but then recovers to the original velocity defect levels once the vortices pass the trailing wing. The acceleration of the axial velocity is sudden as the vortices interact with the downstream wing (see, for example, Fig. 16a). However, this does not mean a jet-like axial velocity profile in the vortex core. The surrounding flow outside the vortex core is also accelerated over the wing. In addition, due to the highly non-axisymmetric nature of the external flow, it is difficult to define the local velocity defect or excess. Nevertheless, upon close examination, there appears to be a velocity defect with respect to the surrounding flow. The acceleration of the vortex streamwise velocity is evident even for the impinging case in Fig. 16b. On the other hand, if the vortex misses the wing, there is small change in its streamwise velocity. Figures 15 and 16 reveal that the features of the streamwise velocity are similar for both co-rotating and counter-rotating vortex cores.
3.5 Unsteady aspects
Figure 17 presents the isosurfaces of the instantaneous vorticity magnitude (coloured by the streamwise vorticity) at αLW = ± 10° for various cases. The co-rotating and counter-rotating vortices are shown in Fig. 17a, b, in the absence of a downstream wing. Helical structures can be observed for both vortices. The characteristic wavelength was estimated to be 0.44c–0.48c. Furthermore, the wavelength does not appear to be affected by the presence of the downstream wing, as shown in Fig. 17c, d for two different cases. In our experiments, we found the vortex core radius (where the tangential velocity is maximum) as a = 0.075c from the ensemble-averaged velocity profiles of the vortex at x/c = −1 in the absence of a downstream wing, for this Reynolds number of Re = 15,000. Taking an average value of λ ≈ 0.46c from Fig. 17, we find that the wavelength normalized by the vortex core radius is λ/a ≈ 6.2 for this Reynolds number of Re = 15,000. It is interesting that this wavelength is not far away from one found (λ/a ≈ 5) in flow visualization at a lower Reynolds number of Re = 5000 (see Fig. 6 and the discussion in Sect. 3.1). However, this wavelength is much shorter than the very long wavelengths of the first helical mode observed in the experiments on wing-tip vortices, leading-edge vortices, and ground vortices (Roy and Leweke 2005; del Pino et al. 2011; Wang and Gursul 2012; Edstrand et al. 2016; Ma et al. 2017), which is on the order of λ/a = O(102) to O(103), corresponding to a range of axial wavenumbers k = 2πa/λ = O(10−3) to O(10−2).
Note that the relatively small wavelengths suggested by the instantaneous velocity measurements and flow visualization in this study (λ/a ≈ 5–6) are not necessarily the most energetic modes. The POD analysis presented in Figs. 9 and 10 already suggests the presence of a helical mode; however, the measurements in one crossflow plane cannot provide an estimate of the axial wavelength. An estimate of the wavelength based on a measured frequency spectrum and an assumed wave speed (i.e., freestream velocity) is not possible either as the PIV system is not a high frame-rate one. However, the volumetric measurements are able to provide this information directly. The Proper Orthogonal Decomposition analysis can be easily extended and performed on the three-dimensional velocity data (see, for example, Sarmast et al. 2014).
Figure 18 shows the four most energetic three-dimensional POD modes for the upstream vortex only (in the absence of the downstream wing) for αLW = 10°. The first mode (about 15% of the total energy) shows two counter-rotating vortex filaments, similar to the vortex dipoles shown in Figs. 9 and 10 in the two-dimensional measurements. The vortex filaments in Mode 1 can be considered to be helical, but their wavelength is very large and only a slight rotation is seen in the measurement volume shown in the figure. The helical vortex filaments are more visible for the higher modes as the wavelength becomes smaller. In Fig. 19, two-dimensional cuts of the vortex filaments are shown at the beginning and the end of the measurement volume for the first two modes. The solid circle indicates the vortex core radius in these plots. By measuring the rotation angle of the vortex dipoles from these plots, we calculated the wavelengths as λ/a ≈ 610 (k ≈ 0.01) for the first mode and λ/a ≈ 115 (k ≈ 0.05) for the second mode. The most energetic mode with k ≈ 0.01 is in agreement with the previous measurements discussed above. In summary, the most energetic helical mode has a very large wavelength, and the smaller wavelengths detected in instantaneous vortices are not among the top four most energetic modes.
We have compared our data for the wavelength (and wavenumber) with those reported in the literature. Table 1 summarizes these data, which were obtained by velocity measurements, flow visualization, and computational simulations. In most cases, the dominant frequency of the velocity fluctuations at a downstream plane was given by these sources, from which the corresponding dimensionless frequency fa/U∞ was calculated. For these cases, the convection speed was assumed to be equal to the freestream velocity and the wavelength normalized by the core radius is summarized in Table 1. Note that, in these cases, except for the results reported by Bailey and Tavoularis (2008), POD analysis in the crossflow plane suggested the existence of helical waves. In other cases, the wavelength was directly obtained from flow visualization or volumetric velocity measurements. Inspection of Table 1 reveals that axial wavenumbers fall into two distinct bands, k = O(10−2) and k = O(1), which are separated by different colours in the table. The two-orders of magnitude difference in the reported axial wavenumbers of the helical mode |m| = 1 are interesting and discussed further below.
The transient energy growth analysis of the vortices (with and without axial flow) predicted that perturbations of azimuthal wavenumber |m| = 1 are amplified (Antkowiak and Brancher 2004; Pradeep and Hussain 2006; Heaton and Peake 2007). This is shown in Fig. 20 as a function of the axial wavenumber, where the theoretical growth rates are taken from Pradeep and Hussain (2006). The Reynolds numbers given in the figure are defined based on the circulation of the vortex, Γ/ν. The symbols show the theoretical predictions of the growth for different Reynolds numbers. There is a peak growth at k ≈ 1.3–1.4 according to the predictions, and there is also a very large growth as k → 0. The inviscid mechanism of growth in the limit of infinitely large wavelengths was discussed by Antkowiak and Brancher (2004), Pradeep and Hussain (2006), and Heaton and Peake (2007). The growth rate becomes infinite as k → 0 for the first helical mode (Heaton and Peake 2007). Hence, the findings in this study and previous observations of very large wavelengths may have a theoretical support. On the other hand, the smaller wavelengths (with less energy) suggested by the instantaneous velocity measurements (k = 1.01) and flow visualization (k = 1.23) in this study are surprisingly close to the theoretical peak at k ≈ 1.3–1.4. It is interesting that the axial wavenumber of Bandyopadhyay et al. (1991) is also very close. Another interesting observation is that the spiraling instability induced by the presence of the wing has a wavenumber close to the theoretical peak (Garmann and Visbal 2015).
Figures 21 and 22 show the two most energetic POD modes for the co-rotating and counter-rotating upstream vortices interacting with the downstream wing. The two cases selected for the interaction of co-rotating vortices in Fig. 21 have been previously presented in detail in terms of their time-averaged vorticity field in Fig. 12. In the first case in Fig. 21a (left column), the upstream vortex has a close interaction with the wing, and exhibits a slight impingement onto the upper surface. Correspondingly, the counter-rotating vortex filaments of the first POD mode appear to be split by the wing due to the interaction. In contrast, for the second case, where the upstream vortex just misses the wing tip, both vortex filaments are visible. In both cases, the vortex pairs of the second modes appear nearly perpendicular to those of the first modes.
Isosurfaces of instantaneous vorticity (top), POD Mode 1 vorticity (middle) and Mode 2 vorticity (bottom), coloured by streamwise vorticity, a Δy/c = − 0.33, Δz/c = 0.15 (POD mode energy percentages: 8.0, 2.8%); b Δy/c = 0.2, Δz/c = 0.15 (POD mode energy percentages: 7.7, 2.5%). αLW = 10°, Re = 15,000
Isosurfaces of instantaneous vorticity (top), POD Mode 1 vorticity (middle) and Mode 2 vorticity (bottom), coloured by streamwise vorticity, a Δy/c = − 0.42, Δz/c = 0 (POD mode energy percentages: 7.7%, 3.7%); b Δy/c = 0, Δz/c = − 0.1 (POD mode energy percentages: 6.2, 4.4%); c Δy/c = 0.2, Δz/c = − 0.15 (POD mode energy percentages: 10.2, 2.9%). αLW = − 10°, Re = 15,000
For the interaction of counter-rotating vortices shown in Fig. 22, three cases are presented (their time-averaged vorticity fields are shown in Fig. 14). In the first case in part (a), shown in the left column, there is a close interaction, but no impingement. As a result, the counter-rotating vortex filaments are visible in the first POD mode; however, we note that there is a substantial increase in the cross-sectional area of the vortex filaments in the streamwise direction. This is interpreted as increased vortex core radius and meandering as the upstream vortex interacts with the wing. In the second case in part (b) (right column), the upstream vortex axis is almost aligned with the leading edge of the wing (see Fig. 14b also), displaying a direct impingement. Correspondingly, the two vortex filaments of the first POD mode are split at the leading edge. The effect of the flow separation on the wing surface also modifies the first mode. In the third case, in part (c), the upstream vortex just misses the wing tip. In this case, the first mode reveals coupling with the tip vortex shed from the downstream wing. The most energetic POD mode again indicates substantial increase in the area of the vortex tubes, suggesting increased vortex core radius and meandering.
4 Conclusions
The interaction of meandering tip vortices with a downstream wing was investigated experimentally using flow visualization, particle image velocimetry measurements, and volumetric velocity measurements. Unlike the previous investigations, both co-rotating and counter-rotating upstream vortices were investigated and the meandering of the vortices was documented. Flow visualization was performed while traversing the upstream wing tip vertically, and the locus of the incident vortex in a crossflow plane past the downstream wing was found to be useful in interpreting the vortex–wing interactions. For counter-rotating vortices, when the wing tips are within a distance of approximately twice the vortex core radius, the locus of the upstream vortex reveals deviations consistent with the formation of a vortex dipole. In this region, the incident vortex may jump from the lower branch to the upper branch. Interestingly, this is the region for which maximum benefits from formation flight are expected. In contrast, for co-rotating vortices, the locus of the incident vortex is much less influenced. Helical disturbances with a wavelength of λ/a ≈ 5 were observed in the incident vortex, and then appeared to excite the downstream vortex, with a possible coupling between the two vortices.
PIV measurements revealed that the incident vortex passes the wing without much change in the time-averaged structure when it is located further away from the wing tip more than roughly twice the vortex core radius or when there is no direct impingement (inboard of the wing). However, there is a much larger effect on the tip vortex shed from the downstream wing. In particular, when the co-rotating incident vortex is outboard, the tip vortex may be completely suppressed. In contrast, the tip vortex may be strengthened by the counter-rotating incident vortex when it is outboard.
When there is no direct impingement and a weak interaction exists, the first two POD modes have vortex dipoles that are perpendicular to each other. They represent a paired first helical mode |m| = 1. There are also very similar modes in the absence of the downstream wing, consistent with the previous observations of streamwise vortices shed from high aspect ratio wings, delta wings, and afterbody vortices. This most energetic mode detected by the three-dimensional POD analysis has a very large wavelength, λ/a = O(102). The wavelength was estimated by calculating the rotation angle of the dipole of the POD mode over a streamwise distance. This is the first ever direct measurement of the dominant wavelength, without other assumptions.
With the volumetric measurements, we were able to capture the details of close and intense interactions, including the direct impingement and split of the incident vortex. There was negligible deviation from the trajectories of the co-rotating incident vortices. In contrast, counter-rotating incident vortices exhibit large spanwise displacements. In most cases, this was attributed to the formation of a vortex dipole. However, in some cases when the strong incident vortex was inboard and the tip vortex of the downstream wing was weak, there was still a large displacement of the incident vortex in the spanwise direction, which appeared to be due to its image vortex. In all cases, sudden acceleration of the incident vortex while passing over the wing is evident.
The instantaneous vorticity obtained from volumetric measurements reveals a characteristic wavelength (λ/a ≈ 6), which is close to that observed in flow visualization. This mode is not among the most energetic modes obtained from the three-dimensional POD analysis. We compared our data with those reported in the literature and found that the axial wavenumber data fall into two bands, k = O(10−2) and k = O(1). Both wavenumber bands show good agreement with the transient energy growth analysis. Observations of very small wavenumbers are consistent with the predictions of infinite growth rate as k → 0 for the first helical mode. The three-dimensional POD analysis also reveals the most energetic modes due to the interaction with the wing. In some cases, the most energetic mode suggests increased meandering as the incident vortex passes the wing and also coupling with the trailing vortex.
References
Antkowiak A, Brancher P (2004) Transient energy growth for the Lamb-Oseen vortex. Phys Fluids 16:1–4
Bailey SCC, Tavoularis S (2008) Measurements of the velocity field of a wing-tip vortex, wandering in grid turbulence. J Fluid Mech 601:281–315
Baker GR, Barker SJ, Bofah KK, Saffman PG (1974) Laser anemometer measurements of trailing vortices in water. J Fluid Mech 65:325–336
Bandyopadhyay PR, Stead DJ, Ash RL (1991) Organized nature of a turbulent trailing vortex. AIAA J 29:1627–1633
Bangash ZA, Sanchez RP, Ahmed A (2006) Aerodynamics of formation flight. J Aircr 43:907–912
Barnes CJ, Visbal MR, Gordnier RE (2015) Analysis of streamwise-oriented vortex interactions for two wings in close proximity. Phys Fluids 27:015103
Barnes CJ, Visbal MR, Huang PG (2016) On the effects of vertical offset and core structure in streamwise-oriented vortex-wing interactions. J Fluid Mech 799:128–158
Berkooz Z, Holmes P, Lumley JL (1993) The proper orthogonal decomposition in the analysis of turbulent flows. Annu Rev Fluid Mech 25:539–575
Bloy AW, Jouma’a M (1995) Trailing vortex effects on large receiver aircraft. J Aircr 32:1198–1204
Bodstein GCR, George AR, Hui CY (1996) The three-dimensional interaction of a streamwise vortex with a large-chord lifting surface: theory and experiment. J Fluid Mech 322:51–79
Bulathsinghala D, Jackson R, Wang Z, Gursul I (2017) Afterbody vortices of axisymmetric cylinders with a slanted base. Exp Fluids 58:60. https://doi.org/10.1007/s00348-017-2343-9
Chen H, Reuss DL, Hung LS, Sick S (2012) A practical guide for using proper orthogonal decomposition in engine research. Int J Engine Res 14:307–319
Chen C, Wang Z, Cleaver DJ, Gursul I (2016) Interaction of trailing vortices with downstream wings. AIAA Paper 2016-1848
Chen C, Wang Z, Gursul I (2017) Unsteady nature of vortex pair in formation flight. AIAA Paper 2017-3306
del Pino C, Lopez-Alonso JM, Parras L, Fernandez-Feria R (2011) Dynamics of the wing-tip vortex in the near field of a NACA 0012 aerofoil. Aeronaut J 115:229–239
Devenport WJ, Rife MC, Liapis SI, Follin GJ (1996) The structure and development of a wing-tip vortex. J Fluid Mech 312:67–106
Edstrand AM, Davis TB, Schmid PJ, Taira K, Cattafesta III, L.N (2016) On the mechanism of trailing vortex wandering. J Fluid Mech 801:R1. https://doi.org/10.1017/jfm.2016.440
Erickson G, Schreiner J, Rogers L (1990) Canard-wing vortex interactions at subsonic through supersonic speeds. AIAA Paper 1990-2814. 17th Atmospheric Flight Mechanics Conference, Guidance, Navigation, and Control and Co-located Conferences
Garmann DJ, Visbal MR (2015) Interactions of a streamwise-oriented vortex with a finite wing. J Fluid Mech 767:782–810
Graftieaux L, Michard M, Grosjean N Combining PIV (2001) POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas Sci Technol 12:1422–1429
Green SI, Acosta AJ (1991) Unsteady flow in trailing vortices. J Fluid Mech 227:107–134
Gursul I, Xie W (1999) Buffeting flows over delta wings. AIAA J 37:58–65
Gursul I, Xie W (2001) Interaction of vortex breakdown with an oscillating fin. AIAA J 39:438–446
Gursul I, Lusseyran D, Rockwell D (1990) On interpretation of flow visualization of unsteady shear flows. Exp Fluids 9:2570266
Han G, Manson W (2005) Inviscid wing-tip vortex behaviour behind wings in close formation flight. J Aircr 42:787–788
Heaton CJ, Peake N (2007) Transient growth in vortices with axial flow. J Fluid Mech 587:271–301
Hummel D (1983) Aerodynamics aspects of formation flight in birds. J Theor Biol 104:321–347
Hummel D (1995) Formation flight as an energy-saving mechanism. Isr J Zool 41:261–278
Inasawa A, Mori F, Asai M (2012) Detailed observations of interactions of wing tip vortices in close-formation flight. J Aircr 49:206–213
Jacquin L, Fabre D, Sipp D, Coustols E (2005) Unsteadiness, instability and turbulence in trailing vortices. C R Phys 6:399–414
Kless JE, Aftosmis MJ, Ning SA, Nemec M (2013) Inviscid analysis of extended-formation flight. AIAA J 51:1703–1715
Leibovich S (1984) Vortex stability and breakdown: survey and extension. AIAA J 22:1192–1206
Leibovich S, Stewartson K (1983) A sufficient condition for the instability of columnar vortices. J Fluid Mech 126:335–356
Lissaman S, Shollenberger CA (1970) Formation flight of birds. Science 168:1003–1005
Lumley JL (1970) Stochastic tools in turbulence. In: Applied Mathematics and Mechanics, vol 12. Academic Press, New York
Ma BF, Wang Z, Gursul I (2017) Symmetry breaking and instabilities of conical vortex pairs over slender delta wings. J Fluid Mech (in print)
Mabey DG (1997) Similitude relations for buffet and wing rock on delta wings. Prog Aerosp Sci 33:481–511
Margaris P, Marles D, Gursul I (2008) Experiments on jet/vortex interaction. Exp Fluids 44:261–278
McKenna C, Bross M, Rockwell D (2017) Structure of a streamwise-oriented vortex incident upon a wing. J Fluid Mech 816:306–330
Pradeep DS, Hussain F (2006) Transient growth of perturbations in a vortex column. J Fluid Mech 550:251–288
Rockwell D (1998) Vortex-body interactions. Annu Rev Fluid Mech 30:199–229
Roy C, Leweke T (2005) Experiments on vortex meandering. FAR-Wake Technical Report AST4-CT-2005-012238, CNRS-IRPHE, also presented in International Workshop on Fundamental Issues related to Aircraft Trailing Wakes, 2008
Sarmast S, Dadfar R, Mikkelsen RF, Schlatter P, Ivanell S, Sorensen JN, Henningson DS (2014) Mutual inductance instability of the tip vortices behind a wind turbine. J Fluid Mech 755:705–731
Sirovich L (1987) Turbulence and the dynamics of coherent structures. I. Coherent structures. Q Appl Math 45:561–571
Vachon M, Ray R, Walsh K, Ennix K (2002) F/A-18 aircraft performance benefits measured during the autonomous formation flight project. AIAA Paper 2002-4492, American Institute of Aeronautics and Astronautics
Wagner G, Jacques D, Blake B, Pacher M (2002) Flight test results of close formation flight for fuel savings. AIAA Paper 2002-4490. American Institute of Aeronautics and Astronautics
Wang Z, Gursul I (2012) Unsteady characteristics of inlet vortices. Exp Fluids 53:1015–1032
Zhang X, Wang Z, Gursul I (2016) Interaction of multiple vortices over a double delta wing. Aerosp Sci Technol 48:291–307
Zhou Y, Zhang HJ, Whitelaw JH (2004) Wing-tip vortex measurements with particle image velocimetry, AIAA Paper 2004-2433, 34th AIAA Fluid Dynamics Conference and Exhibit, Oregon
Acknowledgements
The authors would like to acknowledge the EPSRC strategic equipment Grant (EP/K040391/1 and EP/M000559/1) that made the volumetric velocity measurements possible.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 1 (MP4 2517 KB)
Supplementary material 2 (MP4 7385 KB)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chen, C., Wang, Z. & Gursul, I. Experiments on tip vortices interacting with downstream wings. Exp Fluids 59, 82 (2018). https://doi.org/10.1007/s00348-018-2539-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-018-2539-7