1 Introduction

Water invasion into oil-saturated porous media is relevant to many natural and industrial processes including water infiltration and contaminant transport in soils and groundwater aquifers contaminated by non-aqueous phase liquids (NAPLs), oil recovery, and geological \(\hbox {CO}_2\) storage. Micromodels have been used for decades to study porous media flow under conditions relevant to these applications. Coreflood experiments on rock samples—and to a lesser extent column experiments—are time intensive and require significant volume of test fluids and specialized equipment such as X-ray micro-computed tomography for visualization at the pore scale. In contrast, pore-scale mechanisms in two-dimensional or quasi-two-dimensional micromodels can be readily visualized with off-the-shelf cameras coupled to an optical microscope.

Microfluidic studies of two-phase, oil/water displacement processes typically involve the addition of dye to the aqueous phase to facilitate visualization (e.g., Geistlinger et al. 2016; Frette et al. 1997; Chevalier et al. 2015; Xu et al. 2017; Yun et al. 2017; Kumar Gunda et al. 2011; Xu et al. 2014; Cottin et al. 2010; Yeganeh et al. 2016; Levaché and Bartolo 2014; Datta et al. 2014) unless opaque crude oil is used (e.g., Song and Kovscek 2015; Zhu and Papadopoulos 2012; Bowden et al. 2016). However, many enhanced oil recovery and NAPL-remediation approaches involve the addition of chemical additives such as surfactants and polymers to the water that is injected into the system to displace the oil. Where the aim of a microfluidic experiment is to evaluate the performance of such additives, the addition of dye to the aqueous phase is not desirable as dyes can alter the interfacial properties of the test fluid; in such cases, the oil phase must be dyed instead (e.g., Conn et al. 2014; Zhang et al. 2011; Beaumont et al. 2013; Gauteplass et al. 2013; Nilsson et al. 2013).

In the present paper we demonstrate the use of an oil-soluble dye, Oil Red O (ORO), to study oil displacement in an oil-saturated quasi-monolayer of crushed marble packed in a microfluidic channel, our laboratory model of carbonate rock, by waterflood (brine injection). Injection velocities corresponding to capillary numbers ranging from \(\text {Ca} = \mu _{\text {w}} U_{\text {w}}/\sigma = 9\times 10^{-7}\) to \(9\times 10^{-6}\), where \(\mu _{\text {w}}\) is the dynamic viscosity of the brine, \(U_{\text {w}}\) is the volumetric flow rate of injection per unit bulk cross-sectional area of the packed bed, and \(\sigma\) is the oil/brine interfacial tension, were considered. Oil saturation profiles and their evolution are compared between the lowest and highest \(\text {Ca}\). Two pore-scale displacement mechanisms are identified to explain the contrasting water invasion patterns, and their relative contributions to ultimate oil recovery are calculated (Sect. 3.1). Remaining oil saturation at the end of the waterflood is reported for each \(\text {Ca}\) and compared against previous measurements in micromodels (Sect. 3.3).

2 Materials and methods

The displacement experiments follow the lab-on-a-chip protocol developed by Bowden et al. (2016), with minor modifications. In particular, the microfluidic chip (Dolomite Centre Ltd.) is identical in design as those used previously by Bowden et al. (2016) and Tanino et al. (2015, 2017).

Fig. 1
figure 1

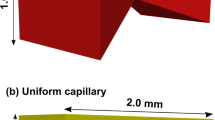
Lab-on-a-chip setup and a scanning electron microscope (SEM) image of crushed marble grains (from Fig. S2, Bowden et al. 2016). Inset depicts the cross section of the gap filters downstream of the packed bed (top right). All lengths are in units of \(\upmu \hbox {m}\). Adapted from Bowden et al. (2016) and Tanino et al. (2015)

Full size image

2.1 Porous medium

The model porous medium was a \(L = 1690\) to \(2400\,\upmu\)m-long quasi-monolayer bed of crushed marble from Carrara, Italy packed in a \(W = 1200\,\upmu\)m-wide, \(H = 55\,\upmu\)m-deep channel etched in soda lime (Fig. 1). The bulk cross-sectional area of the packed bed is \(A = 6.5 \times 10^4 \,\upmu \hbox {m}^2\). The size of the grains is constrained by the dimensions of the microfluidic channel in which they are packed and, as expected, the mean equivalent diameter is approximately the same as the channel depth at \(d_{\text {p}} = 53\pm 24\,\upmu \hbox {m}\) (Fig. 2; Bowden et al. 2016). The mean porosity of the microfluidic analogues is \(\phi =0.27\) (Tanino et al. 2017). The Cartesian coordinates (x, y) are defined as illustrated in Fig. 1; the x-axis is aligned with the mean flow with its origin defined at the upstream end of the packed bed. A new bed was packed for each displacement experiment.

Fig. 2
figure 2

Equivalent grain size distribution in a packed bed (Bowden et al. 2016). Solid line is a normal distribution fitted to data: mean \(53\,\upmu \hbox {m}\), standard deviation \(8\,\upmu \hbox {m}\). Redrawn from Bowden et al. (2016)

Full size image

Single-phase permeability, k, was measured in two packed beds by injecting brine at different flow rates and measuring the resulting pressure upstream of the microfluidic chip, P (ELVEFLOW microfluidic pressure sensor MPS4, resolution \(\pm \, 1.2\) kPa, range − 100 to 690 kPa); the downstream end of the flow line was open to ambient pressure. The permeability was calculated as follows:

$$\begin{aligned} k = \mu _{\text {w}} \frac{\text {d}U_{\text {w}}}{\text {d}(P/L)}, \end{aligned}$$
(1)

where \(\text {d}U_{\text {w}} / \text {d}(P/L)\) is taken as the gradient of the line of best fit to \((U_{\text {w}}, P)\) data in the least-squares sense. The measured values for the two packs, \(k = 5.5\times 10^{-13}\) and \(8.1\times 10^{-13}\) \(\hbox {m}^2\), are in good agreement with Ergun (1952)’s equation for packed columns, which predicts \(k = d_{\text {p}}^{\,\,2} \, \phi ^3/(1-\phi )^2/150 = 7\times 10^{-13} \hbox { m}^2\).

2.2 Fluids

Table 1 Basic properties of the test fluids and their interface at \(21\,^\circ \hbox {C}\) unless otherwise noted
Full size table

The aqueous phase was a solution of 5 wt% NaCl and 1 wt% KCl saturated in limestone, as used previously (Tanino and Blunt 2012, 2013; Tanino et al. 2015; Christensen and Tanino 2017a, b). The oil phase was n-decane (Sigma-Aldrich, \(\ge 99\)%) dyed with ORO (Sigma-Aldrich) at a concentration of \(C = 9\times 10^{-4}\) M. After ORO was added, the solution was filtered through a layer of grade 42 filter paper (\(2.5\,\upmu \hbox {m}\) particle retention, Whatman) to remove any undissolved particles.

Basic properties of the fluids at \(21\,^\circ \hbox {C}\) are summarized in Table 1. The dynamic viscosities of the brine and the oil, (\(\mu _{\text {w}},\mu _{\text {o}}\)), and their densities were measured by rotational viscometry (Anton Paar \(\hbox {SVM}^\text {TM}\) 3000); \(\sigma\) was measured using the du Nouy ring method (Attension Sigma700 force tensiometer, Biolin Scientific AB). The static contact angle of a drop of brine on a polished marble substrate submerged in the test oil, \(\theta _{\text {s}}\), is used as a measure of the local wettability of grain surfaces that come into direct contact with the oil. The substrate was first submerged in brine for a minimum of 12 h at room temperature and then submerged in the test oil in a glass cuvette. After \(t_{\text {a}}=1\) h, the duration over which the packed beds were saturated in the test oil prior to waterflood (Sect. 2.3), a drop of brine (approx. \(10\,\upmu\)L) was dispensed onto the substrate and imaged from the side using a colour camera coupled to a microscope. The contact angle was extracted from each image by fitting a fourth-order polynomial function to the drop profile in polar coordinates (Atefi et al. 2013).

Comparison with analogous measurements on undyed n-decane indicates that the addition of ORO reduces \(\sigma\) towards values more representative of NAPL contaminants (Tuck et al. 2003; Powers and Tamblin 1995; Powers et al. 1996; Dwarakanath et al. 2002) and crude oil under field conditions (Schowalter 1979; Connor 2000; Wood et al. 1991; Sutanto et al. 1990; Øren et al. 1998; Jerauld and Rathmell 1997). A contact angle of \(\theta _{\text {s}} = 76^\circ \pm 2^\circ\) and \(74^\circ \pm 8^\circ\) was measured with and without ORO (Table 1), which is significantly larger than the n-decane/brine dynamic contact angle of \(54^\circ \pm 7^\circ\) measured previously on polished calcite (Christensen and Tanino 2017a). The larger contact angles measured presently are attributed to mineralogical heterogeneities in the marble substrate which are absent from pure calcite crystals.

2.3 Displacement experiments

At the start of each experiment, the packed bed was fully saturated with brine. Next, oil was injected manually until a uniform oil saturation of \(S_{\text {oi}} \simeq 1\) was established; this displacement represents the infiltration of crude oil from source rock into a reservoir or of NAPL into soil or groundwater aquifers. Oil was circulated through the packed bed for \(t_{\text {a}}=1\) h. Finally, brine was injected at a constant volumetric flow rate \(Q_{\text {w}}\) using a syringe pump (Pump 11 elite nanomite, Harvard Apparatus); this displacement step represents waterflood (water injection) schemes in oil reservoirs and ambient flow in soil and in groundwater aquifers. Three \(Q_{\text {w}}\) were considered: \(Q_{\text {w}} = 0.1,0.33\), and 1\(~\upmu\)L \(\hbox {min}^{-1}\); these values correspond to \(U_{\text {w}} = Q_{\text {w}}/A = 26,85\), and \(260\,\upmu\)m \(\hbox {s}^{-1}\), respectively (Table 2). The duration of brine injection varied from 7.5 min (450 pore volumes) for the highest \(U_{\text {w}}\) experiment to 120 min (405 pore volumes) for the lowest \(U_{\text {w}}\) experiment.

Table 2 Summary of experimental conditions
Full size table

2.4 Flow visualization

The absorption spectra of n-decane and \(9\times 10^{-4}\) M ORO in n-decane were measured in the range 215 to 850 nm at room temperature (light source: DT-MINI-2-GS Deuterium Tungsten Halogen UV–Vis–NIR light source, Ocean Optics; detector: USB4000-UV-VIS, Ocean Optics). Like most alkanes, n-decane does not absorb light in the UV–Vis range (Fig. 3, black), while the ORO solution absorbs at all wavelengths up to 600 nm, with peaks at 355 and 515 nm (Fig. 3, red). These peaks are in excellent agreement with those measured in 13 organic solvents by Sidir and Sidir (2015).

Fig. 3
figure 3

Absorption spectra of n-decane (black) and \(9\times 10^{-4}\) M ORO in n-decane (red)

Full size image

During secondary water invasion, the chip was back-lit at wavelengths between 490 and 635 nm (Lumen 1600-LED, Prior Scientific)Footnote 1 and a high-speed 24 bit colour camera (Pixelink PL-B742F) with a global shutter coupled to an optical microscope (Nikon SMZ745T) captured the packed bed in a sequence of still RGB images at a resolution of \(2.4\,\upmu\)m \(\hbox {pix}^{-1}\) and a constant exposure time of 100 ms. Images were acquired at 4.9 fps at the beginning of the experiment for a minimum of 55 pore volumes of water injection after water breakthrough; the acquisition rate was subsequently reduced to 1.0 fps.

2.4.1 Correlation between transmitted light intensity and oil thickness

Fig. 4
figure 4

The ratio of blue-to-red channels, \({\widetilde{i}}\), of the transmitted light a as a function of the path length through a continuous layer of oil at constant dye concentration of \(C = 9\times 10^{-4}\) M and b as a function of C within a packed bed. Superposed in b are the transmission through the same packed bed when it is fully saturated in brine (blue \(\times\)). Each marker depicts a spatial average across a single image and vertical bars depict the standard deviation. Dashed lines are lines of best fit in the least-squares sense. Horizontal bars depict a the variation in particle size reported by the manufacturer and b the uncertainty arising from dilution when preparing the calibration standards (Taylor 1997); where the bars are not visible, they are smaller than the marker size. Insets are raw images of a packed bed fully saturated in brine and in the test oil

Full size image

In the present experiments, ORO is the light attenuating species (Fig. 3). Then, from Beer–Lambert law, light transmission through the packed bed, i, normalized by the incident light, \(I_0\), is related to the local concentration of ORO in the packed bed, c(z), and its molar absorption coefficient, ε, as:

$$\begin{aligned} \frac{i}{I_0} = 10^{-\epsilon \int ^H_0 c(z) \text {d}z}. \end{aligned}$$
(2)

ORO concentration is uniform within a single experiment and thus \(\int ^H_0 c(z) \text {d}z \equiv C h_{\text {o}}\), where \(h_{\text {o}}(x,y)\) is the local, depth-integrated oil thickness. In the present experiments, \(Ch_{\text {o}} \le 5\times 10^{-2}\,\mu\)m M. While \(\epsilon\) for the test oil is not available, values between \(\epsilon = 5\times 10^3\) and \(2\times 10^4\) \(\hbox {cm}^{-1}\) \(\hbox {M}^{-1}\) have been reported for solutions of azo red dye in dodecane of comparable concentration and viscosity (Chiang and Chao 2014). Assuming \(\epsilon =O(10^4)\) \(\hbox {cm}^{-1}\) \(\hbox {M}^{-1}\) for the test oil considered presently, \(\epsilon \, Ch_{\text {o}}\ll 2/\ln (10)\) and Eq. (2) can be approximated by the first two terms of the Maclaurin series expansion:

$$\begin{aligned} \frac{i}{I_0} \approx 1 - \ln (10) \, \epsilon \, C h_{\text {o}}. \end{aligned}$$
(3)

Given the design and the small dimensions of the microfluidic chip we are unable to systematically vary the oil thickness within a packed bed. We, therefore, followed the approach of Zhao et al. (2016) and analyzed the dependence of the transmitted light intensity on oil depth between parallel plates (i.e., \(h_{\text {o}}\)) and dye concentration in a packed bed (i.e., C). Images were acquired at the same exposure time, acquisition rate, and illumination as those acquired during the displacement experiments. The calibration images display significant evidence of a linear correlation between the grey scale intensity and C and \(h_{\text {o}}\), respectively, consistent with Eq. (3). However, we found that the ratio \({\widetilde{i}}(x,y,t) = i_{\text {B}}(x,y,t)/i_{\text {R}}(x,y,t)\), where \(i_{\text {B}}\) and \(i_{\text {R}}\) are the intensities of the blue and red channels, respectively, yields a large dynamic range and partially corrects for non-uniform distribution and instantaneous fluctuations in incident light, so only these are considered in our analysis.

The correlation between the depth of the test oil and the intensity of light transmitted through it was determined by measuring the mean intensity transmitted through a layer of oil of five known thicknesses bound at the top and bottom by a 1.2–1.5 mm-thick soda lime glass slide. \(h_{\text {o}}\) was systematically varied by placing mono-disperse standards (Whitehouse Scientific Ltd.) between the slides to act as precision spacers; standards ranging from \((25.60\pm 0.7)\,\upmu \hbox {m}\) to \((56.28\pm 0.9)\,\upmu \hbox {m}\) were considered. \({\widetilde{i}}\) decreases linearly with increasing \(h_{\text {o}}\) (Fig. 4a), in agreement with Eq. (3).

Similarly, \({\widetilde{i}}\) of light transmitted through an oil-saturated packed bed decreases linearly with the dye concentration over the range \(0 \le C \le 9\times 10^{-4}\) M (Fig. 4b). The large standard deviation is attributed to the presence of the grains, which results in the path length through the oil varying from \(h_{\text {o}}=0\) (i.e., grains span the entire depth of the channel) to H (pores span the entire depth).

Combined, the two dependencies imply that the \({\widetilde{i}}(x,y,t)\) field within a packed bed can be converted into the total depth of oil within a given pixel, \(h_{\text {o}}(x,y,t)\), using a linear calibration curve of the form:

$$\begin{aligned} \left\langle {\widetilde{i}}\,(x,y,t)\right\rangle = \alpha - \beta \left\langle h_{\text {o}}(x,y,t)\right\rangle , \end{aligned}$$
(4)

where \(\alpha \,(>0)\) and \(\beta \,(> 0)\) are fitting coefficients and angular brackets denote a spatial average spanning many pores. Unless otherwise specified, the averaging volume spans the entire width of the packed bed and \(x \pm H\), which is equivalent to \(2H\,W\,/\left( \pi /4 \,{d_{\text {p}}}^2\right) = 60\) grains. The resulting \(\left\langle {\widetilde{i}}\right\rangle\) is a function of (x, t) only.

2.4.2 Determination of initial oil saturation

\(S_{\text {oi}}\) was measured in three packed beds as follows. The packed beds were first fully saturated in the test oil, i.e., the packed bed-averaged oil saturation, \(S_{\text {o}}\), was \(S_{\text {o}}=1\). This state corresponds to \(\langle h_{\text {o}}\rangle = H\phi\). Next, the packed beds were flushed with solvents and fully saturated with brine \(\left( \langle h_{\text {o}}\rangle = S_{\text {o}} = 0\right)\). Finally, the test oil was injected to establish \(S_{\text {oi}}\) in the same manner as in a displacement experiment. At each stage, still images were acquired at the same exposure time, acquisition rate, and illumination as in the displacement experiments.

From each image, \({\widetilde{i}}(x,y,t)\) was extracted and a spatial \(3\times 3\) median filter applied to remove noise. Substituting the values at \(S_{\text {o}}=0\) and \(S_{\text {o}} = 1\) into Eq. (4) yields the expression for the initial oil saturation:

$$\begin{aligned} S_{\text {oi}} \equiv \frac{\left\langle h_{\text {o}}\right\rangle _L (S_{\text {oi}})}{H\phi } = \frac{\left\langle {\widetilde{i}}\right\rangle _L \left( S_{\text {oi}}\right) - \left\langle {\widetilde{i}}\right\rangle _L \left( S_{\text {o}}=0\right) }{\left\langle {\widetilde{i}}\right\rangle _L (S_{\text {o}}=1) - \left\langle {\widetilde{i}}\right\rangle _L (0)}; \end{aligned}$$
(5)

\(\langle \,\,\rangle _L\) denotes a spatial average over the entire length (and width) of the packed bed. In the experiments considered presently, oil injection was performed manually and rapidly to ensure maximum \(S_{\text {oi}}\), and, accordingly, the measured packed bed-averaged value was \(S_{\text {oi}} = 0.97 \pm 0.03\) (standard deviation).

2.4.3 Extraction of oil saturation during waterflood

The depth-averaged oil saturation within the packed bed and its evolution during a waterflood were determined for each acquired image using the same method as above. However, it was not practical to acquire images at \(S_{\text {o}}=1\) during the displacement experiments. Accordingly, the transmitted intensity field at the beginning of water injection, i.e., at zero capillary pressure, was used as the second calibration reference. By analogy with Eq. (5), the width-averaged oil saturation is thus given by the following:

$$\begin{aligned} \widehat{\langle s_{\text {o}}\rangle }(x,t)= & {} \frac{\langle s_{\text {o}}\rangle (x,t)}{\langle s_{\text {o}}\rangle _{\text {max}}(x)} \end{aligned}$$
(6)
$$\begin{aligned}= & {} \frac{\left\langle {\widetilde{i}}\right\rangle (x,t) - \left\langle {\widetilde{i}}\right\rangle \left( S_{\text {o}}=0\right) }{\left\langle {\widetilde{i}}\right\rangle _{\text {min}}(x) - \left\langle {\widetilde{i}}\right\rangle (S_{\text {o}}=0)}, \end{aligned}$$
(7)

where the circumflex denotes normalization by the initial oil saturation at the beginning of the waterflood, \(\langle s_{\text {o}}\rangle _{\text {max}}\). In the present analysis, \(\left\langle {\widetilde{i}}\right\rangle \left( S_{\text {o}}=0\right)\) was approximated by either \(\left\langle {\widetilde{i}}\right\rangle _L\) in images of the packed bed under fully brine-saturated conditions (experiments C0–4, Table 2) or the mean \({\widetilde{i}}\) in the open channel immediately upstream of the packed bed when it is fully saturated in brine (all other experiments). Similarly, \(\left\langle {\widetilde{i}}\right\rangle _{\text {min}} (x)\) was evaluated as the mean intensity within the packed bed averaged over a minimum of 20 images prior to water entering the packed bed.

3 Results

3.1 Pore-scale displacement mechanisms

Fig. 5
figure 5

Water invasion patterns at four instances during a waterflood at \(\text {Ca} = 9\times 10^{-7}\) (top), \(3\times 10^{-6}\) (experiment C0–6, middle), and \(9\times 10^{-6}\) (bottom). From left to right: 30 s prior to water breakthrough, at breakthrough, 5 s after breakthrough, and 200 s after breakthrough. An image at the onset of water injection has been subtracted from each image and a \(3\times 3\) median filter applied; bright pixels represent invading water. Mean flow is left to right. The numbers at the top of each image are \(\widehat{\langle s_{\text {o}}\rangle _L}\). Arrows indicate the location that water first reaches the end of the packed bed (\(x=L\)); experimental conditions are summarized in Table 2. Dashed circles demarcate selected pockets of oil-filled pores. The horizontal white bar at the top left corner of the first image in each row corresponds to 500 \(\upmu\)m. We emphasize that these images are for visual inspection only; we avoid image subtraction in the post-processing for quantitative analysis to ensure that slight movement of the chip does not affect our analysis

Full size image

We first compare the water invasion patterns at the different \(\text {Ca}\). Figure 5 presents snapshots from four instances during three experiments. Specifically, the second column corresponds to the instance that water has reached the downstream end of the packed bed (water breakthrough), taken here to be when \({\widetilde{i}}\) within the gap filters first increases (\(t = t_{\text {b}}\)); the normalized, packed bed-averaged oil saturation at this instance is denoted by \({\widehat{S}}_{\text {ob}}\). The remaining images correspond to 30 s prior to water breakthrough (first column) and 5 s (third column) and 200 s after breakthrough (last column). The corresponding \(\widehat{\langle s_{\text {o}}\rangle _L}\) is shown above each image. For quantitative comparison, the width-averaged oil saturation profiles along the length of the packed bed are presented in Fig. 6.

Fig. 6
figure 6

Instantaneous, width-averaged oil saturation as a function of distance along the packed bed at the beginning of water injection (red), at water breakthrough (black), and 200 s after breakthrough (blue) at \(\text {Ca} = 9\times 10^{-7}\) (a), \(3\times 10^{-6}\) (experiment C0–4, b), and \(9\times 10^{-6}\) (c). Also depicted are intermediate times \(t-t_{\text {b}} = -200.6\) (a green dotted), −121.2 (a green dashed-dotted), −30.0 (a green dashed), and \(-\,3.9\) s (c green dashed), respectively. Arrows indicate \(L - x = 300\,\upmu \hbox {m}\) from the downstream end of the packed bed

Full size image

3.1.1 High Ca regime

At the highest \(\text {Ca}=9\times 10^{-6}\), the invading water formed fingers which merged and split as the front propagated across the length of the packed bed, bypassing pockets of oil-filled pores (dashed circles, bottom row, Fig. 5). During this initial period, \(\widehat{\langle s_{\text {o}}\rangle }(x,t)\) increased from the upstream end of the packed bed up to the advancing water front, beyond which \(\widehat{\langle s_{\text {o}}\rangle } = 1\) (dashed, Fig. 6c). The oil-depleted (i.e., \(\widehat{\langle s_{\text {o}}\rangle } < 1\)) region propagated downstream until it reached the end of the packed bed (black, Fig. 6c), which coincided with the arrival of the leading finger (arrow, bottom row, Fig. 5).

As water injection continued, other fingers propagated into previously unswept pockets, further displacing oil from the packed bed (third column, Fig. 5); \(\widehat{\langle s_{\text {o}}\rangle }\) decayed further at the corresponding, intermediate x (blue, Fig. 6c). Finally, beyond \(t-t_{\text {b}} \approx 55\) s, oil displacement was limited to water in selected water-filled pores expanding into and displacing oil remaining along the edges of that pore (last column, Fig. 5); these isolated events had negligible impact on \(\widehat{\langle s_{\text {o}}\rangle }\).

3.1.2 Low Ca regime

We now consider the lowest \(\text {Ca} \left( = 9\times 10^{-7}\right)\). The water invasion pattern \(t-t_{\text {b}} = 200\) s after breakthrough (top row, last column, Fig. 5) and the corresponding \(\widehat{\langle s_{\text {o}}\rangle _L} = 0.55\) and the mean saturation profile (blue, Fig. 6a) are comparable to those at the highest \(\text {Ca}\).

However, in sharp contrast to the highest \(\text {Ca}\), the depletion of \(\widehat{\langle s_{\text {o}}\rangle }\) took place in two distinct stages. During the first stage, the profile of \(\widehat{\langle s_{\text {o}}\rangle }\) displayed only a weak dependence in x (e.g., dotted and dashed-dotted green, Fig. 6a) as oil saturation decreased more-or-less uniformly across the length of the packed bed from its initial state to \(\widehat{\langle s_{\text {o}}\rangle } = 0.88\pm 0.03\) (dashed green). Remarkably, at the end of this first stage, only a few pores were occupied by water (first column, Fig. 5). Thus, oil depletion evident in \(\widehat{\langle s_{\text {o}}\rangle }(x,t)\) cannot be discerned in the images at the lowest Ca, which indicates that water was distributed at thicknesses smaller than the resolution of the images (i.e., \(\ll 5\,\upmu\)m).

As waterflood continued oil displacement entered a second stage, characterized by a \(\widehat{\langle s_{\text {o}}\rangle }(x)\) profile that increases sharply from \(x=0\) to a finite distance along the packed bed which, as was at highest Ca, corresponds to the leading edge of the (visible) advancing fingers (second column, top row, Fig. 5). Unlike at the higher Ca, however, a continuous path across the length of the packed bed cannot be discerned at breakthrough with only \(x=400\,\upmu \hbox {m}\) \((x/L \approx 0.25)\) invaded by the advancing front (black, Fig. 6a). As waterflood continues, fingers advanced further until the leading (visible) front and the corresponding low \(\widehat{\langle s_{\text {o}}\rangle }\) region reached the end of the packed bed at \(t-t_{\text {b}} \approx 80\) s. Note that the large gradient in \(\widehat{\langle s_{\text {o}}\rangle }(x)\) between \(x/L = 1/3\) and 2/3 at the end of the experiment (blue, Fig. 6a) arises from two large pockets of oil that were bypassed by fingers invading by piston-like displacement (Fig. 5 top row, last column).

We interpret the initial, sub-resolution invasion of water to be precursor film flow along the surface of the grains. Such films have recently been documented in 2D microfluidic cylinder arrays (Geistlinger et al. 2016; Zhao et al. 2016) with coarser elements and in a 3D packed bed of spheres (Datta et al. 2014). Because of their limited thickness, these films only displace a small fraction of oil and oil saturation decreases only slightly behind the film front. Behind the precursor film is a second front driven by water flowing through the center of the pores by piston-like displacement. Water invading via this mechanism spans the available pore space and, accordingly, its displacement path is readily visible and the mean oil saturation behind this second, bulk water front was significantly lower. Comparison of \(\widehat{\langle s_{\text {o}}\rangle }\) at \(t-t_{\text {b}} = -\,30.0\) s (dashed green) and 200 s (blue) indicates that precursor films displaced 12% of the oil initially in place and piston-like displacement displaced a further 35%.

Precursor film flows are driven by spontaneous imbibition and their occurrence indicates that the packed bed was water-wetting, in agreement with the measured bulk \(\theta _{\text {s}}(< 90^\circ )\). To our knowledge, however, precursor films have only been reported under more strongly water-wetting conditions (\(\theta _{\text {s}} \le 50^\circ\)) (e.g., Geistlinger et al. 2016; Zhao et al. 2016; Krummel et al. 2013; Datta et al. 2014; Lenormand and Zarcone 1984), in which precursor film flow gives rise to film swelling, snap-off at the pore throats, and subsequent capillary trapping of oil and, accordingly, is associated with high \(\widehat{\langle s_{\text {o}}\rangle }\) (e.g., Constantinides and Payatakes 2000). The present experiments demonstrate that imbibition can take place even at \(\theta _{\text {s}} \simeq 75^\circ\), but that it does not lead to snap-off. This suppression of snap-off is consistent with previous simulations in pore network models (Nguyen et al. 2006; Al-Futaisi and Patzek 2004).

3.1.3 Intermediate Ca

The intermediate \(\text {Ca} \left( = 3\times 10^{-6}\right)\) corresponds to a transition regime between the low and high Ca limits. The basic features of experiment C0-6 resemble those of the high Ca: water breakthrough coincided with injected water forming a continuous path along the packed bed and emerging at a single point (arrow, middle row, Fig. 5). The leading, dominant finger is narrower than that at the highest \(\text {Ca}\) and only one finger had formed before breakthrough, giving rise to a larger \({\widehat{S}}_{\text {ob}} = 0.76\pm 0.04\). In experiment C0-4, the bulk water front had not reached the downstream end of the packed bed at water breakthrough, resulting in \({\widehat{S}}_{\text {ob}} = 0.85\pm 0.06\) that matches those of the lowest Ca (Table 2).

3.2 Comparison with precursor film flow theory

We now compare our low Ca experiment to the classic model for the invasion length, \(x_{\text {f}}(t)\), by film flow through grain roughness (Lenormand and Zarcone 1984):

$$\begin{aligned} x_{\text {f}}(t) = \frac{1}{2} \sqrt{\frac{d_{\text {r}}}{2} \, \frac{\sigma \cos \theta _{\text {a}}}{\mu _{\text {w}}}} \sqrt{t}, \end{aligned}$$
(8)

where \(d_{\text {r}}\) is the equivalent roughness diameter; following Geistlinger et al. (2016), we replaced \(\sigma\) with \(\sigma \cos \theta _{\text {a}}\) to account for the impact of advancing contact angle, \(\theta _{\text {a}}\), on the capillary pressure.

The depleted oil region propagates from \(x_{\text {f}}=0\) to \(x_{\text {f}} = L = 1690\,\upmu \hbox {m}\) in approximately \(t=80\) s (Fig. 6a). Using Morrow (1975)’s empirical model, the advancing contact angle can be estimated from the measured static angle as \(\theta _{\text {a}} = 1.14\,\theta _{\text {s}} = \left( 86\pm 3\right) ^\circ\). Substituting these values and measured values of \(\mu _{\text {w}}\) and \(\sigma\) into Eq. (8) yields \(d_{\text {r}} = 0.08\)−0.55 μm, which is equivalent to 0.15 to 1% of the equivalent grain diameter. While SEM images indicate that the actual grooves are \(O(1)\,\upmu\)m, they do not occur everywhere on the grains in all grains (Fig. 1). The extracted \(d_{\text {r}}\) is thus in reasonable agreement with the true roughness. Further quantitative comparison with theory requires more precise determination of the precursor film front as it propagates and direct measurement of grain roughness. Both are topics for future work.

3.3 Mean oil saturation

Fig. 7
figure 7

Mean oil saturation as a function of a dimensionless time at \(\text {Ca} = 9\times 10^{-7}\) (red), \(3\times 10^{-6}\) (black, grey), \(9\times 10^{-6}\) (blue) and b Ca at water breakthrough (open circles) and at the end of the waterflood (solid). Vertical bars in b depict the difference between two half-widths of the packed bed. Lateral variation in water distribution due to fingering is most pronounced near water breakthrough and, accordingly, the uncertainty tends to be larger for \({\widehat{S}}_{\text {ob}}\) than \({\widehat{S}}_{\text {or}}\). Dotted lines are a guide to the eye

Full size image

Finally, we consider packed bed-averaged oil saturations (Fig. 7). Oil saturation tends to be higher at the downstream end of the packed bed (Fig. 6), which we attribute to imperfections in the channel cross-section near the intersect between the channel and the gap filters (Tanino et al. 2017). Accordingly, the last \(300\,\upmu \hbox {m}\) of the packed bed was excluded from spatial averaging operations to prevent end effects from unrealistically increasing the mean (arrows, Fig. 6).

Figure 7a presents the depletion of the packed bed-averaged oil saturation as a function of dimensionless time:

$$\begin{aligned} {\widetilde{t}} = \frac{t - t_{\text {b}}}{L} \frac{U_{\text {w}}}{\phi }, \end{aligned}$$
(9)

taken here to be the time relative to water breakthrough normalized by the advective time scale, \(L/(U_{\text {w}}/\phi )\), which governs piston-like displacement. It can be readily seen that after \({\widetilde{t}} = O(10)\), oil displacement ceased at all Ca and \(\widehat{\langle s_{\text {o}}\rangle _L}\) reached its long-time, steady-state value. This transient time falls between \({\widetilde{t}}=O(1)\) typically reported under strongly water-wet conditions e.g., (Salathiel 1973; Mungan 1966; Tanino and Blunt 2012; Christensen and Tanino 2017a) and \({\widetilde{t}} = O(50-1000)\) reported under mixed-wet conditions (e.g., Salathiel 1973; Tanino and Blunt 2013; Christensen and Tanino 2017a), further corroborating the near-neutral wettability indicated by the measured \(\theta _{\text {s}}\). In the discussion that follows, the remaining oil saturation at the end of the waterflood experiment, \({\widehat{S}}_{\text {or}}\), was evaluated as the time-average of \(\widehat{\left\langle s_{\text {o}}\right\rangle _L}\) after \({\widetilde{t}}\,> 100\).

Under the present conditions, \({\widehat{S}}_{\text {ob}}\) decreases monotonically with increasing \(\text {Ca}\) (open circles, Fig. 7b). However, precursor film advances like square root of time through roughness (Geistlinger et al. 2016; Lenormand and Zarcone 1984; Hay et al. 2008), which suggests that the bulk water front will merge with the precursor film front after sufficient amount of time provided that the packed bed is sufficiently long. This in turn implies that values of \({\widehat{S}}_{\text {ob}}\) are not universal under water-wet conditions, but are a function of L as well as \(\text {Ca}\). This is a topic of future work, using longer porous media.

In contrast, the long-time steady state is well defined. \({\widehat{S}}_{\text {or}}\) is constant within experimental uncertainty under conditions considered presently (solid circles, Fig. 7b; Table 2), i.e., \(10^{-6} \le \text {Ca} \le 10^{-5}\). While this weak dependence on Ca is reminiscent of analogous observations in consolidated rock (see, e.g., Tanino et al. 2015, and references therein) and in packed beds of spheres (e.g., Datta et al. 2014) under more strongly water-wet conditions, the pore-scale mechanisms that give rise to it differ. In the present experiments, the weak dependence is attributed to the near-neutral wettability: precursor films do not lead to snap-off and, therefore, do not suppress piston-like displacement nor do they affect ultimate oil recovery.

Waterflood oil displacement is a function of the hydrophilicity of the grains, grain roughness, pore size distribution and pore geometry, viscosity ratio, Ca, and system dimensions, and meaningful comparison of absolute values with other experimental systems is difficult (e.g., Dullien et al. 1989; Xu et al. 2017; Yun et al. 2017; Nguyen et al. 2006; Tanino and Blunt 2013; Vizika et al. 1994). Notwithstanding this, present measurements of \({\widehat{S}}_{\text {or}} \approx 0.52\) are broadly larger than values reported in the literature at comparable Ca, which range from \({\widehat{S}}_{\text {or}}\approx 0.09\) in a 3D packed bed of smooth spheres (Datta et al. 2014, \(\theta _{\text {s}} \approx 5^\circ\)) to \({\widehat{S}}_{\text {or}}\approx 0.25\) in 2D etched pore networks (Vizika et al. 1994, \(\theta _{\text {s}} = 40^\circ\)).

Present measurements are slightly larger than \({\widehat{S}}_{\text {or}}\approx 0.45\) previously measured in a packed bed of smooth, uniform spheres assembled in the same microfluidic channel as that used in the present experiments for a oil/water pair with comparable \(\theta _{\text {s}}\approx 70^\circ\) and a smaller viscosity ratio of \(\mu _{\text {w}}/\mu _{\text {o}} = 10^{-2}\) (Bowden et al. 2016). The difference is largely attributed to the wider grain size distribution in the present experiments. Wider grain size distribution promotes non-uniform invasion of water as the water flows preferentially through the higher permeability paths comprised of larger pores (Fig. 5). While grain roughness is also associated with poor oil displacement and higher \({\widehat{S}}_{\text {or}}\) (e.g., Bowden et al. 2016), the correlation is generally attributed to the roughness serving as conduits for wetting films and promoting snap-off and is thus not expected to have contributed to the difference in \({\widehat{S}}_{\text {or}}\) here.

4 Conclusions

Optical microscopy was used to visualize unsteady liquid/liquid flow in a two-dimensional bed of marble grains, our microfluidic analogue of carbonate rock, where both liquids and the grains were translucent. We applied the technique to measure the depth-averaged oil saturation and its evolution as water was injected at three different rates. In particular, by calibrating transmitted light intensity to local oil thickness, we were able to quantify the volume of sub-resolution precursor water films; such films are not correctly accounted for by segmentation, whereby each pixel is assumed to be either completely filled by oil or to contain no oil.

The measured end-point oil saturation was not a function of injection rate under conditions considered presently. However, oil saturation at early times, specifically at water breakthrough, decreased with increasing injection rate even at capillary numbers as low as \(\text {Ca} = \text{O}\left( 10^{-6}\right)\). These observations were explained in terms of the competition between precursor film flow and piston-like displacement. In sharp contrast to previous studies, precursor film flow did not lead to snap-off and high \({\widehat{S}}_{\text {or}}\) in the present experiments, which we attribute to the near-neutral wettability of the oil/water/marble system considered presently.

Oil displacement at early times has important implications for oil recovery operations, which typically involve the injection of only 1–2 pore volumes of flood water, and geological \(\hbox {CO}_2\) storage schemes. The experiments presented here highlight the importance of considering flow behaviour at pore volumes representative of field operations when evaluating these applications. Microfluidic experiments using translucent solid and liquid phases combined with optical microscopy are a fast, cost-effective tool for this purpose.