Abstract
Spray drying is an important industrial process to produce powdered milk, in which concentrated milk is atomized into small droplets and dried with hot gas. The characteristics of the produced milk powder are largely affected by agglomeration, combination of dry and partially dry particles, which in turn depends on the outcome of a collision between droplets. The high total solids (TS) content and the presence of milk proteins cause a relatively high viscosity of the fed milk concentrates, which is expected to largely influence the collision outcomes of drops inside the spray. It is therefore of paramount importance to predict and control the outcomes of binary droplet collisions. Only a few studies report on droplet collisions of high viscous liquids and no work is available on droplet collisions of milk concentrates. The current study therefore aims to obtain insight into the effect of viscosity on the outcome of binary collisions between droplets of milk concentrates. To cover a wide range of viscosity values, three milk concentrates (20, 30 and \(46\%\) TS content) are investigated. An experimental set-up is used to generate two colliding droplet streams with consistent droplet size and spacing. A high-speed camera is used to record the trajectories of the droplets. The recordings are processed by Droplet Image Analysis in MATLAB to determine the relative velocities and the impact geometries for each individual collision. The collision outcomes are presented in a regime map dependent on the dimensionless impact parameter and Weber (We) number. The Ohnesorge (Oh) number is introduced to describe the effect of viscosity from one liquid to another and is maintained constant for each regime map by using a constant droplet diameter (d \(\sim 700\ \upmu \hbox {m}\)). In this work, a phenomenological model is proposed to describe the boundaries demarcating the coalescence-separation regimes. The collision dynamics and outcome of milk concentrates are compared with aqueous glycerol solutions experiments. While milk concentrates have complex chemical composition and rheology, glycerol solutions are Newtonian fluids and therefore easy to characterize. The collision morphologies of glycerol solutions and milk concentrates are similar, and the regime maps can be described by the same phenomenological model developed in this work. The regime of bouncing, however, was not observed for any of the milk concentrates.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A liquid suspension of solid particles, such as milk, can be converted into a powder by means of a spray drying process. This unit operation is widely used in chemical applications such as paint pigments and ceramic materials production and has multiple applications in pharmaceutical, food and dairy industries Mujumdar (2014). For example, powdered milk is used in the baking industry to keep the bread fresh for a longer time, in pastry dough to make it crispier or in the production of ice cream, milk chocolate and baby food Fontana et al. (2008); Early (1998).
Droplet collision outcomes of glycerol: a bouncing for \({ We}=5.8\), \({B}=0.05\), \({Oh}=0.02\), b coalescence for \({We}=23\), \({B}=0.55\), \({Oh}=0.36\), c reflexive separation for \({We}=41\), \({B}=0.01\), \({Oh}=0.02\) and d stretching separation for \({We}=69\), \({B}=0.74\), \(\hbox {Oh}=0.065\)
Milk powder manufacturing varies, depending on the finished product specification, but it comprehends common heat treatment processes. Whole and skim milk typically has a water content of approximately 87 and 91%, respectively. In a first step, the water is partly removed by evaporation under reduced pressure and low temperature. At this point, the condensed milk typically has a high total solids content of about 48%. Without this first concentration step, very small particles will be produced with a high air content, a low wettability and a short shelf life. The condensed milk is then fed to a spray dryer chamber where it is atomized through a spray nozzle by high pressure, resulting in a distribution of small droplets. The droplet size distribution in spray applications is extremely broad and ranges approximately from 10 to \(100\ \upmu \hbox {m}\). In the work of Han et al. (1997) and Madsen (2006), the Rosin–Rammler distribution Rosin and Rammler (1933) was identified as the most accurate in predicting droplet size distribution for high pressure swirl injector. In the spray chamber, the dispersed suspension is brought in contact with hot air, enabling evaporation of the moisture. As a final process, while the final product is collected, the fine particles are separated from the hot gas stream and recycled to the spray dryer tower by means of a cyclone Fritsching (2016).
The dried product has some advantages over liquid milk, such as an extended shelf life due to the low moisture content. The water activity of the dried material (2.5–5%) is below the level where bacteria can multiply, which corresponds to \(60\%\). A storage of approximately 1 year does not lead to any substantial loss of quality of the powder Sharma et al. (2012). Furthermore, due to its lower bulk volume, the transport and storage of milk powder are more cost-efficient compared to liquid milk and less packaging material is required.
Milk powders may vary in their composition (milk fat, protein, lactose), the heat treatment they receive during manufacture, powder particle size and packaging. Instant powders, for example, should disperse quickly and closely resemble fresh milk without undissolved particles. Some other powders are fortified with vitamins and minerals. A certain powder is therefore produced in order to be suitable to the intended application.
Although the powder morphology is optimized towards the desired characteristics, the properties such as flow ability, water solubility and dustiness are largely affected by the agglomeration and currently still difficult to control. An agglomerate is a combination of small particles forming a permanent larger mass where original particles are identifiable. The size and integrity of the agglomerate depend on the drying process, the contact time, the viscosity for sticking and the collision outcomes of droplets. A substantial amount of droplet collisions is expected near the spray nozzles, due to the high local droplet number density and relative velocity. The droplet size, velocity distribution and initial spray angle are significantly altered by the collision dynamics: coalescence of droplets will produce larger droplets, whereas separation will produce smaller satellite droplets. Figure 1 illustrates four examples of collision outcomes observed in the experiments of this work. The mechanism of bouncing is shown in case (a). The second case (b) is an example of coalescence. The case (c) is a reflexive separation with formation of one relatively large satellite resulting from two droplets impacting on the same axis. The last case (d) occurs at high impact velocity after stretching and consequent separation with a satellite of smaller size. The transition between these collision outcomes is determined by relative velocity, impact angle and droplet size, density and surface tension. Viscosity is also an important factor which has been considered only recently.
The droplets with a large diameter do not evaporate completely, while too small droplets lead to undesired dust particles. Agglomeration is a desired phenomenon in this application and one of the important factors to control the quality of the final powder Sharma et al. (2012); van der Hoeven (2008). As a result of the concentration step and the drying process, the solids content of the milk concentrates increases and correspondingly also the viscosity. The presence of (cow) milk proteins is the cause of a relatively high viscosity of milk concentrates Nitsche (2011). It is expected that high viscosity values largely affect the collision outcomes for milk concentrate droplets. A predictive spray dryer model can support the process development and can contribute to reduction in costs and improvement in product quality in the industrial production of milk powder. The optimization of the spray drying process and of the final product characteristics often requires an experimental campaign with a pilot set-up, which is very expensive and time-consuming.
Spray drying is usually the final step of the processing line and therefore essential to the product quality of the milk powder. Detailed knowledge of collision dynamics in the spray dryers is thus important. Therefore, it is essential to get insight into the droplet collision dynamics of viscous milk concentrates. Many studies Jiang et al. (1992); Willis and Orme (2003); Gotaas et al. (2007); Kuschel and Sommerfeld (2013) focussed on the effect of viscosity on the transition boundaries between different regimes of collision outcome, but a general evaluation of the viscosity contribution for milk collision outcomes is still not available. In this work, we carry out an extensive experimental investigation to be able to quantitatively describe the influence of viscosity. The effect of viscous dissipation is then translated to regime boundary models depending on non-dimensional parameters. Glycerol is chosen as a reference fluid to compare results obtained with milk and to elaborate on the possible role of specific surface interactions in the proposed boundary models for the collision outcomes.
2 Droplet–droplet collisional theory
Droplet collision dynamics received considerable attention over the last few decades, both because of fundamental interest and because of its various applications. A few studies address the effect of viscosity on the collision outcome by means of a numerical approach Dai and Schmidt (2005); Munnannur and Reitz (2007); Planchette et al. (2017); Finotello et al. (2017). The advantage of this approach is the potential to capture all the internal motion of droplets during collision. However, the interface capturing methods are usually computationally very demanding.
Compared to numerical works, a larger number of experimental studies have addressed droplet collisions. An extensive experimental campaign on water droplet collisions was presented by Ashgriz and Poo (1990) for various impact conditions. The investigation concentrated on collision dynamics description and identification of the regimes of coalescence, reflexive and stretching separation. Theoretical models for the collision outcome occurrence have been provided as well. Despite the fact that no viscous dissipation energy is considered, most of the current collision outcome boundary models are still based on Ashgriz and Poo (1990) theory.
In the work of Jiang et al. (1992), a model which explicitly includes the viscosity has been proposed. The experiments were limited to a small range of viscosities, from 0.4 to 3.5 mPas, for water and alkanes. They showed that the onset of reflexive separation shifts to higher We as the ratio of liquid viscosity to surface tension increases. The model was later refined using the Ohnesorge (Oh) number by Qian and Law (1997). Furthermore, Jiang et al. (1992) concluded that the extent of viscous energy dissipation occurring during the initial stage of droplet deformation is independent of the droplet viscosity. Willis and Orme (2000, 2003) conducted an experimental investigation of viscous droplet collisions in a vacuum environment to avoid aerodynamic effects during collisions. Their results showed a proportional dependency of energy dissipation on droplet viscosity, in contradiction with Jiang et al. (1992). Brenn and Kolobaric (2006) extended the model for the prediction of satellite formation after stretching separation of Brenn et al. (2001) by including the effect of viscosity. The model gave good predictions for highly viscous liquids and high We numbers but was not able to describe liquids such as water and alcohol. Gotaas et al. (2007) studied experimentally and numerically the influence of viscosity in a range from 0.9 to 50 mPas, analysing n-decane and mono-, di- and triethylenglycole. In general, it was observed that the coalescence to separation boundaries shift to higher We number for fluids with higher viscosities. They confirmed that the results for the onset of reflexive separation for viscous fluids provided by Jiang et al. (1992) were not valid for relatively high viscosity and a new empirical correlation was presented. In the study of Kurt et al. (2007), the collision behaviour for pure liquids and suspensions was explored. They identified the difficulty of working with suspensions because of instability in the monodispersed droplet chain. The number of satellite droplets was found to increase with viscosity. The opposite behaviour was noticed for fluids with solid particles. Also Kuschel and Sommerfeld (2013) investigated the effect of viscosity by an experimental campaign. For the coalescence-stretching separation boundary, the model of Ashgriz and Poo (1990) was considered inadequate by Kuschel and Sommerfeld (2013) for capillary (Ca) numbers exceeding 0.577. To consider a large viscosity range, they applied a combination of Ashgriz and Poo (1990) and Jiang et al. (1992) models. The boundary between coalescence and reflexive separation was observed only for small solids mass fractions. Sommerfeld and Kuschel (2016) experimentally extended the previous work of Kuschel and Sommerfeld (2013), considering different alcohols and an oil. The derived models are, also in this case, a combination of Ashgriz and Poo (1990) and Jiang et al. (1992) models.
The gas properties in which collision events occur are also a relevant factor determining changes in the bouncing probability. It was observed by Qian and Law (1997) and later confirmed by Krishnan and Loth (2015) that an increase in the gas density stabilizes the interdrop layer, with a consequent increase in bouncing probability. The boundaries between coalescence and both types of separation are instead insensitive to the surrounding gas properties. Estrade et al. (1999) proposed an empirical model for bouncing based on deformation of ethanol droplets. Although the viscous energy dissipation is not accounted for, the model is the most commonly used to develop new correlations to demarcate the bouncing regime.
The transition between bouncing and coalescence is also found in collisions of laminar jets (Bush and Hasha (2004)). In the work of Wadhwa et al. (2013), the non-coalescence regime is due to a thin film of air which keeps the streams separated as in the case of two colliding drops. Surface instabilities are identified as responsible for the governing transitions between the two regimes.
An important contribution in the field of droplet collisions with non-Newtonian fluids is the work of Motzigemba et al. (2002), reporting experiments and numerical simulations on collisions of droplets from aqueous shear-thinning solutions of carboxymethylcellulose (CMC). In this work, glycerol/water mixtures and shear-thinning water/CMC solutions were compared. The zero shear viscosity of the water/CMC solutions was similar to the viscosity of the glycerol/water mixture, but the non-Newtonian droplets experienced deformations that were two times larger than for the Newtonian droplets. Chen et al. (2016), through direct numerical simulation (DNS), concluded that a collision of shear-thinning droplets can be modelled by a collision of Newtonian droplets with an effective viscosity. This finding was supported also by the work of Focke and Bothe (2012).
2.1 Dimensionless collision parameters
Different regimes of droplet collision outcomes are usually indicated in terms of non-dimensional regime maps, often with Weber number We and impact parameter B along the two axes. Because these two dimensionless numbers do not take into account the viscosity, at least one other dimensionless parameter needs to be used.
The Weber number is the ratio between inertia forces and surface tension:
where \(\rho _{\text{d}}\) is the droplet density, \(d_{\text{s}}\) is the diameter of the smallest droplet, \(v_{\text{rel}}\) is the relative velocity and \(\sigma\) is the surface tension. The ratio between \(d_{\text{s}}\) and the large droplet diameter \(d_{\text{l}}\) is the size ratio \(\Delta\).
The impact parameter B is defined, before the moment of impact, as the distance b between the two droplet centres in the plane perpendicular to the relative velocity vector (Fig. 2), normalized by the average droplet diameter:
When B is equal to 0, it is a head-on collision, and when it is 1, it is a grazing collision.
The Ohnesorge number represents the ratio of viscous forces and the combined effect of inertial forces and surface tension:
The capillary number is another non-dimensional parameter accounting for viscosity, directly indicating the ratio of viscous forces and surface tension:
Finally, some authors use the droplet Reynolds number, defined as the ratio of the inertial and viscous forces:
Because these dimensionless numbers are correlated, we only need one other parameter to include the effect of droplet viscosity. For example, when Ca is specified, Oh and Re can be calculated according to:
2.2 Current models for regime boundaries
A model that can be applied for low viscous liquids is the one proposed by Ashgriz and Poo (1990). They assumed that reflexive separation occurs if the effective kinetic energy is larger than \(75\%\) of the nominal surface energy of the merged droplets. The onset for head-on collisions (\(B=0\)) between these regimes corresponds to \(We_{\text{c}}=19\) when \(\Delta\) is 1. More generally, for nonzero values of B, the model for the boundary between reflexive separation and coalescence is given by:
where
For the boundary between stretching separation and coalescence, they found:
where
Jiang et al. (1992) models are valid only for relatively low viscous liquids but their formulation takes into account that a portion of the kinetic energy dissipates because of the viscous flow inside the droplets. For the critical We, demarcating the transition from coalescence to reflexive separation for head-on collisions (\(B=0\)) Jiang et al. (1992) proposed a direct dependency on the viscosity:
with \(C_{1}\) in (m/s). Successively, Qian and Law (1997) modified the viscosity to surface tension ratio with the Oh number and used two constants, \(C_{3}\) related to geometrical parameters and \(C_{4}\) to the surface energy of the deformed droplet. The model for the critical impact parameter demarcating the boundary between coalescence and stretching separation proposed by the same authors is:
where k is a constant. It can be noticed that Eqs. 17 and 18 contain constants which are not dimensionless, and therefore likely to be dependent on the system under consideration. This motivated other authors to develop theories or correlations which are presented in dimensionless form.
The criterion for bouncing, formulated by Estrade et al. (1999), occurs when the droplet initial kinetic energy of deformation does not exceed the energy required to produce a limit deformation. The viscous dissipation was neglected. The model predicts especially well at large Weber numbers.
The shape parameter \(\phi\) depends on the material properties of the liquid and the gas and is determined experimentally. The value reported by Estrade et al. (1999) for ethanol droplets is \(\phi =3.351\). Kuschel and Sommerfeld (2013) found a continuous distribution of the shape factor as a function of viscosity for both PVP K30 and saccharose. Successively Sommerfeld and Kuschel (2016) attributed values between 3.3 and 3.8 for various alcohols.
Table 1 summarizes some of the collision outcome boundaries models mentioned above.
3 Milk properties
The complex chemical composition and rheology of different milk concentrates make the systematic investigation of the viscosity effect on collision dynamics very challenging. The solids fraction generally consists of approximately 36% lactose, 31% fats, 25% proteins, 5% minerals substances and 3% other substances (e.g. organic acids), all by weight. The solids are suspended or dissolved in the water, depending on the type of solid and the size of the corresponding particles Walstra et al. (2005). The total solids content TS is calculated with
The sections below introduce a brief description of the parameters influencing the surface tension and shear viscosity of the milk concentrates.
3.1 Surface tension
Proteins and milk fats are the surface-active constituents causing the surface tension of milk to be lower than that of water Walstra et al. (2005). Milk fats are the largest and lightest component of milk and have the tendency to distribute at the surface. Proteins are present in milk as a colloidal suspension in water, which forms an unimolecular layer at the surface. No work is found in the literature on the surface tension of milk for whole milk concentrates with high total solids content. Jenness et al. (1959) reported relevant values for rennet whey (51–52 mN/m), skim milk (52–52.5 mN/m), whole milk (46–47.5 mN/m), \(25\%\) fat cream (42–45 mN/m) and sweet-cream buttermilk (39–40 mN/m). Kristensen et al. (1997) reported values at \(25\ ^{\circ }{\text{C}}\) for skim milk (47.3 mN/m), \(3.5\%\) milk (41.9 mN/m) and \(38\%\) cream (31.4 mN/m). The surface tension values used for collisions in this work are in the same range.
Besides the total solids content, the surface tension also depends on processes such as homogenization and temperature history Mohr and Brockmann (1930). When milk is for instance exposed to high shear rates, the surface tension decreases due to the release of the surface-active components of the milk fat globule membrane Michalski and Briard (2003).
3.2 Viscosity and rheology
The viscosity of milk concentrates increases exponentially with increasing TS content Snoeren at al. (1984), due to the loss of free motion Hinrichs (1999) and protein–protein interactions which occur more frequently as they are in closer proximity Corredig and Dalgleish (1999), Kessler (2002). The effect of solids content on the viscosity of reconstituted whole milk concentrates at \(46\ ^{\circ }\hbox {C}\) is illustrated in Fig. 3a.
Also the rheological behaviour of milk depends on the total solids content: below \(30\%\) TS content, milk concentrates behave as a Newtonian fluid, while non-Newtonian shear-thinning behaviour is observed for higher TS content milk concentrates Trinh et al. (2007). Also lower values for this critical TS content have been reported, e.g. 22.3% Vélez-Ruiz and Barbosa-Cánovas (1998), \(25\%\) Chang and Hartel (1997), \(20\%\) Morison et al. (2013) and \(15\%\) Solanki and Rizvi (2001). Different values reported can be explained by differences in milk composition combined with processing effects. For a \(50\%\) TS content skim milk concentrate, the effect of shear rate on the apparent viscosity is shown in Fig. 3b.
For these shear-thinning milk concentrates, the viscosity decreases with increasing shear rate. An increased shear rate deforms or rearranges particles, resulting in a lower flow resistance. Thixotropic behaviour (time-dependent behaviour) is observed for milk concentrates above 44% TS content Trinh et al. (2007). This is the result of a breakdown in the microstructure of the material as a consequence of the applied shear. To recover its structure, the milk concentrate must rest for a certain period. It is also reported that the changes in apparent viscosity were irreversible for milk concentrates stored for a long time under high shear Bienvenue et al. (2003). Some other processes, such as whey protein heat denaturation, also irreversibly change the apparent viscosity Fritsching (2016).
The droplets in a spray dryer are exposed to high shear rates. Values reported are in the range of \(10^{4}\)–\(10^{6}\,\hbox {s}^{-1}\) Fritsching (2016), \(10^{3}\)–\(10^{4}\,\hbox {s}^{-1}\) Mezger (2006) and \(10^{5}\,\hbox {s}^{-1}\)Larsson and Orucoglu (2013). An estimation of the shear rate of a droplet collision can be based on the approximation for the shear rate of a droplet collision with a solid surface, as given by Eq. 22 Chandra and Avedisian (1991). It states that the shear rate is proportional to the ratio of the droplet relative velocity divided by the droplet height at maximum spreading.
The viscosity of milk is thus dependent on shear rate, total solids content and time or shear history. But there are more factors influencing the viscosity of the milk. First of all, the state and concentration of the proteins are substantially changing the viscosity. High TS contents have a low pH thus the positive and negative charges attract each other and the protein molecules form large protein clusters, which leads to a high viscosity of the milk concentrate Bienvenue et al. (2003) and Anema and Li (2003). Furthermore, the viscosity increases with increasing concentration of fats.
Another factor that affects the viscosity in a complex way is the temperature Walstra et al. (2005), Snoeren at al. (1984), Westergaard (2004). The significant decrease in viscosity with increasing temperature can be partly explained by the fact that the viscosity of the aqueous solution is lower at higher temperature. In addition, the volume of the proteins in the form of micelles is substantially higher at low temperatures, which consequently increases the viscosity. On the contrary, temperatures above \(70\,^{\circ }\hbox {C}\) lead to the denaturation of whey proteins and a considerable increase in viscosity. This trend is shown in Fig. 3c, where the viscosity profile as a function of temperature is displayed for various whole milk concentrates.
Finally, milk concentrates with a high TS content are strongly susceptible to a process called age thickening, which is the increase in viscosity over time during storage at rest. The mechanism involved in this gelling effect is still not completely clear. The rate of age thickening increases with increasing total solids content and temperature Walstra et al. (2005), Snoeren at al. (1984).
Trinh et al. (2007) investigated age thickening for milk concentrates. Their work shows that no age thickening occurs after 4 h storage at \(45\,^{\circ }\hbox {C}\) for 10, 20, 30 and \(34\%\) TS content milk concentrates, although age thickening was observed for 30 and \(34\%\) TS content after 7 h storage at \(85^{\circ }\hbox {C}\). For concentrates with higher solid contents, they stated that, in order to observe age thickening within 4 h storage, the minimum storage temperature required is 85, 65 and \(45\,^{\circ }\hbox {C}\) for 44, 46 and \(48\%\) TS content, respectively.
4 Materials and methodology
4.1 Liquids characterization
Measured rheology data of investigated milk concentrates. H–B is the Herschel–Bulkley model (Eq. 23)
As previously mentioned, the rheology of milk concentrates is Newtonian for milk concentrates below approximately \(30\%\) TS content and non-Newtonian when the milk is more concentrated. The viscosity of the \(20\%\) TS content concentrate is measured with a viscometer (Fungilab Alpha Series) and a viscosity value of 4.3 cP is found for various shear rate settings and is thus considered exhibiting Newtonian behaviour. The viscosity values of the \(30\%\) TS content and \(46\%\) TS content concentrates are measured with a rheometer (Anton Paar MCR 302). The apparent viscosity as a function of shear rate is given in Fig. 4. Shear-thinning (non-Newtonian) behaviour is found for both \(30\%\) TS and \(46\%\) TS content concentrates. A larger effect of shear thinning is observed for higher TS concentrates.
We propose to fit the shear rheology data of milk solutions with the Herschel–Bulkley (H–B), Bird et al. (1977), model according to:
where \(\tau\) is the shear stress, \(\tau _{0}\) is the yield stress, \(\dot{\gamma }\) is the shear rate, K the consistency index and n the flow index. Because milk is shear thinning \(n<1\). \(\tau _{0}\), K and n are correlated as a function of the TS content based on correlation functions provided by Tetra Pak, Heerenveen (the Netherlands). The same constants are used to fit the measured data of 30 and 46% milk concentrates.
As discussed in the theoretical background, the droplets in a spray dryer are exposed to high shear rates. Reported values are in the range of \(10^{3}\)–\(10^{6}\,\hbox {s}^{-1}\). In our set-up, binary droplet collisions with droplet diameters in the range of 620–770 μm and relative velocities in the range of 0.5–3 m/s are observed. Equation 22 yields an approximation for the shear rate of 800–\(4700\,\hbox {s}^{-1}\). This lower boundary corresponds to the lower boundary of the values reported in the literature. Figure 4 shows that in this range of shear rates (white region with dashed border), the viscosity can be considered constant, but substantially lower than the zero shear rate viscosity. The shear rate range can be calculated from the nozzle diameter of \(300\ \upmu \hbox {m}\) and the volumetric flow rate between 4.5 and 11 ml/min. The shear rate, calculated as the ratio of the jet velocity to nozzle diameter, lays in a range of 860–\(2170\,\hbox {s}^{-1}\). This is very similar to the one calculated with the relative velocity and diameter of the drops.
The viscosity value used in this work is the average value in the expected range of experimental shear rates. The viscosity values used are given in Table 2. It is probably not meaningful to compare the viscosity values to the literature, since most of the values reported are measured at higher temperatures or the work does not specify the shear rate at which the viscosity is measured.
The density of milk concentrates used in this work is based on a correlation provided by Tetra Pak. Density can variate because milk is a natural product and several applied processes (e.g. standardization, homogenization and pasteurization) can influence the density as well. Density values used in this work are given in Table 2.
Milk concentrates were used in collision experiments at \(20\,^{\circ }\hbox {C}\) for a maximum of 3 h to make sure no age thickening effect or contamination influence the results. The surface tension and viscosity values were measured before starting the experiments and later every hour. For 20% TS content, no change in viscosity was observed, while for the 46% TS content, a small increase (ca. 10%) in the viscosity was observed after 3 h. No significant change in surface tension was observed.
A reconstitution method is used to prepare milk concentrates with more reproducible physical properties than fresh milk and to be able to reach relatively high solids (TS) content. Please note that it is known that fresh milk and reconstituted milk do not necessary have the same properties Trinh et al. (2007). A summary of the values used in this work are given in Table 2 together with the properties of glycerol solutions used in this work. A Kruss K20 Force Tensiometer was used to measure the surface tension of the liquids. The surface tension measured for glycerol at \(20\,^{\circ }\hbox {C}\) is very similar to the one from Takamura et al. (2012); Connors (2001). The viscosity and density measurements are in perfect correspondence with the trends described in Cheng (2008). Also for the glycerol mixture, surface tension and viscosity are calculated before and after the experiments, with a maximum usage of the same liquid for 3 h. This procedure enables to minimize contamination and relevant physical property changes.
4.2 Reconstitution of milk concentrates
It is known that the properties of fresh cow’s milk can vary substantially. For this work, it is desirable to perform experiments with constant properties of milk concentrates. The reconstitution method consists of adding water to skim milk or whole milk powder (SMP or WMP). In this work, Arla spray-dried whole milk powder, made from cow’s milk, is used. The milk powder consists of 26% milk fats, 24–28% milk proteins, 36–42% lactose, 5–6% minerals and 3.2% moisture.
The procedure to prepare milk concentrates with controllable chemical properties and various TS contents was provided by Tetra Pak. In the section below, the procedure used to reconstitute milk is described. Batches of 1000 grams are prepared and, depending on the desired TS content, the amount of dry whole milk powder is weighed using a scale (Table 3). Water at approximately \(55\,^{\circ }\hbox {C}\) is positioned in a mixer (IKA RW16 basic overhead stirrer with a range of 40–1200 rpm). Subsequently, the lid of the mixing chamber is locked in place and the stirring speed is set at approximately 370 rpm. The pre-weighted dry milk powder is slowly added through a funnel into the mixing container during a maximum time of 5 min. The mixing process is continued for 4 more minutes. The mixing container is then removed from the mixing chamber and the foam layer, deposited after mixing on the top, is carefully removed with a spoon.
In the next stage, the milk solution is centrifuged at 2000 g for 3 min by a centrifuge (SIGMA 3-30X super-speed refrigerator). The mixing process leads to inclusion of air bubbles, which are removed by the centrifugation step. The centrifugation step also ensures complete homogenization of the milk concentrate. The milk solution is finally cooled in an ice bath at \(5\,^{\circ }\hbox {C}\) until the temperature approaches room temperature. The experiments are performed at atmospheric pressure and room temperature.
4.3 Experimental set-up
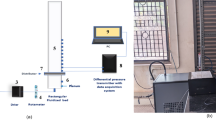
The experimental set-up, illustrated in Fig. 5, is composed of a droplet generator (BUCHI, Switzerland) that produces two streams of monodispersed droplets. The main parts of the droplet generator are the control unit, the producing unit and the syringe pumps. The perturbation of the streams is produced through an oscillating electrical signal at the desired frequency which causes a mechanical vibration of the structure. The frequency for these experiments is in the range of 500–750 Hz. The received vibrations can be adjusted independently for both jets. The liquid is introduced into the producing unit by two 60-ml syringe pumps. The liquid then passes thought the vibration chambers and nozzles of \(300\,\upmu \hbox {m}\). On exiting the nozzle the liquid stream separates into equal size droplets. The droplet chains are brought to collision by two rotating components and a linear component. The collision parameters can be controlled by imposing the nozzle diameter correlated with the droplet diameter, the flow rate of the syringe pumps, which influence the droplet speed before collision, and the frequency, which affects the distance between two consecutive droplets.
The area before and after the collision is recorded by a high-speed camera. The background of this area is a white plastic plate illuminated by a series of LEDs, to optimize the contrast of the droplets with respect to the background.
The angle between the two droplet streams and the vertical axis can be set by rotating components. The y-position (Fig. 6) of the left vibration chamber can be adjusted as well with the purpose to modify the impact parameter. In addition, the x-position of both vibration chambers can be changed to adjust the distance between the two nozzles. Finally, to ensure the two droplet streams to collide in the same plane, the z-position of the left vibration chamber can be adjusted. For this alignment procedure, a second high-speed side camera is added in the collision plane, perpendicular to the front camera. During experiments, the side camera is used to accurately align the two streams in the z direction, while after experiments, this alignment can be visually checked once more for a specific collision. The Davis cameras are operated at a frequency of 4000 Hz and an exposure of \(1/20000\ {\text{s}}\). A Sigma 105 mm f/2.8 EX DG Macro lens is used for the camera in front of the droplet. As the side camera is further away from the droplet streams, it is combined with a Nikon 200 mm f/4 AF-D Macro lens to provide more magnification at a larger distance. The observation area was adapted for different collision outcomes: for coalescence the camera can be positioned closer than for the stretching separation where the rupture of the ligament takes long time. This is the result of a compromise between the possibility of visualizing the entire collision dynamics and, oppositely, of having a high resolution. For each specific collision, the Weber number, the Ohnesorge number and the impact parameter are determined by post-processing the pre-collision area of the recorded video. The area below the collision is used to visually determine the collision outcome.
The choice of using droplet diameters of \(700\,\upmu \hbox {m}\) is due to experimental restrictions. The viscous liquids need a high flow rate from the syringe pumps to be injected through the nozzles. With smaller nozzles diameter than the \(300\,\upmu \hbox {m}\) used in our work, injecting issues occurred in stabilizing the stream breakup. The camera resolution was also an important factor to take into consideration. Our aim is to observe the total collisional event, pre- and post-collision, with a sufficient number of pixels per drop diameter; therefore, we choose a suitable observation frame. With smaller droplet sizes, the process of tracking and analysis of drops would have not been accurate.
4.4 Droplet collision tracking
The parameters affecting impact collision, namely the We, Re, Oh, Ca and B, need to be identified for each event, tracking the drops velocity and position from frame to frame. The recorded images are analysed using MATLAB R2015a and processed following two different procedures, corresponding to before and after collision. If the error of the two streams alignment in the colliding drop pair is greater than \(5\%\) of the droplet diameter, the recording is discarded. Based on a sample of 500 droplets, the mean radius corresponds to 11.35 pixels with a standard deviation of 0.64 pixels. If smaller satellites are visible in the recording before collision or if the difference in the droplet diameter of the streams is greater than \(4\%\), the recordings are discarded and a new optimal frequency is established. The analysis of the pre-collisional part consists of the following steps:
-
The viscosity, density and surface tension of the colliding liquid in the recording are entered in the script. Furthermore, the pixel-to-meter ratio is entered, as well as the average droplet radius. A ruler is used to calibrate the pixel-to-meter ratio, once the camera position is set.
-
The pre-collision area is selected manually, the drops are distinguished from the background using the edge and imfill image analysis commands and the locations of all droplets are determined with the imfindcircles function (step 1–3 in Fig. 7).
-
The frame is divided into two vertical sides so that one droplet from one stream collides with one droplet belonging to the other jet. The drop on the left side is associated with the one on the right side which has the smallest vertical distance. This is illustrated by step 4 in Fig. 7. The pair is labelled with a number which remains the same for the entire recording. For the new pairs appearing in the next frames, new labels are provided.
-
The script now continues with Frame 2. All droplets are again localized, the droplet pair of the colliding droplets is found by using the location of the droplet pair of the previous frame. Once the droplet pair has again been identified, the horizontal and vertical displacements from the previous frame are measured and velocity coordinates are derived. The script continues with the next frame.
-
The process for a pair stops when the circles around the two droplets overlap.
-
With the displacements and position of droplets at the moment of collision, the relative velocity and impact parameter are calculated for each pair in the recording. The distance b between the two droplet centres is calculated according to:
$$\begin{aligned} b=\left| \frac{\Delta y \Delta v_{x} - \Delta x \Delta v_{y}}{v_{\text{rel}}} \right| \end{aligned}$$(24)In case the two drops have no point of contact in the last frame before merging, an extrapolated position, based on the previous velocity and displacement of the drops, is considered for calculating the impact parameter. Therefore, the relevant dimensionless numbers are calculated and then stored in a matrix.
-
When the droplet pairs are detected, a video in which the pair label is shown next to the moving droplets is created.
The procedure corresponding to the post-collision consists of visual analysis of the recording and identification of the collision outcome for each droplet pair. In case of separation, the number of satellites is also registered. The minimum detectable droplet size is of the order 1 pixel, corresponding to approximately 32 μm. Although this is a limitation of the tracking analysis, the satellites size is not the main focus of this work and the regimes boundaries can still be correctly estimated. The time a droplet remains inside the view of the camera is approximately 7.5 ms.
Head-on collisions for 20% TS content milk for increasing We number: a coalescence at \({We}=31.5\) and \({B}=0.001\), b reflexive separation at \({We}=35.2\) and \({B}=0.07\), c reflexive separation with formation of one satellite at \({We}=41.3\) and \({B}=0.02\), d reflexive separation with formation of one satellite at \({We}=59.2\) and \({B}=0.05\), e reflexive separation with formation of one satellite at \({We}=80.4\) and \({B}=0.002\)
5 Results and discussion
5.1 Milk
The milk entering a spray dryer has a high viscosity due to the earlier temperature treatments, meaning that the collision behaviour does not correspond to that of water. In this work, experiments with 46% TS content, corresponding to Oh = 0.44, are carried out. This is the maximum concentration which does not present viscosity variations within 3 h of usage. To observe the reflexive separation regime which occurs for relatively low viscosity liquids such as water, lower values of Oh number (0.05 for 30% TS and 0.022 for 20% TS) are also considered in our experiments. The collision outcomes are discussed in the section below.
The head-on (\(B=0\)) and near head-on collision and the boundary demarcating coalescence and reflexive separation are presented first, followed by the description of the grazing collisions and coalescence to stretching separation regimes.
In Fig. 8, head-on collisions for 20% TS content milk droplets for different Weber numbers are illustrated. It can be seen that in all cases the two droplets merge and deform into a disc-like drop (4 and 5 in the figure) in a time interval of approximately 1 ms. The merged droplets oscillate and relax after some time to a spherical shape (6). In case 8(a), the two droplets merge, deform into a disc-like drop and extend to an ellipsoidal shape (7 and 8). The consequent retraction restores the spherical shape of the merged droplets (12). In the other cases, the Weber number and thus the amount of kinetic energy are increased. The initial kinetic energy is sufficient to break the ligament and reflexive separation occurs. The internal momentum rate is in this case higher than the surface tension force. A very small satellite droplet is formed in case c (\({We}=41\)) and its size increases with increasing Weber number [d (\({We}=59\)), e (\({We}=80\))]. Figure 8e shows that the satellite droplet can be similarly sized as the parent droplets. The range of satellite sizes is 7–\(35\ \,\upmu \hbox {m}\) for \({We}\sim 40\), approximately \(100\ \upmu \hbox {m}\) for \({We}\sim 60\) and 100–\(200\ \,\upmu \hbox {m}\) for \({We}\sim 70\). Moreover, it is possible to observe the ligament breakup behaviour with the initial neck destabilization from the two tip edges and consequent pinch-off (9–12 for cases c, d and e). The total time duration for the collisions illustrated in Fig. 8 is approximately of 5.5 ms. According to Ashgriz and Poo (1990), the large contour of the disc-like shape creates a pressure difference between the inner and outer regions. As a consequence, the disc shape contracts inward (to recover the spherical shape) and the liquid is pushed out from its centre. A stretched liquid cylinder is then formed. When the amount of energy available is sufficient to move the two ends further apart, a liquid bridge is formed that eventually breaks. The head-on onset of reflexive separation for 20% TS milk concentrates is expected to be in between We 32 and 35. This value is substantially higher than the onset for water droplets, which is approximately We = 19 Ashgriz and Poo (1990). From the experiments, we observed that the onset of reflexive separation for the 30% TS content milk concentrate is between We = 44 and We = 51. For the 46% TS content milk concentrate, no reflexive separation was observed even for We = 156.
The stretching separation occurs at sufficiently high B and high relative velocities. Because B is high for two impacting drops only, a part of the droplets become into contact (interacting region), while the peripheral regions have the tendency to continue their motion. The surface energy, responsible for holding the combined droplet, is relative to only the interacting region and thus lower than the kinetic energy. In Fig. 9, the effect of viscosity is shown, illustrating a collision outcome for similar impacting conditions but different milk concentration. A portion of the kinetic energy dissipates because of the viscous flow inside the droplets. The stretching energy available for separating the merged droplets is less and separation becomes more difficult.
A bouncing regime is observed for both head-on collisions (at low We) and grazing collisions (at low and intermediate We) for hydrocarbon droplets Jiang et al. (1992), alcohols, oil and saccarose Kuschel and Sommerfeld (2013); Estrade et al. (1999), but this regime is absent for head-on collisions of water droplets Ashgriz and Poo (1990); Jiang et al. (1992); Kuschel and Sommerfeld (2013); Estrade et al. (1999). In the literature, the presence of a bouncing regime for head-on collisions of hydrocarbons and absence of this regime in water are attributed to the difference in surface tension. Similarly for milk concentrates, no bouncing was observed for head-on collisions at very low We numbers nor for high impact parameters (see Fig. 9). The lowest limit of the Weber number obtained in the experiments of this work is approximately 5.5. If for low relative velocities the promoted coalescence can be attributed to interfacial mechanisms, the same cannot be concluded for collision at high impact parameters, where the surface energy in the interaction region is lower. The phenomenon is therefore more complex and requires further analysis although it is difficult to perform experiments in the region of low We numbers and very high B because of experimental limitations previously mentioned. The demonstration that bouncing does not occur in milk collisions at any concentration is, however, very important for milk spray applications.
5.2 Proposed models
The model proposed by Qian and Law (1997) for the relation between the critical Weber number of reflexive separation (for head-on collision, \({B}=0\)) and the Oh number is:
Later, Gotaas et al. (2007) proposed two different correlations depending on the Oh number:
These models, as well as the critical Weber numbers for water Ashgriz and Poo (1990), the reconstituted milk concentrates and glycerol–water mixture used in this work, are plotted in Fig. 10. The error bars indicate the range of Ohnesorge numbers for the specific regime map and the range of Weber numbers in which the critical Weber is expected to be located. The linear correlation between the critical Weber number of reflexive separation and the Ohnesorge number matches well with the two values found for 20% TS content and 30% TS content. The power function which is proposed for \({Oh}>0.04\), however, overestimates the critical Weber number of glycerol substantially. The linear relation and power function proposed by Gotaas et al. (2007) predict the critical Weber number of 298 and 2295, respectively, for 46% TS content. Our experiments for 46% are limited to a Weber number of 156, for which no reflexive separation is observed.
As discussed in the introduction, the general approach to describe the boundary demarcating coalescence and reflexive separation is to give a horizontal translation to the model of Ashgriz and Poo (1990) for water, with a critical We dependent on the Oh number. The model proposed in this work is a combination of the model by Ashgriz and Poo (1990) for reflexive separation, horizontally translated in the (We, B) map in order to predict a correct onset of reflexive separation, and the model by Jiang et al. (1992) for stretching separation, with two constants fitted to the experimental data on milk. This approach is used also in the recent study of Sommerfeld and Lain (2017). The two fitting constants for water are proposed by Jiang et al. (1992) and for saccharose by Kuschel and Sommerfeld (2013). The model is given by Eq. 27 (reflexive separation coalescence) and Eq. 30 (coalescence-stretching separation).
Here \({{\eta _1}}\) and \({{\eta _2}}\) are geometric factors as introduced by Ashgriz and Poo (1990) (Eqs. 9 and 10).
The model is expressed also in terms of the size ratio, but we only considered equal-sized droplets (\(\Delta =1\)) and \({d}\sim 700 \ \upmu \hbox {m}\) in this work. It follows that the model is valid and limited to binary droplet collisions of milk concentrates with TS contents between 20 and 46% and with equal droplet diameters at atmospheric pressure and room temperature. A representation of the adapted models for reflexive and stretching separation, derived in this work, is shown in Fig. 11.
5.3 Collision regime maps
Figure 12 shows the collision outcome regime maps for constant Oh numbers 0.022, 0.05 and 0.44. The proposed model for the boundaries between coalescence and stretching separation, Eq. 30, is represented by a black continuous line. The coalescence-reflexive separation boundary, Eq. 27, is shown as a black dashed-dotted line. The Ashgriz and Poo (1990) models for water are also provided, dashed line for stretching and dotted line for reflexive, with the purpose of showing the influence of viscosity on the collision outcomes.
Although some overlap is present between the different collision regimes in the transition areas, we can define the boundaries and observe their evolution with increasing viscosity. The overlap can be explained by small differences in droplet size, a small offset within the alignment of the two droplet streams in the z direction and some small changes in the physical properties of the investigated liquids over time.
We can observe that a higher impact parameter is required for low Weber numbers to achieve stretching separation. In addition, the critical Weber number for reflexive separation increases with increasing impact parameter. For our experiments, the critical Weber number of reflexive separation increases from the 20 to the 30% TS content, while for 46% the onset is not observed in the range considered in this work. (Also at We = 156, the outcome is coalescence.) In accordance with the observation of Jiang et al. (1992),Gotaas et al. (2007) and Kuschel and Sommerfeld (2013), the increased viscous dissipation shifts the separation regimes towards higher We numbers, promoting coalescence.
Collision outcome regime maps for binary droplet collision of milk concentrates: milk 20% TS content corresponds to \({Oh}=0.022\), milk 30% TS content to \({Oh}=0.05\) and milk 46% to \({Oh}=0.44\). Blue stars: coalescence, red triangles: reflexive separation, green squares: stretching separation. Continuous line: this work for stretching separation, dashed-dotted line: this work for reflexive separation, dashed line: Ashgriz and Poo (1990) stretching separation, dotted line: Ashgriz and Poo (1990) reflexive separation
Collision outcome regime maps for binary droplet collision of glycerol–water: glycerol 40 vol% corresponds to \({Oh}=0.021\), glycerol 60 vol% TS content to \({Oh}=0.064\) and glycerol 86 vol% to \({Oh}=0.38\). Blue stars: coalescence, red triangles: reflexive separation, green squares: stretching separation, magenta circles: bouncing. Black continuous line: this work for stretching separation; black dashed-dotted line: this work for reflexive separation; black dashed line: Ashgriz and Poo (1990) stretching separation; black dotted line: Ashgriz and Poo (1990) reflexive separation; magenta continuous line: Estrade et al. (1999) bouncing
5.4 Glycerol
Grazing droplet collision for milk concentrates and glycerol solution at similar conditions: a \({We}=40.6\), \({B}=0.61\), \({Oh}=0.022\) for milk 20% and \({We}=41.3\), \({B}=0.63\), \({Oh}=0.021\) for 40 vol% glycerol, b \({We}=61.5\), \({B}=0.63\), \({Oh}=0.049\) for milk 30% and \({We}=61.9\), \({B}=0.64\), \({Oh}=0.068\) for 60 vol% glycerol, c \({We}=97.6\), \({B}=0.68\), \({Oh}=0.44\) for milk 46% and \({We}=97.9\), \({B}=0.68\), \({Oh}=0.38\) for 80 vol% glycerol
For milk droplets, no bouncing regime is observed, neither for very low We numbers where coalescence is found instead, nor for high impact parameters where the merged droplet is separated by stretching. As already anticipated, the complex macromolecular and colloidal composition of milk might lead to surface mechanisms at the collision interface which promote coalescence instead of bouncing as collision outcome. We carried out experiments with glycerol–water mixtures to compare milk with a reference liquid, which is reproducible and stable over time. Although in the literature there are examples of Newtonian droplet collisions for different concentrations, thus also for different Oh number, the aim is to carefully analyse the collision morphology.
Figure 13 shows the three regime maps for glycerol solutions with the phenomenological models for stretching separation (black continuous line) and reflexive separation (black dashed-dotted line) developed in this work for milk concentrates. Glycerol 40% vol has an Oh = 0.021, glycerol 60% vol an Oh = 0.64 and glycerol 80% an Oh = 0.38. As for milk concentrates, the Ashgriz and Poo (1990) models for water are also provided with a dashed line for stretching and a dotted line for reflexive separation. The model for bouncing by Estrade et al. (1999), with shape factor \(\chi _1=3.351\), is represented by the magenta continuous line.
The constants applied to the Jiang et al. model Jiang et al. (1992) and the modified Ashgriz and Poo model Ashgriz and Poo (1990) are fitted on data on water and milk concentrates. The results presented in the glycerol solution regime maps are not used for fitting the models. The model matches well with the experimental results that show the boundary between coalescence and stretching separation. As already discussed in 5.2, the onset of reflexive separation is underpredicted by the modified model of Ashgriz and Poo (1990), possibly due to the nonlinear behaviour of the critical Weber number with respect to the Ohnesorge number for \({Oh}\ge 0.04 .\)
The triple point is the intersection between the regimes of bouncing, coalescence and stretching separation. The Weber number of the triple point does not clearly change between the three glycerol maps. This point is located at \({We}\sim 30\) for all the maps. The corresponding impact parameter increases slightly with higher Ohnesorge number, from \({B}\sim 0.50\) (40 vol%) to \({B}\sim 0.57\) (60 vol%) to \({B}\sim 0.70\) (80 vol%), but the overlap in this area does not allow an accurate description of the triple point position. From Sommerfeld and Kuschel (2016), we are aware that the triple point prediction is difficult also for alcohols and oils because of the large scatter of data around the transition of the three regimes.
Bouncing occurs over the full range of impact parameters in the 40 vol% and 60 vol% glycerol regime maps, while the 80 vol% glycerol solution map shows coalescence for \({We}\sim 10\) and \({B}<0.15\). For even lower Weber numbers, it is expected that coalescence occurs, since the resistance against drainage from the gap between the droplets is substantially lower Qian and Law (1997), Li and Fritsching (2011). This region is the so-called coalescence with minor deformation at lower Weber numbers. Possibly due to the lower limit of the Weber number as a consequence of experimental limitations, which are common in the considered literature, this region is not found.
Glycerol droplets bounce at high Weber numbers only when the impact parameter is high. During the bouncing process, the surfaces deform by flattening. In this process, the initial kinetic energy of the interaction region is converted into surface energy. When the remaining energy is not sufficient to overcome the pressure force, the droplets will bounce apart. At constant Weber number, the initial kinetic energy of the interaction region decreases with increasing impact parameter due to a lower overlap of the droplet upon impact. Therefore, bouncing is still observed for high Weber numbers and high impact parameters.
If the impact parameter is not high enough and the relative velocity is relatively high, stretching separation occurs. As it was for milk, when the ratio between the initial kinetic energy, which stretches out the combined droplet, is higher than the surface energy of the interacting region, there is breakup. Moreover, also for glycerol the stretching separation regime moves towards higher We number when the viscosity is increased.
5.5 Comparison of milk and droplet collision dynamics
In Fig. 14, milk and glycerol collisions are compared for the same impact conditions. From our experiments, no remarkable differences are found with respect to the transition between coalescence and separation regimes.
The onset of reflexive separation for both liquids follows a similar trend. In accordance with other previous work, we can conclude that the curve of the Ashgriz and Poo (1990) model for reflexive separation does not accurately predict the boundary, but the relatively scattered data in this area allow only an approximate prediction.
The boundary between coalescence and stretching separation can be described reasonably well by the same phenomenological model and, as shown in Fig. 14, also the collision dynamics for glycerol solutions and milk concentrates are comparable for similar Weber numbers, impact parameters and Ohnesorge numbers.
Two main differences characterize the two liquids: milk has a complex macromolecular and colloidal structure and exhibits non-Newtonian behaviour, while glycerol has a simpler chemical structure and exhibits Newtonian behaviour (see Fig. 15). It is likely that the complex chemistry of milk at the droplet surface promotes coalescence. To fully understand this phenomenon, further investigations, with other possible reference liquids, are required.
6 Conclusions
The objective of this work was to experimentally investigate the effect of viscosity on binary droplet collisions in a spray dryer, in particular for milk concentrates. To investigate this effect, three milk concentrates with a wide range of viscosity values were used (20, 30 and 46% total solids content). The effect of viscosity was investigated by comparing the three regime maps.
The critical We number for reflexive separation increased with the Oh number. The kinetic energy is dissipated due to viscous flow and thus needs to be higher with higher viscosity to achieve reflexive separation. Similarly, the boundary between coalescence and stretching shifted to the right in the regime map with increasing Oh number.
The second objective of this study was to develop a phenomenological model, describing the collision regime boundaries in the (We, B) map as a function of, among other properties, the liquid viscosity. The experimental results show that the critical We number of reflexive separation can be described as a linear function of the Oh number, at least in the range of Oh numbers investigated for milk concentrates. The model by Ashgriz and Poo (1990) describing the boundary between reflexive separation and coalescence, without viscous dissipation energy effects, is extended by a horizontal translation to take into account the effect of viscosity. The model by Jiang et al. (1992), also taking the effect of viscosity into account, describes the boundary between coalescence and stretching separation and contains two fitting constants, generally determined in the literature by experimental results. These constants are determined based on a fitting method to the experimental data on milk concentrates. The adapted model describes the experimental data well, but slightly underpredicts the boundary for the 46% TS content milk concentrate.
Additionally, binary collision experiments with three aqueous glycerol solutions (40, 60 and 80 vol% glycerol in water) were performed to create glycerol regime maps with Oh numbers in the same range as the milk concentrate regime maps. The boundaries between coalescence and the two types of separation in the glycerol regime maps showed similar trends as in the milk regime maps. However, in contrast to collisions with milk concentrate droplets, glycerol droplets bounce at low collision kinetic energy or high impact parameters.
Finally, we demonstrated that the model proposed in this work for collisions of milk concentrate droplets is applicable to the glycerol regime maps too. Milk and glycerol exhibit similar collision behaviour and develop analogous collision morphologies. Unlike glycerol, milk collisions show no bouncing at any impacting condition and at any viscosity. Further investigation needs to be carried out on the complex colloidal chemistry of milk to investigate the mechanisms promoting coalescence rather than bouncing.
References
Anema SG, Li Y (2003) Association of denatured whey proteins with casein micelles in heated reconstituted skim milk and its effect on casein micelle size. J Dairy Res 70(1):73–83
Ashgriz N, Poo J (1990) Coalescence and separation in binary collisions of liquid drops. J Fluid Mech 221:183–204
Bienvenue A, Jiménez-Flores R, Singh H (2003) Rheological properties of concentrated skim milk: importance of soluble minerals in the changes in viscosity during storage. J Dairy Sci 86(12):3813–3821
Bird RB, Armstrong RC, Hassager O, Curtiss CF (1977) Dynamics of polymeric liquids, vol 1. Wiley, New York
Brenn G, Kolobaric V (2006) Satellite droplet formation by unstable binary drop collisions. Phys Fluids (1994–present) 18(8):087,101
Brenn G, Valkovska D, Danov K (2001) The formation of satellite droplets by unstable binary drop collisions. Phys Fluids (1994–present) 13(9):2463–2477
Bush JW, Hasha AE (2004) On the collision of laminar jets: fluid chains and fishbones. J Fluid Mech 511:285–310
Chandra S, Avedisian C (1991) On the collision of a droplet with a solid surface. In: Proceedings of the Royal Society of London A: mathematical, physical and engineering sciences, The Royal Society 432, pp 3–41
Chang YH, Hartel RW (1997) Flow properties of freeze-concentrated skim milk. J Food Eng 31(3):375–386
Chen X, Focke C, Marschall H, Bothe D (2016) Investigation of elementary processes of non-newtonian droplets inside spray processes by means of direct numerical simulation. In: Process-spray, Springer, Berlin, pp 3–51
Cheng NS (2008) Formula for the viscosity of a glycerol- water mixture. Ind Eng Chem Res 47(9):3285–3288
Connors KA (2001) 5.5 the phenomenological theory of solvent effects in mixed solvent systems. Handb Solv 281
Corredig M, Dalgleish DG (1999) The mechanisms of the heat-induced interaction of whey proteins with casein micelles in milk. Int Dairy J 9(3):233–236
Dai M, Schmidt DP (2005) Numerical simulation of head-on droplet collision: effect of viscosity on maximum deformation. Phys Fluids (1994–present) 17(4):041,701
Early R (1998) Technology of dairy products. Blackie Academic and Professional, London, UK
Estrade JP, Carentz H, Lavergne G, Biscos Y (1999) Experimental investigation of dynamic binary collision of ethanol droplets-a model for droplet coalescence and bouncing. Int J Heat Fluid Flow 20(5):486–491
Finotello G, Padding JT, Deen NG, Jongsma A, Innings F, Kuipers JAM (2017) Effect of viscosity on droplet-droplet collisional interaction. Phys Fluids 29(6):067,102
Focke C, Bothe D (2012) Direct numerical simulation of binary off-center collisions of shear thinning droplets at high weber numbers. Phys Fluids 24(7):59–80
Fontana AJ Jr, Schmidt SJ, Labuza TP et al (2008) Water activity in foods: fundamentals and applications, vol 13. John Wiley, Hoboken
Fritsching U (2016) Process-spray: functional particles produced in spray processes. Springer, Berlin
Gotaas C, Havelka P, Jakobsen HA, Svendsen HF, Hase M, Roth N, Weigand B (2007) Effect of viscosity on droplet-droplet collision outcome: experimental study and numerical comparison. Phys Fluids (1994–present) 19(10):102,106
Han Z, Parrish S, Farrell PV, Reitz RD (1997) Modeling atomization processes of pressure-swirl hollow-cone fuel sprays. Atomization Sprays 7(6):663–684
Hinrichs J (1999) Influence of volume fraction of constituents on rheological properties andheat stability of concentrated milk. Milchwissenschaft 54(8):450–454
Jenness R, Patton S et al (1959) Principles of dairy chemistry. John Wiley, New York
Jiang Y, Umemura A, Law C (1992) An experimental investigation on the collision behaviour of hydrocarbon droplets. J Fluid Mech 234:171–190
Kessler HG (2002) Food and bio process engineering. Dairy Technology. Verlag A, München, pp 56–96
Krishnan K, Loth E (2015) Effects of gas and droplet characteristics on drop-drop collision outcome regimes. Int J Multiph Flow 77:171–186
Kristensen D, Jensen P, Madsen F, Birdi K (1997) Rheology and surface tension of selected processed dairy fluids: influence of temperature. J Dairy Sci 80(10):2282–2290
Kurt O, Fritsching U, Schulte G (2007) Binary collisions of droplets with fluid and suspension particles. ILASS 2007:10–12
Kuschel M, Sommerfeld M (2013) Investigation of droplet collisions for solutions with different solids content. Exp Fluids 54(2):1–17
Larsson N, Orucoglu R (2013) The effect of age thickening in milkpowder production. Master' s thesis, KTH, School of Chemical Science and Engineering (CHE)
Li XG, Fritsching U (2011) Numerical investigation of binary droplet collisions in all relevant collision regimes. J Comput Multiph Flows 3(4):207–224
Madsen J (2006) Computational and experimental study of sprays from the breakup of water sheets. Aalberg University Esbjerg, Denmark
Mezger TG (2006) The rheology handbook: for users of rotational and oscillatory rheometers. Vincentz Network GmbH & Co KG, Hanover
Michalski M, Briard V (2003) Fat-related surface tension and wetting properties of milk. Milchwissenschaft 58(1–2):26–29
Mohr W, Brockmann C (1930) Surface tension measurements of milk. Milchwiss Forsch 10:72–95
Morison KR, Phelan JP, Bloore CG (2013) Viscosity and non-newtonian behaviour of concentrated milk and cream. Int J Food Prop 16(4):882–894
Motzigemba M, Roth N, Bothe D, Warnecke H, Prüss J, Wielage K, Weigand B (2002) The effect of non-newtonian flow behaviour on binary droplet collisions: vof-simulation and experimental analysis. Zaragoza 9:11
Mujumdar AS (2014) Handbook of industrial drying. CRC Press, Boca Raton
Munnannur A, Reitz RD (2007) A new predictive model for fragmenting and non-fragmenting binary droplet collisions. Int J Multiph Flow 33(8):873–896
Nitsche R (2011) Milk protein analysis with the agilent 2100 bioanalyzer and the agilent protein 80 kit. Agilent Technologies, Waldbronn, Germany
Planchette C, Hinterbichler H, Liu M, Bothe D, Brenn G (2017) Colliding drops as coalescing and fragmenting liquid springs. J Fluid Mech 814:277–300
Qian J, Law C (1997) Regimes of coalescence and separation in droplet collision. J Fluid Mech 331:59–80
Rosin P, Rammler E (1933) The laws governing the fineness of powdered coal. J Inst Fuel 7:29–36
Sharma A, Jana AH, Chavan RS (2012) Functionality of milk powders and milk-based powders for end use applicationsa review. Compr Rev Food Sci Food Saf 11(5):518–528
Snoeren T, Brinkhuis J, Damman A, Klok H (1984) Viscosity and age-thickening of skim-milk concentrate. Neth Milk Dairy J (Netherlands)
Solanki G, Rizvi S (2001) Physico-chemical properties of skim milk retentates from microfiltration. J Dairy Sci 84(11):2381–2391
Sommerfeld M, Kuschel M (2016) Modelling droplet collision outcomes for different substances and viscosities. Exp Fluids 57(12):187
Sommerfeld M, Lain S (2017) Numerical analysis of sprays with an advanced collision model. ILASS Europe 2017, 28th conference on liquid atomization and spray systems, 6-8 Sep 2017, Valencia, Spain
Takamura K, Fischer H, Morrow NR (2012) Physical properties of aqueous glycerol solutions. J Pet Sci Eng 98:50–60
Trinh B, Trinh KT, Haisman D (2007) Effect of total solids content and temperature on the rheological behaviour of reconstituted whole milk concentrates. J Dairy Res 74(1):116–123
van der Hoeven M (2008) Particle-droplet collisions in spray drying
Vélez-Ruiz J, Barbosa-Cánovas G (1998) Rheological properties of concentrated milk as a function of concentration, temperature and storage time. J Food Eng 35(2):177–190
Wadhwa N, Vlachos P, Jung S (2013) Noncoalescence in the oblique collision of fluid jets. Phys Rev Lett 110(12):124,502
Walstra P, Walstra P, Wouters JT, Geurts TJ (2005) Dairy Science and technology. CRC Press, Boca Raton
Westergaard V (2004) Milk powder technology: evaporation and spray drying. Niro A/S, Copenhagen
Willis K, Orme M (2000) Experiments on the dynamics of droplet collisions in a vacuum. Exp Fluids 29(4):347–358
Willis K, Orme M (2003) Binary droplet collisions in a vacuum environment: an experimental investigation of the role of viscosity. Exp Fluids 34(1):28–41
Zisu B, Schleyer M, Chandrapala J (2013) Application of ultrasound to reduce viscosity and control the rate of age thickening of concentrated skim milk. Int Dairy J 31(1):41–43
Acknowledgements
The authors gratefully acknowledge the financial support of this work by Tetra Pak CPS, Heerenveen, the Netherlands.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Finotello, G., Kooiman, R.F., Padding, J.T. et al. The dynamics of milk droplet–droplet collisions. Exp Fluids 59, 17 (2018). https://doi.org/10.1007/s00348-017-2471-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-017-2471-2