Boundary layer characterization and acoustic measurements of flow-aligned trailing edge serrations

Abstract

Trailing edge serrations designed to reduce airfoil self-noise are retrofitted on a NACA 0018 airfoil. An investigation of the boundary layer flow statistical properties is performed using time-resolved stereoscopic PIV. Three streamwise locations over the edge of the serrations are compared. An analysis of the results indicates that, while there is no upstream effect, the flow experiences significant changes as it convects over the serrations and toward its edges. Among the most important, a reduced shear stress and modifications of the turbulence spectra suggest beneficial changes in the unsteady surface pressure that would result in a reduction of trailing edge noise. Microphone array measurements are additionally performed to confirm that noise reduction is indeed observed by the application of the chosen serration design over the unmodified airfoil.

1 Introduction

Airfoil self-noise is known to be produced by different aeroacoustic mechanisms, an identification and description of which is available from Brooks et al. (1989). The noise caused by the convection of turbulent eddies over the sharp trailing edge of an airfoil is called turbulent-boundary-layer trailing edge (TBL-TE) noise. This source of noise is dominating in several noise-regulated industrial applications, such as wind turbines (Wagner et al. 1996; Pedersen et al. 2009), urging an investigation over its production mechanisms and mitigation techniques.

Theoretical formulations of TBL-TE noise for conventional straight trailing edges have been proposed using a number of approaches. Examples of these can be found in Amiet (1976), Chase (1972), Howe (1999) and Parchen (1998). An extension of the theory for variable trailing edge shapes has in addition been formulated by Howe (1991). Based on this solution, variable trailing edge shapes have been found to reduce the efficiency at which TBL-TE noise is produced. In particular, a serrated trailing edge, which is shaped as a series of sharp sawteeth, has been identified to be particularly promising for this objective (Howe 1991).

While serrated trailing edges have been acoustically measured in wind tunnels, and their noise reduction effects have been confirmed in Dassen et al. (1996), Moreau and Doolan (2013), Gruber et al. (2010) and Finez et al. (2011), Chong and Vathylakis (2015), the analytic prediction of Howe (1991) yields too optimistic noise reduction levels compared to the experimental observations ($\approx$12 dB compared to ${\lesssim}{7}\,{\hbox {dB}}$ seen in wind tunnel measurements, over a select frequency range). The analytical approach remains nevertheless a valuable starting point for serrations design, as well as being a powerful tool for understanding the baseline mechanisms of noise reduction. It is worth noting that Lyu et al. (2015) has later provided an alternative approach to the Howe (1991) model that includes the hydrodynamic interaction between adjacent serrations, obtaining results that are in better agreement with the noise reduction levels observed in wind tunnel experiments. Azarpeyvand et al. (2013) has further developed Howe’s theory to cover other trailing edge geometries mixing combs and sawtooth shapes, as well as sinusoidal variations over sawtooth baselines. These have been complemented by wind tunnel measurements in Gruber et al. (2013).

The promising results have made serrations an attractive option in the pursuit of reducing the noise from wind turbine blades. Field measurements have been performed, confirming that noise reduction can be obtained in large-scale applications. Examples of these can be found in Oerlemans et al. (2009) and Schepers et al. (2007). Several independent field tests have further been carried out by several industrial players, including LM Wind Power, with whom a full-rotor overall sound pressure level reduction of up to ${3}\,{\hbox {dB}}$ has been obtained (private communication with Jesper Madsen, Chief Engineer, Aerodynamics, LM Wind Power). The research on serration-retrofitted airfoils is thus critical in the pursuit of an improved and more reliable design, based on a scientific understanding of the underlying mechanisms of noise reduction of an unmodified airfoil by trailing edge serrations.

Two potential factors have been proposed that drive the noise reduction. The first is the modification of the flow and surface pressure by the physical presence of the serrations (Jones et al. 2010; Moreau and Doolan 2013; Chong and Vathylakis 2015), and the second leans on a change in the scattering of the surface pressure by the modification of the trailing edge geometry (Gruber 2012; Howe 1991). Despite the two potential factors being assessed, their weight in the final noise reduction is still unknown. The solution of this dichotomy remains critical, as the dominance of either can lead to different preferred optimization approaches for serration design. In this paper, the approach used to address this duality focuses on a characterization of the unsteady flow over the serration, of which the fluctuating pressure on the serration surface argued to be a direct consequence (Blake 2012).

An understanding of the surface pressure fluctuations is critical, as TBL-TE noise is the result of the scattering of surface pressure waves into acoustic pressure waves by the sharp edge, driven by the impedance discontinuity between the wall and the freestream. Nevertheless, while numerical studies such as those of Jones et al. (2010), Sandberg and Jones (2011), Jones and Sandberg (2012) and Arina et al. (2012) have provided field velocity and pressure solutions, as well as unsteady surface pressure information, obtaining the latter experimentally over serrations is difficult due to the relatively large physical size of available transducers with respect to the surface pressure structures, and to the physical thickness of the serrations themselves.

Workarounds have been implemented, for example in Gruber (2012) and Chong and Vathylakis (2015), where serrations have been cut into a flat plate placed at the lower side of a wind tunnel nozzle. In their study, the instrumented side is under a turbulent boundary layer, while the opposite side, from which the measurement instruments protrude, remains in a quiescent state. Although promising, the method cannot be used in airfoil applications due to the disturbances to the flow field that would be generated by the protrusion of microphones or pressure transducers.

On the other hand, advanced non-intrusive measurements techniques such as particle image velocimetry (PIV, Raffel et al. 2007) offer flow information with good temporal and spatial resolution. Studies of the flow field around serrations have been performed previously in Finez et al. (2011), Arce León et al. (2016) and Avallone et al. (2016) using PIV. In Arce León et al. (2016), time-averaged results are used to quantify the level of mean flow modification when serration-flow misalignment is prescribed by applying an angle of attack to the airfoil or setting the serrations with a flap angle. The results are considered in terms of the conditions assumed in Howe (1991), and ultimately concludes that misaligned serrations cause flow effects that are not contemplated in the analytic solution, yet are not enough to explain the discrepancies between the predicted and observed reduction levels, and changes in the acoustic spectra shape.

Gruber (2012) investigated serrations without a detailed focus on the level of flow misalignment. By using a highly cambered airfoil and serrations that protrude straight out from the angled trailing edge, it can be readily assumed that the condition of flow alignment is not met. Flow visualization using smoke has confirmed this in Gruber et al. (2011). In the research of Moreau and Doolan (2013), the condition of flow alignment is more closely achieved by mounting serrations at the trailing edge of a flat plate. Nevertheless, the relatively large angle (${12}^{\circ }$) on the upper side of the flat plate as it narrows to form the sharp trailing edge does not help to ensure that equal flow conditions over the upper and lower serration sides are obtained. The study further focuses on the reduction of tonal noise components due mainly to vortex shedding. A more detailed research on serrations, where flow alignment is obtained, is therefore missing. With this baseline, a more realistic measurement of the boundary layer properties and their change along the serration surface can be achieved without the effect of mean pressure differences between upper and lower surfaces.

Having detailed hydrodynamic information, an implementation of the so-called TNO-Blake prediction model for TBL-TE noise (Parchen 1998; Blake 2012) can further be applied to qualitatively approximate changes to the surface pressure. This model relies substantially on boundary layer information to approximate the noise emission by the scattering of the unsteady surface pressure at the trailing edge. Recent changes, provided by Stalnov et al. (2016), Bertagnolio et al. (2014) and Kamruzzaman et al. (2012), have further shown improvements in predicting TBL-TE noise by using modified boundary layer models and addressing anisotropy in the boundary layer turbulence. Even though an extension of the method to a variable trailing edge shape has not yet been proposed, the model itself can be used to produce a qualitative analysis of the unsteady pressure over the serration surface, and by extension, its scattering into noise at the edge.

The present study uses time-resolved stereoscopic PIV (Arroyo and Greated 1991) to obtain a 3-component planar vector field of the flow over thin trailing edge serrations retrofitted on a NACA 0018 airfoil. No incidence has been prescribed, in order to maintain a balance in the mean pressure between the serration sides, and a Reynolds number of 263,000 is achieved in an open test section wind tunnel. The results are evaluated with a modified TNO-Blake equation (Blake 2012) in order to qualitatively estimate streamwise changes in the surface pressure along the length of the serrations.

While a precise formulation for the noise emissions based on this equation is not possible, this research will expose important differences in the estimated surface pressure between the straight edge airfoil and the serrated edge airfoil. Additionally, streamwise locations of the latter are also observed and discussed.

In order to confirm that the adopted serrations are effectively reducing far-field broadband noise generated at the trailing edge, microphone array measurements are presented.

2 Experimental set-up

The experiments were conducted at the Delft University of Technology vertical wind tunnel (V-Tunnel). It has a contraction ratio of around 60:1. The turbulence intensity has been measured by Ghaemi et al. (2012) to be below 0.5% for a freestream velocity of ${10}\,{\hbox {m/s}}$ at the exit of a cylindrical nozzle of ${60}\,{\hbox {cm}}$ in diameter. In the present set-up, a square nozzle of ${40}\times {40}\,{\hbox {cm}^{2}}$ has been used with ${20}\,{\hbox {m/s}}$ and higher freestream velocities. The turbulence intensity has been verified by stereo PIV statistics to still stay at or below $1\%$ at the present regime.

A NACA 0018 airfoil, reference profile thickness for outboard sections of state-of-the-art wind turbine blades, has been manufactured into an aluminum wing of chord $C={20}\,{\hbox {cm}}$ and span of 40 cm, equal to the test section width. The model has been installed in an ad hoc prepared open test section with two long side plates to approximate the two-dimensional flow condition over most of the wing span.

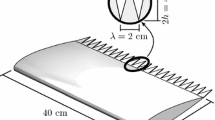
A modular trailing edge design in the airfoil allows inserts to be retrofitted while keeping the surface free from irregularities, as indicated in Fig. 1 (right). The insert used for this set-up is a sawtooth trailing edge serration model with teeth of $2h={4.0}\,{\hbox {cm}}$ length, or $0.2\,C$, and $\lambda = {2.0}\,{\hbox {cm}}$ width, or $\lambda = h$. These dimensions follow the recommendations for serration design of Gruber et al. (2011). In particular, it is suggested that the length required to achieve a noise reduction must comply with $2h\gtrsim \delta$, for $\delta$ the boundary layer thickness. In the present case $2h\approx 4\delta$, as will be discussed in Sect. 3.1.

The serrations are of flat-plate type, made of laser-cut steel, with a constant ${1}\,{\hbox {mm}}$ thickness throughout the span and length, equal to the nominal thickness of the unserrated airfoil trailing edge. At this thickness, they remain stiff with respect to any flow-induced vibration. A schematic of the airfoil and serration dimensions is shown in Fig. 1.

Fig. 1

Airfoil and serration dimensions and detail of the modular trailing edge (right)

All measurements were conducted at $\alpha = {0}^{\circ }$ angle of attack. A freestream velocity of ${20}\,{\hbox {m/s}}$ was chosen for the PIV measurements, resulting in a chord-based Reynolds number of 263,000. This velocity was selected as it is the highest with which time-resolved flow information can be gathered with the current high-speed PIV system. The acoustic measurements were conducted at speeds of 30, 35 and ${40}\,{\hbox {m/s}}$. In this case, the higher velocities were needed in order to distinguish the trailing edge noise from the background noise, especially for the reduced levels obtained when serrations were applied. The reconciliation between the PIV and acoustic measurement velocity differences is addressed in Sect. 3.3.

At the tested velocities, the boundary layer is forced to turbulent transition with randomly distributed roughness elements. The trip tape was constructed by an appropriate density of dispersed carborundum elements of ${0.6}\,{\hbox {mm}}$ nominal size, placed on a thin double-sided tape of ${1}\,{\hbox {cm}}$ width, following guidelines outlined in Braslow et al. (1966). The tape, streamwise-centered at $0.2\,C$, spans the entirety of the airfoil. A stethoscope probe has been used to verify that the boundary layer was tripped and that it remains turbulent downstream until the trailing edge.

2.1 Stereoscopic PIV

Stereoscopic particle image velocimetry (Arroyo and Greated 1991) has been employed to obtain measurements of the three velocity components in a plane aligned with the flow field. The flow was seeded with tracer particles from an evaporated glycol-based solution called SAFEX, producing liquid droplets of about ${1}\,{\upmu \hbox {m}}$. Illumination of the particles was provided by a Quantronix Darwin Duo double cavity Nd:YLF laser, which has an energy of $2\times {25}\,{\hbox {mJ}}$ at 1 kHz. Two high-speed Photron Fastcam SA1 cameras were used, equipped with $1024\times {1024}\,{\hbox {px}}$ resolution CMOS sensors with a pixel pitch of ${20}\,{\upmu \hbox {m}/\hbox {px}}$ and a digital resolution of 12 bit. Two Nikon NIKKOR macro-objective lenses of 105-mm focal length at an aperture of f/5.6 were used for the two cameras, respectively, mounted one perpendicular to the flow field and the second one at a relative angle of ${35}^{\circ }$ with respect to the first. With an overall distance of about ${40}\,{\hbox {cm}}$, the resulting magnification factor is about 0.40, entailing that the particle image on the sensor is limited by diffraction to about ${10}\,{\upmu \hbox {m}}$ (Meinhart and Wereley 2003).

To avoid the problem of peak-locking, potentially present for the available ${20}\,{\upmu \hbox {m}/\hbox {px}}$ pixel pitch of the cameras, defocusing is applied to the raw images by slightly displacing the focus plane from the laser one (Westerweel 1997). The procedure allows keeping the particle images in the range between 1 and 1.5 px and to obtain a stochastic distribution of round-off errors in the computed velocity field.

Since the stereoscopic PIV method requires the cameras to be at an angle with respect to the measurement plane, a Scheimpflug adaptor was used to correct the sensor measurement plane misalignment. The final field of view is the calibrated and dewarped combination of the images of both cameras. A resulting area of $2\times {5}\,{\hbox {cm}^{2}}$ was obtained by cropping the sensor to $512\times {1024}\,{\hbox {px}}$, permitting the same field of view for both time-resolved data and statistics, with a digital imaging resolution of about ${20}\,{\hbox {px}/\hbox {mm}}$. A sample capture of one of the cameras is shown seen in Fig. 2.

Fig. 2

Single camera capture of the airfoil trailing edge side (left), serrations and the tracer particles, illuminated by the laser. The flow goes from left to right. An instantaneous vorticity field from the PIV cross-correlation result is overlaid for illustration purposes

The triggering of the camera shutter and the firing of the laser pulse was controlled by a LaVision HighSpeed Controller. The capture sequence command and data acquisition, along with the data processing, was performed using the LaVision software DaVis8. Two acquisition set-ups were used to capture either time-resolved or uncorrelated flow samples for averaging. Their respective configurations are detailed in the following two subsections. For both, a multi-pass stereo cross-correlation was applied with a final window size of $16\times {16}\,{\hbox {px}}$ (or $0.8\times {0.8}\,{\hbox {mm}^{2}}$). The adjacent windows were overlapped by 75% such that the flow is sampled with a spatial resolution of ${0.8}\,{\hbox {mm}}$ and a vector spacing of ${0.2}\,{\hbox {mm}}$.

Fig. 3

PIV set-up indicating the two camera locations and laser sheet formation with respect to the wind tunnel open test section and the airfoil. The circular-to-square nozzle exit conversion is shown for illustrative purposes

A view of the PIV set-up is shown in Fig. 3. The cameras are located on the side of the airfoil, one perpendicular to the laser sheet and another above it, as previously mentioned. The laser is fired from the side and oriented perpendicular to the airfoil surface by means of a mirror. It is formed into a sheet of about ${1}\,{\hbox {mm}}$ thickness in the field of view region using optical lenses. The bottom part of the wind tunnel nozzle corresponds to the contraction from the tunnel circular exit of ${60}\,{\hbox {cm}}$ to the ${40}\times {40}\,{\hbox {cm}^{2}}$ test section nozzle exit, of which an approximate cutout is illustrated here. The side plates for this set-up are made of Plexiglas to allow optical access for the cameras to the region of interest.

For the serrated edge, three spanwise locations were measured at planes normal to the z axis. A schematic of these locations is shown in Fig. 4, along with the orientation of the coordinate system and the location of its origin. The x axis is oriented parallel to the airfoil chord in the streamwise direction and located at the serration median line of the serration and its root. The z axis is oriented in the spanwise direction, and the y axis is in the wall-normal direction. An auxiliary definition for the orientation of the x and y axes will be given below in Sect. 3.1 for wall-normal measurements over the airfoil surface. This becomes necessary to correct for the difference in angle between the airfoil and the serration surfaces, and adhere to the definition for the boundary layer measurements. The measurement planes are located spanwise in the serration-width normalized locations $z/\lambda =0, 0.25$ and 0.5.

Fig. 4

Wall-normal measurement plane locations over the serration surface. The y axis is positive out-of-plane

2.1.1 Acquisition of the uncorrelated dataset

For simplicity, this set-up will be referred to as the time-averaged measurement for the remainder of the paper. The time separation between image pairs was chosen to be $\Delta t = {50}\,{\upmu \hbox {s}}$, yielding a particle image displacement of approximately 15 pixels in the freestream. A minimum distance to the wall of around $y^+ \approx 10$ was achieved, limited mainly by the finite digital resolution obtained with the set-up, as discussed in the results Sect. 3.1. An acquisition frequency of ${250}\,{\hbox {Hz}}$ was chosen, ensuring that all vector fields are uncorrelated at this flow speed. In total, 2000 time instances were captured per case, for a total of ${8}\,\hbox {s}$ of measurement time.

2.1.2 Time-resolved sample acquisition

For the time-resolved sample acquisition, a continuous set of images is captured for which each individual image serves as the cross-correlation pair for the following time instance. For this purpose, the repetition rate of each of the laser cavities was set to 5000 Hz, while the pulse separation time was set to ${100}\,{\upmu \hbox {s}}$. Being the pulse separation time half with respect to the repetition rate, the raw images can been re-shuffled in order to obtain a time-series of about 10,100 particle images at 10,000 Hz. With this acquisition frequency, a particle displacement of around ${24}\,{\hbox {px}}$ in the freestream was achieved for the ${20}\,{\hbox {m/s}}$ flow velocity (about double the one used for statistics).

2.1.3 Uncertainty analysis for the PIV method

A linear propagation approach (Stern et al. 1999) was used to estimate the typical measurement uncertainty. It was verified a-posteriori using the statistical method introduced in Wieneke (2015).

Bias errors occurring to peak-locking (Westerweel 1997) happen when the particle diffraction spots are imaged with less than a pixel on the camera sensor. As mentioned in the experimental set-up paragraph, the source is thus alleviated by following the technique proposed in Raffel et al. (2007), wherein it is suggested that a slight de-focusing of the images by the lens can bring the apparent particle size to above ${1}\,{\hbox {px}}$. A histogram of the particle displacement is provided in Fig. 5 and shows the success of this approach, giving no evidence of peak-locking. Here, the decimals of the measured velocity magnitudes, $U - \lfloor U \rfloor$, where $\lfloor \cdot \rfloor$ is the floor function, are binned into a histogram, which would show a large deviation toward one or more values, if a peak-locking error would dominate. The line plot represents the cumulative distribution of the binned decimal occurrences, showing a very close approximation to the ideal result.

Fig. 5

Evaluation of the presence peak-locking error by means of a decimal distribution histogram and a cumulative distribution of binned decimal counts

Further, the finite spatial resolution of the resulting velocity fields may limit the capture of flow structures. With the applied multi-pass cross-correlation algorithm, and the application of window deformation, the amplitude of the fluctuations is measured with less than 5% modulation, for window sizes smaller than 0.6 times the characteristic structure length scale (Schrijer and Scarano 2008). Having a window size of $0.8\times {0.8}\,{\hbox {mm}^{2}}$, as specified earlier, flow structures down to ${1.2}\,{\hbox {mm}}$ can thus be measured within 95% accuracy.

An iterative self-calibration procedure was applied to further improve the fitting of the captured planes from the initial location-based calibration, which is based on a known three-dimensional target. The application of the two calibration procedures helps alleviate further aspects such as the lens distortion. A final polynomial fitting used for the mapping of the images is implemented within DaVis and iterated on the raw images, yielding a disparity vector of less than ${0.10}\,{\hbox {px}}$ after self-calibration, considered satisfactory to carry out the stereo cross-correlation (Raffel et al. 2007).

The random errors in the measurement domain have been found to vary with less than 1% in the freestream and around 3% in the inner boundary layer region. The method used to approximate these numbers has been based on the work of Wieneke (2015).

The mean velocity and velocity root-mean-square, or rms, of the fluctuations carry uncertainties that are dependent on the size of the statistical sample. For the present case, the error in the mean velocity reduces to $0.05\%\, {\overline{U}}$, and on the rms to $2\%\, U_{\text {rms}}$.

2.2 Microphone array

Microphone arrays consist of a series of microphones distributed in a particular configuration and are useful tools for sound source localization (Mueller 2002; Benesty et al. 2008). These devices can be used for studying both stationary sources, for example in wind tunnels (Mueller 2002; Sijtsma 2010), or moving ones, such as aircraft flyovers (Merino-Martinez et al. 2016a, b; Snellen et al. 2015).

Acoustic images depicting the estimated locations and Sound Pressure Level (SPL) of the sound sources can be obtained by applying a beamforming algorithm to the acoustic data of the array and considering a scan grid of potential sound sources. These algorithms are based on the phase delays between the emission of the sound at the considered source location and the received signal at each microphone in the array.

There are several beamforming methods available, but the most widely used for aeroacoustic experiments is the delay-and-sum beamforming, also known as conventional frequency domain beamforming (Johnson and Dudgeon 1993; Sijtsma 2010), due to its simplicity, robustness and low computational demand. By evaluating a discrete Fourier transform of the data, an analysis of the frequencies of interest is possible. Moreover, this method provides continuous results when applied to distributed sources (such as trailing edge noise), unlike most deconvolution methods which show instead misleading spots (Dougherty 2014).

For this experiment, microphone array measurements have been employed to quantify the noise reduction capabilities of the adopted serration. An array with 64 microphones and of an effective diameter, D, of ${0.9}\,{\hbox {m}}$ was used, arranged in a multi-arm logarithmic spiral configuration (Mueller 2002; Pröbsting et al. 2016), as shown in Fig. 6. The array was placed ${1.26}\,{\hbox {m}}$ away from the airfoil in the direction normal to the mean camber plane of the airfoil, as illustrated in Fig. 7. The center of the array was aligned in the streamwise direction with the root of the serrations at the trailing edge.

Fig. 6

Microphone distribution of the array. Coordinates are shown in the airfoil system

Fig. 7

Sideways view of the set-up used for the acoustic measurements. The microphone array can be seen on the left of the test section. The front wooden side plate is rendered semi-transparent to indicate the location of the airfoil

The test section was modified from that described in the PIV set-up in order to have longer side plates, terminating ${0.7}\,{\hbox {m}}$ downstream of the airfoil trailing edge. Furthermore, the airfoil leading edge is separated ${0.5}\,{\hbox {m}}$ from the nozzle exit. These measures helped to separate the extraneous noise sources coming from the nozzle and the downstream edges of the side plates from the airfoil trailing edge noise source.

The sampling frequency used was 50 kHz, and the selected sound frequency range of interest extended from 1 to ${5}\, {\hbox {kHz}}$. For each measurement, a recording time of ${60}\, {\hbox {s}}$ was employed. The acoustic data was averaged using time blocks of 2048 samples ($\Delta t={40.96}\,{\hbox {ms}}$) for each Fourier transform and windowed using a Hanning weighting function with 50% data overlap. With these values, the frequency resolution for the source maps is ${24.41}\,{\hbox {Hz}}$. The averaged cross-spectral matrix required for beamforming was obtained after cross-correlating the microphones signals. The expected error (Brandt 2011) in the estimate for the cross-spectrum is, therefore:

$$\begin{aligned} \varepsilon _{r} = \sqrt{\frac{\Delta t}{T_{\text {meas}}}}=2.6\%. \end{aligned}$$

(1)

Considering a normal Gaussian distribution for the measurements (Brandt 2011), the spectral estimate 95% confidence interval is:

$$\begin{aligned} {\hat{G}}_{xx}(1-2\varepsilon _{r})\le G_{xx} \le {\hat{G}}_{xx}(1+2\varepsilon _{r}). \end{aligned}$$

(2)

With the normalized random error calculated in Eq. (1), we obtain:

$$\begin{aligned} 0.948\, {\hat{G}}_{xx}\le G_{xx} \le 1.052\, {\hat{G}}_{xx}\,, \end{aligned}$$

where ${G}_{xx}$ and ${\hat{G}}_{xx}$ are the true and the measured values of the cross-spectrum, respectively.

The rectangular scan grid used for beamforming covered the expected area of noise generation, ranging from $z={-0.22} \,{\hbox {m}}$ to $z={0.22} \,{\hbox {m}}$ in the spanwise direction and from $x={-0.7} \,{\hbox {m}}$ to $x={0.3} \,{\hbox {m}}$ in the streamwise direction, according to the axes defined in Fig. 4, with a distance between grid points of ${1}\,{\hbox {mm}}$. Therefore, the scan grid covered the whole airfoil and went from the nozzle exit until ${0.3} \,{\hbox {m}}$ after the trailing edge using $441\times 1001$ grid points.

The lower boundary of the minimum angular distance at which two different sources can be separated using an array of circular aperture of diameter D can be estimated using the Rayleigh criterion (Lord Rayleigh FRS 1879):

$$\begin{aligned} \varphi =1.22 \frac{c}{f\,D}. \end{aligned}$$

(3)

For the current experimental set-up, the minimum angular distance for the highest frequency considered in this analysis (${5}\,{\hbox {kHz}}$), considering $c={340}\,{\hbox {m/s}}$, is $\varphi ={0.092}\,{\hbox {rad}}$. Thus, the minimum resolvable distance, R, at a distance from the array r of ${1.26} \,{\hbox {m}}$ is $R=r\tan {\varphi }\approx {0.12} \,{\hbox {m}}$. Therefore, the selected spacing between grid points is approximately 120 times smaller than the Rayleigh’s limit distance at that frequency.

Because trailing edge noise is supposed to be a distributed sound source, the source maps were integrated over an area extending from $z={-0.1} \,{\hbox {m}}$ to $z={0.1} \,{\hbox {m}}$ and from $x={-0.06} \,{\hbox {m}}$ to $x={0.06} \,{\hbox {m}}$ (see Fig. 29). This section was chosen to minimize the contribution from extraneous sound sources, while still containing a representative part of the trailing edge (Pagani et al. 2016). The beamforming results in that area were normalized by the value of the integral of a simulated point source of unitary strength placed at the center of the area of integration, evaluated within the same spatial boundaries (Sijtsma 2010). This process was then repeated for each frequency of interest to obtain the acoustic frequency spectra of the trailing edge.

Each microphone was previously calibrated using a pistonphone which generates a ${250}\,{\hbox {Hz}}$ signal of known amplitude. Moreover, the performance of the array itself was assessed and calibrated by using tonal sound generated with a speaker at a known position emitting at several single frequencies: 500, 1000, 2000, 3000, 4000 and ${5000}\,{\hbox {Hz}}$. The SPLs at the center of the array were also measured with a calibrated TENMA 72-947 sound level meter. Therefore, the microphone array was calibrated in both source position and strength detection.

The effect of the shear layer in the acoustic measurements (Amiet 1975) was neglected due to the small angle (<10$^{\circ }$) between the center of the array and the scan area of interest and the considerably low flow velocities employed in this experiment (Salas and Moreau 2016).

3 Results

A study of the results, together with an analysis of the quantities relevant for the noise generation, is here presented. First, a characterization of the boundary layer is shown based on the time-averaged PIV measurements. This is done in order to identify both the effect that the serrations have on the flow directly upstream of the trailing edge, and the mean flow and turbulence parameters pertaining to the flow as it convects over downstream locations of the serration edge.

The statistical description of the flow field in terms of average velocity and Reynolds stresses indicates which regions, within the boundary layer, exhibit larger levels of turbulence intensity. Nevertheless, the correlation between a change in the latter and the pressure fluctuations at the object surface remains complex.

To study such a link, the results will then focus on the elements of the TNO-Blake model based on results obtained from the time-resolved PIV measurements, with the objective of providing a qualitative comparison between the flow at three different locations over the serration edge, and the straight edge. This is done to estimate the level of modification that the flow experiences and evaluate a potential correlation with the noise reduction mechanism of the serrations.

Lastly, the results of the acoustic measurements are presented with the purpose of confirming and quantifying the noise reduction effects that this serration design offers when retrofitted on the used airfoil profile.

3.1 Mean flow characterization of the turbulent boundary layer

In the present section, the mean flow and turbulence statistics of the boundary layer are introduced. Focus is placed on establishing whether there is a measurable effect of the serrations immediately upstream of $x/2h=0$, and on the way the flow in the boundary layer evolves along the serration surface until it encounters its edge at different downstream locations.

Time-averaged measurements are taken with stereoscopic PIV. Data are presented in the wall-normal direction at different streamwise locations over the surface of the airfoil and the serration tooth. Note that, to adhere to the definition of the boundary layer, the wall-normal lines over the airfoil surface and over the serration surface are not parallel. For simplicity, the defined coordinate system will also be rotated accordingly, as indicated in the schematic of Fig. 8, such that y always points in the local wall-normal direction, and $u = \overline{u} + u'$, is the local wall-parallel component of U, where $\overline{u}$ and $u'$ are the time average and fluctuating parts of the flow according to the Reynolds decomposition.

Fig. 8

Schematic of the boundary layer over the airfoil (angled surface on the left) and the serration surface

The streamwise locations are picked ${1}\,{\hbox {mm}}$ ($0.025\, x/2h$) upstream of the respective trailing edge, mainly to avoid the directional ambiguity carried by the vertex between the airfoil and the serration tooth at $x/2h = 0$. This choice of translation in x is kept in all locations for consistency. For simplicity, the $x/2h = -0.025$ will still be referred to as the airfoil trailing edge and written as $x/2h=0$ in the rest of this paper. The locations $x/2h = -0.025, 0.475$ and 0.975, along the serration trailing edge, will be referred to as the serration trailing edge and noted as $x/2h = 0, 0.5$ and 1.0.

To analyze the boundary thickness, the surface-parallel edge velocity, $u_{\mathrm{e}}$, is taken as the velocity at the wall-normal location $y_\delta$ at which the spanwise vorticity, integrated from the closest available wall-normal location, $y_\text {min}$ to $y_\delta , -\int _{y_{\text {min}}}^{y_\delta }\omega _z\left( y \right) \,\mathop {}\!\mathrm {d}y$, stabilizes. This method offers an accurate way to determine the boundary layer edge by virtue of the values of $\omega _z$ being negligibly small beyond it (see Spalart and Watmuff 1993; Balint et al. 1991). The establishment of $u_{\mathrm{e}}$ in this way is preferable over assuming the freestream velocity from the wind tunnel pitot tube measurements, as small deviations (±1%) are expected in the mean flow freestream velocity between different runs, causing variations in the boundary layer locations.

First, wall-normal results at $x/2h=0$ are presented for the straight edge and the 3 spanwise locations for the serrated edge: $z/\lambda = 0, 0.25$ and 0.5. The objective is to establish whether the serration has any measurable effect on the flow close upstream to it. Figure 9 shows the results obtained for the mean streamwise velocity, ${\overline{u}}$. Differences along the wall-normal profile between the straight edge and the serration, or spanwise locations of the latter, are practically absent.

Fig. 9

Wall-normal boundary layer profiles of $\overline{u}/u_{\mathrm{e}}$ at $x/2h=0$

Table 1 Measures of boundary layer thickness at $x/2h =0$

The resulting boundary layer thickness values are given in Table 1 for the different serrated edge spanwise locations and for the straight edge, along with the results from the XFOIL (Drela 1989) simulation on the latter. The values found from the PIV measurements on the straight edge airfoil show a good approximation to the ones reported by XFOIL. As expected from Fig. 9 and the discussed similarity of the ${\overline{u}}$ wall-normal profiles, the values of $\delta _{99}, \delta ^*$ and $\theta$ (respectively, the boundary layer thickness at 99% of the edge velocity, $u_{\mathrm{e}}$, the displacement thickness, and the momentum thickness) are also similar for all measurements, with $\delta _{99}$ having a variation range of $\pm {0.25}\,{\hbox {mm}}, \delta ^*$ of $\pm {0.05}\,{\hbox {mm}}$, and $\theta$ also of $\pm {0.05}\,{\hbox {mm}}$. In the remainder of the article, if not explicitly indicated, $\delta$ will refer to $\delta _{99}$.

The non-dimensional boundary layer profile is shown in Fig. 10 for the resolved vector field above the wall, $y^+>10$. It shows a departure from the log-law expected from a flat plate boundary layer measurement, and instead follows the trend expected for a boundary layer in an adverse pressure gradient (Nagano et al. 1998; Lee and Sung 2008), which is the case at this location over the airfoil surface.

Fig. 10

Non-dimensional boundary layer profile at $x/2h=0$. The dashed lines show the law of the wall and log-law

The skin friction coefficient, defined as $C_f= \mu \left( \partial u / \partial y \right) _{y=0}$, where $\mu$ is the fluid dynamic viscosity, is a guide to the general shape of the boundary layer. It will be discussed later (Sect. 3.2.2) that the intensity of the mean pressure at the surface is found to be especially sensitive to the shear experienced in the boundary layer, for which $C_f$ is an indicator. The direct calculation of $C_f$ is impossible due to the absence of flow data close enough to the wall. Instead, the results presented in Fig. 10 use an estimation of $C_f$ based on a best fit of the data against the log-law. The value found that best collapses the data (allowing for an expected deviation due to the adverse pressure gradient) is found to be approximately $C_f = 1.5\times 10^{-2}$. An XFOIL simulation of the same set-up yields a value of $C_f = 1.87\times 10^{-2}$ at the same streamwise location, $x/2h=-0.025$ (or $x/C = -0.05$). The $C_f$ value of $1.5\times 10^{-2}$ in the XFOIL simulation is reached instead slightly downstream at a streamwise location of $x/2h = -0.14$ (or $x/C = -0.028$). This represents a small deviation of around $0.03\, C$ or $0.11 \, 2h$. The approximation of the friction coefficient is thus considered satisfactory and will be examined later to evaluate its downstream evolution.

The wall-normal profiles of $u'_{\text {rms}}$ and $v'_{\text {rms}}$ at $x/h=0$ are presented in Figs. 11 and 12. Only slight differences are observed between the different locations of the serrated edge and the straight edge. The $u'_{\text {rms}}$ shows higher values, slightly above or around $0.09\, u_{\mathrm{e}}$, at locations near the surface, at around $y/\delta = 0.2$–0.3 The values of $u'_{\text {rms}}$ rapidly decline, reaching an asymptote of around $0.01\, u_{\mathrm{e}}$ by $y \approx 1.1 \delta$.

Fig. 11

Wall-normal profiles of $u'_{\text {rms}}/u_{\mathrm{e}}$ at $x/2h=0$

Fig. 12

Wall-normal profiles of $v'_{\text {rms}}/u_{\mathrm{e}}$ at $x/2h=0$

Values of $v'_{\text {rms}}$ show the same trend as $u'_{\text {rms}}$, but with a lower maxima of around $0.05\, u_{\mathrm{e}}$. The maxima happen at around the same wall-normal location as for $u'_{\text {rms}}$, and the decline is seen to reach minima slightly above that for $u'_{\text {rms}}$, in this case being closer to $y\approx 1.2\delta$.

Having discussed the mean flow properties of the wall-normal data at the $x/2h=0$ location, it is established that the serrations have a negligible effect on the flow immediately upstream. The same analysis will now be applied to the 3 streamwise trailing edge locations of the serrations, at $x/2h = 0, 0.5$ and 1.0.

The measured ${\overline{u}}$ is shown in Fig. 13. Contrary to what was discussed for $x/2h = 0$ in Fig. 9, the velocity profiles seen here for the different cases vary significantly. The straight edge case, and the serration at $x/2h = 0$, are at the same locations as presented before and are included here to facilitate the comparison with the locations further downstream. As the boundary layer develops, the ${\overline{u}}$ profile exhibits an increase in velocity.

Fig. 13

Wall-normal profiles of ${\overline{u}}/u_{\mathrm{e}}$ at different spanwise trailing edge locations of the serration and the straight edge

Figure 14 provides evidence that the two downstream locations agree more closely with the log-law than the previously discussed measurements at $x/2h=0$. A good fit is found between $20<y^+<100$ for $x/2h = 0.5$, and between $50< y^+ < 150$ for $x/2h = 0$. These two profiles also fit closer to non-adverse pressure gradient conditions, from which the measurements at $x/2h=0$ deviate considerably, as was discussed above. The approximation of $C_f$ for $x/2h = 0.5$ yields a value of $C_f = 2.6\times 10^{-2}$ , and for $x/2h=1$, $C_f = 3.3\times 10^{-2}$. Again, for both the serrated and straight edge at $x/2h = 0$, $C_f$ was established earlier to be $1.5\times 10^{-2}$.

Fig. 14

Non-dimensional boundary layer profile measured at different spanwise trailing edge locations of the serration and the straight edge. The dashed lines show the law of the wall and log-law

It can be concluded that the skin friction coefficient increases for downstream locations of the serration edge, and is larger than that of the straight edged airfoil, approximately doubling by the time the flow reaches the tip of the serration. This directly relates to an increase in the boundary layer shear observed near the wall. The velocity shear is later reduced after $y/\delta \approx 0.1$, as confirmed by the mean flow profiles in Fig. 13. This reduced shear in the middle and upper boundary layer, thanks to the lower skin friction of the lower boundary layer which has allowed a larger velocity compared to the same wall-normal locations of the $x/2h=0$ measurements, spans a larger extent of the boundary layer. It will be shown later that, according to Eq. (4), this change ascribes to an expected beneficial change in the qualitative mean pressure values at the surface.

The measured boundary layer thickness parameters for these trailing edge locations are shown in Table 2. The $\delta _{99}$ values appear to shrink downstream, becoming 10% thinner when measured over the tip of the serration at $x/2h=1$ than when done so over $x/2h=0$, but it is very similar between the former and $x/2h=0.5$. The values of $\delta ^*$ and $\theta$ show only small differences downstream.

Table 2 Measures of boundary layer thickness at the trailing edge of the specified spanwise locations

The rms measurements of $u'$ and $v'$ are shown in Figs. 15 and 16. For $u'_{\text {rms}}$, the maxima decrease at trailing edge locations downstream of $x/2h=0$, from around $u'_{\text {rms}}/u_{\mathrm{e}} = 0.095$ to $u'_{\text {rms}}/u_{\mathrm{e}} = 0.085$. The locations of the maxima of $x/2h = 1$ are higher than for the rest of the locations, and stand around $y/\delta \approx 0.4$ instead of between $y/\delta \approx 0.2$ and 0.3. The lower values of $u'_{\text {rms}}$ for $x/2h = 1$ and 0.5 persist at the same wall-normal locations up to around $y/\delta = 1.2$, showing differences of around $u'_{\text {rms}}/u_{\mathrm{e}} = 0.02$ compared to the serrated edge at $x/2h=0$ and the straight edge. The measurement of $v'_{\text {rms}}$ shows the trailing edge location at $x/2h = 0.5$ to have a larger rms than the rest of the presented locations, which is unexpected based on the evolution of the boundary layer downstream of the airfoil.

Fig. 15

Wall-normal profiles of $u'_{\text {rms}}/u_{\mathrm{e}}$ at different spanwise trailing edge locations of the serration and the straight edge

Fig. 16

Wall-normal profiles of $v'_{\text {rms}}/u_{\mathrm{e}}$ at different spanwise trailing edge locations of the serration and the straight edge

3.2 Turbulence statistics and qualitative analysis of surface pressure

In order to establish the effect that the observed boundary layer properties have on the surface pressure, the time-resolved PIV dataset is used here to characterize the different elements of the TNO-Blake surface pressure approximation (Blake 2012),

$$\begin{aligned} {\varPi }_p\left( \omega \right)= & {} \frac{4\pi \rho ^2}{{\varLambda }_{p|z}\left( \omega \right) } \int ^{\delta }_0 {\varLambda }_{y|vv}\left( y \right) U_{\mathrm{c}} \left( y \right) \left[ \frac{\partial u\left( y \right) }{{\hbox {d}}y} \right] ^2\nonumber \\&\times \frac{{\overline{v}}^2\left( y \right) }{U^2_{\mathrm{c}}\left( y \right) } {\varPhi }_{vv}\left( k_x, k_z=0 \right) e^{-2|k|y } \mathop {}\!\mathrm {d}y. \end{aligned}$$

(4)

Here $\rho$ refers to the fluid density, ${\varLambda }_{y|vv}$ refers to the wall-normal integral length scale taken over the flow component $v, U_{\mathrm{c}}$ refers to the wall-normal-dependent convection velocity magnitude, ${\varPhi }_{vv}\left( k_x = \omega /U_{\mathrm{c}}\left( y \right) , k_z=0 \right)$ refers to the wavenumber spectral density of the v flow component where k is the flow component-dependent wavenumber. It can be shown that only $k_x = \omega / U_{\mathrm{c}}\left( y \right)$ contributes to the radiation at frequency $\omega$ (Bertagnolio et al. 2014). An analysis of the wall-normal and streamwise dependence of these values will be given below and the results will be summarized in Sect. 3.2.5. The term ${\varLambda }_{p|z}$ is the spanwise surface pressure integral length scale and is relevant to get a final approximation to ${\varPi }_p$. Unfortunately, as discussed in the introduction, ${\varLambda }_{p|z}$ is technically impossible to quantify in this case due to the unavailability of transducers thin enough for these serrations and is therefore left out of this discussion.

3.2.1 Vertical integral length scale

The vertical integral length scale results, shown in Fig. 17, are calculated as (Kamruzzaman and Lutz 2011)

$$\begin{aligned} {\varLambda }_{y|vv}\left( y\right) = \int _{0.2\delta }^{2\delta } R_{vv}\left( y,\xi _y\right) \mathop {}\!\mathrm {d}\xi _y\,, \end{aligned}$$

(5)

where

$$\begin{aligned} R_{vv} = \frac{\overline{v\left( y \right) v\left( y+\xi _y \right) }}{\sqrt{v\left( y \right) v\left( y+\xi _y \right) }} \end{aligned}$$

(6)

is the correlation coefficient between the signal of v at the wall-normal location y, and that separated by $\xi _y$ in the wall-normal direction. The resulting $R_{vv}$ values for the serrated streamwise location $x/2h = 1$ are presented in Fig. 18 for reference. This results in a more complex prediction of the constructive and destructive interference of the local scattered pressure waves along the edges.

Fig. 17

Wall-normal values of ${\varLambda }_{y|vv}$

Fig. 18

Values of $R_{vv}$ for the serrated-case streamwise location $x/2h = 1$

Overall, a wall-normal variation in ${\varLambda }_{y|vv}$ of around ${3}\,{\hbox {mm}}$ is experienced for all cases, showing similar values between the streamwise measurement locations and an overall increase in integral length scale at locations further from the wall, indicating an increase in turbulent structure size as expected. A similar trend has been observed in Kamruzzaman et al. (2009). There is a difference of values between the cases along the same wall-normal location of no more than ${0.5}\,{\hbox {mm}}$, with the downstream location initially showing lower values, and exhibiting a crossover at $y/\delta =0.6$. The $x/2h=0.5$ location follows the upstream location, either serrated or unserrated, more closely. This similarity suggests that streamwise surface pressure variations are weakly driven by this factor.

3.2.2 Convection velocity and mean velocity shear

A wide variety of methods have been proposed to approximate the convection velocity, a good summary of which is given in Renard and Deck (2015). In the present study, a spectral approach is taken based on Romano (1995) and used in Chong and Vathylakis (2015) to obtain the surface pressure convection velocity. It is obtained using the streamwise cross-spectral density results and evaluating the slope of the phase spectrum over a two-point measurement separation $\xi _x$, as

$$\begin{aligned} u_{\mathrm{c}}\left( y \right) = 2\pi \xi _{x}\frac{\mathop {}\!\mathrm {d}f}{\mathop {}\!\mathrm {d}\phi \left( y,f,\xi _x \right) }\,, \end{aligned}$$

(7)

where $\phi \equiv \arctan \left[ \text {Im}\left( P_{u|12} \right) \text {Re}\left( P_{u|12} \right) ^{-1} \right]$ and $P_{u|12}$ the streamwise velocity component cross-spectral density between streamwise locations $x_1$ and $x_2 = x_1 + \xi _x$. Traditionally, it has been troublesome to obtain the velocity information at $x_2$ since velocity probes located at $x_1$ disturb the flow downstream. Since a non-intrusive measurement technique is adopted in the current study, a wide range of $\xi _x$ is attainable, allowing a deeper evaluation of its dependence on $\phi$.

Since $\xi _x$ is wall-parallel, the streamwise component of the convection velocity, $u_{\mathrm{c}}$, is evaluated instead of the convection velocity magnitude, $U_{\mathrm{c}}$. Since at the chosen locations the wall-parallel component is largely dominant, the wall-normal and spanwise component contributions to the convection velocity are considered negligible, and $u_{\mathrm{c}}\rightarrow U_{\mathrm{c}}$. Though for the sake of rigorousness, $u_{\mathrm{c}}$ is indicated.

The phase, $\phi = \phi \left( y,f,\xi _x \right)$ is dependent on the streamwise location, the frequency and the two-point measurement separation. Having a frequency dependence suggests that turbulent structures of different size might convect at different velocities if $\mathop {}\!\mathrm {d}f / \mathop {}\!\mathrm {d}\phi$ is not constant. It has nevertheless been previously observed that in similar applications the relation between convection velocity and frequency appears to be negligible (Stalnov et al. 2016; Chong and Vathylakis 2015). This is confirmed in Fig. 19, which shows a measure of $\phi$ for $x/2h = 1$ and $y/\delta = 0.9$, and where it is evident that $\phi \left( y/\delta = 0.9, f ,\xi _{x}\right)$ varies linearly over f, with a slope that increases with larger $\xi _{x}$. Only one case is presented for conciseness, but the linearity of $\phi$ with respect to the measured range of f has been separately confirmed for other streamwise and wall-normal locations.

Fig. 19

Contours of $\phi$ (left) as a function of frequency and $\xi _x$. A line plot representation (right) is shown the linear nature of $\phi$. Measurement taken at $x/2h=1$ and $y/\delta = 0.9$

Being the result of an arctangent, the phase result varies as $-\pi \le \phi \le \pi$. A selective procedure has been applied to remove the discontinuities in $\phi$ over the presented frequency range. The signal coherence is seen to break down first at higher frequencies, and more rapidly for locations nearer the wall and for smaller $\xi _x$. Once this has happened, naturally the value of $\phi$ becomes erratic and affects the calculation of $u_{\mathrm{c}}$ by means of its slope. To account for this and keep an accurate calculation of $\mathop {}\!\mathrm {d}f / \mathop {}\!\mathrm {d}\phi$, a procedure was applied by which the values of $f\left( \phi \right)$ are linearly interpolated starting at $f=0$ until the coefficient of determination drops below 0.97. The slope is then calculated from the result of the linear interpolation. Cases for which the coherence was so poor that not enough samples over f were employable (<25% of those available) were discarded.

The resulting convection velocity, calculated from Eq. (7), is shown in Fig. 20. The marker locations represent the mean of $\mathop {}\!\mathrm {d}f/ \mathop {}\!\mathrm {d}\phi$ for the different values of $\xi _x$ tested. The standard deviation of the sample per wall-normal location is represented by the gray region around the mean location.

The dashed line represents the mean convection velocity variation over the boundary layer, fitted with least-squares to the boundary layer log-law equation. The convection velocity is seen to depart slightly from the log-law fit, fact which is highlighted in the left-most plot with horizontal arrows, scaled with the magnitude of the difference between the two values. This difference has a negative maximum at around $y/\delta = 0.3$ and a small positive one at around $y/\delta = 0.7$, becoming negative again at the uppermost region of the boundary layer. A similar behavior is replicated for the rest of the locations. Having established the presented $u_{\mathrm{c}}$ as the mean over a wide range of eddy sizes and events occurring throughout the boundary layer, this departure from the log-law fit might suggest that a tendency for ejection events is experienced at around $y/\delta = 0.3$, and of sweep events for $y/\delta = 0.7$, a discussion of which is presented in Romano (1995), Krogstad et al. (1998) and Ghaemi and Scarano (2013), and is expanded here in Sect. 3.2.3.

The mean flow profile, ${\overline{u}}$, is indicated as a solid line in the plots. The convection velocity is greater than ${\overline{u}}$ below a certain crossover point in the boundary layer. This crossover is located at $y/\delta =0.8$ over $x/2h=0$ for both the serrated and straight edge cases, and around $y/\delta = 0.7$ further downstream at $x/2h = 1$. A similar trend of $u_{\mathrm{c}} > {\overline{u}}$ has been observed in Atkinson et al. (2015) for a turbulent boundary layer over a flat plate, and Buxton and Ganapathisubramani (2011) for a turbulent mixing layer. The degree of difference seen here is larger than that observed by Atkinson et al. (2015) and may be attributed to conditional differences between the two cases, possibly driven by the adverse pressure gradient in the present one. This assumption is supported by the closer match in the downstream location, where, as it was previously discussed, the boundary layer shows a better fit to the log-law.

Fig. 20

Wall-normal convection velocity. From left to right straight edge (cross symbol) and serrated edge at locations $x/2h=0$ (open circle), $x/2h = 0.5$ (puls symbol) and $x/2h = 1$ ( ). Mean u is presented (dash line), as is the log-fitted curve from the convection velocity results (semi solid)

A direct comparison of the convection velocity for the measured streamwise locations for the serrated edge and that of the straight edge is presented in Fig. 21. It can be seen that the trend follows the one observed for the mean velocity in Sect. 3.1, where the velocity near the wall exhibits an increasing as it moves downstream.

Fig. 21

Comparison of the convection velocity for the straight edge and the streamwise measurement locations of the serrated case

The square of the mean velocity vertical shear factor of Eq. (4) is presented in Fig. 22, where the most downstream measurement location $x/2h=1$ exhibits the lowest values throughout the boundary layer, followed by $x/2h=0.5$. A decrease of about ${1}\,{\hbox {s}^{-2}}$ in the maximum value is observed moving downstream between the different measurement stations.

Fig. 22

The square of the vertical shear of the mean velocity

The last remaining velocity-dependent factor in Eq. (4) is $\left[ {\overline{v}}/u_{\mathrm{c}} \right] ^2$, which is presented in Fig. 23. A significant difference is observed between the measurements at $x/2h=0$ and the other streamwise locations. This is due to the wall-parallel flow at the location $x/2h=0$ encountering either the surface of the serrations at approximately an angle of ${11}^{\circ }$ or the flow convecting from the opposite side of the airfoil (with a similar effect). This interaction causes the flow to gain upward momentum relative to the direction parallel to the airfoil surface, increasing the value of ${\overline{v}}$. At the downstream measurement locations, the flow at the edge remains instead relatively invariant in the v component, and thus the value of $\left[ {\overline{v}}/u_{\mathrm{c}} \right] ^2$ becomes driven by the denominator, which is also several times larger than ${\overline{v}}$. The measurement of this factor at $x/2h = 1$ is less than half than that of the measurement at $x/2h=0.5$. As expected, at $x/2h=0$ the measurement is similar for both the serrated and unserrated cases.

Fig. 23

The $\left[ {\overline{v}}/u_{\mathrm{c}} \right] ^2$ factor of Eq. (4)

3.2.3 Reynolds stresses, and sweep and ejection events

The Reynolds stress, evaluated from a quadrant analysis, can give valuable information on turbulent structures that convect in the boundary layer. This information is also relevant as it may provide further understanding of surface pressure peak events. In Chong and Vathylakis (2015), a relational approach between simultaneous pressure peak measurements on the surface is made along with turbulence fluctuation measurements in the boundary layer. Conclusions in their observations indicate that, near the wall, events occurring in the IV quadrant are strongly correlated to surface pressure peaks, and at regions further away from it (near or beyond $\delta$) the II quadrant events appear to contribute more. Separately, Ghaemi and Scarano (2013) find that sweep events are correlated with positive pressure peaks on the surface, and conversely, ejection events are correlated with negative pressure peaks. In a quadrant plot, the II quadrant is associated with ejection events and the IV quadrant to sweep events.

For the purpose of evaluating the Reynolds stress variation over the boundary layer, Fig. 24 shows the values of $-\overline{u'v'}$ for the measured locations. The Reynolds stress values for all streamwise locations reduce quite well to zero at the measured $y/\delta$ location. The downstream serration locations at $z/\lambda =0$ and 0.25 show a noticeably different behavior than for $x/2h=0$, exhibiting much lower values at their maxima, reaching about $-\overline{u'v'}/ u^2_{\mathrm{e}} \approx 3\times 10^{-3}$, or about two-thirds of that which is measured at $x/2h=0$. A similar observation has been made in Gruber (2012).

Fig. 24

Wall-normal profiles of $-\overline{u'v'}$ at trailing edge locations

In order to inspect the correlation of the velocity component fluctuations and perform a relational analysis to the expected surface pressure events, a series of quadrant analysis plots are shown in Fig. 25. Kernel density estimation (kde) contours for the entire time series are shown to more clearly indicate the relational trends observed between the two component fluctuations over the four quadrants. The hyperbola lines $|u'v'| = -6\overline{u'v'}$ are presented, above which are $u'v'$ events that are 6 times larger than the mean Reynolds shear stress (Kim et al. 1987; Lu and Willmarth 1973). The choice of the factor 6 is made to match that of Chong and Vathylakis (2015). In order to avoid overpopulating the plots, only events occurring outside of the $-6\overline{u'v'}$ limit are shown. The measurements over the straight edge are omitted for brevity, but are separately confirmed to be very similar to the measurements of the serrated case at $x/2h=0$.

Fig. 25

Distribution of $u'$ and $v'$ for different wall-normal locations. A kernel density estimation (kde) contours are shown. The hyperbolas correspond to $|u'v'| = -6\overline{u'v'}$ and only events that are larger than this limit are shown to avoid clutter. From left to right, open circle serration vertex at $x/2h=0$; plus symbol serration edge at $x/2h=0.5;$ : serration tip at $x/2h=1.0$

As is expected from the observations made in Fig. 24, away from the wall, at $y/\delta =0.9$, the magnitude of both $u'$ and $v'$ is reduced. The events are also less correlated, indicated by the kde exhibiting a more circular footprint.

At $y/\delta =0.6$ and below, the fluctuation components show an anticorrelation between $u'$ and $v'$, indicated by an elongated kernel density distribution toward the II and IV quadrants. A larger range in the $u'$ direction is present, evidenced by the kde being generally more slanted toward the $u'$ axis. This pattern was also observed in Chong and Vathylakis (2015) and is supported by the larger $u'_{\text {rms}}$ magnitude observed above. There is additionally a marked existence of events having a magnitude bias toward the II quadrant. Most events are nevertheless seen clustered in low values at the IV quadrant, as suggested by the location of the kde peak.

The fluctuations at $y/\delta =0.3$ remain more evenly concentrated between quadrants II and IV, both in the location of the kde peak and in its distribution. A slightly larger range for $u'$ and $v'$ is exhibited. This is expected, as this is the rough location where the rms maxima were observed in Sect. 3.1, as well as from the observations made of Fig. 24.

The measurements nearest to the wall show slightly decreased activity with respect to the mid-boundary layer locations, especially in the wall-normal direction. This is again expected from the observed rms results discussed before. A slight shift in the most-likely event location for $x/2h=0.5$ is observed, indicated by a bias in the kde peak toward the II quadrant. At $x/2h = 1$ , this behavior is also present but more moderate, and at $x/2h=0$ , the peak remains instead centered at the origin.

To simplify the observation of high-intensity events, Fig. 26 is provided, showing the percentage of the total events that comply with $|u'v'|>-6\overline{u'v'}$. In the current results, such events are present for all wall-normal locations, but at $y/\delta > 0.6$ , they are significantly biased toward the II quadrant, thus contributing to both high and low pressure peaks at the surface. Closer to the wall, events are more evenly distributed between quadrants II and IV. Overall, there is a decrease in high-intensity events by up to around 2% moving downstream, which is beneficial for noise reduction as it indicates the convection of less intense surface pressure events at locations close to most of the serration edge. This further implies that each location of the serration edge will contribute differently to noise reduction.

Fig. 26

Percentage of events with $|u'v'| > -6\overline{u'v'}$ occurring at each quadrant, for the different streamwise and wall-normal locations

In relation to the observed variance in the convection velocity as shown in Fig. 20, the measurements at $y/\delta =0.6$ indicate that most events happen in the IV quadrant, suggesting a larger number of sweep events (although events are of lower intensity than events in the II quadrant). This goes in line with the higher convection velocity observed at around this height with respect to the log-law behavior. At around $y/\delta =0.3$, where the convection velocity is lower than the log-law fit, the peak of the kde is well centered, indicating no event bias to either the II or IV quadrants. This is also true for the predominance of high-intensity events, which are also well distributed between the II and IV quadrants. This symmetry inhibits an explanation of the observed convection velocity anomaly based on the Reynolds shear measurements, requiring further investigation.

3.2.4 Turbulent flow spectra

The final factor of Eq. (4) that is evaluated is the wavenumber auto-spectra. To evaluate the results, the frequency-dependent auto-spectra is provided in Fig. 27 for both the streamwise and wall-normal components. As observed in the quadrant analysis above, the fluctuations over u have a larger range, behavior which is reflected here, evidenced by the larger energy of ${\varPhi }_{uu}$ compared to ${\varPhi }_{vv}$, which is about ${7}\,{\hbox {dB}}$ higher at the lowest frequencies presented. Both spectra follow the Kolmogorov $-5/3$ decay well until higher frequencies are reached. This is expected because of limitations in the temporal resolution achieved by the PIV signal-to-noise ratio between the instantaneous flow fields, which settles the maximum measurable frequency to about 3/4 of the Nyquist frequency (Ghaemi and Scarano 2013). It appears to be more sensitive at lower boundary layer location presented, $y/\delta =0.2$, reaching a plateau at around $f={3}\,{\hbox {kHz}}$ for ${\varPhi }_{uu}$. Overall, the results between the streamwise cases are very similar. The most downstream location does present lower energies in frequencies below ${1}\,{\hbox {kHz}}$ for both components, with ${\varPhi }_{vv}$ showing up to a ${3}\,{\hbox {dB}}$ loss.

Fig. 27

The flow frequency-dependent auto-spectra of the wall-parallel component (left) and wall-normal component (right) at two wall-normal locations

The pre-multiplied wavenumber spectra are presented in Fig. 28. Large overall level differences are seen between the different wall-normal locations, reducing greatly for regions in the upper boundary layer. All the streamwise locations exhibit peaks located close to $k_u \approx {100}\,{\hbox {m}^{-1}}$. As expected from the frequency-dependent auto-spectra as shown in Fig. 28, the downstream location of the serrated edge shows lower levels, especially evident at around $y/\delta =0.4$ and below for wavenumbers under $k_u\approx {200}\,{\hbox {m}^{-1}}$. The $k_u$ location of the peak for the downstream measurement appears to suffer a slight increase to around ${150}\,{\hbox {m}^{-1}}$. A variation in the wavenumber suggests changes in the intensity and spectral shape of the acoustic emissions due to modifications in the turbulent structure size and convection velocity. In the present case, the most contributing change appears to be in the intensity, with small variations in $k_{\mathrm{e}}$ across the serration edge.

Fig. 28

The flow wavenumber-dependent pre-multiplied auto-spectra of the wall-normal component at four wall-normal locations

3.2.5 Summary of the flow parameter observations

The different elements of Eq. 4 that are attainable from the hydrodynamic measurements have been considered in the previous sections. Observations clearly indicate that the flow in the boundary layer changes as it convects past the different edge locations of the serration.

In summary, the following findings have been discussed:

• the overall thickness of the boundary layer is reduced as the flow evolves beyond the adverse pressure gradient that is present between the end of the airfoil and the serration surface,

• the vertical integral length remains similar along the boundary layer height between downstream locations,

• the convection and mean velocity suffer changes, mostly seen below $y/\delta = 0.4$, with downstream locations exhibiting higher velocity,

• the shear is reduced downstream as a consequence of this,

• the factor ${\overline{v}}/u_{\mathrm{c}}$ becomes hard to evaluate, given the relatively large downward motion of the flow with respect to the boundary layer line at $x/2h=0$, but the downstream location $x/2h=1$ shows slightly reduced levels with comparison to $x/2h=0.5$,

• the quadrant analysis reveals the presence of turbulent structures in the boundary layer that lead to high pressure peaks on the surface, but suggests a reduction of these events downstream,

• the auto-spectra of the flow indicate that below a certain frequency the downstream location over the serration tip exhibits less energy than the upstream location for both the serrated case and the straight edge case,

• peaks in the wavenumber auto-spectra are present around ${100}\,{\hbox {m}^{-1}}$, with a slight increase seen for the tip location near the surface to about ${150}\,{\hbox {m}^{-1}}$.

The boundary layer integrated results for the different factors are calculated in Table 3 for the different streamwise locations. The product of these factors is also presented, excluding the ${\overline{v}}^2/u_{\mathrm{c}}^2$ factor due to the previously discussed discrepancy in conditions between the $x/2h=0$ and other streamwise locations that is unclear how to account for. There is a noticeable reduction in the levels between the streamwise locations, driven primarily by the shear factor and modified throughout by the thinning boundary layer. This implies a change in the surface pressure intensity, driven by the convecting flow over it. At the same time, this fact suggests that an accurate calculation of the noise emitted at the serration edges requires a streamwise-dependent input of the surface pressure. This limits the direct applicability of Green’s function as it is done in Howe (1991) in the case of serration-retrofitted airfoils. The downstream change in the surface pressure appears nevertheless to be beneficial for the pursuit of lower noise emissions.

Table 3 Boundary layer integrated values for the different elements of Eq. (4)

Proof that the serrations used in the current set-up reduce noise when compared to the unmodified airfoil is provided in the next section. Although the hydrodynamic investigation shows that beneficial changes in the flow and surface pressure are prescribed by the introduction of the serrations, their modification of the scattering efficiency remains a credible and additional driver in the mechanism of noise reduction.

3.3 Beamforming results

In order to assess the influence of the presence of serrations and the flow velocity on the emitted noise levels, the acoustic data from the microphone array was utilized. A set of flow speeds between 30 and 40 m/s was used for the acoustic measurements, within which the airfoil self-noise was well distinguishable from the background noise. While these flow velocities are too high to capture the time-resolved flow data with the current PIV system, it will be shown that the trends recorded between the serrated and the unserrated airfoils are consistent within the ${10}\,{\hbox {m/s}}$ flow velocity range that was tested, and an extension of the conclusions here obtained to ${20}\,{\hbox {m/s}}$ is, thus, achievable.

The source plots for the aforementioned flow velocities and frequencies between 1 and ${5}\,{\hbox {kHz}}$ are gathered in Fig. 29 for both the airfoil with straight trailing edge and the one including serrations. It can be observed that the strongest noise sources are located at the trailing edge in all cases, as expected. In these acoustic images it can readily be noted that higher velocities produce higher noise levels and that the serrations offer quieter results for all cases with respect to the straight trailing edge case in this frequency range.

The frequency spectra obtained from the beamforming source plots for $U_\infty =30, 35$ and ${40}\,{\hbox {m/s}}$ are depicted in Fig. 30. The results are shown in third-octave bands to better distinguish relevant differences between the two cases. The largest noise reductions were observed between 1 and ${2}\,{\hbox {kHz}}$.

Fig. 29

Acoustic source maps obtained for the airfoil with the straight edge (top) and with the serrated edge (bottom) at the freestream velocities indicated in the figures and frequencies between 1 and ${5}\,{\hbox {kHz}}$. The airfoil location is marked by the solid rectangle and the integration area by the dashed rectangle

Fig. 30

Acoustic frequency spectra of the airfoil with straight and serrated edges. The freestream velocity is indicated in the plots, as well as the SPL reduction in decibels

The noise emission differences observed between the straight and serrated edges reflect those in the literature, although none have used the same serration geometry, flow settings and airfoil combination. Results in Moreau and Doolan (2013) show frequency-dependent reductions ranging from 3 to 13 dB on a serrated flat plate which experienced vortex shedding. This situation was not present in the current case. In Gruber et al. (2010), a maximum ${5}\,{\hbox {dB}}$ reduction is observed for a case with a highly cambered airfoil and serrations with a flap angle toward its bottom side. The same reduction level is observed in Qiao et al. (2013) and Finez et al. (2011). These studies have used single microphones or linear arrays. Acoustic beamforming is used in Fischer et al. (2014), where serrations also reduced noise by approximately ${5}\,{\hbox {dB}}$.

The relation between the SPL and the flow velocity, and serration noise reduction can be observed more clearly in Fig. 31, where the integrated noise levels (for frequencies between 1 and ${5}\,{\hbox {kHz}}$) obtained in the acoustic images in Fig. 29 are plotted against the flow velocity for both cases. An approximately constant SPL difference of around ${6}\,{\hbox {dB}}$ is present in all cases. Given the characteristic length of the airfoil tested and the dominance of low-frequency noise in the spectra, the airfoil can be considered as compact Roger and Moreau (2005), Ayton (2016) and Cavalieri et al. (2016). The expected 5th power law dependence of the acoustic power with the flow speed (Ffowcs Williams and Hall 1970; Fink 1977) is also included in Fig. 31, showing a close agreement with both cases. These observations suggest that the noise reduction trend remains significant at the ${20}\,{\hbox {m/s}}$ flow speed.

Fig. 31

Velocity dependence law (straight line) for trailing edge noise emissions compared to the measured noise from the straight and serrated edges

4 Conclusions

Time-resolved flow data was acquired over the unmodified and serration-retrofitted trailing edges of a NACA 0018 airfoil at zero lift. Acoustic measurements were further performed to characterize the noise emissions from both trailing edges, by which the noise reduction benefits of the retrofitted serrations were confirmed, showing reductions of up to ${6}\,{\hbox {dB}}$ with respect to the unmodified configuration.

In order to evaluate the role of the flow in this reduction, statistics have been presented for both configurations and, by means of the TNO-Blake model, were used to form a qualitative approximation of the unsteady surface pressure near the edges. This approach has been favored, as a technical means by which to directly evaluate the latter on thin serrations is absent.

While at the root of the serrations, the flow remains unmodified, considerable changes are experienced as it convects downstream. Parameters of the TNO-Blake model were evaluated, and results indicate that changes in the flow, as it convects downstream, lead to lower intensities in the unsteady surface fluctuations. It is found that these changes were mostly driven by the shear and the boundary layer thickness, which becomes thinner at downstream locations. Additionally, the spectra of the wall-normal component showed a decrease in energy in the lower frequencies and wavenumbers for the location furthest downstream over the serration tooth. A quadrant analysis was further presented, and events known to be related to high-intensity surface pressure peaks were shown to be less prominent downstream.

These findings reveal that, at least when retrofitted on an airfoil, the mechanism of noise reduction by serrations is aided by beneficial changes in the flow that convects over its edges. The variation of the pressure fluctuations in the streamwise direction, and of the flow parameters reported, is such that the local scattered pressure waves might vary along the serration edges. While Lyu et al. (2015) suggests a geometric dependence of the constructive and destructive interference of the local scattered pressure waves along the edges, this variation would make the prediction more complex.