Modelling droplet collision outcomes for different substances and viscosities

Abstract

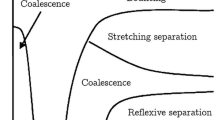
The main objective of the present study is the derivation of models describing the outcome of binary droplet collisions for a wide range of dynamic viscosities in the well-known collision maps (i.e. normalised lateral droplet displacement at collision, called impact parameter, versus collision Weber number). Previous studies by Kuschel and Sommerfeld (Exp Fluids 54:1440, 2013) for different solution droplets having a range of solids contents and hence dynamic viscosities (here between 1 and 60 mPa s) revealed that the locations of the triple point (i.e. coincidence of bouncing, stretching separation and coalescence) and the critical Weber number (i.e. condition for the transition from coalescence to separation for head-on collisions) show a clear dependence on dynamic viscosity. In order to extend these findings also to pure liquids and to provide a broader data basis for modelling the viscosity effect, additional binary collision experiments were conducted for different alcohols (viscosity range 1.2–15.9 mPa s) and the FVA1 reference oil at different temperatures (viscosity range 3.0–28.2 mPa s). The droplet size for the series of alcohols was around 365 and 385 µm for the FVA1 reference oil, in each case with fixed diameter ratio at Δ= 1. The relative velocity between the droplets was varied in the range 0.5–3.5 m/s, yielding maximum Weber numbers of around 180. Individual binary droplet collisions with defined conditions were generated by two droplet chains each produced by vibrating orifice droplet generators. For recording droplet motion and the binary collision process with good spatial and temporal resolution high-speed shadow imaging was employed. The results for varied relative velocity and impact angle were assembled in impact parameter–Weber number maps. With increasing dynamic viscosity a characteristic displacement of the regimes for the different collision scenarios was also observed for pure liquids similar to that observed for solutions. This displacement could be described on a physical basis using the similarity number and structure parameter K which was obtained through flow process evaluation and optimal proportioning of momentum and energy by Naue and Bärwolff (Transportprozesse in Fluiden. Deutscher Verlag für Grundstoffindustrie GmbH, Leipzig 1992). Two correlations including the structure parameter K could be derived which describe the location of the triple point and the critical We number. All fluids considered, pure liquids and solutions, are very well fitted by these physically based correlations. The boundary model of Jiang et al. (J Fluid Mech 234:171–190, 1992) for distinguishing between coalescence and stretching separation could be adapted to go through the triple point by the two involved model parameters C _a and C _b, which were correlated with the relaxation velocity $u_{\text{relax}} = {\sigma \mathord{\left/ {\vphantom {\sigma \mu }} \right. \kern-0pt} \mu }$. Based on the predicted critical Weber number, denoting the onset of reflexive separation, the model of Ashgriz and Poo (J Fluid Mech 221:183–204, 1990) was adapted accordingly. The proper performance of the new generalised models was validated based on the present and previous measurements for a wide range of dynamic viscosities (i.e. 1–60 mPa s) and liquid properties. Although the model for the lower boundary of bouncing (Estrade et al. in J Heat Fluid Flow 20:486–491, 1999) could be adapted through the shape factor, it was found not suitable for the entire range of Weber numbers and viscosities.

Appendices

Appendix 1: Collision boundary models

In this section a brief overview about the boundary line models used for deciding on the collision outcome by using collision maps of the form B = f(We) will be given. Details on the derivation of the equations are given in the respective articles. These models will be also used for comparison with the present experimental data. It should be emphasised that in the present study the colliding droplet properties (i.e. size and substance) are identical and also the environmental conditions were not changed (i.e. air at ambient conditions).

1.1 Model of Ashgriz and Poo (1990)

Ashgriz and Poo (1990) developed two correlations for the boundaries of coalescence and separation. For off-centre collisions only a small portion of the droplets, depending on the impact parameter, come into contact and are partially deformed. This interaction region is stretched until it breaks up, creating satellite droplets. Based on an energy balance the following equation for the boundary between coalescence and stretching separation was derived:

$$ We = \frac{{4\left( {1 + \varDelta^{3} } \right)^{2} \left[ {3\left( {1 + \varDelta } \right)\left( {1 - B} \right)\left( {\varDelta^{3} \phi_{S} + \phi_{L} } \right)} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }}{{\varDelta^{2} \left[ {\left( {1 + \varDelta^{3} } \right) - \left( {1 - B^{2} } \right)\left( {\phi_{S} + \varDelta^{3} \;\phi_{L} } \right)} \right]}} $$

(14)

where

$$ \begin{aligned} & \phi_{\text{S}} = \left\{ {\begin{array}{*{20}l} {1 - \frac{1}{{4\varDelta^{3} }}(2\varDelta - \tau )^{2} (\varDelta + \tau )} \hfill & \quad{{\text{for}}\;h > 0.5d_{\text{S}} } \hfill \\ {\frac{{\tau^{2} }}{{4\varDelta^{3} }}(3\varDelta - \tau )} \hfill &\quad {{\text{for}}\;h < 0.5d_{\text{S}} } \hfill \\ \end{array} } \right.\; \\ & \phi_{\text{L}} = \left\{ {\begin{array}{*{20}l} {1 - \frac{1}{4}(2 - \tau )^{2} (1 + \tau )} \hfill &\quad {{\text{for}}\;h > 0.5d_{\text{L}} } \hfill \\ {\frac{{\tau^{2} }}{4}(3 - \tau )} \hfill &\quad {{\text{for}}\;h < 0.5d_{\text{L}} } \hfill \\ \end{array} } \right. \\ & h = \frac{1}{2}\left( {d_{\text{L}} + d_{\text{S}} } \right)(1 - B) \\ \end{aligned} $$

(15)

and τ = (1 − B)(1 + Δ) are the substitutes of the equation above.

Reflexive separation takes place for near head-on collisions. A torus-like collision complex is created with a thin lamella spanning the torus. After rebound of the liquid, it is stretched and a ligament is formed, which eventually breaks up, forming mostly one large satellite (Brenn et al. 2001). The criterion for reflexive separation is fulfilled, when the effective kinetic energy is larger than 75% of the nominal surface energy of the combined droplets:

$$ We = 3\left[ {7\left( {1 + \varDelta^{3} } \right)^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} - 4\left( {1 + \varDelta^{2} } \right)} \right]\frac{{\varDelta \left( {1 + \varDelta^{3} } \right)^{2} }}{{\varDelta^{6} \;\eta_{\text{S}} + \eta_{\text{L}} }} $$

(16)

The geometrical parameters given in Eq. (16) are:

$$ \begin{aligned} & \eta_{\text{S}} = 2\left( {1 - \xi } \right)^{2} \;\left( {1 - \xi^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} - 1 \\ & \eta_{\text{L}} = 2\left( {\varDelta - \xi } \right)^{2} \;\left( {\varDelta^{2} - \xi^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} - \varDelta^{3} \\ & \xi = \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \right)\;B\;\left( {1 + \varDelta } \right) \\ \end{aligned} $$

(17)

1.2 Model of Jiang et al. (1992)

In contrast to the model of Ashgriz and Poo (1990), the model of Jiang et al. (1992) accounts for viscous dissipation by applying momentum conservation. It has been developed to describe the boundary between coalescence and stretching separation. The final equation for the boundary curve contains two model constants (i.e. C _a and C _b) which can be fitted to the experimental data (see, e.g., Gotaas et al. 2007a, b):

$$ B = \frac{{C_{\text{a}} }}{{We^{1/2} }}\;\left[ {1 + C_{\text{b}} \;\frac{\mu }{\sigma }\;\left( {\frac{{\rho \;d_{1} }}{\sigma }} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} } \right] $$

(18)

1.3 Model of Estrade et al. (1999)

This model has been derived from collision maps obtained experimentally for ethanol droplets and describes the lower boundary of bouncing. A free model constant, the shape factor Ψ (for ethanol the value was found to be 3.351), has been introduced whereby the model can be adapted to fit other droplet collision conditions:

$$ We = \frac{{\varDelta \left( {1 + \varDelta^{\,2} } \right)\;\left( {4\varPsi - 12} \right)}}{{\chi \;\left( {1 - B^{2} } \right)}} $$

(19)

where

$$ \begin{array}{*{20}l} {\chi = 1 - 0.25\;\left( {2 - \tau } \right)^{2} \left( {1 + \tau } \right)} \hfill &\quad {{\text{if:}}\;\tau > 1} \hfill \\ {\chi = 0.25\;\tau^{2} \;\left( {3 - \tau } \right)} \hfill &\quad {{\text{if:}}\;\tau \le 1} \hfill \\ \end{array} $$

(20)

and τ = (1 − B)(1 + Δ) is an additional parameter given in Eq. 20.

Appendix 2

2.1 Summary of the model of Naue and Bärwolff (1992)

The model description is divided into two major parts. In the first part, the concept of process evaluation by means of the information entropy will be explained, and in the second paragraph the derivation of the K-numbers, which may be regarded as a structure parameter, will be presented.

2.2 Concept of process evaluation

The process of vortex development is characterised by a main flow transport and a lateral motion where the latter is feed by the convective flow. The non-dimensional entropy S is a measure of the partitioning of the two characteristic motions where joint entropy is maximised. For evaluating an exponential distributed property f, defined in the interval 0 < f ≤ 1, the non-dimensional entropy is used:

$$ S = - \ln \,f $$

(21)

The entropy production σ can be derived from:

$$ \frac{{{\text{d}}\sigma }}{{{\text{d}}f}} = S $$

(22)

After an integration in the interval f = f _* to f = 1 and the application of a Taylor series expansion a modified ansatz compared to the thermodynamic entropy definition is obtained. The result of the integration of Eq. 22 gives the entropy production:

$$ \sigma_{*} - f_{*} = - f_{*} \;\ln \,f_{*} $$

(23)

The term −f _* ln f _* is called information entropy σ _i* and has been introduced by Shannon (1948) in cybernetics. With the averaged values f _*, σ _* and σ _i* in a residence range, the mean entropy production can be written as follows:

$$ \tilde{\sigma }_{*} - \tilde{f}_{*} = \tilde{\sigma }_{{{\text{i}}*}} $$

(24)

The difference from the equation above is equal to the quality gain which is expressed by the information entropy. A process may be regarded as optimal, if the information entropy is maximised. Now a distinction between competing and sequential processes has been carried out, which is omitted here because of the large amount of equations.

2.3 Optimal processes and derivation of K

Processes in which the information entropy approaches a maximum are considered as optimal processes. Competing processes might have a phase shift to each other, which the authors (Naue and Börwolff 1992) called phase₁ and phase₂ for a two-dimensional process. The maximum of the information entropy can be found by the derivation of the definition equation which yields:

$$ \frac{{{\text{d}}\sigma_{{{\text{i}}*}} }}{{{\text{d}}f_{*} }} = \frac{{{\text{d}}f_{*} \;\ln \,f_{*} }}{{{\text{d}}f_{*} }} = \ln \,f_{*} - 1 $$

(25)

For the optimum one obtains ln(f _*opt) = −1 or f _*opt = 1/e as a solution. The phase shift mentioned above can either be excited or weakened through convection or conduction effects, depending on the sign of phase _n . As a result of these considerations it may be concluded that for optimal processes, waves are optimal phase shifted to each other and develop optimal. In a two-dimensional phase space the values for the optimal phase functions are:

$$ {\text{phase}}_{1} = \frac{1}{e} $$

(26)

$$ {\text{phase}}_{2} = \left( {1 - \frac{1}{{e^{2} }}} \right)^{{\frac{1}{2}}} $$

(27)

The similarity number or structure parameter K (here called structure parameter) will be obtained by considering the interaction of structures (i.e. velocity fluctuations) with the mean flow. The transport of the structures results from the momentum distribution among competing processes. For that, the author considered a pipe flow and asked for the optimal partitioning of the total momentum to the convective transport and the structure movement for the three-dimensional case, with the result that only one meaningful solution for this ratio is obtained:

$$ \phi = - \frac{e - 1}{2\,e} $$

(28)

The process of turbulent velocity fluctuations is of course fully three-dimensional. The momentum velocity v _j is a measure of the distance travelled in a certain time interval ∆t. First it is assumed that the travelled distance is identical in all three directions in space (i.e. isotropic). Hence, a third of the additional travel distance is obtained from:

$$ v_{\text{j}} \;\frac{e - 1}{6\,e}\;\Delta t $$

(29)

The entire volume of the residence, without turbulent velocity fluctuations, within a certain cross-sectional area is given as V ₀ = v _j A _j Δt. On the other hand, with turbulent velocity fluctuations, if the volume is assumed as isotropic, one obtains:

$$ V_{\text{t}} = v_{\text{j}} \;A_{\text{j}} \;\Delta t\;\left( {1 + \frac{e - 1}{2e}} \right) $$

(30)

Consequently, the volume ratio characterising the expansion due to velocity fluctuations is obtained from:

$$ \frac{{V_{\text{t}} }}{{V_{0} }} = 1 + \frac{e - 1}{2e} = \left( {\frac{{s_{\text{t}} }}{{s_{0} }}} \right)^{3} $$

(31)

where s ₀ and s_t are the lengths of the volume edges without and with turbulent fluctuations, respectively. A series expansion yields:

$$ \frac{{s_{\text{t}} }}{{s_{0} }} = 1 + \frac{e - 1}{6e} $$

(32)

The proposed structure parameter K characterises this expansion due to velocity fluctuations or vortex motion for a spherical volume:

$$ K = 2\pi \;\frac{{s_{\text{t}} }}{{s_{0} }} = 2\pi \left( {1 + \frac{e - 1}{6e}} \right) = 6.9451 $$

(33)

The final expression for the structure parameter for a n-dimensional process (i.e. dimensionality of the structures in the phase space) is given by:

$$ K^{n} = \left[ {2\,\pi \left( {1 + \frac{e - 1}{6\;e}} \right)} \right]^{n} $$

(34)