Flow topology and acoustic emissions of trailing edge serrations at incidence

Abstract

The flow past a NACA 0018 airfoil with sawtooth trailing edge serrations has been investigated using stereoscopic particle image velocimetry (PIV). The serration flap angle and airfoil incidence are varied in order to study the effect of secondary flow establishing between the suction and pressure sides of the serrations. The flow topology around the serrations is inferred from the analysis of time-averaged streamlines close to the airfoil surface and from the wall-normal flow velocity in between serrations. Additional PIV measurements with a plane in cross-flow highlight the formation of streamwise vortex pairs. The flow behavior is further characterized in terms of its turbulence statistics. Noise emissions are measured with an acoustic phased array in combination with beamforming. The serrations are found to be effective in reducing noise, and their application is studied for different degrees of airfoil incidence and serration flap angle.

1 Introduction

Broadband airfoil noise emissions that originate due to the interaction of the airfoil turbulent boundary layer with the sharp trailing edge (Brooks et al. 1989) have been shown to be effectively reduced using trailing edge serrations. Evidence of this has been observed in acoustic measurements performed both in wind tunnel experiments (Gruber et al. 2013; Moreau and Doolan 2013; Dassen et al. 1996) and on full-scale wind turbines (Schepers et al. 2007; Oerlemans et al. 2009). For the latter, airfoil self-noise reduction is relevant in relation to the observance of noise limits established by local regulations. Furthermore, experimental studies related to the flow around serrations and surface pressure characterization have also been previously performed (Chong and Vathylakis 2015; Finez et al. 2011; Arce et al. 2015).

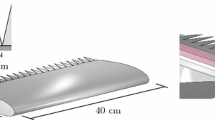
An analytical model for the prediction of the noise emitted from a sawtooth serrated trailing edge has been proposed by Howe (1991a, b). It yields the nondimensional acoustic power spectrum, $\varPsi$, of the serrated trailing edge with respect to the reference spectrum of the straight trailing edge, $\varPsi _{0}$, as a function of serration wavelength, $\lambda$, and amplitude, 2h (see Fig. 1 for the geometric definition of $\lambda$ and 2h)

$$\begin{aligned} \varPsi \left( \omega \right) \approx \frac{\varPsi _0\left( \omega \right) }{1+\left( 4h/\lambda \right) ^2}, \end{aligned}$$

(1)

where $\omega$ is the angular frequency of the acoustic pressure fluctuations.

The above relation has been derived under the assumption of frozen turbulence convected across the trailing edge. In particular, the time-average streamlines are assumed to remain aligned with the freestream direction. For an airfoil at incidence, the transverse fluid motion induced by the pressure unbalance between suction and pressure side limits applicability of the theory as commented by Howe (1991b).

Experimental studies (Gruber et al. 2013; Moreau and Doolan 2013) have reported less effective noise reduction for serrated trailing edges than that predicted with the above-mentioned model. The mismatch could be ascribed to a number of flow parameters which the theory does not account for, and which may lead to a departure from the predicted behavior. A more thorough understanding of the flow field around the serrations is therefore needed to unambiguously identify potential reasons of the discrepancy between the above model and experimental observations.

While wind tunnel experiments have revealed that a reduction in noise is often measured when using serrations, a slight increase in noise at relatively higher frequencies has also been reported (Moreau et al. 2011; Gruber 2012). It has been argued in Dassen et al. (1996) and Oerlemans et al. (2009) that the noise increase at higher frequencies might be due to the misalignment of the serrations with the flow in the wake of the airfoil. Gruber et al. (2011) has ascribed this phenomenon to an increased turbulence activity between the serration teeth.

In order to relate the noise reduction efficiency to flow field effects, the present work combines stereoscopic particle image velocimetry (PIV) and acoustic phased array measurements of sawtooth trailing edge serrations on a NACA 0018 airfoil. The experiments are conducted comparing the serrated trailing edge with the straight edge airfoil. The pressure unbalance between the serration upper and lower surfaces is varied by placing the airfoil at incidence, and accentuated when the inclination of the serrations is also varied.

The time-averaged flow topology is first characterized to determine the streamline distortion. The analysis of the turbulent velocity fluctuations yields the properties of the boundary layer along the serrations. The noise emitted by the serrated trailing edge is monitored with a microphone array yielding the power spectral density of the acoustic pressure fluctuations in the relevant frequency range.

2 Experimental setup

Experiments were conducted in a low-speed wind tunnel with vertical exit (V-Tunnel) operated within the aerodynamics laboratories of the Aerospace Engineering Department at TU Delft. The contraction ratio of 60:1 produces a flow at the exit ($40\times 40{\hbox { cm}^2}$) with turbulence intensity below 1 %. The operating velocity ranges from ${10}\hbox { m/s}$ to ${45}\hbox { m/s}$.

A NACA 0018 airfoil profile has been CNC-machined into an aluminum model with removable trailing edge inserts, a chord $C ={20}\hbox { cm}$ and a span of ${40}\hbox { cm}$. The length of the serrations is $2h={4.0}\hbox { cm}$ with $2h/\lambda = 2$, such that $\lambda ={2.0}\hbox { cm}$ is the serration wavelength (see Fig. 1). The serration panel thickness is ${1.0}{\hbox { mm}}$. When measurements are taken in respect to the straight trailing edge, it is the original trailing edge of the NACA 0018 airfoil which is used.

The relevant parameters inducing an unbalance in the pressure between the serration upper and lower surfaces are the airfoil angle of attack, $\alpha _g$, and the serration flap angle, $\varphi$. Figure 2 shows the convention used, where a positive value of $\varphi$ indicates an inclination of the flap angle toward the airfoil pressure side.

Fig. 1

Dimensions of the airfoil and serrations

Fig. 2

Airfoil cross section and serrated trailing edge flap. Angle of attack, $\alpha$, and the serration flap angle, $\varphi$, are shown

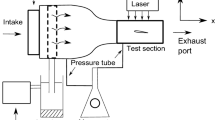
The airfoil was placed at the exit of the wind tunnel and held by means of side plates. Three experimental configurations were needed to measure the flow at three different plane locations, namely the near-wall plane, cross-flow plane, and wall-normal plane. A sketch of the setup for the near-wall plane and the cross-flow plane experiments can be seen in Fig. 3. The wall-normal plane experiment is shown in Fig. 4, right.

Boundary layer transition was forced by a tripping element at $x/C=0.175$. The trip is composed of randomly distributed roughness elements (carborundum with nominal grain size of ${0.6}{\hbox { mm}}$) over a width of approximately ${10}{\hbox { mm}}$. The onset of turbulence past the tripping element was verified with a stethoscope probe. For the baseline configuration ($\alpha = {0}^\circ$), the boundary layer thickness at the airfoil trailing edge was measured with PIV to be $\delta _{99}={15.9}{\hbox { mm}}$. PIV experiments are conducted at freestream velocity $U_\infty ={20}\hbox { m/s}$, corresponding to a chord-based Reynolds number of $2.6\times 10^5$.

Fig. 3

Setup used in the near-wall (camera and laser position shown) and the cross-flow plane measurements

2.1 Stereoscopic PIV

The coordinate system is defined with x, y, and z along the freestream, vertical and spanwise directions, respectively. The origin is located at the trailing edge of the airfoil and at the serration tooth centerline. The velocity vector is represented by the components u, v, and w, in x, y, and z coordinate directions, respectively.

Three-component velocity measurements were conducted using stereoscopic PIV. The air flow was seeded with ${1}{\upmu \hbox {m}}$ tracer particles of evaporated water–glycol-based fog fluid. Illumination is obtained with a Quantronix Darwin Duo, Nd:YLF laser ($2\times {25}{\hbox { mJ}}$ at ${1}{\hbox { kHz}}$) and laser optics is used to form a sheet of approximately ${1.5}{\hbox { mm}}$ thickness.

Fig. 4

Left PIV measurement planes along different direction. Only one of three wall-normal planes is indicated for clarity. Center coordinate system for the near-wall plane. Right position of wall-normal measurement planes

The measurement configurations are illustrated in Fig. 4, left. The near-wall plane ($x-z, y={2}{\hbox { mm}}$) enables to quantify the streamlines distortion and to study the near-wall flow topology. The laser sheet is maintained parallel to the surface of the serrations (see Fig. 4, center), and thus, results are presented based on a coordinate system rotated about the z axis $\left( x_r,y_r,z_r \right)$. The cross-flow plane ($y-z, x={60}{\hbox { mm}}$) inspects the streamwise vortices emanating from the serrated trailing edge. Finally, three wall-normal planes ($x-y, z=0,\lambda /4,\lambda /2$) are chosen that span one serration element and determine the properties of the turbulent boundary layer upstream and spanwise across the trailing edge (see Fig. 4, right).

The imaging system is composed of two Photron Fastcam SA1 CMOS cameras (${1024\times 1024}{\hbox { px}^2}$, pixel-pitch ${20}{\,\upmu \hbox {m/px}}$, 5.4 frames per second) equipped with Nikon NIKKOR macro-objective lenses and Scheimpflug adapters to correct for the misalignment between the object and sensor plane. With about ${50}\hbox { cm}$ distance from the object and an angle of ${40}^\circ$ between the two cameras, the field of view covers an area of approximately $5\times {5}{\hbox { cm}^2}$, resulting in a digital imaging resolution of ${20}{\hbox { px/mm}}$.

Image pairs are acquired with a time separation of ${50}{\upmu \hbox { s}}$ at a rate of ${250}{\hbox { Hz}}$ for a total of 1500 instantaneous measurements (6 s). Image interrogation is performed with LaVision DaVis 8 software using a multi-pass stereo cross-correlation with a final window size of $16\times { 16}\hbox { px}\; (0.8\times {0.8}{\hbox { mm}^2})$. An overlap factor of 75 % between adjacent windows is applied, leading to a vector spacing of ${0.2}{\hbox { mm}}$.

The typical measurement uncertainty is estimated by a linear propagation approach (Stern et al. 1999) and verified a posteriori using the statistical analysis method introduced by Wieneke (2015). The random and bias components are considered. Bias errors due to peak-locking (Westerweel 1997) are associated to the large imaging aperture (f / 5.6) yielding a diffraction spot of only half pixel diameter. This effect is mitigated by slightly defocusing the images (Raffel et al. 2007), bringing the particle image diameter to approximately 1.5 px. The verification is performed inspecting the histogram of particles image displacement, which in this case gives no evidence of peak-locking. The error due to finite spatial resolution depends on the characteristic length to be accurately measured in the PIV velocity fields. With a multi-pass cross-correlation algorithm with window deformation the amplitude of the fluctuation is measured with <5 % modulation when the window size is smaller than 0.6 times the length of the scale to be measured (Schrijer and Scarano 2008). Therefore, with ${0.8}{\hbox { mm}}$ window size, flow structures down to ${1.2}{\hbox { mm}}$ (0.13 % of the boundary layer) can be measured within 95 % precision. Other systematic sources of uncertainty, including calibration errors and lens distortion, are alleviated by iterative steps of a self-calibration procedure with a polynomial mapping of the images, via the DaVis software. A disparity vector smaller than 1px is reached for the stereo calibration (Raffel et al. 2007).

The random components of the uncertainty have been evaluated with a technique following the work of Wieneke (2015), where the degree of particle images matching is quantified with the analysis of the correlation peak width. Random errors vary along the measurement domain with <1 % and approximately 3 % in the freestream and in the inner boundary layer regions, respectively. The uncertainty of the mean of the velocity, and the root mean square (RMS) of its fluctuations, also depends upon the size of the measured ensemble to form the statistics. In the present case, the uncertainty on the mean velocity is 0.01 and 2 % on its RMS.

2.2 Acoustic measurements

The beamforming technique is applied by means of a phased microphone array. The airfoil is installed in the wind tunnel open test section, with side plates, with the airfoil leading edge located ${50}\hbox { cm}$ downstream of the wind tunnel nozzle. The side plates end ${70}\hbox { cm}$ downstream of the airfoil trailing edge. This allows sufficient spatial separation of the noise emanating from the trailing edge from other noise sources. A view of the experimental arrangement can be seen in Fig. 5, and a sample acoustic source map is shown in Fig. 6.

The microphone array consists of 64 electret-condenser PUI AUDIO 665-POM-2735P-R omni-directional microphones. The microphones have a sensitivity of ${-35 \pm 2}{\hbox { dB}}$ (ref. ${1}{\hbox { V/Pa}}$) over a frequency range of 0.2–25 kHz. The array arrangement consists of a multi-arm logarithmic spiral configuration (Mueller 2002; Pröbsting et al. 2015b), designed for the suppression of side lobes below ${-12}{\hbox { dB}}$ over the field of view, and frequency range between 1 and ${5}{\hbox { kHz}}$. The microphone array center is pointed straight toward the center of the airfoil and is located at a distance of ${105}\hbox { cm}$.

Fig. 5

Setup for the acoustic measurements (also used for the PIV measurements on the wall-normal plane)

Fig. 6

Source map for serrated trailing edge with $\alpha _g ={12}^\circ$ and $\varphi ={6}^\circ , U_\infty ={35}\hbox { m/s}, f={4565}{\hbox { Hz}}$. The airfoil location (planform boundary) is indicated with the solid line, and the integration region with the dashed line

Data acquisition is performed during 60 s at a sampling rate of ${50}{\hbox { kHz}}$. The sample block length used is 4096, with an overlap of 50 %, resulting in a frequency resolution of ${24.4}{\hbox { Hz}}$. A Hanning window is applied. The number of independent blocks in the ensemble average is $k=1465$, or $k=2930$ considering the 50 % overlap. The normalized random error of the PSD estimate is given by $1/\sqrt{k}$, which conservatively for $k=1465$ results in $\varepsilon _{\text {rand}}\approx 2.6\,\%$, yielding a 95 % confidence interval of ${\approx }2\varepsilon _{\text {rand}}=\pm 5\,\%$.

A beamforming technique is applied following Sijtsma (2010). The resulting source power distribution is integrated over a region around the trailing edge to obtain the source power. This integration region was centered on the trailing edge and is ${20}\hbox { cm}$ long in the spanwise direction, while it scales with the frequency-dependent beamwidth in the chordwise direction.

2.3 Angle of attack correction

In the acoustic measurements an open test section is necessary and was also used for the wall-normal plane PIV measurements. An indication of the effective angle of attack follows from Brooks et al. (1984), where the effective angle of attack $\alpha$ is corrected from the geometric one, $\alpha _g$:

$$\begin{aligned} \alpha = \alpha _g\frac{1+2\sigma }{\left( 1+2\sigma \right) ^2+\sqrt{12\sigma }}\,, \end{aligned}$$

(2)

where $\sigma = \pi ^2C^2/48H^2$. Here C is the airfoil chord and H is the wind tunnel nozzle height. Applying the corrections on the geometric values used in the experiments gives: $\alpha _g = {12.0}^\circ \rightarrow \alpha ={6.6}^\circ$, and $\alpha _g = {6.0}^\circ \rightarrow \alpha ={3.3}^\circ$. The remainder of the discussion will refer to $\alpha _g$. For the measurements in the cross-flow plane and in the near-wall plane (closed test section) it is assumed that $\alpha \approx \alpha _g$.

3 Results and discussion

3.1 Mean flow topology

Results of the cross-flow plane measurements are presented in Fig. 7, where the vorticity component, $\omega _x$, is shown for different configurations of flap angle and airfoil incidence. The position of the serration tip is projected on the measurement plane.

Fig. 7

Cross-flow measurements showing streamwise vorticity for different permutations of $\alpha _g$ and $\varphi$ and $U_\infty = {20}\hbox { m/s}$. Mean flow direction in v and w is indicated with arrows in the four bottom right frames

The presence of streamwise, counter rotating vortex pairs, emanating from the serrations is evident from these results. It is also shown that the circulation pertaining to these vortices is also more strongly correlated with the serrations flap angle, rather than with the incidence of the whole airfoil. An increase in $\varphi$ by ${3}^\circ$ for $\alpha _g={0}^\circ$, increases the vorticity maximum by over ${1000}{\hbox { s}^{-1}}$. Incrementing $\alpha$ by ${3}^\circ$, keeping $\varphi$ constant at ${0}^\circ$, increases the vorticity by just half the amount.

The vortex pairs produce a vigorous upwash motion in between the serrations and a downwash directly behind the serration tips, resulting from the pressure difference established between the two sides of the serrations once they are placed at an angle with respect to the airfoil chord. Similar flow behavior, with a transverse motion between the teeth toward the suction side, has been reported by Arina et al. (2012).

The streamwise vortices give an indication of secondary motions in the wake, in turn associated with the streamline distortion close to the surface of the trailing edge. These observations suggest consequently that the angle by which turbulent fluctuations are advected across the edge will depart from that of the serrations (defined below as $\theta _0$).

Fig. 8

Color contours of time-averaged wall-normal velocity distribution for $\alpha _g = {6}^\circ$ and $\varphi = {6}^\circ$. Straight trailing edge (left), serrated pressure side (middle), and serrated suction side (right)

The result for the normalized wall-normal flow component, $v_r/U_\infty$, for the case where $\alpha _g = {6}^\circ$ and $\varphi ={6}^\circ$, can be seen in Fig. 8. The measurement of the straight trailing edge (located at $x=0$) is also shown for comparison. The outline of the serrated trailing edge is indicated.

On the pressure side (Fig. 8, middle), the flow is directed into the measurement plane over the entirety of the domain. This indicates that flow passes through it with regions of higher velocity in between adjacent serrations at around half a serration length. The velocity on the suction side (Fig. 8, right) exhibits two streamwise elongated regions with positive wall-normal velocity. These regions are consistent with the formation of streamwise vortices observed in the wake.

Fig. 9

Near surface spanwise velocity (color contours) and a qualitative streamline pattern for varying $\alpha _g$ and $\varphi$. Pressure (top) and suction side (bottom)

The near surface flow distortion is better observed in the measurement of $w_r/U_\infty$ (Fig. 9). The streamlines are affected to a different extent when airfoil angle of attack or serration flap angle is increased. The $w_r$ component of the streamlines has been scaled by a factor of four to clarify the direction to which the streamlines point. The effect of flap angle is again more pronounced than that of the airfoil angle of attack.

The near surface flow at the pressure side (Fig. 9, top) exhibits deflection away from the serration centerline, $z_r/2h = 0$. Instead, the streamlines on the suction side (Fig. 9, bottom) appear to converge toward the tip of the serration tooth. This result indicates that the serration trailing edge angle apparent to the mean flow streamlines is being modified by the secondary flow pattern established as a result of a pressure difference. The most direct implication is a discrepancy to the prediction obtained from the model in Howe (1991b).

In the analytical formulation from Howe (1991b), it is argued that flow properties around a distance $\delta$ from the serration edge are relevant to its noise reduction mechanism. When no airfoil incidence or serration flap angle is applied, the mean flow behavior near the serrations has been shown in Fig. 9 to adhere closely to the above assumption. The most notable modification due to serrations remains the change in the effective angle at which the turbulent flow structures convect over the trailing edge. The latter are responsible for noise generation, with the most effective condition for noise production given by streamlines being orthogonal to the edge.

On the suction side the streamlines tend to align even more with the edge, while on the pressure side the behavior is opposite and the streamlines tend to become normal to the edge. Even under these conditions, the serrations have been shown in multiple studies (Gruber 2012; Moreau et al. 2011) to be effective at reducing noise. This further suggests that, although the main working principle hypothesized by Howe (1991b) (to change the effective angle at which the noise generating flow structures convect over the trailing edge) remains true, the validity of frozen flow properties does not hold true.

The angle formed by the streamlines and the trailing edge plays a primary role in Howe’s model [Eq. (1)]. Therefore, understanding how airfoil incidence or serration flap angle modify the flow behavior and the noise reduction is the relevant question addressed. The actual streamline topology obtained from the PIV analysis explains part of this phenomenon.

Fig. 10

Definition of the flow curvature angle, $\theta$, with respect to the serration trailing edge. Schematic situation on the airfoil pressure side

The angle at which the local streamline passes over the serration trailing edge will be referred to as $\theta$ and is illustrated in Fig. 10. Here $\theta _0$ represents the angle between the undisturbed streamline and the serration trailing edge, and $\gamma$ is the local flow deflection over the trailing edge, such that $\theta = \theta _0+\gamma$. The angle $\gamma$ is positive by a deflection that increases the total angle $\theta$.

The serration geometric parameters in Eq. (1) can be rewritten such that it becomes a function of the trailing edge angle. Since

$$\begin{aligned} \cot \theta _0 = 4h/\lambda \,, \end{aligned}$$

(3)

then, from Eq. (1),

$$\begin{aligned} \varPsi \approx \frac{\varPsi _0}{1+\cot ^2\theta _0} = \varPsi _0\sin ^2\theta _0\,. \end{aligned}$$

(4)

Correcting for the streamline deflection yields $\varPsi \approx \varPsi _0\sin ^2\left( \theta _0+\gamma \right)$.

The maximum observed value of $\gamma$ is charted in Fig. 11 for the pressure side. For $\varphi ={6}^\circ , \gamma$ approaches ${4}^\circ$. Figure 11 shows the difference in decibels between the predicted noise of the serrated trailing edge and that of a straight trailing edge. When the value of $\gamma$ increases, the serration is expected to become less effective in reducing the trailing edge noise. For the cases studied here, the serrations are expected to lose approximately ${2}{\hbox { dB}}$ in noise reduction performance at the highest observed deflection only on the pressure side. A simplifying hypothesis is made here that the boundary layer properties (thickness and shape factor) along with the flow turbulence are unaltered by the presence of the serrations at varying values of $\varphi$.

Fig. 11

Values of $\gamma _{\text {max}}$ for different cases measured over the serration trailing edge (left). Expected influence of $\gamma$ on Eq. (4) (right)

From the suction side, instead, following Howe’s approach, one expects an additional reduction of noise emission since the streamline deflection tends to reduce $\theta$ even further, with the flow becoming more parallel to the trailing edge.

There is evidence (see Blake 2012; Bertagnolio et al. 2014) that the contribution of noise between the pressure and suction sides is not equal and the peak noise level is likely to be strongly driven by the boundary layer thickness, suggesting that for a straight trailing edge airfoil the suction side is the dominant source of noise. Based on the observations made regarding the beneficial direction in which the flow is deflected on the suction side, this leads to the conclusion that the observed streamline distortion would further increase the overall noise reduction. This is not observed, and serration misalignment has instead been linked to an increase in noise in the higher frequencies while maintaining similar levels of reduction in the lower and mid-frequency ranges (Gruber et al. 2011).

Admittedly, it must be retained in mind that the value of $\gamma$ is not constant over the serration trailing edge, which should be considered for a quantitative measurement of it. Considering a correction based on the maximum deflection of streamlines, the result does not come to agree with the large differences (approximately ${6}{\hbox { dB}}$) reported between the analytical solution of the serrated trailing edge noise, and the results current and previous of wind tunnel experiments (Gruber et al. 2013; Moreau and Doolan 2013).

Therefore, further elements are taken into consideration below, first of all the boundary layer thickness, shape factor, and the turbulent fluctuations.

3.2 Boundary layer across serrations

The properties of the flow across the serrations are inspected in three planes spanning one serration element. These measurements were taken with the open test section setup, and as discussed above, the correction of the presented geometric angle of attack must be considered. The wall-normal distance, $y_r$, is normalized with the boundary layer thickness, $\delta$, measured at the straight trailing edge at $\alpha ={0}^\circ$ (see Sect. 2).

Fig. 12

Profiles over the wall-normal coordinate direction of $\overline{u_r}$ for the straight trailing edge and three spanwise locations of the serrated edge for $\alpha _g={0}^\circ$ and $\varphi ={0}^\circ$

When the airfoil is at zero incidence and with zero flap angle, no significant difference is found between the straight edge and the cases with serrations (Fig. 12). At higher angles of attack, namely $\alpha _g={12}^\circ \;(\alpha \approx {6.6}^\circ )$, as shown in Fig. 13, clear differences emerge between the straight and serrated trailing edges. The former shows flow with a lower velocity region in the wake location, which is replicated by the $z/\lambda =0.5$ location of the serrated edge after $x/2h=0.5$, and slightly by the $z/\lambda =0.25$ spanwise location further downstream.

Fig. 13

Profiles over the wall-normal coordinate direction of $\overline{u_r}$ for straight and serrated trailing edge for $\alpha _g={12}^\circ$ and $\varphi ={0}^\circ$. Suction side

The time-averaged streamwise velocity field is presented in Fig. 14. The value of $\alpha _g$ is ${12}^\circ$, and the serrations are placed at $\varphi ={6}^\circ$. The three spanwise measurement locations are presented for the serrated case. Contours of $\overline{u}/U_\infty$ are shown along with the projection of streamlines onto the examined planes.

Fig. 14

Time-averaged streamlines and contours of streamwise velocity component, $\overline{u}$. Straight trailing edge on the upper left, and varying spanwise positions of the serrated edge ($\varphi ={0}^\circ$)

Regions of lower velocity are observed close to the serration for the locations $z/\lambda = 0$ and 0.5. These two planes also exhibit a similar shape in the flow topology close to the serration surface and in its near wake. The flow in the measurement plane between adjacent serrations, $z/\lambda =0.5$, shows notable differences. Here the flow passing through adjacent serration teeth is evident, as shown previously in Fig. 8, as well as its influence on the shape, location, and thickness of the wake region.

3.3 Turbulence statistics

The mean flow topology near the serrations has been presented in the previous section and related to the discussion on serrated trailing edge noise in Howe (1991a, b). A look into the flow behavior from a turbulence statistics point of view will be given here.

Fig. 15

Wall-normal profiles of $u^{\prime }_{\text {RMS}}/U_\infty$ for the straight and serrated trailing edges at different spanwise locations, $\alpha _g={0}^\circ , \varphi ={0}^\circ$

The wall-normal profiles of $u^{\prime }_{\text {RMS}}$ are given in Fig. 15. No large differences are evident between the straight or serrated edges, nor for spanwise variations in the latter. The straight and the serrated edges at $z/\lambda =0.5$ do exhibit similar behavior, with higher fluctuations seen further from $y/\delta =0$, and lower values closer to it. These similarities become more evident further downstream. The measured Reynolds stress, $-\overline{u^{\prime }}\overline{v^{\prime }}$, shown in Fig. 16 show a similar trend, with overall little significant differences between the cases, but with the straight edge departing slightly from the serrated edge, which shows almost no spanwise variation.

Fig. 16

Wall-normal values of $-\overline{u^{\prime }}\overline{v^{\prime }}/U^2_\infty$ for the straight and serrated trailing edges at different spanwise locations, $\alpha _g={0}^\circ , \varphi ={0}^\circ$

Measurements of $u^{\prime }_{\text {RMS}}$ for an airfoil incidence of ${12}^\circ$ (Fig. 17) show notable differences between straight and serrated trailing edges, and also along different spanwise locations of the latter. When $z/\lambda =0$, a behavior similar to what was seen for $\alpha _g={0}^\circ$ for all streamwise locations is experienced. Measurements at $z/\lambda =0.25$ and 0.5 show a distinctly stronger decrease in fluctuation intensity around the wake centerline, an effect which is more apparent for locations further downstream. Values for the off-center spanwise locations are higher than for the $\alpha _g={0}^\circ$ case for regions downstream of $x/2h=0.25$, but remain similar for the $z/\lambda =0$ location.

Fig. 17

Values of $u^{\prime }_{\text {RMS}}/U_\infty$ for the straight and serrated trailing edges on the suction side (top) and pressure side (bottom), for different spanwise locations, $\alpha _g={12}^\circ , \varphi ={0}^\circ$

Fig. 18

Values of $v^{\prime }_{\text {RMS}}$, suction side (top) and pressure side (bottom), for different values of $\alpha _g$ and $\varphi$ for the serrated trailing edge

Measurements of $v'_{\text {RMS}}$ for different values of $\alpha _g$ and $\varphi$ are taken for $z/\lambda =0.25$ and shown in Fig. 18. At the suction side, cases at incidence or with flap deflection show higher values of $v'_{\text {RMS}}$ than for $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$. At $x/2h=0.5$, the serration trailing edge intersects the measurement plane, which reveals a change in the flow structure from this point onwards. Beyond $x/2h=0.5$, the cases with incidence and flap angle exhibit more pronounced differences. In particular, the $v'_{\text {RMS}}$ values are significantly higher above $y_r/\delta \approx 0.25$, reaching maximum values of around $v'_{\text {RMS}}\approx 0.07$ close to $y_r/\delta \approx 0.4$, and exhibiting a similar profile between them. The $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$ case has instead its maximum closer to $y_r/\delta =0$ and remains largely unchanged for the different streamwise locations.

At the pressure side, measurement of $v'_{\text {RMS}}$ for cases at incidence or with flap angle shows higher values than for $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$. For the former, values of $v'_{\text {RMS}}$ also cover a smaller $y_r$ extent before dropping to zero. Translating the above observations in terms of noise generation by the trailing edge requires the evaluation of the intensity and spectrum of the hydrodynamic surface pressure fluctuations that are scattered by it (see Pröbsting et al. 2015a; Bull 1979; Brooks and Hodgson 1981). In the present experiments, the measured amplitude of wall-normal RMS fluctuations and their closeness to the sharp edge is used to infer a trend in the expected sound level that is produced. The higher values seen here for the cases with airfoil incidence or serration flap angle are found to be well in line with the increase of noise emissions that are measured by the serrations at these configurations with respect to the case at $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$. This result is recalled in the discussion of Sect. 3.4.

The Reynolds stress $-\overline{u'_r v'_r}$ of Fig. 19 shows overall higher values than for the zero incidence measurements. The $z/\lambda =0.5$ case approaches the profile of the straight edge for downstream locations, and $z/\lambda =0.25$ follows with less intensity but a similar shape. The serration centerline plane measurements remain distinctly different and follow the shape seen earlier for $\alpha _g={0}^\circ$, but with higher values.

Fig. 19

Values of $-\overline{u'_r v'_r}$ for the straight and serrated trailing edges on the suction side (top) and pressure side (bottom) at different spanwise locations, $\alpha _g={12}^\circ , \varphi ={0}^\circ$

Fig. 20

Values of $-\overline{u'_r v'_r}$, suction side (top) and pressure side (bottom) at different values of $\alpha _g$ and $\varphi$ for the serrated trailing edge

The spatial distribution of $-\overline{u'_r v'_r}$ is illustrated in Fig. 20 at the spanwise location of $z/\lambda =0.25$, where the measurement plane intersects the serration edge at $x/2h=0.5$. Values of $-\overline{u'_r v'_r}$ over the suction side attain a minimum for $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$. Instead, the cases with airfoil incidence and serration flap angle exhibit Reynolds shear stresses approximately three times higher, with the case $\alpha _g={12}^\circ ,\,\varphi ={6}^\circ$ showing the highest. The location of the maxima varies as well between cases, where for $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$ it is approximately at $y_r/\delta =0.25$, and for the other cases it increases from around $y_r/\delta =0.25$ at $x/2h=0$ to $y_r/\delta =0.7$ and 0.5 for $x/2h=1$. At the pressure side, the situation is similar to that observed for the wall-normal fluctuations, with the case $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$ yielding the highest values of $-\overline{u'_r v'_r}$, and also extending over a larger extent of $y_r$ before dropping to zero.

The amplitude of Reynolds shear stresses is associated to the importance of turbulent activity at relatively small scales in the boundary layer (see Ganapathisubramani et al. 2003; Ghaemi and Scarano 2013). In the present context, higher values of $-\overline{u'_r v'_r}$ are therefore associated to a potential increase of sound production in the high-frequency range of the spectrum. The acoustic measurements of serrated edges presented in Sect. 3.4 reveal indeed that cases with larger values of $\alpha _g$ and $\varphi$ are louder than the case at $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$, and even than the straight trailing edge. This is particularly evident at higher frequencies, which could be explained by the behavior of $-\overline{u'_r v'_r}$ and $v'_{\text {RMS}}$.

Fig. 21

Velocity fluctuations of components $u^{\prime }_{\text {RMS}}$ (top) and $v^{\prime }_{\text {RMS}}$ (bottom), for the straight edge (left), and the serrated edge ($\varphi ={0}^\circ$ and ${6}^\circ$) at the spanwise location $z/\lambda = 0.5$ and $\alpha _g={12}^\circ$

To visualize the location of regions with high $u^{\prime }_{\text {RMS}}$ and $v^{\prime }_{\text {RMS}}$ for different cases with $\alpha _g={12}^\circ$, Fig. 21 shows the contour plots for the $z/\lambda =0.5$ plane. The straight trailing edge shows higher $u^{\prime }_{\text {RMS}}$ and $v^{\prime }_{\text {RMS}}$ on the suction side which continues downstream while another region of higher RMS is seen to originate from the trailing edge. This behavior was previously observed in the PIV measurements conducted in Finez et al. (2011). The serrated trailing edge with $\varphi ={6}^\circ$ shows this effect as well, and this region of increased fluctuations is seen to originate from the root of the serrations. The presence of this pattern is not evident in the serrated case with $\varphi ={0}^\circ$. Trailing edge noise is mainly produced by the more effective scattering mechanism related to dipole noise sources than by quadrupole sources in the turbulent wake (Howe and Street 1999). Nevertheless, the considerable increase of turbulence intensity near the serrated trailing edges caused by the misalignment of the serration teeth may indeed be the source of additional sound that has been reported in other studies, for example Gruber et al. (2011), where flow has been measured with hot wire.

Further evidence of the effect of serration misalignment and the increase in turbulence intensity can be seen in the cross-flow plane measurements at the wake of the serrations (Figs. 22 and 23). Higher levels of turbulence intensity can be seen for the u component than for the v component, supporting the observations made in the wall-normal plane. The u component exhibits periodic and alternating up/down facing horseshoe-shaped regions of increased fluctuations behind the tips ($\cup$ shaped), and the roots of the serrations ($\cap$ shaped), with slightly higher $u^{\prime }_{\text {RMS}}$ from the tip regions. The fluctuation intensity of the v component (Fig. 23) shows similar patterns but is instead dominant in the region behind the serration root. This region is also where opposing streamwise vortices are in close proximity (see Fig. 7).

Fig. 22

Velocity fluctuations of the u component in the cross-flow plane

Fig. 23

Velocity fluctuations of the v component in the cross-flow plane

The $\alpha _g={0}^\circ$ and $\varphi ={0}^\circ$ case shows no significant modulation along the spanwise direction. Increasing $\varphi$ causes a rapid increment of velocity fluctuations, which indicates that serrations at incidence cause an increase of turbulent fluctuations, in addition to altering the time-averaged streamlines patterns. Despite the above conditions, in the next section it is shown that the overall effect of serrations remains that of reducing the noise emissions (near ${7}{\hbox { dB}}$ for some frequencies).

Fig. 24

Values of the Reynolds stress $-\overline{u'_r v'_r}$ in the cross-flow plane

Observations in the cross-flow plane downstream of the serrations enable to visualize the spanwise distribution of the Reynolds shear stresses (Fig. 24). The airfoil incidence and the flap deflection introduce a significant increase of $-\overline{u'_r v'_r}$ with respect to the $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$ case. Positive maxima are formed trailing the serration teeth center, whereas negative-valued maxima emanate from the serration valleys. The value of these maxima is two to three times higher than that measured at zero incidence, with a slightly higher peak value originating from the pressure side shear layer. The overall pattern of Reynolds shear stresses is highly correlated with that of the vorticity distribution in Fig. 7, indicating an increase of turbulent kinetic energy production at airfoil incidence and flap deflection. The overall conclusion is that the Reynolds shear stress increase is more pronounced than that of $u^{\prime }$ (approximately 30–50 %) and $v^{\prime }$ (50–70 %), which preludes to an increase of sound production especially at the high-frequency side of the spectrum. In the following section, evidence is gathered on the above increase (also referred to as loss of noise reduction efficiency) of serrations when placed at incidence.

3.4 Noise emissions

Fig. 25

Third-octave sound pressure levels for the straight, and two serrated trailing edges, with $\alpha _g = {0}^\circ$ and $U_\infty = {35}\hbox { m/s}$

The third-octave band sound pressure level, SPL, of the straight trailing edge airfoil and the serrated airfoil can be seen in Fig. 25 for $\alpha _g={0}^\circ$ and $U_\infty ={35}\hbox { m/s}$. The serrations are shown to be effective at reducing the noise emitted by the airfoil trailing edge. Also, there is a marked difference between the noise measured using the serrations with $\varphi ={0}^\circ$ and those with $\varphi ={6}^\circ$.

Results of the measured noise for the serrations relative to the straight edge are shown in Fig. 26. The three airfoil incidence cases and the two serration flap angles are presented for a freestream velocity of ${35}\hbox { m/s}$. The vertical axis represents the measured sound pressure level difference in decibels with respect to the straight trailing edge, where a positive number indicates a reduction in noise and a negative value represents an increase in noise.

At $\varphi = {0}^\circ$ (Fig. 26, top), the serrations offer a reduction of up to ${7}{\hbox { dB}}$ for the frequency band between ${1}{\hbox { kHz}}$ and ${3}{\hbox { kHz}}$. Beyond this upper limit, the reduction vanishes when approaching ${5}\hbox { kHz}$. At $\varphi = {0}^\circ$ the change in angle of attack has only a small effect on the noise reduction.

When the serrations are placed at $\varphi ={6}^\circ$ (Fig. 26, bottom), the noise reduction is less pronounced, to the point that, depending on airfoil incidence, an increase of noise is measured in the higher frequency range. This increase may relate to the presence of high RMS in the flow caused by these high flap or airfoil incidence angles, as discussed in the previous section. The frequency where such inversion occurs is denoted as crossover frequency, $f_0$, and has been reported in detail in Gruber et al. (2010).

Fig. 26

Measured noise differences in third-octave band SPL of serrations relative to the straight trailing edge for $U_\infty = {35}\hbox { m/s}$, for $\varphi ={0}^\circ$ (top) and ${6}^\circ$ (bottom). The noise of the serrated trailing edge of a flat plate according to Howe (1991b) is also presented, for which only the $\alpha _g={0}^\circ$ and $\varphi ={0}^\circ$ case is applicable

The approximation of Howe (1991b) for the noise of a similar serration geometry on the trailing edge of an infinitely thin flat plate under the same flow conditions, without incidence, is also presented in Fig. 26 (solid line). The differences observed with the experimentally measured noise from the serration-retrofitted airfoil are notable. A variation regarding the spectrum shape is persistent, where the present case shows higher reduction at the lower and mid-frequency range presented, and less reduction in the higher frequencies. Instead, the prediction indicates an opposite behavior. This contrast has also been reported in Gruber et al. (2011). Alternatively, a simplistic application of Eq. (4) based on the spectrum of the straight edge in Fig. 26 would be approximated as a constant reduction for all frequencies, thus represented as a straight line, at the same predicted constant reduction discussed above in Fig. 11, indicating an overestimation of at least ${5}{\hbox { dB}}$ over the reduction levels here observed. Its inclusion is omitted for conciseness.

Although the authors have determined that the degree of serration-flow misalignment significantly affects the efficiency at which the serrations reduce noise, the fact that the discrepancies between the predicted and measured levels of reduction are present for the $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$ case, indicates that misalignment by itself cannot be used to explain them. A comprehensive study of the boundary layer flow properties, especially using time-resolved information, could help identify further reasons for this discrepancy. This analysis demands a dedicated scrutiny and is reserved for an independent paper.

4 Conclusions

The mean topology and the turbulence statistics of the flow near trailing edge serrations have been studied using PIV under different degrees of airfoil incidence and serration flap angle. The PIV measurements yield the pattern of streamlines close to the surface of serrations enabling to quantify their departure from the freestream direction. Measurements in the cross-flow plane indicate the presence of streamwise vortices emanating from the serrated edge, with their strength primarily influenced by the serration flap angle. The results of the mean flow measurements are input to a simplified version of the model in Howe (1991b) that estimates relative noise reduction on the basis of the local angle between the flow and the trailing edge.

The study is complimented with acoustic measurements, by which it is shown that the serrated trailing edge effectively reduces the turbulent boundary layer trailing edge noise of the airfoil, although to a lesser extent than that which the prediction suggests. This is consistent with experimental findings reported in the literature. The PIV survey further reveals that, in the $\alpha _{g}={0}^\circ , \varphi ={0}^\circ$ case, the mean flow and turbulence statistics do not exhibit significant changes, yet a noticeable noise reduction is achieved. When serration-flow misalignment is prescribed, the flow undergoes important changes in various mean flow and turbulence statistic measures. Despite this significant departure from the assumed conditions in the Howe model, the noise is still reduced in the lower frequencies of the range measured. At higher frequencies, the noise is instead increased. Changes in turbulence statistics between serration-flow misaligned cases and the $\alpha _g={0}^\circ ,\,\varphi ={0}^\circ$ case serve to explain the observed change in acoustic emissions.