Abstract
The unsteady effect of a periodic pitching motion on the characteristic of a laminar separation bubble on the suction side of a SD7003 aerofoil is investigated by means of time-resolved planar and tomographic particle image velocimetry. The measurements provide information on the separation, transition and vortex roll-up onset as well as the spanwise distribution of vortical structures, for both the dynamic pitching between 4° and 8° and corresponding cases at a static pitch angle. During pitching, a clear hysteresis behaviour is observed for the vortex roll-up position and shedding frequency, showing a strongly delayed recovery of the shear layer with respect to the steady aerofoil case. The development of the shear layer transition exhibits initially 2D Kelvin–Helmholtz rollers that are interrupted, forming Λ-shaped rollers, which eventually evolve into 3D arch-shaped hairpin structures. The 3D analysis of undulated rollers allowed the determination of the rollers streamwise spatial separation for both static and pitching aerofoil cases .
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
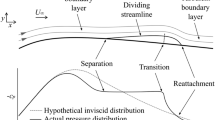
Flow research on aerofoils subjected to a pitching oscillation have predominantly dealt with the high Reynolds number regime that is relevant to aeronautical applications such as wing flutter. As recent developments have witnessed a reduction in size towards small unmanned air vehicles (UAV), the flow over pitching aerofoils at moderate Reynolds numbers \(O(10^4\)–\(10^5\)) has become of increasing interest in relation to small helicopters and ornithopters. At these low Reynolds number conditions, a laminar separation bubble (LSB) is observed to occur, as illustrated in Fig. 1. As a consequence, under such conditions the tendency for flow separation is more critical than at high Reynolds numbers as it deteriorates aerodynamic performances (McMichael and Francis 1997).
One of the first documented experimental observations of a LSB was reported by Jones (1934). Only years later, (Gaster 1966) performed extensive research on the time-averaged characteristics of a LSB, determining the influence of pressure gradient and Reynolds number that lead to short and long bubbles. Notwithstanding these efforts, no physical explanation and criterion for the bubble bursting from short to long bubbles has found general acceptance so far (Diwan et al. 2006). The parameters governing the bubble characteristics were also investigated by Horton (1969) and O‘Meara and Mueller (1987), who described the LSB structure as a locally confined laminar flow separation with a subsequent turbulent reattachment closing the separated region. Downstream of laminar separation the LSB is enclosed by a separated shear layer that divides a recirculating flow region from the outer flow and along which laminar-to-turbulent transition occurs.
Advances in both experimental and computational capabilities enabled detailed studies on the transition mechanism of shear layers, including the receptivity to oncoming disturbances and breakdown to turbulence (Watmuff 1999; Alam and Sandham 2000; Lang et al. 2003). These investigations suggested that the transition and reattachment processes were governed by amplification of Tollmien–Slichting (T–S) waves in the attached boundary layer upstream of separation, the adverse pressure gradient that separates the flow and the amplification of Kelvin–Helmholtz (K–H) instabilities in the separated shear layer. By forcing unsteady 3D disturbance modes (travelling waves) in combination with small amplitude T–S waves in the boundary layer, Marxen et al. (2003) showed that 2D T–S waves affect the position and size of the LSB, whereas a spanwise modulation of forced T–S waves does not influence the transition scenario significantly. These conclusions were based on time- and spanwise-averaged mean flow descriptions as obtained by laser Doppler anemometry and particle image velocimetry (PIV).
Direct numerical simulations (DNS) revealed that the application of volume forcing and low-frequency main flow disturbances to the LSB triggers the K–H instabilities more upstream, reducing bubble size and therefore improving aerodynamic performance (Lou and Hourmouziadis 2000; Wissink and Rodi 2004; Jones et al. 2008). Burgmann and Schröder (2008) demonstrated experimentally a decreasing bubble size as well as an upstream shift of the separation, transition and reattachment locations, when increasing Reynolds number (\(2\times 10^4\)–\(6\times 10^4\)), angle of attack (\(4^\circ\)–\(8^\circ\)) or free stream turbulence intensity level. Similar turbulence level effects had been observed by Ol et al. (2005) in three different facilities at \({Re} = 6\times 10^4\) and an incidence angle of \(\alpha =4^\circ .\)
Further numerical and experimental analyses by Yang and Voke (2001), Lang et al. (2003) showed that transition is the result of amplification of K–H instabilities in the separated shear layer, which leads to the roll-up and subsequent shedding of large vortices at the rear part of the bubble. These results are supported by recent studies from, e.g. Burgmann et al. (2007), Hain and Kähler (2005) and Zhang et al. (2008) who have applied time-resolved planar or stereo scanning PIV in order to gain insight into the temporal development and 3D spatial formation of a LSB on a SD7003 aerofoil, as well as the behaviour of the vortices formed in the shear layer. In their analysis the choice for this specific aerofoil was motivated by the well-developed laminar separation bubble on its suction side. Burgmann et al. (2007) observed that in the process towards reattachment, the K–H instabilities lead to a smooth transition of the LSB, inducing a two-dimensional spanwise vortex roll-up of the separated shear layer. As the two-dimensional rollers entrain fluid from the outer flow and move downstream, they shed from the shear layer and undergo a deformation process into c-shaped vortices, which evolve to arch-like Λ-structures and eventually breakdown into turbulence, showing hairpin-like structures. This process is considered smooth, as no sudden bursting of vortices, i.e. a fluid ejection off the wall, occurs. Similar observations were also obtained from detailed numerical simulations by Visbal et al. (2009).
Moreover, the PIV analyses revealed that the entrainment of high-momentum fluid from the outer flow towards the wall, by the shed vortices, compensates for the effect of the adverse pressure gradient, leading to a closure of the recirculation region by turbulent reattachment. Due to its turbulent nature this reattachment was found to be an unsteady process, where the vortex formation frequency corresponds to the K–H instability frequency (Burgmann et al. 2007), causing a streamwise and vertical flapping motion of the shear layer close to reattachment (Zhang et al. 2008).
Similar to the static angles of attack cases (Rudmin et al. 2013) measured a decreased bubble size and a downstream moving bubble as the incidence angle is increased during quasi-steady pitching motions at a low reduced frequency varying between 0.0011 and 0.0020. The measurements were performed using hot films on the suction side of a NACA-0012 aerofoil. Concerning unsteady pitching motion effects on boundary layer transition, Pascazio et al. (1996), Lee and Basu (1998) and Lee and Petrakis (1999) performed measurements on a NACA-0012 aerofoil oscillating at different reduced frequencies \(k =\pi fc/U_\infty\) and Reynolds numbers, that varied, respectively, from \(k = 0.026\) to \(k = 0.283\) and \({Re} = 1\times 10^5\) to \({Re} = 2\times 10^5.\) During (part of) the pitching motion, a LSB was observed on the upper surface and when present, the boundary layer transition occurred in the separated shear layer. It was shown that, during a sinusoidal oscillating motion, pitch-up delays the onset of separation and boundary layer transition relative to the static case, affecting moreover the reattachment process. As the aerofoil pitches down the opposite effects occur: compared to the relative steady cases separation and transition are found to be promoted and a thinner boundary layer occurs. The transition–laminarisation cycle was observed to follow a slightly asymmetric hysteresis cycle, where the effect is stronger close to the trailing edge as a consequence of the trailing-edge flow separation.
The hysteresis cycle showing the delay of separation on an oscillating NACA-0012 aerofoil was confirmed by Kim and Chang (2009), using surface-mounted hot-wire probes and smoke-wire visualisations. In their investigation they observed that this delay increases with Reynolds number. Lee and Basu (1998) and Lee and Petrakis (1999) attribute these stabilising effects to the convective time lag and the boundary layer improvement effects in unsteady motion as suggested by Ericsson and Reding (1972), where the motion affects the pressure gradient as is shown by the non-stationary Bernoulli equation
with \(\xi = x/c.\) This suggests that for equal angle of attack, \(\alpha,\) the local pressure gradient is more favourable during pitch-up motion when compared to its static situation. Therefore the boundary layer is improved by this more favourable upstream time history. As a result separation is supposed to occur more downstream during pitch up, when compared to the steady case. According to this accelerated mass flow theory the opposite is expected to occur during downward motion.
Wissink and Rodi (2003) showed by DNS simulations at \({Re} = 6\times 10^4\) that a periodically changing inflow affects a LSB on a flat plate due to a time-varying streamwise pressure gradient, causing the boundary layer flow to alternately separate and reattach. As the inflow decelerated, a new separation bubble was formed in each period and it was shown that K–H instabilities tend to form in the shear layer during the oscillating inflow. Similar to the steady case, these instabilities caused the initial roll-up of the shear layer, where the roll-up was followed by 3D Ω-shaped flow structures, which were partially entrained in the new separation bubble. In case of accelerated inflow, a spanwise roll of turbulent flow is shed from the shear layer and after shedding, the remainder of the separated bubble was found to rejoin with the shed turbulent roll while it travels downstream.
Whereas, for a stationary aerofoil, quantitative and qualitative studies of the flow effects have been reported on the LSB characteristics, the dynamic effects, such as those induced by a periodic variation of the incidence angle, have only been observed qualitatively. Therefore, the specific objective of the present work is to perform detailed qualitative and quantitative investigations of the dynamic effects on the LSB characteristics and to analyse the three-dimensional transition and vortex formation phenomena that are induced by a periodical pitching motion of the aerofoil. Time-resolved planar and tomographic PIV measurements have been performed on the suction side of an SD7003 aerofoil at a Reynolds number of \(3\times 10^4\). The applicability of planar PIV to this type of investigation has been demonstrated by Hain et al. (2009), and the feasibility of tomographic PIV as a reconstruction method (in boundary layer flows) can be found in Humble et al. (2009).
The influence of a pitching motion on the LSB are analysed by comparing the transition process on a steady aerofoil at fixed \(4^\circ\), \(6^\circ\) and \(8^\circ\) angle of attack, to that on an unsteady aerofoil, which pitches at a reduced frequency of \(k = 0.2\) between \(4^\circ\) and \(8^\circ\) incidence angle.
2 Experimental methodology
2.1 Experimental model
The investigations are performed on the suction side of a SD7003 aerofoil with a chord length of 80 mm and a span of 400 mm. The aerofoil is made of black anodised aluminium to guarantee a stiff and light structure that minimises laser light reflections and inertial instabilities during the unsteady pitch. Its rotation axis was fixed at 1/4-chord, and the Maxon DC RE 35 Motor has been chosen as the actuator of the push–pull system driving the aerofoil pitching motion. This engine has programmable rpm, position and unit ramp inputs. By regulating the engine’s angular velocity, the system kinematics allowed to impose a sinusoidal motion of the aerofoil’s incidence angle \(\alpha = \alpha _0 +\Delta \alpha \sin (2\pi ft)\), with nominal settings of \(\alpha _0 = 6^\circ\), \(\Delta \alpha = 2^\circ\). The frequency of oscillation \(f = 4.5\) Hz is chosen such that at the desired Reynolds number of \(30 \times 10^4\) the reduced frequency \(k = 0.2\).
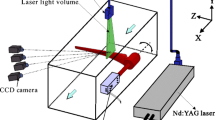
The wind tunnel facility has been used in open exit configuration of \(0.40 \times 0.40\,{\text {m}}^2\) cross-sectional area and fitted with a transparent extension to allow full optical access and to accommodate the actuator for the pitching motion. Figure 2 shows a sketch of the extension box containing the aerofoil in its vertical position.
During the experiments, the velocity is regulated by a pitot tube at \(5.67 \pm 0.04\,{\text {m}}/{\text {s}}\) such that \(Re \approx 30{,}000\). For the flow conditions chosen, previous hot-wire anemometry measurements indicate a turbulence level of \(Tu < 0.2\,\%\) in the centre of the test section.
2.2 Experimental set-up
The measurements are performed using two experimental configurations. Planar TR-PIV is used for quantifying the LSB characteristics in the cross-sectional plane. Tomographic TR-PIV experiments are performed to visualise the 3D dynamics of the vortex roll-up and shedding and the spanwise distribution of vortical structures. The selection of the specific volume used for the Tomographic TR-PIV investigations was based on the results obtained from the planar PIV. Figure 2 shows the configuration views used for both investigations.
Water-based fog droplets of 1 \(\upmu {\text {m}}\) diameter are injected into the test section as seeding particles. The particles are illuminated by a Quantronix Darwin Duo dual oscillator, single-head Nd:YLF laser. The laser light is emitted at 527-nm wavelength and each pulse has a duration of 200 ns and an energy of 25 mJ at 1 kHz. The light scattered is subsequently captured by 2 (for planar PIV) or 4 (for tomographic PIV) LaVision HighSpeedStar cameras with a sensor size of \(1024 \times 1024\) pixels. The acquisition rate of the double frame is 5.4 kHz, yielding an effective vector field acquisition frequency of 2.7 kHz, i.e. 2700 vector fields per second. The data acquisition and analysis is performed by the DaVis 7.4 software from LaVision GmbH. Table 1 shows the set-up parameters chosen for the two experimental configurations.
2.2.1 Planar PIV configuration
In order to detect the LSB at all the desired angle of attack cases and simultaneously satisfy a high spatial resolution, two cameras with 105-mm lenses are used as shown in Fig. 2a. The resulting fields of view captured by each camera, FOV1 and FOV2 in Fig. 3, have a 5 % overlap in order to couple the images by an image stitching routine used in the DaVis software. This results in a total FOV of \(103 \times 54\) mm that allows to capture the flow around the full aerofoil. After stitching, the minimum intensity level present in all images is subtracted from the original images. Subsequently, these images are then normalised by dividing by the local average intensity of the images. As a last image post-processing step, a masking function is applied at the position of the aerofoil surface. The elaborated images are cross-correlated using a \(12 \times 12\) pixel window size with 50 % overlap, leading to a vector pitch of 0.3 mm as shown in Table 1.
2.2.2 Tomographic PIV configuration
The tomographic PIV experiments provide a characterisation of the vortex dynamics and of its spanwise distribution. Literature has shown that the vortex roll-up and shedding occur in the downstream part of the LSB (Burgmann et al. 2007; Burgmann and Schröder 2008). Therefore, the area of interest to be observed during tomographic experiments was selected on the basis of the observations obtained from the planar TR-PIV measurements. The tomographic field of view is chosen such that it captures the vortex roll-up and shedding for both the static and pitching situation. In chordwise direction this yields a FOV that covers at least 85 % of the chord. Furthermore, the measurement volume is dictated by the spanwise dimensions of the characteristic structures expected to occur in the LSB. Burgmann and Schröder (2008) visualised arch-like structures by considering a FOV that covers 30 % of the chord in spanwise direction. The depth of the measurement volume in the direction normal to the aerofoil chord is determined by the height of the bubble, since the characteristic vortices generated scale with this height. To satisfy all conditions, the laser light sheet used illuminates a volume parallel to the aerofoil span and along its suction side and covers a volume of \(50 \times 70 \times 15\) mm. The set-up used is shown in Fig. 2b, indicating the four cameras used to capture the particle motion inside the volume. The cameras form a solid angle of \(30^\circ\) for optimal reconstruction quality, since beyond \(60^\circ\) total aperture angle, an optimal configuration is reached for a 3D tomographic system aperture (see Scarano 2013). All off-axis cameras use 105-mm Nikon lenses, while the upper centre camera uses a 60-mm Nikon lens. Furthermore lens mounted adaptors were used to satisfy the Scheimpflug condition.
The laser sheet, formed by a diverging lens, is deflected by a mirror to illuminate the region of interest. In order to double the light intensity reflected by the tracer particles in the measurement volume, another mirror is installed on the tunnel lower wall to reflect the incoming light. The used camera aperture diameter \(f_\#\) is 5.6. According to \(d_z = 4.88\lambda f_\#^2(1+M)^2(M)^{-2}\) (Raffel et al. 2007) a focal depth of about 2 mm is obtained, where the cameras’ plane of focus is placed in the shear layer region, i.e. the region in which vortex shedding occurs. In the focal plane, the particles are locked to one pixel. Despite the low depth of focus, this choice allowed a good tomographic reconstruction throughout a measurement volume of 6–10 mm thickness, since the image size of particles outside the region of focus is larger, attaining approximately 3–4 pixel. The particle images maintain a disc-like intensity distribution and are reconstructed with sufficient accuracy, according to other measurement indicators (reconstruction intensity profile, percentage of spurious vectors, measurement noise). The 4-pixel size for the out-of-plane particles at the edge of the measurement volume, i.e. for \(\Delta z_0 = 7.0\,\text{ mm }\), is in accordance to both the simplified thin lens equation suggested by Cierpka et al. (2010) and the approximate expression for the blur circle as discussed in Scarano (2013).
The tomographic reconstruction is performed by mapping the particle projections onto the physical space through a calibration procedure discussed by Elsinga et al. (2006). Four calibration, planes were used and by applying self-calibration the error is reduced to less than 0.2 pixel (Elsinga et al. 2006; Wieneke 2008), which permits an accurate reconstruction of the particle position in the 3D volume. Both calibration and its correction are performed by the Davis software. In the post-processing procedure, a last MART smoothing parameter (Elsinga et al. 2006) of 0.5 is used.
The visualisation of the 3D vortical structures in the bubble region is performed by applying the Q-scheme to the data obtained from tomographic PIV. This method is a vortex identification method and considers the positive second invariant of the velocity gradient tensor Hussain and Jeong (1995), which yields for incompressible flows \(Q \equiv \frac{1}{2}(\Vert {\varOmega }\Vert ^2 - \Vert {{\varvec{S}}}\Vert ^2)\), where \(\Vert \mathbf{S }\Vert = [{\text {tr}}](S\;S^{t})]^{1/2}\) \(\Vert {\varOmega }\Vert = [{\text {tr}}(\varOmega \;\varOmega ^{t})]^{1/2}\) and \({{\varvec{S}}}\) and \({\varOmega }\) are the symmetric and antisymmetric components of the velocity gradient tensor.
2.3 Determination of separation bubble characteristics
In determining the bubble characteristic, both the raw particle image data and the post-processed data obtained from planar PIV are used. The separation point, \(x_{{\text {s}}}\), is determined by following by eye the particle movement in the raw PIV data. Based on particle track evaluation allows us to determine the separation point within 1–3 pixels, where the error in measuring particle positions in PIV is considered 1 pixel (\(<\)0.07 % c), while the statistical errors in determining the separation point are found at highest 3 pixel (\(<\)0.2 % c). The time-averaged reattachment location, \(x_{{\text {r}}}\), is found at each angle of attack from the time-averaged streamlines.
The transition location, \(x_\mathrm{tr}\), is determined by considering the line of maximum normalised Reynolds stress, \(\overline{u^{\prime }v^{\prime }}/U^{2}_{\infty }\), above the aerofoil upper surface and along the chord. An example is shown in Fig. 4a. The transition point is defined as the location where the normalised Reynolds stresses starts to increase exponentially along this line, i.e. the location where the logarithmic slope of this Reynolds stress curve changes dramatically; a similar approach was used by Burgmann and Schröder (2008). These results are compared to a second method used by Burgmann and Schröder (2008) and Ol et al. (2005) where the transition location is determined at the chord-wise position at which Reynolds stresses reach a threshold value of 0.001. For simplicity these two methods are referred to as the Transition Exponential Method (TEM) and the Transition Threshold Method (TTM), respectively. Figure 4b illustrates the application of both methods to the data found at \(6^\circ\).
a Lines at which \(\overline{u^\prime v^\prime }/U_\infty ^2\) (dark blue), \(\overline{v^{\prime 2}}\) (light blue) and \(PSD_{\max }(v^\prime )\) (red) are maximum for the steady aerofoil at \(\alpha =6^\circ\). b Determination of transition and vortex roll-up onset locations according to the Exponential, the Threshold and the Wavelet method at \(\alpha =6^\circ\)
The vortex roll-up location, \(x_{{\text {vort}}}\), is determined using a wavelet transform method and is compared to two more conventional methods that were suggested by Burgmann et al. (2007). For these two approaches a Fourier transform analysis is performed to obtain the power spectral density (PSD) field of the \((v^\prime )\) component above the aerofoil upper surface. Then the line of the maximum \({\text {PSD}}_{\max }(v^\prime )\) value is considered, as shown in Fig. 4a. The vortex roll-up location is determined as the location on this line at which \({\text {PSD}}_{\max }(v^\prime )\) shows an exponential rise or where it reaches a threshold value of 0.002 (Burgmann et al. 2007), as shown in Fig. 4a. These conventional methods are only used for the steady aerofoil configuration, since the Fourier transform analysis cannot be used for the pitching aerofoil case. For this reason, the wavelet analysis approach is used as a reference method to determine the vortex roll-up locations for both the steady and pitching aerofoil cases. In this approach the vortex roll-up onset is determined along the line of the \(\overline{v^{\prime 2}}\) maxima, the light blue line shown in Fig. 4a. Along this line the complex Morlet-type wavelet transform analysis is applied to the vertical velocity components \(v^\prime\). This results in a contour plot as, e.g. shown in Fig. 5, where wavelet coefficients are plotted as a function of frequency and location along the line of \(\overline{v^{\prime 2}}\) maxima. As will be shown later, the strongest fluctuations located most upstream along the chord occur at the shedding frequencies. By considering the wavelet coefficients at this frequency, i.e. along line B in Fig. 5, a wavelet curve is obtained as a function of x/c position. This curve is shown in Fig. 4b for the steady case obtained at \(\alpha = 6^\circ\). The vortex roll-up location is defined at the position where the wavelet coefficients increase exponentially along this curve. When applying the wavelet analysis method to the static angle cases, the vortex roll-up onset locations determined deviate less than 3 % chord length from the location found by the more conventional thresholds and exponential growth methods. This validates the method as a convenient tool for the unsteady aerofoil configuration.
The shedding frequency of the generated vortices is determined using three approaches: (1) counting the amount of vortices shed within a known time interval, (2) spectral analyses with the fast Fourier transform (FFT) analysis and (3) wavelet analysis.
The FFT analysis determines the shedding frequencies by considering the frequencies belonging to the PSD\(_{\max }(v^\prime )\) values obtained along the line of maximum PSD\(_{\max }(v^\prime\)) at the location of \(x_{{\text {vort}}}\). This approach can, however, only be used for the static aerofoil cases.
By using the wavelet analysis, the shedding frequencies are determined for both the steady and unsteady cases. The resulting wavelet coefficient contour plots, see, e.g. Fig. 5, show initially high peak values in the close vicinity of the vortex roll-up location and at the specific frequency, which corresponds to the shedding frequency determined by manual counting and the FFT analyses (for the case displayed this occurs at 510 Hz).
The Strouhal number is defined as \(S_t=f_{{\text {shed}}}\theta _{{\text {s}}}/U_{{\text {s}}},\) where \(f_{{\text {shed}}}\) represents the shedding frequency, \(\theta _{{\text {s}}}\) and \(U_{{\text {s}}}\) are, respectively, the momentum thickness and velocity at the boundary layer at separation (Burgmann et al. 2007; Burgmann and Schröder 2008). As these last two parameter cannot be determined accurately from the experiments, their values were estimated from a XFOIL simulation, a two-dimensional panel method with integral boundary layer theory. In the simulation a Reynolds number of \(Re =30\times 10^4\) and transition parameter of \({N} = 7\) are used, where the latter corresponds to a turbulence level of \(Tu = 0.161\,\%\) to resemble the wind tunnel conditions. The simulated separation velocity \(U_{{\text {s}}}\) cannot be used to define the drift velocity \(U_{{\text {drift}}}\) of the shedded vortices. The drift velocity is obtained from the PIV data and is calculated by measuring by hand the displacement of the core of the shedded vortices within a certain time period.
2.3.1 Phase-averaged bubble characteristics for pitching motion
The aerofoil pitch motion induced by the actuation mechanism is determined by using the aerofoils upper surface laser reflections obtained from the raw planar PIV data. Calibration images of the illuminated aerofoil were taken for each experimental run at \(4^\circ\), \(6^\circ\) and \(8^\circ\).
Figure 6 shows an example of the reconstructed motion and reference calibration angles \(4^\circ _{{\text {ref}}}\), \(6^\circ _{{\text {ref}}}\) and \(8^\circ _{{\text {ref}}}\), where the latter are found to deviate slightly from the desired values \(4^\circ\), \(6^\circ\) and \(8^\circ\). The offset of \(0.2^\circ\) represents the misalignment of the camera field of view with respect to the wind tunnel centre line, the \(0^\circ\). Nevertheless, the oscillatory frequency and motion amplitude can be deduced with a reconstruction error of two pixels, i.e. an error of about \(0.1^\circ\).
When actuated, the aerofoil’s motion resembles a sinusoidal mode well. During each experimental measurement of 1 s, the average frequency of oscillation of 4.505 Hz is found, resulting in the desired reduced frequency of \(k\approx 0.2.\) Since the amplitude of motion is slightly higher than \(4^\circ\) each reference angle of interest, i.e. \(4^\circ _{{\text {ref}}}\), \(6^\circ _{{\text {ref}}}\) and \(8^\circ _{{\text {ref}}}\) is passed twice per cycle, once during pitch up and once during pitch down. The bubble characteristics are determined by combining three experimental measurements, which result in 12 independent groups of N subsequent images, each captured in the interval \(t_i - 1/2\Delta {t_1}\) to \(t_i + 1/2\Delta {t_1}\). As a criterion it is chosen that the 12N images should provide a converged result of the bubble characteristics. Furthermore, the time interval \(\Delta t\) should be small enough to consider the flow representable for the specific pitch phase, which limits the value of N.
The number of 12N images to be used to satisfy the convergence criteria, is evaluated by considering the normalised Reynolds stress curves used for the determination of the transition point. The curve obtained from a full data set of one second, 2700 samples, is compared at each steady reference angle to the curves obtained from 12 independent groups of N images of that same experimental run. As a convergence criterion, it is chosen that the deviation is less than 10 %. For the pitching cases through \(\alpha = 4^\circ\) and \(\alpha = 8^\circ\) this condition is satisfied for \(N = 40\) images. During the unsteady motion the actual flow considered varies with \(\pm \Delta \alpha <0.2^\circ\) from its reference angle. When passing through \(\alpha = 6^\circ\), a smaller number of \(N=20\) images was taken due to the faster aerofoil motion at this angle. This choice yields a deviation from the reference curve of 15 % and an offset of \(\pm \Delta \alpha =0.25^\circ\) compared to the reference angle of \(\alpha = 6^\circ _{{\text {ref}}}\). Figure 7 shows an example of the Reynolds stress curves obtained at \(\alpha = 4^\circ\) for the 2700 and the 12N images. It can be noted that for the smaller amount of images the curves are similar and the transition points, as determined by the exponential increase in the Reynolds stresses, do not deviate strongly from the value transition location obtained when using the full data set of 2700 images.
3 Results
3.1 Statistical laminar separation bubble properties
3.1.1 Steady aerofoil
The characteristic shape of a LSB as obtained from the 2D-PIV measurements is shown in Fig. 8, where the time-averaged flow field is given for the aerofoil stationary at \(4^\circ\) angle of attack. Downstream of separation point \(x_{{\text {s}}}\) it shows a distinct recirculation region, which is separated from the outer flow by the separated shear layer. Along this streamline the transition and vortex roll-up locations are indicated. The time-averaged reattachment location \(x_{{\text {r}}}\) is found at the aerofoil trailing edge for the case shown. Table 2 and Fig. 8 show the bubble characteristics determined for the static aerofoil fixed at \(4^\circ\), \(6^\circ\) and \(8^\circ\) angle of attack.
The results shown in Fig. 9a–d are all in agreement with the general trends found by Burgmann and Schröder (2008), Pauley et al. (1990) and Visbal et al. (2009) where the bubble characteristic locations move more upstream as the angle of attack increases. The forward shift of the separation point is a consequence of the increased unfavourable pressure gradient on the aerofoil at higher incidence angles. The transition and vortex roll-up onset move upstream with increasing incidence angle as a consequence of the stronger pressure gradient as well as the higher shear stresses present in the separated shear layer. The stronger shear stresses caused by the thinner boundary layer affect vorticity and vortex roll-up associated to the Kelvin–Helmholtz instabilities, since both are directly related to the transverse velocity gradient (Burgmann et al. 2007; Burgmann and Schröder 2008). It can be noted from Fig. 9d that vortex roll-up and transition occur in the close vicinity of each other for all incidence angles. Eventually, the more upstream-triggered transition and vortex roll-up imply also an upstream shift of reattachment, see Fig. 9a, yielding a bubble length contraction at higher angles of attack. Moreover, the bubble height, defined as the maximum vertical distance between the aerofoil surface and the highest velocity found in the boundary layer, is strongly affected by the change in incidence angle. Figure 9b shows that both bubble height and length decrease with increasing angle, which confirms the observations of Visbal et al. (2009), Ol et al. (2005), Burgmann and Schröder (2008). Furthermore, a comparison of the results at lower and higher Reynolds numbers by Burgmann and Schröder (2008) shows that for the present work the separation and reattachments locations are found, respectively, more upstream and downstream, whereas the transition point is located in between the lower and higher Reynolds number cases. This bubble increase could be explained by the strong influence of the turbulence level on the LSB as was suggested by Burgmann and Schröder (2008) where the LSB was investigated at a higher turbulence level of \(Tu = 1.0\,\%\). Eventhough separation is initiated later for the higher turbulence level the freestream fluctuations lead to a earlier transition compared to the separation. Consequently, the Kelvin–Helmholtz instabilities initiate earlier, which implies a thinner bubble and shorter bubble as a smaller amount of fluid is entrained into the bubble by the vortices.
Characteristic bubble parameters. a Separation point \(x_{{\text {s}}}\) (open) and reattachment location \(x_{{\text {r}}}\) (solid). b Bubble height \(h_{{\text {b}}}\) (open) and length \(l_{{\text {b}}}\) (solid). c Transition onset location \(x_{{\text {tr}}}.\) d Vortex roll-up onset location \(x_\mathrm{vort}\) compared to the transition point \(x_\mathrm{tr}\)
In the process of transition and vortex roll-up, the vortex shedding frequency is found to increase with angle of attack, as shown in Table 2 and Fig. 9d. Nearly identical frequency values were determined by the three methods described in Sect. 2.3 and a Strouhal number varying from 0.06 to 0.09 was found. Since the shedding frequency is related to the characteristic vortex dimension \(\lambda\), which depends on the boundary layer size, and the convective vortex drift velocity, \(U_{{\text {drift}}}\), by \(f \propto U_{{\text {drift}}}/\lambda\), see Davidson (2004), the increase in shedding frequency with angle of attack can be explained by the thinner boundary layer and the increased vortex drift velocity at higher incidence angles.
Furthermore the wavelet coefficient distribution in, e.g. Fig. 5 shows that downstream of vortex shedding dominant fluctuations occur at about half the shedding frequency. As will be discussed later this indicates that for angles \(\alpha \ge 6^\circ\) at times vortex pairing takes place after shedding.
3.1.2 Pitching aerofoil
The two phases of pitching motion, pitch up and pitch down, are considered separately as they present different flow conditions. The separation, transition and vortex roll-up locations and vortex shedding frequencies are determined for the pitching aerofoil as it attains the \(4^\circ\), \(6^\circ\) and \(8^\circ\) for either directions. The subscripts u and d will be used to indicate if the specific angular position is crossed while pitching up or down, respectively. It is noted that during the unsteady motion no full flow separation from the aerofoil surface has been observed.
Figure 10 compares the characteristic bubble properties obtained for the pitching aerofoil with the corresponding results for the aerofoil under static conditions. The pitch motion induces a clear hysteresis loop behaviour of the characteristic bubble locations. The pitch down is seen to promote the instabilities such that the characteristic parameters occur more upstream when compared to the corresponding steady case, although in the initial phase the difference with the steady situation appears minor. During pitch up the opposite occurs, where these three bubble characteristics are delayed and triggered more downstream, while also the discrepancy with the static aerofoil characteristics appears much stronger. A similar hysteresis is found for the vortex shedding frequency, see Fig. 10d, where during pitch down (up) a decreasing (increasing) frequency is measured, which is, however, higher (lower) than for the fixed angle of attack cases.
The hysteresis loop and the time delay of the bubble characteristics are in agreement with the smoke-wire visualisations and multiple hot-film sensor measurements by Kim and Chang (2009) and Lee and Basu (1998), respectively. Both can possibly be attributed to the (un)favourable modification of the boundary layer caused by the moving-wall and accelerated mass flow effects as proposed by Ericsson and Reding (1972), see Eq. (1). It is suggested that during pitch up (down) the pressure gradient may (de)stabilise the flow and postpone (promote) both transition and vortex roll-up. The postponement (promotion) of the characteristic bubble locations implies an increased (decreased) boundary layer thickness and decreased (increased) local supervelocities at shedding, affecting the characteristic size and convective velocity of the vortices and as a consequence the vortex shedding frequency. In fact, both planar and tomographic PIV analyses will show that during pitch up (down) the characteristic vortex length, wavelength \(\lambda _{{\text {vort}}},\) described in the next section, is larger (smaller) and the convective velocity is lower (higher) when compared to its corresponding steady case.
Furthermore, the accelerated mass flow effects could also be the explanation of the approximately equal characteristic values found when pitching through \(4^\circ _u\) and \(8^\circ _d\) in comparison with their respective steady cases. When passing through both incidence angles, the pitching aerofoil has an angular velocity close to zero and therefore the acceleration of the fluid in the separated region becomes negligible. As a consequence just after pitch motion reversal, the pressure lag effects are barely affecting the flow. Moreover, it is noted that the hysteresis is stronger during pitch up, which is in accordance to the qualitative observations of Lee and Petrakis (1999). For the pitch-down motion, the difference of the characteristic locations compared to the steady case is not only smaller, but it is hardly visible between \(8^\circ\) and \(6^\circ\). An explanation for the latter is the relatively small difference in transition locations and the shedding frequencies between the steady cases obtained at \(6^\circ\) and \(8^\circ\). This implies that at these angles the vortical flow structures in the rear part of the bubble, which correlated with the shedding frequency, are of similar size (Davidson 2004). As a consequence, despite the pressure lag introduced by the movement, during pitch down from \(8^\circ\) to \(6^\circ\) degrees the vortical structures are not expected to vary strongly from the steady state structures and so with it the shedding frequency, the vortex roll-up onset and transition locations.
3.2 Dynamics of LSB
The instantaneous flow fields obtained after subtracting the vortex convective velocity from the original velocity component in x-direction are shown in Fig. 11 and indicate the presence of coherent rollers, highlighted with a strong vorticity along the shear layer that separates the bubble from the outer flow. A vortex roll-up and typical cat-eye structures as visualised by De Young (2004) are observed at the downstream end of this shear layer. These structures are found at all three investigated angles for both aerofoil motion cases. The presence of such cat-eye structures was also observed by Burgmann and Schröder (2008) and indicates that the LSB transition is dominated by K–H instabilities as is the case in free shear layer transition. These coherent structures are also observed in the 3D tomographic measurements. The evolution of the vortical structures from its onset to vortex breakdown is revealed best for the static aerofoil at \(\alpha = 6^\circ\) and is shown in Fig. 12.
(Left) evolution of vortical field at \(\alpha =6^\circ\). Vortex visualisation by Q-contours. (Right) dominating positive vorticity \(\omega\) (orange) and vorticity component \(\omega _y\) (grey) until vortex shedding, i.e. \(x/c<0.5\) (top and centre). (Right centre) Detailed hairpin structures showing vorticity components \(\omega _x\) (positive in brown and negative in blue) and positive \(\omega _y\) beyond \(x/c>0.5\). Bottom low-speed streaks at \(U=3\,{\text {m}}/{\text {s}}\) (blue) visualised at the hairpin structures
Initially the vortex roll-up is moved by instabilities that will form a large roller-like 2D vortex filament with uniform distribution in spanwise direction (vortex roll II at \(t_0\) and III at \(t_0 +2\Delta t\)), which will be shed at the rear part of the LSB as the 2D rollers move downstream (vortex roll II at \(t_0+2\Delta t\)). Beyond shedding the 2D filament structure is subjected to 2D disturbances and velocity differences in the boundary layer that deform the filament into a large interconnected 3D structure, which displays a spanwise waviness indicating the onset of arch-like \(\Lambda\)-structures. Examples are shown by vortex roll II at \(t_0+2\Delta t\) in Fig. 12 and at \(t_0\) and \(t_0 + 11\Delta t\) in Fig. 15a. For all three fixed angles of attack considered, the bended structure’s occurrence is not repeated systematically. Also spatially, a non-uniform distribution of the arch-like structures has been detected.
After bending of the roller, for both fixed and pitching angle cases, the 3D vortex roll is found to either pair or not to interact at all with the newly generated vortex roll. At \(4^\circ\) fixed angle of attack and while pitching up or down through this angle no pairing has been observed. However, at higher angles of attack, for both the static and pitching cases, pairing has (often) been observed. Figure 13 considers a pairing while the aerofoil pitches up through \(8^\circ _u\). The time sequence shows that the most downstream vortex I pairs with the newly generated vortex roll II. The occurrence of pairing is confirmed by the peaks found at about half the shedding frequency in the wavelet coefficient contour plots obtained from the wavelet analysis performed on the planar PIV data, as is shown for example in Fig. 5. It must be noted, that the pairing is detected more regularly during pitch up than during pitch down or for the corresponding steady cases. It is suggested that the more regular pairing is related to the increase in supervelocities as incidence angle increases. The velocity contour levels in Fig. 13a show that, during pitch up, the convective velocity of the most upstream vortex roll is higher than for the more downstream roll, promoting the pairing of the two vortex rolls. Moreover, as will be discussed later, the reduction of the characteristic vortex length, \(\lambda _{{\text {vort}}}\), at higher incidence angles facilitates to achieve pairing before interacting with the LSB.
While convected downstream the (paired) vortex roll tends to break down into arc-shaped hairpins that grow in size as the head is lifted and the vortex legs are stretched. Examples of these structures are indicated by the red coloured letters A, B, C, D and E in Fig. 12. The right side of the figure shows how these hairpin structures are accompanied by their typical counter rotating vorticity \(\omega _x\) in the vortex legs, the lifting vorticity \(\omega _y\) in the hairpin head and the low-speed streaks, which occur in between the hairpin legs. The distance between two vortex legs of the arc-shaped hairpins varies from 0.1c to 0.2c, as it is convected downstream. Similar values were also found by Burgmann and Schröder (2008) and Elsinga et al. (2006). At the higher angles of attack, the size of the hairpin structures is strongly related to the interaction between two succeeding vortex rolls, i.e. when pairing occurs, larger hairpin structures are generated compared to the case where no pairing has occurred. This is shown in Fig. 14. Hairpin vortex A, which resulted after pairing, is clearly larger than the hairpin structures found at about \(x/c=0.5\), which occurred without a vortex pairing prehistory. A possible explanation of this difference is the fact that pairing triggers the breakdown of the vortex rolls more downstream, where the shear layer has grown in thickness. As vortical structures scale with this thickness, it seems reasonable to expect larger hairpin structures when pairing occurs. Moreover, two paired vortices increase the energy of the vortex, inducing to a larger structure size.
As a final remark it must be mentioned that, despite using a similar evaluation method, in the experiments no clear supportive evidence could be found for the c-shaped structures, as proposed by Burgmann et al. (2007) and Burgmann and Schröder (2008). The differences might be caused by the height from the wall of the measurement volume analysed during the measurements. The c-shaped distorted vortices detected by Burgmann et al. (2007) are detected very close to airfoil wall as visualisations are performed in the wall-normal coordinate \(0<y/c<0.05.\) In the present work, the visualisation of the K–H vortices undergoing spanwise instability covers the range up to 0.2 chord, where important vortex activity is detected up to \(y/c = 0.1.\) c-Shaped structures can be explained as the lower region of K–H rollers undergoing spanwise undulation. The more pronounced distortions are seen in the upper region (lambda vortices) where the crests of undulated K–H vortices accelerate under the effect of the outer flow velocity and lead to a rapid vortex stretching in the legs region.
3.2.1 Vortex shedding characteristics
The vortex shedding frequency previously determined by planar PIV can be related to the vortex convective velocity, \(U_{{\text {drift}}}\), and a characteristic vortex length scale \(\lambda _{{\text {vort}}}\). The latter is defined as the wavelength corresponding to the separation between two subsequent vortex rolls as indicated in Figs. 11 and 15 for the 2D planar and 3D tomographic PIV analyses, respectively. Due to the tomographic field of view used, the values for \(\lambda _{{\text {vort}}}\) were obtained only for steady and pitching cases at \(4^\circ\) and \(6^\circ\) and can be found in Table 3.
When pitching through \(6^\circ _u\), for both the 2D as the 3D data analysis, the wavelength \(\lambda _{{\text {vort}}}\) has nearly the same values as found at the \(4^\circ\) and the \(4^\circ _u\) cases. Furthermore at \(4^\circ _{u}\) and \(6^\circ _u\) the vortex drift velocities obtained from planar PIV are more or less equal, while higher than for the \(4^\circ\) case. Defining the shedding frequency by the relation \(f_{s} \approx U_{{\text {drift}}}/\lambda _{{\text {vort}}},\) yields approximately equal frequency values for these angles of attack cases, which is in accordance with the results from planar PIV analysis, shown in Fig. 10d. Similarly this shedding frequency relation is approximately valid for the pitch-down trough \(6^\circ _d,\) where the detected characteristic wavelength, convective vortex velocity and shedding frequency differ from the \(6^\circ _u\) case, while being of the same order as for the steady condition at \(6^\circ.\) Again this is in accordance with the data shown in Fig. 10d. Note that the 3D shedding vortex shedding frequency in Table 3 has been calculated from the measured 2D vortex drift velocity and the 3D wavelength and emphasises the similar shedding frequencies found at \(4^\circ\) and \(6^\circ _u.\) The higher value found when pitching up through 4 is explained by the calculating method used, where a high vortex drift velocity is found for this case. The differences in wavelength \(\lambda _{{\text {vort}}}\) and vortex roll-up onset location are visualised in Fig. 15 for the \(6^\circ _{u,d}\) pitching cases. At \(6^\circ _u\) the onset of the vortex roll moves steadily upstream with increasing angle, while at \(6^\circ _d\) the roll-up onset, shedding and breakdown occur more downstream as the aerofoil continues its pitch down. The fact that roll-up and shedding are stimulated more upstream, i.e. where the boundary layer is thinner, results in smaller vortical structures (Davidson 2004) that are convected with higher vortex drift velocity, which explains the higher shedding frequency during pitch down.
4 Summary and conclusions
The effect of an unsteady pitching motion on a laminar separation bubble present on the suction side of a SD7003 aerofoil was investigated by means of time-resolved planar and tomographic particle image velocimetry. As a consequence of the pitch motion, a delay of the laminar separation bubble characteristic locations is observed, resulting in a hysteresis behaviour of the separation, laminar-to-turbulent transition and vortex roll-up onset. The pitch down (up) promotes (delays) the instabilities such that the characteristic locations occur more upstream (downstream) when compared to the corresponding steady angle case. The deviation from the steady characteristics is particularly evident in the pitch-up interval and the latter phase of the pitch-down interval. A similar hysteresis loop is observed for the frequency at which the generated vortex sheds from the shear layer in the rear part of the LSB. During pitch down (up) a decreasing (increasing) frequency is measured, which is higher (lower) than for the fixed angle of attack cases. In particular for the pitch-up cycle, both planar and tomographic PIV analyses showed a relation between the shedding frequency, the characteristic phase-averaged distance between two succeeding undulated vortex rolls and the convective vortex velocity.
Using tomographic PIV the laminar-to-turbulent transition process in the shear layer present at the boundary of the LSB has been visualised. Transition is found to start with the formation of uniformly distributed rollers, representing 2D Kelvin–Helmholtz vortex filaments. Consequently instabilities and velocities differences present at the shear layer cause the filaments to deform with spanwise waviness into arch-like Λ-shaped vortex rollers, while moving downstream. Eventually the further interaction with the environment leads to a breakdown of these rollers into 3D hairpin structures. In addition the 3D reconstruction method allowed the visualisation of the influences of different angle of attack configurations and the pitching motion on the roll-up onset location, the characteristic phase-averaged distance between two succeeding undulated vortex rolls and the pairing behaviour between these vortex rolls. It was found, however, that no major modifications in the vortex structures themselves are induced by the aerofoil pitch motion.
References
Alam M, Sandham ND (2000) Direct numerical simulation of “short” laminar separation bubbles with turbulent reattachment. J Fluid Mech 410:1–28
Burgmann S, Schröder W (2008) Investigation of the vortex induced unsteadiness of a separation bubble via time-resolved and scanning PIV measurements. Exp Fluids 45:675–691
Burgmann S, Danneman J, Schröder W (2007) Time resolved volumetric PIV measurement of the transitional separation bubble of an SD7003 airfoil. Exp Fluids 44:609–622
Cierpka C, Segura R, Hain R, Kähler CJ (2010) A simple single camera 3C3D velocity measurement technique without errors due to depth of correlation and spatial averaging for microfluidics. Meas Sci Technol 21. doi:10.1088/0957-0233/21/4/045401
Davidson PA (2004) Turbulence: an introduction for scientists and engineers. Oxford University Press, Oxford
De Young DS (2004) Theory of jet dissipation. In: X-ray and Radio Connections, Santa Fe NM, 3–6 February 2004
Diwan SS, Chetan SJ, Rhamesh ON On the bursting criterion for laminar separation bubbles. In: Govindarajan, R (ed) Sixth IUTAM symposium on Laminar–Turbulent transition, pp 401–407
Elsinga GE, Scarano F, Wieneke B, van Oudheusden BW (2006) Tomographic particle image velocimetry. Exp Fluids 41:933–947
Ericsson LE, Reding JP (1972) Analytical prediction of dynamic stall characteristics. In: AIAA 5th fluid and plasma dynamics conference, paper no. 72-682, Boston, MA, USA, 26–28 January 1972
Gaster M (1966) The structure and behaviour of laminar separation bubbles. AGARD CP–4:813–854
Hain R, Kähler CJ (2005) Advanced evaluation of time-resolved PIV image sequences. In: 6th international symposium on particle image velocimetry, Pasadena, CA, 21–23 September 2005
Hain R, Kähler CJ, Radespiel R (2009) Dynamics of laminar separation bubbles at low-Reynolds-number aerofoils. J Fluid Mech 630:129–153
Horton HP (1969) A semi-empirical theory for the growth and bursting of laminar separation bubbles. In: Aeronautical research council, CP 1073:
Humble RA, Elsinga GE, Scarano F (2009) Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J Fluid Mech 622:33–62
Hussain F, Jeong J (1995) On the identification of a vortex. J Fluid Mech 285:69–94
Jones BM (1934) Stalling. J R Aeros Soc 38:747–770
Jones LE, Sandberg RD, Sandham ND (2008) Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence. J Fluid Mech 602:175–207
Kim D-H, Chang J-W (2009) Unsteady boundary layer for a pitching airfoil at low Reynolds numbers. J Mech Sci Technol 24:429–440
Lang M, Rist U, Wagner S (2003) Investigation on controlled transition development in a laminar separation bubble by means of LDA and PIV. Exp Fluids 36:43–52
Lee T, Basu S (1998) Measurement of unsteady boundary layer developed on an oscillating airfoil using multiple hot-film sensors. Exp Fluids 25:108–117
Lee T, Petrakis G (1999) Boundary-layer transition, separation, and reattachment on an oscillating airfoil. J Aircraft 37:356–360
Lou W, Hourmouziadis J (2000) Separation bubbles under steady and periodic-unsteady main flow conditions. J Turbomach 122:634–643
Marxen O, Rist U, Wagner S (2003) The effect of spanwise-modulated disturbances on transition in a 2-D separated boundary layer. AIAA paper no. 2003-0789
McMichael JM, Francis MS (1997) Micro air vehicles—toward a new dimension in flight. USA. DARPA, August 1997
Ol MV, Hanff E, McAuliffe B, Scholz U, Kähler CJ (2005) Comparison of laminar separation bubble measurements on a low Reynolds number airfoil in three facilities. In: 35th AIAA fluid dynamics conference and exhibit, 2005-5149, Toronto, Ontario, 6-9 June 2005
O‘Meara MM, Mueller TJ (1987) Laminar separation bubble characteristics on an airfoil at low Reynolds numbers. AIAA J 25:1033–1041
Pascazio M, Autric JM, Favier D, Maresca C (1996) Unsteady boundary-layer measurement on oscillating airfoils—transition and separation phenomena in pitching motion. In: AIAA Journal 96-0035 (ed) AIAA, aerospace sciences meeting and exhibit, Reno, NV, 15–18 January 1996
Pauley LL, Moin P, Reynolds WC (1990) The structure of two-dimensional separation. J Fluid Mech 220:397–411
Raffel M, Willert C, Kompenhans J (2007) Particle image velocimetry: a practical guide, 2nd edn. Springer, Berlin
Rudmin D, Benaissa A, Poirel D (2013) Detection of laminar flow separation and transition on a NACA-0012 airfoil using surface hot-films. J Fluids Eng 135:1104–1110
Scarano F (2013) Tomographic PIV: principles and practice. Meas Sci Technol 24. doi:10.1088/0957-0233/24/1/012001
Visbal MR, Gordnier RE, Galbraith MC (2009) High-fidelity simulations of moving and flexible airfoils at low Reynolds numbers. Exp Fluids 46:902–933
Watmuff JH (1999) Evolution of a wave packet into vortex loops in a laminar separation bubble. J Fluid Mech 397:119–169
Wieneke B (2008) Volume self-calibration for 3D particle image velocimetry. Exp Fluids 45:549–556
Wissink J, Rodi W (2004) DNS of a laminar separation bubble affected by free-stream disturbances. Springer, Berlin
Wissink JG, Rodi W (2003) DNS of a laminar separation bubble in the presence of oscillating external flow. Flow Turbul Combust 71:311–331
Yang Z, Voke PR (2001) Large-eddy simulation of boundary-layer separation and transition at a change of surface curvature. J Fluid Mech 439:305–333
Zhang W, Hain R, Kähler CJ (2008) Scanning PIV investigation on the laminar separation bubble on the SD7003 airfoil. In: 7th international symposium on particle image velocimetry, Rome, Italy, 11–14 September 2008
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nati, A., de Kat, R., Scarano, F. et al. Dynamic pitching effect on a laminar separation bubble. Exp Fluids 56, 172 (2015). https://doi.org/10.1007/s00348-015-2031-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-015-2031-6