Abstract
This article gives an overview of the background-oriented schlieren (BOS) technique, typical applications and literature in the field. BOS is an optical density visualization technique, belonging to the same family as schlieren photography, shadowgraphy or interferometry. In contrast to these older techniques, BOS uses correlation techniques on a background dot pattern to quantitatively characterize compressible and thermal flows with good spatial and temporal resolution. The main advantages of this technique, the experimental simplicity and the robustness of correlation-based digital analysis, mean that it is widely used, and variant versions are reviewed in the article. The advantages of each variant are reviewed, and further literature is provided for the reader.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 BOS technique and its relatives
The BOS technique is similar to the human observation of heat haze, mirage or fata morgana, where local density gradients between the human observer and a distant object distort or even mirror the perceived image (Fig. 1a). A second effect, the shadow effect (Fig. 1b), is visible to the unaided eye, but became more relevant with the advent of optical instrumentation. This effect is generated by a density variation between the light source and a surface of homogeneous brightness and color. The light intensity variations ∆I at each location of the surface are proportional to the second derivative of the air density between the light source and the surface. An image of these inhomogeneous light intensities is called a shadowgraph.
The observation of density gradients in fluid dynamics became important when aerodynamics became transonic. A major driver for improvement and application was the photography of bullets and their flow fields in the work of Ernst Mach at the end of the nineteenth century. The technique most commonly used for fluid density visualization is Toepler’s schlieren photography (Fig. 1c). Its optical setup typically consists of spherical mirrors or lenses and a half aperture, e.g., in form of a knife edge. It captures light intensity variations ∆I proportional to the first derivative of the fluid density.
The closest relative of the BOS methods is laser speckle interferometry (Fig. 1d). The illumination of a screen through the density gradient under investigation is made with laser light that generates a speckled interference pattern. The displacement of this pattern ∆s, which has been evaluated optically and/or digitally, is proportional to the first derivative of density.
The background-oriented schlieren method is also based on the analysis of image displacements. However, the structures are a feature of the background that can be illuminated with incoherent light and imaged through a fluid containing spatial density gradients (Fig. 2). Since digital evaluation and white-light illumination (at least for surface deformation measurements) are also known in speckle interferometry, BOS could also be named “white-light speckle density photography.” However, the name background-oriented schlieren technique is the most common name, as “background oriented” describes the fact that the camera used for the recording focuses onto objects behind the flow under investigation. Additionally, the term schlieren, the old German word for local optical inhomogeneities in (mostly) transparent media, most intuitively tells a fluid experimentalist that the technique quantifies the first spatial derivative of density, integrated along the path of light. In this article, the term “background-oriented schlieren” is always completed by the words “method” or “technique” as the “schlieren” from their definition cannot be background oriented, but only the measurement technique for their visualization.
1.2 Early BOS publications
The first descriptions of the principle and application of the background-oriented schlieren method can be found in publications from 2000. The article from Dalziel et al. (2000) appeared in “Experiments in Fluids” in April and describes several schlieren or moiré techniques that the authors named “synthetic schlieren.” They had in common that parts of the traditional optical setups have been substituted by digital image analysis. Some of these techniques and especially the variant “dot tracking refractometry” basically equal BOS. The application described within this context was the internal wave field in an oscillating cylinder. A second “Experiment in Fluids” article from Raffel et al. (2000a, b) appeared in May. It focused on the BOS principle that utilizes a random dot pattern in the background and described its application to a rotor wake visualization of a helicopter in hovering flight. The patent application of Meier (2002) was published in June. It was submitted on the same day as the publication of Raffel et al. but one year after the manuscript of Dalziel et al. (2000). The application illustrated in the patent application is the diamond-like pattern of a supersonic free jet, which had been recorded by H. Richard. It is also one of the applications described in a conference paper by Richard et al. (2000), which was presented in Lisbon in July 2000. Also described herein is the experimental and computational effort required for subsequent quantitative determination of density. Raffel et al. (2000b) presented in the same year in August in Edinburgh and described applications of the conventional, reference-free and natural background versions of BOS to a large utility helicopter in flight.
2 Setup of the BOS technique
2.1 BOS theory
The background-oriented schlieren technique is based on the relation between the refractive index of a fluid and its density, given by the Lorentz–Lorenz equation, which can be simplified to the Gladstone–Dale equation for gaseous media. The BOS technique can best be compared with laser speckle density photography as described by Debrus et al. (1972) and Köpf (1972) and the improved versions by Wernekinck and Merzkirch (1987) and Viktin and Merzkirch (1998). Like most interferometric techniques, laser speckle density photography preferably utilizes an expanded parallel laser beam, which traverses a compressible flow field or (in more general terms) passes through an object of varying refractive index (i.e., a phase object). However, in contrast to other interferometry, laser speckle patterns are generated instead of interference fringes. Compared with the quantitative optical techniques mentioned above, the BOS method simplifies the recording. The laser speckle pattern, usually generated by the expanded laser beam and a ground glass, is replaced by a (mostly painted or printed) random dot pattern on a surface in the background of the test volume. This pattern preferably has to have the highest spatial frequency that can be imaged with sufficient contrast.
Usually, the recording is performed as follows: First, a reference image is generated by recording the background pattern observed through air at rest in advance of (or subsequent to) the experiment. In the second step, an additional exposure through the flow under investigation (i.e., during a wind tunnel run) leads to a locally displaced image of the background pattern. The resulting images of both exposures can then be evaluated by image correlation methods. Existing evaluation algorithms, which have been developed and optimized, for example, for particle image velocimetry (or other forms of speckle photography), can then be used to determine the displacement of patterns at multiple locations throughout the image. The deflection of a single beam contains information about the spatial gradient of the refractive index integrated along the line of sight (Fig. 3). Details on the theory of ray tracing through gradient-index media are found in Sharma et al. (1982) and Doric (1990).
Assuming paraxial recording and small deflection angles (ɛ y ≈ tan ɛ y ), a formula for the image displacement Δy can be derived for the BOS technique (Raffel et al. 2007)
with the magnification factor of the background, M = z i /Z B, the distance between the dot pattern and the density gradient, Z D, and the deflection angle
The image displacement can thus be rewritten as
with Z A being the distance from the lens to the object and the focal length of the lens, f. Since the imaging system should be focused onto the background for best contrast, we note:
Equation 3 shows that a large image displacement can be obtained for a large Z D and a small Z A. The maximum image displacement for increasing Z D approaches \(\Delta y = f\varepsilon_{y}.\) On the other hand, certain constraints in the decrease in Z A have to be fulfilled in order to image the flow field with sufficient sharpness. The optical system has to be focused on the background in order to obtain maximum contrast at high spatial frequencies for later interrogation, and Eq. 4 applies. At the same time, the sharp imaging of the density gradients would be best at \(Z_{\text{i}}^{{\prime }}\) with
This focusing problem that is inherent with the BOS technique is depicted in Fig. 4. As a consequence of the fact that the system is usually focused on the background, the sharpness of the density gradient under investigation is limited. By introducing the aperture diameter d A and the magnification of the density gradient imaging \(M^{\prime} = Z_{\text{i}}^{{\prime }} /z_{\text{A}},\) a formula for the geometric blur d i (Fig. 4) of a point at Z A can be expressed as:
Additionally, the imaging of the small scales structures in the background is diffraction limited. The following formula holds for the diffraction limited minimum image diameter d d.
where λ is the wavelength of the light (~0.5 μm). The approximation given by (Eq. 8) can be used in order to compute the overall image blur \(d_{\varSigma }\) for the two different sources and to simulate the effect of the underlying convolution of the imaging artifacts:
The following problem arises when trying to optimize the sharpness of BOS recording by minimizing the overall image blur \(d_{\varSigma }\): Larger aperture diameters d A will decrease the diffraction limited minimum image diameter d d (Eq. 7), but increase the geometric blur d i (Eq. 6). However, for most BOS setups, the latter effect is the stronger resulting in small aperture diameters typically being used for BOS recording. This increases the demand for intense background illumination, but also keeps other imaging problems like spherical and chromatic lens aberrations small. Since correlation techniques average over the interrogation window area, the overall image blur \(d_{\varSigma }\) does not lead to a significant loss of information, as long as \(d_{\varSigma }\) is considerably smaller than the interrogation window size.
2.2 BOS example in practice
The following section describes a typical BOS experiment. More complex experimental setups and evaluation methods can be found in the literature which is described in the later sections.
The opening angle of a BOS camera, determined by the focal length of the lens and the sensor format, is chosen in a way that the object’s image covers the full image area. The background pattern is placed at a distance to the object, which is typically smaller than the distance between the object and the camera, but of the same order of magnitude. The f number of the imaging lens (f/d A) is in the order of 11. The typical size of an individual background structure (e.g., a random dot) yields an image on the order of 3–5 pixels. Two- to three-pixel images are better, but can frequently not be reached, because of the diffraction limited imaging at small apertures and the small pixel pitch of today’s cameras. A recording of an undisturbed background (flow-off) and a disturbed background (flow-on) are loaded into the software used for the cross-correlation evaluation (e.g., by PIV software). The peak fitting routine should be adapted to this image size (e.g., 4 pixels). The 3-point peak fitting frequently used for PIV evaluation will yield more measurement noise, when BOS image structures are larger. Conventional cameras can be used as well as scientific cameras, but image format should be uncompressed. Demo versions of suitable software packages can be downloaded from the internet (e.g., PivView and others). The BOS image displacements due to density gradients are usually smaller than that in PIV recordings. In spite of the fact that small image displacements (e.g., <0.5 px) can be determined with high accuracy, the small displacements lead to relative BOS measurement errors that are larger than usually obtained in PIV (e.g., BOS 2–3 % instead of PIV 1 %). Larger image displacements can be obtained for smaller fields of view. The subtraction of the mean displacement helps to see the flow patterns when vector plots are used for visualization. Figure 5 depicts an undisturbed background, recorded as reference (a), the same background behind a laser-induced plasma (b) and the resulting image displacements proportional to the density gradients along the line of sight (c). The displacements are represented as vectors (Fig. 5c). The underlying grayscale represents the radial displacement component at each location. Typical effects that might occur for such thermal applications are: the image blur due the strong density gradients, the reduced image contrast behind the ionization spark and the resulting data dropout in the center of the displacement field.
Background pattern recording a before and b shortly after a density variation was brought into the flow by means of plasma ignition; c vector plot of the displacement correlation between both recordings; gray scales represent the radial component of the displacement vectors (Raffel et al. 2011)
3 Accuracy of BOS
Much of the focus over the recent years has been on analyzing and improving the accuracy of the method. The dynamic range of the technique for most of the applications is of the order of 50:1, and the measurement error has been found to be in the order of 2–3 % percent of the full scale (Elsinga et al. 2004; Hargather and Settles 2012; Vinnichenko et al. 2012). Other authors (Popova (2004), Popova et al. 2008; Gojani and Obayashi 2012; Gojani et al. 2013; Yevtikhiyeva et al. 2009) investigated the influence of various parameters on the measurement sensitivity and resolution of BOS analytically and experimentally and presented several guiding formulae for setting up a BOS system. A large number of papers have been published on methods suitable for a general improvement of accuracy and resolution of BOS. For example, Schröder et al. (2009) used a continuously varying random dot pattern, which was generated by a digital projector, and a long-distance microscope to measure the density fields in micro-nozzle plumes in vacuum. The variation in the pattern behind the steady flow allowed for a significant improvement of the spatial resolution and signal-to noise ratio by the application of the ensemble correlation technique. Atcheson et al. (2009) demonstrated the advantages of optical flow algorithms for BOS. Meier and Rösgen (2013) improved BOS imaging using laser speckle illumination. When more cameras are used, the alignment and optimization of the setup are more difficult. A calibration scheme for multi-camera tomographic setups that compensates the blurring effect and provides consistent results for 3D BOS has been reported by Le Sant et al. (2014). Various authors focused on special imaging configurations and special applications. Delmas et al. (2013) analysed infrared BOS recordings and Hargather and Settles (2011) and Prasanna and Venkateshan (2011) BOS for heating and cooling flow research. Van Hinsberg (2014), e.g., suggested a modification of the classical correction factor for BOS when applied in the near-field and demonstrated the advantage of this approach by the application to an underexpanded supersonic free jet. Vasudeva et al. (2005) investigated a warm air jet in an industrial application. Bichal and Thurow (2010, 2014) used BOS for wavefront sensing. Jensen et al. (2005) performed BOS measurements in cryogenic gas cloud flows, and Clem et al. (2013) compared BOS data recorded from a variety of supersonic jets with corresponding far-field acoustic data.
4 BOS applications in complex facilities
One of the main advantages of the BOS technique—the reduced requirements for optical access—promoted its application in rough industrial environments and complex experimental facilities. Ramanah and Mee (2006) and Ramanah et al. (2007), for example, investigated scramjet flows in hypersonic impulse facility and compared the results with conventional schlieren images. Kirmse et al. (2011) performed combined PIV and BOS measurements in a high-enthalpy shock tunnel at Mach 8. Supersonic facilities such as shock tubes have also been used in order to visualize the shock-heated regions on a sharp cone at Mach 3.8 (Raghunath et al. 2004) and shock waves at Mach 4 (Mizukaki 2010). Transonic flows and the shock waves contained have been examined by Glazyrin et al. (2012) and Znamenskaya et al. (2012). Wake flows behind wind tunnel models have been investigated in case of thermal, centrifugal and compressible effects. Roosenboom and Schröder (2009, 2010) investigated a propeller slipstream wake geometry and Bencs et al. (2011) the wake of a heated cylinder. Reinholtz et al. (2010) investigated jettison motor plumes from an Orion launch abort vehicle model and Wolf et al. (2012) rocket model near-wakes. As optical flow diagnostics are frequently used for research on turbines for aero-engines and power generation, BOS is also useful in this field. Loose et al. (2000) and Alhaj and Seume (2010), for example, used a combined PIV and BOS investigation for the investigation of wake flows in linear turbine cascade facilities. Challenging wind tunnel applications under cryogenic conditions have been reported by Germain and Quest (2005), Loose et al. (2006), and Fey et al. (2010). Combustion research can take advantage of the ability of BOS to visualize and measure heat plumes and flames (Iffa et al. 2011), but also to determine concentration levels of different fuel sprays (Bang and Lee 2013; Lee et al. 2011, 2013; Tillmann et al. 2014) or gas jets as performed by Iffa et al. (2010), Ducasse et al. (2010) and Veser et al. (2011).
Other publications mainly focused on the development of tomographic evaluation methods from multi-camera recordings. It appears that the ideal recording and evaluation methods for the quantitative determination of density and density gradient fields have not yet been found. Currently, the white-light background illumination, grayscale recording, cross-correlation evaluation and tomographic analysis are the most common techniques for recording and evaluation in quantitative measurements.
5 Stereo- and multi-camera recording for flow structure localization
For quasi two-dimensional flows, a single camera perspective is sufficient to identify the positions of the structures in the flow. However, the accuracy of those BOS applications will not be as good as similar results from conventional schlieren photography or shadowgraphy. This is due to the reduced resolution of the displacement analysis and the fact that BOS uses divergent viewing instead of parallel beams. The BOS method can, however, easily be applied to three-dimensional flow fields, due to the reduced complexity of its recording. For many applications, a two-camera setup is sufficient to allow for the measurement of the position of flow structures in three-dimensional space.
This approach was applied by Klinge et al. (2003) who utilized a stereoscopic BOS system for the localization of a wing-tip vortex in a transonic wind tunnel. Schairer et al. (2013) conducted stereoscopic BOS measurements for the tip vortex localization on a full-scale helicopter model in a large wind tunnel facility using epipolar geometric analysis. Bauknecht et al. (2015) used the same method also in combination with photogrammetry for the three-dimensional reconstruction of a large part of the blade tip vortices of a flying helicopter from multi-camera BOS images. The procedure for density gradient localization consists of at least two steps:
5.1 Two-dimensional structure identification
In preparation for a 3D localization, the positions of the flow structures under investigation have to be determined from the evaluated displacement images to get their 2D positions in each camera plane. Bauknecht et al. (2015), for example, describe a semiautomatic detection algorithm for finding discrete points on vortex lines. Starting from manually selected points close to the vortex filaments, a stepwise cross-correlation between cuts orthogonal to the main vortex axis in combination with a polynomial-based predictor is applied. A spline curve is then fitted to the discrete points on each vortex filament by means of a least squares procedure.
5.2 3D vortex locations determination by epipolar analysis and photogrammetry
For the 3D reconstruction of the geometry of a solid object with photogrammetry, discrete markers or prominent points on its surface are usually imaged and identified in multiple measurement images of a multi-camera system. In order to apply the same reconstruction algorithms to invisible and continuous objects such as vortices, corresponding points on the vortex lines have to be identified in the images of all cameras (see “correspondence problem” in Meyn and Bennett 1993).
One possible solution for this is the application of the epipolar geometry method (Hartley and Zisserman 2003), which imposes geometric constraints on pairs of camera images, as shown in Fig. 6. Epipolar geometry uses the pinhole camera model and is based on the idea that a plane defined by an object space point P (e.g., a point on a 3D vortex segment) and its projections P A and P B onto the image planes of two cameras (A, B) can be used to establish geometric dependence between P A and P B. If only P A and the corresponding optical center O A are known, the line through these two points can be projected as an epipolar line in the image plane of camera B (red line in Fig. 6). The projected point P B corresponding to P A must be located on this epipolar line. If the vortex on which P is located on can be identified in both projections, as shown in Fig. 6, the point P B can be found by intersecting the epipolar line with the corresponding projected vortex in the image plane of camera B. The constraint imposed by epipolar geometry can be written as
with the coordinates of the corresponding points in the images A and B and the 3 × 3 fundamental matrix F. This fundamental matrix can be estimated given at least seven corresponding point pairs in the two images. In the study described by Bauknecht et al. (2015), the fundamental matrices were estimated for all possible camera combinations in the multi-camera setup.
Principle of the epipolar geometry (after Schairer et al. 2013), showing the projected camera plane points P A and P B of the 3D point P and the corresponding red epipolar line
The intersection points of the epipolar lines with the corresponding 2D vortex projections were computed and used in the reconstruction process. The 3D reconstruction of the vortex positions was carried out using pairs of cameras and the stereo-photogrammetry technique. A result is shown in Fig. 7, depicting a large part of the vortex system of a full-scale BO 105 helicopter in hovering flight.
Reconstructed vortices from a BO 105 in ascending hovering flight. Measured vortex center lines color-coded (Bauknecht et al. 2015)
6 Tomographic BOS analysis
The idea of an expansion of the BOS technique for the determination of three-dimensional density fields by multi-camera recording and tomographic evaluation was presented in early publications (e.g., Raffel et al. 2000a, b; Meier 2002). However, as BOS techniques were initially slow in attracting experimentalists, it took some years before the theory and application of tomographic evaluation were presented.
6.1 Density determination of 2D flows
It is generally possible to use a finite difference approximation or a Poisson solver to integrate the density gradient field to determine the relative density field in the flow. If the absolute density is known at one point in the observation area, this can be used to determine the density at all points in the flow quantitatively. However, any non-two-dimensionality in the flow field will distort the results, since the BOS method is a line-of-sight integrating technique. A first step toward the determination of the density distribution by computation of the Poisson equation for BOS data of two-dimensional transonic flows has been presented by Richard et al. (2000) and Richard and Raffel (2001). However, a more complete analysis by tomographic algorithms is required in order to deal with three-dimensional density fields.
6.2 Density determination of axisymmetric flows
van Hinsberg and Rösgen (2014) and Van Hinsberg (2014) used the principle of ray tracing and the ring discretization method to obtain the theoretical deflections and apparent shifts of an axisymmetric supersonic underexpanded free jet. They also described a modification of the classical correction factor for BOS applications in the near-field. The density field of axisymmetric flows can also be computed from the schlieren data after applying an Abel or Fourier transform inversion algorithm. In this case, the transform algorithm rebuilds the density field from ray deflections. This has been shown, for example, by Venkatakrishnan (2005), Venkatakrishnan and Suriyanarayanan (2009) and Sourgen et al. (2004, 2012). Kindler et al. 2007 applied the tomographic reference-free BOS method for the study of rotor blade tip vortices. Ota et al. (2011) demonstrated that the Algebraic Reconstruction Technique (ART) can also be used in order to derive density distributions. According to them, the ART method is favorable for applications where a wind tunnel model is in the line of sight.
6.3 Density determination for complex flows
Some of the publications on the density determination for complex flows deal with investigations of an asymmetric mixture of jets (Venkatakrishnan et al. (2011) or an asymmetric cold streak in a turbine engine’s exhaust jet (Adamczuk et al. 2013; Hartmann et al. 2015). If single jets were investigated by tomographically evaluated BOS recordings, the authors aimed for the description of the unsteady effects. Todoroff et al. (2014) reconstructed instantaneous 3D flow density fields of an unsteady air jet by a new direct regularized 3D BOS method. Atcheson et al. (2008) and Berger et al. (2009) applied tomographic BOS to unsteady gas flows.
Goldhahn and Seume (2007) and Goldhahn et al. (2009) described the tomographic reconstruction by a filtered back-projection algorithm and applied the method to determine the density distribution of asymmetric underexpanded free air jets out of a double-hole orifice. The 3D density field was reconstructed in planes perpendicular to the jets axis. They justified the assumption of parallel projection in the case of small opening angles of the camera lens used. The principle of the reconstruction process can be described as follows:
The refractive index is related to the density by the Gladstone–Dale equation:
where n is the refractive index and G is the Gladstone–Dale constant. A relation between the angle of deflection and the first derivative of the refractive index was derived by Fomin (1998). By applying Eq. (2), this expression can be modified as:
In order to apply computerized tomography, secondary radial axes s and t were established on the plane YZ. Figure 8 shows these secondary radial axes. Different recording projections can be obtained by rotating the axis s by an angle θ for a range of 180°. By taking enough projections through the object, the Fourier plane is successively filled with values that describe the object. A single light ray in a line \(s = {\text{const}}\), with \(s = z\;\cos \varTheta + y\;\sin \varTheta\), will be deflected by an angle \(\varepsilon (s,\varTheta )\) (see Liu et al. (1989) for a detailed description):
where the integral is calculated along a line \(s = {\text{const}}\). Equation 12 basically represents Eq. 11 adapted to the radial axes. In order to compute the density reconstruction, the convolution back-projection method can be applied (Goldhahn and Seume 2007).
Secondary radial axes s–t (Liu et al. 1989)
Hence, by using Fourier transforms, the density distribution can be obtained,
where the density reconstruction is a convolution of the projections under ɛ(s, θ) with a filter function q(s).
7 Pulsed illumination BOS
Pulsed illumination has also been used frequently in order to capture unsteady features of the flow under investigation. Kumar et al. (2011) used a pulsed white-light source using a Xenon flash lamp with a maximum repetition rate of 1000 Hz and pulse duration of 5–10 μs for the visualization of micro-jets. In some cases, a Xenon stroboscope was placed behind a semitransparent background pattern for increased efficiency of the illumination (e.g., Augenstein et al. 2001; Rouser et al. 2011; Ramanah et al. 2007). The latter used a Movistrob 400 (Bamberg and Bormann Electronic Gmbh) with a maximum light intensity of 550 lux and a pulse width of about 8 µs. Kirmse et al. (2011) used an Nd:YAG laser generating pulses of 25 ns in combination with optical band path filters in front of the camera in order to minimize the influence of the self-luminosity of the high-enthalpy flow under investigation. Yamamoto et al. (2014) utilized a laser stroboscope with a pulse width of 20 ns as an illumination source (CAVITAR, Finland). Jin et al. (2011) also used an Nd:YAG laser. Experimental efforts were required in order to avoid laser speckles to interfere with the evaluation of the background image displacement analysis.
An increasingly large number of researchers use high intensity LEDs. Electronic drivers push the amperage to multiple times the level of continuous operation. As a consequence, exposure times were defined by the duration of the light pulse, not by the shutter of the cameras. A highly over-driven pulsed LED was used by Bencs et al. (2011) and Raffel et al. (2012) (HardSoft) and customized LED collimated arrays, for example, by Hernandez et al. (2013).
8 Retroreflective BOS
When it comes to large-scale and short-exposure BOS applications, even in favorable laboratory conditions, illumination becomes one of the limiting factors. The use of retroreflective materials for BOS backgrounds greatly enhances the efficiency of short duration pulsed light sources of limited pulse energy. Highly efficient illumination is important in two ways: First, the smaller the lens aperture, the more the intensity of light required. As mentioned earlier, a small aperture will reduce image blur and therefore yield greater sensitivity in detecting smaller phase objects yielding higher spatial resolution. Second, motion blur should be minimized by reduced exposure times. Retroreflective materials provide the most efficient return of light from speckled backgrounds, when on-axis lighting is used, because retroreflection does not follow the inverse-square law of lighting suffered by diffuse background. Heineck et al. (2010, 2012) describe several installations of retroreflective BOS (RBOS) systems to visualize shock waves, the vortices from a full-scale helicopter rotor and a jet in cross-flow in facilities and location never accessed prior to this development. The RBOS technique has been applied by Schröder et al. (2014) for the measurement of the jet of an Airbus A320 with four instantaneously operated high resolution high-framing-rate cameras.
9 High-framing-rate BOS
A recent technical improvement for BOS applications is the increasing availability of CMOS sensors with the active pixel sensor (APS) technology in which, in addition to the photodiode, a readout amplifier is incorporated into each pixel. This, together with highly parallel readout electronics storage devices, allows for the recording and handling of up to a few thousand frames per second at acceptable noise levels. Several of the BOS experiments presented in the literature describe the use of these cameras. In many cases, they allowed for good temporal resolution of the flow phenomena under investigation.
Rouser et al. (2011), for example, determined the time-accurate flow field of a pulsed detonation driven turbine. Kessler et al. (2005) used BOS for hydrogen detection and the observation of a hydrogen explosion at a 1 kHz frame rate. Kushner et al. (2015) used a high-speed PIV laser to obtain 20-kHz laser speckle RBOS movies of a sweeping jet actuator.
Mizukaki (2010) investigated transonic vortex rings discharged from the open end of a shock tube at 10 kHz frame rate and , together with co-workers, the wave propagation of an explosion at 100 kHz (Mizukaki et al. 2015). The very high framing-rate capability of the BOS technique was demonstrated in 2014 when Yamamoto et al. (2014) investigated the evolution of a shock wave pressure induced by a laser pulse in a liquid-filled thin tube using an ultra-high-speed video camera with 5 MHz frame rate. The pressure field was obtained by solving the Poisson equation.
10 BOS velocimetry
During the past decades, several velocimetry techniques have been proposed which do not require tracer particles to be added to the flow. One of them utilizes BOS. The “PIV analysis” of BOS displacement fields can be performed and provides a spatially resolved estimate of local convection velocities. Jonassen et al. (2006), for example, used the prevalent eddies in a turbulent flow as Lagrangian flow tracers. Convection velocities have also been determined by Settles (2010) who applied BOS and other optical density gradient methods for the visualization of thermal plumes and used the method for “seedless PIV” (BOS velocimetry).
Bühlmann et al. (2014) used a “PIV analysis” of the measured BOS displacement field itself to perform a spatially resolved estimate of the local advection velocities. Due to the need for naturally occurring density gradients, the applicability of their method is limited to turbulent compressible or thermal flows. Other authors used their BOS time-series data similarly to measure velocities of the density gradient generated by vortices, concentration or temperature gradients or shock waves (e.g., Jin et al. 2011). However, the velocities measured represent the velocities of the structures, for example the vortex convection speed or the speed of the compression shock, but not necessarily the local fluid velocity. Density tagging velocimetry (DTV) has been proposed to overcome this problem (Raffel et al. 2011). The DTV method is an optical technique for pointwise velocity measurements based on the detection and tracking of a local refractive index or density variation which is intentionally induced in the flow by two subsequently recorded BOS images. The local density variation, “density tag,” acts as a tracer particle that is transported by the fluid flow. The density tagging method used was based on pulsed laser-induced ionization. The same tagging method can also be used in order to determine the speed of the resulting shock wave. Assuming that the laser pulse is strong enough to ionize the fluid, but weak enough to create only a weak shock wave, the changes in pressure and density can be assumed to occur isentropically. The shock wave’s propagation speed can then be approximated by the speed of sound which, for an ideal gas, is given by:
This relation between temperature and speed of sound can be used to estimate the temperature around the point of plasma ignition, neglecting heat transfer and disruptive effects of the shock wave to the flow field, such as non-local density or pressure changes (Kähler and Scholz 2003; Raffel et al. 2012). However, it has also been found that the method allows for a limited accuracy as the ignition itself is intrusive and the structure’s expansion is not necessarily symmetric.
11 Color BOS
The increasing availability and resolution of color cameras lead to the development of color BOS (CBOS) that has recently been used for a number of BOS applications. In order to get an improved analysis of color images, the CBOS processing takes the fact into account that digital cameras have sensors for the colors red, green and blue. According to Leopold (2007) and Leopold et al. (2010), data from the sensors should directly be stored without any treatment or compression in a file with a special raw format. Due to the decomposition into the three colors, eight elementary dot patterns can be extracted from the image (Fig. 9):
Extraction of the eight elementary dot patterns from the colored background image (Leopold 2007)
-
three patterns based on the unfiltered red, green and blue color channels of the camera,
-
three patterns based on dots which contain mainly one base color (pure red, green or blue dots),
-
one pattern based on dots with a significant amount of at least two colors (secondary colors), and
-
one pattern for the uncolored areas, the so-called black dots.
The assessment of the image distortion can be achieved by treating each of the eight elementary patterns separately. An average intensity value for each location is determined by the value obtained at the location itself and by the results from interpolations between the opposite neighboring values. A standard deviation criterion, which the intensities used for the averaging must satisfy, can be used in order to increase the accuracy of the procedure. Various publications report the advantages of the method and the determination of density distributions of axisymmetric flows (Leopold et al. 2010; Ota et al. 2012, 2015; Sourgen et al. 2012). One of the advantages of the CBOS technique is its ability to treat regions of high refractive index gradients with the associated blurring of the background pattern (see, e.g., Fig. 5) by a shift of one of the base color patterns. Details of this procedure are described by Leopold et al. (2014).
12 Natural background BOS
The use of natural formation backgrounds for detecting refractive index gradients is intuitive since many effects, such as heat haze or mirage, can be seen in nature even without any instrumentation. The first question that needs to be answered while planning to visualize those effects with electronic equipment for measurements is the selection of the best-suited background.
Different quality indicators were introduced by Kindler et al. (2007), Hargather and Settles (2010a, b) and Bauknecht et al. (2014) to assess the suitability of different background images for BOS measurements. The earlier indicators are based on the signal-to-noise ratio of the autocorrelation of a background image. Plotted versus interrogation window size, it allows identifying suitable backgrounds and gives an indication of the obtainable spatial resolution. The second method introduced by Bauknecht et al. is based on the cross-correlation of two images of the same background, which have been recorded by different cameras. Based on the displacement field of the two images, the inverse of the variance of the rotation ω z is calculated. This quality indicator is independent of residual misalignments of the two images, is not negatively affected by the autocorrelation of image noise and allows for a more direct evaluation of the backgrounds in a realistic BOS setup than the previously suggested methods. An analysis of natural backgrounds (Fig. 10) based on the cross-correlation of image pairs is taken from Bauknecht et al. (2014). Figure 11 contains plots of the quality indicator over interrogation window size for the corresponding background patterns in Fig. 10. The graph indicates that larger interrogation window sizes decrease the correlation noise, at the cost of measurement resolution and accuracy.
Example cutouts of the natural backgrounds used for the current study with increasing structure sizes from left to right. Contrast enhanced for clarity (Bauknecht et al. 2014)
Despite this, obvious trend images have to be evaluated at small interrogation window sizes (e.g., 8–16 px) in order to resolve the small scales. For these backgrounds and magnifications, small-scale scree (Fig. 10b) was best suited as a natural background. Smaller structures like grass (Fig. 10a) and larger structures as shown in (Fig. 9c–e) show higher variances in the rotation of the displacement field.
This quality indicator is especially suited for the background selection for large-scale tests outside the laboratory. In addition to the flight tests described by Bauknecht et al. (2015), other examples for this sort of measurements include explosions of gas (Sommersel et al. 2008) and C4 (Mizukaki et al. 2012). The image subtraction method and the (conventional) BOS correlation method have been found to be suited for this task (Hargather 2013).
13 Reference-free BOS
The reference-free BOS method (Raffel et al. 2000b, 2014; Bauknecht et al. 2014) can be used if the density variation under observation does not cover the whole field of view, leaving some parts of the image almost free of distortions. These parts can serve as a reference for a second measurement image, in which the density structures are located in front of another part of the background, rather than requiring an image without a phase object as a reference.
This is useful for experiments where camera and background move with respect to each other, for example, for cameras that are airborne and/or track a rapidly moving object.
There are two basic principles on how to achieve the necessary shift of the density structures between the two images and hence how to realize a reference-free setup: the stereoscopic configuration and the monoscopic/paraxial configuration. In the stereoscopic configuration, two cameras record images at the same time but from different angles (see Fig. 12). If properly set up, the density variation is in front of different parts of the common background. Correlating the two images, the density variation appears twice in the resulting displacement field, but in different positions and with a different sign. As the background is viewed from different angles, it must be reasonably planar. Because of the simultaneous acquisition of both images, the background may change over time without influencing the measurement. If the density gradient under consideration moves relative to the background, as is the case for the blade tip vortices of a helicopter, the monoscopic/paraxial configuration can be realized. In principle, two images of the same background are recorded at consecutive points in time from one location. The evaluated displacement field of these two pictures features the density variation at both points in time, but with a different sign. For this setup, either a single camera with a short interframing time (monoscopic configuration) or two paraxially mounted cameras triggered with a short time delay (paraxial configuration) are required. In the paraxial setup, the cameras have to be mounted very close together and the distance to the background has to be large enough for the alignment error to be negligible.
Reference-free BOS setup (Raffel et al. 2000b)
A drawback of this method is that the integration of the density field from the displacements is not or not easily possible, as the reference pictures are not entirely free of density variations. The major advantage over the stereoscopic setup, however, is the straightforward implementation for out-of-the-laboratory experiments. Because both cameras must be close to each other, they can be mounted on the same tripod or can easily be operated airborne (Kindler et al. 2007; Bauknecht et al. 2014). It is then possible to move both cameras simultaneously while keeping the object of interest within the field of view.
14 Free surface BOS
Another alternative application of BOS is the observation of free surface flows. Moisy et al. (2009), for example, recorded a background pattern through a liquid. The liquid was contained in a tank with a transparent bottom allowing for an optimization of the background pattern distance Z D. With this approach, the topography of the liquid’s interface could be determined by a numerical integration of the displacement field. The main limitation of the method, namely the ray crossing (caustics) due to strong curvature and/or large surface pattern distance, was presented additionally. Jin et al. (2010) and Plaksina et al. (2012) presented an experimental investigation of near-surface small-scale structures at water–air interface and found that the temperature measurement sensitivity is generally better than 0.1 K for such an application by comparing the result with infrared measurements. Tokgoz et al. (2012) conducted temperature and velocity measurements inside a thin fluid layer using background-oriented schlieren and PIV methods by placing a reflective surface to one side of the test section.
15 Conclusions
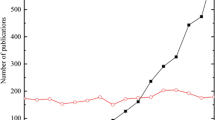
Presently, BOS is frequently used as an “easy-to-use” visualization of flows having density gradients due to varying temperature or pressure. Its strength lies in the simplicity of a basic setup, and this allows for its application in experimental environments which are unsuited for other measurement techniques. This advantage has further been developed to a state where BOS can be used for a large number of investigations in various fields. Due to new camera designs and the rapid development in the area of digital imaging and image processing, higher signal-to-noise ratios and increased resolution counteract the main disadvantage of the BOS, which is the limited resolution inherent with the statistical displacement computation. It can be seen in Fig. 13 that the number of publications is still growing. More and more frequently the pure qualitative flow visualization is replaced by a more sophisticated analysis of the images allowing for three-dimensional density determination. A clear recent trend for laboratory investigations is the recording with high-framing-rate cameras frequently used together with LED illumination and retroreflective material.
Coupling BOS with other optical flow techniques such as PIV, LIF and thermography has also enjoyed success and serves fluid mechanical research and development of machinery. Table 1 depicts the number of BOS applications that have been performed together with another optical flow metrology.
Within the past 15 years, the background-oriented schlieren techniques have developed from a robust and simple flow visualization to an increasingly accurate method for the measurement of complete density fields at very high framing rates. The combination of its application with other sophisticated flow metrologies further increases the completeness of the information obtained from fluid flow experiments. The ongoing improvement of the technique is driven by the continuing demand for high-quality experimental data for CFD validation and improvement of physical models of complex flows and the rapid development of illumination, image recording and image processing techniques.
Abbreviations
- A, B:
-
Cameras
- C s :
-
Speed of sound
- d A :
-
Lens aperture diameter
- d d :
-
Diffraction limit image diameter
- d i :
-
Geometric blur image diameter
- \(d_{\varSigma }\) :
-
Overall blur image diameter
- F :
-
3 × 3 Fundamental matrix
- f :
-
Lens focal length
- G :
-
Gladstone–Dale constant
- I :
-
Image intensity
- M :
-
Background image magnification
- M′:
-
Density gradient magnification
- n :
-
Refractive index
- n 0 :
-
Reference refractive index
- O A,B :
-
Origins camera coordinate systems
- P :
-
Point in the observation area
- q(s):
-
Filter function
- R :
-
Specific gas constant
- T :
-
Gas temperature
- s, t :
-
Secondary axes
- X, Y, Z :
-
Coordinates in object space
- x, y, z :
-
Coordinates in image space
- P A, P B :
-
Projections of P in images A and B
- Z A :
-
Distance lens—schlieren
- Z D :
-
Distance schlieren—background
- z i :
-
Distance lens—image plane
- γ :
-
Adiabatic index
- ∆I :
-
Local variation in image intensity
- ∆s :
-
Local image displacement
- ∆y :
-
Image displacement in y direction
- ε y :
-
Light deflection in y direction
- ε(s, Θ):
-
Light deflection in radial coordinates
- λ :
-
Wavelength of light
- γ :
-
Adiabatic index
- ρ :
-
Density
- \(\rho_{\infty }\) :
-
Reference density
- ρ*:
-
Normalized density \(\rho /\rho_{\infty }\)
- Θ :
-
Radial coordinate
- ω z :
-
z component of rotation
References
Adamczuk R, Hartmann U, Seume J (2013) Experimental demonstration of analyzing an engine’s exhaust jet with the background-oriented schlieren method. Paper AIAA-2013-2488, AIAA ground testing conference, San Diego
Alhaj O, Seume JR (2010) Optical investigation of profile losses in a linear turbine cascade. ASME Turbo Expo 2010: power for land, sea and air. Glasgow, UK
Atcheson B, Ihrke I, Heidrich W, Tevs A, Bradley D, Magnor M, Seidel HP (2008) Time-resolved 3d capture of non-stationary gas flows. ACM Trans Gr 27(5):132
Atcheson B, Heidrich W, Ihrke I (2009) An evaluation of optical flow algorithms for background oriented schlieren imaging. Exp Fluids 46(3):467–476
Augenstein E, Leopold F, Richard H, Raffel M (2001) Schlieren techniques in comparison: the background oriented method versus visualization with holographic filters. Paper 1191, 4th international symposium on particle image velocimetry, Göttingen
Bang SH, Lee CS (2013) Comparison between background oriented schlieren (BOS) technique and scattering method for the spray characteristics of evaporating oxygenated fuels. Optik 124(15):2147–2150
Bauknecht A, Merz CB, Raffel M, Landolt A, Meier AH (2014) Blade-tip vortex detection in maneuvering flight using the background-oriented schlieren technique. J Aircr 51(6):2005–2014
Bauknecht A, Ewers B, Wolf C, Leopold F, Yin J, Raffel M (2015) Three-dimensional reconstruction of helicopter blade tip vortices using a multi-camera BOS system. Exp Fluids 56(1):1–13
Bencs P, Szab S, Bords R, Zhringer K, Thvenin D (2011) Synchronization of particle image velocimetry and background oriented schlieren measurement techniques. In: Proceedings of the 8th Pacific Symposium on flow visualization and image processing, Moscow
Berger K, Ihrke I, Atcheson B, Heidrich W, Magnor MA (2009) Tomographic 4d reconstruction of gas flows in the presence of occluders. In: Proceedings of the vision, modeling, and visualization workshop 2009, Braunschweig
Bichal A, Thurow B (2010) Development of a background oriented schlieren based wavefront sensor for aero-optics. Paper AIAA-2010-4842, 40th fluid dynamics conference and exhibit, Chicago
Bichal A, Thurow BS (2014) On the application of background oriented schlieren for wavefront sensing. Meas Sci Technol 25(1):015001
Bühlmann P, Meier AH, Ehrensperger M, Rösgen T (2014) Laser speckle based background oriented schlieren measurements in a fire backlayering front. In: 17th international symposium on applications of laser techniques to fluid mechanic, Lisbon
Clem MM, Brown CA, Fagen AF (2013) Background oriented schlieren implementation in a jet-surface interaction test. Paper AIAA-2013-0038, 51st AIAA aerospace sciences meeting including the new horizons forum and aerospace exposition, Grapevine
Dalziel SB, Hughes GO, Sutherland BR (2000) Whole-field density measurements by ‘synthetic schlieren’. Exp Fluids 28(4):322–335
Debrus S, Francon M, Grover CP, May M, Robin ML (1972) Ground glass differential interferometer. Appl Opt 11:853–857
Delmas A, Le Maoult Y, Buchlin JM, Sentenac T, Orteu JJ (2013) Shape distortions induced by convective effect on hot object in visible, near infrared and infrared bands. Exp Fluids 54(4):1–16
Doric S (1990) Ray tracing through gradient-index media: recent improvements. Appl Opt 29:4026–4029
Ducasse ML, Dubois J, Amielh M, Anselmet F (2010) Experimental investigation of a turbulent variable density jet impinging on a sphere. In: Proceedings of the 15th international symposium on applications of laser techniques to fluid mechanics, Lisbon
Elsinga GE, Van Oudheusden BW, Scarano F, Watt DW (2004) Assessment and application of quantitative schlieren methods: calibrated color schlieren and background oriented schlieren. Exp Fluids 36(2):309–325
Fey U, Konrath R, Kirmse T, Ahlefeldt T, Kompenhans J, Egami Y (2010) Advanced measurement techniques for high Reynolds number testing in cryogenic wind tunnels. Paper AIAA-2010-1301, 48th AIAA Aerospace Sciences Meeting, Orlando
Fomin NA (1998) Speckle photography for fluid mechanics measurements. Springer, Berlin. ISBN:3540637672
Germain E, Quest J (2005) The development and application of optical measurement techniques for high Reynolds number testing in cryogenic environment. Paper 4584, 3rd AIAA aerospace sciences meeting, Reno
Glazyrin FN, Znamenskaya IA, Mursenkova IV, Sysoev NN, Jin J (2012) Study of shock-wave flows in the channel by schlieren and background oriented schlieren methods. Optoelectron Instrum Data Process 48(3):303–310
Gojani AB, Obayashi S (2012) Assessment of some experimental and image analysis factors for background-oriented schlieren measurements. Appl Opt 51(31):7554–7559
Gojani AB, Kamishi B, Obayashi S (2013) Measurement sensitivity and resolution for background oriented schlieren during image recording. J Vis 16(3):201–207
Goldhahn E, Seume J (2007) The background oriented schlieren technique: sensitivity, accuracy, resolution and application to a three-dimensional density field. Exp Fluids 43(2–3):241–249
Goldhahn E, Alhaj O, Herbst F, Seume J (2009) Quantitative measurements of three-dimensional density fields using the background oriented schlieren technique. In: Imaging measurement methods for flow analysis. Springer, Berlin, pp 135–144
Hargather MJ (2013) Background-oriented schlieren diagnostics for large-scale explosive testing. Shock Waves 23(5):529–536
Hargather MJ, Settles GS (2010a) Natural-background-oriented schlieren imaging. Exp Fluids 48(1):59–68
Hargather MJ, Settles GS (2010b) Recent developments in schlieren and shadowgraphy. Paper AIAA-2010-4206, 27th AIAA aerodynamic measurement technology and ground testing conference, Chicago
Hargather MJ, Settles GS (2011) Background-oriented schlieren visualization of heating and ventilation flows: HVAC-BOS. HVAC R Res 17(5):771–780
Hargather MJ, Settles GS (2012) A comparison of three quantitative schlieren techniques. Opt Lasers Eng 50(1):8–17
Hartley R, Zisserman A (2003) Multiple view geometry in computer vision, 2nd edn. Cambridge University Press, UK. ISBN:978-0-5215-4051-3
Hartmann U, Adamczuk R, Seume JR (2015) Tomographic background oriented schlieren applications for turbomachinery. Paper AIAA-2015-1690, 53rd AIAA aerospace sciences meeting, Kissimmee. doi:10.2514/6.2015-1690
Heineck JT, Schairer ET, Kushner LK, Walker LA (2010) Retro-reflective background oriented schlieren (RBOS). Proceedings of the 14th international symposium on flow visualization, Daegu
Heineck JT, Kushner LK, Schairer ET, Walker LA (2012) Retro-reflective background oriented schlieren (RBOS) as applied to full-scale UH-60 blade tip vortices. In: Proceedings of the American Helicopter Society Aeromechanics Specialists’ conference, San Francisco, pp 722–727
Hernandez R, Heine B, Schneider O, Chernukha P, Raffel M (2013) Visualization and computation of quantified density data of the rotor blade tip vortex. New results in numerical and experimental fluid mechanics VIII, Springer, Berlin, pp 321–329, ISBN:978-3-642-35679-7
Iffa ED, Aziz ARA, Malik AS (2010) Concentration measurement of injected gaseous fuel using quantitative schlieren and optical tomography. J Eur Op Soc 5:10029
Iffa ED, Aziz ARA, Malik AS (2011) Gas flame temperature measurement using background oriented schlieren. J Appl Sci 11(9):1658–1662
Jensen OS, Kunsch JP, Rösgen T (2005) Optical density and velocity measurements in cryogenic gas flows. Exp Fluids 39(1):48–55
Jin J, Lutzky AE, Mursenkova IV, Vinnichenko NA, Znamenskaya IA, Glazyrin FN (2010) Application of BOS method for analysis of the flow after surface discharge. In: Proceedings of the 21st international symposium on transport phenomena, Kaohsiung City
Jin J, Mursenkova IV, Sysoev NN, Vinnichenko NA, Znamenskaya IA, Glazyrin FN (2011). Experimental investigation of blast waves from plasma sheet using the background oriented schlieren and shadow methods. J Flow Vis Image Proc 18(4)
Jonassen D, Settles G, Tronosky M (2006) Schlieren for turbulent flows. Opt Lasers Eng 44:190–207
Kähler CJ, Scholz U (2003) Investigation of laser-induced flow structures with time-resolved PIV, BOS and IR technology. In: Proceedings of the 5th international symposium on particle image velocimetry, Busan
Kessler A, Ehrhardt W, Langer G (2005). Hydrogen detection: visualisation of hydrogen using non-invasive optical schlieren technique BOS. In: Proceedings of the international conference of hydrogen safety, Pisa
Kindler K, Goldhahn E, Leopold F, Raffel M (2007) Recent developments in background oriented schlieren methods for rotor blade tip vortex measurements. Exp Fluids 43(2–3):233–240
Kirmse T, Agocs J, Schröder A, Schramm JM, Karl S, Hannemann K (2011) Application of particle image velocimetry and the background-oriented schlieren technique in the high-enthalpy shock tunnel Göttingen. Shock Waves 21(3):233–241
Klinge F, Kirmse T, Kompenhans J (2003) Application of quantitative background oriented schlieren (BOS): investigation of a wing tip vortex in a transonic wind tunnel. Paper F4097, PSFVIP-4, Chamonix
Köpf U (1972) Application of speckling for measuring the deflection of laser light by phase objects. Opt Commun 5:347–350
Kumar R, Ali MY, Alvi FS, Venkatakrishnan L (2011) Generation and control of oblique shocks using microjets. AIAA J 49(12):2751–2759
Kushner LK, Heineck JT, Storms BS, Childs RE (2015) Visualization of a sweeping jet by laser speckle retro-reflective background oriented schlieren. Paper AIAA-2015-1690, 53rd AIAA aerospace sciences meeting, Kissimmee
Le Sant Y, Todoroff V, Bernard-Brunel A, Le Besnerais G, Micheli F, Donjat D (2014) Multi-camera calibration for 3D BOS. In: Proceedings of the 17th international symposium on applications of laser techniques to fluid mechanic, Lisbon
Lee J, Kim N, Lee H, Min K (2011) The measurement of penetration length of diesel spray by using background oriented schlieren technique. SAE technical paper 2011-01-0684
Lee J, Kim N, Min K (2013) Measurement of spray characteristics using the background-oriented schlieren technique. Meas Sci Technol 24(2):025303
Leopold F (2007) The application of the colored background oriented schlieren technique (CBOS) to free-flight and in-flight measurements. In: Proceedings of the 22nd international congress on instrumentation in aerospace simulation facilities, Pacific Grove
Leopold F, Sourgen F, Klatt D, Jagusinski F (2010) The application of the colored background oriented schlieren technique to the reconstruction of the density field. In: Proceedings of the 14th international symposium on flow visualization, Daegu
Leopold F, Ota M, Jagusinski F, Maeno K (2014) Algebraic reconstruction of the unsteady density field around a spike-tipped model at supersonic speed using the colored background oriented Schlieren technique. In: Proceedings of the 16th international symposium on flow visualization, Okinawa
Liu TC, Merzkirch W, Oberste-Lehn K (1989) Optical tomography applied to speckle photographic measurement of asymmetric flow with variable density. Exp Fluids 7:157–163
Loose S, Richard H, Dewhirst T, Raffel M (2000) Background oriented schlieren (BOS) and particle image velocimetry (PIV) applied for transonic turbine blade investigations. Paper 28-2, laser techniques for fluid mechanics, Lisbon
Loose S, Richard H, Bosbach J, Thimm M, Becker W, Raffel M (2006) Optical measurement techniques for high Reynolds number train investigations. Exp Fluids 40(4):643–653
Meier G (2002) Computerized background-oriented schlieren. Exp Fluids 33(1):181–187
Meier AH, Rösgen T (2013) Improved background oriented schlieren imaging using laser speckle illumination. Exp Fluids 54(6):1–6
Meyn LA, Bennett MS (1993) Application of a two camera video imaging system to three-dimensional vortex tracking in the 80- by 120-foot wind tunnel. In: Proceeding of AIAA 11th applied aerodynamics conference, Monterey, CA, USA
Mizukaki T (2010) Visualization of compressible vortex rings using the background-oriented schlieren method. Shock Waves 20(6):531–537
Mizukaki T, Tsukada H, Wakabayashi K, Matsumura T, Nakayama Y (2012) Quantitative visualization of open-air explosions by using background-oriented schlieren with natural background. In: Proceedings of the 28th international symposium on shock waves, vol 1. Springer, Berlin, pp 465–470
Mizukaki T, Borg S, Danehy PM, Murman SM, Matsumura T, Wakabayashi K, Nakayama Y (2015) Background-oriented schlieren for large-scale and high-speed aerodynamic phenomena. Applications for turbomachinery. Paper AIAA-2015-1690, 53rd AIAA aerospace sciences meeting, Kissimmee. doi:10.2514/6.2015-1692
Moisy F, Rabaud M, Salsac K (2009) A synthetic schlieren method for the measurement of the topography of a liquid interface. Exp Fluids 46(6):1021–1036
Ota M, Hamada K, Kato H, Maeno K (2011) Computed-tomographic density measurement of supersonic flow field by colored-grid background oriented schlieren (CGBOS) technique. Meas Sci Technol 22(10):104011
Ota M, Kato H, Maeno K (2012) Three-dimensional density measurement of supersonic and axisymmetric flow field by colored grid background oriented schlieren (CGBOS) technique. Int J Aerosp Innov 4(1):1–12
Ota M, Leopold F, Noda R, Maeno K (2015) Improvement in spatial resolution of background-oriented schlieren technique by introducing a telecentric optical system and its application to supersonic flow. Exp Fluids 56(48). doi:10.1007/s00348-015-1919-5
Plaksina YY, Uvarov AV, Vinnichenko NA, Lapshin VB (2012) Experimental investigation of near-surface small-scale structures at water-air interface: background oriented schlieren and thermal imaging of water surface. Russ J Earth Sci 12(4):4002
Popova EM (2004) Processing schlieren-background patterns by constructing the direction field. J Opt Technol 71(9):572–574
Popova EM, Kompenhans J, Skornyakova NM (2008) Investigation of the accuracy of the background oriented schlieren method. In: Proceedings of the 13th international symposium of flow visualization, Nice
Prasanna S, Venkateshan SP (2011) Construction of two dimensional temperature field from first derivative fields. Exp Thermal Fluid Sci 35(6):1019–1029
Raffel M, Richard H, Meier GEA (2000a) On the applicability of background oriented optical tomography for large scale aerodynamic investigations. Exp Fluids 28(5):477–481
Raffel M, Tung C, Richard H, Yu Y, Meier GEA (2000b) Background oriented stereoscopic Schlieren (BOSS) for full scale helicopter vortex characterization. In: Proceedings of the 9th international symposium on flow visualization, Edinburgh
Raffel M, Willert C, Wereley S, Kompenhans K (2007) Particle image velocimetry, 2nd edn. Springer, Berlin. ISBN 987-3-540-72307-3
Raffel M, Hernandez-Rivera R, Heine B, Schröder A, Mulleners K (2011) Density tagging velocimetry. Exp Fluids 51(2):573–578
Raffel M, Raiser D, Schuster F, Mulleners K (2012) Applications of density tagging velocimetry. In: Proceedings of the 16th international symposium on applications of laser techniques to fluid mechanics, Lisbon, Portugal
Raffel M, Heineck JT, Schairer E, Leopold F, Kindler K (2014) Background-oriented schlieren imaging for full-scale and in-flight testing. J Am Helicopter Soc 59(1):1–9
Raghunath S, Mee DJ, Rösgen T, Jacobs PA (2004) Visualization of supersonic flows in shock tunnels, using the background oriented schlieren technique. In: Proceedings of the AIAA Australian aerospace student conference, Sydney
Ramanah D, Mee DJ (2006) Scramjet flow visualization using background oriented schlieren in hypersonic impulse facilities. Paper AIAA-2006-8004, 14th AIAA/AHI space planes and hypersonic systems and technologies conference, Canberra
Ramanah D, Raghunath S, Mee DJ, Rsgen T, Jacobs PA (2007) Background oriented schlieren for flow visualisation in hypersonic impulse facilities. Shock Waves 17(1–2):65
Reinholtz CK, Heltsley FL, Scott KE, Rhode MN (2010) Visualization of jettison motor plumes from an Orion launch abort vehicle wind tunnel model using background-oriented schlieren. Paper AIAA-2010-1736, US Airforce T and E Days, Nashville
Richard H, Raffel M (2001) Principle and applications of the background oriented schlieren (BOS) method. Meas Sci Technol 12(9):1576
Richard H, Raffel M, Rein M, Kompenhans J, Meier GEA (2000) Demonstration of the applicability of a background oriented schlieren (BOS) method. Paper 15-1, laser techniques for fluid mechanics, Lisbon
Roosenboom EW, Schröder A (2009) Qualitative investigation of a propeller slipstream with background oriented Schlieren. J Vis 12(2):165–172
Roosenboom EW, Schröder A (2010) Image-based measurement techniques of increased complexity for industrial propeller flow investigations. Paper AIAA-2010-4210, 27th AIAA aerodynamic measurement technology and ground testing conference, Chicago
Rouser KP, King PI, Schauer FR, Sondergaard R, Goss LP, Hoke JL (2011) Time-accurate flow field and rotor speed measurements of a pulsed detonation driven turbine. Paper AIAA-2011-577, 49th AIAA aerospace sciences meeting, Orlando
Schairer ET, Kushner LK, Heineck JT (2013) Measurements of tip vortices from a full-Scale UH-60A rotor by retro-reflective background oriented schlieren and stereo photogrammetry. In: Proceedings of the 69th AHS annual forum, Phoenix
Schröder A, Over B, Geisler R, Bulit A, Schwane R, Kompenhans J (2009) Measurements of density fields in micro nozzle plumes in vacuum by using an enhanced tomographic background oriented schlieren (BOS) technique. 9th International symposium on measurement technology and intelligent instruments, Saint-Petersburg
Schröder A, Geisler R, Schanz D, Agocs J, Pallek D, Schroll M, Klinner J, Beversdorff M, Voges M, Willert C (2014) Application of image based measurement techniques for the investigation of aeroengine performance on a commercial aircraft in ground operation. 17th International symposium on applications of laser techniques to fluid mechanic, Lisbon
Sharma A, Kumar DV, Ghatak AK (1982) Tracing rays through graded-index media: a new method. Appl Opt 21:984–987
Settles GS (2010) Important developments in schlieren and shadowgraph visualization during the last decade. In: Proceedings of the 14th international symposium on flow visualization, Daegu, p 267
Sommersel OK, Bjerketvedt D, Christensen SO, Krest O, Vaagsaether K (2008) Application of background oriented schlieren for quantitative measurements of shock waves from explosions. Shock Waves 18(4):291–297
Sourgen F, Haertig J, Rey C (2004). Comparison between background oriented schlieren measurements (BOS) and numerical simulations. Paper AIAA-2004-2602, 24th AIAA aerodynamic measurement technology and ground testing conference, Portland
Sourgen F, Leopold F, Klatt D (2012) Reconstruction of the density field using the colored background oriented schlieren technique (CBOS). Opt Lasers Eng 50(1):29–38
Tillmann W, Abdulgader M, Rademacher HG, Anjami N, Hagen L (2014) Adapting of the background-oriented schlieren (BOS) technique in the characterization of the flow regimes in thermal spraying processes. 23(1–2):21–30. doi:10.1007/s11666-013-0018-5
Todoroff V, Le Besnerais G, Donjat D, Micheli F, Plyer A, Champagnat F (2014) Reconstruction of instantaneous 3d flow density fields by a new direct regularized 3dBOS method. In: Proceedings of the 17th international symposium on applications of laser techniques to fluid mechanic, Lisbon
Tokgoz S, Geisler R, van Bokhoven LJA, Wieneke B (2012) Temperature and velocity measurements in a fluid layer using background-oriented schlieren and PIV methods. Meas Sci Technol 23(11):115302
van Hinsberg NP (2014) A modification of the classical correction factor for digital background oriented schlieren when applied in the near-field. In: Proceedings of the 17th international symposium on applications of laser techniques to fluid mechanic, Lisbon
van Hinsberg NP, Rösgen T (2014) Density measurements using near-field background-oriented schlieren. Exp Fluids 55(4):1–11
Vasudeva G, Honnery DR, Soria J (2005) Non-intrusive measurement of a density field using the background oriented schlieren (BOS) method. In: Proceedings of the 4th Australian conference on laser diagnostic in fluid mechanics and combustion, Adelaide
Venkatakrishnan L (2005) Density measurements in an axisymmetric underexpanded jet by background-oriented schlieren technique. AIAA J 43(7):1574–1579
Venkatakrishnan L, Suriyanarayanan P (2009) Density field of supersonic separated flow past an afterbody nozzle using tomographic reconstruction of BOS data. Exp Fluids 47(3):463–473
Venkatakrishnan L, Wiley A, Kumar R, Alvi F (2011) Density field measurements of a supersonic impinging jet with microjet control. AIAA J 49(2):432–438
Veser A, Kuznetsov M, Fast G, Friedrich A, Kotchourko N, Stern G, Schwall M, Breitung W (2011) The structure and flame propagation regimes in turbulent hydrogen jets. Int J Hydrogen Energy 36(3):2351–2359
Vinnichenko NA, Uvarov AV, Plaksina YY (2012) Accuracy of background oriented schlieren for different background patterns and means of refraction index reconstruction. In: Proceedings of the 15th international symposium flow visualization, Minsk
Viktin D, Merzkirch W (1998) Speckle-photographic measurements of unsteady flow processes using a highspeed CCD camera. In: Proceedings of the 8th international symposium on flow visualization, Sorrento, Italy
Wernekinck U, Merzkirch W (1987) Speckle photography of spatially extended refractive-index fields. Appl Opt 26:31–32
Wolf C, Klei C, Buffo R, Hörnschemeyer R, Stumpf E (2012) Comparison of rocket near-wakes with and without nozzle simulation in subsonic freestream conditions. Paper AIAA-2012-3019, 42nd AIAA fluid dynamics conference and exhibit, New Orleans
Yamamoto S, Tagawa Y, Kameda M (2014) The evolution of a shock wave pressure induced by a laser pulse in a liquid filled thin tube using the background-oriented schlieren technique. In: Proceedings of the 17th international symposium on applications of laser techniques to fluid mechanics, Lisbon
Yevtikhiyeva OA, Skornyakova NM, Udalov AV (2009) An investigation of the error of the background schlieren method. Meas Tech 52(12):1300–1305
Znamenskaya I, Vinnichenko N, Glazyrin F (2012) Quantitative measurements of the density gradient on the flat shock wave by means of background oriented schlieren. In: Proceedings of the 15th international symposium on flow visualisation, Minsk
Acknowledgments
The author would like to acknowledge the contributions of A. Bauknecht, F. Leopold, K. Mulleners, K. Kindler, E. Schairer, J.T. Heineck, A.D. Gardner and R. Sujith in the form of results, descriptions and annotations to the article.
Author information
Authors and Affiliations
Corresponding author
Additional information
In memory of our friend Hugues Richard.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Raffel, M. Background-oriented schlieren (BOS) techniques. Exp Fluids 56, 60 (2015). https://doi.org/10.1007/s00348-015-1927-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-015-1927-5