Skip to main content
SpringerLink
Log in

Use of PIV to highlight possible errors in hot-wire Reynolds stress data over a 2D rough wall

  • Research Article
  • Published:
Experiments in Fluids Aims and scope Submit manuscript

Abstract

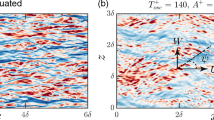
Particle image velocimetry (PIV) measurements are carried out in a turbulent boundary layer over a 2D rough surface consisting of transverse square bars. The aim of this work is to investigate a possible cause for the near-wall X-wire measurement errors observed on similar rough surfaces. The PIV measurements do not show the anomalous near-wall deficit of Reynolds stresses as measured with X-wires over the same surface. An extensive flow visualization analysis of the PIV data for a spacing between the roughness elements of p = 7k (k is the roughness element height) shows the occurrence of large-scale inward (sweeps) and outward (ejections) motions with a period of about 10.6δ/U 0 (δ and U 0 are the boundary layer thickness and the free-stream velocity). While these motions dominate the near-wall region and contribute almost equally to the Reynolds shear stress −‹uv›, the mean outward deviation from the mean flow direction is stronger than the inward deviation. Also, when the roughness spacing is reduced to p = 3k, the outward deviation reduces significantly more than the inward deviation. The results support the argument that the outward motions, which can have an instantaneous deviation angle of more than 50° in the case p = 7k, make the X-wire probe inefficient for detecting the ejection events (associated with the outward motions), particularly if the apex angle of the X-wire is not optimized for capturing the strong flow ejections with large deviations. The results explain in part the disparate information on the effect of the roughness on the Reynolds stresses in the outer region of the turbulent boundary layer over rough walls.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Acharya M, Escudier M (1987) Turbulent flow over mesh roughness. In: Durst F, Launder BE, Lumley JL, Schmidt FW, Whitelaw JH (eds) Turbulent shear flow 5. Springer, Berlin, pp 176–185

    Chapter  Google Scholar 

  • Antonia RA, Djenidi L (2009) On the outer layer controversy for a turbulent boundary layer over a rough wall. IUTAM Symposium on the physics of wall-bounded flows on rough walls, July 07–09, Cambridge, UK

  • Antonia RA, Luxton RE (1971) The response of a turbulent boundary layer to a step change in surface roughness Part 1. Smooth to rough. J Fluid Mech 48:721–761

    Article  Google Scholar 

  • Balachandar R, Patel V (2002) Rough wall boundary layer on plates in open channels. J Hydraul Eng 128:947–951

    Article  Google Scholar 

  • Chin CY, Djenidi L, Antonia RA (1995) Low-Reynolds number effects in a turbulent boundary layer. Exp Fluids 19:61–68

    Google Scholar 

  • Djenidi L, Elavarasan E, Antonia RA (1999) Turbulent boundary layer over transverse square cavities. J Fluid Mech 395:271–294

    Article  MATH  Google Scholar 

  • Djenidi L, Antonia RA, Amielh M, Anselmet F (2008) A turbulent boundary layer over a two-dimensional rough wall. Exp Fluids 44:37–47

    Article  Google Scholar 

  • Furuya Y, Miyata M, Fujita H (1976) Turbulent boundary layer and flow resistance on the plates roughened by wires. Trans ASME J Fluids Eng 98:635–644

    Article  Google Scholar 

  • Ikeda T, Durbin PA (2007) Direct simulations of rough walls. J Fluid Mech 571:235–263

    Article  MATH  Google Scholar 

  • Jimenez J (2004) Turbulent flows over rough walls. Ann Rev Fluid Mech 36:173–196

    Article  Google Scholar 

  • Kameda K, Mochizuki S, Osaka H (2004) LDA measurements in roughness sublayer beneath a turbulent boundary layer developed over two-dimensional square rough surface. In: Proceedings of the 12th international symposium on applications of laser techniques to fluid mechanics, (CDROM-paper 28.3), July 12–14, Lisbon, Portugal

  • Kitzhofer J, Ergin FG, Jaunet V (2012) 2D least squares matching applied to PIV challenge data (Part 1). In: 16th International symposium on applications of laser techniques to fluid mechanics, July 09–12, Lisbon, Portugal

  • Krogstad P-A, Antonia RA (1999) Surface roughness effect in turbulent boundary layer. Exp Fluids 27:450–460

    Article  Google Scholar 

  • Krogstad P-A, Antonia RA, Browne LWB (1992) Comparison between rough- and smooth-wall turbulent boundary layer. J Fluid Mech 245:599–617

    Article  Google Scholar 

  • Krogstad P-A, Antonia RA, Browne LWB (1994) Structure of turbulent boundary layers on smooth and rough walls. J Fluid Mech 277:1–21

    Article  Google Scholar 

  • Kunen JMG (1984) On the detection of coherent structures in turbulent flows, PhD Thesis, Delft University Press

  • Lee S-L, Sung HJ (2007) Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J Fluid Mech 584:125–146

    Article  MATH  Google Scholar 

  • Lee S-L, Kim JH, Sung HJ (2008) PIV measurements of turbulent boundary layer over a rod-roughened wall. Int J Heat Fluid Flow 29(6):1679–1687

    Article  Google Scholar 

  • Lee JH, Lee S-L, Kim K, Sung HJ (2009) Structure of the turbulent boundary layer over a rod-roughened wall. Int J Heat Fluid Flow (in press). doi:10.1016/j.ijheatfluidflow.2009.08.002

  • Leonardi S, Orlandi P, Smalley RJ, Djenidi L, Antonia RA (2003) Direct numerical simulations of turbulent channel with transverse square bar on one wall. J Fluid Mech 491:229–238

    Article  MATH  Google Scholar 

  • Li JD, Perry AE (1989) Proceedings of the 10th AFMC, University of Melbourne, December, 11th–15th, pp 7.9–7.12

  • Lu SS, Willmarth WW (1973) Measurements of the structure of the Reynolds stress in turbulent boundary layer. J Fluid Mech 60:481–571

    Article  Google Scholar 

  • Mulhearn PJ (1978) Turbulent flow over a periodic rough surface. Phys Fluids 21:1113–1115

    Article  Google Scholar 

  • Mulhearn P, Finnigan JJ (1978) Turbulent flow over a very rough, random surface. Bound Layer Met 15:109–132

    Article  Google Scholar 

  • Perry AE, Lim KL, Henbest SM (1987) An experimental study of the turbulence structure in smooth- and rough-wall boundary layers. J Fluid Mech 177:435–466

    Article  Google Scholar 

  • Pokrajac D, McEvan I, Nikora V (2008) Spatially averaged turbulent stress and its partitioning. Exp Fluids 45:73–83

    Article  Google Scholar 

  • Rao KN, Narasimha R, Narayanan MAB (1971) The ‘bursting’ phenomenon in a turbulent boundary layer. J Fluid Mech 48:339–352

    Article  Google Scholar 

  • Raupach MR, Tom AS, Edwards I (1980) A wind-tunnel study of turbulent flow close to regularly arrayed rough surfaces. Bound Layer Met 18:373–397

    Article  Google Scholar 

  • Roussiniva VT (2009) Turbulent structures in smooth and rough open channel flows: effect of depth, PhD Dissertation, University of Windsor, ON, Canada

  • Smalley RJ, Antonia RA, Djenidi L (2001) Self-preservation of rough wall turbulent boundary layer. Eur J Mech B-Fluids 20:591–602

    Article  MATH  Google Scholar 

  • Spalart PR (1988) Direct simulation of a turbulent boundary layer up to Rθ = 1410. J Fluid Mech 187:61–98

    Article  MATH  Google Scholar 

  • Tachie MF, Adane KK (2007) PIV study of shallow open channel flow over d- and k-type transverse ribs. J Fluids Eng 129:1058–1072

    Article  Google Scholar 

  • Volino RJ, Schultz MP, Flack KA (2007) Turbulent structure in rough- and smooth-wall boundary layers. J Fluid Mech 592:263–293

    Article  MATH  Google Scholar 

  • Volino RJ, Schultz MP, Flack KA (2009) Turbulent structure in a boundary layer with two-dimensional roughness. J Fluid Mech 635:75–101

    Article  MATH  Google Scholar 

  • Volino RJ, Schultz MP, Flack KA (2011) Turbulent structure in boundary layer over periodic two- and three dimensional roughness. J Fluid Mech 676:172–190

    Article  MATH  Google Scholar 

  • Wallace JM, Eckelmann H, Brodkey RS (1972) The wall region in turbulent shear flow. J Fluid Mech 54:39–48

    Article  Google Scholar 

  • Zhang Y, Che D (2012) Effects of two-dimensional V-shaped grooves on turbulent channel flow. Exp Fluids 52:315–328

    Article  Google Scholar 

Download references

Acknowledgments

L.D. and R.A.A. acknowledge the support from The Australian Research Council. L.D., F.A. and M.A. wish to thank the Ecole Centrale de Marseille for its financial contribution to this project.

Author information

Authors and Affiliations

  1. Discipline of Mechanical Engineering, University of Newcastle, Newcastle, Australia

    Lyazid Djenidi & Robert A. Antonia

  2. CNRS, IRPHE, UMR7342, Aix Marseille Université, Marseille, France

    Muriel Amielh

  3. ECM, IRPHE, UMR7342, Aix Marseille Université, Marseille, France

    Fabien Anselmet

Authors
  1. Lyazid Djenidi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Robert A. Antonia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Muriel Amielh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Fabien Anselmet
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lyazid Djenidi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Djenidi, L., Antonia, R.A., Amielh, M. et al. Use of PIV to highlight possible errors in hot-wire Reynolds stress data over a 2D rough wall. Exp Fluids 55, 1830 (2014). https://doi.org/10.1007/s00348-014-1830-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00348-014-1830-5

Keywords

Search

Navigation