Turbulent boundary-layer control with plasma spanwise travelling waves

Abstract

Arrays of dielectric-barrier-discharge plasma actuators have been designed to generate spanwise travelling waves in the turbulent boundary layer for possible skin-friction drag reductions. Particle image velocimetry was used to elucidate the modifications to turbulence structures created by the plasma spanwise travelling waves. It has been observed that the plasma spanwise travelling waves amalgamated streamwise vortices, lifting low-speed fluid from the near-wall region up and around the peripheries of their cores to form wide ribbons of low-speed streamwise velocity within the viscous sublayer.

1 Introduction

1.1 Transverse wall motions

The turbulent boundary layer can be considered as an assortment of coherent structures that are dispersed quasi-periodically in space and time (Head and Bandyopadhyay 1981; Robinson 1991; Hutchins et al. 2005). The hairpin vortices extend from the wall to the edge of the boundary layer and agglomerate to form hairpin packets (Zhou et al. 1999; Adrian 2007). The legs of hairpins form quasi-streamwise vortices and play an important role in maintaining wall turbulence (Choi 1989). The upwash side of quasi-streamwise vortices collect low-speed fluid within the viscous sublayer. This causes the appearance of low-speed streaks (Kline et al. 1967), which ultimately leads to ejection events (Corino and Brodkey 1969)—the expulsion of low-speed fluid into the outer regions of the boundary layer. The downwash side of quasi-streamwise vortices causes sweep events and the transfer of momentum from the outer regions of the boundary layer into the wall. The sweep events have been shown to be the major contributor to turbulent skin friction (Kravchencko et al. 1993; Orlandi and Jiménez 1993). Therefore, one way to achieve skin-friction drag reduction is to suppress sweep events, which can be achieved by controlling turbulence structures within the boundary layer.

Skin-friction drag reduction by transverse wall motions have received a lot of interest over recent years: see Karniadakis and Choi (2003) and Quadrio (2011) for reviews. Being inspired by results from Bradshaw and Pontikos (1985), who observed that a sudden spanwise pressure gradient temporarily suppressed the production of turbulence, Jung et al. (1992) created a spanwise-wall oscillation by introducing the spanwise velocity at the wall of the form,

$$\begin{aligned} w=A{\sin}\left( \omega t\right) , \end{aligned}$$

(1.1)

where $w$ is the spanwise velocity, $A$ is the amplitude of oscillation, $T=2\pi /\omega$ is the forcing period and $t$ is time. They used a direct numerical simulation (DNS) to find that a harmonic spanwise velocity (or pressure gradient) can suppress the turbulence production. This led to a 40 % reduction in skin-friction drag when the period of oscillation was $T^{+}\left( =Tu_{\tau }^{2}/\nu \right) \approx 100$. Here, $u_{\tau }$ is the friction velocity and $\nu$ is the kinematic viscosity. An experimental investigation soon followed (Laadhari et al. 1994), which verified the numerical predictions by showing that the velocity and Reynolds stresses in the near-wall region of the boundary layer were reduced with a spanwise-wall oscillation. The reduction in skin-friction drag was later experimentally quantified by Choi et al. (1998). They found a 45 % reduction in skin-friction drag when the spanwise-wall oscillation was optimised by a non-dimensional wall speed. Furthermore, they suggested that the drag reduction mechanism was due to the twisting of the near-wall turbulence structure caused by the periodic Stokes layer over the oscillating wall. This caused negative spanwise vorticity and reduced the near-wall velocity gradient, leading to a reduction in wall shear stress. Bandyopadhyay (2006) also suggested that the drag reduction mechanism with spanwise-wall oscillation was caused by the cyclic reorientation of the near-wall vorticity by the oscillating wall. However, Dhanak and Si (1999) proposed that the drag reduction mechanism may be related to weakening of sublayer streak instabilities, which in turn led to weakening of coherent structures in the near-wall region of the boundary layer. A similar explanation has recently been given by Touber and Leschziner (2012). They found that an optimum period of oscillation was determined by streak-formation and streak-amplification time scales. They observed that when the strain vector generated by the oscillating wall rapidly changed sign, the sublayer streaks were disrupted and weakened, causing a reduction in skin-friction drag. However, as the period of oscillation increased, the strain vector changed slowly with time. This allowed streaks to form and grow in the direction of the strain vector and resulted in poorer control. Moreover, Ricco et al. (2012) studied numerically spanwise-wall oscillation in a turbulent channel flow. They observed that the turbulent kinetic energy and coefficient of friction decreased due to a transient increase of turbulent entrophy on the initiation of the oscillating wall. In addition, Blesbois et al. (2013) and Moarref and Jovanovic (2012) have recently shown that the linear analysis of the Navier–Stokes equations can be used to elucidate structural and statistical information of the response of the turbulent flow to a transverse oscillatory wall motion.

A circular-wall oscillation was investigated experimentally by Choi and Graham (1998) and later with DNS by Quadrio and Sibilla (2000) and Nikitin (2000). The oscillation was created by rotating the body of a circular cylinder around its axis. The experimental and numerical investigations found a 25 % and up to a 40 % reduction in skin-friction drag, respectively. The discrepancy in these results was thought to be due to Reynolds number effect (Touber and Leschziner 2012) as the experimental study of Choi and Graham (1998) was conducted at a Reynolds number one order of magnitude higher than any previous investigation.

Another type of forcing has also been investigated. Du and Karniadakis (2000) applied spanwise travelling waves along the wall of a turbulent channel flow and achieved a 30 % reduction in skin-friction drag. In their DNS study of Lorentz forcing, the spanwise travelling waves were implemented using the following form,

$$\begin{aligned} F_{z}=Ie^{-\frac{y}{\triangle }}\sin \left( \kappa _{z}z-\omega t\right) , \end{aligned}$$

(1.2)

where $F_{z}$ is the force in the spanwise direction, $I$ is the forcing amplitude, $\triangle$ is the penetration depth and $\lambda _{z}=2\pi /k_{z}$ is the spanwise wavelength and $k_{z}$ is the spanwise wavenumber. Du et al. (2002) demonstrated that a skin-friction drag reduction of 30 % can be obtained when a product of amplitude, $I$, period, $T^{+}$ and penetration depth, $\triangle$ remained constant. They then found that application of spanwise travelling waves led to the amalgamation of the sublayer streaks into a wide ribbon of low-speed fluid. An experimental investigation of spanwise travelling waves was conducted by Breuer et al. (2004), who implemented the spanwise travelling waves using electromagnetic actuators in a turbulent channel flow. Xu and Choi (2006) performed a similar experiment in a water flume to observe up to a 30 % reduction in skin-friction drag. They also carried out flow visualisations in the near-wall region of the boundary layer to observe the formation of wide ribbons of low-speed fluid during spanwise travelling-wave control.

Spanwise travelling waves have also been implemented with an out-of-plane motion of a flexible wall. This was first studied numerically by Zhao et al. (2004). In their DNS, they observed a skin-friction drag reduction of 30 % when a forcing period of $T^{+}=50$ was used to excite the flexible wall. They attributed the drag reduction to the change in boundary-vorticity flux, which was generated by the acceleration of the deforming wall. This caused the suppression of quasi-streamwise vortices within the boundary layer. A further numerical investigation was conducted by Klumpp et al. (2011). In their large-eddy simulation (LES), the out-of-plane motion of a spanwise surface wave was implemented in a turbulent channel flow and achieved a skin-friction drag reduction of 9 %. They ascribed the drag reduction mechanism to the attenuation of wall-normal vorticity fluctuations and not to the redistribution of streamwise vorticity, which was present in both drag reducing and drag increasing cases. Itoh et al. (2006) and Tamano and Itoh (2012) studied experimentally a flexible wall in a turbulent boundary layer. They observed a skin-friction drag reduction of the order of 10 %, associated with a reduction in sweep intensity and an increase in the contribution of Reynolds stress by inward-wall interactions. Tomiyama and Fukagata (2013) conducted a DNS of a spanwise travelling wave implemented by a wavy wall. They observed that the longitudinal vortices were lifted away from the wall and weakened leading to a drag reduction of 13 %.

Investigations on the spanwise travelling waves have been carried out by either a Lorentz forcing or a deformable wall. The limitation with Lorentz forcing is that it can only work in a liquid flow, such as sea water, while a deformable wall has difficulties in practical implementation. Here, we have investigated into the use of dielectric-barrier-discharge (DBD) plasma actuators to generate spanwise travelling waves in air.

1.2 Dielectric-barrier-discharge plasma

Dielectric-barrier-discharge (DBD) plasma actuators are usually comprised of an upper and a lower electrode separated by a thin dielectric material: see Fig. 1. The upper electrode is exposed to the air flow, and the lower electrode is encapsulated between the dielectric and aerodynamic surface. Application of several kV of AC power at kHz frequency between the upper and lower electrodes causes the air around the exposed electrode to become ionized and a plasma is formed (Moreau et al. 2013).

Fig. 1

Schematic representation of a DBD plasma actuator used in the present study a cross-section and b dimensions

DBD plasma actuators have been used for separation control of aerofoils (Corke et al. 2010, 2011; Whalley et al. 2013), vortex shedding control of bluff bodies (Munska and McLaughlin 2003; McLaughlin et al. 2004; Jukes and Choi 2009), delaying laminar-to-turbulent transition (Grundmann and Tropea 2007, 2008, 2009) and noise reduction of cavity flows (Huang and Zhang 2008). Wilkinson (2003) created a spanwise flow oscillation in the turbulent boundary layer with DBD plasma actuators by applying a frequency modulating input to a pair of lower electrodes on either side of an upper electrode. However, the plasma was formed on both sides of the upper electrode causing wall jets to collide. Later, Jukes et al. (2006) created a spanwise flow oscillation in the turbulent boundary layer using two sets of asymmetric plasma actuators, which was studied using hot-wire anemometry. A skin-friction drag reduction of up to 45 % was observed from this study.

Elam (2012) carried out a DNS investigation in order to simulate the experimental study of Jukes et al. (2006), showing a drag reduction of 47 %. Elam (2012) also numerically investigated a plasma standing wave. The standing wave translates the time-dependent forcing of spanwise-wall oscillation (1.1) into a stationary counterpart by introducing spanwise velocity that is modulated in the streamwise direction. He observed a skin-friction drag reduction of 52 %, similar to the findings of Viotti et al. (2009). Extensive surveys of the literature detailing DBD plasma physics, operating principles, actuator designs and flow control strategies can be found in recent reviews by Moreau (2007), Corke et al. (2010) and Wang et al. (2013).

2 Experimental set-up and procedure

2.1 Test facility

Boundary-layer measurements with spanwise travelling waves were performed in a low-speed, closed-return wind tunnel. The test section was 3 m long and had an octagonal cross-section with dimensions of $508 \times 508\; \hbox {mm}^{2}$. The turbulent boundary layer was developed over a smooth flat plate set in the upper part of the test section. The flat plate was 3 m long and 22 mm thick, with a super-elliptic shape leading edge with a semi-major axis of 75 mm. A flap was attached at the trailing edge to adjust the pressure gradient to nearly zero. The boundary layer was tripped to fix the transition point using an array of 3 mm diameter rods that were 10 mm high. These were placed 100 mm downstream of the leading edge and covered a streamwise distance of 60 mm. Boundary-layer measurements were taken 2.2 m downstream of the trip. The free-stream velocity was set at $U_{\infty }=1.8$ m/s, where the free-stream turbulence intensity was 0.24 %. The turbulent boundary-layer thickness was $\delta =90$ mm at the measurement station, where the viscous sublayer thickness was around 1 mm. The Reynolds number based on friction velocity was $Re_{\tau }\left( =\delta u_{\tau }/\nu \right) =435$ and the shape factor was $H\,=1.46$. The friction velocity was obtained by the Clauser plot method based on hot-wire data (not shown), matching to the log-law by Schlichting (1979). The value of $u_{\tau }$ obtained with this method was within 5 % of the value obtained by least-squares linear fitting the hot-wire data in the linear region of the viscous sublayer (Hutchins and Choi 2002). Measurements of spanwise travelling waves in quiescent air were also conducted inside the wind tunnel. For these experiments, a 1.5-m-long section was sealed to create a closed chamber to ensure that the flow induced by the DBD plasma actuators was not influenced by any drafts.

Throughout this paper, $x$, $y$ and $z$ denote the streamwise, wall-normal and spanwise directions where $x=0$ is 2.05 m downstream of the test-plate leading edge, $y=0$ is the location of the wall and $z=0$ is set at 50 mm from the wind tunnel centre line. The capitalised symbols $U$, $V$ and $W$ and lower case symbols, $u$, $v$ and $w$ are used to indicate the total and fluctuating velocities in the streamwise, wall-normal and spanwise directions, respectively. Phase-averaged quantities are indicated by triangular brackets (e.g. $\langle U\rangle$) and time-averaged quantities are denoted with an over bar (e.g. $\overline{U}$). The superscripts (e.g. $U^{+}$) are to show viscous scaling with canonical friction velocity, $u_{\tau }$.

2.2 Plasma actuators

Plasma actuator sheets used in this study had dimensions of $408 \times 336\; \hbox {mm}^{2}\; \left( x^{+}=xu_{\tau }/\nu = \hbox {2,045}, {z}^{+} = \hbox {1,685}\right)$. They were photochemically etched from a copper-clad Mylar sheet ($250\,\upmu \hbox {m}$ thick, dielectric constant $\varepsilon =3.1$) and flush mounted into the test plate of the wind tunnel. Each actuator sheet consisted of 24 copper electrodes, powered by a set of high-voltage sinusoidal RF inputs. The upper and lower electrodes were 2.5 and 6 mm ($z^{+}=13$ and $z^{+}=30$) in width, respectively, had an active length of 338 mm $\left( x^{+} = \hbox {1,700}\right)$ and protruded only $18\, \upmu \hbox {m} \left( y^{+}=0.09\right)$ from the wall: see Fig. 1b.

Fig. 2

Schematic of spanwise travelling-wave excitation to show cross-section of the plasma actuators for a unidirectional spanwise travelling waves, b bidirectional spanwise travelling waves, c plasma forcing with unidirectional spanwise travelling waves and d plasma forcing with bidirectional spanwise travelling waves. $\lambda ^{+}=500$ (100 mm) and $T^{+}=82$ (208 ms)

The spanwise travelling-wave actuator sheets could be configured to produce unidirectional or bidirectional spanwise travelling waves. Here, schematic representations of unidirectional and bidirectional spanwise travelling waves are shown in Fig. 2a, b, respectively. The spanwise travelling waves used four discrete forcing phases to push fluid in the spanwise directions. For each forcing configuration, the plasma actuators were operated in sequence from phase (i) to phase (iv) for a duration of $T^{+}$ each: see Fig. 2c, d, which show the forcing profiles with time for the unidirectional and bidirectional spanwise travelling waves, respectively. The wavelength $\lambda$ for both forcing configurations was 100 mm $\left( \lambda ^{+}=500\right)$. The travelling-wave actuator arrays were repeated three times across the width of each actuator sheet so that spanwise travelling waves are generated over a span of 3$\lambda$. The spatial and temporal spanwise forcing imposed by the plasma actuators creates streamwise vorticity in the cross-stream (y-z plane) of the flow.

Fig. 3

Schematic of spanwise travelling-wave excitation through phases (i)–(iv) for a unidirectional spanwise travelling waves and b bidirectional spanwise travelling waves

The unidirectional spanwise travelling waves were created by operating a single plasma actuator at a time during each phase of forcing: see Fig. 3a. Therefore, four plasma actuators were used per wavelength, which were separated by a distance of $\lambda /4=25$ mm $\left( z^{+}=125\right)$. During phase (i), the plasma actuator generates a body force to the right. This entrains and accelerates fluid from around the phase (i) actuator towards the phase (ii) actuator. The phase (ii) actuator is then operated, which entrains and accelerates the fluid from the first phase of forcing towards the phase (iii) actuator. The phase (iii) actuator is then operated, which entrains and accelerates the fluid collected during the first two phases of forcing further to the right towards the phase (iv) actuator. Once the phase (iv) actuator has operated, fluid has been transported across one wavelength of the travelling wave in a period of $T^{+}$.

The bidirectional spanwise travelling waves were created with a similar principle to the unidirectional forcing, although in this case two plasma actuators are operated in two opposing directions simultaneously during each phase of forcing. Hence, the bidirectional spanwise travelling wave used eight plasma actuators per wavelength, with opposing actuators separated by a distance of $z = 56\; \hbox {mm}\,\left( z^{+} = 280\right)$. The plasma actuators for the bidirectional spanwise travelling waves are illustrated in Fig. 3b with the actuators firing in the positive spanwise direction (to the right) coloured black and those firing in the negative spanwise direction (to the left) coloured red. At the end of phase (i), the fluid surrounding the phase (i) actuators is entrained and accelerated towards the middle of the two phase (i) actuators. The phase (ii) actuators are then operated, which entrain and accelerate the fluid collected during phase (i) towards the middle of the two phase (ii) actuators. Then, the phase (iii) actuators are activated to entrain and accelerate the fluid collected during the first two phases of forcing (to the right in Fig. 3). Once the phase (iv) actuators have operated, fluid has been transported across one wavelength of the travelling wave in a period of $T^{+}$.

The spatial and temporal scales of the bidirectional forcing actuator sheet used to design our experiments are based on Xu and Choi (2006), who obtained a 30 % reduction in skin-friction drag in a water channel experiment using Lorentz forcing. For the data presented throughout this paper, the sinusoidal voltage input to the plasma actuator sheet was fixed at $E=7\; \hbox {kV}_{{\rm p-p}}$ with a frequency of $f=25$ kHz and applied with a forcing period of $T=208$ ms $\left( T^{+}=82\right)$, requiring up to 12 power supplies.

2.3 Experimental equipment and techniques

Time-resolved 2D and stereoscopic particle image velocimetry (PIV) from TSI were used to obtain the velocity field in the turbulent boundary layer with spanwise travelling waves. The system consisted of up to two Photron APX-RX cameras, a New Wave Research Pegasus PIV laser and a TSI 9307-6 oil droplet generator. Olive oil droplets with a nominal size of $1\,\upmu \hbox {m}$ were used to seed the flow through three flush-mounted spanwise slots in the upstream of the DBD plasma actuator sheet. For the 2D PIV measurements, the laser sheet was aligned in the x-z plane parallel to the wall at $y=1\; \hbox {mm}\; \left( y^{+}=5\right)$ in the mid-span of the DBD plasma sheet, with a field of view of $100 \times 100\,\hbox {mm}^{2} \,\left( x^{+}=500, \,z^{+}=500\right)$. The stereoscopic PIV measurements in the y-z plane were taken at $x^{+}=200$ with a field of view of $40 \times 100\,\hbox {mm}^{2} \,\left( y^{+}=200,z^{+}=500\right)$. For each experiment, the spanwise travelling waves were created continuously for 14 forcing periods $\left( 14T^{+}\right)$. Image pairs were acquired at a frequency of 750 Hz for the last 3 of the 14 forcing periods. The time delay between each pair of frames was typically $200\,\upmu \hbox {s} \; \left( t^{+}=0.075\right)$ or $75\, \upmu \hbox {s}\; \left( t^{+}=0.028\right)$ for the 2D and stereoscopic measurements, respectively. Data processing was performed using INSIGHT 3G software from TSI using a cross-correlation algorithm to generate velocity vectors over a $32 \times 32\; \hbox {pixel}^{2}$ interrogation area with 50 % overlap. This gave a spatial resolution of $1.6 \times 1.6\,\hbox {mm}^{2} \left( x^{+}=y^{+}=z^{+}=8\right)$ for both the 2D and stereoscopic PIV measurements. In total, 156 flow realisations were taken over one forcing period. Each experiment was repeated 17 times, capturing cumulatively 51 forcing periods. This allowed a time-resolved phase-average over one forcing period with spanwise travelling-wave excitation, enabling the changes in turbulent boundary-layer structure to be analysed. We estimate that the uncertainties in velocity fluctuations measured with the PIV system are typically 6 %, agreeing well with the uncertainty analysis of (Westerweel 1997). Since vorticity measurements require an estimation of a velocity gradient and Reynolds stresses require an estimate of a product of velocity fluctuations, we estimate that the uncertainties in these quantities are typically 12 %.

Experiments in quiescent air were conducted using a similar time-resolved PIV system, consisting of a pulsed copper vapour laser and a Photron Fastcam SA-3 camera. Here, glycerine droplets with nominal size of $1\, \upmu \hbox {m}$ were used as seeding particles. The laser sheet was aligned with the actuator mid-span illuminating the y-z plane. Here, image pairs were taken at a frame rate of 500 Hz, with the time delay between frames being typically 200–400 $\upmu \hbox {s}$. In total, 156 flow realisations were taken over one forcing period and each experiment was repeated 5 times.

The Stokes numbers of the seeding particles used throughout this study were <0.1. This ensured that the seeding particles followed the fluid flow closely with tracing errors being <1 % (Tropea et al. 2007).

Fig. 4

Streamwise vorticity with unidirectional spanwise travelling waves in quiescent air (a–h) at a $\frac{1}{8}T$, b $\frac{2}{8}T$, c $\frac{3}{8}T$, d $\frac{4}{8}T$, e $\frac{5}{8}T$, f $\frac{6}{8}T$, g $\frac{7}{8}T$, h $T$, streamwise vorticity with unidirectional spanwise travelling waves in the y-z plane of the turbulent boundary layer (i–p) at i $\frac{1}{8}T^{+}$, j $\frac{2}{8}T^{+}$, k $\frac{3}{8}T^{+}$, l $\frac{4}{8}T^{+}$, m $\frac{5}{8}T^{+}$, n $\frac{6}{8}T^{+}$, o $\frac{7}{8}T^{+}$, p $T^{+}$ and diagram of forcing along the spanwise direction (q–x) showing q phase (i), r phase (i), s phase (ii), t phase (ii), u phase (iii), v phase (iii), w phase (iv) and x phase (iv). $\lambda ^{+}=500$ (100 mm) and $T^{+}=82$ (208 ms). Turbulent boundary-layer data are scaled with canonical $u_{\tau }$. The white contours of negative $\lambda _{2}$ illustrate the locations of vortical flow structures

3 Results

3.1 Induced flow with spanwise travelling waves

3.1.1 Spanwise travelling waves in quiescent air

Initially, the spanwise travelling waves were studied in quiescent air in order to gain insight into how the plasma actuators, when operated sequentially, entrain and accelerate the nearby air to transport fluid in the spanwise direction. Figure 4a–h shows the phased-averaged vorticity created by unidirectional spanwise travelling waves in quiescent air. The data in quiescent air have been phase-averaged over 5 forcing periods. In this figure, data are presented in intervals of $T/8$ throughout the four phases of actuation and the phase of the actuation is illustrated on the right hand side of the figure: see Fig. 4q–x. The location of the activated plasma actuator and the direction of the DBD plasma wall jet are indicated under each image. Here, the travelling wave moves from left to right, in the positive spanwise direction. On initiation of DBD plasma, the fluid ejected laterally by plasma forcing is replenished by entrainment from above the plasma actuator. This leads to a generation of circulation during the formation of a starting vortex (Whalley and Choi 2010, 2012). At the end of phase (i), a starting vortex has developed and moved along and away from the wall in the positive spanwise direction. The core of the starting vortex is located at $y\approx 10\, \hbox {mm}$ and can be identified by a roll-up into a negative vortex, shown by white contours of negative $\lambda _{2}$ (Jeong and Hussain 1995): see Fig. 4b. Plasma forcing during phase (ii), Fig. 4c, d, causes a creation of another starting vortex, which entrains a previously formed starting vortex generated by the forcing from phase (i). During this process, the two co-rotating vortices coalesce, thrusting the fluid in the positive spanwise direction (to the right in Fig. 4). At the end of phase (iii), Fig. 4f, the wall jet begins to wrap up around the starting vortex due to its own induction. By the end of phase (iv), Fig. 4h, the near-wall fluid has been transported over one wavelength of the travelling wave. In other words, unidirectional spanwise travelling waves thrust the near-wall fluid in the positive spanwise direction by the vortices created in sequence (Choi et al. 2011).

Fig. 5

Streamwise vorticity with bidirectional spanwise travelling waves in quiescent air (a–h) at a $\frac{1}{8}T$, b $\frac{2}{8}T$, c $\frac{3}{8}T$, d $\frac{4}{8}T$, e $\frac{5}{8}T$, f $\frac{6}{8}T$, g $\frac{7}{8}T$, h $T$, streamwise vorticity with bidirectional spanwise travelling waves in the y-z plane of the turbulent boundary layer (i–p) at i $\frac{1}{8}T^{+}$, j $\frac{2}{8}T^{+}$, k $\frac{3}{8}T^{+}$, l $\frac{4}{8}T^{+}$, m $\frac{5}{8}T^{+}$, n $\frac{6}{8}T^{+}$, o $\frac{7}{8}T^{+}$, p $T^{+}$and diagram of forcing along the spanwise direction (q–x) showing q phase (i), r phase (i), s phase (ii), t phase (ii), u phase (iii), v phase (iii), w phase (iv) and x phase (iv). $\lambda ^{+}=500$ (100 mm) and $T^{+}=82$ (208 ms). Turbulent boundary-layer data are scaled with canonical $u_{\tau }$. The white contours of negative $\lambda _{2}$ illustrate the locations of vortical flow structures

Phase-averaged vorticity created by bidirectional spanwise travelling waves in quiescent air is shown in Fig. 5a–h. Here, the plasma actuators fire in opposing directions during each phase of forcing, and the travelling wave moves in the positive spanwise direction. This causes two starting vortices to develop and move towards each other by the end of phase (i): see Fig. 5b. By the end of phase (ii), Fig. 5d, there is a region of fluid encapsulated within the first 10 mm of the wall between $25\,\hbox {mm}<z<50\,\hbox {mm}$. This region of fluid continues to move in the positive spanwise direction during the forcing in phase (iii) and phase (iv): see Fig. 5e–h. As this region of fluid is being transported along the wall, there is a highly vortical flow structure developing throughout the four phases of excitation. In order to understand how fluid is being transported in the spanwise direction, we analyse the developing vorticity throughout phase (iii) and phase (iv) as shown in Fig. 5d–g. Figure 5d shows two counter-rotating vortices at the end of phase (ii). The vortices have concentrated regions of positive and negative vorticity in their cores, where the secondary vorticity due to the no-slip boundary condition is wrapped around the periphery of each vortex. Here, the negative vortex core formed by the positive spanwise plasma forcing is located at $z\approx 50$ mm, while the positive vortex core formed by the negative spanwise plasma forcing is located at $z\approx 75$ mm. Both vortex cores are located at a wall-normal distance of $y\approx 10$ mm. Figure 5e shows the beginning of phase (iii) where two newly activated plasma actuators are producing two more starting vortices. Throughout this phase of forcing, the plasma actuator produces the negative vorticity at $z\approx 70$ mm, which rolls up into a vortex in the vicinity of the existing positive vortex located at $z\approx 75$ mm. Due to vortex induction, the positive and negative vortices lift each other away from the wall. The plasma actuator continuously entrains and accelerates the nearby fluid creating negative vorticity that ultimately leads to an expulsion of the positive vortex away from the wall: see Fig. 5e, f. Simultaneously, the negative secondary vorticity formed around the periphery of the positive vortex is amalgamated with the vorticity of the negative vortex, moving in the positive spanwise direction. The lifting of the positive vortex away from the wall allows the two negative co-rotating vortices close to the wall to coalesce around $z\approx 65$ mm: see Fig. 5f. By the beginning of phase (iv), there is an elongated single vortex of negative vorticity spanning from $z\approx 50$ mm to $z\approx 80$ mm, which is being pushed further in the positive spanwise direction during phase (iv): see Fig. 5g. The coalescing of co-rotating vortices and complex interaction of counter-rotating vortices during each phase of forcing are essential for the transport of fluid in the positive spanwise direction by bidirectional spanwise travelling waves.

3.1.2 Spanwise travelling waves in the turbulent boundary layer

Figure 4i–p shows the phase-averaged streamwise vorticity created by unidirectional spanwise travelling waves in the y-z plane of the turbulent boundary layer. The travelling wave moves from left to right in the figure, while the boundary-layer flow moves into the plane of the paper. There are remarkable similarities between the development of unidirectional spanwise travelling waves in the turbulent boundary layer with that in quiescent air: see Fig. 4a–h. For example, at the end of phase (i), Fig. 4j, there is a formation of a single streamwise vortex clearly identified by a concentrated region of negative streamwise vorticity in its core and by contours identified by negative $\lambda _{2}$. The streamwise vortex is generated by twisting and folding of spanwise vorticity at the tip of each plasma actuator, which causes streamwise vorticity to roll-up and evolve as a spatially developing starting vortex: see Jukes and Choi (2013). This mechanism differs from the creation of a starting vortex in quiescent air, which is generated by the entrainment of fluid directly above the plasma region: see Whalley and Choi (2012). Even so, the magnitude and core location of the streamwise vortices generated within the turbulent boundary layer and those in quiescent air are very similar. Plasma forcing during phase (ii) creates another streamwise vortex, which entrains the streamwise vortex generated during forcing in phase (i): see Fig. 4k, l. The same process of vortex creation and amalgamation continues throughout the next two phases: see Fig. 4m–p. Hence, the development of unidirectional spanwise travelling waves in the turbulent boundary layer and in quiescent air are very similar: streamwise vortices are generated in sequence, which move as a single vortex during the four phases of travelling-wave excitation.

The development of streamwise vorticity throughout all four phases of actuation by bidirectional spanwise travelling waves in the turbulent boundary layer is presented in Fig. 5i–p next to the corresponding data in quiescent air. Since the bidirectional spanwise travelling waves are generated by plasma forcing in two opposing directions during each phase of forcing, two streamwise vortices move along the wall throughout the forcing in phase (i): see Fig. 5i, j. We see a positive streamwise vortex interacting with the negative streamwise vortex in phase (i) at $z^{+}\approx 100$. The development of streamwise vorticity throughout phase (ii) is given in Fig. 5k, l, showing the generation of two additional streamwise vortices and interaction with a positive streamwise vortex at $z^{+}\approx 275$. The same process of streamwise vortex creation and interaction between the positive and negative streamwise vortices is apparent throughout phase (iii) and phase (iv): see Fig. 5m–p. Figure 5l shows the streamwise vorticity at the end of the second phase of forcing where there are two counter-rotating streamwise vortices with cores located at $z^{+}\approx 250$ and $z^{+}\approx 425$. On comparison with data in quiescent air, Fig. 5d, there is a compact region of negative streamwise vorticity spanning from $z^{+}\approx 100$ to $z^{+}\approx 300$. The plasma forcing in phase (iii) generates two additional streamwise vortices, Fig. 5m, n. The actuator firing in negative spanwise direction creates a positive streamwise vortex at $z^{+}\approx 50$, while the actuator firing in the positive spanwise direction creates a negative streamwise vortex at $z^{+}\approx 350$. Similar to the observation in quiescent air, the negative streamwise vortex forms a counter-rotating pair with the positive streamwise vortex generated during phase (ii). These counter-rotating vortices lift each other away from the wall by the induction on to each other, allowing the two co-rotating negative streamwise vortices to coalesce at around $z^{+}\approx 350$. The plasma forcing throughout phase (iv) is shown in Fig. 5o, p, which thrusts the negative co-rotating streamwise vortices further in the positive spanwise direction.

The qualitative behaviour in the development of streamwise vorticity in the turbulent boundary layer is very similar to that in quiescent air, as shown in Fig. 5. We see, however, that the strength of vorticity being generated during the plasma actuation is slightly different between the two cases. There are two possible reasons for these differences. Firstly, the experiments in quiescent air, as shown in Fig. 4, were conducted using eight of the twenty-four electrodes on the actuator sheet. This meant that the spanwise travelling waves were generated only over a span of one wavelength. On the other hand, the experiment in the turbulent boundary layer was conducted with twenty-four electrodes over a span of three wavelengths. Secondly, data in quiescent air were captured during the first period of plasma forcing, whereas the data in the turbulent boundary layer were taken during the last three of 14 forcing periods. These may have yielded differences observed in streamwise vorticity development during the bidirectional spanwise travelling waves in the turbulent boundary layer.

Fig. 6

Spanwise velocity, fluctuating streamwise velocity and wall-normal vorticity profiles at $y^{+}=5$ with a unidirectional spanwise travelling waves and b bidirectional spanwise travelling waves at (i) $\frac{1}{4}T^{{+}}$, (ii) $\frac{1}{2}T^{{+}}$, (iii) $\frac{3}{4}T^{{+}}$ and (iv) $T^{{+}}$. $\lambda ^{+}=500$ (100 mm) and $T^{+}=82$ (208 ms). Scaled with canonical $u_{\tau }$

In order to demonstrate the creation of spanwise travelling waves, the spanwise velocity, fluctuating streamwise velocity and wall-normal vorticity profiles in the turbulent boundary layer at $y^{+}=5$ are shown in Fig. 6 for two different arrays of plasma actuators. These profiles were obtained from 2D PIV data in the x-z plane and have been space-averaged in the streamwise direction over a distance of $x^{+}=500$ ($x=100$ mm). The velocity and vorticity profiles generated at the end of each phase of forcing with unidirectional spanwise travelling waves are shown in Fig. 6a. Here, the unidirectional spanwise travelling waves create a well-defined positive spanwise velocity in a bell-shaped profile with an amplitude of $\langle W^{+}\rangle \approx 22.$ This can be seen throughout four phases of forcing as the unidirectional spanwise travelling waves sweep across the near-wall region of the turbulent boundary layer. The region of positive spanwise velocity is accompanied by a region of low-speed streamwise velocity, both of which extend over a distance of $z^{+}\approx 300$ in the direction of spanwise movement. We can also see that a region of high-speed streamwise velocity precedes the region of low-speed streamwise velocity, spanning over a distance of $z^{+}\approx 200.$ The peak in positive streamwise velocity leads the peak in positive spanwise velocity by $z^{+}\approx 50,$ while the minimum streamwise velocity is found when the region of positive spanwise velocity falls to zero. Since the spanwise velocity is nearly uniform along the length of the plasma actuators (i.e. $\partial W/\partial x\approx 0$), the wall-normal vorticity can be given by $\omega _{y}\approx \partial U/\partial z.$ In other words, the wall-normal vorticity is generated with the spanwise change of streamwise velocity, as shown in Fig. 6.

The spanwise velocity profiles with bidirectional spanwise travelling waves have a two-bump profile with an amplitude of $\langle W^{+}\rangle \approx 12$ as two plasma actuators are operated in opposing spanwise directions in each phase of forcing: see Fig. 6b. At the end of phase (i), there is a low-speed streamwise velocity region spanning $100<z^{+}<250$, which is pushed by the travelling waves in the positive spanwise direction from phase (ii) and phase (iii). A small, high-speed streamwise velocity region at $z^{+}\approx 150$ is a result of a downwash associated with the entrainment during the plasma actuation (Whalley and Choi 2012). At the end of phase (ii), there is also a region of low-speed streamwise velocity which spans $25<z^{+}<150.$ This low-speed streamwise velocity region moves in the positive spanwise direction during the plasma forcing from phase (iii) and phase (iv). It should also be noted that by the end of phase (i) there is a similar region of low-speed streamwise velocity which spans $z^{+}>400$ due to the plasma forcing from phase (iv). Similar to unidirectional spanwise travelling waves, the bidirectional spanwise travelling waves create large spanwise variations in high-speed streamwise velocity. They therefore produce regions of positive and negative wall-normal vorticity, forcing alternating low- and high-speed streamwise velocity streaks within the viscous sublayer.

Fig. 7

Fluctuating streamwise velocity in the x-z plane of the turbulent boundary layer at $y^{+}=5$ showing a no-control data, b unidirectional spanwise travelling waves at $\frac{3}{4}T^{+}$ and c bidirectional spanwise travelling waves at $\frac{3}{4}T^{+}.$ Scaled with canonical $u_{\tau }$

Fig. 8

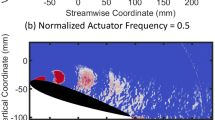
A comparison of data in the y-z plane at $x^{+}=200$ and in the x-z plane at $y^{+}=5$ of the turbulent boundary layer with unidirectional spanwise travelling waves (a–f) at $\frac{3}{4}T^{+}$ showing a streamwise vorticity (y-z plane), b fluctuating streamwise velocity (y-z plane), c wall-normal velocity (y-z plane), d Reynolds shear stress (y-z plane), e spanwise velocity (y-z plane), f fluctuating streamwise velocity (x-z plane) and with bidirectional spanwise travelling waves (g–l) at $\frac{3}{4}T^{+}$ showing g streamwise vorticity (y-z plane), h fluctuating streamwise velocity (y-z plane), i wall-normal velocity (y-z plane), j Reynolds shear stress (y-z plane), k spanwise velocity (y-z plane) and l fluctuating streamwise velocity (x-z plane). Scaled with canonical $u_{\tau }.$ The white contours of negative $\lambda _{2}$ illustrate the locations of vortical flow structures

3.2 Changes in turbulent boundary-layer structure

3.2.1 Phase-averaged spanwise travelling waves

The change in near-wall structure of the turbulent boundary layer in the x-z plane at $y^{+}=5$ with plasma spanwise travelling waves is shown in Fig. 7. Here, the spanwise travelling waves are moving in the positive spanwise direction. The low- and high-speed streaks without plasma flow control can be seen in Fig. 7a meandering through the flow with characteristic streak spacing of $z^{+}\approx 100.$ The modifications to the near-wall turbulence structure with unidirectional spanwise travelling waves are shown in Fig. 7(b). Here, plasma forcing is applied at $z^{+}\approx 350,$ as shown underneath the figure. This phase of forcing pushes a wide ribbon of low-speed streamwise velocity in the positive spanwise direction over $z^{+}>400,$ as observed in the sequence of Fig. 6a. A similar result is obtained with bidirectional spanwise travelling waves: see Fig. 7c. Here, plasma forcing is applied at $z^{+}\approx 100,$ $z^{+}\approx 350$ and $z^{+}\approx 600$ (not shown), which leads to ribbons of low-speed streamwise velocity over $z^{+}<50,$ $150<z^{+}<300$ and $350<z^{+}<500.$ The ribbon of low-speed streamwise velocity centred around $z^{+}\approx 200$ can be clearly identified in the near-wall streamwise velocity profile shown in Fig. 6b: see the profiles at the end of phase (iii).

Velocity measurements in the y-z plane of the turbulent boundary layer taken at $3T^{+}/4$ in a plane at $x^{+}=200$ are shown in Fig. 8 along with x-z plane data from Fig. 7 for further comparison. Here, it should be noted that the data shown in the x-z and y-z planes were not acquired simultaneously. Figure 8a, g shows the streamwise vorticity with unidirectional and bidirectional spanwise travelling waves, respectively. The unidirectional spanwise travelling waves have a streamwise vortex located at $z^{+}\approx 375,$ as identified by $\lambda _{2}$ vortex identification technique, having a strong negative streamwise vorticity with circling arrows of $V{\text{-}}$ and $W{\text{-}}$ components of velocity. The bidirectional spanwise travelling waves show a large elongated negative streamwise vortex centred at $\left( y^{+},z^{+}\right) \approx \left( 50,350\right),$ which is interacting with a positive streamwise vortex located at $\left( y^{+},z^{+}\right) \approx \left( 100, 400\right),$ which was generated during the second phase of forcing. There is another positive streamwise vortex located at $z^{+}\approx 50,$ which has been generated by plasma forcing from a succeeding travelling wave: see Fig. 3b. The streamwise vortices generated during unidirectional and bidirectional spanwise travelling-wave forcing are entraining low-speed streamwise velocity from the near-wall region around their peripheries. This leads to a reduction in streamwise velocity inside the boundary layer up to a wall-normal distance of $y^{+}\approx 100$ and $y^{+}\approx 200$ for the unidirectional and bidirectional spanwise travelling waves, respectively: see Fig. 8b, h. Figure 8e shows the spanwise velocity generated by the unidirectional spanwise travelling waves. Here, the spanwise velocity is positive up to the centre of the streamwise vortex core. A similar observation can be made with the bidirectional spanwise travelling waves, Fig. 8k. Here, both positive and negative spanwise velocities are generated as two plasma actuators are operated in opposing spanwise directions. These velocities extend up to $y^{+}\approx 50.$ The regions of upwash and downwash created by the unidirectional and bidirectional spanwise travelling waves are shown in Fig. 8c, i, along with the $-uv^{+}$ Reynolds shear stress shown in Fig. 8d, j, respectively. With both forcing configurations, the regions of downwash coincide with the locations of the plasma actuators, and with the regions of high-speed streamwise velocity in the near-wall region: see Fig. 8f, l. Moreover, wide ribbons of low-speed streamwise velocity are found immediately upstream of the streamwise vortices travelling in the positive spanwise direction.

Fig. 9

Distribution of phase-averaged $-uw^{+}$ Reynolds stress in the x-z plane at $y^{+}=5$ and $-uv^{+}$ Reynolds stress in the y-z plane at $x^{+}=200$ along with the distribution of fluctuating streamwise velocity, fluctuating wall-normal velocity and white contours of negative $\lambda _{2}$ to illustrate the location of vortical flow structures for a unidirectional spanwise travelling waves with plasma forcing at $\frac{3}{4}T^{+}$ and b bidirectional spanwise travelling wave with plasma forcing at $\frac{3}{4}T^{+}$. The black and white numerals indicate the locations of turbulence events. Scaled with canonical $u_{\tau }$

The formation of wide ribbons of low-speed streamwise velocity play an important role in the drag reduction mechanism (Du and Karniadakis 2000; Du et al. 2002). Indeed, the modification of sublayer streaks into wide ribbons of low-speed fluid is a recurring and prominent observation of spanwise travelling-wave control in the present study. Shown in Fig. 9 are the effects of the plasma-induced streamwise vortices on the production of Reynolds stresses within the turbulent boundary layer, and on the formation of wide ribbons of low-speed streamwise velocity within the viscous sublayer. Here, the plasma spanwise travelling waves are moving in the positive spanwise direction (to the right in Fig. 9). The production of $-uv^{+}$ Reynolds stress is shown in the y-z plane at $x^{+}=200$ along with $-uw^{+}$ Reynolds stress in the x-z plane at $y^{+}=5$. The streamwise vortices created by the plasma spanwise travelling waves can be seen to the right of the image by the white contours of negative $\lambda _{2}$ superimposed on backgrounds of fluctuating streamwise and wall-normal velocities. The numerals, I to IV, indicate the quadrants in the Reynolds stress distribution, and the location of the operated plasma actuators are shown under each image. Figure 9a shows the unidirectional spanwise travelling waves at the end of the third phase of forcing. The unidirectional forcing creates a streamwise vortex that lifts low-speed fluid outwards from the near-wall region of the boundary layer by vortex induction. The upwash side of the streamwise vortex causes an ejection event (Q-II event), which creates the positive $-uv^{+}$ Reynolds stress within the boundary layer. The downwash side of the streamwise vortex creates an inward-wall event (Q-III event) as the low-speed streamwise velocity, which is lifted from the near-wall region and wrapped around the periphery of the streamwise vortex, is entrained back into the wall. Hence, the streamwise vortex, which is travelling in the positive spanwise direction, leads to the production of Q-II and Q-III turbulence events. These events contribute directly to the formation of the wide ribbon of low-speed streamwise velocity within the viscous sublayer, which is illustrated by the positive $-uw^{+}$ Reynolds stress. In addition, a sketch of the mechanism of the action of the induced vortices for the unidirectional spanwise travelling waves is shown in Fig. 10a. Here, we see the travelling streamwise vortex which collects the low-speed streamwise velocity from within the near-wall region of the boundary layer and forms a wide ribbon of low-speed fluid which is propelled from left to right in the direction of the travelling wave.

Fig. 10

Sketches of the mechanism of the action of the induced vortices for a unidirectional spanwise travelling waves and b bidirectional spanwise travelling waves

The distribution of Reynolds stresses with bidirectional spanwise travelling waves is shown in Fig. 9b. Here, the plasma actuator operating in the positive spanwise direction produces an elongated vortical flow structure of positive sign, which is interacting with a streamwise vortex formed during the second phase of forcing, interacting to form separate but compact regions of negative $\lambda _{2}$. The induction of streamwise vortices lifts low-speed streamwise velocity from the near-wall turbulent boundary layer producing a positive $-uv^{+}$ Reynolds stress at $z^{+}\approx 350$. The downwash side of the streamwise vortex causes a Q-III turbulence event at $z^{+}\approx 200$, creating a wide ribbon of low-speed streamwise velocity in the viscous sublayer. The plasma actuator thrusting fluid in the negative spanwise direction creates a negative streamwise vortex, which causes Q-II and Q-III turbulence events by vortex induction; this actuator is forming the plasma spanwise travelling wave for the preceding wavelength of the travelling-wave actuator sheet. The low-speed ribbon is illustrated by a band of positive and negative $-uw^{+}$ Reynolds stress in the x-z plane. The downwash generated by the plasma actuator, which is driving fluid in the positive spanwise direction, creates a region of negative $-uw^{+}$ Reynolds stress at $z^{+}\approx 300$, whilst the downwash that is thrusting fluid in the negative spanwise direction creates a region of positive $-uw^{+}$ Reynolds stress at $z^{+}\approx 100$. A sketch of the mechanism of the action of the induced vortices for the bidirectional spanwise travelling waves is shown in Fig. 10b. Here, the wide ribbon of low-speed fluid which is formed by the induction of the two counter-rotating streamwise vortices is being propelled in the direction of the spanwise travelling wave. We see a streamwise vortex, which was generated during a previous phase of forcing, being lifted up and away from the wall by vortex induction. This process, the generation of two counter-rotating streamwise vortices and the lifting of a positive streamwise vortex away from the wall, occurs during each phase of bidirectional forcing.

Huang et al. (2011) conducted a DNS study of a spanwise travelling wave generated by a Lorentz force at the wall of a turbulent channel flow. They observed that the spanwise travelling wave created streamwise vortices, which travelled in a spanwise direction, causing Q-II and Q-III turbulence events that contributed to the formation of a wide ribbon of low-speed streamwise velocity within the viscous sublayer. Huang et al. (2011) also found that the streamwise vortices suppressed the quasi-streamwise vortices in the turbulent channel flow, which led to significant weakening of sublayer streaks in the intrinsic flow. Our experimental results with plasma actuators confirm these findings.

It must be noted that a discrete spatial forcing of plasma actuators generates streamwise vortices each time they are activated, resulting in a spanwise velocity profile that resembles either half a sinusoid or a two-bump shape depending on the forcing configuration: see Fig. 6. These are very similar to the non-ideal forcing profiles employed by Du et al. (2002).

4 Concluding remarks

In this experimental investigation, we have shown that it is possible to create spanwise travelling waves for turbulent boundary-layer control using two different types of DBD plasma actuator arrays. The DBD plasma actuator arrays were configured to produce either unidirectional or bidirectional spanwise travelling waves. The unidirectional spanwise travelling waves operated a single plasma actuator in the positive spanwise direction in each phase of forcing, whereas the bidirectional spanwise travelling waves operated two plasma actuators in opposing spanwise directions. We have shown that the unidirectional spanwise travelling waves created streamwise vortices in sequence, which formed a single travelling streamwise vortex. In contrast, the bidirectional spanwise travelling waves created counter-rotating streamwise vortex pairs, which interacted and lifted each other away from the wall to form a compact region of streamwise vortices. We observed that the streamwise vortices lift low-speed streamwise velocity from the near-wall region up and around the peripheries of their cores, leading to a modification of Q-II and Q-III turbulence events and a formation of the wide ribbons of low-speed streamwise velocity within the viscous sublayer.

The discrete spatial and temporal forcing of plasma actuators employed in the present experiment generated a streamwise vortex each time a plasma actuator was operated. This resulted in a spanwise velocity profile that resembled either half a sinusoid or a two-bump shape similar to the non-idealised forcing of Du et al. (2002). A prominent and recurring observation of spanwise travelling-wave control was a generation of wide ribbons of low-speed velocity within the viscous sublayer as shown in a DNS study (Du and Karniadakis 2000).