An advection-based model to increase the temporal resolution of PIV time series

Abstract

A numerical implementation of the advection equation is proposed to increase the temporal resolution of PIV time series. The method is based on the principle that velocity fluctuations are transported passively, similar to Taylor’s hypothesis of frozen turbulence. In the present work, the advection model is extended to unsteady three-dimensional flows. The main objective of the method is that of lowering the requirement on the PIV repetition rate from the Eulerian frequency toward the Lagrangian one. The local trajectory of the fluid parcel is obtained by forward projection of the instantaneous velocity at the preceding time instant and backward projection from the subsequent time step. The trajectories are approximated by the instantaneous streamlines, which yields accurate results when the amplitude of velocity fluctuations is small with respect to the convective motion. The verification is performed with two experiments conducted at temporal resolutions significantly higher than that dictated by Nyquist criterion. The flow past the trailing edge of a NACA0012 airfoil closely approximates frozen turbulence, where the largest ratio between the Lagrangian and Eulerian temporal scales is expected. An order of magnitude reduction of the needed acquisition frequency is demonstrated by the velocity spectra of super-sampled series. The application to three-dimensional data is made with time-resolved tomographic PIV measurements of a transitional jet. Here, the 3D advection equation is implemented to estimate the fluid trajectories. The reduction in the minimum sampling rate by the use of super-sampling in this case is less, due to the fact that vortices occurring in the jet shear layer are not well approximated by sole advection at large time separation. Both cases reveal that the current requirements for time-resolved PIV experiments can be revised when information is poured from space to time. An additional favorable effect is observed by the analysis in the frequency domain whereby the spectrum becomes significantly less prone to aliasing error for the super-sampled data series.

1 Introduction

The increase in the performance of high-speed PIV hardware with diode-pumped solid-state lasers and large-format CMOS imagers (Hain et al. 2007) has marked an important advancement in fluid mechanics research. These developments enable the investigation of unsteady and turbulent flows processes with temporal resolution for moderate flow velocity (typically up to 10 m/s). Most documented experiments are conducted at repetition rate in the range between 1,000 and 5,000 Hz, which is largely sufficient for water flows and slow air flows. The repetition rate becomes largely insufficient in aerodynamic problems where the air flow velocity may approach 100 m/s. At a fixed power output for the high-speed lasers, the pulse-energy/repetition-rate trade-off often imposes lower recording rates in order for the scattered light to be detected by the CMOS imager. At higher frame rates, the active pixel region decreases and the available laser pulse energy is not more than 1 or 2 mJ, which explains why only very few experiments are reported that exceed 20 kHz (Wernet 2007; van Oudheusden et al. 2011).

Conversely, PIV measurements of acceptable spatial resolution often lack sufficient temporal information, especially when compared with traditional point-wise techniques like hot-wire anemometry (HWA) and Laser Doppler Anemometry (LDA). This limitation hampers the quantitative evaluation of dynamic flow features in the temporal and frequency domain.

On a more qualitative side, the visualization of dynamical phenomena is often performed by animating the temporal series of PIV measurements. The interpretation of the sequence becomes increasingly difficult when the time separation between frames is larger than the time taken by a flow structure to travel across a given point.

The increased interest in simultaneous evaluation of velocity and pressure field from time-resolved PIV (PPI, planar pressure imaging, Liu and Katz 2006; de Kat et al. 2008; Charonko et al. 2010) and its applications for aeroacoustics (Haigermoser 2009; Lorenzoni et al. 2009; Morris 2011) requires measurement conditions at the limit of PIV hardware specifications. As a result, PIV has been mostly applied for the detailed description of the spatial flow organization and high-resolution time, and frequency analyses are typically made with point-wise instruments such as LDA or HWA.

The latter scenario does not take into account that time-resolved PIV measurements often contain correlated information both in space and in time, along the fluid trajectories. The velocity field measured by PIV should not be regarded as an ensemble of separate velocity measurements, which does not exploit the full potential of the information provided by the experiment.

Perhaps, the most striking example is the use of Taylor’s hypothesis of frozen turbulence, applied in various forms by several works. Previously, the hypothesis has been used to determine spatial length scales from the temporal signal obtained by a point-wise anemometer (Tennekes 1975). In most PIV applications, the hypothesis is invoked to extend the measurement domain from planar to 3D using the temporal sequence (pouring time in space). Similarly, Brede et al. (1996) performed measurements behind a circular cylinder by a plane perpendicular to the free-stream and inferred the spatial organization of secondary motion (A-mode and B-mode, Williamson 1996) in the Kármán wake. Van Doorne and Westerweel (2007) investigated transitional pipe flows using high-speed stereo PIV and obtained 3D iso-contours of streamwise vorticity from the measurements in a plane perpendicular to the symmetry axis.

The use of Taylor’s hypothesis in turbulence has received much attention in that it enables inferring information in the wavenumber space from the frequency domain analysis performed at a single point. However, caution should be taken for a quantitative use of this model to study large-scale coherent structures in shear flows in that the determination of a convection velocity is non-trivial when structures interact with each other such as during the pairing of vortices in jets (Zaman and Hussain 1981). The simplistic model of a single convection velocity for all scales or wavenumbers is reported to introduce artifacts leading to misinterpretation of the flow physics as recently discussed by del Álamo and Jiménez (2009), who recognized the bimodal energy spectrum in wall bounded turbulence as a measurement artifact introduced by Taylor’s approximation.

When the time separation between successive measurements produces a particle displacement comparable with the light sheet thickness, Ganapathisubramani et al. (2007) showed that it is possible to estimate the out-of-plane components of the velocity gradient by simply assuming advection is valid between subsequent measurements, yielding the measurement of the complete velocity gradient tensor in a turbulent flow.

Other approaches that make use of physical models to improve the tracking accuracy of imaged tracers motion have been proposed such as the optical flow method, introduced by Horn and Schunck (1981). Techniques specifically tailored for PIV applications have later been also investigated (Okuno et al. 2000). Recently, a hybridization of cross-correlation and dense estimators for fluid motion were investigated by Heitz et al. 2008.

In contrast with the above works, the use the advection principle in time-resolved PIV sequences with a configuration such that the measurement plane contains the dominant convection has received little or no attention. The current approach does not aim at increasing the spatial dimensions of the measurement domain, instead it enables to enrich the temporal sequence adding more samples.

The approach may be shortly worded as pouring Space in Time. Two major consequences are expected from this method: (1) the point-wise temporal resolution of PIV time-sequences can be increased beyond the PIV recording rate of the system and (2) point-wise time-aliasing effects can be largely reduced when using the combined spatial and temporal information.

The latter topic has also been investigated in the framework of digital filtering (Gobbi et al. 2006) of atmospheric turbulence data for the reduction in aliasing effects when estimating the spectrum of wind velocity from sonic anemometers.

The present work concentrates upon the first point. The potential impact on the second aspect is only addressed by an example, and its demonstration is left open for further investigations.

The concept is demonstrated experimentally making use of PIV time series from measurements where all temporal fluctuations are sampled at a much higher rate than that dictated by the Nyquist criterion. Moreover, the experiments are conducted under well-controlled laboratory conditions with favorable illumination and imaging, and the image sequences are analyzed with multi-frame correlation to reduce random errors. This approach provides PIV time series that can be considered as ground truth to verify the validity of the method. Sub-sampled time series are then extracted from the raw data and the reconstructed time-sequence is compared with the original data.

The paper contains first a short discussion of the advection principle and its relation to the flow timescales and required measurement frequency. Then, a section is devoted to the description of the numerical approach followed for the time super-sampling of the PIV sequence. The investigation of the applicability of the method in real experiments is structured in two parts with planar and three-dimensional experiments.

2 Background on the advection model

For a time-resolved PIV measurement, the acquisition frequency f _acq of image pairs (double-frame mode) or single exposures (single-frame continuous mode) determines the rate at which instantaneous velocity fields are obtained. For the analysis in the frequency domain, Nyquist criterion dictates that the rate at which individual samples should be acquired to avoid the aliasing phenomenon is at least twice the maximum frequency present in the signal. Obeying the latter condition, a faithful reconstruction of the signal temporal sequence is possible by interpolation. Similarly, Nyquist principle can be applied to the spatial domain to determine the length scale of the smallest resolvable fluctuation. In this case, the criterion states that the smallest resolvable wavelength λ is not smaller than twice the interrogation volume W _S (window size), unless a window weighting function is applied (Nogueira et al. 1999).

There is however a fundamental difference between the sampling process in the space and time domain for PIV. While in the temporal domain, the sampling is regarded as instantaneous and as such no analogue filtering technique can be applied, in the spatial domain, the response function of the cross-correlation analysis (finite size of the interrogation window) can be assimilated to an analogue linear filter, which makes the signal band-limited. The phenomenon of unstable waves growth can be regarded as spatial aliasing, which can be easily overcome by filtering the velocity field in between subsequent iterations (Schrijer and Scarano 2008).

Considering a flow with local convective speed V _conv, a measured fluctuation of length scale λ will pass through the local measurement point within an Eulerian timescale τ _Eul = λ/V _conv. Therefore, the acquisition frequency for the given experiment with PIV (or any other system with a stationary probe) will depend upon the flow speed in the hypothesis that the measured fluctuations are dominated by convection (e.g., turbulence in the far wake or in the outer boundary layer). The required measurement frequency for the considered length scale in an Eulerian frame of reference must be chosen obeying Nyquist criterion and reads as:

$$ f_{\text{Eul}} > 2{{V_{\text{conv}} } \mathord{\left/ {\vphantom {{V_{\text{conv}} } \lambda }} \right. \kern-\nulldelimiterspace} \lambda }. $$

(1)

For typical aerodynamic problems, where the flow speed may attain values in the order of 100 m/s, it is nearly impossible to perform, with currently available systems, any time-resolved measurement complying with the Nyquist principle for velocity fluctuations with length scales below the centimeter (f _Nyquist ~ 20 kHz). In contrast, for the same case, PIV measurements can be easily designed in such a way that the spatial resolution resolves spatial fluctuations of the velocity field in the order of a millimeter. Knowledge of the instantaneous spatial velocity distribution allows, in principle, the flow pattern at future or past time instants to be predicted if the convective motion in the fluid is known. This concept is at the basis of Taylor’s hypothesis of frozen turbulence. The correspondence between temporal delay and a spatial shift under this hypothesis leads to the well-known property of the space–time correlation function (Hinze 1975):

$$ R\left( {{\mathbf{X}};{\mathbf{X}} + {\mathbf{V}}_{\text{conv}} \cdot {\text{d}}\tau ,t;t + {\text{d}}\tau } \right) = 1, $$

(2)

where velocity fluctuations are considered at the new convected spatial location ${\mathbf{X}} + {\mathbf{V}}_{\text{conv}} \cdot {\text{d}}\tau$ at a time dτ later. In the hypothesis that velocity fluctuations are passively advected over a small temporal interval dτ (which occurs when ${{\sqrt {\overline{{v^{'2} }} } } \mathord{\left/ {\vphantom {{\sqrt {\overline{{v^{'2} }} } } {\left| {{\mathbf{V}}_{\text{conv}} } \right| \ll 1)}}} \right. \kern-\nulldelimiterspace} {\left| {{\mathbf{V}}_{\text{conv}} } \right| \ll 1)}},$ the above property is rewritten as:

$$ v\left( {{\mathbf{X}} + {\mathbf{V}}_{\text{conv}} \cdot {\text{d}}\tau ,t + {\text{d}}\tau } \right) = v\left( {{\mathbf{X}},t} \right). $$

(3a)

Equation 3a is valid only for small temporal delays dτ, even for a uniform convective field. For larger discrete time intervals (say t ^′), it is necessary to integrate along fluid path trajectories, still under the hypothesis of passive advection, and Eq. 3a becomes

$$ v\left( {{\mathbf{X}} + \int\limits_{\tau = 0}^{\tau = t'} {{\mathbf{V}}_{\text{conv}} \cdot {\text{d}}\tau } ,t + t^{'} } \right) = v\left( {{\mathbf{X}},t} \right), $$

(3b)

where it is required to evaluate V _conv implicitly at the current spatial location in the integral of the flow trajectory that is being integrated. Equation 3b forms the basis for techniques proposed in this paper: using the spatially distributed velocity field, an estimate of the velocity fluctuation at delayed time instants with respect to the actual measurement time is obtained. This approach is particularly suited to the three-dimensional velocity measurements where the velocity vector field is known in a volumetric domain, and the transport of turbulent fluctuations can be predicted along all three spatial coordinates. The technique can also be applied in planar PIV measurements provided that the dominant motion is aligned with the measurement plane. The approaches suggested in this paper can be regarded as an important development of previous works, in which the scopes were the enrichment of spatial information from single-sensor and planar measurements.

For instance, Cenedese et al. (1991) investigated the validity of Taylor’s hypothesis in highly turbulent flows by using a two-points Laser Doppler anemometer, concluding that the approximation is essentially correct for small separations and large structures. Instead, eddy deformation is the most responsible for the decrease in space–time correlation. It should be added that a drop in space–time correlation is introduced by moving from a three-dimensional convection field to a two-points or planar reference system. This limitation can be overcome when all the convective velocity vector components are determined by a three-dimensional measurement.

The introduction of the advection model involves a Lagrangian approach in the measurement of the temporal evolution of the signal with the consequence that the timescale of temporal fluctuations can be significantly longer that the corresponding fluctuation observed from an Eulerian standpoint. Following Koeltzsch (1999), the ratio between the Lagrangian and Eulerian timescales is dependent upon the relative amplitude of turbulent fluctuations with respect to the convective velocity:

$$ \frac{{\tau_{\text{Lag}} }}{{\tau_{\text{Eul}} }} = \alpha \frac{{\left| {{\mathbf{V}}_{\text{conv}} } \right|}}{{\sqrt {\overline{{v^{'2} }} } }}, $$

(4)

with α varying between 0.35 and 0.8. The resulting increase in the timescales for convected turbulence going from the Eulerian frame of reference to the Lagrangian one indicates the potential increase in effective measurement frequency for a PIV time-sequence (f _Lag < f _Eul).

3 Pouring Space in Time by Time Super-Sampling

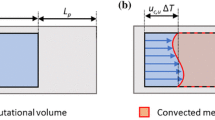
Let us consider a three-dimensional unsteady flow field, where a fluid parcel P moves along a trajectory Γ. The fluctuation of a generic property G is measured at two time instants t ₁ and t ₃ (separated by the inverse of the measurement rate Δt) while transiting at the positions X ₁ and X ₃. The situation is schematically depicted in Fig. 1, where the property G travels along a single coordinate X. The spatial distribution of G is transformed from the time instant t ₁ (red line) to t ₃ (green line). The value of G at an intermediate time instant t ₂ and at the position X ₂ is unknown. A simple prediction of the location of the parcel P may be obtained by the backward projection starting from location X ₂ by the local advection velocity V(X ₂, t ₁) (V _conv = const in the simplest case of frozen turbulence) during the time interval t ₂ − t ₁ = Δt/2. The latter corresponds to the passive transport of the fluid parcel along the local streamline crossing the location X ₂ and estimated at time t ₁. The estimate can be also obtained from the subsequent time instant t ₃ by a forward projection from location X ₂ by the local advection velocity V(X ₂, t ₃) in the time interval t ₃ − t ₂ = Δt/2.

Fig. 1

Schematic principle of temporal super-sampling under advection assumption. Left: spatial distribution of G at two time instants. Right: temporal evolution of G at a location X ₂

In a two-dimensional or three-dimensional problem, where the convection velocity varies in space and time, the prediction of the position at the intermediate time step is not as straightforward as in the case of a uniform stream transporting small amplitude fluctuations. The position of the fluid parcel at time t ₂ may be estimated from the local convective velocity known in X ₂ at time t ₁ and t ₃. The origin and arrival positions to X ₂ can be approximated by a Taylor expansion truncated at the first order that reads as:

$$ {\mathbf{X}}_{1} = {\mathbf{X}}_{2} - {\mathbf{V}}_{\text{conv}} \left( {{\mathbf{X}}_{2} ,t_{1} } \right) \cdot {\raise0.7ex\hbox{${\Updelta t}$} \!\mathord{\left/ {\vphantom {{\Updelta t} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}} + o(\Updelta t^{2} ) $$

(5a)

$$ {\mathbf{X}}_{3} = {\mathbf{X}}_{2} + {\mathbf{V}}_{\text{conv}} \left( {{\mathbf{X}}_{2} ,t_{3} } \right) \cdot {\raise0.7ex\hbox{${\Updelta t}$} \!\mathord{\left/ {\vphantom {{\Updelta t} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}} + o(\Updelta t^{2} ) $$

(5b)

when the velocity at position X ₁ and X ₃ and time instants t ₁ and t ₃, respectively, is obtained by the spatial interpolation; the above equations can be used to estimate the velocity of the fluid parcel in X ₂ at t ₂, which simply reformulates Eq. 3a:

$$ {\mathbf{V}}\left( {{\mathbf{X}}_{2} ,t_{2} } \right) = {\mathbf{V}}\left( {{\mathbf{X}}_{1} + {\mathbf{V}}_{\text{conv}} \cdot {\raise0.7ex\hbox{${\Updelta t}$} \!\mathord{\left/ {\vphantom {{\Updelta t} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}},t_{1} } \right), $$

(6a)

$$ {\mathbf{V}}\left( {{\mathbf{X}}_{2} ,t_{2} } \right) = {\mathbf{V}}\left( {{\mathbf{X}}_{3} - {\mathbf{V}}_{\text{conv}} \cdot {\raise0.7ex\hbox{${\Updelta t}$} \!\mathord{\left/ {\vphantom {{\Updelta t} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}},t_{3} } \right), $$

(6b)

The estimates of V(X ₂, t ₂) obtained from Eq. 6a (forward) and 6b (backward) do not generally coincide. This may be due to inaccuracies of the advection model and to measurement noise, which is notably uncorrelated between subsequent time instants. Therefore, a closed-form of the estimate is proposed here that provides temporal continuity. A linear combination of Eq. 6a and 6b is obtained introducing weighting coefficients based on the temporal distance from the actual sample. The forward and backward predictions of the flow property are combined together as follows:

$$ {\mathbf{V}}\left( {{\mathbf{X}}_{2} ,t_{2} } \right) = \tfrac{1}{2}{\mathbf{V}}\left( {{\mathbf{X}}_{1} ,t_{1} } \right) + \tfrac{1}{2}{\mathbf{V}}\left( {{\mathbf{X}}_{3} ,t_{3} } \right). $$

(7)

Equation 7 is easily generalized for velocity samples placed anywhere in between the two measurements. The result reads as:

$$ {\mathbf{V}}\left( {{\mathbf{X}}_{2} ,t_{2} } \right) = \frac{{t_{3} - t_{2} }}{\Updelta t}{\mathbf{V}}\left( {{\mathbf{X}}_{1} ,t_{1} } \right) + \frac{{t_{2} - t_{1} }}{\Updelta t}{\mathbf{V}}\left( {{\mathbf{X}}_{3} ,t_{3} } \right), $$

(8)

Equation 8 now more closely approximates the solution of Eq. 3b than 3a. This equation is valid also for a non-uniform velocity distribution and relies on the assumption that the velocity fluctuations are transported passively. Note that for the case that large local curvature exists in the convective velocity field, more sophisticated approaches should be considered. For instance, a better approximation of Eq. 3b is investigated by Moore et al. (2010) who applied Lagrangian paths to determine the material derivative from PIV data. Despite the above limitations, still Eq. 8 is found to provide a good basis for the numerical implementation of the advection model.

The procedure outlined above, however, cannot be explicitly applied to data measured by PIV in that the velocity of a fluid parcel is only known at a single time instant and the fluid trajectory is not directly available. In fact, the positions X ₁ and X ₃ are unknown and need to be estimated evaluating Eq. 5a and 5b. Once that the positions are obtained, the velocity is evaluated by spatial interpolation with 2D or 3D cubic splines. Once the velocity at X ₂ and t ₂ is estimated, the evaluation of V _conv is refined averaging the values of the velocity at the beginning and end of the trajectory. After two to three iterations, the result of the calculation does not exhibit any significant change.

As a result, one or more intermediate temporal samples of the flow velocity are obtained between the actual measurements making use of spatial and temporal information. This aspect may be regarded as transferring information from dense measurement in the spatial domain to the temporal domain where samples are separated by larger intervals. Therefore, the overall approach is worded as pouring Space in Time.

An important parameter governing the super-sampling procedure is the super-sampling factor SSF, i.e., the number of steps introduced in between two subsequent measurements. The resulting time step is δt = Δt/SSF, where Δt is the time separation between subsequent recordings and corresponds to 1/f _acq. The overall method will be referred to as time super-sampling (TSS) in the remainder of the present paper.

4 Range of application and theoretical limits

The flow configurations where the TSS method is expected to yield a significant increase in the measurement temporal resolution are those where small-scale turbulence is transported by means of a uniform stream (e.g., grid turbulence) or in moderately sheared flows with a significant advection motion (e.g., boundary layers and wakes). In these cases, a significant separation exists between Eulerian and Lagrangian timescales. A net increase in temporal resolution, however, is only achieved if the temporal sampling rate f _acq is below the ratio of convective velocity V _conv and the smallest resolvable length scale (the interrogation window size).

$$ f_{\text{acq}} < {{V_{\text{conv}} } \mathord{\left/ {\vphantom {{V_{\text{conv}} } {W_{S} }}} \right. \kern-\nulldelimiterspace} {W_{S} }} $$

(9)

The latter ratio also represents the maximum temporal frequency f _max that can be obtained starting from the available spatio-temporal information present in the measurement. The technique effectively increases the temporal resolution if the flow exhibits velocity fluctuations at length scales comparable to the window size or smaller. An estimate of such length scales can be obtained by the velocity spatial auto-correlation, as proposed in the examples, and the corresponding timescale is obtained by multiplying it by the local convective velocity.

The temporal resolution achievable by the TSS technique does not only depend upon the super-sampling factor, but is theoretically limited by the spatial resolution of the measurement.

The same concept may be further clarified considering the time domain. Assume that uncorrelated velocity samples are spaced by a distance not smaller than the interrogation window size W _S . Assume also the path travelled by a fluid parcel between subsequent snapshots, ΔX = V _conv·Δt, to be larger than a single interrogation window. Therefore, the time separation δt applicable between spatially uncorrelated samples should obey the condition δt · V _conv/W _s  > 1 in order not to include redundant information from the spatial velocity field. Interestingly, the latter expression is analogous to the Courant–Friedrichs–Lewy condition (Hirsch 1990) for the stability of the numerical solution of certain partial differential equations. However, in the present case, stability is not an issue, and adopting time steps smaller than the above will result in obtaining temporally correlated information.

A simple and physics-based criterion to establish the optimum value of δt (connected to the super-sampling factor SSF = Δt/δt) corresponds to the length scale of the velocity spatial fluctuations (estimated by auto-correlation) divided by the local velocity.

An additional theoretical limit of the TSS method is the approximation of quasi-rectilinear trajectories of the fluid parcels. The regions where the flow curvature radius R _C is smaller than the travelled path ΔX will be affected by errors due to distortion of the actual trajectories. This aspect emerges clearly from the experimental analysis of the transitional jet. As a simple criterion, one may require that Δt _max < R _C / V _conv. Furthermore, for planar experiments, it should be considered that only a projection of the flow trajectories is available and any fluctuation due to the out-of-plane motion cannot be accounted for by the advection equation based on the planar measurement domain. The errors arising from the three-dimensional motion in planar PIV experiments are of complex nature and depend upon several parameters, which will not be dealt with in the present study.

4.1 A posteriori estimate of the reconstruction accuracy

A simple criterion is proposed that establishes the accuracy of the TSS approach based on the measured data. The main principle is that the estimate at the intermediate time between two measurements (t + Δt/2) should correspond, except for errors arising from the TSS technique and errors due to the measurement noise. When Eq. 6a and 6b are evaluated separately, they yield an independent estimate of the velocity at time t ₂. The a posteriori error estimate is given by the standard deviation of the difference between the forward and backward evaluation. The relative error is obtained with normalization either to a reference velocity (Eq. 10) or to the amplitude of turbulent fluctuations:

$$ \varepsilon_{{r,{\text{TSS}}}} = \frac{100}{{V_{\infty } }} \cdot \left\{ {\frac{1}{N}\left[ {\sum\limits_{n = 1}^{N} {\left( {u_{{{\text{TSS}},n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - u_{{{\text{TSS}},n + 1 - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \right)^{2} } + \sum\limits_{n = 1}^{N} {\left( {v_{{{\text{TSS}},n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - v_{{{\text{TSS}},n + 1 - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \right)^{2} } } \right]} \right\}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} . $$

(10)

The subscript TSS, n + 1/2 indicates the velocity estimated at the time instant t + Δt/2 obtained from the measurement at time t, whereas TSS, n + 1−1/2 indicates that obtained from the following measurement sample. In the present work, the error is evaluated directly by comparing the reconstructed velocity to the actual measurement (Eq. 11). In the remainder, Eq. 10 is evaluated and compared with the direct error, yielding a good agreement.

5 Experimental verification

The applicability of the method for PIV data is verified making use of the two and involving planar as well as 3D (tomographic) measurements of turbulent shear flows.

The first application is the near wake of a NACA-0012 airfoil at chord Reynolds number of 370,000. The hypothesis of frozen turbulence holds reasonably well in this flow regime. Measurements are performed at a rate close to the limit of state-of-the art high-speed PIV equipment (20 kHz) in order to measure the velocity field at a rate approximately 4 times higher than that required to fully resolve the dynamics of the measurable flow scales. The second case is a circular jet at Re = 5,000 measured by tomographic PIV, which involves a free shear layer undergoing transition. Therefore, the flow conditions are far from the condition of advected turbulence. Also in this case, the measurements are performed with redundant time resolution (approximately 10 times higher) with respect to the timescales exhibited in the flow. The condition of highly time-resolved measurements from both experiments enables to consider the raw data series as an accurate reference to estimate the errors involved with the time super-sampling technique.

The analysis is conducted first qualitatively, by the inspection of the spatial flow pattern and the distortions inherent to the super-sampling technique. Furthermore, the velocity time history at relevant locations is inspected, yielding information on the signal degradation in the time domain. The error is quantified on a statistical basis evaluating the standard deviation of the difference between the raw velocity field and that reconstructed by TSS. As a term of comparison, also the error committed by a point-wise time super-sampling with linear interpolation (e.g., according to Gobbi et al. 2006) between samples is shown. The frequency domain analysis is performed only for the planar measurements, where the duration of the experiment allows the amplitude spectra to be evaluated with converged statistics. The main parameter varied throughout the analysis is the super-sampling factor SSF.

5.1 Planar PIV of the near wake of a NACA airfoil

Experiments are conducted to study the dynamical phenomena at the origin of acoustic noise emission from airfoils with sharp trailing edge (Ghaemi and Scarano 2011). The investigation is conducted in a low-speed wind tunnel at free-stream velocity of 14 m/s over a NACA-0012 airfoil of 40 cm chord length placed at zero incidence. The chord-based Reynolds number is 370,000, and the boundary layer transition is forced at a position 30% chord by a tripping device. The Reynolds number based on the momentum thickness of the boundary layer at the trailing edge is Re _θ  = 1,500. Table 1 summarizes the measurement conditions.

Table 1 Trailing edge experiment measurement conditions

The acquisition rate of 20 kHz is achieved firing each of the two lasers at 10 kHz with a time delay of 50 μs. A recording sequence of one second duration includes 20,000 samples. The region of interest indicated in Fig. 2 is the near wake of the airfoil, where the two turbulent boundary layers come to interact. In these conditions, the hypothesis of frozen turbulence holds reasonably well in that no flow reversal occurs, and the typical level of velocity fluctuations encountered in the flow is one order of magnitude smaller than the convection velocity. The digital resolution of the measurement is 20 pixels/mm, and the interrogation is performed with a window size of 20 pixels (1 mm) and an overlap factor of 75%. As a result, velocity fluctuations of wavelength larger than approximately two millimeters are spatially resolved. Based on Eq. 1, the minimum temporal sampling rate that avoids aliasing of the passage of structures of 1 mm-length scale traveling at a velocity of 6 m/s is 6 kHz. The assumption is a conservative estimate of the needed measurement rate that does not take into account the actual spectrum of turbulence. The Eulerian timescale is estimated from the temporal auto-correlation function of the vertical velocity fluctuations: the 1/e decay time is found to be 0.2 ms, corresponding to approximately 5 kHz, which indicates that the spectrum of turbulent fluctuations occupies the entire measurable range of scales.

Fig. 2

Instantaneous velocity field after a NACA-0012 airfoil. Velocity vectors and color coded streamwise velocity component. The black circle indicates the position where the velocity time history is considered. Raw data (top) and reconstructed with SSF = 12 (bottom). Data on the edge is reconstructed taking values from outside the measured domain

The frequency spectrum estimated from the measurements at 20 kHz is expected to fully resolve the temporal fluctuations and, as such, will be considered unaffected by aliasing. Therefore, the raw data will be considered as reference data for comparison in the time and frequency domain analyses.

The velocity time history in Fig. 3a illustrates that from data sub-sampled at 3.3 kHz (SSF = 6), most of the velocity fluctuations can be retrieved with the TSS approach. Notable exceptions are the fluctuations at highest frequency and small amplitude. These small fluctuations are ascribed to measurement noise, and they cannot be (nor it is desirable that they are) captured by the current advection-based approach. Amplitude modulation becomes clearly noticeable only at SSF = 24 for the present case (Fig. 3b).

Fig. 3

Time history of vertical velocity component (expressed as pixels displacement). SSF = 6 (a) and 24 (b)

A global norm of the error is introduced to quantify the discrepancy between the data reconstructed by the point-wise interpolation or the TSS method and the reference data. The quadratic difference ε _TSS of the local velocity normalized by the free-stream value is displayed in Table 2 for the chosen values of SSF.

$$ \varepsilon_{\text{TSS}} = \frac{100}{{V_{\infty } }} \cdot \left[ {\frac{1}{N}\sum\limits_{n = 1}^{N} {\left( {u_{{{\text{TSS}},n}} - u_{n} } \right)^{2} + \left( {v_{{{\text{TSS}},n}} - v_{n} } \right)^{2} } } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} $$

(11)

Table 2 Measured intensity of turbulent fluctuations, measurement error, and a posteriori error estimate of super-sampled time series at (X,Y) = (10, 0 mm)

The difference between the raw data and the super-sampled series at SSF = 6 is in the order of 0.2 pixels, which is slightly in excess of the measurement noise observed in the raw data. An estimate of the latter is obtained by comparing the raw data with the data series super-sampled with SSF = 2, where both series are sampled at a frequency above Nyquist criterion and their difference can only be ascribed to measurement noise, which is not correlated between subsequent snapshots. This result indicates that a significant part of the discrepancy (approximately 70%) is due to the noise-averaging effect of the super-sampling procedure, rather than a spatio-temporal filtering. The fact that the spectral content of the time series remains practically unaltered up to SSF = 24 further supports the above hypothesis. The intensity of turbulence fluctuations in Table 2 is reported to slightly decrease, from 6.9 to 6.4% (normalized to the free-stream velocity) when the temporal separation between measurements is increased to 24 times the original. The effect is more pronounced for the point-wise linear interpolation, where the fluctuations drop to 4.8%, due to the underestimated fluctuations in between subsequent samples (Fig. 3b). The quadratic error with respect to the raw data is approximately 1% at SSF = 2, which is ascribed to the above mentioned noise-averaging effect.

In the last column, the values of the error estimated a posteriori are compared with the actual error. The estimated error is slightly below the actual one; however, the values and trend are in rather good agreement. This confirms that ε _r,TSS can be taken as a reliable error estimator for the TSS technique.

The length of the present dataset allows the signal to be analyzed in the frequency domain by means of amplitude spectra estimated with the Welch algorithm (Welch 1967). The time series composed of 20,000 samples is divided into 50 blocks of 800 samples (overlapping by 50%) and each one is weighted by a Hamming window.

Three values of SSF are considered. The graphs in Fig. 4 compare the spectrum obtained from the measurement performed at 20 kHz (solid black line) with that of the sub-sampled series (filled delta) and that of the super-sampled series (hollow circles) obtained from the sub-sampled data.

Fig. 4

Amplitude spectrum of vertical velocity component. Raw measurement at f _acq = 20 kHz (black solid line). Raw data after sub-sampled data (filled blue delta). Super-sampled data to the original rate from the sub-sampled series (hollow red circles). Super-sampling factor SSF = 6 (a), 12 (b), and 24 (c)

When the original data is sub-sampled by a factor 6, the resulting sampling rate of 3.3 kHz falls slightly below the maximum frequency expected in the signal at 6 kHz. As a result, the last part of the amplitude spectrum (approximately the frequency range above 1 kHz) in Fig. 4a becomes affected by errors due to aliasing. In contrast, the spectrum obtained starting from the same sub-sampled series with the TSS technique fully recovers the energy distribution of the reference data. The only difference is observed in frequency range beyond 4 kHz, where the raw data spectrum begins to flatten due to the effect of measurement noise. Instead, the super-sampled spectrum continues monotonically toward a lower noise level. This behavior should not be regarded as any extension of the measurement dynamic range, but is ascribed to the averaging effect of the TSS method, by which every sample is obtained as a linear combination of two independent velocity measurements (Eq. 7).

Sub-sampling by a factor 12 (sampling rate 1.67 kHz), one observes a largely distorted spectrum (Fig. 4b) due to aliasing effects that compromise the energy distribution also in the low frequency range (below 500 Hz), with the appearance of spurious peaks not corresponding to any physical mode. The super-sampled result from this sub-sampled series still follows the raw data spectrum with a good agreement for the entire frequency range, which indicates that Lagrangian timescales for this flow are not shorter than 1.2 ms (1/833 Hz).

Finally, the spectrum obtained when sub-sampling by a factor 24 (sampling rate 416 Hz) severely truncates the energy distribution in the frequency domain, and large part of the energy escapes the frequency range (0–416 Hz). As a result, the spectrum is entirely corrupted by aliasing. Although here the TSS technique appears to retrieve the trend of the raw data spectrum and not to overestimate the energy content at low frequency, one may notice that starting from the Nyquist limit for the sub-sampled series, the energy of the spectrum obtained with TSS slightly underestimates that of the reference data, to a maximum of approximately 10% at a frequency of 4 kHz.

Interestingly, the present case shows no visible limit for the maximum value of SSF, indicating that Lagrangian and Eulerian timescales are separated by at least one order of magnitude (τ _Lag > 10 τ _Eul). In fact, the Eulerian sampling requires a rate of at least 6 kHz, whereas the data reconstruction by TSS with samples taken at 833 Hz still returns an acceptable spectrum of the velocity fluctuations, resulting in an increase in temporal resolution of one order of magnitude.

5.2 Tomographic PIV of a circular jet

The experiment features a submerged water jet issued at a velocity of 0.45 m/s from a contoured nozzle with of 10 mm exit diameter (Re = 5,000). Time-resolved tomographic PIV experiments are performed to investigate the role of coherent flow structures in the production of acoustic noise in subsonic jets. For a detailed description of the experimental apparatus and flow conditions, the reader is addressed to the study of Violato et al. (2010). The laminar flow laminar at the exit undergoes shear layer transition with Kelvin–Helmholtz vortex rings that undergo vortex pairing in the first three diameters. Growth of azimuthal disturbances and the subsequent transition to the three-dimensional regime occur within five diameters. The high-speed tomographic system (see Table 3) is composed of a Quantronix Darwin-Duo Nd:YLF diode-pumped laser illuminating a cylindrical domain of 30 mm diameter and operates at 1 kHz repetition rate. Four LaVision High Speed Star 6 CMOS cameras compose the imaging system with an aperture of 90 degrees. The particles displacement between recordings is 0.4 mm (8 voxels) at the jet exit. Tomograms of 600 × 600 × 1,000 voxels are produced with DaVis 7.4 and analyzed with volume deformation iterative multigrid (VODIM, Scarano and Poelma 2009) with interrogation volumes of 2 × 2 × 2 mm³ (40 × 40 × 40 voxels). The use of ensemble correlation averages over four exposures (3 pairs) decreases the measurement precision error to approximately 0.05 voxels.

Table 3 Parameters of jet experiment by tomographic PIV

The vortex rings are formed at a rate of approximately 30 Hz (Strouhal number of 0.67); therefore, each shedding process is described by more than 30 snapshots. The minimum frequency to describe the flow pattern is visualized by an axial data slice where velocity vectors and velocity axial component contours are shown (Fig. 5). The three-dimensional pattern of vortices is visualized with iso-surfaces based on the Q-criterion (Hunt et al. 1988). Two axi-symmetric vortex rings are present in the region close to the nozzle exit, whereas the ring above (Y/D = 2.5) exhibits azimuthal waves and is contracted under the action of a larger structure above it, which will later involve it in a pairing/leapfrogging event. The axial flow is accelerated inside vortex rings causing inward radial flow at their trailing region.

Fig. 5

3D velocity field from tomographic PIV. Reconstructed velocity field with TSS. From left to right: SSF = 1 (raw), 6, 12, 24. Iso-surface of Q-criterion for vortex detection

A visual inspection of the reconstructed velocity pattern at SSF = 6 (Fig. 5) shows no significant difference with respect to the raw data. At SSF = 12, the coherence of the circular motion in the vortex cores is slightly degraded; however, the topology of the vortex pattern based on the Q-criterion visualization is mostly retained. Only at SSF = 24 are important artifacts are introduced, both in terms of the velocity vector field as well as the Q-criterion. These are particularly prominent in the upper part of the flow, where smaller flow scales are formed, which are visibly reduced in their amplitude. Also in the lower part of the domain, the vortex shedding is not well modeled by advection and non-linear effects such as strong streamlines curvature and acceleration cannot be compensated for by the advection model. This is not surprising, when one considers that the sampling time interval becomes ΔT = 24 ms, which largely exceeds half the time taken by a shedding event (ΔT _shed = 34 ms).

The time history of the axial and radial velocity directly shows the effect of data sub-sampling and reconstruction by TSS (Fig. 6). Also, a point-wise linear interpolation of sub-sampled data is shown for comparison. For SSF = 6 (f = 133 Hz), both the reconstruction based on linear interpolation (dashed blue line) as well as the super-sampled series follow the reference data with good agreement. At a sub-sampling factor of 24 (f = 42 Hz), the linear reconstruction becomes largely aliased as opposed to the TSS reconstruction that follows the major fluctuations in the raw data.

Fig. 6

Measured velocity time history (expressed as voxels displacement) evaluated at X/D = 0 and Y/D = 3.5. Axial displacement for SSF = 6 (a) and 24 (b). Radial displacement for SSF = 6 (c) and 24 (d)

It is important to remark that lowering the measurement rate in time-resolved tomographic PIV experiments enables operating the system at higher pulse energy, which in turn enables the measurement over a larger domain. This is considered an important factor, in that time-resolved tomographic PIV measurements in air flows are currently limited by the laser power budget and often the energy scattered by the particle tracers is barely sufficient for the measurement. Moreover, the trade-off between acquisition frequency and image resolution of many camera systems can be now tipped more toward increasing image resolution with less direct loss in terms of temporal resolution.

Based on Eq. 1, the smallest resolvable timescale is given by the ratio between the interrogation volume length and a reference convective velocity. In the present experiment, τ = W _S /V _jet, yielding 4 ms, which corresponds to 250 Hz. Nevertheless, the latter represents only the maximum temporal frequency that can be resolved based on the spatial resolution of the measurement.

The temporal auto-correlation function of the three velocity components from the raw data is used to estimate the actual frequency content. The 1/e decay time ranges from 8 ms in the near region and for the axial and radial components to 12 ms in the more turbulent region (Y/D > 4) for all three components. The corresponding frequency is approximately 100 Hz, which is less than that obtained based only on the window size and convective velocity. Therefore, one may conservatively establish that the minimum sampling rate for the present experiment is 100 Hz.

The global error norm is extended to three-dimensional data and normalized to the jet exit velocity V _jet according to the expression below and:

$$ \varepsilon_{\text{TSS}} = \frac{1}{{V_{\text{jet}} }} \cdot \left[ {\frac{1}{N}\sum\limits_{n = 1}^{N} {\left( {u_{{{\text{TSS}},n}} - u_{n} } \right)^{2} + \left( {v_{{{\text{TSS}},n}} - v_{n} } \right)^{2} + \left( {w_{{{\text{TSS}},n}} - w_{n} } \right)^{2} } } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} $$

(12)

The largest discrepancy between the velocity reconstructed by super-sampling and the reference data is observed along the jet shear layers (Fig. 7). Vortex shedding and vortex pairing introduce large relative velocity fluctuations and a strong streamline curvature, which is considered to be the cause of increasing errors for large values of SSF. The data series at SSF = 6 exhibit a relative error within 3%, which may be considered negligible as it is in the same order of the typical measurement uncertainty for tomographic PIV. The local linear interpolation has a similar distribution of the error, indicating that the frequency content of the signal does not exceed 200 Hz. At SSF = 12 and 18, the discrepancy attains approximately 9 and 15% for the linear interpolation. The TSS reconstruction reduces the error to 6 and 10%, respectively, which may be considered acceptable for flow-visualization purposes. When the sampling frequency is reduced to 42 Hz (SSF = 24), both linear interpolation and the TSS method suffer from significant distortions with error levels exceeding 25 and 15%, respectively. One can observe that the region most affected by errors tends to include the jet axis at a distance larger than 2 diameters for the linear interpolation. This is ascribed to the effect of turbulent fluctuations transported in the inner part of the jet, which are largely smeared by a point-wise reconstruction. The TSS method appears to compensate for most of the errors in the inner part of the jet, and the region affected by largest errors remains the highly sheared interface. Nevertheless, the reduction in the acquisition frequency associated with the use of the TSS technique is less pronounced in this case. According to the obtained results, one may conclude that a measurement rate of about 50 Hz (SSF = 18) is sufficient when a discrepancy of 10% between the reconstructed series and the raw data is allowed. This corresponds to half the measurement rate with respect to the estimated sampling frequency based on the temporal auto-correlation function of the velocity.

Fig. 7

Relative error (ε _TSS) in the axial plane as a function of the super-sampling factor. Left-to-right SSF = 6,12,18,24. The left-side half figure is relative to local linear interpolation. The right-side half figure is the error from TSS

6 Conclusions

An advection model is proposed to numerically increase the temporal resolution of time-resolved PIV measurements. The approach makes use of the space–time features of time-resolved PIV measurements and is based on the estimation of the fluid parcels transport in the hypothesis that their velocity remains frozen. The maximum theoretical increase depends upon the ratio between the timescales of turbulent fluctuations evaluated from a Lagrangian and an Eulerian reference frame. The range of application of the method is discussed, and the main parameters governing the potential increase in temporal resolution are identified, which include the measurement rate as well as the spatial resolution.

The effectiveness of the approach is assessed by the experiments conducted at a measurement time-rate well beyond the maximum frequency exhibited in the flow, which provide a valid reference for the error analysis.

The application to the NACA-0012 airfoil wake flow demonstrates more clearly the potential of this technique both for flow visualization and to avoid the aliasing phenomenon when performing the analysis in the frequency domain. In this case, even the largest sub-sampling factor considered (SSF = 24) returns an amplitude spectrum in rather good agreement with the raw data, clearly indicating the suitability of the method to obtain higher frequency information from the TSS method applied to PIV time series. The increase in temporal resolution is estimated to be approximately one order of magnitude.

The application of the TSS method for 3D data obtained by tomographic PIV is particularly interesting because of its potential to reduce the needed measurement rate. The latter is very relevant for volumetric measurements in view of both the required laser power and computational effort needed to produce and evaluate tomograms. The results show that the reference data can be reconstructed starting from a time series taken at a significantly lower measurement rate. However, the jet experiment shows that in free-shear layers, the errors associated with the advection model increase more rapidly as the time separation between measurements becomes larger. Under these conditions, the increase in temporal resolution appears to be limited to a factor 2.

The study does not cover all possible numerical procedures aiming at time super-sampling but shows with some evidence that the information available in PIV time series can be used more efficiently when a spatio-temporal coherence of the signal can be hypothesized.

Appendix

The time super-sampling method in pseudo code and implemented as a Matlab macro. For conciseness, the instructions are given only for one coordinate (X) and velocity component (U) and for planar data.