Abstract
Astigmatism or wavefront deformation, microscopic particle tracking velocimetry (A-μPTV) (Chen et al. in Exp Fluids 47:849–863, 2009; Cierpka et al. in Meas Sci Technol 21:045401, 2010b) is a method to determine the complete 3D3C velocity field in micro-fluidic devices with a single camera. By using an intrinsic calibration procedure that enables a robust and precise calibration on the basis of the measured data itself (Cierpka et al. in Meas Sci Technol 22:015401, doi:10.1088/0957-0233/22/1/015401, 2011), accurate results without errors due to spatial averaging or bias due to the depth of correlation can be obtained. This method takes all image aberrations into account, allows for the use of the whole CCD sensor, and is easy to apply without expert knowledge. In this paper, a comparative study is presented to assess the uncertainties of two state-of-the-art methods for 3C3D velocity field measurements in microscopic flows: stereoscopic micro-particle image velocimetry (S-μPIV) and astigmatism micro-particle tracking velocimetry (A-μPTV). First, the main parameters affecting all methods’ measurement uncertainty are identified, described, and quantified. Second, the test case of the flow over a backward-facing step is analyzed using all methods. For comparison, standard 2D2C μPIV measurements and numerical flow simulations are shown as well. Advantages and disadvantages of both methods are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With the increasing complexity of micro-fluidic devices such as micro-mixers, micro-bioreactors, and micro-heat exchangers, among others, three-dimensional flows become an important challenge. Although the Reynolds numbers for the majority micro-fluidic devices are too low to generate turbulence, the numerical simulations are often impossible due to complex boundary conditions such as electrokinetic or electrophoretic forces, electric or magnetic field or due to multiphase effects or chemical reactions. Therefore, the μPIV (particle image velocimetry) method, introduced by Santiago et al. (1998) as an experimental tool for the measurement of 2D2C (two-dimensional, two-components) velocity fields in micro-fluidic devices, has become one of the most wide-spread techniques in micro-fluidics. Unfortunately, there are some inherent limitations, as the technique relies on volume illumination:
-
the spatial resolution of the depth direction is determined by the imaging optics’ depth of focus and thus limited to several μm
-
out-of-focus particles also contribute to the cross-correlation (depth of correlation) and, hence, introduce a bias in the measurements
-
only 2C2D velocity fields can be measured.
The improvement and adaptation of the macroscopic μPIV technique are still ongoing processes. Reviews of the state of the art of μPIV and of its relevant applications were published by Lindken et al. (2009) and Wereley and Meinhart (2010). Several methods have been proposed to extend the velocity reconstruction to the third component. Reviews about advanced 3D methods can be found by Lee and Kim (2009); Chen et al. (2009) and Cierpka et al. (2010b). One method consists of using different viewing perspectives. Stereoscopic μPIV (S-μPIV), derived from μPIV, takes advantage of a stereoscopic microscope to observe the flow field in the measurement region from two slightly different viewing angles. The in-plane particle image displacement observed by two cameras under different angles can be used to estimate the in-plane velocity by 2D cross-correlation. The third component is then reconstructed by the in-plane velocities as will be explained in detail in Sect. 2 Another approach is the tomographic reconstruction of the particle distribution in the volume, after which 3D cross-correlation is applied to obtain the 3D velocity field. An inherent problem for multi-camera approaches is the need for a very precise calibration and the small viewing angles applied (Lindken et al. 2006). Thus, their applicability, especially for the tomographic methods, to micro-fluidic devices seems to be quite limited, and alternative imaging approaches are necessary. Recently, in-line holography (Lee and Kim 2009; Ooms et al. 2009) was applied to 3D velocity field measurements in microscopic channels. However, the numerical reconstruction process is rather time consuming, and the optical setup has to be built with great care to have an acceptable accuracy of the out-of-plane velocity. To overcome the difficulties of the complex calibration procedure in holography and multi-camera techniques, a method using just one camera is favorable. The depth coding via three pinholes in the imaging system is a smart technique, estimating the particle’s depth position via two-dimensional images (Pereira and Gharib 2002; Willert and Gharib 1992). With the three pinholes, a particle is imaged as a triplet. The distance between the edges of the triplet is related to the depth position. This concept is more robust than holography and was successfully applied to micro-fluidics by Yoon and Kim (2006). Aside from masking the optics, there are other methods that rely on breaking the axis symmetry of an optical system. This allows for the coding of the depth position of particles in a 2D image. By later reconstruction of the particles’ position in real space, the velocity field can be evaluated by correlation algorithms or tracking methods. So far, a bent dichroic mirror (Ragan et al. 2006), diffraction gratings for multi-planar imaging (Angarita-Jaimes et al. 2006), an optical filter plate at an angle (van Hinsberg et al. 2008), and the observation under an angle (Hain and Kähler 2006) was used. For micro-fluidic applications, cylindrical lenses were successfully used by Chen et al. (2009) and Cierpka et al. (2010b). The approach based on cylindrical lenses, especially, is a very powerful and simple method, which allows for the extension of existing 2D measurement systems to fully 3D measurements. Kao and Verkman (1994) applied this technique to the measurement of the position of fluorescent particles in living cells. Today astigmatic imaging is commercially used in nearly every CD or DVD player to precisely determine the distance between CD and laser head. A big advantage of this approach is the possibility to adjust the measurement depth and resolution by changing the focal length of the cylindrical lens. The use of the recently presented intrinsic calibration procedure (Cierpka et al. 2011) makes the technique easy applicable without special expert knowledge.
Therefore, the S-μPIV and A-μPTV approaches will be studied and discussed in the following. In order to determine the accuracy and uncertainty of both techniques, measurements of the flow over a backward-facing step will be compared with standard μPIV as well as numerical simulations. The backward-facing step flow was chosen, since it offers a velocity field that is well known and mainly one directional prior to the step. Furthermore, it has a very pronounced out-of-plane component shortly downstream of the step. Other groups have also verified their 3D measurement methods with backward-facing step flows (Chen et al. 2009; Yoon and Kim 2006; Bown et al. 2006). A combined stereo PIV/PTV approach was used by Bown et al. (2006). They measured the flow over a 232-μm step in a 466-μm high channel. Glycerol was used as working fluid, resulting in a Re h = 0.004. The flow was investigated with stereoscopic μPIV at 23 different planes in the z-direction. The accuracy of the correlation-based results was found to be limited by the misalignment or non-overlapping of the two focal planes of the stereo microscope. To improve the accuracy, a super resolution PTV approach was applied. Using a PTV, algorithm allows to restrict valid measurements only to strongly focused particles, which decreases the effect of the depth of correlation. The authors reported uncertainties for the averaged vector map in the order of 0.35 μm/s (3% of the mean velocity) for the in-plane components, and 0.82 μm/s (7% of the mean velocity) for the out-of-plane component of the correlation-based velocity estimation. The uncertainty was decreased to 2 and 3% for the in-plane and out-of-plane velocity, respectively, with the PTV algorithm. Unfortunately, the way the uncertainties were determined was not reported, and a comparison is therefore difficult. Chen et al. (2009) used a cylindrical lens with \(f_{\hbox{cyl}} = 500\,\hbox{mm}\) to measure a \(600\,\upmu\hbox{m}\) range at a \(170\,\upmu \hbox{m}\) backward-facing step, inside a 500 μm high channel. The uncertainty for the depth position was reported to be \(2.8\,\upmu\hbox{m}\) for the calibration images. Unfortunately, no uncertainty of the single measurements was given. The measured RMS value of the velocity was \(3.3\,\upmu\hbox{m/s}\), even though \(2.8\,\upmu\hbox{m/s}\) was expected from the measurement uncertainty. This is above one third of \(u_{\infty}.\) The investigated Reynolds number was Re h = 0.0015. The images were taken in single frame mode, probably with continuous laser light illumination and are of higher quality than double frame images with very short laser light pulses. The separation time between successive images in the study was \(\Updelta t = 2\,\hbox{s}\). The authors stated that 3,000 images were acquired, which takes 100 min. This and the very low Reynolds number are far beyond realistic ‘Lab-on-a-chip’ applications, which range in the order of \(Re_h = 1,\ldots,100\). For these devices the acquisition of double frame images in a short time, which suffer from large noise levels, is necessary.
2 Experimental setup
2.1 The backward-facing step flow, numerical simulation, and conventional μPIV
For the sake of a proper comparison, all experiments were performed in the same micro-channel to avoid variations in the boundary conditions. The micro-channels are fabricated out of elastomeric polydimethylsiloxane (PDMS) on a 0.6-mm thick glass plate by the Institute for Microtechnology of the Technical University Braunschweig. They possess inlet and outlet cross-sectional areas of \(500 \times 150\,\upmu\hbox{m}^{2}\) and \(500 \times 200\,\upmu\hbox{m}^{2}\), respectively. The channel was approximately 30 mm in length, with the backward-facing step at about 15 mm from the inlet to assure fully developed flow conditions upstream of the step. The flow in the channel was seeded with polystyrene latex particles, fabricated by Microparticles GmbH. The particle material was pre-mixed with a fluorescent dye, and the surface of the latex micro-spheres was later PEG modified to make them hydrophilic. Agglomeration of particles at the channel walls can be avoided by this procedure, allowing for long duration measurements without cleaning the channels or even clogging. The particles showed very high fluorescence signals that allowed for the extension of the measurement depth for the astigmatic measurements (Cierpka et al. 2011). To investigate the downward flow close to the step in greater detail with standard μ-PIV, an additional measurement was performed with a channel allowing optical access from the side. The data were evaluated using the single pixel procedure outlined by Scharnowski et al. (2010).
The mean diameter of the monodisperse particle distribution was \(d_P=2\,\upmu\hbox{m}\) (standard deviation = \(0.04\,\upmu\hbox{m}\)) for the A-μPTV measurements and \(d_P = 1\,\upmu \hbox{m}\) for all PIV measurements. The fluid was distilled water, which was pushed by a high precision Nexus 3000 syringe pump (manufactured by Chemix) with constant flow rate through the channel. The Reynolds number based on the step height was Re h = 3.75 and based on the hydraulic diameter of the inlet, \(Re_{\hbox{HD}}=17.3\). For the illumination of the particles, a two cavity frequency-doubled Litron Nano S Nd:YAG laser system was used. The image recording was performed with the DaVis 7.4 software package from LaVision. The images were acquired in double exposure mode, where the camera shutter is activated two times. The time delay between the two successive frames was set to \(\Updelta t = 200\,\upmu\hbox{s}.\) 1,000 images were recorded at each z-position for all three techniques. The A-μPIV measurements, as well as the 2D2C conventional μPIV measurements, were performed using an Axio Observer Z.1 inverted microscope by Carl Zeiss AG with a LD-Plan Neofluar objective with a numerical aperture of NA = 0.4 and a magnification of M = 20×. To reconstruct the velocity field in the volume from conventional PIV, the raw image pairs were preprocessed and cross-correlated. Preprocessing consisted of subtracting the sliding minimum over time, followed by the same substraction in space to decrease non-uniformities and back-reflections. These steps are followed by a bandwidth filter and constant background subtraction, used to sort out particle agglomerations and eliminate the remaining background noise. 2D velocity fields were measured for seven equidistant planes inside the channel, starting from \(z = 37\,\upmu\hbox{m}\) and ending at \(z=177\,\upmu\hbox{m}\). The image pairs were cross-correlated with the DaVis 7.2 software package from LaVision. A normalized multi-pass algorithm with a final interrogation window size of 32 × 32 pixels was used with 50% overlapping of the interrogation windows with an average of 3–5 particle images per window. Since the flow was laminar and stationary, the vector fields were averaged to get the final vector fields.
For the numerical flow simulation, the micro-channel was modeled with a solid modeler to extract the micro-channel boundaries; the boundaries were meshed in CD-adapco STAR-CCM+ 4, and a finite volume model was set for a laminar and viscid fluid with a constant density (water). The computational domain exceeded 600,000 hexahedral cells. In the step region, four times the channel width, the mesh size was equal to \(6.25\,\upmu\hbox{m}\) (1/80 of step width) to ensure an optimal velocity resolution. The no-slip condition was set at the boundaries of the computational domain. At the inlet, the velocity was set to match the Reynolds number of the experiment. At the outlet, the pressure was set to a reference value. To avoid entrance effects, two flow extensions were located at the inlet and the outlet; uniform boundary conditions were set at a distance of twenty times the channel width. The steady solution converged using the implicit solver in 500 steps; the relative errors of residuals of continuity and momentum were less than 10−6.
2.2 Stereoscopic μPIV
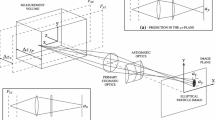
For the S-μPIV measurements, an upright stereoscopic microscope, with a common main objective (CMO) lens configuration (Leica M165 FC) was used. The CMO design uses a large-diameter objective lens, through which both the left and right channels view the object. The optical axis of the objective is normal to the object plane, therefore there is no inherent tilt of the image at the CCD focal plane, and the left and right images are viewed by the CCD cameras, theoretically with no convergence as can be seen in Fig. 1. The corresponding direct linear transform for the conversion between the image and object spaces can be derived using geometric optics:
where, \(\Updelta X_1',\Updelta Y_1'\) and \(\Updelta X_1',\Updelta Y_1'\) are the projection of a displacement vector (x, y, z) in the image space of camera 1 and camera 2 respectively, and \(\Uptheta_1,\Uptheta_1,\alpha_1,\alpha_2\) are angles as defined in Fig. 1. Equation 1 is derived under the assumption that the working distance of the lens is much larger than the displacement in the axial direction. In a real system, the transform is typically more complex than the one in Eq. 1 due to distortions and aberrations induced by imperfections of the lens or by refraction between different media (e.g., glass and water of the micro-channel). Therefore, an empirical calibration is required. For the presented measurements, a stereo-lens Planapo 2×, with NA = 0.282 was used, in combination with the internal zoom lens system of the microscope, which was set to achieve a total magnification of M = 20×, at the CCD of the cameras. Images were taken with two double-frame cameras with 4 k × 2.6 k pixels CCD sensors (PCO 4000). The calibration was performed using a calibration plate with a grid reticule where the lines were 50 μm apart from each other. The grid was displaced along the axial direction, with steps of \(2\,\upmu\hbox{m}\), using a piezoelectric stage (PZ 400 SG, Piezosystem Jena GmbH) with a resolution of \(7.5\,\hbox{nm}\). A multi-plane polynomial function of third order was used to fit the calibration curves (displacement of the grid crosses in the image space of cameras 1 and 2 as a function of the axial position of the grid). A self-calibration procedure (Kähler et al. 1998) was subsequently used to account for further distortions introduced by the geometry of the step channel.
A major problem in S-μPIV measurements is given by the possible mismatch of the two focal planes caused by optical aberrations and imperfections in the construction of the microscope. In S-μPIV, as well as in μPIV, volume illumination is used and the measurement volume observed by one camera corresponds to its focal plane. The evaluated 3D velocity vectors result from the recombination of the 2D velocity fields observed by cameras 1 and 2, under the assumption that their measurement volumes are exactly co-spatial. The thickness of the measurement volume can be estimated using the depth of correlation (Olsen and Adrian 2000). A misalignment of the two cameras’ measurement planes with respect to each other introduces an additional bias error, especially when velocity gradients are present (Rossi et al. 2010). What is more important, this error cannot be corrected since it inherently depends on the design and construction of the microscope.
In order to quantify the misalignment, the focal planes of cameras 1 and 2 were reconstructed taking images of the calibration reticule at different heights and using a local focus function based on the variance of image intensity (Sun et al. 2004). The procedure was repeated with the reticule surrounded by air and submerged under 200 μm of distilled water, analogous to the experimental conditions used to record the images of particles inside the backward-facing step, filled with water. The reconstructed focal planes for cameras 1 and 2 in air and water are reported in Fig. 2.
It can be observed that the focal planes are curved and overlap only partially, even when the finite thickness of the measurement volume is considered. Particularly for the case in water, in the region where the velocity measurements on the backward-facing step were taken, a mean difference of \(4.1\,\upmu\hbox{m}\) was estimated between the two focal planes, with a maximum of \(11.2\,\upmu\hbox{m}\). This error is only negligible when the depth of the measurement volume is large compared to the mismatch. However, an additional error is introduced by averaging the velocity measurement through the depth of correlation in this case. For this setup, using \(1\,\upmu\hbox{m}\) diameter particles, the depth of correlation was estimated to be equal to \(30\,\upmu\hbox{m}\), which means that in the worst case one-third of the measurement thickness was not correlated. This can already lead to substantial systematic errors (Kähler 2004). With regards to the PIV analysis, the images were first pre-processed using a sliding minimum filter for background removal and a smoothing median filter for image random noise reduction. Subsequently, an ensemble correlation over 1,000 images per plane was calculated, using a multipass algorithm with final interrogation window of 64 × 64 pixels and 50% overlap. The vector fields were recombined using the empirical calibration to reconstruct the third velocity component. The results were later organized on a Cartesian grid with the same grid size as the results of the conventional μPIV, with \(\Updelta x = \Updelta y = 15\,\upmu\hbox{m}\) and \(\Updelta z = 29\,\upmu\hbox{m}\).
2.3 Astigmatism μPTV
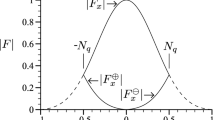
The depth coding of the particle position on the images is achieved by a cylindrical lens in the imaging system. Similar setups were used in previous studies (Chen et al. 2009; Cierpka et al. 2010b). The cylindrical lens for the current investigation had a focal length of \(f_{\rm cyl} = 100\,\hbox{mm}\) and was directly placed in front of the CCD chip (Cierpka et al. 2010a). The curvature of the cylindrical lens only acts in one direction and causes two focal planes in the x and y-axis to be formed. For the setup used here, these planes are separated by \(\Updelta z \approx 45.2\,\upmu \hbox{m}\) in the measurement volume. Particles that are close to one focal plane, e.g. the x-axis focal plane, appear as small and sharp images in that axis. They are now far from the in-focus plane in the y-direction and result in defocused, larger images in the y-axis. Thus, an elliptical image is formed on the CCD sensor, with a small horizontal axis, denoted as a x , and a large vertical axis, denoted as a y . By evaluating the particle image’s width and height, the depth position can be found using a calibration procedure. The position in the xy-plane is determined by a wavelet-based algorithm, which gives reliable results with subpixel accuracy up to high background noise levels (Cierpka et al. 2010b). The ratio between background and signal intensity was below 0.1 for the measurements presented, which results in an error of 0.05 pixels for the in-plane position. This relates to an absolute error of \(0.031\,\upmu\hbox{m}\) in the x-direction and \(0.038\,\upmu\hbox{m}\) in the y-direction. For the final procedure, image preprocessing is applied to the images. First, a sliding minimum over time is subtracted to remove background noise. Smoothing and segmentation filters are then used to highlight regions of possible particle candidates. Based on this initial guess for particle positions, the algorithm determines a x , a y , x, and y in the originally background-subtracted images. For the details of the particle image detection algorithm, the interested reader is referred to Cierpka et al. (2010b).
As for the stereoscopic PIV, the uncertainty of the following results is strongly affected by the accuracy of the calibration. In previous studies, the calibration of the depth position was built on the differences of the axis a x − a y (Chen et al. 2009) or on the ratio a x /a y (Cierpka et al. 2010b). Both methods showed good results in the region between the two in-focus planes but are ambiguous beyond this region. The measurement depth would therefore be limited to the region between the two in-focus planes. Since the particles are rather narrowly distributed in size (\(d_P = 2\,\upmu\hbox{m}, \hbox{standard deviation} = 0.04\,\upmu\hbox{m}\)) and the quality of the fluorescent dye allows for the reliable detection of strongly defocused particles images, it was possible to extend the measurement depth using the values for the axis a x and a y directly. Assuming the particle image is a sum of the tracer particles size, diffraction and defocussing and that all three terms can be approximated by a Gaussian function, the model developed by Olsen and Adrian (2000) can be used to describe the particle image diameter \(a\left({z}\right)\). With the added assumption that the working distance of the lens is significantly larger than z, the particle image diameter can be estimated by the following equation (Meinhart and Wereley 2003; Rossi et al. 2010):
where, d p denotes the particle diameter, λ is the wavelength of the emitted light, n 0 the refractive index of the immersion medium of the lens, and M and \(\hbox{NA}\) the magnification and numerical aperture of the lens, respectively. Equation 2 represents the arc of a hyperbola described by the general formula:
where, F is the position of the in-focus plane. As Eq. 2 also remains valid for the principal axis, when the cylindrical lens is included in the system, the following functions can be introduced to describe the particle image diameters in the x and y-directions:
where, F xz and F yz are the positions of the respective in-focus planes for the x and y-directions, and c 3 and c 6 are additional terms to account for an offset along the ordinate axis. Since the distance between F xz and F yz in physical space is known, the best approximation can be used as a calibration function to relate a x and a y to z. There are certain advantages of this intrinsic calibration. For example, the measurement volume depth is not limited by distance between the in-focus planes of the setup, and the optical path through the different media does not change between calibration and experiment. Furthermore, no complicated scanning procedure is needed and the image preprocessing is the same for calibration and measurement as well. All image aberrations are taken into account and since the calibration is based on all data points, the highest statistical relevance is achieved. A complete explanation of the calibration procedure is given in Cierpka et al. (2011). Knowing the particle position in the volume at two different time instants t and \(t+\Updelta t\) allows for an estimation of the first order approximation of the particles’ velocity. To find matching particles, a simple nearest neighbor PTV algorithm was applied in the 3D space.
The determination of a x and a y was done using an auto correlation-based algorithm. Although very sparse seeding was used, prior to this step each identified region of a possible particle image was checked for overlapping particles. The used criteria were a maximum allowed perimeter of the region where a particle is assumed and, a test, if the center of an identified region belongs to a particle image (i.e. has a higher intensity as the background). For ideal conditions, two of the four values of Eq. 4 are equal and give the depth position of the particles. However, due to small variations in the particle size distribution and the determination of their width and height, the data points scatter around the ideal solution. The determination of z was therefore made by finding the value that minimizes the Euclidean distance between the two measured points a x and a y to the calibration curve. The standard deviation between the estimated particle position \(z_{\rm est}\) and the position given by Eq. 4 gives an impression regarding the uncertainty of a single measurement and was calculated to be \(\sigma (z-z_{\rm est}) = 3.14\,\upmu\hbox{m}\). Using this calibration, the maximum measurement depth was \(104\,\upmu\hbox{m}\). Therefore, the position uncertainty in the depth direction of a single measurement, without traversing, is 6% of the measurement depth. However, for a single measurement, this would result in an uncertainty of about \(15.7\,\hbox{mm/s}\) for the present conditions with a maximum volume depth of \(104\,\upmu\hbox{m}\). A reduction of the volume thickness would decrease this uncertainty significantly. To compare the results, one has to consider that for the cross-correlation; approximately 6–10 particle images should be present in an interrogation area. The data were later interpolated on a Cartesian gird and showed a good convergence of the mean value in one volume element. The difference between the mean values of a certain number i = I of data points that belong to one grid volume and all the data points i = N in the same volume \((\Updelta x = \Updelta y = 10 \,\upmu\hbox{m}, \Updelta z = 10 \,\upmu\hbox{m}), \epsilon_w = \left|\Upsigma\epsilon_{wi=I}/I - \Upsigma\epsilon_{wi=N}/N\right|\) is a measure of convergence. Taking 10 particle images the difference is \(\epsilon_w = 1.4\,\hbox{mm/s}\). The average number of data points that contribute to a grid volume element was 50, which gives a difference of \(\epsilon_w \approx 0.38\,\hbox{mm/s}\). It should be mentioned at this point, that this approach leads to any desired accuracy, as the technique is free of systematic evaluation errors in contrast to PIV. The measurement volume’s depth depends on the microscope’s magnification and the focal length of the cylindrical lens, as well as on the detection level of the camera, the power of the laser, and the quality of the fluorescent dye.
For the study presented here, approximately 50% of the data points are within a span of \(34.5\,\upmu\hbox{m}\), centered at the mid-point between the two focal planes, and 90% fall between a span of \(59.6\,\upmu\hbox{m}\). To cover the whole channel, overlapping data were acquired at eight different z-positions.
For each z-level, around 50,000 valid particle pairs were identified with a simple nearest neighbor algorithm. This gives a valid vector for 65% of the total particle images per frame, which was about 50–80. The 36% loss of pairs is due to the motion of particles out of the measurement volume in all directions, the excluding of overlapping particles in one of the two frames and due to the larger uncertainty for the determination of the position in z-direction. In the current study, a simple nearest neighbor algorithm was used for the tracking step. If a more sophisticated algorithm will be applied, it is supposed that the loss of pairs will significantly decrease. Less particle images per frame occur for the measurements closer to the wall, since a part of the measurement volume was already outside of the channel. The data of all individual particles were filtered by a global histogram filter in order to remove obvious outliers. A local universal outlier detection algorithm for PTV data proposed by Duncan et al. (2010) was additionally used. The authors proposed a weighting of the neighboring values by their distances. The normalized residuum or fluctuation at the position r *0 was set to be lower than 2 for valid data, taking the 10 closest neighboring points into consideration. Rejecting data with a residuum higher than 2 for one of the three velocity components result in an outlier removal of <4%. In total, 390,000 vectors were considered to be valid and were used for the following analysis. The data were then interpolated onto a Cartesian grid with a grid size of \(\Updelta x = \Updelta y = 10\,\upmu\hbox{m}, \Updelta z = 10\,\upmu\hbox{m}\) and 25% overlap. Using this interpolation, approximately 50 single PTV measurements points contribute to the mean at each point in the Cartesian grid. As a measure for the uncertainty of the measurements, the standard deviation of the single measurements \(\hbox{std}\left(u_i-u_{\rm mean}\right)\) can be calculated. However, this quantity is strongly affected by the grid size in regions of high gradients. Therefore, it was evaluated upstream of the step (\(x <-50\,\upmu\hbox{m}\)), where a laminar channel flow profile is present, and v and w have a zero mean, and the scatter of the single PTV data points is purely caused by the measurement technique. The mean standard deviation in that region was \(0.95\,\hbox{mm/s}\) for v and \(3.7\,\hbox{mm/s}\) for w. The uncertainty for the out-of-plane component is 4.9% of \(u_{\infty}\), which is four times higher than for the in-plane component with 1.3% of \(u_{\infty}\).
3 Results
In Fig. 3, slices of the streamwise velocity u are shown for the simulation (top), the S-μPIV (middle), and the A-μPTV (bottom). The flow direction is from left to right. Both 3D measurement techniques show the expected velocity profiles for Poiseuille flow. The velocity is higher upstream of the step and then decreases because of the expansion of the channel. The influence of the channel wall is also clearly visible within the measured channel volume. The influence of the step is not very pronounced in the u-component.
In Fig. 4, the out-of-plane component w is visualized by isosurfaces of w = −4.5 mm/s. In addition, a slice with the streamwise velocity component in the center of the channel is presented. Immediately after the step, the flow goes downward and follows the contour of the step. Upward flow, further downstream from the step, was estimated by the simulation to be at a maximum with \(w = 0.2\,\hbox{mm/s}\) and could not be experimentally resolved. For the measurements with the stereo microscope, a region of downward flow was also found at \(x \approx 400\ldots600\,\upmu\hbox{m}\), which is caused by the fact that the two focal planes do not exactly overlap and therefore an artificial out-of-plane motion is detected by the reconstruction. Nevertheless, the size of the downward flow region is very well captured, whereas it is slightly underestimated by the astigmatic-μPTV technique.
To quantify the overall agreement, the velocity of the flow simulation was interpolated at the grid points of the experimental results. Based on this, the standard deviation of \(u_{\rm exp}-u_{\rm sim}\) is given in Table 1. For the in-plane components, the differences between simulation and results from S-μPIV and A-μPTV are in the same order, but lower by a factor of two than for standard μPIV. For the out-of-plane component, the best agreement can be achieved with the A-μPTV technique. However, a more detailed comparison is possible by using actual velocity profiles. Since the data are sampled on Cartesian grids, where the nodes do not overlap exactly, velocity values for certain coordinate ranges are presented. In Fig. 5, profiles for the streamwise velocity component are shown for the center plane of the channel (\(-11<y<11\,\upmu\hbox{m}\)). In the upper figure, the profile corresponds to a position immediately downstream of the step and in the lower figure, the profile corresponds to approximately two step heights downstream of the step.
The lower velocity in the profile close to the step can be seen in all measurements. However, close to the step, the velocity estimated by the conventional μPIV measurements is underpredicted. This effect is caused by the depth of correlation, since the gradient in that region is very pronounced. Conventional and S-μPIV are highly affected by the depth of correlation if no special precautions are taken (Rossi et al. 2010). For the S-μPIV measurements, special care was given to image preprocessing, which decreases this effect and the profiles match the simulation considerably better in the middle of the channel. Nevertheless, close to the walls, the velocity is overestimated. The A-μPTV approach is not affected by the bias due to depth of correlation and shows consisting results with the numerical simulation. Especially in the regions of high gradients, the results are closer to the numerical simulation, compared to the correlation-based methods. Another advantage of the PTV approach is the spatial resolution in the z-direction, which is not limited by the number of planes used for scanning, as is in both PIV approaches; instead, its limitation is determined by the number of data points acquired. The most challenging task lies in the measurement of the in-plane and out-of-plane components in regions with strong out-of-plane velocity. In Fig. 6, velocity profiles for u and w are shown for a region in the center of the channel, immediately above the step (\(55<z<66\,\upmu\hbox{m}\)). Since the out-of-plane component cannot be measured with conventional μPIV in the same channel, an identical channel with optical access from the y-direction was fabricated. The single pixel PIV technique (Kähler et al. 2006) was used to evaluate the w velocity component with high spatial resolution of \(\Updelta x = \Updelta z = 0.5\,\upmu\hbox{m}\). However, the absolute velocity is underestimated by these measurements. The most likely explanation is the fact that a small difference in the geometry of two micro-channels would result in different flow fields as already pointed out. Nevertheless, the region of the step and the size of the region with downward flow is well predicted. The downward flow is also clearly indicated by both 3D techniques. S-μPIV and A-μPTV both give results that resemble the simulation. The absolute value for the velocity and the size of the region with downward flow are well predicted by both methods. However, for the S-μPIV, a region of upward flow is detected for \(x>150\,\upmu\hbox{m}\). This effect is not physical and is caused by non overlapping focal planes as already mentioned. A compensation by post processing is not possible. The results for the A-μPTV are much more scattered and show values of negative w. Nevertheless, these measurements are closer to the results of the simulation. The larger scatter is caused by the fact that, on average, 50 particles contribute to one data point, whereas for the stereoscopic measurements on average, approximately 11 particles were found in an interrogation window of 64 × 64 pixels. Considering a depth of correlation of 30 μm, this leads to a particle volume concentration of \(c_{SPIV} \approx 6.4 \times 10^{-4} \,\hbox{particles}/\upmu \hbox{m}^3\). For the A-μPTV technique, sparse seeding is required and only around 80 particles are present in a volume of \(10\times10\times10\,\upmu\hbox{m}^3\) (including ≈ 50 valid particle pairs). Dividing this value by the 1,000 frames over which the particles were detected, the final particle concentration is \(c_{SPIV} \approx 8 \times 10^{-5}\) particles/μm3, and thus 8 times lower than for the stereoscopic measurements. The vector yield per frame is for the stereoscopic technique 1 vector in a volume of 15 × 15 × 30 μm3 and thus \(n_{SPIV} \approx 1.5\times 10^{-4} \) vectors/μm3. For the A-μPTV, one gets 0.05 vectors per frame in a volume of \(10\times10\,\upmu\hbox{m}^3\), which results in a vector yield of \(n_{SPIV} \approx 0.5\times 10^{-4}\) vectors/μm3. The total number of vectors in the volume determined by the SPIV method is therefore three times larger than for the A-μPTV method. For the same amount of vectors, one would have to measure twice as long with astigmatism PTV. However, the spatial resolution of the averaged field is increased by 1.5 for the in-plane resolution and a factor of 3 for the out-of-plane resolution. Furthermore, the uncertainty for the in-plane velocity shows similar values for both techniques, whereas the uncertainty of the out-of-plane velocity is slightly lower for the A-μPTV method.
On the lower part of Fig. 6, the streamwise velocity is presented. Conventional μPIV is included as well but shows poor performance in the region above the step. Beyond the step, the velocity is significantly underestimated although the profile was taken at \(z = 60\,\upmu\hbox{m}\). The boundary layer of the bottom wall, prior to the step, cannot be well resolved, and the measured velocity is much too low. S-μPIV performs slightly better but overpredicts the velocity upstream of the step. Nevertheless, beyond the step, the profile matches the simulation quite well. The best match between experiments and simulation upstream of the step is achieved by the A-μPTV although the velocity is slightly underestimated downstream of it.
4 Conclusion and outlook
The following conclusions can be drawn from the analysis:
-
μPIV gives reliable 2D2C results, but in regions of strong gradients (in-plane and out-of-plane direction) and strong out-of-plane motion, the technique fails at providing reliable results.
-
S-μPIV gives reliable 2D3C results, but due to the unavoidable mismatch of the focal planes, systematic errors appear that cannot be compensated digitally. To minimize the error, or at least to know the extent to which the results will be biased, the focus function has to be evaluated for both cameras.
-
By scanning the measurement plane, average 3D3C velocity fields can be estimated with S-μPIV but no instantaneous 3D3C velocity fields can be obtained.
-
A-μPTV provides instantaneous 3D3C velocity information and allows for the study of unsteady volumetric flow phenomena.
-
For A-μPTV, the accuracy of the velocity components in x- and y-direction is not effected by the measurement volume depth and is comparable to correlation-based methods.
-
The uncertainty of the instantaneous out-of-plane velocity estimation by A-μPTV increases with increasing measurement volume depth but, for mean values, it decreases below the corresponding value of the μPIV due to the absence of systematic evaluation errors.
-
An advantage of the A-μPTV technique, compared to the correlation-based methods, is that the results do not suffer from the influence of the depth of correlation and a higher resolution in depth direction can be achieved.
-
Since with longer measurement time the mean distance between the vectors is decreasing for the A-μPTV technique, it is possible to increase the spatial resolution for the average flow fields in all three dimensions. In case of S-μPIV, the spatial resolution cannot be increased by acquiring more images. Thus high gradients are always underestimated.
The analysis indicate that the A-μPTV technique is already a very robust, reliable, and accurate tool for the estimation of 3D3C velocity fields in micro-fluidics. The future potential of the technique lies in the possible extensions:
-
Since the particle positions are known in the whole volume, the particle distribution can be used to reconstruct interfaces between fluids to characterize the mixing process at the micro-scale (Mastrangelo et al. 2010; Rossi et al. 2011).
-
Using time-resolved A-μPTV imaging, the Lagrangian trajectories of the particles can be determined and the complete motion (velocity and acceleration) or the interaction of particles in time and space can be fully reconstructed (Kumar et al. 2011).
-
A-μPTV can be used to determine the full 3D velocity information as well as a scalar distributions such as temperature, ph-value, or pressure fields by combining the underlying imaging technique with particles whose fluorescent emission is a function of these physical properties.
References
Angarita-Jaimes N, McGhee E, Chennaoui M, Campbell HI, Zhang S, Towers CE, Greenaway AH, Towers DP (2006) Wavefront sensing for single view three-component three-dimensional flow velocimetry. Exp Fluids 41:881–891. doi: 10.1007/s00348-009-0737-z
Bown MR, MacInnes JM, Allen RWK, Zimmerman WBJ (2006) Three-dimensional, three-component velocity measurements using stereoscopic micro-PIV and PTV. Meas Sci Technol 17:2175–2185. doi: 10.1088/0957-0233/17/8/017
Chen S, Angarita-Jaimes N, Angarita-Jaimes D, Pelc B, Greenaway AH, Towers CE, Lin D, Towers PD (2009) Wavefront sensing for three-component three-dimensional flow velocimetry in microfluidics. Exp Fluids 47:849–863. doi: 10.1007/s00348-009-0737-z
Cierpka C, Rossi M, Segura R, Kähler CJ (2010a) Comparative study of the uncertainty of stereoscopic micro-PIV, wavefront-deformation micro-PTV, and standard micro-piv. In: 15th Int. Symp. on applications of laser techniques to fluid Mechanics, Lisbon, Portugal
Cierpka C, Segura R, Hain R, Kähler CJ (2010b) A simple single camera 3C3D velocity measurement technique without errors due to depth of correlation and spatial averaging for micro fluidics. Meas Sci Technol 21:045401. doi: 10.1088/0957-0233/21/4/045401
Cierpka C, Rossi M, Segura R, Kähler CJ (2011) On the calibration of astigmatism particle tracking velocimetry (APTV) for microflows. Meas Sci Technol 22:015401. doi:10.1088/0957-0233/22/1/015401
Duncan J, Dabiri D, Hove J, Gharib M (2010) Universal outlier detection for particle image velocimetry (PIV) and particle tracking velocimetry (PTV) data. Exp Fluids 21:057002. doi: 10.1088/0957-0233/21/5/057002
Hain R, Kähler CJ (2006) Single camera volumetric velocity measurements using optical aberrations. In: 12th Int. Symp. on Flow Visualization, Göttingen, Germany
Kähler CJ (2004) The significance of coherent flow structures for the turbulent mixing in wall-bounded flows. DLR Research report, FB 2004-24, ISSN 1434–8454
Kähler CJ, Adrian RJ, Willert C (1998) Turbulent boundary layer investigations with conventional and stereoscopic particle image velocimetry. In: 9th Int. Symp. on applications of laser techniques to fluid mechanics, Lisbon, Portugal
Kähler CJ, Scholz U, Ortmanns J (2006) Uwall-shear-stress and near-wall turbulence measurements up to single pixel resolution by means of long-distance micro-PIV. Exp Fluids 41:327–341. doi: 10.1007/s00348-006-0167-0
Kao HP, Verkman AS (1994) Tracking of single fluorescent particles in three dimensions: use of cylindrical optics to encode particle postition. Biophys J 67:1291–1300
Kumar A, Cierpka C, Williams S, Kähler CJ, W ST (2011) 3D3C velocimetry measurements of an electrothermal microvortex using wavefront deformation PTV and a single camera. Micro Nano 10:355–365. doi:10.1007/s10404-010-0674-4
Lee SJ, Kim S (2009) Advanced particle-based velocimetry techniques for microscale flows. Microfluid Nanofluid 6:577–588. doi: 10.1007/s10404-009-0409-6
Lindken R, Westerweel J, Wieneke B (2006) 3D micro-scale velocimetry methods: A comparison between 3D-μPTV, stereoscopic μPIV and tomographic μPIV. In: 13th Int. Symp. on applications of laser techniques to fluid mechanics, Lisbon, Portugal
Lindken R, Rossi M, Grosse S, Westerweel J (2009) Micro-particle image velocimetry (μPIV): Recent developments, applications, and guidelines. Lab Chip 9:2551–2567. doi: 10.1039/b906558j
Mastrangelo F, Rossi M, Cierpka C, Segura R, Kähler CJ (2010) Reconstruction of the interface between two fluids in microfluidic-mixers using astigmatic particle imaging. In: 2nd European Conference in Microfluidics, Toulouse, France
Meinhart CD, Wereley ST (2003) The theory of diffraction-limited resolution in micro particle image velocimetry. Meas Sci Technol 14:1047–1053. doi: 10.1088/0957-0233/14/7/320
Olsen MG, Adrian RJ (2000) Out-of-focus effects on particle image visibility and correlation in microscopic particle image velocimetry. Exp Fluids 29:S166–S174. doi: 10.1007/s003480070018
Ooms TA, Lindken R, Westerweel J (2009) Digital holographic microscopy applied to measurement of a flow in a T-shaped micromixer. Exp Fluids 47:941–955. doi:10.1007/s00348-009-0683-9
Pereira F, Gharib M (2002) Defocussing digital particle image velocimetry and three-dimensional characterization of two phase flows. Meas Sci Technol 13:683–694. doi: 10.1088/0957-0233/13/5/305
Ragan T, Huang H, So P, Gratton E (2006) 3D particle tracking on a two-photon microscope. J Fluorescence 16:325–336. doi: 10.1007/s10895-005-0040-1
Rossi M, Cierpka C, Segura R, Kähler CJ (2010) On the effect of particle image intensity and image preprocessing on depth of correlation in micro-PIV measurements. In: 15th Int. Symp. on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal
Rossi M, Cierpka C, Segura R, Kähler CJ (2011) Volumetric reconstruction of the 3D boundary of stream tubes with general topology using tracer particles. Meas Sci Technol Under review
Santiago JG, Wereley ST, Meinhart CD, Beebe DJ, Adrian RJ (1998) A particle image velocimetry system for microfluidics. Exp Fluids 25:316–319
Scharnowski S, Hain R, Kähler CJ (2010) Estimation of Reynolds stresses from PIV measurements with single-pixel resolution. In: 15th Int. Symp. on applications of laser techniques to fluid mechanics, Lisbon, Portugal
Sun Y, Duthaler S, Nelson BJ (2004) Autofocusing in computer microscopy: selecting the optimal focus algorithm. Microsc Res Tech 65(3):139–149. doi: 10.1002/jemt.20118
van Hinsberg NP, Roisman IV, Tropea C (2008) Three-dimensional, three-component particle imageing using two optical aberrations and a single camera. In: 14th Int. Symp. on applications of laser techniques to fluid mechanics, Lisbon, Portugal
Wereley ST, Meinhart CD (2010) Recent advances in micro particle image velocimetry. Ann Rev Fluid Mech 42:557–576. doi: 10.1146/annurev-fluid-121108-145427
Willert C, Gharib M (1992) Three-dimensional particle imaging with a single camera. Exp Fluids 12:353–358
Yoon SY, Kim KC (2006) 3D particle and 3D velocity field measurement in a microvolume via the defocussing concept. Meas Sci Technol 17:2897–2905. doi: 10.1088/0957-0233/17/11/006
Acknowledgments
Financial support from Deutsche Forschungsgemeinschaft (DFG) in frame of the priority program SPP 1147 and the research group FOR 856 (Mikropart) is gratefully acknowledged. The authors also would like to thank Stefanie Demming and the Institute for Microtechnology at the Technische Universität Braunschweig for their kind support which is gratefully appreciated.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Cierpka, C., Rossi, M., Segura, R. et al. A comparative analysis of the uncertainty of astigmatism-μPTV, stereo-μPIV, and μPIV. Exp Fluids 52, 605–615 (2012). https://doi.org/10.1007/s00348-011-1075-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00348-011-1075-5