Flow around a NACA0018 airfoil with a cavity and its dynamical response to acoustic forcing

Abstract

Trapping of vortices in a cavity has been explored in recent years as a drag reduction measure for thick airfoils. If, however, trapping fails, then oscillation of the cavity flow may couple with elastic vibration modes of the airfoil. To examine this scenario, the effect of small amplitude vertical motion on the oscillation of the shear layer above the cavity is studied by acoustic forcing simulating a vertical translation of a modified NACA0018 profile. At low Reynolds numbers based on the chord (O(10⁴)), natural instability modes of this shear layer are observed for Strouhal numbers based on the cavity width of order unity. Acoustic forcing sufficiently close to the natural instability frequency induces a strong non-linear response due to lock-in of the shear layer. At higher Reynolds numbers (above 10⁵) for Strouhal number 0.6 or lower, no natural instabilities of the shear layer and only a linear response to forcing were observed. The dynamical pressure difference across the airfoil is then dominated by added mass effects, as was confirmed by numerical simulations.

1 Introduction

Within the European (EU) project (VortexCell2050 2005) a relatively thick wing has been the subject of study. From a structural-strength viewpoint, in order to carry a larger load thick wings are beneficial. However, flow separation will deteriorate the aerodynamic performance of such a wing. Trapping a vortex induced by flow separation is a remedial measure that has already been proposed by Ringleb (1961). The first successful application in a flight experiment was reported by Kasper (1977). However, attempts to reproduce the result of Kasper in a wind tunnel failed (Kruppa 1977). In 1980–1996 Lev Schukin designed an aircraft “EKIP”, in which trapped vortices prevented large-scale separation (US patent No. 5.417.391; Russian patent 14.10.1991, No. 2015941). Theoretical models, such as Bunyakin et al. (1998), Chernyshenko (1995) have shown that vibrations can have a stabilising effect on a flow with a trapped vortex. Optimal control of trapped vortices by suction and blowing at the wall has been considered by Iollo and Zannetti (2001). The effect of placing cavities in a plane wall with an adverse pressure gradient is discussed by Margason and Platzer (1997). These studies did not consider potential coupling of vortex shedding with elastic oscillation modes of the wing. As a first step we consider here the effect of a vertical translational motion of the wing on the flow around a thick wing with a cavity. We consider a cavity with a generic geometry, see Fig. 1, which is not optimised to obtain flow control. The dead water region of the cavity is separated from the main flow by a shear layer. The question is whether oscillations of this shear layer will lock-in to vertical translational oscillations of the wing. We are focussing on the dynamic response of this complex geometry rather than using it for the study of boundary layer separation control.

Fig. 1

Geometry of one of the airfoils with a cavity

The objective of the present paper was to gain insight into the dynamical behaviour of an airfoil with a cavity, by flow visualisations and experimental measurements. One of the airfoils with a cavity is shown in Fig. 1. More details about the airfoils are given in Sect. 2 We will compare the results of experiments with the results for a standard airfoil without cavity, thin airfoil theory, and numerical simulations. Calculation of the unsteady forces on conventional wings, due to rotational and vertical translational motions, has been thoroughly investigated and documented (Theodorsen 1935; Fung 1955). A wing with cavity, however, may show different dynamical behaviour which is not captured by the conventional theories. In this paper, we will focus on both steady flow and a vertical translation motion at low amplitude of the airfoil simulated in the wind tunnel via acoustic forcing. The dynamical behaviour of the airfoils with and without cavities will be investigated using local pressure measurements, flow visualisation and hot-wire anemometry.

A large amount of research has been devoted to rectangular cavities in plane walls. In contrast, not much information is available for the case of a cavity placed in an airfoil. For cavities in plane walls, it is known that a cavity can display a first shear layer instability mode when the Strouhal number, $St_W=\frac{f W} {U_{\infty}}$, is approximately 0.5 (or 1 for the second shear layer mode), where W is the width of the cavity opening, f is the frequency in Hz and $U_{\infty}$ is the free stream velocity (Rockwell and Naudasher 1978, 1979).¹ The cavity may also give rise to a cavity wake mode described by Gharib and Roshko (1987), although this mode is rarely observed in experiments (Gloerfelt et al. 2002; Larchevêque et al. 2007).

Based on the aforementioned literature about cavity flows, we may expect oscillations of the shear layer over the cavity. These oscillations may be enhanced by (and/or couple with) vibrations of the wing, possibly leading to high amplitude oscillatory forces on the wing and a dynamical behaviour very different from that of a conventional wing without cavity. Vibrations of the airfoil are expected to organise the flow in two ways. They are expected to synchronise vortex shedding in the spanwise direction, in particular along sharp edges, such as the trailing edge of the wing and the edges of the cavity. Similarly the vibrations of the airfoil might force the separated shear layer.

Periodic vortex shedding from bluff bodies or cylinders, placed with its axis normal to the flow, has a limited coherence in the spanwise direction. Typically a coherence length of 6 diameters is observed (Blevins 1985). The lateral coherence length of this vortex shedding is increased by an order of magnitude by applying an acoustic field corresponding to a velocity perturbation of the order to 2% of the main flow velocity (Blevins 1985). This lock-in of the vortex shedding is also known to occur as a result of mechanical oscillations of the cylinder (Blevins 1991).

In shallow cavity flow configurations, shear layer instabilities occur, resulting into hydrodynamic oscillations that can qualitatively be described by a feedback loop (Rockwell and Naudasher 1978; Rockwell 1983; Gloerfelt 2009). The pulsation amplitude and coherence of vortex shedding are known to be increased strongly by acoustic feedback due to the presence of an acoustical resonator (Rockwell 1983). In our case we impose acoustic perturbations of the velocity normal to the main flow with amplitudes up to 5% of the main flow velocity. In a similar way as for the cylinder (Blevins 1985) and for deep cavity flows (Rockwell 1983), we expect that this acoustical forcing will trigger the shear layer instability, leading to the formation of coherent vortex structures. This trigger will be uniform in the spanwise direction (along the wing, normal to the main flow direction). Therefore, we expect a two-dimensional model to be fairly accurate for the flow in the cavity. Further, down along the wing and in the wake, turbulence will breakdown the coherent vortical structures and make the flow essentially three dimensional.

In order to achieve Strouhal numbers St _W  = 0.5 or St _W  = 1.0 for the cavities considered here, the reduced frequency $k=\frac{\Upomega c}{2U_{\infty}}$, based on the chord length of the airfoil, should be 7.5 for the first shear layer mode and 15 for the second shear layer mode. Due to these rather high values of the reduced frequency, the oscillations of the shear layer are not anticipated to affect classical wing bending-torsion flutter modes, but they could potentially contribute to undesirable high-frequency structural vibrations.

Using conventional plunging experiments on airfoils, where the airfoil is physically vertically translated with respect to the wind tunnel, it will be difficult to reach high values of the reduced frequency. Therefore, we apply a different method in this paper, where the airfoil is fixed to the wind tunnel and the flow is transversely modulated by an acoustic standing wave, which is driven by loudspeakers. The fundamental difference between oscillating an airfoil in a uniform steady free stream and placing a fixed airfoil in an oscillating free stream is the presence of a uniform time-dependent pressure gradient which drives the oscillating flow. The frequency of the acoustical excitation is chosen in order to maximise the amplitude of the transversal resonant duct mode. At this frequency, the standing wave appears to be reasonably uniform in the spanwise direction. The acoustical pressure distribution is determined from 4 piezo electrical pressure transducers mounted flush on the wall of the wind tunnel. From these measurements, the acoustic velocity transversal to the main flow is calculated.

First, in Sect. 2, the experimental facilities and methods are described. Then, in Sect. 3, flow visualisations at low Reynolds number are presented and compared to numerical simulations of the incompressible Navier–Stokes equations for two-dimensional flow. Hot-wire measurements at low Reynolds number are also presented in this section. Then, in Sect. 4, the experimental data obtained at high Reynolds numbers are described. These consist of local pressure and hot-wire measurements with and without external forcing. Finally, the conclusions are provided in Sect. 5.

2 Experimental methods

In this paper, we will present experimental data obtained in a water channel and a wind tunnel, respectively. This section gives a brief description of these experimental facilities. The airfoils are manufactured out of extruded aluminium and approximate the NACA0018 profile definition within an accuracy of 0.2 mm. All three airfoils have a chord length c = 165 mm and a rounded trailing edge with a radius of 0.5 mm. The standard NACA0018 airfoil is shown in Fig. 2a. The geometry shown in Fig. 2b will be referred to as the airfoil with cavity A, the one in Fig. 2c will be referred to as the airfoil with cavity B. The cavity opening W = 34 mm, which is about 20% of the chord length c. The angle of attack, denoted by α, is defined positive as indicated in Fig. 2a. The cavity shapes considered in this paper are not optimised for trapping a vortex, rather they were optimised for quick manufacturing. The cavities are milled at an angle of 70° with respect to the chord line. The internal shape of the cavity is circular with a radius of 15 mm. Both cavities have the same internal shape; however, cavity A has sharp edges on both the upstream and downstream sides of the cavity, whereas cavity B has a short extension plate at the upstream edge while the downstream edge is rounded with a radius of 4 mm. The geometry of cavity B is designed to approach the generic geometries considered in the VortexCell2050 project.

Fig. 2

Geometries of NACA0018 airfoil without cavity (a), with cavity A (b) and with cavity B (c). The location of pressure transducers is indicated by the arrows (see Table 1). The chord length c = 165 mm and the width of the cavity opening W = 34 mm

In order to measure the pressure at the airfoil surface, the airfoils are equipped with dynamic pressure transducers (Kulites). The location of these transducers is shown in Fig. 2b, c by the arrows. The types of pressure transducers, the mounting locations, are listed in Table 1. The leading edge of the airfoil is located at x/c = 0. The standard airfoil is equipped with pressure transducers at locations 1, 2 and 3. The airfoil with cavity A has pressure transducers at locations 1, 2, 3 and 4. The airfoil with cavity B is equipped with the nine pressure transducers indicated in Fig. 2c.

Table 1 Specification of the pressure transducers and their location x/c for each airfoil

2.1 Water channel

The water channel has a width of 30 cm and a length of 7 m, in which flows with velocities up to 0.25 m/s can be reached. This corresponds to a maximum Reynolds number, based on the chord length, of $4.1\times 10^4$. The airfoil geometry is that of the airfoil with cavity A. The airfoil section has a spanwise width of 150 mm and is bounded at the ends by transparent Plexiglas end plates of dimensions 30 × 20 cm² and a thickness of 5 mm, to minimise end effects and create quasi-two-dimensional flow over the airfoil, see Fig. 3. The upstream edges of the end plates are rounded (circular) to prevent flow separation, and the airfoil is mounted in the middle of the end plates. The airfoil is placed vertically in the water channel at a distance of 1.1 m downstream of the inlet contraction and the water depth is set to 155 mm, such that the free surface just touches the upper end plate, while the other end plate is resting on the bottom of the channel (Fig. 4). This ensures no-slip boundary conditions on both ends of the cavity rather than free-slip at the upper end of the airfoil when it extends above the free water surface. A digital photocamera is mounted above the water surface to capture snapshots of the flow. Dye is injected manually into the cavity. Figure 4 shows a schematic of the setup in the water channel. The flow is illuminated by a horizontal light sheet, which is created by light from two slide projectors that passes through a slit of 3 mm in black paper.

Fig. 3

NACA0018 airfoil with cavity A, mounted in between two perspex end plates

Fig. 4

Side view of the setup in the waterchannel

2.2 Wind tunnel setup

The test facility is a low-speed wind tunnel with a test section with square cross section 500 × 500 mm² and a length of 1,000 mm. The maximum velocity in the test section is 67 m/s, which corresponds to a free stream Mach number of 0.19 at room temperature. The turbulence intensity in the empty test section is less than 0.2% in a frequency range of 0.1 Hz–5 kHz for the velocity range considered here.

In each of the two opposite side walls of the test section, a circular hole with a diameter of 200 mm, covered with fabric, has been made. On the outside of the test section, two loudspeakers (JBL 2206H) are mounted over these holes, one on each side of the test section. The loudspeakers are not fixed to the test section but mounted on an independent rigid aluminium frame. The slit between the test section wall and the strip of the loudspeaker is filled with a 5-mm-thick rim of closed-cell foam. This provides an acoustical seal with a minimum of mechanical contact. The speakers are connected in series and opposite phase, such that both membranes have displacements in the same direction with respect to each other. The speakers are driven by an amplifier (QSC RMX2450) which in turn is driven by a sinusoidal signal from a function generator (Yokogawa FG120). Piezoelectric pressure transducers (either PCB 116A or Kistler 7031) are mounted in the side walls of the test section in order to measure the acoustic field inside the test section. The amplitude of the transversal acoustic velocity in the centre of the wind tunnel v′, is computed from the signals of pressure transducers in the side walls of the wind tunnel.

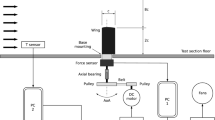
In the middle of the test section, an airfoil can be mounted vertically. The spanwise length of the airfoils is 495 mm such that the aspect ratio is 3. At the spanwise ends, there are small gaps of 2 mm. The angle of attack α can be set with an accuracy of 0.5 deg. For α = 0°, the blockage in the test section is 2%. A sketch of the experimental setup is shown in Fig. 5.

Fig. 5

Sketch of the test section with speakers and airfoil installed. The direction of the main flow is given by the arrow

The function generator is tuned to the first transversal eigenfrequency (f = 331 Hz) of the wind tunnel with the wing installed, creating a transversal standing wave. An important non-dimensional number in acoustics is the Helmholtz number $He=\frac{\pi c}{\lambda}$, with λ the acoustic wavelength. If He ² ≪ 1, the acoustic field around the airfoil is called “compact” and can be locally approximated by an incompressible potential flow. In this case, the airfoil in an acoustically forced flow is expected to be similar to moving the airfoil normal to the main flow in a steady uniform flow. In our experiments, He ² ≈ 0.25, which may not be negligibly small compared to unity. This should be kept in mind when the experimental data are compared to an incompressible flow theory. As already mention in Sect. 1, the main difference between an airfoil in such an acoustically forced flow and a physically vertically translating airfoil in a uniform flow is the presence of a time-dependent pressure gradient. In the experimental data presented in this paper, this pressure gradient contribution has been subtracted to ease comparison with a translating motion of the airfoil.

All signals from the pressure transducers and the signal from the function generator are recorded with a National Instruments data acquisition system (NI SCXI-1000). The data are post-processed using a lock-in method, which allows the extraction of the component of the pressure signal at the excitation frequency and determine its phase. The phase of all the signals is determined with respect to the signal generated by the function generator which is driving the amplifier of the speakers. A Hilbert transform is used to obtain a complex harmonic function from the reference signal.

The value of the reduced frequency k can be varied by adjusting the free stream velocity $U_{\infty}$. For the current setup, reduced frequencies in the range of 2.5 < k < 10 can be obtained. In our measurements, the Reynolds number, $Re_c=\frac{U_{\infty}c}{\nu}$, with ν the kinematic viscosity of the fluid, was varied from $3\times 10^4$ to $7\times 10^5$. Due to the limited sensitivity of the pressure transducers in the wing, unsteady pressures on the wing are only measured in the range $2\times 10^5<Re_c<7\times 10^5$. As we have flow separation at the sharp upstream edge of the cavity, this flow separation in not sensitive to the Reynolds number. For additional details and validation of the method, we refer to Olsman et al. (2010).

3 Low Reynolds numbers ($Re_c\leq 10^5$)

In this section, the results of flow visualisations in the water channel are presented and compared to numerical simulations. Then the results of hot-wire measurements of the shear layer, at low Reynolds number, $Re_c=O(10^4)$, performed in the wind tunnel are discussed. For these Reynolds numbers, the boundary layer flow over the profile is essentially laminar.

3.1 Flow visualisations without external forcing

In order to illustrate the shear layer modes, we performed flow visualisations in the water channel without external forcing at a Reynolds number, $Re_c=2 \times 10^4$. We also compare these flow visualisations with the results of numerical simulations of the incompressible Navier–Stokes equations for two-dimensional flow.

The numerical method is an immersed boundary (IB) projection method described by Taira and Colonius (2007, Colonius and Taira 2008). The solid body of the airfoil is represented on a regular Cartesian grid by a set of discrete forces that are in turn regularised (smeared) on the grid. At these discrete body points, the no-slip condition is exactly enforced. The equations are discretised with a second-order finite-volume method, and a streamfunction-vorticity formulation is used in a staggered grid arrangement. Due to the streamfunction formulation, the divergence-free constraint of the velocity field is exactly satisfied (to machine precision). The immersed boundary treatment gives rise to a first-order error in the momentum equations near the surface of the body; empirical convergence studies presented in Taira and Colonius (2007) show better than first-order accuracy in the L2 norm. Further details regarding the numerical method can be found in the aforementioned references.

Turbulence, and hence the transition to turbulence, cannot be computed using this two-dimensional numerical method. In a real three-dimensional flow, turbulence will cause a dramatic increase in the dissipation, due to the energy cascade from large to small vortical scale. In contrast, enforced two-dimensionality will cause small-scale structures to merge into larger structures (self-organisation of the flow) by the mechanism of the inverse energy cascade.

Figure 6 shows the flow visualisations in the water channel as well as plots of the vorticity obtained from the numerical simulations for angles of attack, α, ranging from −6° to +6°, for NACA0018 with cavity A. The angle of attack is defined positive as indicated in Fig. 2a. Flow visualisations are on the left, and the corresponding vorticity plots from the numerical simulations are on the right. In all the plots, the direction of the flow is from left to right and $Re_c=2\times10^4$. Positive vorticity (counter clockwise rotation) is indicated by red and negative vorticity is denoted by blue.

Fig. 6

Oscillations of the shear layer above the airfoil with cavity A as visible in the flow visualisation experiments in the water channel (left panels) and in the vorticity plots obtained from the numerical simulations (right panels), for $Re_c=2 \times 10^4$ and for various values of α. The levels in the vorticity plots are in the range $-40< \frac{\omega c}{U_{\infty}}<40$ (positive vorticity (counter clockwise rotation) is indicated with red, negative vorticity is indicated with blue)

The agreement between the experiments and simulations is fair. However, in the experiments we can see the actual roll-up of the shear layers, whereas in the numerical simulations we do not see this in much detail. We must note here that the dye in the experiments is a passive tracer while the vorticity shown from the numerical results is not. In the flow visualisations, we observe a transition to turbulence near the trailing edge, especially for high positive angles of attack. This transition to turbulence quickly spreads the dye and diffuses the vortices. Downstream of the trailing edge of the wing, the dye has been spread out by turbulence and we do not recognise any vortices. In the two-dimensional flow numerical simulations, turbulence does not occur and we observe a laminar well-organised flow field even downstream of the trailing edge. In the numerical results, we observe in general two vortices of opposite sign inside the cavity. In the experiments, we observe one of these two vortices clearly, and the second vortex is probably too weak to be identified.

For zero angle of attack, Fig. 6e–h, we observe that the shear layer is switching between the first (Fig. 6e, f) and second (Fig. 6g, h) shear layer mode. We see this for both the experiment and the numerical simulation. However, the first shear layer mode is more violent in the simulation. In the simulation, the vorticity in the cavity is observed to be largely ejected during each cycle of oscillation, which is not apparent in the dye visualisation.

We also conducted numerical simulations of vertically translating airfoils. In the numerical method, the translating motion of the airfoil is simulated as a time-dependent oscillatory velocity, by prescribing the velocity fluxes at the cell interfaces in the entire computational domain. Because the method solves the incompressible Navier–Stokes equations, the Helmholtz number is zero and the forcing is uniform.

We performed these numerical simulations for NACA0018 without cavity, NACA0018 with cavity A and NACA0018 with cavity B, for $\alpha=0^{\circ}, Re_c=2 \times 10^4$ and a forcing amplitude of $v'/U_{\infty}=5 \times 10^{-2}$, with v′ the forcing velocity amplitude in the direction perpendicular to the direction of the free stream velocity $U_{\infty}$. The resulting lift force and pressure differences over the airfoils, at x/c = 0.133 and x/c = 0.49, of these numerical simulations display only minor deviations with respect to Theodorsen’s theory in the range of reduced frequencies 1 < k < 15. This is not surprising because the equivalent translation amplitude relative to the chord length is small $1.5 \times 10^{-3}<\frac{v'}{2kU_{\infty}}<2.5\times 10^{-2}$.

Although we do observe oscillation of the shear layer and vortex shedding from the cavity, it appears from the numerical simulations that the lift force and local pressure differences at x/c = 0.133 and x/c = 0.49 are not significantly affected by these oscillations and vortex shedding downstream of the cavity. The lift force and pressure differences are actually dominated by the added mass of the airfoil. Further details about this can be found in Olsman (2010)

3.2 Hot-wire anemometry at low Reynolds numbers

At low Reynolds numbers ($Re_c\le 10^5$), the boundary layer upstream of the cavity is laminar. The cavity shear layer displays (“natural”) self-sustained oscillations that do not involve an acoustic resonance. The Strouhal number of these oscillations is in reasonable agreement with data from the literature for shallow rectangular cavities in a plane wall at low Mach numbers. Above $Re_c=2\times10^5$, these natural self-sustained oscillations disappear, which is not the behaviour found in the literature for shallow rectangular cavities. Also, the response of the shear layer to external acoustic forcing changes dramatically at that Reynolds number. Below $Re_c=10^5$, the shear layer responds to external forcing. This response is particularly strong when the Strouhal number of the forcing is not too far from the Strouhal number corresponding to the natural oscillations of the shear layer. In that case, one observes “lock-in” which means that the natural oscillations are suppressed and the oscillations at the forcing frequency are strong. Above $Re_c=2\times 10^5$, no non-linear lock-in response to forcing could be detected by the hot-wire. This is a very surprising result in contradiction with other observations on related rectangular cavities. From literature, we would have expected a shear layer mode around St _W  = 0.5, which is not observed for positive angle of attack in the wind tunnel experiments. Whistling modes are observed around St _W  = 1 or higher Strouhal numbers, which have frequencies close to the transverse resonance frequencies of the test section. This therefore deserves further research.

At low velocities corresponding to the Reynolds number of the numerical simulations and water channel experiments ($Re_c=O(10^4)$), pressure transducers are not sensitive enough to detect flow fluctuations. We use hot-wire anemometry in a wind tunnel order to allow measurements at these low flow velocities.

The hot-wire probe (one-dimensional Dantec P5511, wire thickness 5 μm) can be used for velocities above 1 m/s. Our probe is fixed to the bottom of the test section, as shown in the schematic drawing in Fig. 7. The probe holder consists of a small tube with a diameter of 6 mm and a length of 200 mm, which is reinforced at the rear by means of a copper plate of 2 mm thickness and 20 mm width. The hot-wire is located at 200 mm from the bottom wall of the test section.The tube with the copper plate is fixed to the bottom of the test section, such that the copper plate at the rear is aligned along the flow direction. Inside the tube, a narrower tube is fitted, which holds a small construction in which the hot-wire is mounted horizontally. The narrower tube can rotate inside the wider tube, which allows the positioning of the hot-wire with an accuracy of 1 mm. The hot-wire is positioned at 145 mm up from the bottom of the test section. The position of the hot-wire will be given in a coordinate system fixed to the airfoil, with the origin at the upstream edge of the cavity and the x-axis parallel to the chord line, see Fig. 8. The position of the hot-wire probe is made non-dimensional with the width of the cavity opening W. The upstream edge is at the origin while the downstream edge of the cavity is located close to (x/W, y/W) = (1, 0). The difference between the downstream edge of the cavity and (x/W, y/W) = (1, 0) is due to the fact that the line joining the edges of the cavity is not exactly parallel to the chord line.

Fig. 7

Sketch of the hot-wire mounting inside the test section

Fig. 8

Definition of the coordinate system used for the positioning of the hot-wire

All hot-wire signals are recorded with a data acquisition system (National Instruments) at a sampling frequency of 12 kHz. The time signals are post-processed with a Fast Fourier Transform, using averaging over windows, with 50% overlap and on every window a Hanning window is applied. The width of the windows is approximately 1.3 s and a total of 150 windows are typically used for the averaging.

Here, we present measurements taken on the airfoil with cavity A, see Fig. 2b. The hot-wire is positioned just upstream of the downstream edge of the cavity. The largest flow oscillations of the shear layer are expected close to the downstream edge of the cavity. Figure 9 shows the time-averaged velocity profile over the shear layer for α = +5° and $Re_c=3.3 \times 10^4$. The magnitude of the velocity is made non-dimensional with the free stream velocity $U_{\infty}$. The free stream velocity $U_{\infty}$ is measured for α = 0° with the hot-wire positioned at $(\frac{x}{W},\frac{y}{W})=(1.7,1.8)$. We see that the shear layer has an approximate thickness of 0.1W≈3 mm and that the air inside the cavity is almost stagnant.

Fig. 9

Measured mean velocity profile across the shear layer over cavity A as a function of y/W, for $Re_c=3.3 \times 10^4, \alpha =+5^{\circ}$. Since the hot-wire moves in a circular path, the position x/W is not constant, 0.7 < x/W < 0.93

We need to be careful in interpreting the hot-wire signal because the hot-wire measures the absolute value of the velocity in the direction perpendicular to the wire. A purely sinusoidal time dependence of the velocity around zero at a frequency f would result in a hot-wire signal with a fundamental frequency at 2f. At the outer edge of the shear layer, this problem does not occur because the velocity never vanishes, due to the contribution of the main flow. We expected problems at the inner cavity side of the shear layer. However, for all the measurement locations within the shear layer of Fig. 9, we observed only one dominant peak in the frequency domain. Even at the inner side of the shear layer, we did not observe a frequency doubling. We therefore conclude that the measured frequency is the actual oscillation frequency of the shear layer.

At a Reynolds number of $Re_c=3.3 \times 10^4$, we observe a signal typical for a laminar flow, with distinct peaks in the frequency domain. Such natural hydrodynamic instability is commonly observed in shallow cavities (Rockwell and Naudasher 1978; Gloerfelt 2009). Figures 10, 11, 12, 13, and 14 show a short sample of the hot-wire signal (on the left) and the corresponding averaged power spectrum (on the right) for different values of the angle of attack α. On the upper horizontal axis of the frequency domain plots, the Strouhal number St _W is plotted. The magnitude of the velocity is made non-dimensional with the free stream velocity $U_{\infty}$, and time is made non-dimensional with the ratio of the free stream velocity and the chord length c of the airfoil. At each angle of attack, the hot-wire position is such that $0.2\leq \overline{|\mathbf{u}|}/U_{\infty}\leq 0.7$, which ensures that the hot-wire is inside the shear layer. For α = +5°, in Fig. 11, also the hot-wire signal and power spectrum are shown with an acoustic forcing of $v'/U_{\infty}=2.5 \times 10^{-2}$.

Fig. 10

Time and frequency domain data for the airfoil with cavity A at $Re_c=3.3 \times 10^4$ and α =  +10°. Hot-wire position: (x/W, y/W) = (0.66, 0.20). No acoustic forcing

Fig. 11

Time and frequency domain data for the airfoil with cavity A at $Re_c=3.3 \times 10^4$ and α =  +5°. Hot-wire position: (x/W, y/W) = (0.89,  −0.0094). Without (unforced) and with an acoustic forcing of $v'/U_{\infty}=2.5 \times 10^{-2}$ (forced). The peaks at 51 and 78 Hz correspond to St _W  = 0.6 and St _W  = 0.9, respectively

For α =  +10° (Fig. 10), no peak in the spectrum is present and the time signal oscillates in a larger range from $\overline{|\mathbf{u}|}/U_{\infty}\approx 0.2$ up to $\overline{|\mathbf{u}|}/U_{\infty}\approx 0.7$. Most likely the flow separates upstream of the cavity and is turbulent at the position of the hot-wire. At α =  +5° (Fig. 11), a clear narrow peak in the spectrum at 51 Hz is observed. This corresponds to a Strouhal number based on the width of the cavity opening of $St_W=\frac{fW} {U_{\infty}}=0.6$, which indicates the presence of the first shear layer mode. We also observe a lower peak at 78 Hz, corresponding to St _W  = 0.9, which might corresponds to the second shear layer mode. With the acoustic forcing switched on, a large peak at the forcing frequency of 332 Hz appears, but no clear peak appears at the second harmonic of the forcing frequency at 664 Hz. A peak at the second harmonic would indicate non-linear effects, such as the roll-up of the shear layer. With forcing, the peaks at the natural oscillation frequencies 51 Hz and 78 Hz remain. Also, the hot-wire signals with and without acoustic forcing are very similar (Fig. 11a). These are all indications that the shear layer only responds linearly to the acoustic forcing, which might be due to the low Reynolds number and the correspondingly thick shear layer. An alternative, more plausible, explanation is that the forcing Strouhal number, St _W  = 3, is too high compared to the modes of the cavity flow. This is confirmed by the measurements of the amplitude dependency of the response, which will be discussed later. As shown in Fig. 12, for α = 0° we also observe two peaks, respectively at 53 and 83 Hz (St _W  = 0.6 and St _W  = 0.9); however, now the peak at 83 Hz is dominant. As shown in Figs. 13 and 14, for α = −5° and α = −10° the dominant peaks are located around 80 Hz, which corresponds to St _W  = 0.9.

Fig. 12

Time and frequency domain data for the airfoil with cavity A at $Re_c=3.3 \times 10^4$ and α = 0°. Hot-wire position: (x/W, y/W) = (0.92,  −0.045). No acoustic forcing. The peaks at 53 and 83 Hz correspond to St _W  = 0.6 and St _W  = 0.9, respectively

Fig. 13

Time and frequency domain data for the airfoil with cavity A at $Re_c=3.3 \times 10^4$ and α = −5°. Hot-wire position: (x/W, y/W) = (0.93,  −0.054). No acoustic forcing. The peak at 80 Hz corresponds to St _W  = 0.9

Fig. 14

Time and frequency domain data for the airfoil with cavity A at $Re_c=3.3 \times 10^4$ and α = −10°. Hot-wire position: (x/W, y/W) = (0.95,  −0.077). No acoustic forcing. The peak at 76 Hz corresponds to St _W  = 0.9

For α < 0° only the second shear layer mode is present. For α ≥ 0° two peaks appear, which could be due to a mix of the first and second shear layer mode.

We now increase the Reynolds number at fixed angle of attack, α = +5°, and show the hot-wire signal and power spectra with and without acoustic forcing. Figure 15 shows the hot-wire signal and power spectrum at $Re_c=6.3 \times 10^4$ without acoustic forcing and with an acoustic forcing of $v'/U_{\infty}=2.5 \times 10^{-2}$ and f = 332 Hz. Without acoustic forcing a low peak at 108 Hz is observed and a high peak at 270 Hz, corresponding to St _W  = 0.6 and St _W  = 1.6, respectively. The subsequent peaks are higher harmonics of the peak at 270 Hz. With the acoustic forcing switched on, the peaks at 108 and 270 Hz (and the higher harmonics) disappear and peaks at the forcing frequency of 332 Hz and its higher harmonics (664 Hz) appear. Also, a peak at the first subharmonic appears at 166 Hz. An example of a non-linear effect causing a subharmonic (period doubling) is the periodic alternation between injection and subsequent ejection of a vortex. The alternating injection and subsequent ejection of a vortex is repeated periodically, resulting into period doubling. This behaviour is illustrated by the numerical simulations of (Hofmans 1998) (page 178, Fig. 6.28). Here, the shear layer clearly locks in at the forcing frequency at St _W  = 2.0. Also, the hot-wire signals are different. With the acoustic forcing switched on, the velocity fluctuations are more irregular. At this Reynolds number ($Re_c=6.3 \times 10^4$) the lock-in of the shear layer to the forcing frequency occurs even for extremely low forcing amplitudes, such as $v'/U_{\infty}=3.5 \times 10^{-4}$. In the spectrum with acoustic forcing, there also appears a peak at 4 Hz (not shown), which is likely to be a global oscillation of the entire wind tunnel flow.

Fig. 15

Time and frequency domain data for the airfoil with cavity A at $Re_c=6.3 \times 10^4$ and α = +5°. Without (unforced) and with an acoustic forcing of $v'/U_{\infty}=2.5 \times 10^{-2}$ (forced). Hot-wire position: (x/W, y/W) = (0.89,  −0.0094). The peaks in the spectrum without acoustic forcing at 108 and 270 Hz correspond to St _W  = 0.6 and St _W  = 1.6, respectively

Figure 16 shows the time signal and power spectrum at α = +5° and $Re_c=1.0 \times 10^5$. The data are shown without acoustic forcing and with an acoustic forcing of $v'/U_{\infty}=1.4 \times 10^{-3}$. Here, also the peak at 4 Hz is present, both with and without acoustic forcing. This means the peak at 4 Hz is independent of the velocity, which is in agreement with the assumption that this is a global oscillation of the wind tunnel. Without acoustic forcing, we also observe two frequencies of the shear layer, a low peak at 460 Hz and a high peak at 915 Hz, which correspond to St _W  = 1.7 and St _W  = 3.4, respectively. With acoustic forcing, we again observe high peaks at the forcing frequency of 332 Hz and its higher harmonics. We do not observe a subharmonic at 166 Hz. The peaks at 460 and 915 Hz have disappeared. The shear layer response to the acoustic forcing is stronger compared to the case of $Re_c=6.3\times 10^4$. This is due to the fact that the Strouhal number of the forcing St _W  = 1.2 is now close to the natural cavity mode St _W  ≈ 1. If we compare Figs. 15a, 16a, we observe that the flow oscillations are much larger for $Re_c=1.0\times 10^5$, while the forcing amplitude is lower.

Fig. 16

Time and frequency domain data for the airfoil with cavity A at $Re_c=1.0 \times 10^5$ and α = +5°. Without (unforced) and with an acoustic forcing of $v'/U_{\infty}=1.4 \times 10^{-3}$ (forced). Hot-wire position: (x/W, y/W) = (0.93,  −0.044). The peaks in the spectrum without acoustic forcing at 460 and 915 Hz correspond to St _W  = 1.7 and St _W  = 3.4, respectively

When the shear layer locks in at the forcing frequency, we expect the Fourier coefficient of the hot-wire signal at the forcing frequency to be independent of the forcing amplitude. This is due to the saturation of the shear layer response. The acoustic forcing only triggers the shear layer instability. In Fig. 17, the shear layer response at the forcing frequency, determined by a lock-in procedure, is plotted as a function of the forcing amplitude. The response at the forcing frequency and the plunging velocity amplitude is made non-dimensional with the free stream velocity $U_{\infty}$. We see that for $Re_c=3.3\times 10^4$ the response is nearly linear, which means that there is no lock-in with the natural shear layer oscillation modes. However, at $Re_c=6.3\times 10^4$ and $Re_c=1.0\times 10^5$, the shear layer response shows a very different behaviour. For $v'/U_{\infty}<10^{-2}$, the response is at least an order of magnitude larger compared to the case of $Re_c=3.3\times 10^4$ and does not grow linearly with the forcing amplitude. This confirms that the signal is due to a lock-in of the shear layer oscillation to the acoustic forcing. Because the forcing frequency is fixed in our experiments (first transversal mode of the test section), we cannot discern whether the difference in receptivity of the shear layer is due to an increase in the Reynolds number Re _c or a decrease in the Strouhal number St _W . We suspect here that the Strouhal dependency is dominant for $Re_c\leq 10^5$.

Fig. 17

Shear layer response as a function of the forcing amplitude $v'/U_{\infty}$ for three values of the Reynolds number Re _c , based on the chord length. The response at St _W  = 3.8 is linear, in contrast to the strong non-linear response at St _W  = 1.2 and St _W  = 2.0

Similar distinction between “stable, lightly damped” (linear) oscillation and “self-sustained-oscillation” (strong lock-in) is observed by Rowley et al. (2006).

The strong response of the shear layer to the forcing is expected to be due to the fact that the excitation frequency at $Re_c=6.3\times10^4$ is close to a natural instability mode of the cavity, which is observed without excitation. The change in Re _c from $3.3\times10^4$ to $6.3\times 10^4$ has only a minor effect on the boundary layer thickness and does not induce the transition to turbulence in the boundary layer. Therefore, this change in boundary layer thickness cannot explain the strong difference in coupling between the shear layer and the imposed acoustical oscillation. This is similar to the effect of vibration on vortex shedding in the wake of a cylinder. Lock-in between the elastic oscillation and vortex shedding only occurs if the natural Von Karman shedding frequency is close to the vibration frequency (Blevins 1991). Hence, we do not expect a strong Reynolds number dependency, and the drastic change in shear layer response is expected to be a Strouhal number effect. For a more firmly established conclusion, experiments should be carried out with different chord lengths of wind tunnel widths. This allows the Reynolds number and Strouhal number to be varied independently.

The measurement presented in this section has also been taken for the airfoil with cavity B. The results of these experiments are similar to the results presented in this section, obtained for cavity A.

From the snapshots, such as the ones shown in Fig. 6e–l, we can estimate the hydrodynamic wavelength, $\Uplambda$, which is the distance between the vortices appearing close to the airfoil surface downstream of the cavity. The hydrodynamic wavelength is made non-dimensional with the width of the cavity opening W. For the first shear layer mode, we expect $\Uplambda/W\approx 1.0$ while $\Uplambda/W\approx 0.5$ for the second shear layer mode. The estimated values of the ratio $\Uplambda/W$ are listed in Table 2. For the calculation of $\Uplambda/W$ from the hot-wire experiments, we assumed a convective velocity of $0.5U_{\infty}$. The agreement between the estimates from experiments and numerical results of $\Uplambda/W$ is good for positive angles of attack. However, for negative angles of attack, the numerical solutions display a first shear layer mode, while the experiments show the second shear layer mode.

Table 2 Ratios of the hydrodynamic wavelength over the width of the cavity opening, $\Uplambda/W$

4 High Reynolds numbers ($Re_c>10^5$)

In the present section, the results at higher Reynolds number ($Re_c>10^5$) are presented. We will present measurements of the time-averaged pressure coefficient at the airfoil surface, hot-wire measurements in the shear layer and experimental data on the unsteady difference in local pressure coefficient.

4.1 Measurements of the pressure coefficient

The time-averaged surface pressures are measured for different values of the angle of attack, without acoustic forcing. Plots of the time-averaged pressure coefficient, $C_p=\frac{2(p-p_{\infty})} {\rho U_{\infty}^2}$, with ρ the density and $p_{\infty}$ the free stream pressure, are shown in Fig. 18a–c as a function of the angle of attack α, for $Re_c=4.4 \times 10^5$. The pressure coefficient was measured at four locations, the leading edge, the lower and upper surface at 13.3% of the chord downstream of the leading edge and for the airfoils with cavity the pressure inside the cavity was measured (these correspond to locations 1, 2, 3 and 4, indicated in Fig. 2c).

Fig. 18

Experimental values of the time-averaged pressure coefficient C _p as a function of the angle of attack, α, for NACA0018 (squares), NACA0018 with cavity A (circles) and NACA0018 with cavity B (triangles) at different locations on the airfoil surface. $Re_c=4.4 \times 10^5$. The locations of the pressure transducers are indicated by the numbers in the legend, which correspond to the numbers in Fig. 2; Table 1

The pressure coefficients at the leading edge, as shown in Fig. 18a, show only small differences between the three airfoils. While cavity B displays a shift in the stagnation point towards positive angles, it is, however, remarkable that for NACA0018 with cavity A the pressure coefficient, starting from α = 0°, both in positive and negative directions, first increases and then decreases. This might indicate a non-monotonous change in the location of the stagnation point, which is not easily explained. For α < −16° or α > 16° the pressure coefficient of NACA0018 with cavity A displays a sharp increase, which indicates separated flow.

On the upper surface, Fig. 18b, the curves of NACA0018 with cavity B display lower values of the pressure coefficient compared to the airfoil with cavity A or without cavity. Note that the upper side of the airfoil corresponds to the suction side of the airfoil for positive angles of attack. The curves all display an increase in pressure for α > 12°, which is due to flow separation.

The pressure coefficient on the lower surface of NACA0018 with cavity A and B, Fig. 18c, displays significantly lower values compared to the airfoil without cavity. This is especially true for negative angles of attack, which corresponds to the suction side of the airfoil. For α < −12° the pressures increase, again due to flow separation.

Figure 18d shows the values of the pressure coefficient inside the cavity for NACA0018 with cavity A and B. At this location, no significant deviations are observed between the two different cavity geometries.

It is worth mentioning that the time-averaged pressure coefficients measured with the acoustic forcing switched on yield virtually the same time-averaged values as obtained without the acoustic forcing.

Based on the flow visualisations and low Reynolds number simulations, we expect vortex shedding downsteam of the cavity, see Sect. 3.1 We attempt to detect this periodic vortex shedding from the cavity by cross-correlating the time signals of the local surface pressure downstream of the cavity, pressure transducers 5, 6 and 7 in Fig. 2c. The cross-correlation of these time signals obtained from the numerical simulations of the flow around the airfoil with cavity A yields clear sinusoidal signals as a function of the time lag, with a clear dominant correlation peak with a height of 0.7 at a convective velocity of 63% of the free stream velocity.

The airfoil with cavity B is equipped with three pressure transducers downstream of the cavity. Cross-correlation of the time signal from these pressure transducers, however, does not yield a clear signal as a function of the time lag, for $2 \times 10^5<Re_c<5\times 10^5$. Only at α = 15°, a single peak with a height of 0.1 in the cross-correlation is present, which yields a convective velocity of 75% of the free stream velocity. The appearance of a single peak may be an indication of turbulence that is convected downstream. A periodic vortex shedding would result in an oscillating cross-correlation as a function of the time lag. Only a single peak is no indication of periodic vortex shedding.

4.2 Hot-wire anemometry at high Reynolds numbers

Figures 19 and 20 show the frequency spectra of the hot-wire signals for $Re_c=2.0 \times 10^5$ and $Re_c=4.4 \times 10^5$ and α = +5°. Both results without acoustic forcing and with acoustic forcing are shown.

Fig. 19

Frequency spectrum for the airfoil with cavity A at $Re_c=2.0 \times 10^5$ and α = +5°. Without (unforced) and with an acoustic forcing of $v'/U_{\infty}=1.8 \times 10^{-2}$ (forced). Hot-wire position: (x/W, y/W) = (0.89,  −0.0094)

Fig. 20

Frequency spectrum for the airfoil with cavity A at $Re_c=4.4 \times 10^5$ and α = +5°. Without (unforced) and with an acoustic forcing of $v'/U_{\infty}=1.0 \times 10^{-2}$ (forced). Hot-wire position: (x/W, y/W) = (0.95,  −0.055)

For both Reynolds numbers, we observed low frequency peaks in the spectrum (not shown) which correspond to the blade passing frequency of the fan of the wind tunnel. For $Re_c=2.0\times 10^5$, these peaks are located at 13 and 21 Hz. In the spectrum for $Re_c=4.4\times 10^5$, these peaks are at 26, 53 and 105 Hz.

The hot-wire signals with and without acoustic forcing are similar except for a peak at the forcing frequency of 332 Hz. Additionally, there is a high peak at 358 Hz and a low peak at 316 Hz, for $Re_c=4.4 \times 10^5$. The appearance of these secondary peaks is caused by amplitude modulation of the signal with the oscillation at 26 Hz. For $Re_c=2.0 \times 10^5$, we also observe these secondary peaks near the forcing frequency.

For $Re_c=2.0 \times 10^5$ the Strouhal number of the acoustic forcing St _W  = 0.6 and for $Re_c=4.4 \times 10^5$ this is St _W  = 0.3. The Strouhal number St _W is not far removed from the expected first natural hydrodynamic mode of the cavity. However, in both cases we do not observe natural oscillations of the shear layer nor do we observe a strong lock-in response of the shear layer with the acoustic forcing. For $Re_c=2.0\times 10^5$, we do observe a generation of higher harmonics of the forcing frequency (Fig. 19). These higher harmonics are, however, lower than the fundamental by at least one order of magnitude. We do observe a low natural peak at St _W  = 5 for $Re_c=2.0 \times 10^5$ and a low natural peak at St _W  = 2.9 for $Re_c=4.4 \times 10^5$. The origin of these peaks remains an open question.

4.3 Measurements of the local unsteady pressure difference

In the preceding section, we have presented hot-wire measurements. In order to get an indication of the unsteady lift force on the airfoils, we will measure unsteady local surface pressures. Linearised potential flow theory as described by Theodorsen (1935), Fung (1955) shows that the local pressure difference at 13.3% of the chord downstream of the leading edge provides a good indication of the lift force. We will refer to the linearised potential flow theory for a flat plate as “Theodorsen’s theory” in this section. All the experimental results presented in this section have been corrected for the presence of the time-dependent pressure gradient to enable direct comparison with Theodorsen’s theory.

4.3.1 NACA0018 with cavity A

With the acoustic forcing, the pressure difference over the airfoil was measured using pressure transducers 1 and 3. From these pressures, a non-dimensional pressure difference was computed which is presented in the frequency domain as an amplitude and corresponding phase. This non-dimensional pressure difference is given by

$$ \Updelta C_{pu} = \frac{2(p_1-p_3)}{\rho U_{\infty} v'}. $$

(1)

Here, ρ is the density. The extra underscript u is used to emphasise that this is a difference in unsteady pressure coefficient.

Figure 21a, b display the amplitude and corresponding phase, respectively, for the airfoil without cavity and the airfoil with cavity A. The angle of attack is zero and the forcing amplitude $\frac{v'}{U_{\infty}}$ varies from $6.5 \times 10^{-3}$ to $97 \times 10^{-3}$. The solid line with open square markers shows the experimental results for NACA0018 without cavity, the results of NACA0018 with cavity A are shown by the dashed line with open squares and the dotted line shows the result of Theodorsen’s theory. Only small deviations are observed between NACA0018 without cavity and NACA0018 with cavity A. The main difference is a steeper increase in $|\Updelta C_{pu}|$ as a function of k for NACA0018, compared to NACA0018 with cavity A. This is most likely due to a difference in added mass between the two airfoils. We should note here that Theodorsen’s theory is an incompressible theory which corresponds to He ² = 0 and in our experiments He ² ≈ 0.25. The effect of a finite Helmholtz number is to increase the amplitude of $\Updelta C_{pu}$ and to lower the phase, with respect to Theodorsen’s theory (Olsman et al. 2010). Further deviations are expected due to viscous effects and complex wake structures, which are neglected in the theory of Theodorsen.

Fig. 21

Experimental $\Updelta C_{pu}$ values at x/c = 0.133, as a function of the reduced frequency k, for NACA0018 without cavity (squares) and NACA0018 with cavity A (circles) and the result of Theodorsens theory (dotted line). α = 0° and $1.9 \times 10^5 < Re_c < 7.8 \times 10^5$

Similar measurements as shown in Fig. 21a, b have been taken for difference angles of attack and different forcing amplitudes. These measurements revealed no significant deviation with respect to the results shown in Fig. 21a, b.

4.3.2 NACA0018 with cavity B

Figure 22a, b show the results of the measurement with acoustic forcing for NACA0018 with cavity B. Again these results do not indicate any significant deviations compared to the results obtain with the clean airfoil and the airfoil with cavity A. The values of $\Updelta C_{pu}$ were also computed from the signals from transducers located at 9 & 5 and 8 & 7. Figure 23a, b display the amplitude and corresponding phase of $\Updelta C_{pu}$ as a function of the reduced frequency, at x/c = 0.490 for α = 0°. In Fig. 24a, b the amplitude and corresponding phase of $\Updelta C_{pu}$ are shown as a function of the reduced frequency, at x/c = 0.851 and α = 0°. These measurements yield similar graphs as Fig. 22a, b and are close to the results of linearised potential flow theory for a flat plate.

Fig. 22

Experimental amplitude and corresponding phase of $\Updelta C_{pu}$ at x/c = 0.133, as a function of the reduced frequency k, for the airfoil with cavity A (circles), the airfoil with cavity B (triangles) and the result of Theodorsen’s theory (dotted line). $\alpha=0^{\circ}, 1.8 \times 10^5 <Re_c< 7.8 \times 10^5$ and the forcing amplitude $6.5 \times 10^{-3} \leq v'/U_{\infty}\leq 73 \times 10^{-3}$

Fig. 23

Experimental amplitude and corresponding phase of $\Updelta C_{pu}$ at x/c = 0.490, as a function of the reduced frequency k, for cavity B for $\alpha=0^{\circ}, 1.8 \times 10^5 <Re_c< 7.8 \times 10^5$ and a forcing amplitude $2.5 \times 10^{-2} \leq v'/U_{\infty}\leq 18.6 \times 10^{-2}$

Fig. 24

Experimental amplitude and corresponding phase of $\Updelta C_{pu}$ at x/c = 0.851, as a function of the reduced frequency k, for cavity B for $\alpha=0^{\circ}, 1.8 \times 10^5 <Re_c< 7.8 \times 10^5$ and a forcing amplitude $2.5 \times 10^{-2} \leq v'/U_{\infty}\leq 18.6 \times 10^{-2}$

Based on the experimental results presented in the previous sections, we conclude that in the range of reduced frequencies tested, the pressure differences over the airfoils are dominated by the added mass effect of the airfoil.

5 Conclusions

Flow visualisations, numerical simulations and wind tunnel measurements have been presented for three different airfoils, one without cavity and two with a different cavity geometry (A and B). Results with and without acoustic forcing have been described. The presence of periodic vortex shedding was identified by flow visualisations, numerical simulations of the Navier–Stokes equations for two-dimensional flow and hot-wire measurements.

Experiments at low Reynolds numbers ($Re_c\leq 10^5$) show natural oscillations of the shear layer across the cavity in a NACA0018 airfoil that correspond mainly to the second hydrodynamic mode St _W ≈ 1 and are close to the first transversal transversal acoustic resonance frequency of the wind tunnel test section. An exception to this is that at zero angle of attack, both the first (St _W ≈ 0.5) and the second (St _W ≈ 1) hydrodynamic mode appear intermittently.

Upon acoustically forcing the shear layer, one finds a linear response of the shear layer for St _W  = 3.8, while for St _W  = 2.0 and St _W  = 1.2 we observe a strongly non-linear response, indicating a lock-in of the shear layer at the forcing frequency.

At higher Reynolds numbers ($Re_c>10^5$), we do not observe, for positive angle of attack, natural oscillations of the shear layer, nor does the shear layer respond non-linearly to the acoustic forcing. This is most unexpected and deserves further research.

The influence of the cavity on the time-averaged pressure coefficient is most prominent at the suction side of the airfoil for negative angles of attack. Here, the pressure coefficient of NACA0018 with cavity B attains a lower value compared to NACA0018 and NACA0018 with cavity B attain even lower values compared to NACA0018 with cavity A.

Measurements of the local unsteady difference in pressure coefficient do not show significant deviations between the airfoil with cavity A and the airfoil without cavity. The deviations observed between the experimental data and linearised potential flow theory are partially due a relatively large value of the Helmholtz number in the experiments He = 0.5. Comparison of experimental data of the airfoil with cavity A with the results obtained for the airfoil with cavity B yields very similar results. Numerical simulations at low Reynolds number for a vertically translating airfoil yield nearly identical results for the local pressure differences over the airfoil and the lift force, for NACA0018 and NACA0018 with cavity A and B.

For the case of a vertically translating airfoil, placement of a cavity of the dimensions and geometry described in this paper does not display a significant deviation in the local unsteady pressure differences and lift force compared to the same airfoil without cavity or linearised potential flow theory for a flat plate, in the range of reduced frequencies 2.5 < k < 11. The lift forces and pressure differences across the airfoil are mainly determined by the effect of the added mass of the airfoil.