Full 3D-3C velocity measurement inside a liquid immersion droplet

Abstract

We describe a tomographic PIV system for the measurement of the internal flow in a droplet over a stagnant and a moving surface. The flow condition is representative of the flow in an immersion droplet applied in a liquid immersion lithography machine. We quantify the accuracy and reliability of the measurements and compare the shape of the reconstructed measurement volume to shape measurements by means of shadowgraphy. First results indicate the internal flow pattern near the receding contact line, showing a small recirculation region.

1 Introduction

In semiconductor fabrication, immersion lithography has been considered as a means to further improve the spatial resolution. By replacing the air (${n}_{\rm air}\approx\,1.0$) in the gap between a lens and an object (a silicon wafer) with water (${n}_{\rm water}\approx$ 1.44) for 193 nm UV light, the optical resolution in the image plane is enhanced (French and Tran 2009). The spatial resolution is given by $\delta\,=\,k\lambda/\hbox{NA}$ where k is the process coefficient with k ≃ O (1), λ the light wavelength, and NA the numerical aperture of the lens, $\hbox{NA}\,=\,{n}\cdot\sin\theta$, where θ is the half viewing angle. Current immersion systems can improve the resolution quality down to the order of tens of nanometers (Mulkens et al. 2004; Owa and Nagasaka 2008), which is an enhancement of about 30–40%.

Besides the advantage of higher optical resolution, immersion lithography also poses a couple of difficulties and challenges. In semiconductor production, usually the substrate (wafer) is moved underneath the optical lithographic lens. The biggest challenge then is to keep the liquid phase uniform without defects. With speeds in the range of 1 m/s, the main concerns for wafer defects are (1) water left behind (watermarks) and (2) a loss of resist-water adhesion (air gap) and bubble entrainment at the leading edge of the immersion droplet. To further increase yield, manufacturers of lithographic immersed-lens scanners wish to increase the wafer speed even further. Schuetter et al. (2006) studied the transitions of the dynamic contact angle for the immersion droplet until the maximum substrate speed, about 0.4 m/s, where the droplet starts to break up. Riepen et al. (2008) reported the evolution of dynamic contact angles as a function of the rotational speed where the substrate is rotated with respect to a liquid immersion droplet. The receding contact angles evolve from a round shape to a cusp shape when the substrate has a velocity less than 0.73 m/s. Above the critical velocity, the liquid droplet begins to break up (‘pearling’) at the downstream side of the immersion droplet. This critical velocity depends on fluid, gap heights, contact angles, and so on.

In a different geometry, similar studies were performed on a moving droplet on an inclined substrate, albeit at a much lower Reynolds number ($\hbox{Re}\,=\,O$(1)), i.e., almost within the Stokes flow regime. Podgorski et al. (2001) showed that the initially rounded perimeter of the drop exhibits a singularity at the rear of the drop when the capillary number exceeds a critical value. Snoeijer et al. (2005) attempted to apply conventional planar particle image velocimetry (PIV) to measure the internal flow field. However, the measured flow field rather represents the average fluid motion over the whole depth of the droplet. A theoretical model was suggested to understand the mechanism of the droplet motion. In the Stokes flow regime, the theoretical model is derived from the lubrication theory taking into account the small slope of the liquid--air interface with respect to the solid plane (Limat and Stone 2004). However, in the case of the immersion droplet at a higher value of the Reynolds number, it is difficult to obtain a theoretical model.

Therefore, to allow for a further understanding of the fluid motion in a liquid immersion droplet under realistic conditions, the droplet flow field needs to be investigated experimentally. Kang et al. (2004) performed a quantitative measurement of lateral flow fields of an evaporating droplet by a direct ray tracing method, and Lu et al. (2008) measured the internal flow of electro-wetting-on-dielectric (EWOD)-driven droplet by conventional PIV. However, due to the complex nature in contact line dynamics, the volumetric measurement of all velocity components of the flow inside the entire droplet shape is desirable. To measure the volumetric flow field, several methods are proposed. Scanning light-sheet (Brücker 1995), holography (Hinsch 2002; Sheng et al. 2009), defocusing digital particle image velocimetry (DDPIV) (Pereira et al. 2000, 2007), tomographic particle image velocimetry (Elsinga et al. 2006), and 3D particle tracking velocimetry (Maas et al. 1993) are the most typical approaches. Recently, Pereira et al. (2007) investigated the 3D flows of evaporating droplet by using μDDPIV with an inverted microscope.

In this paper, the internal flow of the liquid immersion droplet on a moving substrate is investigated by means of tomographic PIV. This measurement technique is capable of simultaneously measuring all three velocity components (referred to as 3D-3C). The paper is structured as follows. First, the experimental setup and measurement technique are explained in detail. Next, the pre- and post-processing for 3D-3C data will be elucidated followed by a discussion of the measurement accuracy based on the assessment of the relative measurement examined by means of the continuity equation. Tomographic PIV is applied to determine the complex flow topology of the immersion droplet at Re = 200 for the first time. From this result, we can assess the internal flow field of the liquid immersion droplet. The results may lead to strategies that can achieve the flow control and to optimized designs of the immersion lithographic system.

2 Experimental setup

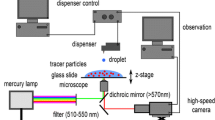
The experimental setup is shown in Fig. 1. A transparent glass wafer with a highly uniform hydrophobic surface coating (static contact angle, θ _s ≈ 90°) is used. The working fluid is distilled water with a dynamic viscosity μ = 10⁻³ Pa$\cdot$s, a surface tension $\gamma\,=\,70\,\hbox{mN}/\hbox{m}$, and a density $\rho\,=\,10^{3}\,\hbox{kg}/\hbox{m}^{3}$. We consider a liquid immersion droplet with a diameter (D) of 2 mm and a height (h) of 200 μm as shown in Fig. 2a. The wafer spins with a velocity of $V_{w}\,=\,1.0\,\hbox{m}/\hbox{s}$ at the position of the droplet, so that the flow conditions are characterized by a capillary number ($\hbox{Ca}\,=\,\mu V_{w}/\gamma$) of 0.014 and a Reynolds number ($\hbox{Re}\,=\,\rho V_{w}h/\mu$) of 200. At these conditions, the immersion droplet exhibits a wedge shape at the rear. In particular, Fig. 2b,c shows that the droplet begins to lose mass (referred to as ‘pearling’) at a critical velocity of around 1.4 m/s.

Fig. 1

Illustrations of the experimental setup. Top an overview of the facility. Bottom left four PIV cameras are mounted on a custom-made microscope at the bottom of the setup. Bottom right the customized stereo microscope, simplified immersion hood and pre-loaded device

Fig. 2

Shadowgraphy results: the side view of a the entire liquid immersion droplet on the stagnant substrate ($V_{w}\,=\,0\,\hbox{m}/\hbox{s}$), b the tail of the immersion droplet on the moving substrate with $V_{w}\,=\,1.3\,\hbox{m}/\hbox{s}$, and c the tail of the immersion droplet on the moving substrate with $V_{w}\,=\,1.4\,\hbox{m}/\hbox{s}$. The dash-dot lines indicate the surface of the substrate(wafer)

Figure 3 depicts a schematic of the experimental facility. A constant immersion film (droplet) is generated by a so-called immersion needle as shown in the red dashed line on the top right in Fig. 3. The measurement volume coincides with the total droplet volume. At the center of the immersion needle, the working fluid is supplied to the droplet. It is extracted through an annular trench around this center supply inlet. This simplified configuration represents a more complex immersion hood of an actual lithography machine. The inlet volume flow rate is constant at a rate of 39.34 ml/min with an uncertainty of ±2% of the full scale. To extract air and liquid at the same time through the annulus, a vacuum pressure of −0.5 bar is applied during the measurements. This condition generates a certain constant droplet volume for both a moving and a stagnant wafer. Furthermore, the immersion needle is installed near the edge of the 12-inch wafer, which spins with a constant angular velocity that results in a constant velocity at the position of the droplet. Due to the large radial droplet position, the local movement of the wafer with respect to the needle can be considered nearly uniform translational. The surface of the immersion needle is aligned with the wafer surface in parallel as much as possible. The rotation table consists of a vacuum chuck at the center to hold and rotate the wafer. Four vacuum pre-loaded (VPL) air bearings support the horizontal position and level of the wafer.

Fig. 3

Schematic of the experimental setup. The upper half shows the liquid immersion droplet system consisting of the simplified immersion hood and the flow controller for the inlet and outlet flows. In addition, the lower half shows the stereoscopic measurement system

For the visualization of the motion of the fluid inside the droplet, the recirculating fluid is seeded with 1.28-μm tracer particles (Microparticle GmbH) that are fluorescent (Rhodamine-B) and that have a polyethylene glycol (PEG) coating. This coating avoids particle coagulation and attachment of particles to the wafer surface and to the free droplet surface. The fluorescence is excited by illumination with laser light from a pulsed frequency-doubled Nd:YLF laser, which emits light with a wavelength of 527 nm. A separate stirring device maintains a homogeneous particle density. The PEG-coated particles in water possess a slightly negative surface charge, whereas the immersion needle showed a weak positive charge promoting the attachment of particles to the surface. Therefore, the immersion needle is grounded to maintain electrical neutrality, which reduces the number of particles sticking to the surface significantly.

The optimal particle image density is a compromise between the spatial resolution, the number of ghost particles, and the cross-correlation signal-to-noise ratio. The inflow impinges vertically downward on the wafer, and the outflow is extracted upward as shown in Fig. 4. Hence, the illumination with the laser through the microscope lens is parallel to the inflow and outflow directions. Hence, the laser beam illuminates the whole droplet. As a consequence, the background noise reaches a rather high level, which requires a proper image processing to reduce the effects of image background noise (see Sect. 3.1). The resulting image density (N _I ) is $5.38\,\times\,10^{-1},\,N_{I}\equiv CA_{I}\Updelta z_{0}/M_{0}^{2}$, where C is the mean number of particles per unit volume ($\hbox{m}^{-3}),\,M_{0}$, the magnification of the lens, $\Updelta z_{0}$, the depth of field (m), and A _I , the image interrogation area ($\hbox{m}^{2}$). In this experiment, the particle volume fraction is 2.5% in aqueous suspension of 0.2 ml and then the particles are diluted in 500 ml distilled water. In the present condition, there is a low image density condition, N _I  < 1. Directly counting particle images from raw images yields a value of around 0.034 ppp (particles per pixel), which corresponds to a source density N _S ≃ 0.09. The whole pre- and post-processing and calibration procedures are performed by means of a commercial code (Davis 7.4, LaVision GmbH).

Fig. 4

Schematic of the volume illumination for the immersion droplet where δz is the depth of field, h the height of the droplet, D the diameter of the droplet. At the top right, a close-up of the stationary droplet with the cylindrical coordinate system (r, θ, Z) is given

For the velocity measurements, we apply four CCD cameras, each with a resolution of 1,376 × 1,040 pixels and a 12-bit dynamic range. In this experimental condition, the equivalent dimension of a single pixel in the object domain is almost 4 μm. The camera (LaVision Imager Intense) has a high quantum efficiency of about 48% at 580 nm. To observe the flow field inside the droplet, the entire droplet volume needs to be accessed without any distortion for instance caused by reflection or refraction at the free surface. Therefore, four cameras are mounted on an inverted custom-made microscope. The optical path of each camera is off-axis through a single microscope objective lens with a magnification of 1.5. The offset angle between the optical axes of the cameras is about α≈ 20°, as shown in Fig. 5. The laser beam diameter L _d is almost 5 mm. As shown in Fig. 5, the custom-made microscope is installed below at about 30 mm from the wafer surface. The depth of field is given approximately by $\Updelta z_{0}\cong4(1+1/M_{0})^{2}{f^{\#}}^{2}\lambda$, where $\Updelta z_{0}$ is the depth of field; M ₀, the magnification of the lens; f ^#, the f-number of the lens; λ, the wavelength of the light. For the given optical parameters, we have $\Updelta z_{0}\approx 120$ μm.

Fig. 5

The geometry of the cross-sectional stereo microscope with CCD cameras. The focal length f is about 31 mm and the inner aperture is about 7 mm inside the lens. The particles inside the immersion droplet are volumetrically illuminated at 527 nm wavelength. The optical filters installed in front of each CCD camera only transmit light with wavelengths longer than 535 nm

The wafer is provided from Silicon Valley Microelectronics, Inc. and has a diameter of $300\pm0.3\,\hbox{mm}$ and a local thickness of $0.70\pm0.05\,\hbox{mm}$. A highly uniform hydrophobic surface wafer that is coated with a photoresist is applied by ASML Holding NV. To our best knowledge, there are no glass wafers, with a global flatness at a micron precision within the domain of commercial mass products. Only special custom-made wafers at extremely high price levels might provide values of overall flatness in the order of only a few micron. Therefore, for a constant droplet height, we applied a mechanical device that maintains a fixed reference position of the substrate. To establish this, we first record the height deviation of the edge of the wafer from the lateral camera as a function of time, so that we can obtain the topological characteristics of the wafer. Then, to control the height deviation, we properly mount a mechanical limitation to slightly push the wafer to a certain distance below a reference position (50 μm proved to be sufficient). Owing to this device, a global flatness of the wafer during rotation is controlled within ±1 μm as shown in Fig. 6. The input velocity (${V}_{w}$) is a nominal value of the system. Therefore, we determine the rotational speeds by measuring the topological characteristics of the wafer as a function of time. Hence, the measured wafer speed (${V}_{m}$) has the uncertainty around 0.7% compared with the nominal velocity on the system, as shown in Table 1. Additionally, since the photoresist coating wafer is very sensitive to contact with water, the duration of the contact with water should be minimized.

Fig. 6

Effect of the pre-loaded device. The height deviation ($\Updelta h$) is examined by measuring the topological characteristics of the edge of the wafer as a function of time. All dash-dot lines indicate the variation of the glass wafer without the pre-loaded device being applied, and solid lines present the controlled results with the pre-loaded device lowered on the wafer surface

Table 1 Accuracy of the rotational table by varying rotational speeds where V _w is the input value and V _m is the measured value

3 Pre- and post-processing for 3D-3C data

3.1 Image processing

As can be seen in Fig. 4, the entire droplet volume is illuminated by using laser light passing into the droplet parallel to the inflow and outflow direction. As a consequence, parts of the flow field inside the water supply device, i.e., a flow region located vertically above the droplet volume, are also being illuminated, causing a rather strong background illumination (see Fig. 7a). The image-processing steps necessary to minimize this background illumination are as follows. The main steps are based on spatial and temporal image processing. First of all, we performed a temporal image processing reducing the effects of e.g., laser reflections at the droplet interface, dust on the glass wafer, out-of-plane particles, and similar effects. For the temporal filtering, each intensity value at every pixel is first averaged over all images. Secondly, the computed mean pixel gray value is subtracted at each pixel, i.e.,

$$ I^{\prime}_{i, j}(X, Y)=I_{i, j}(X, Y)-\frac{1}{N}\sum^{N}_{i=1}I_{i, j}(X,Y), $$

(1)

where $I_{i, j}\left(X, Y\right)$ is the intensity value at every pixel for the camera $j,\,j\,=\,1\ldots 4, I^{\prime}_{i, j}$, the new intensity value after this temporal filter processing, i is the index of the image, and N is the total number of images. The result is shown in Fig. 7b. The aforementioned step is useful in the case of steady flow. Additionally, a spatial filtering is applied to remove the remaining noise in the images. A spatial 3 × 3 pixel sliding minimum filter, which subtracts the calculated local minimum from the local intensity, has been applied to all individual images. If necessary, the temporal and spatial filtering should be repeated until reasonable particle image fields are obtained. To enhance the visibility of the particle images with respect to the noisy image background, a 3 × 3 Gaussian smoothing filter is applied as a final step (Guezennec and Kiritsis 1990).

Fig. 7

Effects of the image processing. a Original PIV image; b image after temporal filtering; c after additional spatial filtering and 3 × 3 Gaussian smoothing filtering

3.2 3D calibration and correction

For the 3D calibration, a calibration target is traversed across several planes along the height of the measurement volume (i.e., the droplet). To reproduce the actual experimental conditions, the liquid should be present between the calibration target and the substrate. From this calibration, the geometric mapping function is obtained as a third-order polynomial (Soloff et al. 1997), which can be written as:

$$ \begin{aligned} x&= a_{0}+a_{1}X+a_{2}X^{2}+a_{3}X^{3}+a_{4}Y+a_{5}Y^{2}\\ &\quad+a_{6}Y^{3}+a_{7}XY+a_{8}X^{2}Y+a_{9}XY^{2}, \end{aligned} $$

(2)

$$ \begin{aligned} y&= b_{0}+b_{1}X+b_{2}X^{2}+b_{3}X^{3}+b_{4}Y+b_{5}Y^{2} \\ &\quad +b_{6}Y^{3}+b_{7}XY+b_{8}X^{2}Y+b_{9}XY^{2}, \end{aligned} $$

(3)

where the calibration coefficients a _i and b _i depend on the depth position. Note that despite the image mapping and reconstruction via the calibration process, it is often impractical to achieve a perfect overlap of all reconstructed images in multi-camera PIV measurements. Therefore, in addition, to match corresponding particle images in the volume, the possible mismatch, or disparity, of the particle positions for each of the four cameras is resolved by applying a volumetric self-calibration. Wieneke (2008) first described a volumetric self-calibration that is based on the computation of the 3D positions of matching particles by triangulation. After applying this procedure, the average mapping errors for the case of stationary substrate are reduced from 0.03 to 0.01 pixels (see Fig. 8a, b). For the moving substrate, the errors decrease from 0.04 to 0.02 pixels (see Fig. 8c, d). In both cases, the disparity errors are less than 0.2 μm. In the case of the immersion droplet on the moving substrate, there is an image disagreement in image results caused by differences in refractive indexes. As a consequence, the disparity errors in both cases are a little bit different.

Fig. 8

Mapping errors for all cameras in a plane located at a vertical position $z \approx\,0.1\, \hbox{mm}$ volume self-calibration of before (a) and after (b) in the stationary droplet on the stagnant substrate ($V_{w}\,=\,0.0\,\hbox{m}/\hbox{s}$), before (c) and after (d) in the dynamic droplet on the moving substrate ($V_{w}\,=\,1.0\,\hbox{m}/\hbox{s}$)

3.3 Tomographic reconstruction

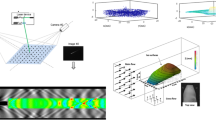
For 3D-3C velocity measurements, the tomographic reconstruction of 3D particles distributions is adopted (Elsinga 2008). As can be seen in Fig. 4, tracer particles are illuminated by a pulsed light source within a volume and their images are recorded simultaneously from four viewing directions using CCD cameras. Reconstructing the 3D particle distribution by tomography is an inverse procedure using the relation between image planes and the real space as established by a 3D calibration and correction procedure (see Sect. 3.2). The 3D intensity distribution is reconstructed in a $2.5\,\times\,2.1\,\times\,0.4\,\hbox{mm}^{3}$ volume discretized with 606 × 510 × 106 voxels using the MART (multiplicative algebraic reconstruction technique) algorithm with 5 iterations and with the relaxation parameter μ  =  1. The resulting distribution of the average intensity profile in the reconstructed volumes is plotted against the depth coordinate in Fig. 9. This 3D reconstructed intensity profile provides important information on the position of the droplet with seeding particles as well as the depth of field. Moreover, the average reconstructed intensity inside the measurement volume relative to the background intensity outside can be regarded as a measure for the reconstruction accuracy.

Fig. 9

Distribution of average intensity peaks in depth. The red dash lines indicate the position of the immersion droplet height, h, and the blue dash-dotted lines indicate the depth of field of the current setup, $\Updelta z_{0}$

To increase the effective particle image density, the reconstructed 3D intensity volumes are averaged over 25 individual reconstructed volume pairs. This is possible when the flow is steady. This effectively increases the seeding density while keeping relative low amount of ghost particles. The 3D-3C velocity vectors of each data set are obtained by means of 3D particle image pattern cross-correlation. The particle image displacement within a chosen interrogation volume (8 × 8 × 8 voxels) with 50% overlap is obtained by the 3D cross-correlation of the reconstructed particle distribution at the two exposures. The measured vector field contains 147 × 132 × 15 velocity vectors. The final vector results are averaged over 30 data sets (for the immersion droplet on a moving substrate) and 40 data sets (for the immersion droplet on a stagnant substrate).

The final result occasionally has vectors outside the liquid immersion droplet although actual particles must evidently be inside the droplet. This is due to ghost particles outside the measurement domain (Elsinga et al. 2010). In the case of tomographic PIV, the intensity information from actual and ghost particles both contribute to the cross-correlation. Therefore, further image processing is required to identify the internal flow field of the liquid immersion droplet. To eliminate spurious vectors, every vertical plane to a mask is applied by considering the largest intensity gradient that represents the position of the droplet interface using average reconstructed intensity field.

4 Results and discussion

4.1 Error estimation

To assess the dynamic range, reliability, and accuracy of our measurement system, the mass conservation in every sub-volume is examined in the form of the continuity equation. Given that the fluid flow is approximated as incompressible, an estimate for the continuity equation has a relative error distribution for all voxels that can be expressed as (Adrian and Westerweel 2010)

$$ \overline{\left(\frac{\partial u}{\partial x}+\frac{\partial v} {\partial y}+\frac{\partial w}{\partial z}\right)^{2}}\cong\left(\frac{\sigma_{\Updelta x}}{D_{I}\Updelta t}\right)^{2}, $$

(3)

where $\sigma_{\Updelta x}$ [pixel] is the overall error amplitude for the displacement; D _I the dimension of the square and non-overlapping interrogation domain [pixel] in the cross-correlation procedure; and $\Updelta t$ the time delay between two frames ($\Updelta t=10$ μs). The relative measurement error in every sub-volume is considered. Figure 10 presents the histogram of the relative error in the form of the continuity equation. The width of the distribution in Fig. 10 indicates the error of the measurement; the fitted Gaussian distribution has a standard deviation of (a) 0.0246 [pixel/pixel] and (b) 0.0251 [pixel/pixel], respectively. Hence, given that D _I   =  8 pixel, it is found through (3) that $\sigma_{\Updelta x}\,=\,0.2$ pixel. This error is consistent with a typical measurement uncertainty reported for tomographic PIV (Elsinga 2008).

Fig. 10

The histogram of the relative error of the liquid immersion droplet on a the stagnant substrate and b moving substrate. The data distribution is fitted by a Gaussian curve to determine the relative error in the form of the continuity equation where ${\vec{u}}$ has three velocity components, ${\vec{u}}=({u,v,w})$. The standard deviation evaluated from the fit is a 0.0246 [pixel/pixel] and b 0.0251 [pixel/pixel], respectively

Furthermore, we check the mass conservation at $z\,=\,100$ μm of the immersion droplet on the stagnant substrate. Due to the characteristics of flow field, the mass flow rate must be zero at that plane. The mass flow rate for the inlet and outlet is 0.5 g/min. The relative error for the mass conservation at the middle plane of the stationary droplet is found to be about 2% with respect to the inlet flow, which is 39.34 g/min.

4.2 3D Flow field

Two exemplary cases are examined: a drop on the stationary substrate and a drop on the moving substrate. Note that all figures in this section depict the fluid field in absolute velocity in the stationary frame of coordinates of the immersion needle. Very close to the substrate, this yields velocities identical to the local velocity of the wafer.

In the case of the stationary substrate, the internal flow field is largely defined as shown in the inset of Fig. 4. The inflow is driven by pressure at the center, and the outflow is extracted out by the vacuum pressure. This global flow pattern is indeed reflected in Fig. 11 showing the full 3D-3C velocity vector results in the stationary droplet. The selected planes are separated by 100 μm. We show the in-plane (x, y) vectors and the contours for the out-of-plane velocity. The flow pattern has a radial symmetry, although the velocity distribution is not perfectly axis-symmetric. This is because the outlet is connected only to one side of the immersion needle, and hence the flow field is slightly skewed to that side. Alternatively, a non-parallel alignment of the immersion needle and substrate could also be a reason for the asymmetry.

Fig. 11

Full 3D-3C velocity distribution in the stationary droplet, $V_{w}\,=\,0\,\hbox{m}/\hbox{s}$ with injection and extraction of fluids through the immersion needle; a Full 3D-3C scan of the flow field where the depth of the individual scanned plane is about 100 μm and b the flow field at the middle of the droplet, (at $z \approx 100$ μm). The vectors show the in-plane (x, y) velocity components, and the contour represents the out-of-plane velocity component

As can be seen in Fig. 12, in the case of a moving substrate, the wafer spins with a velocity of $V_{w}\,=\,1.0\,\hbox{m}/\hbox{s}$ at the position of the droplet. We used shadowgraphy to determine the projected external drop shape. For observing the lateral droplet shape, another CCD camera is installed on top of the x−y translation stage with micron resolution. The droplet has an advancing contact angle of about 145° and a receding contact angle of about 30°. The contact angle is measured from the image of the shadowgraph. At the rear of the droplet, the shape has an opening half-angle of about 60°. The superimposed vectors in Fig. 12 represent the 3D-3C velocity measured by tomographic PIV. The vector planes are cross-sectional results. The internal flow of the immersion droplet is shown, which exhibits a complex, but symmetric, flow pattern. There is a small circulation region near the corner of the droplet (see Fig. 12a). This region is related to the force balance of the viscous force, surface tension, and outlet pressure, as shown in Fig. 12c. The bottom result shown in Fig. 12b presents the flow field above the substrate ($z\approx$ 10 μm). A detailed inspection of the flow near the moving contact line indicates that particles follow the contact line. The velocity gradient of the flow field is related to the substrate speed, surface tension and outlet pressure. Furthermore, there is a fast flow region near the rear outlet trench where the fluid is extracted from the droplet. Therefore, the rear trench of the immersion needle should be considered as an important parameter to extract fluid.

Fig. 12

3D-3C vector field and shadowgraphy of the immersion droplet for Re = 200; a side view at the cross-sectional plane (y  =  0) where θ _a is the advancing contact angle and θ _r is the receding contact angle, b bottom view at $z \approx 10$ μm and ϕ is the half corner angle, and c illustration of the force balance near the corner of the droplet. Here, the vector colors are the magnitude of the velocity in three dimensions

This experiment involves non-uniform optical properties of the media, e.g., different indices of refraction for air, substrate, and water. In Fig. 12, only few data could be obtained near the top of the advancing part of the droplet as a result of the rather large advancing contact angle, which limits the view in that part of the droplet.

The full 3D-3C flow field shown in Fig. 13 reveals the velocity distribution and streamlines inside the liquid immersion droplet on the moving substrate at Re = 200. The vectors indicate 3D-3C components of the velocity and the iso-contours represent the out-of-plane velocity component. Furthermore, the external shape (i.e., free surface) of the liquid immersion droplet is indicated in white, i.e., where the velocity magnitude is zero. Directly above the substrate, the flow direction is the same as the direction of the substrate motion, due to the viscous drag, as shown in Fig. 14a. At $z \approx 30$ μm, the flow field of the front part of the droplet begins to flow toward the trench of the immersion needle, as shown in Fig. 14b. On the other hand, in Fig. 14c, d, e, the main flow is converging to the rear of the droplet, and there is a small flow region with reversed flow at the corner of the droplet. The small reversed flow region becomes smaller as the plane increases its position in the z-direction, as shown in Fig. 14c, d. Figure 14e shows the fast flow region that is nearby the rear trench of the immersion needle, where there still is a small reversed flow region. Schuetter et al. (2006) and Riepen et al. (2008) showed that the droplet tail becomes longer as long as the substrate speed increases. The size of the reversed flow region near the corner of the droplet is related to the length of the droplet tail. The droplet will break up when the viscous force, surface tension, and outlet pressure are no longer balanced. Consider Fig. 2b, c, when the viscous drag force is further increased, i.e., the wafer speed approaches the critical velocity ($V_{w}\,=\,1.4\,\hbox{m}/\hbox{s}$), the liquid immersion droplet begins to show ‘pearling’.

Fig. 13

Full 3D-3C velocity distribution and iso-contour plot in the liquid immersion droplet on the moving substrate ($V_{w}\,=\,1.0\,\hbox{m}/\hbox{s}$) at Re = 200, where the vectors show 3D-3C velocity components and the iso-contour represents the out-of-plane velocity component. The red boxes show the streamline results at the cross-sectional planes ($y\,=\,0.0, 0.3, 0.6\,\hbox{mm}$) where the streamline colors indicate the magnitude of w velocity. The white surface contour indicates the external shape of the liquid immersion droplet on the moving substrate

Fig. 14

Full 3D-3C velocity distributions (colors) and streamlines (black) in the liquid immersion droplet ($V_{w}\,=\,1.0\,\hbox{m}/\hbox{s}$) at Re = 200; Shown are five scan planes at a $z \approx 0$ μm b $z \approx 30$ μm, c $z \approx 60$ μm, d $z \approx 120$ μm, and e $z \approx 180$ μm; vector colors represent the magnitude of the velocity in the three dimensions

In this experimental case, the immersion droplet breaks up, when the critical dimensionless numbers are the capillary number of 0.02 and Reynolds number of 280. From the point of view of hydrodynamics, the Reynolds number is a general dimensionless number to characterize the flow field. However, according to Podsorski et al. (2001) and Riepen et al. (2008), the instability result is similar even though the Reynolds number is different. In this case, the capillary number is more important parameter to determine the droplet breakup. The capillary number represents the relative effect of viscous forces versus surface tension. By Laplace’s theorem, the surface tension is expressed as

$$ \Updelta p = \gamma \kappa=\gamma\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right), $$

(4)

where $\Updelta p$ is hydrostatic pressure, γ is the surface tension, κ is the mean curvature of the surface, and ${R_{1}}$ and ${R_{2}}$ are the principal radii of the curvature. The hydrostatic pressure is the pressure difference between the inside and outside surfaces. According to (5), by varying $\Updelta p$, we can change the curvature of the surface. Riepen et al. (2008) showed this by changing the ambient pressure distribution, and they increased the critical speed of the wafer in the immersion lithography system. In this experimental setup, the dynamic surface tension can be determined from the extraction force. Intuitively, as long as the extraction pressure is increased, the tail of the droplet is decreased. Therefore, in the immersion lithography system, the capillary number would be properly defined by considering the pressure as the additional parameter.

5 Conclusion

For the first time, the complex internal flow of a liquid immersion droplet on a moving substrate has been investigated by using tomographic PIV. The technique allows to obtain the full 3D-3C velocity vector fields. Current results help to understand the internal flow field of the liquid immersion droplet at relatively high Reynolds number, ($\hbox{Re}\,\gg1$). The location of the measurement data is consistent with the shape of the droplet determined by means of shadowgraphy. The limited view on certain parts of the droplet can be improved, provided that the advancing contact angle is decreased. In addition, reducing the strong reflection light at the droplet interface improves the quality of the data near the free surface. The consistency of the measured data is quantified by means of the continuity equation for an incompressible fluid. We observe the separation flow region near the tail of the droplet. This is related to the droplet instability resulting in the rupture of the droplet tail. However, further investigation will be necessary to study these issues in detail. Future work will address a parameter study related to the flow instability as a function of the height of the droplet, different inlet and outlet conditions, different surface condition of the wafer (i.e., applied coatings), and the velocity of the substrate (wafer).