1 Introduction

1.1 Background and motivation

Droplets and their associated phenomena have been investigated since Worthington (1876) observed the “finger pattern” and central jet formation as droplets splashed on a plate. A variety of fields can benefit from a better understanding of droplet impacts, for example,with optimum deposition and surface covering in spray cooling and coating processes (Aziz and Chandra 2000; Pasandideh-Fard et al. 2001) and internal combustion engines (Moita and Moreira 2007). In addition, the estimation and design of gas–liquid separation equipment in the oil and gas industry can benefit from the understanding of droplet impacts (Austrheim 2006; Johnsen 2007; Dorao et al. 2009). For example, scrubbers should be designed such that minimum splashing occurs on the liquid film. In a heat exchanger, the most efficient heat transfer occurs where the working fluid and walls are in contact, while the splashing droplets reduce heat transfer, as droplets suspended in the gas phase contribute little to the heat transfer. Hence, it is very important to understand the phenomena to accurately estimate and design the equipment.

1.2 Literature review

There have been two main research areas found in the literature dealing with high-inertia-energy impact related to the transition from coalescence to splashing/jetting. The first is the characterization of the threshold between coalescence and splashing/jetting, and the second is the formation and evolution of the characteristic parts such as the central jet and crown.

In most of the investigations (Worthington 1876; Hobbs and Osheroff 1967; Engel 1967; Macklin and Metaxas 1976; Stow and Hadfield 1981; Rodriguez and Mesler 1985; Cai 1989; Shin and McMahon 1990; Cossali et al. 1997, 1999; Wang and Chen 2000; Manzello and Yang 2002; Šikalo et al. 2002; Šikalo and Ganić 2006; Vander Wal et al. 2006a, b; Huang and Zhang 2008), the droplet diameters are relatively “large” on a millimetric level (diameter above 1 mm) with relatively low velocities (below 5 m/s), while very few focused on micro-level droplets (diameter below 1 mm), where strong effects from viscous and capillary forces can be important in the impact processes. Furthermore, the diameters had a narrow range of variation (Engel 1967; Stow and Hadfield 1981; Cossali et al. 1997, 1999; Manzello and Yang 2002; Šikalo et al. 2002; Šikalo and Ganić 2006; Vander Wal et al. 2006a, b).

The generalization of the rules for the regime transitions and process evolutions requires the usage of fluids with varying physical properties. Water has been the only experimental fluids in Stow and Hadfield (1981), Rodriguez and Mesler (1985), Cai (1989), Shin and McMahon (1990), Cossali et al. (1999), and it has been the main experimental fluid in the other investigations. Except for the investigations in Vander Wal et al. (2006a, b), most of the other investigations included fewer than three experimental fluids. The limited variety of the experimental fluids may restrict the generalization of the coalescence-jetting/splashing models.

Table 1 shows a summary of the literature treating coalescence/deposition–splashing/jetting. The research subject, fluids and parameters are listed in the table. D and V denote the droplet diameter and impinging velocity, respectively.

The threshold between the low-energy-collision phenomena, deposition or coalescence, to the high-energy-collision phenomena, jetting or splashing, has been the most studied subject. Some investigations (Rodriguez and Mesler 1985; Wang and Chen 2000; Manzello and Yang, 2002; Rioboo et al. 2003; Vander Wal et al. 2006a) characterized the threshold of splashing/jetting without presenting models (denoted by “threshold” in Table 1), while others (Stow and Hadfield 1981; Hsiao et al. 1988; Mundo et al. 1995; Cossali et al. 1997; Vander Wal et al. 2006b; Huang and Zhang 2008) presented empirical models using dimensionless parameters (denoted by “threshold model” in Table 1).

The other main subject was the evolution of a central jet, crown and deposition (Hobbs and Osheroff 1967; Cai 1989; Shin and McMahon 1990; Cossali et al. 1999). The jetting formation can be based on different types of singularities in waves, including gravitational and capillary types. The capillary type of singularity by Faraday instability was described and characterized by using power law relations in Hogrefe et al. (1998), Zeff et al. (2000), and another capillary type of singularity related with bubble entrainment which was studied by Bergmann et al. (2006) with the focus on bubble formation and breakup. It must be pointed out that the jetting criterion was different from the splashing criterion which required the breaking of the crown, and among those investigations listed in Table 1, only Rodriguez and Mesler (1985), Hsiao et al. (1988), Huang and Zhang (2008) studied the threshold of jetting.

In general, there are two methods of generating droplets. The first method generates single millimetric droplets by using a dropper, which is normally a needle or a fine tube. Most of the investigations listed in Table 1 used this method. The second method generates a mono-dispersed droplet stream from a nozzle by applying the Plateau-Rayleigh instability (Lord Rayleigh 1878, 1879) where the surface tension acts to part a liquid jet into small droplets. The droplets generated from the instability are normally sub-millimetric, and the generation frequency is much higher than that from the dropper method. The main advantage of the second method is that micro-level droplets can be generated, but it is often difficult to isolate one impact process from neighboring impacts. In order to capture these high-velocity processes, a high-speed, high-resolution camera with a short exposure time is required.

1.3 Dimensional analysis

Droplet impact phenomena are very complex as many different variables and mechanisms are included in the impact processes. Rein (1993), Mundo et al. (1995) listed many variables and mechanisms that can affect the impact processes, and they can be classified into three categories:

  1. 1.

    Properties of the fluids: transport and thermodynamic properties such as surface tension, viscosity, density etc.

  2. 2.

    Surface conditions: smooth or rough, yielding or unyielding etc.

  3. 3.

    Kinematic parameters: impact velocity, impact angle, droplet size, film movement etc.

Table 1 Overview of literature on transition between coalescence and splashing/jetting
Full size table

The numerous variables and mechanisms make the processes difficult to characterize quantitatively by using one or a few of them. In order to reduce the complexity of the problem and to study the phenomena comprehensively by covering all or most of the dominant variables and mechanisms, dimensional analysis can be used.

There were some assumptions regarding the parameters and effects involved in this impinging process. Willis and Orme (2003), Xu et al. (2005) showed that the ambient gas can affect the impact outcome, and it was pointed out that splashing was inhibited in a vacuum environment because the threshold level denoted by the Weber number increased in a vacuum environment. In this investigation, all the experiments were carried out with ambient gases at the atmospheric pressure (1.15 kPa for n-pentane), and the ambient gas effects on the impact can thus be considered invariant and negligible. Chandra and Avedisian (1991) showed that droplets impinging on a heated surface exhibited different characteristics from the impingement on a non-heated surface, and jetting was formed and fostered by the levitation of droplets impinging on a heated surface, especially above the Leidenfrost temperature. In the present investigation, all the experiments were carried out in a phase-equilibrium state, and thus any non-isothermal effects to the impingements were neglected.

It has been stated previously in the literature that while gravity-related effect can be described by the Bond number \(\left(Bo=\frac{\rho{g}D^2}{\sigma}\right)\) or the Froude number \(\left(Fr=\frac{V}{\sqrt{gD}}\right),\) the effect from gravity on the phenomena of droplet impacts is typically not important (Mundo et al. 1995; Cossali et al. 1997). However, as the droplet size decreases into the sub-millimetric range, the surface-tension effect becomes significantly more important than the gravitational effect. Therefore, when a relatively wide span of diameters is considered, such as in the experiments presented in this paper, it is possible that the effect from gravity may need to be included in the phenomena generated in droplet-pool interactions. A similar reasoning can be done for the viscous effect as for the surface-tension effect. In this work, a threshold model using the Froude number \(\left(Fr=\frac{V}{\sqrt{gD}}\right)\) and the Capillary number \(\left(Ca=\frac{\mu V}{\sigma}\right)\) is presented in Sect. 3.3. The Froude number relates the inertia and the gravity, and the Capillary number relates the viscosity and the surface tension.

Most of the investigations (Stow and Hadfield 1981; Hsiao et al. 1988; Mundo et al. 1995; Cossali et al. 1997; Rioboo et al. 2003; Vander Wal et al. 2006b; Huang and Zhang 2008) selected two or less dimensionless parameters, which covered the dominant effects, to form threshold models. For weighting the effects from inertia, viscosity and surface tension, these investigations used combinations of the Weber number \(\left(We=\frac{\rho DV^2}{\sigma}\right),\) the Reynolds number \(\left(Re=\frac{{\rho DV}}{{\mu}}\right)\) and the Ohnesorge number \(\left(Oh=\frac{\mu}{\sqrt{\rho\sigma D}}\right)\) in their models for coalescence and splashing/jetting. As the Reynolds number can be expressed using the Ohnesorge number and the Weber number \(\left(Re=\frac{\sqrt{We}}{Oh}\right),\) the models of Hsiao et al. (1988), Mundo et al. (1995), Cossali et al. (1997), Vander Wal et al. (2006b), Huang and Zhang (2008) can be written in the form

$$ We\cdot {Oh}^{a}=b, $$
(1)

where a and b are the characterized model constants. Due to the different experimental fluids, impingement targets and definitions for splashing and jetting etc., the model constants vary from investigation to investigation. Table 2 lists the experimental fluids, impacted objects, focused regimes and the model constants.

Table 2 shows that except Hsiao et al. (1988), the investigations weight the effects from the viscosity by using a non-zero exponent on the Ohnesorge number. Viscosity effects were not considered in Hsiao et al. (1988), possibly because a low-viscosity fluid, mercury, was used in the experiment, and the original model in Hsiao et al. (1988) used the square-rooted Weber number which reduced the sensitivity to the Weber number in the threshold. In this table, the other models show stronger effects from the viscosity than the model of Hsiao et al. (1988). It must be pointed out that the jetting models (Hsiao et al. 1988; Huang and Zhang 2008) used experimental data of the impacts of millimetric-level droplets which are different from the sub-millimetric droplets in this study. In Sect. 3, it will be shown that the literature model, Eq. (1), is not able to characterize the threshold of coalescence-jetting in detail for the impacts of the sub-millimetric level droplets of relatively high-viscosity fluids (above the viscosity of water, 0.89 mPa s), and a We-Oh model with a correction term is proposed.

It can be seen from the review of previous work that more information on the transition from coalescence to jetting of micro-level droplets is needed. This work provides a study of discretized, sub-millimetric sized droplets impinging on deep liquid pools. Five fluids are studied with droplet diameters from below 0.1 mm to a maximum of 0.7 mm. The effects from liquid-phase physical properties are studied to suggest two models which can assist in generalizing new fluids.

1.4 Definition of regimes

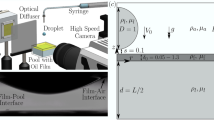
In our investigations, there are four main regimes for the droplet-pool impingement, which are schematically shown in Fig. 1, in which V and D denote the velocity and diameter of the impinging droplet. There are two coalescence regimes associated with high and low collision energy levels, and the transition between jetting and the high-energy-collision coalescence is the main subject in the present work. Schematic drawings for jetting and coalescence are shown in Fig. 2a, b, respectively. The criterion used for identifying jetting is the observation of the primary central jet or the secondary droplets ejected from the central jet as shown in Fig. 2a. This criterion is different from the splashing criterion used in many of the investigations such as Mundo et al. (1995), Cossali et al. (1997), Wang and Chen (2000), Vander Wal et al. (2006a) etc., in which the breaking of the crown into small secondary droplets is used as the criterion for splashing. Coalescence, shown in Fig. 2b, is when impinging droplets merge into the pool, and the impacts create weaker and smoother waves than in jetting.

Fig. 1
figure 1

Droplet-pool impingement regimes

Full size image
Fig. 2
figure 2

Schematic drawing for jetting and coalescence

Full size image

2 Experimental methods

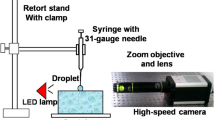
The experimental methods comprise the experimental setup, experimental fluids and image-processing routines. A detailed description of the experimental setup and the image-processing routines can be found in Zhao (2009), Zhao et al. (2010), and a short summary is given in the following.

The experimental setup is shown in Fig. 3, and it includes three parts:

  • Phenomena-generation: the phenomena were generated inside a gas-tight test cell. The droplets were generated by the Plateau-Rayleigh instability, and a nozzle for generating a stream of mono-dispersed droplets was mounted on the lid of the test cell. The droplet diameter and velocity were changed via the pressure exerted in the liquid reservoir and the orifice diameter, for which different sizes of mounted pinholes were used. The deep liquid pool was generated by fully filling an optical cuvette. The high impact frequency of the droplet stream was efficiently reduced by using a rotating shutter (Zhao et al. 2010), for which the working principle is shown in Fig. 4. The mono-dispersed droplet stream was chopped by the shutter (a copper tube with a pair of slits) mounted on an electric motor, and a large number of the droplets impinging on the shutter surface was thrown out of the camera focus and the liquid surface. To generate different impinging frequencies, the “shutter speed”, the opening time for droplets passing through, was controlled by varying the rotating speed of the motor (1,000–10,000 revolutions per minute). In this investigation, the impinging frequency was reduced from above 5,000 Hz to lower than 200 Hz on average. The evolution time for a single impingement, including the recovery of the surface, vary from case to case (see Fig. 9a with an evolution time around 2 ms and Fig. 9d with an evolution time of more than 5 ms), and in our investigation, the maximum evolution time in most of the cases was 8–10 ms corresponding to an impinging frequency of 100–125 Hz, which was higher than the frequency (60 Hz) indicated for isolated impacts (Zhbankova and Kolpakov 1990). Furthermore, during the data processing, each impact included in the experimental database was verified by inspection to be qualitatively isolated.

  • Light source: the backlight was a white light LED collimated by different optical lenses.

  • Data acquisition: a high-speed camera mounted with a long-distance microscope and a close-focus lens was used to capture the fast-evolving phenomena. The data was transferred and stored in a computer for analysis. The camera was operated with a resolution of 576 × 288 pixels, and at this resolution, the frame rate was 9,216 frames per second (fps). The exposure time was from 5 to 10 μs.

Table 2 Comparison of parameters in model (1) from different studies
Full size table
Fig. 3
figure 3

Schematic drawing of the experimental setup

Full size image
Fig. 4
figure 4

Working principle of the rotating shutter

Full size image

The images were processed by using ImageJ (Abramoff et al. 2004) to obtain the droplet information such as the cross-sectional area, x and y coordinates etc., and a script was used to analyze the data for getting the fundamental parameters including diameter, impinging velocity and angle. Based on the experimental methods, the maximum uncertainties of different parameters are estimated and given in Table 3.

The physical properties of the experimental fluids appear in the dimensionless parameters, and thus they are critical for characterizing the threshold between coalescence and jetting. Five fluids, distilled water, technical ethanol, n-pentane, methanol and 1-propanol, were investigated. The physical properties of the experimental fluids were taken from the literature, except those of technical ethanol, which were measured in our laboratory, due to insufficient information on water content. The experiments with n-pentane were carried out at 40°C in the pure saturated vapor of n-pentane, and the other experiments were carried out at 25°C in air saturated with fluid vapor. Table 4 lists the experimental fluids and the liquid-phase physical properties.

3 Results and discussion

This section is divided into two parts. The first part describes and discusses the experimental data ranges of the fundamental parameters (diameter and velocity) and the experimental observations. The second part is devoted to the characterization of the threshold between coalescence and jetting.

3.1 Experimental data range and observations

The velocity and diameter of coalescence and jetting for distilled water, technical ethanol, n-pentane, methanol and 1-propanol are shown in Fig. 5a–e, respectively.

Fig. 5
figure 5

Coalescence and jetting map for the experimental fluids

Full size image

The same nozzles were used in all the experimental runs, while, as can be seen from the figures, the droplets were generated with different diameter and velocity ranges depending on the fluid properties. Experimental runs using n-pentane and methanol with relatively low viscosity and surface tension (see Table 4) presented more narrow velocity ranges than the other three fluids. This was due to the fact that, with n-pentane and methanol, the droplet generation and breaking-up became irregular, which meant that there were more small droplets of different sizes with stronger deformations and more thrown-off droplets (i.e. more background noise). The impingement condition was characterized by high-frequency impact and more wavy pool surfaces, all of which hindered a further increase in velocity. The low viscosity and surface tension were the main causes for the irregular droplet breaking-up and severe oscillations of droplet and pool surface. Low viscosity dissipated less kinetic energy, and low surface tension required less kinetic energy to generate and break surface. Hence, more kinetic energy was maintained and made the flow chaotic.

Another noteworthy characteristic is that, for approximately the same diameter range, the transitions between coalescence and jetting occur with different velocity ranges for the experimental fluids. The velocity and diameter ranges for coalescence and jetting of the experimental fluids are listed in Table 5. In this table, experimental runs of distilled water and technical ethanol contain data from low-energy-collision coalescence, and it is not separated from the high-energy-collision coalescence. Even though the velocity and diameter ranges varied among the experimental runs, it can be seen from both Fig. 5a–e, Table 5 that the jetting data from all experimental runs cover a diameter range of approximately 0.15–0.40 mm. However, the transitional velocity between coalescence and jetting was different. It was found that the experimental runs of n-pentane and methanol shifted to jetting at lower velocity ranges, 2–3 ms for n-pentane and 3–5 ms for methanol. The other fluids with higher viscosities and surface tensions transited to jetting at a higher velocity range of approximately 5–9 ms. The liquid density and surface tension between methanol and the other two alcohols (technical ethanol and 1-propanol) are approximately the same, while the transitional velocity was much lower for methanol than for the other two alcohols. This indicates that it is the high viscosity that leads to the higher transitional velocity between coalescence and jetting. It is concluded that more kinetic energy is needed for a higher viscosity fluid to reach jetting, and this may be explained by the stabilization effect of the viscous force. The effect from the surface tension cannot be seen directly. Even though the experimental run of n-pentane shows the lowest transitional velocity, it may be difficult to draw a conclusion that lowering the surface tension will reduce the transitional velocity by directly comparing the data, as the lowest transitional velocity may be mainly due to the low viscosity of n-pentane.

A comparison of the jetting of different fluids can be used to investigate the effect of the surface tension, see Fig. 6 for technical ethanol and Fig. 7 for distilled water. Characteristic steps of crown, secondary droplets from central jet (C.j. drop) and swelling wave (swell.wav.) are shown.

Fig. 6
figure 6

Non-broken crown and secondary droplet from central jet of ethanol: D = 0.17 mm, V = 8.9 m/s

Full size image
Fig. 7
figure 7

Swelling wave and secondary droplet from central jet of distilled water: D = 0.21 mm, V = 8.9 m/s

Full size image

Figure 7 shows that the impact of a distilled water droplet with larger diameter and higher velocity (i.e. higher kinetic energy, because the density of distilled water is also higher than that of technical ethanol) does not form a crown but a swelling wave. Figure 6 shows that the impact of a technical ethanol droplet with lower kinetic energy forms a crown. As shown in Fig. 6a, the rim is not completely smooth, and this indicates that an instability forms at the rim. The fact that technical ethanol with higher viscosity required less kinetic energy to reach jetting indicates that in this case, the low surface tension of technical ethanol leads to a more unstable rim shown in Fig. 6a. This is because more kinetic energy is needed for breaking and generating new surface for a fluid with higher surface tension, so that high surface tension makes the flow phenomena more stable.

Figure 8 shows the sequential steps of the high-energy-collision coalescence, and only the surface wave after the impact is observed in this regime.

Fig. 8
figure 8

High-energy-collision coalescence of a methanol droplet: diameter D = 0.30 mm, vertical velocity V y  = 2.2 m/s, velocity V = 2.2 m/s

Full size image
Fig. 9
figure 9

Four types of jetting. a Jetting type 1: a methanol droplet, diameter D = 0.27 mm, vertical velocity V y = 4.4 m/s,velocity V = 4.5 m/s. b Jetting type 2: a 1-propanol droplet, diameter D = 0.28 mm, vertical velocity V y =7.3 m/s, velocity V = 7.3 m/s. c Jetting type 3: an n-pentane droplet, diameter D = 0.22 mm, vertical velocity V y =5.2 m/s, velocity V = 5.2 m/s. d Jetting type 4: an n-pentane droplet, diameter D = 0.26 mm, vertical velocity V y =5.9 m/s, velocity V = 5.9 m/s.

Full size image

Four different types of jetting were observed during the experimental runs, which are shown in Fig. 9a–d. In general, these four types of jetting exhibit stronger waves than observed in Fig. 8, and compared to coalescence, the most distinguishable observation in jetting is the appearance of either central secondary droplets or a primary central jet. The characteristic steps of the four types of jetting displayed in Fig. 9a–d distinguish them from each other:

  • Jetting type 1: In Fig. 9a, a crown-like wave (crown) is not formed, but a lower swelling wave is observed. A primary central jet is not observed, but one or more central secondary droplets are ejected.

    Table 3 Estimated uncertainties of different parameters (±%)
    Full size table
    Table 4 Physical properties of the experimental fluids
    Full size table
    Table 5 Velocity and diameter ranges for coalescence and jetting of the experimental fluids
    Full size table

  • Jetting type 2: In Fig. 9b, a crown is formed, but it does not break. Both a central secondary droplet and a primary central jet are observed. The secondary droplets in jetting type 1 and 2 are tiny (less than 0.01 mm), and their velocities are high (about 10 m/s).

  • Jetting type 3: In Fig. 9c, a crown is formed, and its rim breaks into small secondary droplets (splashing). An unbroken primary central jet is observed.

  • Jetting type 4: In Fig. 9d, splashing occurs, and the primary central jet ejects much larger secondary droplets with much lower velocity than in the jetting type 1 and 2.

For a given fluid, a higher kinetic impinging energy will lead to the formation of a crown with a more unstable rim. For instance, Cossali et al. (1997), Vander Wal et al. (2006b) showed that coalescence transited to splashing when the Weber number was increased. The jetting of n-pentane shown in Fig. 9c, d occurred with a lower kinetic impinging energy than the jetting of 1-propanol shown in Fig. 9b, while displaying a more unstable crown and central jet formations by the breaking of the crown and a higher central jet. The observations agree with the conclusion, which is drawn from the analysis of the velocity and diameter ranges of the fluids, that a fluid (e.g. n-pentane) with much lower viscosity and surface tension than another fluid (e.g. 1-propanol, distilled water) requires less kinetic energy to turn to a high central jet and breaking of the crown.

In summary, both low viscosity and low surface tension correspond to less kinetic energy loss and thus give an unstable crown and a high central jet.

3.2 We-Oh model for coalescence-jetting threshold

The impact regimes of coalescence and jetting can be separated by a threshold described by a mathematical expression, and in order to find the most suitable expression, proper regression methods need to be applied. Before introducing the two regression methods employed in the present work, two definitions regarding the data points, which are in regimes separated by a threshold line, must be clarified:

  • Uncertain points: the data points of one regime found in a range where the majority of points are from another regime.

  • Certain points: the data points of one regime found in a range where the majority of points are from the same regime.

Figure 10 shows an example which contains two regimes, Regime 1 and Regime 2, and a threshold is needed for separating the two regimes. The threshold line represents the transition from one regime to another. The following two regression methods are employed in the present work:

  • Least points method: the characterization gives the least number of uncertain points.

  • Least squares method: the characterization gives the minimum sum of square distances to the uncertain points.

Fig. 10
figure 10

An example of data regression for finding the threshold between two regimes

Full size image

In this investigation, the characterizations from the two different methods give almost identical characterizations.

3.2.1 Classical We-Oh model

The first attempt was made to curve-fit the coalescence-jetting threshold using the classical We-Oh model shown by Eq. (1), in which the constants a and b had to be determined. A trial and error method was used to search for the solutions of a in the range [−1,−0.3] with a step of 0.01 and b in the range [0,8000] with a step of 1, and the least squares method was employed. It must be mentioned that certain compromise must be made due to the fact that the best solution, which gave the least sum of squares, for an experimental fluid was always different from the best solution for another fluid, and thus we used the solution that gave the minimum sum of squares for all fluids. The classical We-Oh model that we found was with different values of a and b from those shown in Table 2:

$$ We\cdot Oh^{-0.77}=5573. $$
(2)

The characterized thresholds by the classical We-Oh model, Eq. (2), for distilled water, technical ethanol, n-pentane, methanol and 1-propanol, are plotted in Fig. 11a–e, respectively, using the curves with hollow triangles. Two models from Hsiao et al. (1988), Huang and Zhang (2008) are shown. In Fig. 11a, coalescence-jetting threshold data (hollow-star markers) used in Rodriguez and Mesler (1985) are also plotted, and the data are listed in Table 6.

Fig. 11
figure 11

Coalescence-jetting threshold characterized using the classical We-Oh model (2) and the corrected We-Oh model (3)

Full size image

In general, the classical We-Oh model shown by Eq. (2) can separate the two regimes with a relatively small numbers of uncertain points, especially for the fluids with low viscosity and surface tension, such as n-pentane and methanol, in Fig. 11c, d, respectively, and it agreed well with Rodriguez and Mesler (1985) on the threshold with millimetric impinging droplets. However, its deficiency was found for fluids with high viscosities (e.g. distilled water, technical ethanol and 1-propanol). For distilled water, technical ethanol and 1-propanol shown in Fig. 11a, b and e, the classical We-Oh (Eq. 2) underestimated the threshold Weber number at relatively high Ohnesorge numbers (i.e. small droplet diameter), while overestimated the threshold Weber number at relatively low Ohnesorge numbers (perhaps due to the high surface tension, this overestimation was not obvious for distilled water, see Fig. 11a). For instance, in Fig. 11e, the classical model overestimated for Oh < 0.025 and underestimated for Oh > 0.03. Our assumption was that, in a sub-millimetric diameter range, the effects from the surface tension and viscosity cannot be well addressed by the classical We-Oh model (Eq. 2). On the other hand, for n-pentane with both low surface tension and viscosity, Eq. (2) worked well, since neither surface tension nor viscous effects were strong.

3.2.2 Corrected We-Oh model

In order to capture the threshold variations more closely for fluids with a relatively high viscosity (\(\mu>0.89\hbox{mPa}\cdot\hbox{s}\) in this investigation), the classical We-Oh model was corrected so that the coalescence-jetting thresholds were more sensitive to the Ohnesorge number, i.e. droplet diameter. A corrected We-Oh model,

$$ We\cdot {Oh}^{-0.57+\frac{\hat{\gamma}}{D}}=1705, $$
(3)

was proposed to improve the classical model (Eq. 2) for fluids with a relatively high viscosity. In the corrected model (3), a reference diameter \((\hat{\gamma})\) was introduced, so as to make the threshold level more sensitive to the diameter change.

The characterized thresholds by the corrected We-Oh model (3), for distilled water, technical ethanol, n-pentane, methanol and 1-propanol, are plotted in Fig. 11a–e, respectively, using the curves with hollow circles. The reference diameter, \(\hat{\gamma},\) for each fluid is denoted in the figures. The figures show several characteristics:

  • Compared with the classical model (1), the corrected model (3) with the reference diameter is capable of following the sharp threshold change for relative high-viscosity fluids. The difference in the threshold variation of the two correlations is readily seen by comparing their curves (triangles for the classical and circles for the corrected model).

    Table 6 Coalescence-jetting threshold data extracted from Rodriguez and Mesler (1985)
    Full size table

  • The literature models (Hsiao et al. 1988; Huang and Zhang 2008) show significant discrepancies when compared to the experimental data of the present work, where the dominant droplet diameter is in the sub-millimetric range. However, as the Ohnesorge number decreases, i.e. the diameter increases, the discrepancy between the corrected model (3) and the literature models gradually diminishes. Figure 11a shows that the threshold data of millimetric-level droplets from Rodriguez and Mesler (1985) agree well with the correlation (3). Compared with the corrected model (3), the literature models fit the threshold data of Rodriguez and Mesler (1985) less well, while the discrepancy between the literature models and the present threshold data in the millimetric range is not that large. This may suggest that the literature models may only be valid for “large” droplets in the millimetric range.

  • The reference diameter, \(\hat{\gamma},\) varies with fluid properties. There are two aspects regarding the reference diameter:

    • Compared with the reference diameters for the fluids, when the impinging droplet diameter is larger than 3 mm, the influence of the correction term \(\left(\frac{{\hat{\gamma}}}{ {D}}\right)\) in correlation (3) can be neglected, and the correlation can be simplified into a classic threshold formulation,

      $$ We\cdot {Oh}^{-0.57}=1705. $$
      (4)

      As the droplet diameter decreases, the correction term in correlation (3) becomes more significant. In order to point out the condition at which the simplified correlation (4) must be corrected, a criterion is set as when the diameter is below \(D=100\hat{\gamma}.\) The reason for this criterion is that the exponential term, \(-0.57+\frac{{\hat{\gamma}}}{ {D}},\) in the corrected model (3) starts to deviate significantly from the constant −0.57 as \(\frac{{\hat{\gamma}}}{{D}}\geq0.01.\) So, the reference diameter can be considered as a diameter level at which the threshold becomes very sensitive to the diameter change. Below this level, assumed to be \(D=100\hat{\gamma},\) the surface tension and viscous forces cause the threshold to deviate from the classical form. Furthermore, since the surface tension and viscosity vary between fluids, the reference diameter will also be a function of fluid properties.

    • In this study, fluids with higher ratio of viscosity to surface tension \(\left(\frac{{\mu}}{{\sigma}}\right)\) have larger reference diameters, which indicates a larger threshold increase than that of the classic model formulation as the droplet diameter decreases. The explanation is that the increase in viscosity dampens the formation of jetting due to its nature of dissipating energy, while the increase in surface tension fosters the formation of jetting as it assists in breaking the secondary droplet from the central jet due to the Plateau-Rayleigh instability. Thus, a fluid with a relatively high viscosity and low surface tension, both of which inhibit the formation of jetting, needs more kinetic energy, i.e. a more significant threshold change (the increase of Weber number in Fig. 11a–e), to form jetting. It must be pointed that the conclusion that high surface tension is an advantageous condition for jetting is not contradictory to the conclusion in Sect. 3.1 that low surface tension favors the formation of an unstable crown. This is because the formation of the secondary central droplets, rather than the formation of an unstable crown, is the criterion for jetting.

In order to generalize the corrected We-Oh model (3), the reference diameter needs to be known. We will now present a method for calculating the reference diameter. We assume that the reference diameter, \(\hat{\gamma},\) is primarily a combination outcome of the physical properties, the density (ρ), viscosity (μ) and surface tension (σ) of a liquid. More specifically, the expression of \(\hat{\gamma}\) for an uncharacterized fluid x can be written as

$$ \frac{{\hat{\gamma}_{x}}}{{\hat{\gamma}}} = \left(\frac{{\rho_{x}}}{ {\rho}}\right)^{A_{\hat{\gamma}}} \cdot \left(\frac{{\mu_{x}}}{ {\mu}}\right)^{B_{\hat{\gamma}}} \cdot \left(\frac{{\sigma_{x}}}{ {\sigma}}\right)^{C_{\hat{\gamma}}}, $$
(5)

herein, \(\hat{\gamma}, \rho, \mu\) and σ are the calibration values from the experimental run of 1-propanol in the present study, and \(A_{\hat{\gamma}}, B_{\hat{\gamma}}\) and \(C_{\hat{\gamma}}\) are the exponents for density, viscosity and surface tension, respectively. When the liquid properties of an uncharacterized fluid (ρ x , μ x and σ x ), are known, the reference diameter, \(\hat{\gamma}_{x},\) can be calculated through the above equation.

By a trial and error method, the following solution is found:

$$ \frac{{\hat{\gamma}_{x}}}{{\hat{\gamma}}} = \left(\frac{{\rho_{x}}}{ {\rho}}\right)^{1.82} \cdot \left(\frac{{\mu_{x}}}{{\mu}}\right)^{0.6} \cdot \left(\frac{{\sigma_{x}}}{{\sigma}}\right)^{-0.96}. $$
(6)

The trial ranges for the exponents, A, B and C, are [−8,8], [−2,2] and [−2,2], correspondingly, and the step sizes are set to 0.02. The trial and error method gives a number of solutions with good margins to the trial ranges, and the solutions make reasonable predictions of the reference diameter. The best solution is chosen from those solutions according to the rule that the best solution gives the minimum root sum square (RSS) of the number of uncertain points for all fluids. In the present study, the deviation between the calculated values and experiment-fitted values is within 9%.

3.3 Fr-Ca model for coalescence-jetting threshold

The second attempt of characterizing the coalescence-jetting threshold is by using a Fr-Ca correlation,

$$ Fr=\beta \cdot {Ca}^{1.6}, $$
(7)

in which Fr and Ca denote the Froude number \(\left(Fr=\frac{V}{\sqrt{gD}}\right)\) and the Capillary number \(\left(Ca=\frac{\mu V}{\sigma}\right),\) respectively. The Froude number relates the inertia to gravitational forces, and the Capillary number relates the viscous force to the surface-tension force. β modifies the threshold level for different fluids.

The thresholds from the Fr-Ca correlation (7) (Fr-Ca model) are shown in Fig. 12a–e for distilled water, technical ethanol, n-pentane, methanol and 1-propanol, respectively.

Fig. 12
figure 12

Coalescence-jetting threshold characterized using the Fr-Ca model (7)

Full size image

As can be seen, the regimes of coalescence and jetting can be well distinguished by using the Fr-Ca correlation (7), which agrees well with the threshold data in millimetric range (Rodriguez and Mesler 1985). However, the quantities of β vary for the experimental runs of different fluids.

Similar to the generalization for the corrected We-Oh model (3), β can be assumed to be the products of the density (ρ), viscosity (μ) and surface tension (σ). More specifically,

$$ \frac{\beta_{x}}{\beta} = \left(\frac{\rho_{x}} {\rho}\right)^{A_{\beta}}\cdot \left(\frac{\mu_{x}}{\mu}\right)^{B_{\beta}} \cdot \left(\frac{\sigma_{x}}{\sigma}\right)^{C_{\beta}}. $$
(8)

By a trial and error method, the following solution is found:

$$ \frac{{\beta_{x}}}{{\beta}} = \left(\frac{{\rho_{x}}}{ {\rho}}\right)^{0.27} \cdot \left(\frac{{\mu_{x}}}{ {\mu}}\right)^{-1.80} \cdot \left(\frac{{\sigma_{x}}}{ {\sigma}}\right)^{1.45} $$
(9)

The trial ranges for the exponents, A β, B β and C β, were [−2, 5], [−3, −1] and [0, 3], correspondingly, and the step sizes were set to 0.01. In the present study, the deviation between the calculated values and experiment-fitted values is less than 10%.

3.4 Constraints in the We-Oh and Fr-Ca correlations

While the classical form of We-Oh correlation (2) presented in previous investigations can be used to describe the coalescence-jetting threshold for fluids with both low viscosity and low surface tension, the sub-millimetric droplets presented in this work with viscosities higher than 0.89 mPa s cannot be well described in detail using this basic form. The correction factors needed to describe the sub-millimetric droplets with high viscosities suggest that the previous We-Oh correlation is not universal over the whole droplet size range.

It must be pointed out that the model parameters, including the reference diameter \((\hat{\gamma})\) in the corrected We-Oh correlation (3) and the parameter β in the Fr-Ca correlation (7), varied with fluids, and it was assumed that this was mainly due to the different physical properties which we had been unable to capture with dimensionless parameters. These model parameters were characterized by curve-fitting for the experimental fluids, and our assumption that their values were dependent of the liquid properties enabled us to present a method using the correlations Eqs. (6) and (9) to predict the model parameters for a non-characterized fluid. This suggested method for generalizing the corrected We-Oh and Fr-Ca correlations solved the practical problem of quantifying the unknown parameters in the models, while a theoretical explanation for these model parameters requires further work. The simplified form (4) drops the correction term, but it is only valid for relatively large droplets above millimetric level.

On the other hand, even though both the corrected We-Oh correlation (3) and the Fr-Ca correlation (3) can well describe the coalescence-jetting threshold within the data range in the present study, the gravitational effect appeared in the Fr-Ca correlation, due to the use of Froude number, but not in the We-Oh correlation. However, the droplet diameter (D) in the exponent in Eq. (3) may be seen as a way of including a droplet size effect and hence a gravitational effect. Nevertheless, the Bond number \(\left(Bo=\frac{\rho gD^2}{\sigma}\right)\) was below about 0.05 for most of our data points (above 95%), showing that the gravitational force was small compared to the surface-tension force.

4 Conclusions

The investigation of coalescence and jetting of droplets impinging vertically on a deep liquid pool of the same fluid was carried out using five experimental fluids. The transition between coalescence and jetting was analyzed and compared to previous literature results.

From the comparison of the transitional velocity between coalescence and jetting for different fluids, as well as the comparison of the jetting observations, it can be concluded that both low viscosity and low surface tension foster the formation of an unstable crown and a high central jet, but not the breaking of the jet, which is promoted by low viscosity and high surface tension.

We present two models to describe the transition between coalescence and jetting using We and Oh. A classical We-Oh model of the form (2) typically used in the literature (Rodriguez and Mesler 1985; Hsiao et al. 1988; Huang and Zhang 2008) cannot reproduce the threshold trends for fluids with high viscosities. A corrected We-Oh model of the form (3) can characterize the boundary between coalescence and jetting well, but it requires the use of a reference diameter, \(\hat{\gamma}\) to properly account for droplets in the sub-millimetric range where viscous and surface effects may be significant. Different fluids have different values for the reference diameter.

A Fr-Ca model (7) can also be used to characterize the threshold of coalescence-jetting for the droplets in the sub-millimetric range, and it performs similarly to the corrected We-Oh model (3). A parameter (β), which varies with fluid properties, must be used to fit the threshold levels of different fluids.