Wake visualization of a heaving and pitching foil in a soap film

Abstract

Many fish depend primarily on their tail beat for propulsion. Such a tail is commonly modeled as a two-dimensional flapping foil. Here we demonstrate a novel experimental setup of such a foil that heaves and pitches in a soap film. The vortical flow field generated by the foil correlates with thickness variations in the soap film, which appear as interference fringes when the film is illuminated with a monochromatic light source (we used a high-frequency SOX lamp). These interference fringes are subsequently captured with high-speed video (500 Hz) and this allows us to study the unsteady vortical field of a flapping foil. The main advantage of our approach is that the flow fields are time and space resolved and can be obtained time-efficiently. The foil is driven by a flapping mechanism that is optimized for studying both fish swimming and insect flight inside and outside the behavioral envelope. The mechanism generates sinusoidal heave and pitch kinematics, pre-described by the non-dimensional heave amplitude (0–6), the pitch amplitude (0°–90°), the phase difference between pitch and heave (0°–360°), and the dimensionless wavelength of the foil (3–18). We obtained this wide range of wavelengths for a foil 4 mm long by minimizing the soap film speed (0.25 m s⁻¹) and maximizing the flapping frequency range (4–25 Hz). The Reynolds number of the foil is of order 1,000 throughout this range. The resulting setup enables an effective assessment of vortex wake topology as a function of flapping kinematics. The efficiency of the method is further improved by carefully eliminating background noise in the visualization (e.g., reflections of the mechanism). This is done by placing mirrors at an angle behind the translucent film such that the camera views the much more distant and out-of-focus reflections of the black laboratory wall. The resulting high-quality flow visualizations require minimal image processing for flow interpretation. Finally, we demonstrate the effectiveness of our setup by visualizing the vortex dynamics of the flapping foil as a function of pitch amplitude by assessing the symmetry of the vortical wake.

1 Introduction

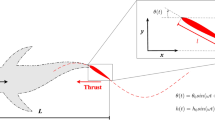
Marine fish that live and hunt in the water column (pelagic piscivorous fish) are both fast and efficient swimmers. Many of such fish, like tuna, have slender tails (caudal fins) and propel themselves primarily with their tail beat; hence they are referred to as thunniform swimmers (e.g., Sfakiotakis et al. 1999). Thunniform swimmers operate at a Reynolds number of 1,000 and up (Webb and Weihs 1986). The fluid mechanics of the heaving and pitching tails is governed by the generation and shedding of vortices (e.g., Triantafyllou et al. 1993; Sfakiotakis et al. 1999). These vortices influence swimming performance through their interactions with the tail. The nature of these vortex interactions depend on the foils kinematics and are not fully understood (Lentink et al. 2007). To better understand the vortex dynamics of thunniform swimmers, scientists often model the tail with a simple, non-flexible, pitching and heaving foil (Fig. 1) (Triantafyllou et al. 1993). Studying such simple foil geometry, kinematics and dynamics is a fair first approximation of thunniform swimmers.

Fig. 1

The tail (caudal fin) of a thunniform swimmer (e.g., tuna and many sharks) forms the main source of propulsion. The tail can be effectively approximated as a heaving and pitching foil

Here we present a novel experimental setup for studying such a flapping foil in a soap film tunnel. Soap films provide an important advantage compared with conventional setups using digital particle image velocimetry (DPIV): the vortical flow can be visualized and filmed time and space resolved without image correlation. Gharib and Derango (1989) illustrated the effectiveness of such setups for studying many types of two-dimensional flows. Rutgers et al. (2001) developed a simple and high quality soap tunnel (driven by gravity) that has eliminated many of the challenges of earlier designs (e.g., Gharib and Derango 1989; Couder et al. 1989). Georgiev and Vorobieff (2001) improved this setup for low flow speeds. Couder et al. (1989) studied vibrating cylinders in a static soap film, they were probably the first to actively drive an object similar to a flapping foil in a soap film. Zhang et al. (2000) studied freely flapping flags in a soap film tunnel, such fluid-structure interactions are also relevant for understanding anguilliform swimming of fish larvae, eels and swimming snakes. To our knowledge we were the first to actively flap a foil in a soap film tunnel (Lentink et al. 2007).

A soap film consists of a thin sheet of water stabilized by soap molecules on the surfaces. The soap molecules give the film elasticity, which mediates the propagation of disturbances through the film in the form of elastic Marangoni waves (Couder et al. 1989). Couder et al. (1989) and Chomaz and Costa (1998) showed that the in-plane dynamics of thin soap-films dominate the out-off-plane dynamics if the film speed is significantly lower than the Marangoni wave speed (elastic Mach number significantly smaller than 1). Hence “sub-sonic” soap-films can be regarded as 2D fluids. Chomaz and Costa (1998) further showed that a soap film obeys the 2D incompressible Navier–Stokes equations provided that the elastic Mach number is significantly lower than 1 and the initial film thickness variations are small. In the same paper Chomaz and Costa show that the vorticity field in the film is correlated to thickness variations of the soap-film. Rivera et al. (1998) showed that the correlation between the thickness and vorticity field in the wake of a grid of cylinders, generating 2D turbulence, remains strong well beyond 19 cylinder diameters downstream (region of interest 50 mm downstream; cylinder diameter 2.7 mm). Here we will study the vortical flow generated by a flapping foil less than 10 chord lengths downstream. Hence we may expect a particular strong correlation between the vorticity and thickness field. Thickness variations in a soap film can be visualized by illuminating the soap film with monochrome light, which results in interference fringes (Rutgers et al. 2001). Filming these fringes time and space resolved enables the quantitatively study of vortex dynamics in soap-films. This makes slow and uniform soap-films ideally suited for studying two-dimensional vortex dynamics at sub-sonic speeds.

Here we quantitatively describe our set-up and illustrate its effectiveness for studying the topology of the vortical wake of a harmonically flapping foil. We chose a dimensionless wavelength and flapping amplitude of the foil that is relevant for thunniform swimmers. Subsequently we qualitatively study the symmetry of the vortical wake of the flapping foil as a function of pitch amplitude.

2 Dimensionless parameterization of a flapping foil

The kinematics of a two-dimensional foil can be described using different dimensionless variables; we chose an approach inspired by the work of Williamson and Roshko (1988). We have published this approach (Fig. 2) elsewhere (Lentink et al. 2007). We describe the harmonic kinematics of a heaving and pitching foil with a dimensionless wavelength λ*, dimensionless amplitude A*, geometric angle of attack amplitude (or pitch angle) A _α,geo and Reynolds number Re. The dimensionless wavelength λ* represents the number of chord lengths travelled forward during one full flap period of the foil:

$$ \lambda ^{*} = \frac{{U_{\infty } }} {{fl}}, $$

(1)

in which U _∞ is the free stream velocity, f the flapping frequency and, l the foil length. The dimensionless amplitude A* represents the amplitude of the foil excursion A with respect to the foil length l:

$$ A^{*} = \frac{A} {l}. $$

(2)

The amplitude-based Strouhal number St _A is equal to the ratio of dimensionless amplitude A* and dimensionless wavelength λ*, and scales with the maximum induced angle of attack at mid-stroke (see Fig. 2; Eq. 4):

$$ St_{A} = \frac{{A^{*} }} {{\lambda ^{*} }}. $$

(3)

The effective angle of attack amplitude A _α,eff is equal to the angle of attack amplitude induced by the flapping foil minus the geometric angle of attack amplitude, A _α,geo (the pitch amplitude):

$$ A_{{\alpha ,{\rm eff}}} = {\rm arctan} {\left( {2\pi St_{A} } \right)} - A_{{\alpha ,{\rm geo}}} . $$

(4)

The time-averaged velocity U _ave of the flapping foil can be approximated as follows (Lentink and Gerritsma 2003):

$$ U_{{\rm ave}} \approx {\sqrt {U_{\infty } ^{2} + {\left( {4Af} \right)}^{2} } }. $$

(5)

Based on this average velocity we define the time-averaged Reynolds number, Re that represents the relative importance of inertia versus viscosity in the flow:

$$ Re = Re_{\infty } {\sqrt {1 + {\left( {4 St_{A} } \right)}^{2} } },\,{\text{in}}\;{\text{which}}\;Re_{\infty } = \frac{{U_{\infty } l}} {\nu }, $$

(6)

note that ν is the kinematic viscosity.

Fig. 2

A graphical representation of the non-dimensional parameters of a sinusoidally flapping foil: dimensionless wavelength, λ*, dimensionless heave amplitude, A*, amplitude-based Strouhal number, St _A , geometrical angle of attack amplitude, A _α,geo effective angle of attack amplitude, A _α,ef and the stroke-averaged Reynolds number, Re (adapted from Lentink et al. 2007)

3 Flapping foil mechanism

The foil is a flat plate and its kinematics is generated with a mechanism that can generate nearly perfect sinusoidal heave and pitch kinematics. Our first mechanism generated kinematics with a small asymmetry because the design is based on a crank-shaft mechanism (Lentink et al. 2007). Here we present and describe an improved flapping mechanism that can generate symmetric sinusoidal kinematics.

The foil has a thickness t of 0.2 mm and length l of 4 mm (relative thickness 5%). It is made out of a thin piano-steel wire bend into an “L” shape. The horizontal part of the “L” functions as the foil (in the soap film), while the vertical part is mounted to the flapping mechanism (Fig. 4b). The foil is mounted such that its axis of rotation is located at approximately 1/4 foil length behind the leading edge. The leading edge of the foil is naturally rounded as a result of bending the wire, while the trailing edge is more or less blunt (flat) as a result of cutting the wire.

The harmonic heave and pitch kinematics of the foil are generated by two coupled mechanisms. A single mechanism consists of a high-inertia constant-RPM spinning disk (aluminum) that drives a light-weight sled (aluminum) of which a schematic is shown in Fig. 3. The disk is connected with a pin (brass) to a rod (carbon fiber tube) that is connected to the sled. Simple Nylon and Brass bearings and proper lubrication resulted in a smoothly running mechanism that can generate both a sine (translation of rod) and cosine (translation of sled). The frequency of these harmonics is determined by the disk’s RPM, while the radius at which the pin connects the disk to the rod (and hence the sled) determines the amplitude of the harmonic. Both the heave and pitch amplitude can be varied independently (at the same frequency), because we used two coupled disk-sled mechanisms to generate both the heave and pitch kinematics, which we further explain in Fig. 4.

Fig. 3

Working principle of our flapping mechanism. The spinning disk (constant RPM) is connected to the rod (by a pin fixed with bearings), and the rod is connected to the sled that slides over two (horizontal) rails. The rod moves up and down with a sine, while the sled moves left and right with a cosine. The cosine of the sled is used to drive the heave of the foil while the sine of the rod drives the pitch of the foil. We use one such mechanism to generate the heave kinematics (using the sleds cosine) and another one to generate the pitch kinematics (using the rods sine). We coupled the disks of both mechanisms such that they operate at the same frequency, phase locked (Fig. 4)

Fig. 4

Overview of flapping mechanism (a) and detailed photo (b) (the upper part of the mechanism is indicated with “1”, the lower part with “2”). The flap mechanism consists of two rotating disks driven by an electric motor (water cooled). The upper disk (see b) is connected to a sled such that it generates the harmonic stroke kinematics (Fig. 3). We mounted the foil on the upper sled. The lower disk is connected to the lower sled with a rod that drives the harmonic pitch kinematics of the foil. The pitch kinematics is transferred by 0.2 mm piano steel wires, which slide through a flexible Teflon tube, to the upper sled were they connect to a pulley on which the foil is mounted. The whole mechanism is shielded by two mirrors set at an approximate angle of 45°

The mechanism allows presetting the heave amplitude (0–6 chord lengths), the geometrical pitch amplitude (0°–90°) and the phase difference between pitch and heave (0°–360°). The mechanism is driven by a reduced electric motor (water cooled) that spins at moderate frequencies (4–25 Hz). Additionally we can also preset the stroke plane angle of the flapping foil with respect to the free-stream velocity of the soap-film, which is relevant for flapping flight, e.g., insects (David 1978).

We determined how accurate the mechanism can generate harmonic kinematics by tracking the foil in the soap film tunnel with our high speed video. For our error analysis we considered three flap periods to determine the error in heave amplitude (ε _A ), pitch amplitude (ε _Aα ), heave-pitch phase-difference (ε_φ) and frequency (ε _f ) (Fig. 5). We determined the error using a best fit method (cftool Matlab 7, method: least squares, algorithm: trust-region) for kinematics generated at different heave amplitudes (1 and 4 chord lengths), pitch amplitudes (0°, 45°, 60°) and frequencies (4–21 Hz), see Table 1. The heave-pitch phase-shift is set to 90° [Read et al. (2003) showed that a flapping foil produces maximal thrust for such a phase shift]. We normalized the data with respect to these input variables in our error analysis. The variable range considered (Table 1) comprises the most extreme cases that we can obtain with our setup. Hence our error analysis can be considered a worst case analysis. We found that the mechanism accurately produces harmonic (sinusoidal) pitch and heave kinematics (Fig. 5). The maximum (local) deviation from ideal sinusoidal kinematics occurs at maximum excursion and is less than 5%, but this is an extreme value, it is typically less than 2%. Hence our new mechanism does not produce perfectly sinusoidal kinematics (as any other mechanism would) but it does generate significantly more sinusoidal kinematics than our earlier design (Lentink et al. 2007).

Fig. 5

Measured pitch and heave kinematics fitted with sine and cosine functions to determine the accuracy of our mechanism (note that we made the kinematics dimensionless with respect to the frequency (here 23 Hz), amplitude (here 1l) and geometric angle of attack amplitude (here 60°) in Table 1). The subsequent error indicators are the heave amplitude error ε_A, the pitch amplitude error, ε_Aα the phase error, ε_φ and the frequency error ε_f

Table 1 Variables used in error analysis (Fig. 6)

The average root mean square error (RMSE) of the present mechanism is small for both the pitch and heave kinematics (<0.02), Fig. 6. The results of the error analysis for the four flap variables are given in Fig. 6, they represent simply the difference between the intended value and the observed value of the flap parameters. Within one image sequence of three periods (part of a run of orders of magnitude more periods) we did not find significant fluctuations. Hence, the errors in Fig. 6 represent the resolution at which we can predetermine the parameters of the mechanism that define the flap kinematics. From this analysis we conclude that the harmonics generated with our mechanism can be preset reasonably accurately (under worst case conditions) with errors close to 0.05. Note that the frequency error is particular low, less than 0.01. Further note that phase shifts (errors) do not influence the symmetry of the foils kinematics provided that this shift is constant, as found for our mechanism. We found that such phase shifts are due to a misalignment of the top and bottom disk in the mechanism (Fig. 4).

Fig. 6

Error analysis of the kinematics generated by the mechanism compared with ideal harmonic kinematics [black lines indicate average; filled circles indicate individual measurements and correspond to Table 1; triangle not part of average (measured at 4.5 Hz)]. Left, RMSE for both heave and pitch kinematics, showing that the kinematics are indeed harmonic. Right, mean relative errors in heave amplitude ε _A , pitch amplitude ε _Aα , phase ε_φ (with respect to the maximum phase error 360°) and frequency ε _f . All errors are of order 0.05 (5%) or less. At low frequency (4.5 Hz) we found that the amplitude error (but not the other errors) is significantly lower than at high frequency (∼20 Hz). We expect that this is due to the inertial loading on the mechanism

4 Soap film tunnel

Our soap film tunnel generates a constant velocity soap film that runs between two wires, driven by gravity. We based our design (Fig. 7) on the simple and effective soap tunnel designed by Rutgers et al. (2001) and Georgiev and Vorobieff (2001). The frame of the current design is made out of cast iron and steel and is therefore more rigid than our first light weight soap tunnel build out of glass fiber tubes (Lentink et al. 2007). Our soap solution consists of tap water and 3% Dawn dishwasher detergent (Dawn “Manual pot and pan detergent”, Professional line, USA). In the current literature there is still considerable controversy with respect to the exact viscosity of soap-films (Rutgers et al. 1996). One of the most extensive studies to date has been performed by Martin and Wu (1995), they determined that the kinematic viscosity of a soap-film consisting of a 4% Dawn soap solution (Dawn “Manual pot and pan detergent”, Professional line, USA) is in the order of 10⁻⁶ m² s⁻¹, we adapt this value in our study. We stored the soap solution in a 1-l reservoir (Fig. 7a) and pumped it with a peristaltic pump (1,000 Mity Flex, Fig. 7b) into a 2 m high, constant height, “overflow” reservoir (Fig. 7c). The soap solution then flows from the reservoir through tubing into a valve (Fig. 7d) that regulates the mass flow. From the valve the soap solution flows to two parallel 1 mm thick nylon wires that gradually diverge (Fig. 7, section I), which results in a stable flowing soap-film. The two Nylon wires run parallel (separation: 0.06 m) along the test section (Fig. 7, section II), in which the flow velocity is approximately constant in flow direction. The flapping foil is inserted in this test section. The soap film continues flowing from the test section along two converging wires (Fig. 7, section III) into the drain (Fig. 7e) from where the film flows into the main reservoir, which completes the cycle.

Fig. 7

The soap film tunnel consists of a frame that spans two Nylon tunnel “walls”. The frame is set at an inclination of 5°. The tunnel has a diverging section (I), a test section (II) in which the foil is placed in the film, and a convergent section (III). The main components of the soap tunnel are: the main reservoir (a), a medical pump (b), a constant-height reservoir (c), a valve (a micrometer that constricts the tubing) (d) and a drain (e)

The soap film speed and thickness can be controlled by two parameters once the Nylon wires are fixed to the frame: first, the valve (control of mass flow) and second, the tilt angle of the film with respect to the horizon (preset of gravitational component in flow direction). Reducing the flow at the valve results in slower and thinner films, while reducing the tilt angle results in slower and thicker films. Super-critical film speeds, at elastic Mach numbers (ratio of film speed over elastic wave speed) of order one, can be obtained at large tilt angles (up to 90°) when the valve is wide open (Rutgers 1999). Under “supersonic” conditions, at flow speeds up to 4 m s⁻¹ and higher, “shockwaves” can occur in the film (Rutgers 1999; Wen et al. 2003). Such flows are not relevant for fish and should be avoided, also because flows at high elastic Mach numbers do not correlate with transonic and supersonic fluid dynamics in air or water (Wen and Lai 2003). For studying subsonic flows, our goal, tilt angles need to be low. For a tilt angle of 5° (at low mass flow, not measured) we obtained a thick film (not measured) with an average speed of 0.25 m s⁻¹, which is 50% slower than “The slowest soap-film tunnel in the Southwest” (Georgiev and Vorobieff 2002). At lower speeds, typically lower than 0.15 m s⁻¹, flow separation starts to occur at the end of the test section near the Nylon wires. For every run we tuned our valve to obtain the lowest possible speed without flow separation. Our optimally tuned soap-films produced nice plug-like velocity profiles in the test section (Fig. 8). Note that we measured the velocity profile over a width of 34 mm, compared with the 60 mm width of the test section (Figs. 8, 9). These profiles were obtained by tracking small pollutants in the soap film, which we filmed with a RedLake^® MotionPro digital high speed video. Pollutant tracking was performed manually with a dedicated Matlab program. We tracked pollutants (diameter of order 10 pixels) over the full width of the camera image (of order 1,000 pixels), which resulted in good tracking accuracy (better than 1%). The measured velocity profiles in the area of investigation in the test section are shown in Fig. 9. The velocity profiles are reasonably flat, while the average film speed is non-constant over a time period of several hours. Hence we measured the velocity profile several times during a measurement cycle to account for these slow fluctuations in our experiments. We always determined the average velocity over the whole heave excursion (twice the amplitude) in order to obtain good average velocities for the non-dimensional variables that depend on this velocity (dimensionless wavelength and Reynolds number).

Fig. 8

Foil in the test section of the soap film tunnel (34 × 41 mm). The non-flapping foil generates small vortices downstream. Nylon wires (1 mm thick) that bound the test section are indicated with thick horizontal lines

Fig. 9

The normalized (plug-like) velocity profiles as measured in the soap tunnel. We chose velocities at which no flow separation would occur in the test section; on average we obtained our slowest films without separation at 0.25 m s⁻¹

5 Visualization setup

The flapping foil in the soap film generates shear layers that roll up into vortices. The resulting vorticity field correlates strongly with thickness variations in the soap-film (Rivera et al. 1998). We visualize the thickness variations by illuminating the film with monochromatic light of a sodium lamp (SOX, wavelength 590 nm,) and film the reflected interference fringes at high speed (Fig. 10). The intensity of the reflected light changes from light to dark and vise versa for thickness variations that approach a quarter of the wavelength of the light source (Fig. 10). To acquire both a high spatial and temporal resolution a RedLake^® high speed digital camera is used to record the interference fringes in the soap film. The camera settings are: resolution of 1,280 × 1,024 pixels at 500 frames per second. To eliminate intensity fluctuations in the recordings we used a special 30 kHz SOX lamp (Philips) (Palmer and Beach 1995). We further improved the image quality by reducing the background reflections (noise) viewed by the camera through the translucent soap film. The light reflected by the mechanism formed the main source of noise in the images. After trying several alternative solutions (e.g., spray painting the mechanism black, shielding it with black paper, etc.) we found that putting mirrors (at an angle of approx. 45°) between the mechanism and film worked best (Fig. 4). These mirrors reflect the little light from the distant, out of focus, black laboratory wall into the camera, which resulted in negligible image noise.

Fig. 10

Interference fringes reflected by a soap film that is illuminated with a monochromatic light source. We capture these fringes with digital high-speed video

6 Vortex wake symmetry of a flapping foil

The heave and pitch variables of our flapping foil setup can be set as follows; A* = 0–6, A _α,geo = 0°–90°, λ* = 3–18 and the phase difference between heave and pitch can be set between 0° and 360°. The Reynolds number of the foil in our soap tunnel is of order thousand. The ranges of these parameters are representative for thunniform swimmers (including the Reynolds number; Webb and Weihs 1986). The caudal fin and its beat are approximated with a flat plate and harmonic kinematics. We focus our experimental study on how foil kinematics affects vortex wake symmetry. Several CFD studies have shown that the vortex wake and the corresponding forces generated by a symmetrically flapping foil can be asymmetric (e.g., Lewin and Haj-Hariri 2003; Lentink and Gerritsma 2003). Symmetry is relevant for thunniform swimmers because force asymmetries can result in net turning moments, which complicate straight swimming in fish. Here we show how a soap tunnel could potentially be used to effectively explore the parametric space of a flapping foil to identify asymmetric vortical wakes. For this study we focus on the influence of pitch amplitude on wake symmetry for a fixed amplitude A* = 3 and dimensionless wavelength λ* = 11 at a Reynolds number of order 1,000 while varying the geometric angle of attack A _α,geo = [0°, 15°, 25°, 45°]. Recently we have made a much broader parametric study with our soap tunnel that will be published elsewhere.

We assess the wake symmetry by making series of 99 triggered photos at a fixed flap phase. We then high-pass filter the individual images and subsequently calculate the average filtered image (Fig. 11) for four phases; 0°, 90°, 180° and 270°. If the vortex wake is symmetric, then the vortical fields must be anti-symmetric for 180°-out-of-phase triggered images (Fig. 11). We developed a simple procedure that enables a graphical check for wake symmetry: we add two 180°-out-of-phase locked images using different RGB channels. The first phase is represented by an orange image and the second by a mirrored pink image. If the two wakes overlap they produce a red image (Fig. 11) and one can assess wake symmetry by eye. We did this for all four pitch angles and found that wake symmetry strongly depends on pitch angle for the heave amplitude and dimensionless wavelength considered (Fig. 11).

Fig. 11

Wake visualization of a flapping foil in a soap film. We first filter the raw images (I _a ) using the Matlab 7.0 gradient and median (3 × 3) filter (I _b ) and than average 99 subsequent filtered frames (I _c ), these 99 images were all shot at the same flapping phase. We then assess the symmetry of the wake as a function of the geometric angle of attack (A_α,geo); note that the resulting effective angle of attack is also indicated (A_α,eff): II–V. The symmetry of the wake can be assessed qualitatively by comparing the average images at the start of the up- and down stroke (indicated with a, b). We subsequently reflect the upstroke wake “b” with respect to the horizontal centerline, in orange, and add it to the downstroke wake “a” in pink. Hence the overlapping parts of the wake become red (c)

Our experiments show that high effective angles of attack result in large vortices and wakes. When the effective angle of attack becomes small, an array of small vortices are generated along the foils path, similar to (but larger than) the wake shed by the non flapping foil at the same speed (Fig. 8). The vortex wake asymmetry is most likely due to non-linear near-vortex-wake interactions, as found by Williamson and Roshko (1988) for vibrating cylinders. How the vortex interactions in the wake and the interactions with the foil induce the wake asymmetry is largely unclear. In some cases the asymmetry is due to vortex merging or tearing (Lentink et al. 2007), but not for the foil kinematics considered here as we did not observe such vortex interactions. There are two sources of imperfections in the experimental setup that could potentially result in wake asymmetry: first flow asymmetry, because our plug like velocity profiles are slightly asymmetric. We do not expect this to result in the wake asymmetry, because wake asymmetry also occurs in close to perfectly symmetrical CFD simulations (e.g., Lewin and Haj-Hariri 2003). The influence of flow asymmetry could, however, be tested in future CFD studies. Second asymmetries in the kinematics generated by the mechanism, these are however small, we again note that wake asymmetry also occurs for close to perfectly symmetrical kinematics in CFD simulations (e.g., Lewin and Haj-Hariri 2003). Note, however, that the symmetry of the tail beat kinematics of fish and the background flow in which they swim in their habitat is not perfectly symmetric either (a detailed study of the level of symmetry of both swimming kinematics and background flow does not exist to our knowledge). Finally despite small asymmetries in our setup we found both symmetric and asymmetric wake patters while varying the geometric angle of attack amplitude in our experiment. Hence we conclude that we found experimental evidence for vortex wake asymmetry generated by a (to good approximation) symmetrically flapping foil in a soap tunnel. This finding is similar to findings by others in three-dimensional water tunnels (e.g., Jones et al. 1996) and two-dimensional CFD simulations (e.g., Lewin and Haj-Hariri 2003).

7 Concluding remarks

We presented a novel soap tunnel setup to effectively study the vortex dynamics of a pitching and heaving foil. The visualization of the vortex dynamics is based on the strong correlation between the vorticity field and thickness variations in the soap film. A high-frequency monochromatic SOX lamp enabled us to film the resulting interference fringes (due to thickness variations) of the soap film at high speed–time and space resolved.

The soap film can flow as slow as 0.25 m s⁻¹ in our setup, 50% slower than previously published setups (Georgiev and Vorobieff 2002), which is essential for operating at both high and low dimensionless wavelengths. Low stride lengths are obtained when the mechanism flaps at maximum frequency. The mechanism itself generates accurate and symmetric harmonic kinematics at all frequencies. We can preset the parameters of the harmonics (the heave amplitude, pitch amplitude, phase difference and flap frequency) with an error close to 5% or less.

To analyze the flow, we filtered and subsequently averaged a large series of images (n = 99). We then compared the average filtered images shot at a constant-phase with similar images shot at a 180° phase difference. We demonstrated the usefulness of such an approach for assessing the wake symmetry qualitatively. We could not find any reliable numerical method to assess the wakes asymmetry quantitatively; to our knowledge this is an open question.

The main advantage of our setup is that it facilitates a detailed and efficient study of the vortex wakes generated by flapping foils. The experiments are time-efficient—they only take 10 min per run, which is much faster than numerical simulations of similar flows on a high-end PC, which can take up to 30 days. Hence our experimental approach is ideally suited for a time-efficient study of the different vortex wake modes in the large parametric space of a flapping foil.

The main restrictions of our method are: it is limited to low Reynolds numbers, has a simplistic foil geometry and a fixed kinematics pattern (harmonic, two-dimensional), and the flow fields in the soap film are intrinsically two-dimensional. Within these constraints one can, however, use the results obtained with our setup as an efficient first order approximation of the more complicated three-dimensional flows generated by swimming animals such as thunniform swimmers. Interestingly we found, like others, asymmetric wakes for symmetric foil kinematics. The question emerges if thunniform swimmers encounter such wake modes during straight swimming.