Expansive Growth vs. pH Reflects a Poisson Point Process of Binding/Unbinding Events in Plant Cell Walls

Abstract

The paramount role of $\mathrm{pH}$ and temperature $\left(T\right)$ in the expansive growth of a plant coleoptile/hypocotyl non-meristematic zone or plant and fungal cells was examined within the framework of the underlying chemical bond statistics in order to reproduce an experimental plot of growth vs. $\mathrm{pH}$. Here, according to the definition, $\mathrm{pH}=\mathrm{pH}\left({\mu }_{{\mathrm{H}}^{+}}\left(T\right), T\right)$ is considered as a function of the chemical potential of the H⁺ (hydronium) ions (${\mu }_{{\mathrm{H}}^{+}})$, as well as an implicit and explicit function of $T$. The derivation of the $\mathrm{pH}$ and $T$ dependent expansive growth distribution from the Poisson statistics of the “tethers” that reproduce the chemical bonds between microfibrils was determined. The probability distribution for the attachment/detachment/reattachment events of the tethers that are connected to the microfibrils in the elongation zone was obtained. The two distinct but interrelated modes of the expansive growth, which are known as “acid growth” and “auxin growth” were distinguished in the analytic model, while the acid growth hypothesis was verified and confirmed at the semi-empirical and microscopic levels for the first time. Moreover, further perspectives, in which the macroscopic variables $\left(P, V, T\right)$ with $P$ standing for the turgor pressure and $V$ for the cell volume, and the microscopic variables, ${E}^{{\varvec{d}},{\varvec{r}}}$, which represent the binding energies of the detachment/reattachment events at the expense of ATP energy, and ${\mu }_{{\mathrm{H}}^{+}}$ can occur simultaneously, were identified. With a few assumptions that are partly based on experimental data it was possible to synthesise a link between the microscopic, explicit statistical explanation of bond dynamics and the macroscopic rheological properties of the cell wall at a given $\mathrm{pH}$ and temperature. A statistical description that predicted the importance of $\mathrm{pH}$ and temperature-dependent chemical potential of the H⁺ ions in microscopic events that result in growth would be supposedly applicable across scales.

Introduction

This article explores the role of $\mathrm{pH}$ and temperature dependence of expansive growth of plant cells using an approach of dynamic bond statistics in the cell wall. Attempts have been made to incorporate $\mathrm{pH}$ and temperature into basic analytical models describing the expansive (diffusive) growth of walled organisms and the effect of these two factors on the attachment/detachment/reattachment of the cellulose–hemicellulose bonds and their effect on growth.

The paper presents preliminary results from the model and comparisons to experimental measurements of growth induced by changes in $\mathrm{pH}$. The main (new) results are summarised below:

• Introduction of binomial/Poisson and Boltzmann statistics into expansive growth of plants.

• Derivation of $\mathrm{pH}$- and $T$-dependent expansive growth distribution.

• Interpretation of “acid growth” and “auxin growth” at the microscopic level.

• Recapitulation of the “acid growth hypothesis” at the microscopic level.

• Potential application to experiments in vivo or in vitro.

• Potential application for plant cell, coleoptile, hypocotyl.

Plant cells are surrounded by cell walls, which consist of a network of interconnected polymers with diverse biochemical and mechanical properties. The lowered $\mathrm{pH}$ is thought to activate wall loosening enzymes and agents like expansins (Cosgrove 2000a), resulting in increased extensibility of the cell wall and promotion of growth. Auxin (indole-3-acetic acid, IAA) is the plant hormone that stimulates cell elongation by increasing wall extensibility via activation of genes encoding cell wall-related proteins and increasing the apoplast acidification (Majda and Robert 2018 for review). The role of auxin in expansive growth has been the subject of many experiments and has been described in numerous mathematical models (Smithers et al. 2019 for review). Also multiscale models encoding physical relationships that bring new understanding to plant physiology and development have been proposed (Jensen and Fozard 2015 for review). Plant cells have been correctly recognised to be open systems (Barbacci et al. 2015) that dissipate energy (Pietruszka and Olszewska 2020) and exchange entropy (Pietruszka 2021) and matter with the environment. The role of biotic and abiotic factors during the expansive growth of plant cells has been studied intensely by many researchers, and analytic models that elucidate the expansive growth have been proposed (e.g. Pietruszka 2020 and papers cited therein). The commonly accepted physiological explanation of the underlying mechanism of growth of Hager et al. (1971) and Cleland (1971) has been widely recognised as the “acid growth hypothesis” (Hager 2003 for review).

In plant cells that are confined by a cell wall, growth requires modification of the cell wall and its properties to allow it to undergo turgor pressure. It has been hypothesised that this modification may be due to a decrease in apoplastic $\mathrm{pH}$, stimulated by auxin which activates membrane-bound proton pumps. The current model (as reviewed by Arsuffi and Braybrook 2018) is based on a decrease in apoplastic $pH$ which leads to changes in the cell wall leading to growth. It has to be noted, that auxin promotes also expression of genes encoding proton pumps and potassium channels (Philippar et al. 2004).

Recently, data obtained using advanced microscopic techniques such as X-ray and transmission electron microscopy was taken into account when expansive growth was described using an analytic model (Sridhar et al. 2018). Two decades earlier Veytsman and Cosgrove (1998) calculated free energy and estimated the entropy of an expanding plant cell. They showed that the yield threshold is the net outcome of the thermodynamics of the wall polymer interactions (see also Dyson et al. 2012; Pietruszka 2011). Their microscopic model of the expanding plant cell wall had two components, in which the first component was the elasticity of the macromolecules, while the second one was the network of hydrogen bonds. Based on these assumptions, they were able to find a new expression for the wall stress in the modified Lockhart (1965) equation. However, the dependence on the two most important environmental factors beyond light illumination, namely $T$ and $\mathrm{pH}$, was not taken into account, and the calculations where performed at a set (room) temperature of 300 K. The first statistical model that showed expansive growth for plant and fungal cells as spring (“tethers”) dynamics at a molecular level was developed by Sridhar et al. (2018). However, also this model did not take into account the existence of the fundamental dependence on $\mathrm{pH}$ and $T$ during the expansive growth of plant cells.

The plant cell wall is a strong fibrillar network that gives each cell its stable shape (Cosgrove 2001). To enlarge, cells loosen the chemical bonds in this network, which enables them to expand under turgor pressure. The mechanical properties are modulated through the control of the biochemical composition and the degree and nature of interlinking between the cell wall polysaccharides (Bidhendi and Geitmann 2016). The phenomenological models such as those of Lockhart (1965) have provided a macroscopic understanding of the expansive growth process. However, such models lack a connection to the molecular processes that underlie the network rearrangements in the wall—the existing wall is extended and rearranged in a large part by the slippage of the wall polymers. Sridhar et al. (2018) filled this gap by introducing the statistics of tethers (chemical bonds), which are connected to the microfibrils and constitute the mechanical scaffold of the extending primary wall. These bonds are governed by the Poisson point process, which has the property that each point is stochastically independent of all of the other points in the process. An advantage of this dynamic approach is its consistency with previous findings (expressed by the Ortega equation), while a disadvantage is its lack of T and $\mathrm{pH}$, which are crucial for the development of plants. Nonetheless, the presence of the viscoplastic and viscoelastic ingredients that are mapped onto the statistics of independently acting springs (tethers) is very attractive. The detachment and attachment events that cause the irreversible deformation of the expanding wall seem to be realistic in the first order of approximation (independent events, tethers acting as a parallel assembly of springs). However, a statistically based reasoning that shows the growth/$\mathrm{pH}$/T relationships has not yet been proposed.

Living entities are not timeless structures. Conversely, they are immersed in time. Therefore, the proper description of growth processes (not states) cannot be static, but dynamic, and in the temperature context—thermodynamic. Therefore, non-equilibrium thermodynamics should describe the physical context of growth. To describe the growth of an individual cell, it is necessary, inter alia, to formulate a constitutive model of the cell wall (Jensen and Fozard 2015). Typically, this can be achieved either by adopting an empirically obtained formulation (e.g. Lockhart 1965) or by deriving relationships based on underlying molecular processes. It turns out that both approaches in which an idealised cell wall, built by the stochastic self-organisation (Pietruszka and Olszewska 2020) of microfibrils and hemicelluloses, and a semi-empirical pattern (Pietruszka 2020), can provide a common description that includes the micro- and macroscopic features of the model. System components (chemical bonds) that undergo statistical distributions can be related to changes in cell volume by decisive factors of growth such as chemical potential (and hence $\mathrm{pH}$) and temperature.

Here I show that the expansive growth distribution of the plant coleoptile/hypocotyl non-meristematic zone vs. $\mathrm{pH}=\mathrm{pH}\left({\mu }_{{\mathrm{H}}^{+}}\left(T\right), T\right)$ reflects the binomial/Poisson statistics in plants. This is due to the fact that $\mathrm{pH}$ is a function of the chemical potential of H⁺ ions and an implicit (through ${\mu }_{{\mathrm{H}}^{+}}$) and explicit function of $T$.

Because the network of microfibrils and tethers is composed of complex polysaccharides and proteins that can dynamically mediate the underlying structure, this apparently simple fact would enable the possible outcomes to be predicted and strict manipulations of a growing plant cell or tissue to be performed at the level of molecules (in the lab) in order to obtain the optimum growth that is parameterised by $\mathrm{pH}$ and T. Moreover, a new analytic tool for probing the different modes of the intrinsic relationships in a system that is composed of the cytoplasm/membrane/wall of a growing plant cell can be anticipated. The low number of model parameters that are required can help to achieve this objective.

Cell Wall Rearrangement During Plant Development Morphogenesis: A Statistical Model

Methodological Notes

Occam's razor, the principle (attributed to William of Occam) that in explaining a thing no more assumptions should be made than are necessary, was used for many biological effects, like the modulation of pectin chemistry, which has an ambiguous effect (increased and decreased cell wall stiffness in vivo) on the properties of the primary cell wall (Bidhendi and Geitmann 2016), to enable us to construct—at first approximation—the analytical model capable of roughly explaining the observed (macroscopic) phenomena. Because the mechanisms underlying expansive growth of plant cells are similar in mono- and dicots species (Cosgrove 2000b), such as Arabidopsis (Arabidopsis thaliana) or the sunflower (Helianthus annuus) which are usually used for basic experiments, we take a more general model for a coleoptile/hypocotyl or a single plant cell.

This model is based on compatibility with the previously published model by Sridhar et al. (2018) (and Pietruszka 2011, 2020), where I introduce both $\mathrm{pH}$ and temperature, which has not been done before. In the Sridhar’s model, the system is a single cell with twisting tip growth. However, it is mathematically constructed using the attaching or detaching tethers to microfibrils, and therefore only these events can be found in the derived equations. A similar procedure for cells containing microfibrils and attachment/detachment events was used in the present article, hence the resulting equations also do not depend on the orientation of the microfibrils with respect to the growth direction. The latter statement implies that the statistical description of the microscopic events that result in growth would presumably apply to different systems (plant species) and at all scales.

Preliminaries

In addition to light illumination in the process of photosynthesis, temperature and $\mathrm{pH}$, the latter of which is expressed by the chemical potential, are the most influential environmental cues for plant growth. Just as temperature determines the flow of energy, the chemical potential ($\mu$) determines the flow of matter. However, both of these quantities enter into the definition of $\mathrm{pH}$ (Covington et al. 1985) through

$$\mathrm{pH}={\mathrm{log}}_{10}{\mathrm{e}}^{-\frac{{\mu }_{{\mathrm{H}}^{+}}-{\mu }_{{\mathrm{H}}^{+}}^{0}}{RT}},$$

(1)

where ${\mu }_{{\mathrm{H}}^{+}}$ (${\mu }_{{\mathrm{H}}^{+}}^{0}$) is the chemical (reference) potential of the H⁺ (hydronium) ions, ${\mu }_{{\mathrm{H}}^{+}}= {\mu }_{{\mathrm{H}}^{+}}(T)$, and R denotes the gas constant. The microscopic state of a system can be expressed through $\mathrm{pH}$ in a collective manner. For brevity, ${\mu }_{{\mathrm{H}}^{+}}\equiv \mu$ throughout the article.

The beta probability density function (Polyanin and Chernoutsan 2011) for 0 ≤ x ≤ 1 and the shape parameters α and β > 0 create the power function of the variable x

$${f}_{\mathrm{beta}}\left(x, \alpha , \beta \right)=\mathrm{const}\times {x}^{\alpha -1}{\left(1-x\right)}^{\beta -1}=\frac{{x}^{\alpha -1}{\left(1-x\right)}^{\beta -1}}{\underset{0}{\overset{1}{\int }}{u}^{\alpha -1}{\left(1-u\right)}^{\beta -1}\mathrm{d}u}=\frac{1}{B\left(\alpha , \beta \right)}{x}^{\alpha -1}{\left(1-x\right)}^{\beta -1},$$

(2)

where B = B(α, β) is the normalisation constant. In the following text, x = $\mathrm{pH}$ and “$\mathrm{pH}$” is hereafter treated as being a non-separable variable name. For compliance, the $\mathrm{pH}$ value is scaled to the range [0, 1] by dividing by 14. The numerical values of the shape parameters α and β will be considered further.

Model Description

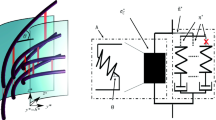
Let us denote |a > , |d > and |r > as attachment (connection), detachment (disconnection) and reattachment (reconnection) events (or states), respectively (see Fig. 1 and the caption; note that the Phycomyces case under consideration is only needed to visualise the model being developed, while the upcoming equations do not contain any species-specific data, symmetries or variables and are therefore applicable for the expansive growth of plant and fungal cells). Let us also assume that the total number of initially ($t={t}_{0}$) attached tethers |a > in the appropriate unit volume $\delta V$ ($V={\sum }_{i}\delta {V}_{i}$) of the wall is n and the number of detached states |d > is k (hereafter, the ‘melting’ of the tethers); we assume k ≤ n—the number of detachments cannot exceed n. Furthermore, the reattached states |r > can only be counted from the limited number of detached states m < k, which we further refer to as tether ‘quenching’ that acts in order to dynamically ensure the integral stability of a growing plant (cell wall); note that k and m are not entirely independent, given that only detached tether can reattach. Henceforth, I will assume a constraint—the conservation of the quantity of attached states per unit length that is required to guarantee the structural integrity of the expanding wall (|a > states remain anchored to the microfibrils beyond the elongation zone). Although the considerations appear to be general, for the focus of attention the specific process of expansive growth that we are trying to describe using our model may be somewhat similar to that described in Sridhar et al. (2018) for Phycomyces. Actually, any selective reversible bonding (e.g. hydrogen bonding) will produce the discussed effects. However, even in this restrictive formulation, the problem seems to be complicated.

Fig. 1

Illustration of the expanding cylindrical cell wall in the longitudinal direction that was used in the proposed statistical model of a network of slipping microfibrils (note that microfibrils are not oriented parallel to the longitudinal axis) that are connected by tethers (partially re-constructed for compatibility after Sridhar et al. 2018). The attachment/detachment/reattachment {|a > , |d > , |r >} events/states are shown (see text). The states in the statistical ensemble are either zero or one—there is no distinction for the elastic and viscoelastic stretch in the model. The reattachment events of the growth zone (magnified fragment) are assumed to occur mainly in the slippage zone (pink). The system is immersed in a thermostat (environment) at temperature T (Color figure online)

Derivation of the Model Equations

Since the |a > , |d > and |r > states are statistically independent in the first approximation, a binomial distribution can be assumed. For the |a > and |d > states, the probability density function (PDF) reads

$${f}_{1}\left(X=\left.k\right|n, {p}_{{\varvec{d}}}\right)=\frac{1}{{2}^{n}}\left(\genfrac{}{}{0pt}{}{n}{k}\right){p}_{{\varvec{d}}}^{k}{\left(1-{p}_{{\varvec{d}}}\right)}^{n-k}$$

(3)

and for the |d > and |r > events, one gets

$${f}_{2}\left(Y=\left.m\right|k, {p}_{{\varvec{r}}}\right)=\frac{1}{{2}^{k}}\left(\genfrac{}{}{0pt}{}{k}{m}\right){p}_{{\varvec{r}}}^{m}{\left(1-{p}_{{\varvec{r}}}\right)}^{k-m}$$

(4)

since ${f}_{1}$ as well as ${f}_{2}$ satisfy normalisation conditions:

$$\sum_{k=0}^{n}{f}_{1}\left(k|n, {p}_{{\varvec{d}}}\right)=1$$

and

$$\sum_{m=0}^{k}{f}_{2}\left(m|k,{ p}_{{\varvec{r}}}\right)=1.$$

In Eqs. (3)–(4) the symbol $\left(\genfrac{}{}{0pt}{}{n}{k}\right)=\frac{n!}{k!\left(n-k\right)!}$ is the Newton symbol and $n\ge k\ge m$. The probability ${p}_{{\varvec{d}}}\equiv P\left({\varvec{d}}\right)$ for the detachment and ${p}_{{\varvec{r}}} \equiv P\left({\varvec{r}}\right)$ for the reattachment events, the latter of which has fewer or equal events compared to the detachment ones, was assumed. Combining both distributions given by Eqs. (3) and (4), a description of the |a >  = >|d >  = >|r > process (attachment =  > detachment =  > reattachment) can be obtained in the form of the total probability density function

$${f}_{t}\left(n, m|{p}_{{\varvec{r}}}, {p}_{{\varvec{d}}}\right)={f}_{2}\left(X=\left.m\right|k, {p}_{{\varvec{r}}}\right){f}_{1}\left(Y=\left.k\right|n, {p}_{{\varvec{d}}}\right),$$

(5)

where X and Y are independent random variables. On the other hand, the truncated form of Eq. (2) has been used successfully in order to describe expansive growth vs. $\mathrm{pH}$ dependence in plants (see SI Table 1 and SI Fig. 1a in Pietruszka 2020). There, the α and β shape exponents were estimated to be α = 1.87 ± 0.02 and β = 3.17 ± 0.06 in the case of the “acid growth” of maize (Pietruszka 2020), where “acid growth” refers to the ability of the plant cells and plant cell walls to elongate or expand quickly at low (acidic) $\mathrm{pH}$. The experimental data that was used for this very accurate interpolation originated from the work of Hager (2003). Henceforth, following Hager’s (2003) “Zuwachs”, an assumption is being made: the length of a coleoptile/hypocotyl in the direction of elongation is proportional to the actual PDF (state during steady growth) multiplied by the appropriate unit length, e.g. μm; the greater the probability, the greater the expansion for a given $\mathrm{pH}$. The biological explanation of the similarity of the shape of the distributions may be related to the increasing number of tether detachments/reattachments as the chemical potential level of the H⁺ ions varies reaching a maximum at critical value ${\mu }_{{\mathrm{H}}^{+}}^{c}$(corresponding to growth maximum) and then follow the negative slope associated with the depletion of available bonds causing the detachment/reattachment events to expire.

Last observation related to the qualitative similarity of both distributions may lead to a comparison of both approaches to obtain an approximate equation for the cumulative distribution functions (this assumption, difficult to analytically verify, is further numerically validated by the Eq. (7)— see “Model Verification: Connection to Experimental Data for Sunflower Hypocotyls” section and Fig. 2):

Fig. 2

a Asymmetric probability density function (PDF) for the attachment/detachment/reattachment events that were governed by the Poisson point processes in the cell wall (imitating “acid growth”) as a function of the number k (or density in %) of the detachment events |d > as described by Eq. (7). The model parameters were equal to: total number of initially attached tethers n = 100 (= 100%), probability for the detachment events p_d = 0.1 (yellow), 0.15 (magenta) and 0.2 (blue) and for the reattachment events p_r = 0.075. Note the qualitative similarity of the blue line to SI Fig. 1a (“acid growth”) in Pietruszka (2020); also compare with Fig. 2 in Hager (2003). b Asymmetric “heavy tail” probability density function (PDF) for the attachment/detachment/reattachment events that were governed by the Poisson point processes in the cell wall (imitating “auxin growth”) as a function of the number k (or density in %) of the detachment events |d > as described by Eq. (7). The model parameters were equal to: n = 100, p_r = 0.02 (blue), 0.03 (magenta) and 0.04 (yellow), and p_d = 0.2. Note the similarity of this plot to SI Fig. 1a (“auxin growth”, inset) in Pietruszka (2020). c Probability density function (PDF) for the attachment/detachment/reattachment events governed by the Poisson point processes in the cell wall as a function of the number k (or density in %) of the detachment events |d > , as described by Eq. (7). The model parameters were equal to: n = 100, p_d = 0.2, p_r = 0.04 (magenta); p_d = 0.2, p_r = 0.02 (blue). The filled area corresponds to the auxin action (“auxin growth”) that was beyond the “acid growth” and arose as a result of the reattachment events in the cell wall (Color figure online)

$$\frac{1}{B\left(\alpha , \beta \right)}\underset{0}{\overset{\mathrm{pH}}{\int }}{{\mathrm{pH}}^{^{\prime}}}^{\alpha -1}{\left(1-{\mathrm{pH}}^{^{\prime}}\right)}^{\beta -1}\mathrm{d}\left({\mathrm{pH}}^{^{\prime}}\right)\approx \sum_{k=m}^{{k}_{\mathrm{max}}\le n}{f}_{2}\left(\left.m\right|k,{ p}_{{\varvec{r}}}\right){f}_{1}\left(\left.k\right|n, {p}_{{\varvec{d}}}\right),$$

$$=\frac{1}{{2}^{2n}}\left(\genfrac{}{}{0pt}{}{n}{m}\right){\left({p}_{{\varvec{r}}}{p}_{{\varvec{d}}}\right)}^{m}{\left[2-{p}_{{\varvec{d}}}\left(1+{p}_{{\varvec{r}}}\right)\right]}^{n-m},$$

(6)

where the latter expression was obtained for the maximum number of detachment events ${k}_{\mathrm{max}}=n$ (the relationship between the parameters of the left and right sides of the equation will be explained later). In such heuristically motivated Eq. (6) the number of |d > and |r > events can, in principle, be experimentally determined (e.g. in per cent or as bond density, i.e. the number of bonds per a sufficiently small volume) in the growing wall. Note that the system temperature and chemical potential are implicit and explicit in Eq. (6), since they both enter the definition of $\mathrm{pH}$, Eq. (1). Equation (6) relates the macroscopic variables $\mathrm{pH}$ and $T$, on the one hand, and on the other hand, a microscopic finite number of the chemical bonds (tethers) that contribute to the process of the expanding cell wall in a unified account that is based on the position of the chemical potential of hydrogen ions ${\mu }_{{\mathrm{H}}^{+}}$. It looks as though—see the upper limit of the integral and the sum in Eq. (6)—the value of $\mathrm{pH}$, and consequently, the level of ${\mu }_{{H}^{+}}$, play a role similar to ${k}_{\mathrm{max}}$ in the sum, which is also controlled by the level of ${\mu }_{{\mathrm{H}}^{+}}$. Hence, roughly speaking, the change of the parameter ${k}_{\mathrm{max}}$ can be interpreted as being relative to the change of the chemical potential ${\mu }_{{\mathrm{H}}^{+}}$, and correspondingly—$\mathrm{pH}$ in a system.

Moreover, for large n the binomial distribution transforms into the Poisson distribution. Then, Eq. (6) reads:

$$\frac{1}{B\left(\alpha , \beta \right)}\underset{0}{\overset{\mathrm{pH}}{\int }}{\mathrm{pH}^{\prime}}^{\alpha -1}{\left(1-\mathrm{pH}^{\prime}\right)}^{\beta -1}\mathrm{d}\left(\mathrm{pH}^{\prime}\right)\approx \left(n-k\right)\left(\begin{array}{c}n\\ k\end{array}\right)\underset{0}{\overset{1-{p}_{{\varvec{d}}}}{\int }}{t}^{n-k-1}{\left(1-t\right)}^{k}\mathrm{d}t\times \left(k-m\right)\left(\begin{array}{c}k\\ m\end{array}\right)\underset{0}{\overset{1-{p}_{{\varvec{r}}}}{\int }}{t}^{k-m-1}{\left(1-t\right)}^{m}\mathrm{d}t.$$

(7)

A binomial distribution is used to model the probability of the number of successes that can be expected from $n$ trials with a probability $p$. The Poisson distribution is a special case of the binomial distribution when $n$ goes to infinity, while the expected number of successes remains fixed. The Poisson distribution is used as an approximation of the binomial in cases in which n is large and p is small. Assuming λ_d and λ_r (λ_d ≥ λ_r) as the rate parameters for the Poisson distribution (see Kingman 1993), a convenient (alternative) formula for further experimentation can be proposed

$$\frac{1}{B\left(\alpha , \beta \right)}\underset{\mathrm{pH}}{\overset{\mathrm{pH}+\Delta\mathrm{pH}}{\int }}{\left({\mathrm{pH}}^{\prime}\right)}^{\alpha -1}{\left(1-\mathrm{pH}^{\prime}\right)}^{\beta -1}\mathrm{d}\left(\mathrm{pH}^{\prime}\right)\propto \frac{{\lambda }^{m}{\mathrm{e}}^{{-\lambda }_{r}}}{m!}\frac{{\varepsilon }^{k}{\mathrm{e}}^{-{\lambda }_{d}}}{k!}$$

(8)

which, potentially, can considerably reduce the number of free parameters. Here, parameters k and m stand for actual number of |d > and |r > events. λ (or ε) parameter can be thought of as the expected number of events (bond melting or quenching, respectively) in the $\Delta \mathrm{pH}$ interval that is being considered.

To summarise, the assumption about the independent Poisson processes led us to consider the binomial and, further, the Poisson distributions, as describing the |d > and |r > events that occur in the elongating primary wall of a cell. Moreover, Eq. (7), via a coupling to the beta Euler distribution, should potentially deliver the set of microscopic parameters $\left\{k,m\right\}$ instead of—and connected with—the shape parameters $\alpha$ and $\beta$ in the beta Euler distribution. However, to prove its applicability, experiments are required, which are beyond the scope of this theoretical work (besides, there are also experimental limitations to measure apoplastic $\mathrm{pH}$). Nonetheless, model calculations (simulations and interpolations) and the procedure of fitting representative experimental data that are presented below show that we are heading in the right direction.

Results and Discussion

In this work, the scenario of statistically independent (non-interacting, Sridhar et al. 2018), but also uncorrelated and non-overlapping tethers, representing viscous stresses associated with crosslink detachment and reformation in the wall, is followed.

Numerical Calculations

Model Analysis: Acid vs. Auxin Growth

Auxin is a plant hormone that promotes cell elongation, hence “auxin growth”. Auxin-induced growth of primary tissues was explained by the acid growth theory which states that IAA activates the PM-H⁺-ATPase (PM for “plasma membrane”) and therefore enhances proton efflux into the cell wall (Rayle and Cleland 1970; Hager et al. 1971). The increased apoplastic $\mathrm{pH}$ or decreased $\mathrm{pH}$ in cytoplasm and $\mathrm{pH}$ changes that are strongly connected with the physiological activity of proton pump in the plasma membrane and can influence elongation growth through concentrations of sugars (Sukhov 2016; Sukhov et al. 2017). In addition, IAA levels in the seedlings have been shown to be increased by temperature (Gray et al. 1998). Auxin influence proton pump and, thereby, may change the probabilities ${p}_{{\varvec{r}},{\varvec{d}}}$ in our model.

Hence, the next step was to execute numerical calculations of the right hand side (RHS) of Eq. (7). The exemplary results are shown in Fig. 2 (see the captions, for brevity), where “acid” and “auxin” growth are demonstrated using the model parameters. Note the qualitative similarity of the plots in Fig. 2a, b to SI Fig. 1a (compare with the “acid growth” or “auxin growth”—inset, respectively) in Pietruszka (2020). There the similarity of both curves shows that the effective influence of temperature (inverse) or $\mathrm{pH}$ for elongating growth of plant cells is—in approximation—comparable (SI Fig. 1.1 in Pietruszka 2020). Using Eq. (7) and the same set of parameters (for clarity, here we assume probabilities ${p}_{{\varvec{d}}}$ as mainly connected with “acid”, while ${p}_{{\varvec{r}}}$ with “auxin” growth, respectively, see also the comment below) as in Fig. 2a, b, the role of the “auxin growth” (either endo- or exogenous) that was beyond the “acid growth” was exposed (filled area in the plot in Fig. 2c representing auxin-enhanced H⁺-pumping), which has an interesting interpretation that is connected with the existence of the reattachment events, which can be treated as active processes, in the model. These |r > states, which can be created at new locations (sites) after each cyclic (Fig. 1—‘moving window’ reference frame, conserving the number of events during growth) expansion step (bond quenching) may ensure the stable elongation of a system. Note that even in the diffuse growth there is addition and recycling of cell wall material otherwise the cell would burst due to extended thinning if it continues to just stretch.

Auxin, which is a growth-promoting substance (Went 1928) that is presumably located at the growing tip could, among others, ensure cell wall synthesis via the reattachment of new bonds in the elongation zone, thus making the wall more “plastic” or stretchy (Heyn 1940) while maintaining its integrity. This reasoning is in agreement with the fact of the rapid diffusion of auxin (Cholodny 1927) from the lighted to the shaded side of the coleoptile, which causes the quick reinforcement of the diluted convex wall (to secure the structural integrity) by the active |r > processes at the extending (shaded) side (see Fig. 1 in Pietruszka and Lewicka 2006, for illustration). Besides, in the |a >  = >|d >  = >|r > scheme that is presented here, the extensibility and the yield threshold (under turgor pressure) of the cell walls can easily be accommodated by the acid growth theory. Moreover, when the entire system is correlated and the stress–strain relations are fulfilled (Pietruszka 2013; Pietruszka and Olszewska 2020), the simultaneous extension of the cell wall at the sub-apical region may be involved in the pollen tube oscillation(s), thus broadening the potential applicability of the presented formalism. However, unlike diffusion growth, in which the cell expands evenly along its length, specialised cells such as pollen tubes and hairs show apical growth involving local vesicular movement of the wall material (Jensen and Fozard 2015), which is beyond this conjecture and should be taken with caution.

Model Verification: Connection to Experimental Data for Sunflower Hypocotyls

Since the distribution on left hand side of the above equations has already been estimated (Pietruszka 2020) with exceptionally high accuracy (determination coefficient R² ≈ 0.99), the parameters on the right side of the equations above can in principle also be determined (using a fitting procedure, e.g. FindFit procedure in Mathematica, Wolfram Research) and a comparison of α, β shape exponents with the resulting parameters of the right side of Eq. (7) can be made. For illustration and preliminary verification of the model, numerical solution of the RHS of Eq. (7) tailored (fitted) to the suitable experimental data, comparing growth under different buffers, presented, after Hager (2003), is shown in Fig. 3 [for details of the experimental plots and procedures for the left side of Eq. (7), see SI Fig. 1a (and inset) in Pietruszka 2020 and further numerical analysis by a stand-alone ready-to-use computer program presented in Kosek and Pietruszka 2021, see also paragraph below]. It turned out that the obtained probability density distribution better adapts to the experimental growth data caused by auxin (b) than acid (a) growth, which is a natural consequence of the theory of acid growth and the so-called PM-H⁺-ATPase (auxin growth in part relies on acid growth). Note that the probability ${p}_{{\varvec{d}}}$ for the detachment events |d > and ${p}_{{\varvec{r}}}$ for the reattachment events |r > is different from the quantity $k$ or $m$ of detached or reattached tethers in that processes, respectively. It should be noted that the number $k/n$ can be interpreted as the percentage of bond detachment processes in relation to all bonds in the volume elements under consideration.

Fig. 3

Relative elongation scaled vs. pH (red dots) and probability density function (PDF, blue curve), both normalised (unitless), for the attachment/detachment/reattachment processes taking place in the cell wall as a function of the number k of the detachment events |d > as described in Eq. (7). For comparison, the same simulation (fit) parameters were used for both panels: total number of initially attached tethers n = 100, number of reattached tethers m = 1, probability for the detachment events p_d = 0.08 and probability for the reattachment events p_r = 0.05; panel a “acid growth” and b “auxin growth”. Experimental data (red dots) for sunflower hypocotyls (rescaled and fitted in Pietruszka 2020 to the Euler beta function—solid red and solid green line) comes from Hager (2003). Note that in both cases, the peaks appear at the low (acidic) pH. The latter statement means that there is a maximum elongation at a defined number (density) of detachment events, corresponding to the specific pH value in macroscopic measurement (Color figure online)

Model Implementation Procedure

In short, only three steps are needed for practical application.

• (1) Calculation of the increase in cell volume from the initial volume and $\mathrm{pH}$ changes (measurement) at a fixed ambient temperature and constant turgor pressure (Pietruszka 2020).

• (2) Determining the values of shape parameters α and β on the basis of Eq. (21) in Pietruszka (2020). For this purpose, in Kosek and Pietruszka (2021), a ready-to-use stand-alone computer program is written on open scientific software (System for Algebra and Geometry Experimentation, SAGE).

• (3) Determining the values of the parameters of the RHS of Eq. (7), as in the above paragraph, using the fitting procedure. The latter requires the experimental data set of relative elongation vs. $\mathrm{pH}$ (dots in Fig. 3) in the form: data = {{x₁, y₁}, {x₂, y₂},…,{x_N, y_N}}, and any FindFit[…] procedure, like in Mathematica, or its equivalent find_fit(data, model) in SAGE (open access), where “model” refers to the RHS of the Eq. (7).

The latter parameters define the microscopic state (participation of bond detachment/attachment processes) corresponding to the macroscopic (growth) state of the plant coleoptile/hypocotyl/cell and conditions of the optimum growth using Eq. (21) in Pietruszka (2020).

Chemical Potential and Temperature

Even though the explicit dependence for the chemical potential on temperature, ${\mu }_{{\mathrm{H}}^{+}}\left(T\right)$, remains unknown, the role of the “elusive” chemical potential (Baierlein 2001) of the H⁺ ions has been introduced in the diffusive growth and state transitions scenario (e.g. by splitting bonds between the microfibrils) in the cell wall (Pietruszka 2020 and papers cited therein). The lack of an analytic dependence can be temporarily bypassed by assuming ${\mu }_{{\mathrm{H}}^{+}}\left(T\right)={\mu }_{{\mathrm{H}}^{+}}$ and remaining at the $\mathrm{pH}$ level notation. Nonetheless, determining the dependence of the chemical potential on temperature may itself constitute an intriguing research task.

Fortunately, the unambiguous temperature dependence in expansive growth has already found its empirical (Went 1953; Yan and Hunt 1999) and semi-phenomenological (SI Fig. 1b and 1.1 in Pietruszka 2020) description in the form of a growth coexistence curve, which is interpolated—again—by the beta probability density function albeit with α = 3.52 ± 0.02 and β = 1.93 ± 0.01 shape parameters, respectively. This fact can be re-introduced and analysed in a similar way as the $\mathrm{pH}$/expansive growth dependence in the Eqs. (6)–(8) of the latter work, although a mirror symmetry should be applied (SI Fig. 1.1, ibid.).

Further Estimates

The role of temperature cannot be sufficiently appreciated until the dependence of the chemical potential on $T$ is known. In a 0th-approximation, the detachment parameter k might be the best candidate for establishing the relationship with the chemical potential (Baierlein 2001; Matlak and Pietruszka 2000; van der Marel 2004) as it changes the state of a system from state |d, k > to |d, k − 1 > . Moreover, detachment events |d > with the probability

$$P({\varvec{d}}; k, k- 1) =\frac{1}{Z}\sum_{j=1}^{{k}_{\mathrm{max}}=n}{\mathrm{e}}^{-\frac{{E}_{j}^{{\varvec{d}}}-\mu N}{{k}_{\mathrm{B}}T}}$$

(9)

need energy ${E}_{j}^{{\varvec{d}}}$ at a given site “j” for the bond splitting that is connected with the chemical potential ${\mu =\mu }_{{H}^{+}}$ at a given temperature $T;$ notation ${\varvec{d}}; k, k- 1$ means that only $\left\{\left|{\varvec{d}}, k>\to \right|{\varvec{d}}, k-1>\right\}$ processes enter the sum. In Eq. (9), $N={\sum }_{i=\{{\varvec{a}},{\varvec{d}},{\varvec{r}}\}}{n}_{i}$ while the symbol $Z$ denotes the partition function for the entire system and ${k}_{\mathrm{B}}$ is the Boltzmann constant. Note that increasing $k$ by one unit results in a decrease in $n-k$ by one unit, where $n$ is the initial number of the |a > states of a system. On the other hand, the reattachment events would give rise to the probability

$$P\left({\varvec{r}}; m, m+1\right)=\frac{1}{Z}\sum_{j=1}^{m<k}{\mathrm{e}}^{-\frac{{E}_{j}^{{\varvec{r}}}-\mu N}{{k}_{\mathrm{B}}T}},$$

(10)

where ${E}_{j}^{{\varvec{r}}}$ corresponds to the energies for the bonding events $\left\{\left|{\varvec{r}}, m>\to \right|{\varvec{r}}, m+1>\right\}$ that, in general, may be different from the initially attached states’ energies. Again, because these events are assumed to be uncorrelated (although the condition $m<k$ introduces correlations into the system), from the initial assumption of independent events, the joint probability P would approximately read

$$P\left(E={E}^{{\varvec{r}},{\varvec{d}}}; {\mu }_{{\mathrm{H}}^{+}}, T\right)\cong P({\varvec{r}}; m, m+ 1)P({\varvec{d}}; k, k-1).$$

(11)

Note that Eqs. (9)–(11) introduce the chemical bond disconnection/reconnection events (of discrete energies ${E}^{{\varvec{r}},{\varvec{d}}}$) at an ambient temperature and a chemical potential ${\mu =\mu }_{{\mathrm{H}}^{+}}$ (Fig. 4), which can be performed at the expense of the ATP energy in the process known as PM-H⁺-ATPase. The higher the temperature the melting/quenching processes of the tethers are the more probable (Fig. 4). That will give rise to attain a faster cell wall expansion at the optimum (critical) temperature, which will also be discussed later. This interpretation can lead to the formulation of a $\mathrm{pH}\left({\mu }_{{\mathrm{H}}^{+}}\left(T\right),T\right)$ dependence as the microscopic foundation of “acid growth hypothesis” (note the explicit and entangled dependence of $\mathrm{pH}$ on temperature). Since all of the events {|a > , |d > and |r >} in the model are assumed to be statistically independent (uncorrelated) and therefore, represented by random variables, the solution of this problem at this level of refinement is exact.

Fig. 4

Probability for the detachment/reattachment events that were governed by Poisson point processes in the cell wall as a function of the chemical potential of H⁺ ions, Eq. (11)—with no correlations present, parameterised by temperature: 283.15 K = 10 °C (yellow), 293.15 K = 20 °C (magenta) and 303.15 K = 30 °C (blue). The model parameters were equal to: ${E}^{{\varvec{d}}}=0.055$ eV, ${E}^{{\varvec{r}}}=0.05$ eV, where we assumed ${E}^{{\varvec{d}}}\equiv {E}_{j}^{{\varvec{d}}}$ and ${E}^{{\varvec{r}}}\equiv {E}_{j}^{{\varvec{r}}}$ for every site “j”, for simplicity. The Boltzmann constant ${k}_{\mathrm{B}}=1.38\times {10}^{-23}$ J/K; energy conversion from electron volt to Joule: E_(eV) = E_(J) × 6.241509 × 10¹⁸ (Color figure online)

Weak correlations, which originate from the constraint $m<k$ (reattachment event, can occur providing that the detachment event has occurred), can be introduced into the system of tethers by considering the conditional probability $P\left({\varvec{r}}|{\varvec{d}}\right):=\frac{P\left({\varvec{r}}\cap {\varvec{d}}\right)}{P\left({\varvec{d}}\right)}$, where the nominator is unknown and must be determined. However, assuming Boltzmann distribution, it can be calculated from the formula $P\left({\varvec{r}}\cup {\varvec{d}}\right)=P\left({\varvec{d}}\right)+P\left({\varvec{r}}\right)-P\left({\varvec{r}}\cap {\varvec{d}}\right)$. From the set theory argument, since $P\left({\varvec{d}}\right) \propto \frac{k}{N}$ and $P\left({\varvec{r}}\right) \propto \frac{m}{N}$ and $P\left({\varvec{a}};{\varvec{d}}\cup {\varvec{r}}\right)=P\left(N\right)=1$, we get

$$P\left( {\user2{r}|\user2{d}} \right) \cong 1 - {\text{e}}^{{ - \frac{{E^{\user2{r}} - E^{\user2{d}} }}{{k_{{\text{B}}} T}}}} - N{\text{e}}^{{ - \frac{{E^{\user2{d}} - \mu N}}{{k_{{\text{B}}} T}}}}.$$

(12)

The expression of the RHS of Eq. (12) is presented in Fig. 5, where the transition area in the vicinity of the “critical” value of the chemical potential ${\mu }_{\mathrm{c}}={\mu }_{{\mathrm{H}}^{+}}^{\mathrm{c}}$ is plotted. Note that above $\mu ={\mu }_{\mathrm{c}}$, $P\to 1$. The latter can be interpreted as meaning that below a certain value of $\mu \to {\mu }_{\mathrm{c}}$, there are not enough |d > states that are accessible for reattachment. Then, at about $\mu \cong {\mu }_{\mathrm{c}}$, many states may detach/reattach, thus causing a state transition (and expansion) in the evolving cell wall (cf. Pietruszka 2020). Above the “critical” value of the chemical potential ${\mu }_{\mathrm{c}}$, all states are available for expansion and can be reattached in the growth shift zone (Fig. 1). This scenario precedes, however, in line with the “acid growth hypothesis”—note that “acid growth” has been observed when the auxin-depleted segments of maize were submerged in an acid buffer solution; the segments began their elongation growth immediately (“acid growth”), whereas the auxin-induced growth (“auxin growth”) began after a delay (lag phase), as is shown in Fig. 1 in Hager (2003). The character of the plot in Fig. 5 would apparently reproduce the former case.

Fig. 5

Conditional probability $P=P\left({\varvec{r}}|{\varvec{d}}\right)$ for the detachment/reattachment events that were governed by Poisson point processes in the cell wall as a function of the level of the chemical potential of H⁺ ions. Calculated in the presence of weak correlations in the system of tethers, as described by Eq. (12). The model parameters were equal to: ${E}^{{\varvec{d}}}=0.0251$ eV, ${E}^{{\varvec{r}}}=0.0255$ eV; T = 22.27 °C. Note that if ${E}^{{\varvec{d}}}={E}^{{\varvec{r}}},$ $P\left(x\right)=1-\left(1+N\right)\mathrm{exp}\left(-x-a\right)$, where $x=\frac{\mu N}{{k}_{\mathrm{B}}T}$ and $a={E}^{{\varvec{d}}}$. Compare with Fig. 4 in Pietruszka and Olszewska (2020) for the existence of an optimal growth resonance peak in Hyacinthus orientalis L. pollen tubes

Potential Applicability of the Framework to Pollen Tubes

Another microscopic interpretation is provided by a comparison with Figs. 4 and 5 in Pietruszka and Olszewska (2020) for Hyacinthus orientalis L. and Nicotiana tabacum L. pollen tubes, and SI Fig. 1 in Pietruszka (2020). In the first article, a change in ambient temperature, and therefore the energy that is supplied to a system (here: elongating pollen tube), creates resonance states for two temperatures (and the corresponding energies): germination $({E}_{\mathrm{ger}}$) and optimum (${E}_{\mathrm{opt}}$). In the language of our model, i.e. for diffusive growth, it looks as though in ${E}_{\mathrm{ger}}$ the bonds are mainly detached and that the system—plant cell wall—is ready for expansion, while in ${E}_{\mathrm{opt}}$, reattachment and detachment events occur simultaneously that enable quick and stable elongation. Changing the chemical potential with temperature “selects” the appropriate states (bonds) for this implementation. However, further shifting of the chemical potential with temperature does not cause an increase in elongation because the available free bonds (detached states) begin to expire. The elongation gain ceases, which is consistent with the observation. Assuming a permanent (i.e. with a constant velocity) displacement of the “observation window”, the entire process will reproduce a sigmoid growth curve (see for instance Fig. 9 in Pietruszka 2020), and is fully compatible with the existence of the maximum at the optimum temperature and $\mathrm{pH}$ (see Fig. 6 and compare with SI Fig. 1.1 in Pietruszka 2020). Taken together, the use of Boltzmann statistics will not cause the expected unlimited monotonic increase in elongation as a function of temperature for all physiological temperatures. On the contrary, this process will reach its maximum at the equilibrium (critical) temperature between detachment and reattachment events. There will also be a well-defined cut-off energy, above which the increase in length will be zero (ibid.).

Fig. 6

The Lorentz resonances (green dashed line) of a spectral exponent $\beta$ (solid red line) at the energies ${E}_{1}$ and ${E}_{2}$ corresponding to germination and optimum growth events (Pietruszka 2021) in case of pollen tubes (compare also with Figs. 4, 5 and the paragraph “Temperature-induced sudden onset of coherent action in pollens—Lorentz resonances” in Pietruszka and Olszewska 2020). Envelope curve (blue) superimposed for illustrative purposes is a usually observed elongation as a function of the reduced ($T/{T}_{\mathrm{max}}$, unitless) temperature (Went 1953; Yan and Hunt 1999). Presumably, the energies ${E}_{1}$ and ${E}_{2}$ (corresponding to germination and optimum growth temperatures) are indistinguishable for a mature plant (when ${E}_{1}$ tends to ${E}_{2}$), which means that the maxima of both curves (growth and resultant Lorenz curve) overlap in this case. Because of the statistics, for multi-cellular organs like coleoptile/hypocotyl (segment) the Lorentz maximum at ${E}_{2}$ will expected to be smeared out, possibly explaining the broad shape of the temperature-dependent expansion curve (blue), see also SI Fig. 1.1 in Pietruszka (2020). The asymmetry of this curve seems due to the cut-off energy at temperature $T=1$, when the detachment events expire altogether (Color figure online)

In the above context, it is also worth noting that although the role of auxin for single cells such as root hairs and pollen tubes is still unknown, the critical exponent and entropy calculated for extracellular ionic fluxes perturbed by IAA or 2-4D (2,4-dichlorophenoxyacetic acid, synthetic auxin) vs. normal state (control) were recently obtained in Pietruszka and Olszewska (2020). These data may be included in further studies, however, tip growing cells like root hairs and pollen tubes, grow by localised exocytosis at the apex of methyl esterified pectins that decrease cell wall viscosity locally (Hepler et al. 2013; Adhikari et al. 2020 for review), being apparently incompatible with the proposed model. This limitation can be circumvented in calculations by assuming that the lower viscosity can be modelled with a reduced (diluted) overall number of chemical bonds in the model equations.

Final Comment and Short Summary

Noteworthy, the Lockhart constant, which was redefined in Pietruszka (2020) from a constant ${\varPhi }_{0}$ to a form that was dependent on $\mathrm{pH}$ and T

$$\varPhi =\varPhi \left(\mathrm{pH}, T\right)\propto {T}^{\alpha -1}{\left(1-T\right)}^{\beta -1}{\mathrm{pH}}^{\beta -1}{(1-\mathrm{pH})}^{\alpha -1}{\varPhi }_{0}$$

(13)

together with the canonical Lockhart equation, can be combined with the appropriately modified (by temperature) Eq. (7), thereby providing a new integro-differential equation, where the macroscopic $\left(P, V, T\right)$ and the microscopic set of variables $\left\{{p}_{{\varvec{d}}},{ p}_{{\varvec{r}}}, k, m\right\}$ or $\left\{{E}^{{\varvec{d}},{\varvec{r}}}, \mu \right\}$ occur concurrently. The solution of the latter can provide mutual information and anticipate simultaneous predictions about the micro- and macro-state of an evolving system, which would enable the fine tuning of the parameters that correspond to the different environmental cues of a biotic (endo- or exogenous) or abiotic character. This is, however, an extended issue that needs further investigations. Nevertheless, this work is an attempt to introduce explicitly statistical (binomial, Poisson and Boltzmann) distributions to model the cell wall during expansive growth, and I believe that the concomitant presence of the microscopic (${E}_{j}^{{\varvec{d}},{\varvec{r}}}$, ${\mu }_{{\mathrm{H}}^{+}}$) and macroscopic—$\mathrm{pH}$ and $\left(P, V, T\right)$ observables will facilitate significant insights on the cell wall dynamics at a molecular level.

The temperature dependence of the chemical potential of hydrogen ions appears to be a key part of the expansive growth of the cell wall (Hoffmann et al. 2020). While some discussions have been made regarding the critical value of the chemical potential (${\mu }_{{\mathrm{H}}^{+}}^{\mathrm{c}})$ to initiate detachment events, the direct implications of the form of ${\mu }_{{\mathrm{H}}^{+}}$ as a function of temperature were not discussed. I have to admit that little is known about this key relationship, and it is still an open research question.

Conclusions

In this study, I attempted to establish the thermodynamic basis of expansive plant growth, in particular, the contribution of “acid growth” where low $\mathrm{pH}$ induces fast expansion and “auxin growth” where endogenous or exogenous auxin induces rapid expansion. By introducing formal statistical reasoning (chemical bond dynamics in the detachment and reattachment of cell wall microfibrils), it was possible to generate a probability density function, Eq. (7), that resembled growth depending on $\mathrm{pH}$ or temperature distribution (Pietruszka 2020). Then, with a few assumptions that are partly based on experimental data (for example, low $\mathrm{pH}$ triggers detachment of cell wall microfibrils, auxin triggers low $\mathrm{pH}$, but also an active process of reattachment), it was possible to synthesise a link between the microscopic, explicit statistical explanation of bond dynamics and the macroscopic rheological properties of the cell wall at a given $\mathrm{pH}$ and temperature, which then permitted an interpretation of the non-monotonic growth behaviour with respect to $\mathrm{pH}$ and temperature to be proposed. Equation (12), which elucidates how such a non-monotonic behaviour translates into a phase transition, is particularly significant.

The problem of the chemical and physical nature of the reversible interactions between the cell structural elements, which are important for understanding expansive growth, was investigated on a thermodynamic basis (Veytsman and Cosgrove 1998) through the free energy of the expanding cell wall. When searching for a preliminary description of the microscopic irreversible processes that lead to the expansion of cell walls, I further examined the Sridhar et al. (2018) dynamic approach. Therefore, the current model is a combination of the latter with the $\mathrm{pH}$ and $T$ macroscopic quantities (having strictly molecular bases) essentially governing growth through the Poisson process and the generalised Lockhart equation. Such modelling could provide noteworthy predictions to test the contribution of the so-called acid growth in diverse plant systems, from the whole-plant level to single cells.

As it was recently suggested, the common denominator that is responsible for the expansive growth of the cell wall seems to be the temperature-dependent chemical potential of the H⁺ ions (Pietruszka 2020). This idea, which is in accordance with the “acid growth hypothesis” (already encoded in the definition of $\mathrm{pH}$ itself), was qualitatively/quantitatively validated in the presented semi-empirical model at the microscopic level. As a result, the well-known hypothesis of Hager and Cleland, which had been experimentally verified by many authors for almost five decades and which was confirmed in this model analysis at the microscopic level, should acquire the full status of the “acid growth theory” in plant science. “The acid growth theory (Rayle and Cleland 1992) of auxin-induced cell elongation is (still_MP) alive and well”.