1 Introduction

Acetylene plays an important role in the formation and nucleation of soot particles and polycyclic aromatic hydrocarbons (PAHs) in all hydrocarbon flames due to the H-abstraction/C2H2-addition sequences in soot formation and growth [1]. The concentration of C2H2 can vary considerably over very small spatial and very short temporal scales. Therefore, the detection of C2H2 in flame conditions can contribute to understanding physical and chemical processes during soot formation. It can also help to control the emission of soot particles which have adverse effects on the environment and health. However, due to the harsh environment background in the sooting flames, such measurement is not trivial.

Laser polarization spectroscopy (PS), which is a coherent laser diagnostic technique, has been developed to offer non-invasive detection of minor combustion species with higher accuracy [2]. Compared with other nonlinear laser techniques, PS has the advantage of high intensity, and its experimental setups are relatively simple. The background influence can be reduced by a high-quality pair of crossed polarizers so that the signal from the target species can be discriminated from the surrounding environment [3].

PS has been applied in the UV/visible range based on electronic transitions of OH, C2, NH [4,5,6], and two-photon electronic transitions of NH3 and CO [7]. However, only limited species can be measured in this spectral range. Many important species, such as CO2, C2H2, and CH4, cannot be probed by UV/visible PS as they do not possess accessible transitions. Mid-infrared laser polarization spectroscopy (IRPS) has been introduced as a tool to detect molecules in the mid-IR (2–5 um) via ro-vibrational transitions [3]. By probing molecular vibrational transitions, it is expected that the influence of molecular collisions on the signal will be reduced.

IRPS has been successfully applied in various hydrocarbon flames to detect infrared active species, such as CH4, CO2, HCl, and HCN, in the mid-IR (2–5 um) range via rovibrational transition [8, 9]. For example, Li et al. performed the first IRPS measurement in laminar flames to detect CO2 and H2O at atmospheric pressure [10], followed by the measurement of OH and H2O at low-pressure laminar flames [11]. However, the application of IRPS on C2H2, which is the main precursor of soot particles and PAHs, is scarce. Recently, Sun et al. [12] reported a quantitative measurement of C2H2 in a sooty flame, however, this was only performed at one fixed location in the flame with the calibration performed separately in a different location. To the authors' knowledge, there is no spatially resolved systematic IRPS measurement of C2H2 in the flame that has been previously reported in the literature.

This work reports on the use of IRPS to quantitively measure C2H2 in C2H4/air laminar premixed sooty flames, using a McKenna burner at atmospheric pressure. The fundamental rovibrational transitions of C2H2 were probed at the wavelength of around 3.1 μm in the near IR range. The IRPS spectra were recorded at the height above the burner surface (HAB) from 3 to 11 mm for spatially resolved measurement. The Chemkin model, at equivalence ratios of 1.3 and 1.5, was used to determine the calibration factor between the measured IRPS signals and the C2H2 mole fractions, \({\chi }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}}\). The paper divides into the experimental details, calibration, and the quantitative measurement of C2H2 along with the soot volume fraction at different heights above the burner. Finally, the collisional effect from the major combustion species is evaluated and discussed.

2 Experimental setup

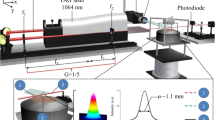
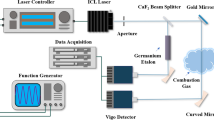
The experiment setup was organized into three parts, which are a laser system to generate the infrared radiation at a spectral region around 3.1 μm, a McKenna burner to produce premixed C2H4/air sooty flame, and a laser diagnostics system with signal detection. Figure 1 shows a schematic diagram of the setup used in this work. The gas temperature at different HAB was measured by a 75 μm-diameter uncoated Pt/Pt-R thermocouple (Omega). The measured values were corrected based on the heat radiation loss method [13, 14]. The fine-wire thermocouple was selected to minimize conductivity and radiation effects and other catalytic effects at the junction.

Fig. 1
figure 1

Experimental setup of IRPS for C2H2 detection in premixed C2H4/air flames. M mirror; BS beam splitter; B burner; P polarizers; WP waveplate; BD beam dump; L lens; D1 detector for the input laser power measurements; D2 detector for the IRPS signal; Pre-AMP pre-amplifier. The arrows indicate the direction of laser propagation

Full size image

Flat premixed C2H4/air flames were produced in a water-cooled McKenna burner, which had a porous plate with a diameter of 60 mm. A steel plate of 80-mm diameter was employed at a height of HAB = 21 mm to stabilize the flames. To ensure the homogeneous mixing of gases, the mixture of C2H4 and air was transferred through a 10-m Teflon pipe from the mass flow meter to the burner. The total flow rate of C2H4 and air was controlled at 5 L/min. Additionally, nitrogen gas was controlled at the flow rate of 1 L/min and used as co-flow to shield the flames. The burner was traversed vertically with a resolution of 1 mm to perform the measurement at different HAB.

The second harmonic of an injection-seeded Nd:YAG laser (Quantel, YG980), operated at 532 nm, was used to pump a tuneable dye laser (Quantel, TDL90) running with the mixture of laser dyes LDS 798 and LDS 765 purchased from Luxottica/Exciton. The output of the dye laser was then difference frequency mixed with a part of the Nd:YAG fundamental infrared 1064 nm beam in a mixing unit with a lithium niobate (LiNbO3) crystal. Subsequently, a tunable IR laser beam was generated at the wavelength of around 3.1 µm with the power of 1.5 mJ per pulse. The linewidth (FWHM) of the seeded Nd:YAG laser and the tuneable dye laser is 0.005 cm−1 and 0.05 cm−1, respectively. This results in a linewidth (FWHM) of ~ 0.05 cm−1 of the mid-IR beam at 3.1 μm. A wavelength meter (Bristol Instrument, 821B) was used to monitor the change in the wavelength of the dye laser during wavelength scanning.

A 632.8 nm HeNe laser was further overlapped with the IR beam in the first CaF2 beam splitter (BS1) to visualize the IR beam path and facilitate alignment. After passing the second beam splitter (BS2), ~ 4% of the IR beam was reflected and used as the probe beam, while the remaining transmitted IR beam was used as the pump beam.

The pump and the probe beams were focused by f = 500 mm and f = 750 mm CaF2 lens, respectively. A quarter-wave plate was placed in the path of the pump beam to generate a circular polarization, which enhances the P and R branches of C2H2 detection.

The burner was placed between two crossed IR polarizers (YVO4) in the path of the probe beam. The probe beam was crossed with the strong pump beam at the detection volume in the center of the burner with a crossing angle of approximately 5○. After passing the detection volume, the pump beam was blocked by a beam dump, while the probe beam emerged parallel using an f = 750 mm CaF2 lens (L3) and then focused by an f = 100 mm CaF2 lens (L4) to a liquid-nitrogen-cooled indium-antimonide (InSb) detector (Hamamatsu Photonics, P5968-060).

Additionally, in order to monitor the input laser power, ~ 4% of the probe beam was reflected to an amplified IR detector (Thorlabs, PDA10PT-EC) using a beam splitter (BS3). After being triggered by the Nd:YAG laser, both the laser power signal and the IRPS signal of C2H2 could be simultaneously collected and stored in a 1-GHz oscilloscope to avoid errors associated with the input power fluctuation.

3 Numerical analysis

According to Demtröder [15], the PS signal can be given by the following equation when two polarizers are perfectly crossed and there is no other birefringent optics between the two polarizers:

$${I}_{\mathrm{IRPS}}\cong {I}_{\mathrm{probe}}\left(\xi +{\left(\frac{\Delta \alpha l}{4}\right)}^{2}L\left(\omega \right)\right),$$
(1)

where \({I}_{\mathrm{probe}}\) is the intensity of the probe beam; ξ is the leakage through the crossed polarizers; l is the interaction distance between the pump and probe beams along the probe beam path; L(ω) is the line shape function; Δα is the induced dichroism, which can be expressed as follows:

$$\Delta \alpha =N{\cdot f}_{B}\bullet {\sigma }^{2} \cdot \frac{{I}_{\mathrm{pump}}{\tau }_{\mathrm{pump}}}{\mathrm{\hslash }\omega }\cdot {\xi }_{J{J}^{\mathrm{^{\prime}}}}$$
(2)

where N is the number of molecules or radicals; fB is the Boltzmann fraction; σ is the polarization-independent absorption cross-section; \({I}_{\mathrm{pump}}\) is the intensity of the pump beam; \({\tau }_{pump}\) is the pulse width of the pump beam; ω is the laser wavelength, and ξJJ’ is the polarization numerical factor.

At atmospheric pressure and following IR excitation, the collision broadening is significantly larger than the Doppler broadening. Thus, the Lorentzian function was selected to demonstrate the line shape: [16]

$$L\left(\omega \right)={\left(\frac{1}{1+{(2\left(\omega -{\omega }_{0}\right)/(\Delta {\omega }_{self}+\Delta {\omega }_{foreign}))}^{2}}\right)}^{n},$$
(3)

where ω0 is the center wavelength; ∆ωself and ∆ωforeign are the line-broadening due to the self and the buffer gas collisions, respectively; and n is the Lorentzian power fitting factor, which is 3 for non-saturated pump energy in this work. The integration over the fitting lines and the maximum intensity at the center wavelength was used to present the integral and maximum IRPS intensities, respectively.

4 Chemical kinetic model

The flames with lean conditions were simulated using the premixed laminar burner-stabilized flame model in the Chemkin-Pro Software package. The mechanism developed at the University of Southern California (USC) was selected to conduct chemical kinetic analysis for simulating the mole fraction of C2H2. The mechanism used in this work is the “High-Temperature Combustion Reaction Model of H2/CO/C1-C4 Compounds” with 784 reactions including a comprehensive reaction model of ethylene combustion [17]. The maximum number of grid points was 250 to provide grid-independent results and other solver parameters of this model were set as their default values. The Chemkin simulation was conducted, by imposing the measured temperature profiles, for Φ = 1.3 and 1.5. The Chemkin model is used to calibrate the simulated C2H2 mole fractions, \({\chi }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}}\), from the experimental IRPS signals to obtain the quantitative calibration factor. Then, the IRPS intensities of the sooty flame were calibrated to their mole fractions by the calibration factor. The mole fractions of C2H2 as a function of the height above the burner were well resolved at different sooty flame conditions.

5 Results and discussion

Figure 2 presents the dependence of the IRPS signal intensity on the pumping laser power. The dependence was measured by varying the pump laser power with different neutral density filters and using the mixture of 2.5% acetylene and N2. In this work, the maximum laser energy of the 3.1 μm mid-IR beam was 1.5 mJ, which contributes to the maximum pump laser energy of 1.44 mJ. The quadratic dependence in Fig. 2 indicates the laser power is still within the unsaturated regime because the PS signal is expected to be the square of the pump laser power (\({I}_{\mathrm{IRPS}}^{\mathrm{Unsaturated}}\propto {I}_{\mathrm{pump}}^{2}\)) under unsaturated conditions and to be independent of the pump laser power under saturated conditions [4].

Fig. 2
figure 2

Dependence of the IRPS signal intensity on the pumping laser power. The black line presents the fitting of the data points. The pump energy used in this work is 1.44 mJ

Full size image

Shown in Fig. 3, a typical example of measured and simulated IRPS spectra of C2H2 are collected in a flame with Φ = 2.1 and HAB = 5 mm. For the simulated spectrum of C2H2, the parameters of line position and intensity were extracted from the HITRAN database [18], and the line profile was characterized by the Lorentzian function. The measured spectra were compared with the simulated spectra to identify the location of the transition lines. According to Fig. 3, a strong vibrational transition P(19) line is marked and selected as the candidate line in this work due to its high intensity and lower interference from the background noise, under flame conditions. As described in Eqs. (1) and (2), some weak transitions with small absorption cross-section, σ, may not be detectable using unsaturated IRPS, where the pump energy was not sufficiently high.

Fig. 3
figure 3

Simulated and measured IR spectra of C2H2 in the flame with Φ = 2.1 and HAB = 5 mm

Full size image

To obtain a high-resolution IRPS signal of the P(19) line, a low-speed wavelength scan was performed within a narrow spectral range from 3248.3 to 3248.8 cm−1. Figure 4 shows the IRPS scan of the P(19) line in flame with Φ = 2.3 at HAB of 5 mm, 7 mm, and 10 mm. The scan wavelength interval was 0.00167 cm−1 between two consecutive measurements.

Fig. 4
figure 4

Typical examples of IRPS line shape of P19 transition for C2H2 in (a) the cold flow and the high-temperature flame with Φ = 2.3 at (b) HAB = 5 mm, (c) HAB = 7 mm, and (d) HAB = 10 mm. The red lines indicate the Lorentzian-cubed fitting for the measurement data

Full size image

It is clear from Fig. 4(b) to (c) that although the IRPS intensity decreases with the increasing HAB, the signal linewidth at different HAB is very similar. Under flame conditions, the linewidth is both temperature- and pressure-dependent due to the collision broadening and Doppler broadening. The full-width-half-maximum (FWHM) Doppler width may be calculated as a function of temperature, T, following Demtröder: [19]

$$\Delta {\omega }_{D}={\omega }_{0}\sqrt{\frac{8kTln 2}{m{c}^{2}}},$$
(4)

where \({\omega }_{0}\) is the center wavelength; c is the speed of light; k is the gas constant; m is the molecular mass. The bimolecular collision broadening of a spectral line can be corrected for the temperature effect using [20, 21],

$$\Delta {\omega }_{C}\propto {\gamma }_{0}{\left(\frac{{T}_{0}}{T}\right)}^{0.7},$$
(5)

where \({\gamma }_{0}\) is the collision broadening coefficient at the reference temperature \({T}_{0}\). According to Eqs. (4) and (5), the Doppler width increases with the temperature, while the collision width has an opposite trend. At atmospheric pressure, the collision broadening is larger than the Doppler broadening for the non-saturated IRPS signal; therefore, the signal linewidth is dominated by collision broadening and decreases with increasing temperature. However, this change is not obvious in flames when the temperature is more than 1000 K [12]. In order to study the effects of linewidth, the IRPS intensity of the P(19) line was estimated by two methods, which are the integration of the signal intensity over the whole wavelength and the maximum intensity at the center wavelength. The comparison between the two methods is used to investigate the effect of collision width on IRPS intensities.

On the other hand, as a non-linear technique, the IRPS signal intensity is proportional to the laser power cubed (\({I}_{\mathrm{IRPS}}^{\mathrm{Unsaturated}}\propto {I}_{\mathrm{pump}}^{2} \cdot {I}_{\mathrm{probe}}\)). The slightly noisy signal can be caused by the unsaturated laser power and pulse-to-pulse laser energy, due to the nature of frequency mixing used to generate the mid-IR tunable laser radiation.

Figure 5 shows the effect of pump beam scattering on the IRPS signal. Compared to pump-off, the background level of pump-on is increased by 15%. As the energy of the probe beam is much lower than the pump beam, the scattered light is mainly contributed by the pump beam and further results in the increase of background level. Although pump scattering can be reduced by increasing the crossing angle between the probe beam and the pump beam, however, a large crossing angle may cause a weaker IRPS signal due to a smaller detection volume. Therefore, the crossing angle used in the experiment is 5° to achieve relatively less pump scattering, but sufficient IRPS signal intensity. On the other hand, compared to the IRPS signal, the fluctuation of the background level is only 1% of the maximum IRPS intensity. Thus, the effect of pump scattering can be neglected in this work.

Fig. 5
figure 5

Effect of pump beam scattering on IRPS signal. The dashed line in the insert figure shows the average background level with and without pump beam scattering

Full size image

To be able to calibrate the IRPS signal intensity in flame conditions, the mole fraction of C2H2 was varied by changing the HAB in Φ = 1.3 and 1.5. For these two Φ’s, Chemkin is expected to produce reliable results [22, 23] and the mole fraction of C2H2 is high enough to be used for the calibration.

Figure 6 shows the square roots of the experimental IRPS intensities as a function of the simulated mole fractions of C2H2 for Φ = 1.3 and 1.5 flame conditions. The experimental signals at different HAB are compared with the Chemkin model in Fig. 6(a) and (c) and present good agreement. Two methods, i.e., the integral IRPS intensity and the maximum IRPS intensity, are presented. The integral IRPS intensity is presented by summing the signal intensity over the whole wavelength, while the maximum IRPS intensity is estimated by summing the signal intensity at the center wavelength (\({\omega }_{0}\) ± 0.09 cm−1). The line fitting in Fig. 6 (b) and (d) shows the calibration equation. Both methods yield a consistent trend, however, the maximum IRPS intensity shows a larger variance.

Fig. 6
figure 6

Comparison between the simulated \({\chi }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}}\) using the Chemkin model and the experimental IRPS signal estimated using the square root of (a) the integral IRPS intensity and (c) the max IRPS intensity for Φ = 1.3 and 1.5. The line fitting in (b) and (d) represents the calibration equation

Full size image

According to Eqs. (1) and (2), the IRPS intensity is proportional to the square of the mole fraction of the investigated species. Therefore, both quantities are connected by a single calibration factor. Based on a simple linear fitting, the calibration factor, C1, for line maximum was found to be 2.48 × 10–3. The line integration calibration factor, C2, was 1.45 times C1. The confidence level and an R-squared value were 95% and 0.977 and 0.939 for the line integration method and the line maximum method, respectively.

As the integral IRPS intensity has a better agreement between the experimental and modeling results, it has been selected to infer the C2H2 mole fraction from the IRPS intensity for the sooty flames in the subsequent measurements, namely Φ = 1.7, 2.1, and 2.3.

On the other hand, the difference between calibration using the integral IRPS intensity and the maximum IRPS intensity is caused by the effects of linewidth, which is decreased with increasing temperature. It should be mentioned that although the maximum IRPS intensity does not consider the effect of linewidth, its calibration still can be fitted well by a linear equation with a relatively high R-squared value. This indicates that the effect of linewidth is not obvious in the C2H4/air flames, which is consistent with the work reported by Sun et al. [12].

Figure 7 shows the mole fraction of C2H2 as a function of the height above the burner surface for the sooty flame with Φ = 1.7, 2.1, and 2.3. The C2H2 mole fraction at each data point is calibrated from the corresponding line integration calibration factor, C2. The HAB was elevated from 3 to 10 mm for spatial-resolved measurement. The error bars are calculated based on the three repetitive measurements. As fuel-rich flames can promote the formation of C2H2, more C2H2 species are detected in the flame with a higher equivalent ratio. From Fig. 7, the first observed C2H2 mole fraction appeared at HAB of 3 mm and measured as 2003 ppm, 2217 ppm, and 2495 ppm, for Φ = 1.7, 2.1, and 2.3, respectively. The mole fraction increased as the HAB increased to reach the maximum value of 2296 ppm, 2807 ppm, and 3478 ppm, for Φ = 1.7, 2.1, and 2.3, respectively. According to the background level and the slope from Fig. 6(b), the Limit of Detection (LoD) was calculated as 35 ± 5 ppm.

Fig. 7
figure 7

Discrepancy between the experimental and the simulated C2H2 mole fraction using Chemkin for rich flame flames condition at Φ = 1.7, 2.1, and 2.3

Full size image

In addition, the location of the peak mole fraction of C2H2 also varies with the flame conditions. When the equivalent ratio increases from 1.7 to 2.3, the peak mole fraction of C2H2 shifts from the HAB of 4–5 mm. On the other hand, when increasing HAB, the signal reduction of C2H2 could be contributed by the formation of PAHs and soot in the upward direction. It was observed that the mole fraction reaches a plateau region at HAB of ~ 8 mm. This mole fraction profile is similar to the results in C2H4/air flames with Φ from 1.77 to 2.37 reported by Otti et al. [24], where the fuel-rich flames exhibit a greater peak mole fraction of C2H2 and the mole fraction decays with increasing HAB until ~ 7 mm.

On the other hand, Fig. 7 also compares the scaled IRPS results with the Chemkin simulated results for Φ = 1.7, 2.1, and 2.3. Compared with the measured results, the simulated results have a higher peak mole fraction of C2H2 and its location also shifts to the higher HAB. This discrepancy becomes more obvious when increasing the equivalent ratio. At Φ = 2.3, the simulated peak mole fraction of C2H2 and its location are approximately 750 ppm and 2 mm higher than the measured results, respectively. The clear discrepancy between the measured and computed \({\chi }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}}\) values is evident of the limitation to applying Chemkin in rich flame conditions because the prediction of soot formation is unavailable in this Chemkin model. As C2H2 is consumed during the formation of soot, the higher mole fraction of C2H2 was predicted in the simulated results, especially in the highly sooting conditions. A similar discrepancy was also observed by Bennett et al. in ethylene laminar flame [25].

One of the advantages of IRPS is its quantitative nature. This is because molecular collisions are not so pronounced as, for example, in Infrared Laser Induced Fluorescence (IRLIF). Molecular collisions may impact the IRPS signal in two ways, namely, in the form of reorientation and energy transfer. The former results in losing the orientation memory created by the pump beam and the latter changes the overlapping integral between the laser line width and the absorption line width, because of the collisional line broadening. For the short effective pulse length, estimated as 4 nsec, the numbers of kinetic collisions in C2H2-N2 and C2H2-CO2 systems are less than 5 and less than 1, respectively. In other words, molecular collisions are dominated by N2, and prior knowledge of the mixture fractions may not be necessary.

To be able to evaluate the effect of the collisional broadening of the major species, we assume a linear combination of the collisional broadening based on C2H2–N2 and C2H2–CO2. The effective collisional broadening coefficient, taken into consideration only CO2 and N2, is approximately given as follows:

$${\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-\mathrm{x}}\approx {\chi }_{{\mathrm{N}}_{2}}\cdot {\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-{\mathrm{N}}_{2}}+{\chi }_{{\mathrm{CO}}_{2}}\cdot {\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-{\mathrm{CO}}_{2}},$$
(6)

where \({\chi }_{{\mathrm{N}}_{2}}\) and \({\chi }_{{\mathrm{CO}}_{2}}\) are the mole fraction of N2 and CO2, respectively, and \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-{\mathrm{N}}_{2}}\) and \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-{\mathrm{CO}}_{2}}\) are broadening coefficients caused by N2 and CO2, respectively. For the P(19) transition, the collisional broadening coefficients \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-{\mathrm{N}}_{2}}\) and \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-{\mathrm{CO}}_{2}}\) is 0.073 cm−1 atm−1 and 0.082 cm−1 atm−1, respectively [26, 27].

Figure 8(a) shows the spatial-resolved temperature profile measured by the thermocouple, while Fig. 8(b) presents the spatial-resolved profiles of the mole fraction of N2 and CO2 for the flame with Φ = 1.5. Figure 8(c) shows the value of \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-\mathrm{x}}\) as a function of HAB for the flame with Φ = 1.5 and 2.3. Although the mole fraction of N2 decreases as the increasing HAB while CO2 has an opposite trend, the mole fraction of N2 is more than 20 times higher than that of CO2, which makes the collisional broadening coefficients \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-{\mathrm{N}}_{2}}\) dominates the total collisional broadening coefficients \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-\mathrm{x}}\). Therefore, according to Fig. 8(c), the values of \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-\mathrm{x}}\) are around 0.074 cm−1 atm−1 for both flames, which is very similar to the collision broadening coefficient of N2. In addition, comparing the selected flames with Φ = 1.5 and 2.3, the \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-\mathrm{x}}\) of Φ = 1.5 is slightly higher than that of Φ = 2.3, which is caused by more CO2 produced in the less sooty flame. However, this variance is only less than 0.5%. It further reveals the change of linewidth is not obvious in the CH4/air flame.

Fig. 8
figure 8

Measured spatially resolved profiles of (a) the temperature and (b) the mole fraction of N2 and CO2 for the flame with Φ = 1.5, and (c) total collisional pressure broadening coefficients of C2H2, \({\gamma }_{{\mathrm{C}}_{2}{\mathrm{H}}_{2}-\mathrm{x}}\), as a function of the height above the burner for the flame with Φ = 1.5 and 2.3

Full size image

Figure 9 shows the spatially resolved profiles of temperature, C2H2 mole fraction, and soot volume fraction for the premixed C2H4/ air flame under sooty conditions with Φ = 2.1 and 2.3. The lowest detectable value C2H2 mole fraction was 2217 ppm, and 2495 ppm, for Φ = 2.1, and 2.3, respectively, observed at HAB of 3 mm. The gas temperature at HAB = 3 mm was determined to be 1400 ± 30 K. As the LoD was evaluated to be ~ 60 times smaller than the lowest recorded C2H2 mole fraction, we can conclude that the production of C2H2 is subject to a critical gas temperature of 1400 ± 30 K. The mole fraction of C2H2 increases to the maximum when the maximum flame temperature is achieved. For example, at Φ = 2.3, the mole fraction of C2H2 is found to reach the maximum at the flame temperature of ~ 1500 ± 30 K. The soot volume fraction was reported by Axelsson et al. using the LII technique under similar gas flows and flame conditions as in this study [28]. The soot particles are found to start forming at the location where the mole fraction of C2H2 reached the maximum. The soot volume fraction increases significantly with the decaying trend of the C2H2 mole fraction. It corroborates the role of C2H2 in the formation of soot and the inception temperature of soot formation is ~ 1500 ± 30 K. This is in a very good agreement with the recent study of Algoraini et al. who report a soot inception temperature in low-pressure C2H4/Air premixed flames as 1465 ± 66 K. [14] It is interesting to conclude that the critical soot inception temperature is the same as the gas temperature where \({\chi }_{{{\mathrm{C}}_{2}\mathrm{H}}_{2}}^{\mathrm{max}}\) was detected.

Fig. 9
figure 9

Measured spatially resolved profiles of temperature, C2H2 mole fraction, and soot volume fraction for the premixed C2H4/ air flame under sooty conditions with (a) Φ = 2.1 and (b) Φ = 2.3. The flame temperature is measured by the thermocouple, and the soot volume fraction is reported by Axelsson et al. using the LII technique

Full size image

In addition, even in highly sooting conditions, e.g., when Φ = 2.3, the soot volume fraction at HAB = 10 mm is 280 ppb, the C2H2 mole fraction is still detectable. It further provides confidence that the IRPS method reported in this paper is suitable to measure the combustion species in such sooting flame conditions. It is also the first time that the measurement of C2H2 is performed systematically using nonintrusive techniques along with the formation of soot particles, where the calibration was evaluated at flame conditions.

6 Conclusion

Quantitative measurement of C2H2 was demonstrated in the premixed rich C2H4/air flame under atmospheric pressure using IRPS. The high-resolution IRPS signal was recorded by probing the ro-vibtational transition P(19) within a narrow spectral range from 3248.3 to 3248.8 cm−1. The C2H2 mole fraction was calibrated from the square root of the recorded IRPS intensity using a linear equation. The calibration factors for the two methods, i.e., the line integration and line maximum, were 3.60 × 10–3 and 2.48 × 10–3, respectively. More C2H2 species were detected in the flame with a higher equivalent ratio. The first observed mole fraction appeared at HAB of 3 mm and measured as 2003 ppm, 2217 ppm, and 2495 ppm, for Φ = 1.7, 2.1, and 2.3, respectively. The mole fraction increased as the HAB increased to reach the maximum value of 2296 ppm, 2807 ppm, and 3478 ppm, for Φ = 1.7, 2.1, and 2.3, respectively. The location of the maximum mole fraction of C2H2 was found to shift to a higher location within fuel-rich flames. When the Φ increased from 1.7 to 2.3, the peak mole fraction of C2H2 shifted from the HAB of 4 mm to 5 mm. After HAB for \({\chi }_{{{\mathrm{C}}_{2}\mathrm{H}}_{2}}^{\mathrm{max}}\), the C2H2 mole fraction was decreased to a plateau region at HAB of ~ 8 mm. In addition, the clear discrepancy between the measured and computed C2H2 mole fraction is evident of the limitation to applying Chemkin in rich flame conditions because the prediction of soot formation is unavailable in this Chemkin model. The C2H2 LoD was determined as 35 ± 5 ppm with the present setup at atmospheric pressure conditions. The total collisional pressure broadening coefficient of C2H2 was found to be dominated by the N2-broadening coefficients. Its value was ~ 0.074 cm−1 atm−1 and varied within a range of only 0.5% under the other flame conditions. For Φ = 2.1 and 2.3, the mole fraction of C2H2 increased to the reach \({\chi }_{{{\mathrm{C}}_{2}\mathrm{H}}_{2}}^{\mathrm{max}}\), at the maximum gas temperature. It was found that the critical soot inception temperature is the same as the gas temperature where \({\chi }_{{{\mathrm{C}}_{2}\mathrm{H}}_{2}}^{\mathrm{max}}\) was detected, namely at 1500 ± 30 K. The detected C2H2 signal in the flame with high soot volume fraction provides confidence that the IRPS is capable to measure the combustion species in sooty flames. The quantitative and high-sensitive IRPS measurement reported in this work demonstrates the potential applications in flame environments to help understand physical and chemical processes. IRPS can be used as a tool to perform quantitative measurements of other important species such as NH and OH with alternative fuels in the future.