1 Introduction

Adaptive optics with deformable mirrors have predominately been used in astronomy to correct for atmospheric aberrations in order to rectify and produce clearer more visible images [1, 2]. Various types of deformable mirrors exist, the most widely adopted are the bimorph and piston-based deformable mirrors. Bimorph deformable mirrors consist of two poled piezoelectric ceramic wafers, covered with a thin glass membrane that is deformed in order to achieve wavefront control. Piston-based deformable mirrors, classified as segmented deformable mirrors, consist of arrays (of a variety of geometries - square, circular, hexagonal, etc.) of rigid, segmented mirrors [3]. In order to achieve surface deformation with such segmented mirrors, a voltage is applied to each mirror electrode, giving rise to a controlled actuator stroke [4]. Predominately, deformable mirrors have been used in adaptive optics setups to correct for optical aberrations present in incoming wavefronts [5, 6].

Apart from wavefront correction, both forms of deformable mirrors have found applications in beam shaping. Due to their high-power handling capabilities, they are particularly useful for the spatial control of high power beams. These mirrors have been applied to intra-cavity compensation of low-order wavefront aberrations to improve beam quality [7, 8], achieve mode matching [9] and perform fast switching between stable and unstable resonator configurations [10]. It has been shown that these mirrors can be engineered to withstand radiation power densities up to 3 kW/cm\(^2\) for continuous sources and roughly 1010 W/cm\(^2\) for pulsed sources [11]. External to the laser cavity, these deformable mirrors have also shown wavefront correction and distribution compensation with both wide and small aperture mirrors [12,13,14,15]. Extending this to spatial-profile control, these mirrors have been demonstrated to produce elliptical and rectangular super-Gaussian and annular beam-shapes [16,17,18] and Bessel modes via a magnetic fluid-based liquid deformable mirror [19].

Although segmented deformable mirrors cause light to diffract due to the spacing between the segments [20], they are ideal for phase singularity beam shaping since the segments can be individually controlled to reproduce a spiral configuration. For example, Robert et al reported the creation of optical vortices by using an Iris AO S37-X deformable mirror consisting of 37 hexagonal actuators [21], where they formed a discontinuous reflective surface by altering each actuator to form a spiral configuration in a piston-tip-tilt fashion. The topological charge carried by the resulting modes was verified with the use of a Michelson interferometer to produce an interference pattern with a reference plane [22]. The generation of both zero and higher-order Bessel-Gauss beams have also been reported, whereby a segmented deformable mirror having 37 hexagonal segments in a honeycomb configuration was used. First the deformable mirror was used as a reflective axicon to generate the zero-order Bessel beam, and then it was programmed to produce a 2\(\pi\) spiral phase for the creation of higher-order Bessel beams [23]. However, these spatial modes are often not of a high fidelity (or correlation) with their desired “true” spatial profile. Spatial Light Modulators (SLMs), on the other hand, have been used extensively to produce spatial modes [24,25,26,27,28] of very high-fidelity for a variety of applications. These applications range from mode-division multiplexing [29], quantum information protocols [30,31,32], advanced adaptive optics systems [33], laser material processing [34,35,36], and brightness enhancement [37]. The advantage of SLMs is that they span a wide range of wavelengths (from visible through to near-infrared and in some cases mid-infrared), while offering instantaneous and rewritable amplitude, phase and polarization control, allowing for the creation of high-purity modes [38,39,40,41,42], independent wavelength control [43], as well as hundreds of structured modes from a single device [44], ranging from LG [45, 46] HG [17], IG [47], BG [48, 49], azimuthal OAM modes [50, 51] and non-diffracting beams [52, 53]. SLMs have also been applied to intra-cavity beam-shaping [54], as well as interferometrically combining resulting modes to create vector beams [55,56,57,58,59].

Since only a few publications have been dedicated to the implementation of deformable mirrors for low-fidelity beam-shaping, we propose first understanding the effect of the various deformable mirror parameters on the resulting spatial profile capabilities. In order to investigate such, we implement a dynamically addressable technology (in the form of a SLM) to act as a test-bed in simulating the various deformable mirror parameters (as depicted in Fig. 1). SLMs are well suited to this task since their discrete pixel arrangement and finite number of phase steps is exactly analogous to the discrete number of mirror segments and finite actuator positions associated with deformable mirrors. Here, we investigate the effect the mirror segment arrangement [such as, the number of mirror segments and their geometrical orientation (namely, Cartesian or radial)] has on the fidelity of the resulting structured mode. This assists in accelerating the decision-making process in determining which deformable mirror arrangement is best suited to achieve the desired spatial profile.

2 Theory and experimental realization

Figure 1 illustrates the conceptual implementation of the experimental simulator. An ideal phase profile, (shown in Fig. 1 as \(\exp (i \ell \phi )\) with \(\ell = 3\)) is divided into N segments of arbitrary geometry with each segment corresponding to a single simple linear actuator within the deformable mirror array. Each actuator is assumed to have a stroke S and precision p allowing for a total phase modulation (in reflection) of \(4\pi S/\lambda\) in S/p discrete steps (where \(\lambda\) is the wavelength of the illuminating light). Each region of the segmented phase profile is assigned a value from the list of S/p allowed actuator positions which results in a phase nearest the average value of the region. The discretized phase map is converted to a phase only hologram and displayed on an SLM.

Fig. 1
figure 1

The modulator simulation process depicted conceptually. The ideal phase profile is divided into a given number of segments according to the selected geometry. Each segment is assigned the nearest allowed phase based on the simulated modulators actuator stroke S and actuator precision p. The final phase map, discretized both transversely and in amplitude, is converted to a phase only hologram and displayed on an SLM

Full size image

To quantify the impact of segment number and geometry on beam quality we define a Figure of Merit (FoM) as:

$$\begin{aligned} \begin{aligned} \text {FoM} = \frac{{\varvec{\sum }}\left( I_{0}^{r} - \bar{I_{0}^{r}}\right) \left( I_{m}^{r} - \bar{I_{m}^{r}}\right) }{\sqrt{{\varvec{\sum }}\left( I_{0}^{r} - \bar{I_{0}^{r}}\right) ^2{\varvec{\sum }}\left( I_{m}^{r} - \bar{I_{m}^{r}}\right) ^2}}\times \frac{{\varvec{\sum }} I_{m}^{r}}{{\varvec{\sum }} I_{0}^{r}}, \end{aligned} \end{aligned}$$
(1)

where \(I_{0}^{r}\) and \(I_{m}^{r}\) are the desired and measured intensity profiles within a region of interest r. \({\varvec{\sum }}\) represents the sum over all coordinates and, \(\bar{I_{0}^{r}}\) and \(\bar{I_{m}^{r}}\) are the average intensities. The first term of Eqn. 1 defines the transverse correlation between the measured and desired intensity profiles within some region r. The second term defines the efficiency i.e., the ratio between the ideal and measured total energy within the region of interest. A deformable mirror capable of perfect beam shaping would result in beams with a FoM of 1.

Fig. 2
figure 2

Eq. 1 as a function of the segment stroke S and the number of segments for a vortex beam with \(\ell =3\). The subpanels A and B illustrate the trace of Eqn. 1 along each axis at the positions indicated by the solid green and red dashed lines respectively. C, D, and E, show the simulated transverse intensity profiles of the modulated beam at the points indicated in the density plot

Full size image

Figure 2 depicts the effect of segment stroke S and segment number on Eq. 1 for a vortex beam with \(\ell =3\). As the stroke of each segment is increased from \(0.25\lambda\) to \(0.5\lambda\) (effectively increasing the modulation from \(\pi\) to \(2\pi\)) the FoM improves, as indicated by the plot corresponding to the dashed red trace line (Fig. 2B). This is further illustrated by comparing Figs. 2E and D. In Fig. 2E, the limited stroke S of the modulator is unable to produce the required phase (despite the relatively large segment number) resulting in an output which is essentially unmodulated. Additionally, the FoM improves as the number of transverse segments comprising the modulator increases (Fig. 2A). Figure 2C shows that for low segment numbers near \(S = 0.5\lambda\) the modulator is able to introduce an optical vortex, but the final beam remains highly distorted. Together these findings are consistent with the intuition that the highest fidelity beam shaping (Fig. 2D) is achieved by modulators with at least a \(2\pi\) modulation capability and a large number of transverse segments.

Fig. 3
figure 3

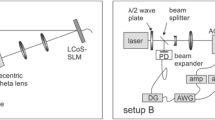
The experimental setup depicted conceptually for the case of a \(4\times 4\) Cartesian modulator. The hologram representing the modulator is displayed on an SLM illuminated by a Gaussian beam from a HeNe laser. The first order diffraction is passed through a lens of focal length f and the resultant intensity profile recorded by a camera at the focal plane

Full size image

An advantage of our approach is its ease of implementation as shown conceptually in Fig. 3. The SLM (a HoloEye Pluto 2) is illuminated by a Gaussian beam from a HeNe laser with the beam being sufficiently small so as to avoid the edges of the hologram. The first order diffraction is passed through a lens of focal length \(f = 500\) mm and the resultant intensity profile recorded by a Spiricon SP300 camera at the focal plane. For the remainder of this work, we assign values of 5 \(\mu\)m and 1 nm to S and p, respectively, in line with commercially available devices, and assume independent modulator segments.

In the following section we examine the effect of segment number and geometry on the FoM for a selection of transverse beam profiles specifically, a Cartesian flattop, an Orbital Angular Momentum (OAM) free annular, and, an \(\ell = 3\) vortex beam.

3 Results and discussion

Figure 4 illustrates how as the number of transverse segments comprising the modulator increases so too does the figure of merit. At low segment numbers the modulators ability to reproduce complex phase profiles is limited as evidenced by the aliasing in the left most phase panel of Fig. 4. This aliasing both directs energy away from the region of interest and distorts the transverse intensity profile of the beam resulting in a low figure of merit. As the number of segments is increased (and the phase profile better approximated), the fidelity of the beam within the region of interest increases while the energy lost to side lobes decreases, resulting in a figure of merit which asymptotically approaches one.

Fig. 4
figure 4

The influence of the number of mirror segments on the figure of merit. The theoretical and measured results are shown as solid black and red dashed lines respectively. The offset between the two curves is due to the limited dynamic range of the camera and can be accounted for using a constant offset correction of 0.13. The top panels illustrate the measured intensity and hologram phase at the locations indicated by the risers, 32, 64, and, 112 transverse segments respectively. The lines in the intensity panels illustrate the agreement in the transverse structure between the measured (red dashed) and simulated (solid black) beams

Full size image
Fig. 5
figure 5

The minimum number of segments required to produce an OAM free annulus with a FoM \(\ge 90\%\) in the Cartesian (left) and radial (right) arrangements. The top row illustrates the relevant segment geometry, note that the number of segments depicted has been reduced to aid in visualisation. The middle row shows the ideal phase profile when mapped to the segments in each configuration. The bottom row shows the measured intensity profile with the insets in the upper corner showing the ideal beam profile. The text indicates the FoM for each beam. The lines in the intensity panels illustrate the agreement in the transverse structure between the measured (red dashed) and simulated (solid black) beams

Full size image

Figure 5 illustrates that the number of modulator segments required to achieve a beam with a specific FoM is contingent on the compatibility between the segment geometry and the phase profile. Specifically, modulators having segment geometries which match the underlying phase profile can produce beams of either, comparable quality with fewer segments, or, higher quality with the same number of segments. In the Cartesian configuration, although the final FoM is slightly higher, a large number of segments (101\(\times\)101) are required to reduce the aliasing in the phase (Fig. 5 middle row left panel) to acceptable levels. By contrast, since the desired phase profile is radially symmetric, a modulator comprised of only concentric rings is able to accurately reproduce the phase profile with a relatively low number of total segments (50 concentric rings).

Fig. 6
figure 6

The effect of rotating the phase profile of a vortex beam (with \(\ell = 3\)) on the FoM. As the phase profile is rotated through \(\theta\), the discontinuities in the phase profile move into (and out of) alignment with the discontinuities between segments changing the degree of aliasing in the phase profile and by extension the FoM of the measured beam. The top panels illustrate the measured intensity and phase (mapped to the segments) at the locations indicated by the risers, \(0^{\circ }\), \(11^{\circ }\), and, \(20^{\circ }\) respectively. Note that the intensity panels have been independently normalized to aid in visualization

Full size image

To further examine the effect of segment geometry a second radially symmetric case (depicted in Fig. 6) was considered. Specifically, a modulator with 50 radial segments (as with the radial case in Fig. 5) was constructed however, each radial segment was further divided into a number of azimuthal segments. The inner most disk of the modulator comprised 9 azimuthal segments with the number of azimuthal segments per concentric ring increasing linearly towards the perimeter of the modulator. The ability of this modulator to produce a vortex beam (with \(\ell = 3\)) is depicted in Fig. 6.

There are two important findings contained in Fig. 6. First, whilst the vortex and OAM free annular beams (Fig. 5) have comparable radial symmetry in their intensity profiles, the azimuthal discontinuities in the phase of the vortex beam necessitate the use of a modulator with at least some degree of azimuthal control. This further highlights that the ability of a modulator to produce a given beam type is closely related to the compatibility between the segment geometry and the underlying phase profile, rather than the ultimate intensity distribution. Second, the alignment of phase discontinuities with discontinuities between the modulator segments can have a significant impact on the FoM of the final beam. Figure 6 illustrates how as the phase profile for the vortex beam (with \(\ell = 3\)) is rotated the discontinuities in the phase profile move into (and out of) alignment with the discontinuities between segments. This alignment then changes the degree of aliasing in the phase profile and by extension the FoM of the measured beam. This effect is cyclic with a periodicity controlled by the relationship between the number of azimuthal segments in the modulator and the number of discontinuities in the phase profile. We stress that whilst we have demonstrated this effect for radial geometries, it can be readily extended to any combination of phase profile and segment structures. Further, the effect emphasises how careful selection, and implementation, of modulator geometries is key in realising high quality structured beams from modulators with limited (often low) numbers of segments.

4 Conclusion

We have examined how the ability of a segmented deformable mirror to produce structured beams is impacted by the number of mirror segments it comprises as well as by their geometry. We have demonstrated a simple and flexible deformable mirror simulator (based on an LCoS-SLM) capable of producing beams in close agreement with theoretical predictions. Finally, we have highlighted the importance of the compatibility between the segment structure and the underlying phase profile of the desired beam. We expect this work to be a valuable reference point for the implementation of deformable mirrors in the context of high power structured light.