1 Introduction

In-situ measurements of temperature and mole fraction of major species are crucial for improving the understanding of the chemical kinetics and pollutant formation in combustion [1, 2]. Spontaneous Raman scattering (RS) is a widely used in-situ laser-diagnostic technique for combustion and other gas-phase reactive flows. This non-intrusive, simultaneous measurement technique is perfectly suitable for the high-temperature and high-pressure combustion environment considering that the signal intensity is proportional to the number density. The flame temperature and the mole fraction of major species can be obtained from the Raman spectra with little dependence on calibration. However, RS is limited by its weak signal and thus its high sensitivity to interference signals, especially in sooting flames. Considering that the typical Stokes RS intensity is on the order of 10–3 of laser-induced Rayleigh scattering [3], its signal can be easily influenced by different sources of interference, e.g., laser-induced fluorescence (LIF) of polycyclic aromatic hydrocarbon (PAHs), laser-induced incandescence (LII) of soot particles, and flame emissions. Thus, the Stokes RS is mainly applied to clean, non-sooting, and stable flames.

Many methods have been developed to isolate RS from the interference signals based on different RS properties [4]. The first approach is to select the excitation laser wavelength under which the RS signal is strong while the LIF and LII signals are weak. The RS intensity IR is inversely proportional to the fourth power of laser wavelength λ, i.e., IR ∝ 1/λ4. Thus, the shorter the laser wavelength, the stronger the RS intensity [5]. At the same time, an ultraviolet laser beam is likely to induce LIF of radicals, while an infrared laser beam can cause LII of soot particles [6]. Rabenstein and Leipertz [7] found that the 355-nm laser pulse is particularly suitable for RS in hydrocarbon sooting flames. Dreyer et al. [8] showed that the signal-to-noise ratios (SNR) of RS in C3H8/air flames are comparable at the excitation laser wavelengths of 532 and 355 nm. Egermann et al. [9] indicated that the interference signals under 266 nm excitation are stronger than that under 355 nm excitation in a heavily sooting flame, while the RS signal under 355 nm excitation is located closer to the fluorescence in the spectrum than that under 266 nm excitation. Taking all factors into account, a 355-nm laser was chosen for the RS collection of sooting flames in the present work.

The second approach is to make use of RS polarizability. Considering that LIF and LII signals are depolarized [10], clean RS signals can be obtained by subtracting signals from different polarization directions. The RS signals with different polarization directions can be excited by two sequential superimposed laser beams with different polarization directions [11, 12] or captured by two imaging systems for signals with different polarization directions [8, 9, 13,14,15]. Nevertheless, this strategy has some limitations considering that (1) the LIF/LII signals are not 100% depolarized, indicating some remaining LIF/LII signals still exist after processing the collected RS signals; (2) the data processing needs two measurements to get clean RS signal.

The third approach is to utilize the different lifetime between RS and interference. The RS lifetime is approximately 10–12 s or less, which is much smaller than the lifetime of LIF (10–10–10–5 s) and LII (~ 10–7 s) [5]. A Kerr gate can be used to separate RS from the collected signals [16,17,18]. Another method based on different lifetime is to use a picosecond-gated camera or a photomultiplier tube [19,20,21]. These time-domain methods need the picosecond-level pulse laser and the laser energy is usually limited to a few mJ to avoid the breakdown. Furthermore, this kind of technique is also expensive and not easy-to-implement.

Besides those approaches to suppress interference signals, many strategies have also been developed to enhance the SNR of RS. The most direct way is to maximize the laser intensity considering that RS increases proportionally with the laser intensity. However, a laser-induced breakdown will occur when the laser irradiance exceeds the breakdown threshold. Kojima et al. [22] and Magnotti et al. [14, 23] established a beam stretcher with multiple optical ring cavities to broaden the laser pulse duration and avoid breakdown. However, the optical ring cavities are usually complex, expensive, and hard to align. Dreyer et al. [8] and Egermann et al.[9] utilized a long-focal length lens to avoid the breakdown by lowering the laser fluence at the focal point. Another approach is to reflect the laser beam into the measurement volume again by prisms/mirrors [24,25,26,27,28] or by a specially designed optical cavity, to achieve the cavity-enhanced Raman spectroscopy (CERS) [29]. It is necessary to mention that the long-focal length lens and CERS will lower the spatial resolution due to the larger focal volume. It is a trade-off between Raman scattering intensity and spatial resolution. Other methods like coherent anti-Stokes-Raman spectroscopy (CARS) or stimulated Raman spectroscopy (SRS) can also highlight the RS of the specific molecule [3, 5]. Nevertheless, those kinds of approaches are either hard to implement or expensive.

In this paper, we introduce a short-gated RS method using nanosecond 355-nm laser pulses, which is relatively low-cost and easy-to-implement. Several strategies from both experimental and simulation perspectives have been utilized to separate RS from interference signals and enhance the SNR. Here, we focus on the counterflow diffusion flame, which is widely used to study particle formation and high-temperature flame kinetics. Considering that counterflow diffusion flame can be assumed to be axisymmetric, the RS intensity can be enhanced with the cost of lower spatial resolution. The proposed RS method was applied in a counterflow diffusion flame and validated by numerical simulation results.

2 Experimental method

2.1 Laser diagnostic setup

The schematic of the laser-diagnostic setup is presented in Fig. 1. A frequency-tripled Q-switch Nd: YAG laser (Brilliant B, Quantel) with a wavelength of 355 nm operating at a repetition rate of 10 Hz and a pulse duration of approx. 5 ns was employed as the excitation source. The full laser power of approx. 125 mJ/pulse was chosen to maximize the RS signal intensity. The polarization of the laser beam was horizontal at the output of the laser head and then was rotated to the vertical direction by an image rotator before focusing into the flame by a plano-convex UV spherical lens with a focal length of 300 mm. On the spectra measurement side, two plano-convex UV spherical lenses were used to collect the RS signal into the slit of the spectrometer (ISOPLANE SCT 320, Princeton Instruments) after passing through an image rotator and a UV polarizer filter. The UV polarizer filter was set in the horizontal direction (along the x-axis) to pass the horizontal-polarized signals, as the vertical-polarized RS signal was rotated by the image rotator. The grating was chosen to be 1800 groove/mm, and the slit was set to 150 μm, which resulted in a spectral resolution of 15.23 cm−1. The signal was then split into spectra and then imaged onto an ICCD camera (PI-MAX 4, Princeton Instruments, 1024i-Gen II RB fast gate). The spatial resolution of the whole spectra collection system was measured to be10.6 μm/pixel. The ICCD gate time setting has an accuracy of 0.01 ns.

Fig. 1
figure 1

Schematic of the laser-diagnostic setup. The purple arrows indicate the laser polarization direction

Full size image

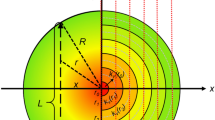
To avoid laser-induced breakdown occurring at full laser power, an additional cylindrical lens with a focal length of 1700 mm was placed behind the 300-mm spherical lens on the laser beam path. Figure 2 shows the three-dimensional sketch of the focusing laser beam profile and the beam profiles at five different positions that were recorded qualitatively by a beam profiler with a resolution of 36 μm/pixel (LBS-100, Spiricon). The laser beam was focused in the horizontal direction (x-axis) by the cylindrical lens and was not changed in the vertical direction (z-axis). The beam diameter in the vertical direction (z-axis) was controlled by the 300-mm spherical lens and measured to be 0.13 mm by the ICCD camera, while the beam width in the horizontal direction (x-axis) was measured to be 1.2 mm by the beam profiler. The RS signal was integrated along the slit corresponding to 10.8 mm along the laser line for sufficient SNR, which takes the advantage of the aberration-free design of the spectrometer. Thus, the focal point of the measurement is point D and the measurement volume was 1.2 mm × 10.8 mm × 0.13 mm (x–y–z). The spatial resolution of 0.13 mm in the vertical direction (z-axis) is higher than that in the directions along the x- and y-axis. Because the measurements were carried out in a laminar counterflow diffusion flame with its spatial distribution uniform in the x–y plane, a low spatial resolution in the x–y plane was acceptable.

Fig. 2
figure 2

Three-dimensional sketch of the extended focal volume of the laser beam and the beam profiles at the points of A–E. Their points are equally spaced with a distance of approx. 30 mm. Point D is the focal point of the spherical lens along the x-axis and also the focal point of the measurement. Point B is the focal point after the spherical lens and the cylindrical lens along the z-axis

Full size image

2.2 Burner and flames

The short-gated RS method was demonstrated in the measurement of temperatures and major species in a counterflow diffusion flame with soot particle formation. Details of the counterflow burner can be found in our recent studies [30,31,32]. A schematic picture of the counterflow burner is shown in Fig. 3. The gases of ethylene and nitrogen were mixed and fed through the lower nozzle. The flow rates of N2 and C2H4 were 3.09 SLM (standard liter per minute) each. The air flowed through the upper nozzle with a flow rate of 7.06 SLM as the oxidizer. The co-flow of N2 was used to stabilize the flame and isolate the experiment volume from ambient air. The soot volume fractions in the counterflow diffusion flame were measured by LII and calibrated by laser extinction measurements. The LII signal of the soot particles was collected by an ICCD camera (Andor, iStarDH334T) with a 75 ns gate width and a 116 ns delay after the laser pulse. The soot particles were generated at a height above the burner (HAB) of approx. 9.5 mm near the flame reaction zone and were transported towards the stagnation plane at a HAB of approx. 7.5 mm. More details about the LII measurement can be found in our recent work [30,31,32]. The maximum soot volume fraction of the current experimental condition is approx. 0.1 ppm. This method has also been applied to flame conditions with higher soot volume fractions in our recent work, so the lower nozzle was heated to 400 K to vaporize the blended liquid fuels [28,29,30].

Fig. 3
figure 3

Schematic figure of the counterflow burner, where the inset shows the LII results of the counterflow diffusion flame

Full size image

3 Results and discussion

3.1 Time-resolved spectral analysis

To find the most appropriate gate delay for the collection of clean RS signals, the ICCD gate time was accurately controlled in this work. Time-resolved spectra at different delay times were collected at the HAB of 9.5 mm. The starting time of the ICCD gate delay, which is defined with respect to the trigger signal, was set to sequentially shift from 80 to 95 ns with an interval of 1.5 ns, while the gate width was kept at 5 ns. A total of 11 spectra with the shifting delay time were collected and each spectrum was averaged over 50 single frames. Figure 4 shows four spectra with different delay times. The N2 Stokes RS spectra are identified at around 386 nm with the Raman shift of 2330 cm−1. The spectral profile was fitted to measure temperatures. The RS spectra mainly interfere with three sources of signals including CH-LIF signals at 2363 cm−1, CN-LIF at 2290 cm−1 [33], and a broadband spectrum.

Fig. 4
figure 4

Time-resolved Raman spectra including LIF as the interference. The spectra were taken at four different gates at the HAB of 9.5 mm. Each spectrum is an average of 50 acquisitions

Full size image

When the gate time is 83–88 ns, the N2 Stokes RS at 2330 cm−1 is stronger than the LIF signal. As the gate is further delayed to 84.5–89.5 ns, the RS reaches its maximum, and LIF signals show an increasing trend. At the gate time of 87.5–92.5 ns, the LIF signals reach their maximum and the RS starts to decline. At the gate time of 90.5–95.5 ns, the RS is overlapped by the LIF signals.

Figure 5a further demonstrates the baseline-corrected signal intensities of these spectra as a function of the delay time. The CH LIF @ 2363 cm−1, N2 Raman scattering @ 2330 cm−1, and broadband emission averaged intensity in the range of 1670–1690 cm−1 were considered. The baseline-corrected signal intensity for each point in Fig. 5a is an integral of the signal generated by the laser pulse over a gate width of 5 ns, as indicated by the black arrows. The Rayleigh scattering was used as the time flag of the laser pulse. The time-resolved Rayleigh scattering was measured using a sequentially shifted 3-ns ICCD gate width and fitted by a convolution function between a Gaussian distribution (i.e. laser pulse temporal profile) and a square function (i.e. the gate time). Figure 5b shows the fitted laser pulse profile. The maximum point of the laser intensity profile occurs at the ICCD delay time of approx. 87.5 ns and is thus denoted as a relative delay time of 0. More details can be found in our supplementary materials. Figure 5c summarizes the SNR of RS and LIF spectra at different delay times. The SNR is evaluated with the signal as the peak intensity of the baseline-corrected spectrum and the noise as the standard deviation of the baseline.

Fig. 5
figure 5

a Temporal profile of N2 RS, CH LIF, and broadband emissions under the laser pulse; b laser pulse profile by fitting with the Gaussian function; c SNR of N2 RS and CH LIF. Black dash line indicating the boundary of the gate and the shadow area represents the integration region from − 4.5 to 0.5 ns

Full size image

As shown in Fig. 5a, the RS reaches the maximum earlier than LIF because the RS can be seen as an instantaneous process, while the intensity of LIF signal rise slower than Raman scattering due to the complete process of absorption, excitation, collision, and emission [5]. Thus, the gate delay time can be chosen appropriately to obtain a strong RS signal intensity and acceptable interference signals from LIF. We successfully performed RS measurement in the counterflow diffusion flame with the soot volume fraction of 0.15 ppm [32]. For the case with a soot volume fraction higher than 0.2 ppm, the current experimental setup may not be applicable.

In comparison, the broadband spectrum shows a rapid increase and slow decay. A possible reason is that the broadband emission may consist of broadband Raman and LIF signals of PAH which could be formed in flames or generated during the laser ablation of soot particles. In many studies, it is observed that the LIF signal has a fast-decaying component with a characteristic time of ~ 1 ns [34, 35]. We checked the spectrum in different polarization directions by tuning the UV polarizer to vertical or horizontal directions. When changing the polarization to the vertical direction, the broadband emission decreases but not extinguishes, which indicates that both polarized RS and depolarized LIF contribute to the broadband emission. At a further delay, the PAH LIF signal becomes more dominant. It is deduced that the LII signals of soot may not be significant here, because the LII signals usually occur between 400 and 800 nm [36]. Based on the above analysis, the collection time was set to − 4.5 to 0.5 ns in the following measurement, corresponding to the ICCD gate delay time of 83 ns after the trigger signal of the laser pulse and the gate width time of 5 ns, to obtain a strong Raman scattering and acceptable interference signals from LIF.

3.2 Nonlinear fitting of RS spectrum

The collected RS spectrum was then directly compared with the simulated RS spectrum to fit the temperature. Based on the theory of quantum mechanics, the RS is induced by the energy exchange from the inelastic collisions between molecules and photons. The modified vibrational and rotational energy of molecules is then reflected in the shifted radiation frequency. Depending on whether the molecules gain or lose energy, Stokes-Raman scattering (\({\nu }_{s}={\nu }_{0}-\Delta \widetilde{\nu }\)) and Anti-Stokes-Raman scattering (\({\nu }_{as}={\nu }_{0}+\Delta \widetilde{\nu }\)) occurs. The shifted wavenumber is a function of the energy level of the molecule:

$$\begin{array}{*{20}c} {\Delta \tilde{\nu } = \tilde{G}\left( {v^{\prime}} \right) - \tilde{G}\left( {v^{\prime\prime}} \right) + \tilde{F}\left( {J^{\prime}} \right) - \tilde{F}\left( {J^{\prime\prime}} \right)} \\ \end{array}$$
(1)

the superscript ′ indicates the final energy state, the superscript ″ indicates the initial energy state, v is the vibrational quantum number, and J is the rotational quantum number. For diatomic molecules, the vibrational term \(\widetilde{G}\left(v\right)\) and the rotational term \(\widetilde{F}\left(J\right)\) can be described as:

$$\begin{array}{*{20}c} {\tilde{G}\left( v \right) = \tilde{\nu }_{e} \left( {v + 1/2} \right) - x_{e} \tilde{\nu }_{e} \left( {v + 1/2} \right)^{2} ,} \\ \end{array}$$
(2)
$$\begin{array}{*{20}c} {\tilde{F}\left( J \right) = \left( {B_{e} - \alpha_{e} \left( {v + 1/2} \right)} \right)J\left( {J + 1} \right) - \left( {D_{e} + \beta_{e} \left( {v + 1/2} \right)} \right)J^{2} \left( {J + 1} \right)^{2} .} \\ \end{array}$$
(3)

here, \({\widetilde{\nu }}_{e}\), \({x}_{e}\), \({B}_{e}\), \({\alpha }_{e}\), \({D}_{e}\), and \({\beta }_{e}\) are molecule-specific constants [3, 37, 38]. The intensity for individual Stokes RS with a collection solid angle at \(90^\circ\) can be calculated by:

$$\begin{array}{*{20}c} {I_{{v^{\prime},J^{\prime}}} = \frac{{\alpha_{zz}^{2} \pi^{2} \left( {\nu_{0} - \Delta \tilde{\nu }} \right)^{4} }}{{ \in_{0}^{2} }} \cdot N_{i} \cdot p_{{v^{\prime\prime},J^{\prime\prime}}} \cdot I_{laser} } \\ \end{array}$$
(4)

where \({\alpha }_{zz}\) is the polarizability matrix element of vertically polarized scattering induced by vertically polarized laser; \({\nu }_{0}\) is the laser wavenumber; \({\epsilon }_{0}\) is the permittivity of free space; \({N}_{i}\) is the number density of molecule i; \(p_{{v^{\prime\prime},J^{\prime\prime}}}\) is the population distribution of the initial energy state with \(v^{\prime\prime},J^{\prime\prime}\), which is prescribed by the Boltzmann distribution; and \({I}_{laser}\) is the laser irradiance [5]. According to the Placzek polarizability theory and selection rules of diatomic molecules, the polarizability matrix element \({\alpha }_{zz}\) can be expressed as:

$$\begin{array}{*{20}c} {\Delta v = + 1, \Delta J = 0,\quad \overline{\overline{{\left( {\alpha_{zz} } \right)^{2} }}} = \left( {v + 1} \right)\frac{h}{{8c\pi^{2} \Delta \tilde{\nu }}}\left[ {\left( {\alpha^{\prime}} \right)^{2} + \frac{4}{45}b_{{J^{\prime},J^{\prime\prime}}} \left( {\gamma^{\prime}} \right)^{2} } \right],} \\ \end{array}$$
(5)
$$\begin{array}{*{20}c} {\Delta v = + 1,\Delta J = \pm 2,\quad \overline{\overline{{\left( {\alpha_{zz} } \right)^{2} }}} = \left( {v + 1} \right)\frac{h}{{8c\pi^{2} \Delta \tilde{\nu }}}\left[ {\frac{4}{45}b_{{J^{\prime},J^{\prime\prime}}} \left( {\gamma^{\prime}} \right)^{2} } \right],} \\ \end{array}$$
(6)

where c is the speed of light, \({\alpha }^{\mathrm{^{\prime}}}\) and \({\gamma }^{\mathrm{^{\prime}}}\) are the mean and anisotropy invariants of the derived polarizability tensor [39], and \(b_{{J^{\prime},J^{\prime\prime}}}\) is the Placzek-Teller coefficient [5].

The population distribution pv,J as well as αzz determine the line intensity for each vibration-rotational transition at the wavenumber shift of \(\Delta \widetilde{\nu }\). By accumulating each line with broadening in a Voigt shape, the Stokes-Raman profile at \(\Delta v=1, \Delta J=0,\pm 2\) can then be simulated and utilized to fit the experimental spectra. The fitting process involves the baseline fitting of the broadband spectrum and the nonlinear fitting of the Raman spectra after the baseline subtraction. In the present work, the Raman spectra fitting utilized a nonlinear fitting function ‘lsqnonlin’ that is based on the trust-region-reflective algorithm, which is completed by MATLAB. More details of the nonlinear fitting method can be found in the supplementary materials and the whole program for the simulation of the Raman spectrum has been uploaded on GitHub [40].

Figure 6 demonstrates the baseline fitting (red line) and N2 RS spectrum fitting (blue line) of the flame at the HABs of 6.94 mm, 8.49 mm, and 11.07 mm. These three positions correspond to the low-temperature region, the sooting flame region, and the high-temperature region, respectively.

Fig. 6
figure 6

Baseline fitting (red line) and N2 Raman spectrum fitting (blue line) of flame at (a) HAB of 6.94 mm, (b) HAB of 8.49 mm, and (c) HAB of 11.07 mm corresponding to the low-temperature region, the sooting region, and the high-temperature region, respectively

Full size image

The total intensity of Stokes RS was utilized to obtain the mole fraction of major species. According to a theoretical analysis by Schrotter and Klockner [41], the total intensity of the vibration–rotation band can be simplified as that of the pure vibrational transition averaged over all orientations of the molecule [5]. This fact indicates that the temperature influences the integrated RS intensity IR in two ways: (1) IR is inversely proportional to the vibrational partition function \(\left(1-{e}^{-hc{\widetilde{\nu }}_{e,i}/kT}\right)\); (2) IR is proportional to the number density Ni of species i which is then inversely proportional to the temperature according to the ideal gas law. Therefore, at a given temperature T, the total intensity of RS IR,i of the species i can be calculated by a reference condition with the temperature of \({T}_{0}\) and the mole fraction of \(x_{0}\) to obtain the mole fraction of xi according to

$$\begin{array}{*{20}c} {x_{i} = \frac{{I_{R,i} }}{{I_{R,0} }}\cdot\frac{T}{{T_{0} }}\cdot\frac{{\left( {1 - e^{{ - hc\tilde{\nu }_{e,i} /kT}} } \right)}}{{\left( {1 - e^{{ - hc\tilde{\nu }_{e,i} /kT_{0} }} } \right)}}\cdot x_{0} } \\ \end{array}$$
(7)

3.3 Demonstration in the counterflow diffusion flame

The short-gated RS method was then utilized in the measurement of temperature and species of the ethylene–air diffusion flame with soot particle formation. Figure 7 demonstrates the measured temperature profile of the flame at each HAB with its temperature profile simulated using the FlameMaster code [42]. The 1D FlameMaster simulation was performed based on a kinetic mechanism referred to ITVMech. The mechanism involving 185 species and 2171 reactions is built on the well-validated C0-C4 core by Blanquart et al. [43] and the PAH model of Narayanaswamy et al. [44]. Soot formation and growth were modeled by the Hybrid Method of Moments (HMOM) closure approach [45]. More details of the simulation can be found in our previous work [32]. The measurement precision is evaluated by the standard deviation of 5 measurements. Figure 8 shows the accuracy and standard deviation of measured temperature as a function of HAB. The standard deviation of the measured temperatures in the sooting region is approx. ± 75 K. In addition, it should be noted that the deviation in the low-temperature region is generally higher than that in the high-temperature region because the sensitivity of the RS spectral profile at low temperatures is lower than that at high temperatures. In the high-temperature non-sooting region, the standard deviation of the measured temperature is approx. ± 50 K, while it reaches up to approx. ± 130 K in the low-temperature region. Besides the influence of sooting and the low sensitivity of RS spectral profile at the low-temperature region, the fitting procedure also contributes to the uncertainty and accuracy of measurements. Using the nlparci function in MATLAB with confidence intervals of 95%, the fitting uncertainties were calculated to be around ± 10 K in the low-temperature region, ± 13.8 K in the high-temperature region, and ± 27.8 K in the sooting region. The accuracy of the measurement is evaluated by comparing it with the numerical simulation. In general, the measured temperature profile matches well with the simulation. The measurement accuracy of the peak temperature can reach approx. 30 K. The large difference between experiment and simulation at the HAB of 12-15 mm is caused by the uncertainties of the mass flow rates and HAB measurement, as well as the boundary condition of simulations. The measurement accuracy has no big difference between the sooting region and non-sooting regions.

Fig. 7
figure 7

The measured and simulated temperature profile of the ethylene flame

Full size image
Fig. 8
figure 8

The accuracy and standard deviation of measured temperature at different HABs

Full size image

Figure 9 further demonstrates the typical RS spectra of O2, C2H4, and N2 at different HABs in the counterflow burner after subtracting the baseline of these spectra. The baselines of these spectra were fitted by the 2nd-order polynomial curve after the peaks (O2, C2H4, and N2) of the full original spectra were removed. The O2 spectra at the Raman shift of 1528–1578 cm−1 and C2H4 v3 spectra at 1314–1369 cm−1 were integrated and processed to evaluate the mole fractions of O2 and C2H4, respectively. The RS intensity from the N2 fitted spectrum was used to evaluate N2 mole fraction. The C2H4 v3 was chosen considering its stronger intensity than the C2H4 v2 signal and its spectral location farther away from other interference signals (Raman and LIF signals of PAHs). Besides, when the spectra were integrated, the crosstalk between signals need to be considered. The most significant crosstalk occurs between the C2H4 v3 Raman signal (1314–1369 cm−1) and the CO2 Raman signal (peak @ 1285 cm−1 and 1388 cm−1). As the cross-section of the CO2 Raman signal is much smaller than that of the C2H4 v3 peak, the crosstalk-induced deviation of the mole fraction of C2H4 is limited to ~ 0.01. For the species of N2 and O2, the reference was chosen to the point at the HAB of 15 mm with \(x_{\text {N}_2}\) of 0.79 and \(x_{\text {O}_2}\) of 0.21, while for the species of C2H4, the reference poxint was chosen to be at the HAB of 7 mm with the \(x_{{\text {C}_2}{\text {H}_4}}\) of 0.50.

Fig. 9
figure 9

Raman scattering of different species at different HABs after subtracting the baseline

Full size image

Figure 10 shows the measured mole fractions of N2, O2, and C2H4. The measurement uncertainty was derived according to Eq. 7 based on the uncertainties of the total RS intensity IR and that of the measured temperatures T, which were estimated by their respective standard deviations. Compared with the temperature measurement, the deviations of molar fractions are larger due to the accumulated uncertainties from both IR and T. Figure 11 shows the accuracy and standard deviation of the measured values. The measured values match well with the simulation results considering the superposition of temperature measurement uncertainties and flame conditions. The standard deviation of N2, O2, and C2H4 shows that a large uncertainty occurs at the boundaries with low temperatures, which is caused by the inaccuracy of the temperature measurement during the RS spectra fitting.

Fig. 10
figure 10

The comparison of measured and simulated mole fractions of N2, O2, and C2H4

Full size image
Fig. 11
figure 11

The standard deviation and accuracy of measured mole fraction of N2, O2, and C2H4 at different HABs

Full size image

4 Conclusion

This study demonstrates a short-gated spontaneous Raman scattering diagnostic method in a counterflow diffusion flame with the soot volume fraction at the level of 0.1 ppm. The optical setup with spherical and cylindrical lenses avoids the laser-induced breakdown and guarantees a high laser intensity. The short gate is elaborately controlled to suppress the LIF from PAHs and radicals. As a cost of strong Raman scattering, the spatial resolution is lower. The temperature can be then obtained by fitting the Raman scattering with simulated N2 Stokes-Raman spectra, based on which the mole fraction can be further evaluated. As validation, the temperature and mole fraction in an ethylene–air counterflow diffusion flame was measured. The measured temperatures and mole fractions of major species (C2H4, O2, N2) agree well with the simulation results in both sooting and non-sooting regions, indicating a good accuracy of the proposed method. This experimental setup is now only applicable for 1D flat flames due to low spatial resolution. Compared to other existing methods, this new method does not require complex equipment and can achieve calibration-free temperature measurements, showing the potential for in-situ laser diagnostics of other multiphase chemical reacting flows in an easy-to-implement and low-cost way.