1 Introduction

Frequency selective surfaces (FSS) are artificial surfaces made of periodically patterned thin metallic layers. Based on the periodicity, FSSs act as frequency filters for selected propagating waves. FSSs are commonly used in frequency-dependent electromagnetic (EM) waves applications, such as filters, perfect absorbers, antenna and radar [1,2,3,4]. FSSs can transmit angle- and polarization-independent waves, as it does not rely on surface modes but on a cavity angle-independent mode [5]. Using origami fold/unfold tuning enables transforming single band static FSS to dual band dynamic FSS [6]. This technique increases the degrees of freedom as both symmetric and anti-symmetric modes are excited because of the strong coupling and suitable orientation of the elements.

On the other hand, metasurfaces typically have periodicity much smaller than the wavelength, which are designed in terms of average fields and effective macroscopic properties. Also, metasurfaces have an inclusion response as artificial meta-atoms surface [7]. Similarly, Huygens’ metasurfaces (HMS) are planar arrays of meta-atom particles of subwavelength size, the array is formed of a balanced electric and magnetic polarizable particles (dipoles), which are defined as an array of Huygens’ sources [8]. Based on both electric and magnetic properties, HMS can be designed for many applications such as low or high reflection and antenna beam forming [9]. Like aperture-type FSS, extra-ordinary transmission (EOT) is related to a 2D periodic array of holes in an opaque surface [10]. The transmission from FSS is possible to reach 100% around the resonance frequency of the holes where commonly the hole dimensions are larger than one-half of the period. Unlike the predicted reduction of the transmission with the hole radius, EOT phenomenon appears with very small holes where the design depends on the lattice period rather than the hole radius [11].

Silver (Ag) is one of the most common metals in plasmonic surface design because of its convenient plasmon frequency, high sensitivity, and naturally low ohmic losses at optical frequencies [12]. On the other hand, Ag surfaces applications still face a problem of quick oxidation in many technologies [13].

A theoretical study of EOT through subwavelength hole arrays in optically thick silver films was presented by Martin et al. [14, 15], where they used thickness \(=320\) nm (\(\approx \lambda\)) and the model was applied for square and circular holes. In the long-wavelength limit, the study showed that the transmission coefficient depends on hole area, not shape. Also, in 2011, for thickness \(=320\) nm, transmission through subwavelength centered-polygonal hole arrays in silver film was numerically investigated, the study observed new hybrid transmission characteristics in octagonal and decagonal hole array [16]. Numerical modeling for nano-structured plasmonic surfaces is regularly performed with different techniques, such as wave concept iterative procedure (WCIP) [17], finite difference time domain (FDTD) [18], finite element method (FEM) [19] and hybrid FDTD/GSM [20, 21]. Numerical approaches are considered more flexible and applicable to wide practical problems compared to analytical models. It can accommodate arbitrary geometries and include a wide range of device physics parameters. That is why it is widely used in FSS modeling studies [22,23,24].

Although analytical modeling has more limitations than numerical modeling and is not suitable for all frequency ranges and cell dimensions, it is still a sufficient and quick tool to estimate the main parameters and responses. One of the most common analytical methods in designing plasmonic filters is the equivalent circuits. It was used for different shapes in the literature in microwaves frequencies, where the metal is considered as the perfect electrical conductor (PEC) [25,26,27]. On the other hand, in optical frequencies, metals are no more suitable to be considered as perfect electrical conductors because of the frequency-dependent parameters such as permittivity and conductivity. The equivalent nanocircuit model(ENC) is one of the most common methods which presents a quick and simple way for surface design, but it still has some limitations and deviations than numerical results. Since 2005, Nader Engheta et al. presented some studies in ENC for optical range nano-antennas [28,29,30]. 1D dielectric/metal/dielectric analytical model in optical frequencies was presented in 2011 [31]. Although circular hole array filters were modeled numerically [23, 24, 32], but up to our knowledge no analytical ENC models were presented for circular holes filter in optical spectrum.

Despite the deviation of ENC results, it still provides fast and easy way to estimate the main characteristics of the transmission spectra compared to the simulation methods and helps reaching better design using optimization techniques. That makes it preferable for FSS applications like filtering , antenna and radar, while doing full-wave simulations is still needed to fine tune the optimized design.

In this work, we present an analytical model that is based on equivalent nanocircuit theory to study circular hole arrays in thin silver plasmonic films. The model is extended for square holes. The model is compared with numerical calculations from COMSOL Multiphysics simulator [33].We used the FEM numerical solver in the simulator to solve the frequency domain form of Maxwell’s equations, as FEM is considered a very efficient method to deal with different structures and is convenient to simulate the nano hole array under discussion. The model achieved good matching with published experimental and numerical results.

2 Structure and model

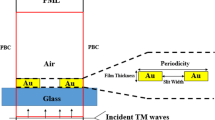
As shown in Fig. 1, the structure contains a silver surface of periodic hole array with radius r, diameter d, periodicity l, and surface thickness t. Using silver parameters from Johnson and Christy [34], the equivalent nanocircuit can be modeled by studying one unit cell due to the symmetry. The model is based on the impedance matching method because of its simplicity and capability to explain fundamental phenomena like extra-ordinary transmission (EOT)[10, 35].

Fig. 1
figure 1

Schematic of the hole array FSS

Full size image

It is worthy to note that the metal in the optical frequencies has an additional resistance compared to the lower frequencies where the metal is considered as a PEC. So, the impedance in the metal region is dominantly inductive with parallel resistance \(Z_{L}\), whereas the impedance in the air hole is dominantly capacitive \(Z_\textrm{c}\). As shown in Fig. 2b, \(Z_\textrm{c}\) represents the impedance in the circular cavity, whereas, \(L_{1,2}\) and \(R_{1,2}\) represents the components of the inductance impedance \(Z_{1,2}\) in the metallic film.

Fig. 2
figure 2

a Schematic of the top view of the unit cell, b equivalent circuit of the unit cell, c the connection of the cell equivalent circuit in with zero-order impedance approximation, d the connection of cell equivalent circuit with high-order impedance approximation

Full size image

As shown in Fig. 2a, the inductance impedance in the metal is divided into two parts; \(Z_{L_1}\) and \(Z_{L_2}\). \(Z_{L_2}\) is estimated approximately from the analogy of the air cavity as a metallic disk removed from the metallic film. So, we used a series equivalent impedance \(Z_1\) and a metallic impedance analogous to the hole impedance \(Z_2\) to calculate \(Z_{L_2}\) as follows [36, 37]

$$\begin{aligned}&Z_{L_1}= \dfrac{jL}{\omega ~ \epsilon _0~ \epsilon _\textrm{m} (L-2r)t}, \end{aligned}$$
(1)
$$\begin{aligned}&Z_{L_2}=Z_1-Z_2, \end{aligned}$$
(2)

where

$$\begin{aligned}&Z_1= \dfrac{jL}{\omega \epsilon _0 \epsilon _\textrm{m} (2r)t} ~ ,~ Z_2= Z_\textrm{c}/\epsilon _\textrm{m}, \end{aligned}$$
(3)
$$\begin{aligned}&Z_{L_2}=j~\dfrac{4r+L}{\omega \epsilon _0 \epsilon _\textrm{m} (2r)t}, \end{aligned}$$
(4)

where \(\omega\) is the angular frequency,\(\epsilon _0\) is the permittivity of free space, \(\epsilon _\textrm{m}\) is the relative permittivity in the metal.

According to the simplified capacitance formula \(C_z=\epsilon _{0} \epsilon _r {\text {Area/length}}\), where, \(C_z\) is the capacitance, \(\epsilon _0\) is the permittivity of free space, \(\epsilon _r\) is the dielectric constant and Z is the impedance. The impedance can be estimated as \(Z=j/(\omega C_z\)), The same simplified procedure was presented previously for square arrays in the infrared regime [36, 37]

In the circular air hole-filled cavity, as shown in Fig. 3, we divided the area in the capacitance relation into infinitesimally small rods of area \(t \times \textrm{d}y\) and length 2x and approximate the capacitance inside the hole \(C_{Z_\textrm{c}}\) as follows

$$\begin{aligned}&C_{Z_\textrm{c}}=\int _{-r}^{r} \dfrac{\epsilon _0 t}{2x} \,\textrm{d}y, \end{aligned}$$
(5)
$$\begin{aligned}&C_{Z_\textrm{c}}=~\dfrac{\epsilon _0 ~t ~\pi }{2} , \end{aligned}$$
(6)
$$\begin{aligned}&Z_\textrm{c}=\dfrac{2j}{\omega ~\epsilon _0 ~ t~ \pi }. \end{aligned}$$
(7)
Fig. 3
figure 3

Circular hole capacitance approximation

Full size image

The above approximation is valid for small holes \((d<L/2)\), as shown in Fig. 2c, where the zero-order surface impedance approximation \((Z_\textrm{S}=Z_0/\sqrt{\epsilon _r })\) is enough to compensate for the metal loss, where \(Z_0=\sqrt{\mu _0/\epsilon _0}\) is the free space impedance. As the hole radius increases, higher order impedance (\(Z_{\textrm{ho}}\)) should be considered, especially the capacitance impedance for TM modes, as shown in Fig. 2d. Both TM and TE frequency-dependent impedance are calculated from circular waveguide approximation as in [38]

$$\begin{aligned} Z_{TM}=-jZ_0 \sqrt{\left( \dfrac{\lambda }{\lambda _\textrm{c}}\right) ^2-1}, \end{aligned}$$
(8)

where \(\lambda _\textrm{c}\) is the cutoff wavelength of TM modes (m, n) for a circular waveguide of radius a, \(\lambda _\textrm{c}=2\pi a/\chi _{mn}\) , and \(\chi _{mn}\) is the nth root of mth Bessel function \(J_{m} (\chi )\)

On the other hand, TE modes impedance equals

$$\begin{aligned} Z_{TE}=\dfrac{jZ_0}{\sqrt{\left( \dfrac{\lambda }{\lambda _\textrm{c}} \right) ^2-1}}, \end{aligned}$$
(9)

where the cutoff wavelength \(\lambda _\textrm{c}=2\pi a/\chi '_{mn}\) , and \(\chi '_{mn}\) is the nth root of mth Bessel function derivative \(J'_{m}(\chi ')\).

With the thickness limitation mentioned in Sect. 2.1, field attenuation inside the hole can be neglected and transmission coefficient is calculated from S-parameter \(T=\mid S_{21}\mid ^2\) [36], where

$$\begin{aligned}&S_{21}=S_{11}+1, \end{aligned}$$
(10)
$$\begin{aligned}&S_{11}=\dfrac{Z_{\textrm{eq}}-Z_0}{Z_{\textrm{eq}}+Z_0 } ,{} & {} Z_{\textrm{eq}}=\dfrac{Z_0 Z}{Z_0+Z}, \end{aligned}$$
(11)

where \(Z_{\textrm{eq}}\) represents the total equivalent impedance (Z) parallel to the free space impedance \(Z_0\).

2.1 The electric nanocircuit model limitations

We are considering the EM problem of insulator–metal–insulator (IMI), where the incident waves are in the z direction (normal to the surface) and \(E_x\) is tangent to the surface of the interface. At the interface between the dielectric (with positive real dielectric constant \(\epsilon _2\)) and the metal (with dielectric function \(\epsilon _1 (\omega )\)), at frequencies below the bulk plasmonic frequency (\(\omega _p\)), the dispersion equation of surface plasmon polariton (SPP) propagating at the interface is [39]:

$$\begin{aligned} \beta =k_0 \sqrt{\dfrac{\epsilon _1 \epsilon _2}{\epsilon _1+\epsilon _2 }}, \end{aligned}$$
(12)

where \(\beta\) is the propagation constant of the traveling wave, and \(k_0=\omega /c\) is the wave vector of the wave propagating in vacuum. The non-zero imaginary part of \(\beta\) is associated with attenuation of the surface plasmon, where the energy of the surface plasmon decreases by a factor (1/e) at the propagation length \((L_p=1/(2 Im(\beta ) ))\). On the other hand, the propagation constant of the guided modes inside both the metal \((\gamma _\textrm{m})\) and the dielectric \((\gamma _\textrm{d})\) are calculated as:

$$\begin{aligned} \gamma _\textrm{m}=\dfrac{-ik \epsilon _\textrm{m}}{\sqrt{(\epsilon _\textrm{m}+\epsilon _\textrm{d} )}}~ , ~\gamma _\textrm{d}=\dfrac{ik \epsilon _\textrm{d}}{\sqrt{(\epsilon _\textrm{m}+\epsilon _\textrm{d} )} }. \end{aligned}$$
(13)

The EM field of the SPP is maximum at the metal–dielectric interface and decays in the direction perpendicular to the interface. The field decreases by a factor of 1/e at the penetration depth \(l_{p,i}=1/{\text {Re}}({\gamma _i})\), where i represents metal or dielectric media [40]. For thick metal films (thicker than penetration depth), the SPP consists of two weakly coupled propagating plasmons on the two surfaces of the metal film. For the above analysis, we propose that the equivalent circuit model is more accurate and valid in thin film plasmonic surfaces (thickness \(\le\) 100 nm for silver)

Considering the Fabry–Perot resonance [41], the resonance mode (\(\nu _q\)), at which constructive interference occurs between the incident beam and the circulating beam is at

$$\begin{aligned}&\nu _q~=~ q \Delta \nu _{\textrm{FSR}}, \end{aligned}$$
(14)
$$\begin{aligned}&\nu _q~=~ \dfrac{q}{t_{\textrm{RT}}}, \end{aligned}$$
(15)

where q is the mode index, \(t_{\textrm{RT}}\) is the round-trip time, and \(\Delta \nu _{\textrm{FSR}}\) is the free spectral range [42]. From the thickness limitation, the first Fabry–Perot resonance mode which occurs approximately at \(\nu _1=2 t/c\) , where c represents the speed of light, is out of the frequency range of interest (200–900 nm).

The model can be extended to arbitrary incident angle, the dependence of the impedance on the incident angle is studied in references [43, 44]. for the metallic grid impedance

$$\begin{aligned}&Z_{\textrm{grid}}=Z \times \xi , \end{aligned}$$
(16)
$$\begin{aligned}&\xi =1-k_0^2 {\text {sin}}^2(\theta )/2 k_{\textrm{eff}}^2, \end{aligned}$$
(17)

where \(k_{\textrm{eff}}=k_0 \sqrt{\epsilon _{\textrm{eff}}}\) is the effective wave number, \(k_0\) is the wave number in free space, and \(\epsilon _{\textrm{eff}}\) is the effective permittivity. Free space impedance for different incident angle is estimated as follows:

$$\begin{aligned}&Z_{0,{\text {TM}}}=Z_0 {\text {cos}}(\theta ), \end{aligned}$$
(18)
$$\begin{aligned}&Z_{0,{\text {TE}}}=Z_0/{\text {cos}}(\theta ). \end{aligned}$$
(19)

3 Results

For comparison purposes, we define two figures of merit to demonstrate the relative deviation between the analytical ENC model and numerical results; the peak-wavelength deviation \(D_\lambda\) , at which the maximum transmission takes place, and the transmission deviation \(D_{\textrm{T}}\), as follows:

$$\begin{aligned}&D_\lambda \, (\%)=\dfrac{(\mid \lambda _{\textrm{EC}}-\lambda _{\textrm{num}}\mid )}{\lambda _{num}} \times {100}\%, \end{aligned}$$
(20)
$$\begin{aligned}&D_{\textrm{T}}\, (\%)=\dfrac{(\mid T_{\textrm{EC}}-T_{\textrm{num}} \mid )}{T_{\textrm{num}} }\times 100 \%, \end{aligned}$$
(21)

where \(\lambda _{\textrm{EC}}\)and \(\lambda _{\textrm{num}}\) are the peak wavelengths of both ENC model results and COMSOL calculations, respectively, and \(T_{\textrm{EC}}\) and \(T_{\textrm{num}}\) are the maximum transmission of ENC results and COMSOL calculations. The parameters, \(D_\lambda\) and \(D_{\textrm{T}}\) are defined to illustrate the deviation from the numerical study either in the wavelength of the peak or the maximum transmission value, which are very important in optical filtering application. It is worthy to mention that the deviation in the maximum transmission is not necessarily occurring at the same wavelength .

For comparison, the model is simulated, numerically, by COMSOL Multiphysics Software, which is considered as one of the most suitable tools for simulating different plasmonic structures.

3.1 Hole size effect

As shown in Fig. 4, increasing the hole diameter results in more light transmission. The equivalent nanocircuit achieved good matching for small holes where the diameter is smaller than half the periodicity with only zero-order impedance approximation with a deviation of peak-wavelength and transmission about 3% and 6.6%, respectively, as mentioned in Table 1. On the other hand, ENC of large holes requires additional high-order impedance approximation.Higher-order modes are presented to expand the ENC model in large hole sizes and to reduce the deviation between the model and numerical results. The periodicity and thickness were kept constant (\(L=200\) nm, \(t=50\) nm), where the hole diameter changes with respect to it in three domains: \(d=40\) nm \((d<L/2),~ d=100\) nm \((d=L/2)\), and \(d=140\) nm \((d>L/2)\).

Fig. 4
figure 4

Transmission for different hole radius: \(d=40\) nm \((d<L/2),~ d=100\) nm \((d=L/2)\), and \(d=140\) nm \((d>L/2)\) at \(L=200\) nm and \(t=50\) nm

Full size image
Table 1 Deviation of ENC model from COMSOL calculations for different radii at \(L=200\) nm and \(t=50\) nm
Full size table
Fig. 5
figure 5

Transmission spectrum and electric field distribution from numerical simulation at the transmission first peak(\(\lambda ~=~320\) nm), dip (\(\lambda ~=~375\) nm) and second peak (\(\lambda ~=~400\) nm) at \(L= 200\) nm, \(d=100\) nm and thickness \(t = 60\) nm

Full size image

3.2 Thickness effect

As shown in the transmission spectrum from numerical simulation, Fig. 5, it has three main features to be examined: first peak at \(\lambda ~=~320\) nm, a dip at \(\lambda ~=~375\) nm, and a second peak at \(\lambda ~=~400\) nm.

For the first peak, increasing the thickness does not affect the wavelength of the peak, as shown in Fig. 8, where the wavelength of the first peak is almost constant at \(\lambda ~=~320\) nm for different thicknesses. This can be explained from the diffraction theory and electric field distribution around the hole edge shown in Fig. 5a.

When light scatters through subwavelength apertures in very thin perfect metal film, it diffracts at the edges, as shown in Fig. 6a, with a transmission related to both hole radius and light wavelength by factor \((r/\lambda )^4\) [45]. However, the transmission in a non-zero thickness hole is characterized by waveguide properties where the transmission is exponentially small above the cutoff wavelength \(\lambda _\textrm{c}\) [11]. Although the cutoff frequency of cylindrical waveguide only depends on the hole radius, the skin depth in real metal increases the cutoff frequency when is taken into account.

Fig. 6
figure 6

a Diffraction of visible light through a subwavelength hole in an infinitely thin film, b the realistic non-zero thickness cylindrical hole with a radius smaller than the wavelength

Full size image

On the other hand, the second peak results from SPP where the electric field is concentrated at the hole edge and the EM wave propagates along the surface as shown in Fig. 5c.The second peak is highly affected by the thickness increase as the coupling between the two surfaces SPP decreases, as shown in Fig. 7. As explained in Sect. 2.1, as the field decays by factor of 1/e at the penetration depth inside the metal. That’s why decoupling is clear at thickness \(t>100\) nm.

Fig. 7
figure 7

Electric filed in y–z plane view for different thicknesses from numerical simulation with \(d=100\) nm and \(L=200\) nm, showing the decoupling between SPP at both surfaces at thickness \(t>100\) nm

Full size image
Fig. 8
figure 8

Transmission for different thickness at diameter 100 nm

Full size image
Table 2 Deviation of ENC model from COMSOL calculations for different thicknesses at \(L=200\) nm and \(d=100\) nm
Full size table

As shown in Fig. 8, comparing the ENC results and COMSOL calculations shows the model sufficiency in estimating both peak-transmission wavelength, and transmission value. The maximum deviation of peak-wavelength is about 6%, whereas the transmission deviation is about 21%, as mentioned in Table 2.

3.3 Comparison with previously reported results

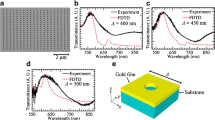
For validation purposes, we compared the proposed ENC model with the experimental measurements reported in [46] for a gold surface structured with a circular hole array (the diameter of the aperture is 200 nm and the periodicity of the array is 600 nm), in which the holes were fabricated through 120 nm thick gold and 80 nm thick silicon nitride layers.

Adjusting the conductivity and structure dimensions values to compensate the actual loss and fabrication varieties in the experimental measurements (as shown in Fig. 9), the ENC results were accurate within 3% of the reported values [46].

Fig. 9
figure 9

Comparison between experimental [46] measurements, numerical calculations, and ENC results for transmission through surface structured with a hole array

Full size image

As shown in Fig. 9, despite the model is efficient in estimating the main peaks locations, it could not detect the secondary peaks because of the approximations in the analytical model where \(d<L/2\) as discussed in Sect. 3.1. This is acceptable for example in designing filters, where a designer is more concerned with the main peaks. So, the model can avoid the long numerical calculation times if used by CAD tools for designing the main features. Once a design is decided on, the designer can do a detailed study or sensitivity analysis in full-wave simulators if needed [47, 48].

4 Model discussion and extension to other cases

In this section, we demonstrate that with suitable impedance representation, ENC modeling can be applied for different hole shapes. In addition to the conventional circular hole shape, other shapes were fabricated such as square[49], rectangle [50] and hexagon [51] hole arrays.

As an example, we apply the ENC model for square hole array shown in Fig. 10. The main modeling procedure is based on representing the metal region with inductance impedance and dielectric regions with capacitance impedance. A previous study of square metal (ITO) plasmonic surface was presented in infrared region with similar procedure [36].

Fig. 10
figure 10

a Schematic of the top view of the square hole unit cell, b equivalent circuit of the unit cell

Full size image

The impedance in both metal and air regions are estimated as follows:

$$\begin{aligned}&Z_\textrm{c}=\dfrac{j}{\omega \epsilon _0 t}, \end{aligned}$$
(22)
$$\begin{aligned}&Z_{L_1}=j \dfrac{d}{\omega \epsilon _0\epsilon _\textrm{m} (L-d) t}, \end{aligned}$$
(23)
$$\begin{aligned}&Z_{L_2}=j \dfrac{L-d}{\omega \epsilon _0 \epsilon _\textrm{m} L t}. \end{aligned}$$
(24)
Fig. 11
figure 11

Transmission for different hole side length

Full size image
Table 3 Deviation between ENC model results and COMSOL calculations for different side lengths at \(L=200\) nm and \(t=40\) nm
Full size table

As shown in Table 3, the transmission is estimated for three values of the square hole side length; representing three different domains compared with the periodicity (\(<L/2 , =L/2 , >L/2\)). The ENC results achieved good matching with COMSOL calculations especially in estimating the peak-transmission wavelength, as shown in Fig. 11, which increase the reliability of the model in designing filters.

5 Conclusion

We present a simple and efficient theoretical model for hole array in plasmonic silver surface. The model extends the conventional equivalent circuit approach to the optical frequencies where the metal cannot be considered as perfect conductor. Applying the model for circular hole array with different radii and thickness shows the simple model effectiveness in designing FSS with hole arrays for optical applications. The model is compared with experimental measurements and numerical model calculations built by COMSOL Multiphysics and showed an acceptable deviation for an analytical model. The ENC model can be a good basis for designing FSS in CAD tools in the future rather than the need for full-wave simulators.