1 Introduction

Forming the intensity distribution in a beam of light using a mask is a widespread strategy with many different applications. For example, in integrated circuit manufacturing different types of masks are used to pattern the photo-resist on a wafer substrate as accurately as possible. While binary masks only alternate between no and full illumination, with a phase mask the interference of different mask sections is utilized and the full amount of incoming light can be exploited.

Similarly, the amplitude and phase distribution of a laser beam can be influenced by a mask in one position to produce a predefined intensity distribution in a different position further down the propagation direction. In such a beam forming process, the used mask is usually called a diffractive optical element (DOE). DOEs are typically fabricated lithographically in a procedure of repeated resist coating, exposure, development, and etching, to produce a discrete number of height levels on the surface of a transparent substrate. The phase information is then encoded in the path difference inside and outside of the transparent material. While the fabrication method allows for structural features with very high resolution down to the nanometer scale, it usually requires an extensive multi-step process under clean room condition, which has to be repeated for every new mask design.

An alternative to a DOE can be realized by a spatial light modulator [1]. Here, the necessary optical phase shift is generated by a liquid crystal array, where the refractive index of each pixel can be changed electronically. Controlled by a video signal, such a device offers great flexibility and speed. On the other hand, system cost is still high and cooling can be an issue at higher intensities.

In this paper, we study the possibility to fabricate an array of predefined phase shifts by a direct laser-writing process. It is well known, that the non-linear interaction of ultra-short pulsed lasers with a transparent medium enables a three-dimensional in-volume modification of optical materials [2]. Especially at moderate intensities just above the modification threshold the induced structural changes lead to a permanent change of the refractive index in optical glass. Such refractive index modifications have been used to fabricate all kinds of optical devices, i.e., wave guide structures [3], volume Bragg gratings [4], Fresnel zone plates [5, 6], and others. Typically the change in refractive index is on the oder of \(\varDelta n \approx 10^{-3} ... 10^{-2}\), leading to a necessary \(2\pi\)-modification length in the micrometer range. While often a microscope objective is used to generate a very small focal volume, some techniques show, that a more loose focusing together with higher pulse energy is also sufficient to create refractive index modifications [7]. We adopt such a strategy, using a typical industrial laser micromachining setup. With a ps-laser source at \(\upmu\)J-level pulse energy and a standard galvo scanner, we create refractive index modifications in a block of BK7 glass that can be used as a tunable phase shift in a mask design.

The paper is structured as follows. First, we discuss the related physical processes, the experimental parameters of a single refractive index modification, and how we realize a tunable phase shift (Sect. 2). Next, we outline the iterative Fourier transform algorithm, which we use to calculate the necessary phase distribution for an image with a given intensity pattern (Sect. 3). Afterwards, we describe the fabrication process and its relevant parameters, present examples of fabricated phase masks and compare the corresponding theoretical and experimental image data (Sect. 4). In the end (Sect. 5), we summarize our results and discuss possible further improvements.

2 Realizing a tunable phase shift

2.1 Energy deposition mechanism

In principle, the modification of a transparent material inside a volume relies on the deposition of energy in the focal region of an ultra-short pulsed laser. While a band gap greater than the photon energy permits propagation without substantial linear absorption, the increasing intensity close to the focus induces non-linear absorption processes like multi-photon ionization (MPI) or tunneling ionization (TI). A typical threshold for the onset of MPI in glass is on the order of \(~10^{12}-10^{13}~{\hbox {W}}/{\hbox {cm}}^2\). The creation of first free electrons above the band gap then enables a self-enhancing process of electron acceleration and collision dynamics, substantially increasing the electron density by an avalanche ionization (AI). The relative amount of MPI, TI, and AI in the overall absorption process thereby strongly depends on the pulse duration and peak power [8]. As a result an electron plasma is created and the absorbed energy is converted into thermal energy by electron-phonon interaction with a relaxation time of ten to several hundreds of picoseconds. Remaining thermal energy can also accumulate over many pulses and change the absorption characteristics for subsequent pulses. When enough energy has been deposited in a spatially finite region, the formation of several types of modifications are possible [2]. For moderate energies, a positive change of refractive index will result, usually attributed to a change of the local density (termed type I modification in the literature). For higher energies, also negative changes of the refractive index are possible, combined with induced birefringence (type II modifications) [9]. A more recent work shows that a continuous transfer of the two regimes in terms of induced stress and density is possible [10]. For still higher energies the creation of voids and crack structures are observed. An interesting way to exploit induced birefringence has been demonstrated in so-called geometric phase optical elements (GPOEs). Here, the spatial orientation of laser-induced nano-gratings is used to encode phase information into the local polarization state of the wavefront [11, 12].

Fig. 1
figure 1

Phase-contrast image of refractive index modifications created with 1000 pulses at 100 kHz. As indicated, the beam propagation direction is into the negative z-direction and the pulse energy is increased from left to right

Full size image

2.2 Accessible parameter range

In our setup, we use an industry standard regenerative amplifier at \(\lambda =1030\) nm as a laser source. It can deliver pulses with energies of \(E_p=50\) \(\upmu\)J at a repetition rate of \(f_r=1\) MHz. With a pulse duration just under 1 ps (\(t_0=994\) fs sech autocorrelation fit), we are reaching a peak power of about \(P_{peak}=0.88 (\sqrt{2}) E_p/t_0\cong 44\) MW, where \({{\,\mathrm{arcosh}\,}}(\sqrt{2})\cong 0.88\) is a pulse shape specific factor assuming a sech pulse shape. Focusing down to a spot size of \(2 w_0\cong 25\) \(\upmu\)m, a peak intensity of \(I=2 P_{peak}/\pi w_0^2=1.8\cdot 10^{13} {\hbox {W}}/{\hbox {cm}}^2\) results. This intensity is already above the threshold for the non-linear interaction, such that a substantial amount of the pulse energy can be absorbed. Unfortunately, at the same time, the non-linear interaction strongly influences the propagation towards the focus by self-focusing due to the Kerr-effect and the formation of single or even multiple filament structures [8, 13, 14]. Because of the non-linear nature of the underlying phenomena, this renders the spatial formation of the resulting plasma quite susceptible to small variations in pulse energy and beam profile. It not only prevents a good localization of the deposited energy but also leads to an unwanted statistical variation in the targeted refractive index modifications. To some extend, this effect can be mitigated by stronger focusing and a microscope objective has been routinely applied. However, in our case, we are using a more simple system with a galvo scanner which is quite flexible but limited to a moderate focusing of \(\text {NA}=0.05\). Therefore, we adopt a different strategy and reduce our pulse energy below the threshold of a single pulse modification. Instead, we use the incubation effect of many pulses to still deposit enough energy but with strongly reduced filament structures.

In the following parameter study, we determine the most suitable parameters to create a refractive index modification with a stable and preferably small size. For simplicity and cost, we use small blocks of BK7 glass as our transparent material. Due to the material dependence of the non-linear interaction (i.e., due to a different band gap) we would expect, that we would have to scale the resulting parameters for other types of glasses. Qualitatively, we find the same type of propagation and modification behavior as has been found in fused silica [8, 14]. With our samples, we use phase-contrast microscopy [15] at a view from the side of the sample (namely the viewing direction is the y-direction perpendicular to the propagation direction of the writing laser which is the negative z-direction). The images make phase changes visible, in the way that a positive refractive index change (\(\varDelta n>0\)) appears darker. In Fig. 1 we show the refractive index modifications created with 1000 pulses at a reduced rate of 100 kHz and different pulse energies. One can clearly see, that also in a multi-pulse incubation a higher pulse energy leads to less localization and more filamentation. The best result in this case we obtained at a pulse energy of about 20 \(\upmu\)J. Here, the overall deposited energy is just above the threshold to create a modification at all. At the same time, the modification is as small and localized as possible, compared to higher pulse energies. Looking at the number of pulses, we apply to one location, we find, that in our parameter range a number of several 100 to 1000 is suitable (see Fig. 2). Obviously, the threshold for a stable creation of a modification also depends on the used pulse energy. With 40 \(\upmu\)J, already 250 pulses are sufficient to create a modification. Due to the higher pulse energy, it is significantly broader and more inhomogeneous in the lateral dimension compared to 1000 pulses applied at 20 \(\upmu\)J. To reach a more homogeneous profile and a higher lateral resolution, a smaller pulse energy combined with a higher number of pulses seems more favorable.

Fig. 2
figure 2

Variation of the number of pulses. Fixed parameters are a pulse energy of 40 \(\upmu\)J at 100 kHz

Full size image

The third parameter which has an important influence is the time interval between the individual pulses applied (see Fig. 3). If this interval is to small, the correspondingly fast heat deposition will create a crack structure with unwanted interfaces. On the other hand, if the interval is to long, the incubation effect is not strong enough any more to create a modification at all. A good compromise for our case is in the range of 10 \(\upmu\)s, such that we use a reduced repetition rate of 100 kHz.

Fig. 3
figure 3

Variation of the time interval between individual pulses. Fixed parameters are a pulse energy of 20 \(\upmu\)J and 1000 pulses applied. For a time interval of 1 \(\upmu\)s a crack structure was created

Full size image

2.3 Tunable phase shift by superposition

Looking at the presented parameter study, we find that a refractive index modification with good localization and minimum variation can be created by applying 500–1000 pulses with 20 \(\upmu\)J pulse energy at 100 kHz repetition rate. Such a modification has a length of about \(z=200\) \(\upmu\)m, a width of \(w=10-15\) \(\upmu\)m, and a refractive index change on the order of \(\varDelta n=10^{-3}\). The phase shift created at a wavelength \(\lambda\) is given by

$$\begin{aligned} \varDelta \varphi = 2 \pi \varDelta n \frac{z}{\lambda }. \end{aligned}$$
(1)

If we assume a visible wavelength of \(\lambda =500\) nm, this already results in \(40\%\) of a \(2 \pi\) phase shift, such that a controllable phase shift from \(0-2 \pi\) seems in reach. However, tuning the phase shift by a variation of \(\varDelta n\), for example by changing the pulse energy or the number of pulses does not really seem feasible, since the same parameters will change the length and width of the modification. Another possibility which turns out to be more suitable is the elongation of a modification. Correspondingly, we create several overlapping modifications in a line from bottom to top by shifting the focus position opposite to the beam direction. Due to the superposition, one might expect that the resulting refractive index will exhibit an inhomogeneous axial profile. In Fig. 4, we show two example results in the same side view as before.

Fig. 4
figure 4

A modification can be elongated by superposition of several modifications created at a shifted focus position. In the left part of the figure 500 pulses with 20 \(\upmu\)J and in the right part 1000 pulses with 15 \(\upmu\)J have been applied for each individual modification. Both experiments show a gradual elongation by superimposing \(1-50\) modifications at \(\varDelta z=10\) \(\upmu\)m axial distance. The lateral distance is \(\varDelta x=10\) \(\upmu\)m

Full size image

The results show that depending on the used number of pulses and the pulse energy, a certain amount of saturation in the modification development can lead to a very smooth form of superposition. We use a focus shift of \(\varDelta z=10\) \(\upmu\)m and decrease the number of pulses or the pulse energy compared to a single modification to account for the additional concentration of energy due to the overlap. Comparing the two example results in Fig. 4, we see that reducing the pulse energy to 15 \(\upmu\)J (right part of figure) is more effective for a smooth form than reducing the number of pulses to 500 (left part of figure). The result is an axially homogeneous modification with a tunable length much smaller than the length of a single modification. The length scale of \(\varDelta z=10\) \(\upmu\)m should be suitable to realize the desired tunable phase shift in a range of \(0-2 \pi\) with sufficient resolution.

3 Calculating the phase distribution

Aiming to generate a predefined target intensity distribution, the question arises, how we can calculate a corresponding phase distribution. We assume, that for a known phase distribution \(\varDelta \varphi (x,y)\) in a mask together with a predefined source amplitude E(x, y), i.e., a laser beam profile, the resulting intensity distribution \(I(x',y')\) can be calculated as shown in diffraction theory [16]. We do this in the far field limit by taking the Fourier transform and the absolute value squared,

$$\begin{aligned} I(x',y')=\left| \int _{-\infty }^{\infty } E(x,y) e^{-i \varDelta \varphi (x,y)} e^{2 \pi i (s_x x + s_y y)} dx dy\right| ^2, \end{aligned}$$
(2)

where the target-plane coordinates \(x'=s_x \lambda l\) and \(y'=s_y \lambda l\) are expressed by the spatial frequencies \(s_x, s_y\) , the wavelength \(\lambda\) and the propagation length l. However, to inversely calculate an unknown phase distribution from a given intensity distribution amounts to a phase retrieval problem, with no closed-form solution. Instead, we use an iterative Fourier transform algorithm by Gerchberg and Saxton [17], that extracts the unknown phase by going back and forth between the known intensity distributions of source and target plane. As shown in Fig. 5, the algorithm starts with the source amplitude \(E_{sc}=\sqrt{I_{sc}}\) together with an initial random phase. In each iteration step, the combination of amplitude and phase is transferred from the source plane to the target plane and back by (inverse) Fourier transformation. In the target plane, the resulting phase is kept and the amplitude is replaced by the target amplitude \(E_{tg}=\sqrt{I_{tg}}\). In the same way, in the source plane again the phase is kept and the amplitude is replaced by the source amplitude \(E_{sc}\).

Fig. 5
figure 5

Iterative Fourier transform algorithm to extract the unknown phase from a given source and target intensity distribution

Full size image

Since the phase information in each plane depends on the amplitude information in the other plane, the iteration extracts a phase distribution consistent with forming the target distribution from the given source. We numerically implement such an algorithm with a source and target distribution discretized on a two-dimensional array. With a power of two as grid size N (i.e., \(N_{xy}=2^5=32\) or \(N_{xy}=2^6=64\)) we can speed up the numerical fast Fourier transform. A typical quality check can be done by calculating the following scalar product in the target plane,

$$\begin{aligned} \langle \tilde{E} , \tilde{E}_{tg} \rangle = \int _{-\infty }^{\infty } \tilde{E}(s_x,s_y)^* \tilde{E}_{tg}(s_x,s_y) ds_x ds_y \in [0,1], \end{aligned}$$
(3)

to measure the overlap of the image distribution calculated from the retrieved mask \(\tilde{E}\) and the target distribution \(\tilde{E}_{tg}\). From this integral a value of one corresponds to a \(100\%\) matching result. If we use a number of 30 iteration cycles in the algorithm, we can calculate the phase array in just a few seconds reaching \(>97\%\) overlap.

4 Results and discussion

With the individual tunable phase shift from Sect. 2 and phase data calculated with the algorithm described in Sect. 3, we can now proceed to fabricate a phase mask for a given target intensity. But in the practical implementation several parameters still have to be optimized.

First, we do not know the exact amount of refractive index change we induce. From the fact that a 10 \(\upmu\)m thick modification appears as a clearly visible change of intensity in our phase-contrast images, we can estimate it to be on the order of \(\varDelta n \approx 10^{-3}\). This value is also consistent with similar parameters from literature [18,19,20,21]. At the same time, our calculations show that a mismatch of 20% already strongly degrades the target quality and the target virtually disappears with a phase shift too large by a factor of two. We thus first approach the correct amount of phase shift with a simple test pattern using a square frame as a target distribution (see Fig. 7). We gradually vary the \(2\pi\)-modification length corresponding to different estimates of \(\varDelta n\). Rounding off the resulting modification length to multiples of \(\varDelta z=10\) \(\upmu\)m, we fabricate a series of phase masks. After running the laser-writing process with the optimized writing parameters of 15 \(\upmu\)J and 1000 pulses at 100 kHz, we produce each diffraction pattern with the beam of a Helium–Neon laser (\(\lambda =632,8\) nm) on a screen at \(l=0.7\) m distance. We do not observe any polarization dependence of the resulting image. In the range of \(\varDelta n \approx 10^{-3}\), the expected target distribution appears and we find that with a value of \(\varDelta n = 1.5 \cdot 10^{-3} (\pm 5\%)\) it can be reproduced best.

Fig. 6
figure 6

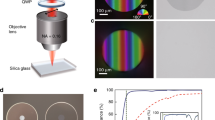
Phase-contrast image of a size \(N_{xy}=32\) phase mask from a top view. The focal plane of the microscope is in the top z-layer on the left side of the image and about in the center on the right side. Since the microscope depth of field is much shorter than the typical modification length, different layers of the mask become visible

Full size image

Next, the continuous phase values resulting from the algorithm have to be discretized in a meaningful manner. The method, we presented in Sect. 2 can in principle produce a near continuous modification length. But since we realize the corresponding shift of focus by moving a z-stage motorized with a stepper which is much slower than the xy-dynamics of our scanning head, this would lead to an impractical amount of time-consuming z-steps. Instead, we restrict the phase data to \(N_z=8\) discrete levels and finish all modification parts on the same z-level before moving the stage to the next higher level (see Fig. 6). Comparing the target quality of continuous and discretized masks with Eqn. 3, we find that the overlap is still \(>95\%\). This seems acceptable considering, that lithographically fabricated DOEs usually come with a discretization down to \(N_z=4\) levels or are even realized as binary phase masks. With this strategy, we achieve a processing time of about 8-9 minutes for a size \(N_{xy}=64\) array which accumulates from the jump and writing time of about 16 ms per individual modification. At the same time, the distance of the discrete z-levels is then given by

$$\begin{aligned} \varDelta z=\frac{\lambda }{\varDelta n N_z}=53 ~\upmu \text {m}. \end{aligned}$$
(4)

This is well below the length of a single modification of about 200 \(\upmu\)m such that the different layers are smoothly connected.

Fig. 7
figure 7

Square frame target intensity distribution produced with a Helium–Neon laser on a screen at \(l=0.7\) m distance. On the left side of the image, a pixel size of \(\varDelta x=12\) \(\upmu\)m has been used, on the right side \(\varDelta x=9\) \(\upmu\)m

Full size image

Another parameter that strongly influences the target quality is the pixel size, the lateral distance \(\varDelta x\) of the individual modifications. As can be seen in Fig. 7, most prominently the size of the diffraction pattern and correspondingly the distance to the next higher-order diffraction is given by the law of a diffraction grating applied to the pixel array. This distance \(x'_{max}\)is then given by

$$\begin{aligned} x'_{max}=\frac{\lambda }{\varDelta x} l, \end{aligned}$$
(5)

leading to an image size of about 3.7 cm and 4.9 cm, which is well reproduced in case of the two examples shown in Fig. 7. Obviously, a smaller pixel size not only leads to a larger diffraction image but also has the potential to increase the image quality. On the other hand, we are limited by the lateral size of the modification which is approximately \(9-10\) \(\upmu\)m. For a smaller pixel size, neighboring modifications start to overlap, influencing their respective radial density profile and changing the corresponding amount of phase shift. Furthermore, with a pixel size of \(\varDelta x=9\) \(\upmu\)m and \(N_{xy}=64\) we already reach a mask size of \(x_{max}=\varDelta x N_{xy}=576\) \(\upmu\)m which is just about the size of our Helium-Neon laser beam of \(2 w_0=500\) \(\upmu\)m.

Considering the thickness of the mask, one could expect that beam propagation effects of the imaging laser inside the mask volume do influence the produced diffraction images. The overall length scale of the elongated modification is about three orders of magnitude larger than the wavelength such that we deal with a mask thickness of about \(0.5-1.0\) mm. On the one hand, this is intrinsically necessary since the refractive index change is only on the order of \(\varDelta n \approx 10^{-3}\). On the other hand, looking at the Rayleigh length of the imaging laser of about 28 cm, we see that the beam diameter and wavefront curvature only change in a negligible way inside the mask volume. Similarly, with a Fresnel number \(F\gg 1\), local diffraction inside the mask does not play a role. In essence, the effect of our mask should be independent of the thickness.

To test our fabrication method with a more advanced target distribution, we fabricate several phase masks with the above parameters where the produced feature size is in the range of \(1/10 -1/20\) of the overall image size. As an example, we present in Fig. 8 the results for a smiley face. Measuring the efficiency of the produced image by again calculating the overlap (see Eqn. 3), we find a value of \(>76\%\) compared to the numerically calculated diffraction image and a value of \(>60\%\) with respect to the initial target distribution. On the one hand, the result shows the general feasibility of our developed method. On the other hand, there is certainly room for improving the quality of the diffraction image. While the general features of the target distribution can clearly be identified, two aspects degrade the image.

Fig. 8
figure 8

Smiley face as an example for a more advanced pattern on a \(N_{xy}=64\) and \(\varDelta x=9\) \(\upmu\)m grid. On the left side we show the original target distribution together with the numerically calculated diffraction image. On the right side we show the measured distribution on the screen as a photograph and the same picture converted to the numerical color scheme

Full size image

In the center of the image, the zero-order non-diffracted laser beam is still strongly visible. This could cheerfully be interpreted as growing a nose to the smiley, which is meaningful in the sense that the zero-order beam can sometimes be included as a wanted feature of the target. In general, it is a well known problem for the application of DOEs. It is always present to some extend, as it is caused by non-exact phase shift values due to tolerances in the fabrication leading to an incomplete destructive interference at the image center. Methods for mitigation include using a mechanical mask to block it off, illumination with a divergent or angled beam, adding more phase levels, or certain precompensation strategies in the mask design.

Furthermore, there is a quite strong background of scattered intensity that lowers the overall contrast of the image. We attribute this scattering mainly to the diffraction at the individual modification. While the overall mean phase shift of a single pixel can be tuned to just the right amount, we cannot prevent a scattering at the transverse spatial profile of the corresponding modification. This profile is not homogeneous as it is implicitly given by the focal profile of the ultra-short pulsed laser and the non-linear absorption mechanism described in Sect. 2.1. The resulting refractive index profile is approximately the imprint of a rotationally symmetric density variation. It seems that we can achieve a better homogeneity in axial direction (z-direction) due to the superposition of individual modifications. Still some tapering at the first and last z-level occurs (see Figs. 4 and  6). An interesting question that remains, is if there exists an optimized scanning strategy that works with lateral overlap and the combination of adjacent pixels to permit a spatially more homogeneous phase shift on the pixel level.

While at the moment, the inhomogeneous profile is intrinsic to the presented fabrication method, its influence can certainly be reduced just by scaling down the modification size relative to the influenced beam profile, i.e., with smaller fabrication laser wavelength, a smaller focus volume, or a bigger illumination beam diameter. This should for example become apparent, when a mask with our current feature size is applied to the beam at the entrance aperture of the scanner in our micromachining setup. Here, a beam diameter of \(2 w_0=10\) mm is used such that the relative feature size of the mask would be smaller by a factor of 20 compared to the presented results with the additional benefit of a larger wavelength. Influencing the phase profile of the fabrication laser beam offers further interesting perspectives and options to tailor the machining focus. In a similar way, a related method has been used to machine the surface of an optical substrate with a combination of material removal by an ultra-short pulsed laser and a following polishing step by a carbon-dioxide laser [22]. The produced axicon optics is capable of forming an elongated machining focus typical for a Bessel beam.

5 Summary and outlook

In summary, we have developed a fabrication method that uses a direct laser-writing process to encode a phase mask into the volume of an optical glass substrate. As a first step, we have worked out a parameter set for the non-linear absorption process to create a stable and reproducible refractive index modification in BK7. The superposition of several modifications enabled us to elongate the modification to a variable length. Using the corresponding tunable phase shift as the single pixel unit of an array, we created a laser machining recipe to implement the full phase mask as a set of \(N_z=8\) discrete layers in a machining time of about 8–9 min for a mask size of \(64\times 64\) pixels. With first successfully written masks, we determined our induced refractive index change to be \(\varDelta n = 1.5 \cdot 10^{-3} (\pm 5\%)\). It followed, that our discrete step size for a single z-layer is given by \(\varDelta z=53\) \(\upmu\)m for an illumination wavelength of \(\lambda =632.8\) nm. With a suitable test pattern, we investigated the influence of several parameters on the quality of the targeted diffraction image. We showed, that a pixel size down to roughly the lateral diameter of a single modification (\(\varDelta x=9\) \(\upmu\)m) is feasible and compared the experimentally measured image size to the prediction from diffraction theory. In the context of mask size, we also discussed how the diffraction image of our mask depends on the pixel size and at the same time should be independent of the thickness. Looking at a more advanced test pattern, we demonstrated the general feasibility of our developed method and discuss its main current limitations. Besides the visibility of the zero-order beam, we identified scattering at the inhomogeneous modification profile as the most important issue. Here, we are currently limited by the size of the individual modification itself, enforcing a compromise between a better resolution and the overlap of adjacent modifications. As we have discussed, a smaller focal volume, a bigger illuminating beam size, or a possibly adapted scanning strategy could help to improve image quality. Since a smaller focal volume could be achieved by using a higher focusing NA, new industrial developments towards a galvo-scannable microscope objective open up a promising way to implement our method with a higher resolution while maintaining high scanning speed. Looking at the overall work-flow, we also want to point out, that the iterative Fourier transform algorithm could benefit from further improvement. One problem is that, due to mathematical ambiguity, there exists a certain tendency for the algorithm to incorporate the symmetric mirror image of the target into the phase mask. This is of course only visible for non-symmetric target distributions and actually a slight feature of the smiley mouth can be found in the numerically calculated diffraction image in the region of the smiley eyes in Fig. 8. A possible solution to remove the mathematical ambiguity could be to include additional illumination directions into the phase-retrieval calculation as used in ptychographic imaging methods [23]. Another possible improvement is that there do exist methods to integrate the necessary discretization of the phase mask already into the iterative Fourier transform algorithm. As a result, the phase error due to the discretization can be partly avoided.