Lifetime reductions and read-out oscillations due to imperfect initial level preparations of atoms in a long-lived DLCZ-like quantum memory

Abstract

Entanglement between a spin-wave qubit (memory qubit) and a photonic qubit is a basic building block for quantum repeaters. Duan-Lukin-Cirac-Zoller (DLCZ) scheme, which generates spin waves via spontaneous Raman scattering (SRS) of Stokes photons in atomic ensemble, provides a promising way to generate such entanglement. In a recent work [arXiv: 2006.05631, accepted by communications physics], DLCZ-like quantum memory that generates long-lived atom-photon entanglement has been experimentally demonstrated, where magnetic-field-insensitive (MFI) coherence is used to store spin waves. For realizing such MFI spin-wave storage, the atoms have to be initially prepared in a specific Zeeman sublevel, which is achieved by applying optical pumping lasers. Here, we demonstrate the memory lifetimes for the cases that the atoms are perfectly and imperfectly prepared in the specific Zeeman level, respectively. The experimental results show that the spin waves associated with magnetic-field-sensitive (MFS) and MFI coherences will be simultaneously created for the case that the atoms are imperfectly prepared in the Zeeman sublevel. Thus, the read outs will experience decay oscillations due to interferences between the two spin waves and the memory lifetime will be shorten due to dephasing of MFS coherence. A detailed theoretical analysis has been developed for explaining the experimental results. The present work will help one to understand decoherence of spin waves (SWs) and then enable one to obtain optimal lifetime of the entanglement storage in the cold atoms.

1 Introduction

Entanglement distribution over long distances is crucial for long-distance quantum communication [1,2,3] and large-scale quantum networks [4, 5]. Due to transmission losses in quantum channels and the no-cloning theorem for quantum states, direct entanglement distribution over long distances (>500 km) is limited [2]. Quantum repeaters (QRs) [1, 2, 6] provide a possible way to achieve long-distance entanglement distribution. In QRs, long distances are divided into short elementary links, each link comprises two nodes [6]. Every node may be formed by a quantum interface that generates quantum correlation or entanglement [6] between a spin wave (atomic memory) and a photon. In an elementary link, the photon from each node is sent to the center station between two nodes in the link for Bell-state measurement (BSM). A successful BSM projects the two nodes in an entanglement state. Via entanglement swapping between two adjacent links, entanglement can be extended the full distances. To practically realize a QR, an attractive approach is the Duan-Lukin-Cirac-Zoller (DLCZ) protocol [1, 2], which generates spin-wave-photon quantum correlation or entanglement via spontaneous Raman scattering (SRS) in atomic ensembles. Over the past decade, the quantum interfaces that generate spin-wave-photon quantum correlation or entanglement through SRSs [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] or storage of photonic quantum correlation or entanglement [37,38,39] in atomic ensembles have been demonstrated.

In QRs, quantum memories (QMs) allow for the storage of generated entanglement in elementary links and then remove probabilistic steps in entanglement generations [2, 40]. For this, the QMs are required to have long lifetimes [2, 40]. For achieving long-lived QMs, decoherence of the spin waves in cold atoms was widely studied [14,15,16,17,18, 30, 35, 41]. It has been pointed out that atomic motions and inhomogeneous broadening of the spin transitions causes spin-wave dephasing [2]. The motion-induced decoherence is suppressed by using collinear configuration [14, 15, 35, 41] to lengthen spin-wave wavelengths or loading the atoms in optical lattices [16,17,18, 30]. The decoherence resulting from inhomogeneous broadening of spin transitions can be reduced by using magnetic-field-insensitive (MFI) coherences for the spin-wave (SW) storage [14,15,16,17,18, 30, 35]. For perfectly storing a SW as the MFI coherence, the atoms have to be initially prepared in a specific Zeeman sublevel by optical pumping lasers [14,15,16,17,18, 30, 35]. In this case, one can create a SW only associated with MFI coherence via SRS [14,15,16,17,18, 30, 35]. In the past decade, the long-lived DLCZ-like memory has been demonstrated for the case that the atoms are prepared in the single specific Zeeman sublevels in the cold atoms [14,15,16,17,18, 30, 35]. Also, for the case that the atoms are un-polarized, the DLCZ-like memory has been demonstrated [16]. However, the influence of the imperfect preparation of the initial Zeeman level on DLCZ-like memory lifetime remains largely unexplored. Here, based on the experiment set up that were used for achieving a long-lived DLCZ memory [35], we demonstrated retrievals of the spin waves for the cases that the atoms are imperfectly prepared into the specific Zeeman level. In this case, the spin waves associated with magnetic-field-sensitive (MFS) coherence are also created and the interference between the read outs from MFS and MFI spin waves will appear, which in turn results in fast decay and oscillations in the read outs and then decrease the memory lifetime. The present results will help one to understand decoherence of the SWs and then enable one to obtain optimal lifetime of the entanglement storage in DLCZ scheme using cold atoms.

2 Experimental method

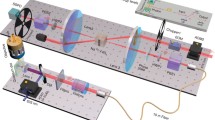
The experiment set up, as shown in Fig. 1a, is similar to the previous work [35]. A cloud of cold ⁸⁷Rb atoms loaded by a magneto-optical trap (MOT) serves as the medium for DLCZ-like quantum memory. The cold atomic ensemble was centered in a polarization interferometer formed by two beam displacers (labeled by BD1 and BD2 in Fig. 1a). For generating spin-wave-photon entanglement, we built a single optical channel (labeled by red lines) that goes through the PI to collect and detect both the Stokes and retrieved photons, which is contrast to the previous work, where, three optical channels are built for generating multiplexed spin-wave-photon entanglement. The optical channel is pre-aligned with a light beam. The light beam emits from a single-mode fiber at the left site (labeled by ${\text{SMF}}_{T}$) and then enters into BD1. The BD1splits the H- and V-polarization components of the beam into two modes $A_{R}$ and $A_{L}$, corresponding to the two arms of optical channel, Exiting from BD1, the two components of the beam parallel propagate in a horizontal plane, with the separation of 4 mm. The optical elements including two identical lenses (labeled by L1 and L2 in Fig. 1a) and two beam transformation devices (labeled by BTD1 and BTD2 in Fig. 1a) are inserted in the polarization interferometer, where BTD1 (BTD2) is formed by two lenses, which shrinks (expand) the two beams by a factor F [35]. For realizing effective spin wave (SW) storages, we use lens L1 to focus the two modes at the center of the atoms. To suppress decoherence due to atomic motions, we have to store SWs to be long wavelength, which in turn require the angles $\vartheta_{R,L}$ of the two modes $A_{R}$ and $A_{L}$ relative to the write beam to be reduced to very small values [15, 41]. The angles are calculated from $\vartheta_{R,L} = B_{f} /2f$, where B_f denotes the beam separation of the two arm modes on the lens L1, and $f$ the focal length of L1. To reduce the values of the angles significantly, we selected $f = 1.425 {\text{m}}$ and used BTD1 to reduce the beam separation by a factor of F=2. After BTD1, the two arms propagate parallel to L1 and has a separation of $B_{f} = 2\;{\text{mm}}$. We then obtain small angles $\vartheta_{R,L} = 0.04^{0}$. After passing through the atoms, the two crossed beams are transformed to parallel beams by L2. Then, the two beams go through BTD2 and are expanded by the same factor F=2. Next, the two beams pass through BD2, which combines the two arm modes into single spatial modes. Finally, the light beam is coupled to the single-mode fiber on the right site (labeled SMF_S in Fig. 1a) with efficiency of 70.6% (71.5%) for H-polarization (V-polarization).

Fig. 1

Overview of the experiment. a Experiment setup for the spin-wave-photon entanglement generation. The double optical channels (S_R and S_L) both are labeled as red lines, are used for propagating H- and V-polarized Stokes photon, which are encoded into the photonic qubit. Two spin waves (M_R and M_L) that are simultaneously created with the Stokes fields (S_R and S_L), are used to encode into the spin-wave qubit. In the ideal atomic preparation, the photonic qubit is well entangled with the spin-wave qubit [details see Eq. (6)]. The channel that is labeled by green line is used for the propagations of the write and read beams. PC: phase compensator; QW: λ/4 wave-plate; BD: beam displacer, PBS: polarization beam splitter; BTD: beam transformation device; SMF: single-mode fiber; BS1 (BS2): Non-polarizing beam splitter, whose reflectance (transmission) is 10% (90%). The write (W) beam is aligned along the z-axis via BS1, and the read (R) beam is along the opposite direction to the write beam via BS2; OSFS: optical-spectrum-filter set, which can attenuate the write (read) beam by a factor of $2.7 \times 10^{ - 9}$ ($3.7 \times 10^{ - 9}$) and transmit the Stokes (anti-Stokes) fields with a transmission of ~ 65%. $B_{0}$: Bias magnetic field (~ 4G). b and c The atoms are fully and partially prepared in the Zeeman state $\left| {a, m_{a} = - 1} \right\rangle$, respectively. d The atoms are un-polarized (equally populated in the Zeeman sublevels of the level $\left| a \right\rangle$). e and f Write and read processes for the case that the atoms are initially prepared in the Zeeman sublevel $\left| {a, m_{a} = - 1} \right\rangle$ and $\left| {a, m_{a} = 0} \right\rangle$, respectively. g Time sequence of an experimental cycle.

The relevant ⁸⁷Rb atomic levels $\left| a \right\rangle = \left| {5S_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} ,F = 1} \right\rangle$, $\left| b \right\rangle = \left| {5S_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} ,F = 2} \right\rangle$, $\left| {e_{1} } \right\rangle = \left| {5P_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} ,F^{\prime} = 1} \right\rangle$ and $\left| {e_{2} } \right\rangle = \left| {5P_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} ,F^{\prime} = 2} \right\rangle$ are shown in Fig. 1(b–f). The experiment is carried out in a cyclic fashion [see time sequence Fig. 1(g) for details]. After the atoms are trapped in a magneto-optical trap (MOT), we apply a bias magnetic field (~ 4G) along z-direction to define quantum axis. As shown in Fig. 1(b), we prepare the atoms into the hyperfine level $\left| a \right\rangle$ by applying pumping laser beams P1 and P2. Furthermore, the atoms may be prepared into the specific Zeeman sublevel $\left| {a, m_{a} = - 1} \right\rangle$ by applying a $\sigma^{ - }$-polarized pumping laser beam P3. For the case that the power of P3 is large enough ($\sim 300\,{\mu W}$, here), the atoms will be perfectly prepared into the Zeeman sublevel $\left| {a, m_{a} = - 1} \right\rangle$ [see Fig. 1(b)], corresponding to $p_{ - 1} = 1$ and $\, p_{0} = p_{ + 1} = 0$, where $p_{ \pm 1,0}$ is the atomic populations in the three Zeeman sublevels $\left| {a, m_{a} = \pm 1,0} \right\rangle$. If not, the atoms will be imperfectly prepared into the Zeeman sublevel $\left| {a, m_{a} = - 1} \right\rangle$, which corresponds to the case of $p_{ - 1} \, < 1$ and $\, p_{0} > 0$ [see Fig. 1(c)]. Especially for P3=0, i.e., the atoms are un-polarized, we have $p_{ - 1} { = }p_{0} = p_{ + 1} = 1/3$ [Fig. 1(d)]. Next, we start DLCZ memory generation. At the beginning of a trail, a write pulse of 20MHz blue-detuned to the $\left| a \right\rangle \to \left| {e_{2} } \right\rangle$ transition is applied to the atoms. For the atoms that are prepared in the Zeeman sublevel $\left| {a, m = - 1} \right\rangle$ [Fig. 1(e)], the write pulse will induces the Raman transition $\left| {a,m_{a} = - 1} \right\rangle \to \left| {b,m_{b} = 1} \right\rangle$ ($\left| {a,m_{a} = - 1} \right\rangle \to \left| {b,m_{b} = - 1} \right\rangle$) via $\left| {e_{2} ,m^{\prime} = 0} \right\rangle$, which may emit $\sigma^{ - }$-polarized [$\sigma^{ + }$-polarized) Stokes photons and create simultaneously SW excitations associated with the coherence $\left| {m_{a} = - 1} \right\rangle \leftrightarrow \left| {m_{b} = 1} \right\rangle$ ($\left| {m_{a} = - 1} \right\rangle \leftrightarrow \left| {m_{b} = - 1} \right\rangle$], where $\left| {m_{a} = - 1} \right\rangle \leftrightarrow \left| {m_{b} = 1} \right\rangle$ and $\left| {m_{a} = - 1} \right\rangle \leftrightarrow \left| {m_{b} = - 1} \right\rangle$ are the MFI and magnetic-field-sensitive (MFS) coherences, respectively. For the atoms that are populated in the Zeeman sublevel $\left| {a, m = 0} \right\rangle$, the write pulse will induces the Raman transition $\left| {a,m_{a} = 0} \right\rangle \to \left| {b,m_{b} = 2} \right\rangle$ $\left( {\left| {a,m_{a} = 0} \right\rangle \to \left| {b,m_{b} = 0} \right\rangle } \right)$ via $\left| {e_{2} ,m^{\prime} = 0} \right\rangle$ [see Fig. 1(f)], which may emit $\sigma^{ - }$-polarized ($\sigma^{ + }$-polarized) Stokes photons and create simultaneously SW excitations associated with the coherence $\left| {m_{a} = 0} \right\rangle \leftrightarrow \left| {m_{b} = 2} \right\rangle$ ($\left| {m_{a} = 0} \right\rangle \leftrightarrow \left| {m_{b} = 0} \right\rangle$), where $\left| {m_{a} = 0} \right\rangle \leftrightarrow \left| {m_{b} = 2} \right\rangle$ and $\left| {m_{a} = 0} \right\rangle \leftrightarrow \left| {m_{b} = 0} \right\rangle$ are MFS and clock (i.e., MFI) coherences, respectively. If the Stokes photon emits into the $A_{R}$ ($A_{L}$) mode and moves rightward, it is denoted as $S_{R}$ ($S_{L}$). For the case that the Stokes photons are $\sigma^{ - }$-polarized, they will be transformed into H (V) –polarized photon by a λ/4 plate labeled as QW_1S (QW_2S). The H (V) –polarized $S_{R}$ and $S_{L}$ modes will be combined to form a Stokes polarization qubit $S$ at the output of the BD2. Then, the photonic polarization qubit $S$ couples to ${\text{SMF}}_{s}$ and enter into detectors. While, for the case that the Stokes photons $S_{R}$ and $S_{L}$ are $\sigma^{ + }$-polarized, they will be transformed into V (H) –polarized photon by QW_1S (QW_2S). After BD2, the V (H) –polarized $S_{R}$ and $S_{L}$ modes will be removed out of the optical channel and are abandoned.

3 Theoretical analysis

The creation of a single $\sigma^{ - }$-polarized Stokes photon $S_{R}$ ($S_{L}$) corresponds to the creation of one SW excitation in the mode $M_{R}$ ($M_{L}$) , which is defined by the wave-vector $k_{{M_{R} }}^{{}} = k_{W} - k_{{S_{R} }}^{{}}$ ($k_{{M_{L} }}^{{}} = k_{W} - k_{{S_{L} }}^{{}}$), where $k_{W}$ denotes the wave-vector of the write pulse, and $k_{{S_{R} }}$ ($k_{{S_{L} }}$) that of the Stokes photon $S_{R}$ ($S_{L}$). The single SW excitation in the mode $M_{R}$ and $M_{L}$ may be written as:

$$\left| {1_{R} } \right\rangle = \left( {X_{ - 1} \sqrt {p_{ - 1} } \left| {1^{ - } } \right\rangle_{R} + X_{0} \sqrt {p_{0} } \left| {1^{ + } } \right\rangle_{R} } \right)/\sqrt {\left( {X_{ - 1} } \right)^{2} p_{ - 1} + \left( {X_{0} } \right)^{2} p_{0} }$$

(1a)

$$\left| {1_{L} } \right\rangle = \left( {X_{ - 1} \sqrt {p_{ - 1} } \left| {1^{ - } } \right\rangle_{L} + X_{0} \sqrt {p_{0} } \left| {1^{ + } } \right\rangle_{L} } \right)/\sqrt {\left( {X_{ - 1} } \right)^{2} p_{ - 1} + \left( {X_{0} } \right)^{2} p_{0} } ,$$

(1b)

where $\left| {1^{ - } } \right\rangle_{R}$ and $\left| {1^{ - } } \right\rangle_{L}$ ($\left| {1^{ + } } \right\rangle_{R}$ and $\left| {1^{ + } } \right\rangle_{L}$) denotes one SW excitation associated with the MFI (MFS) coherence $\left| {m_{a} = - 1} \right\rangle \leftrightarrow \left| {m_{b} = 1} \right\rangle$ ($\left| {m_{a} = 0} \right\rangle \to \left| {m_{b} = 2} \right\rangle$), $X_{{m_{a} }} = C_{{m_{a} ,1,m_{a} + 1}}^{{F_{a} ,1,F_{{e_{2} }} }} C_{{m_{a} + 1,\alpha ,m_{a} + 1 + \alpha }}^{{F_{{e_{2} }} ,1,F_{b} }}$ ($m_{a} = - 1,0$) is the product of the relevant Clebsch-Gordan coefficients. From this expression, we have $X_{ - 1} = \sqrt {1/3}$, $X_{0} = \sqrt {2/3}$. We denote excitation probability as $\chi$ for each mode. For $\chi \ll 1$, the joint state of the light-atom system can be written as:

$$\left| \Psi \right\rangle = \left| 0 \right\rangle + \sqrt {\chi /2} \left[ {\left| {H_{S} } \right\rangle \left| {1_{R} } \right\rangle + \left| {V_{S} } \right\rangle \left| {1_{L} } \right\rangle } \right] + O(\chi ),$$

(2)

where, $\left| 0 \right\rangle$ is the vacuum part, $\left| {H_{S} } \right\rangle$ $\left( {\left| {V_{S} } \right\rangle } \right)$ denotes the H (V) -polarized Stokes photon of the qubit $S$, $\left| 1 \right\rangle_{R}$ $\left( {\left| 1 \right\rangle_{L} } \right)$ one excitation in the SW mode $M_{R}$ $\left( {M_{L} } \right)$.

The Stokes photonic qubit $S$ is guided into a polarization-beam splitter (labeled as ${\text{PBS}}_{S}^{{}}$) after the ${\text{SMF}}_{S}$. The two outputs of the ${\text{PBS}}_{S}^{{}}$ are sent to the single-photon detectors $D_{{S_{1} }}^{{}}$ and $D_{{S_{2} }}^{{}}$, respectively. Once a photon is detected by detector $D_{{S_{1} }}^{{}}$ or $D_{{S_{2} }}^{{}}$, a SW excitation, which is stored in the SW mode $M_{R}^{{}}$ or $M_{L}$ $,$ is heralded. After a storage time t, we apply a read beam that counter-propagates with the write beam to convert the SW excitation $\left| {M_{R} } \right\rangle$ or $\left| {M_{L} } \right\rangle$ into an anti-Stokes photon $T_{R}^{{}}$ or $T_{L}^{{}}$. The retrieved anti-Stokes photon $T_{R}^{{}}$ ($T_{L}^{{}}$) is emitted into the spatial mode determined by the wave-vector constraint $k_{{T_{R} }}^{{}} = - k_{{S_{R} }}^{{}}$ ($k_{{T_{L} }}^{{}} = - k_{{S_{L} }}^{{}}$), i.e., it propagates in the arms $A_{R}$ ($A_{L}$) in the opposite direction to the $S_{R}$ ($S_{L}$) photon. The $T_{R}^{{}}$ ($T_{L}^{{}}$) photon is $\sigma^{ + }$-polarized and transformed into the H (V) -polarized photon by a λ/4 plate labeled QW_1T (QW_2T) in Fig. 1a. After BD1, the $T_{R}^{{}}$ and $T_{L}^{{}}$ fields are combined to form a polarization qubit ($T$). After BD1, the photonic qubit $T$ goes through a phase compensator (labeled as PC in Fig. 1a). Then, the photonic qubit couples to a single-mode fiber (${\text{SMF}}_{T}$) and then passes through a $\lambda /2$ plate. Finally, the qubits $T$ impinge on a polarization-beam splitter (PBS_T). The two outputs of the PBS_T are sent separately to detectors $D_{{T_{1} }}$ and $D_{{T_{2} }}$ for detections. After the detections, the atoms are prepared in the initial state via optical pumping. If no Stokes photon is detected during the write pulse, the atoms are pumped directly back into the initial state. Subsequently, the next trial starts.

After the storage time t, the SWs $\left| {M_{R} } \right\rangle$ and $\left| {M_{L} } \right\rangle$ will evolve into $\left| {1_{R} (t)} \right\rangle = \left[ {\sqrt {p_{ - 1} /2} \left| {1^{ - } } \right\rangle_{R} {\text{e}}^{{ - \, \frac{t}{{2\tau_{1, - 1} }}}} {\text{e}}^{{ - it\omega_{ - 1,1} }} + \sqrt {p_{0} } \left| {1^{ + } } \right\rangle_{R} {\text{e}}^{{ - \, \frac{t}{{2\tau_{0,2} }}}} {\text{e}}^{{ - it\omega_{0,2} }} } \right]/N_{f} ,$ (3a)

$$\left| {1_{L} (t)} \right\rangle = \left[ {\sqrt {p_{ - 1} /2} \left| {1^{ - } } \right\rangle_{L} {\text{e}}^{{ - \, \frac{t}{{2\tau_{1, - 1} }}}} {\text{e}}^{{ - it\omega_{ - 1,1} }} + \sqrt {p_{0} } \left| {1^{ + } } \right\rangle_{L} {\text{e}}^{{ - \, \frac{t}{{2\tau_{0,2} }}}} {\text{e}}^{{ - it\omega_{0,2} }} } \right]/N_{f} ,$$

(3b)

respectively, where, $N_{f} = \sqrt {\left( {\sqrt {p_{ - 1} /2} } \right)^{2} + \left( {\sqrt {p_{0} } } \right)^{2} }$ denotes normalized factor, $\tau_{ - 1,1}$ and $\tau_{0,2}$ are decay times associated with the MFI and MFS coherences, $\omega_{ - 1,1}$ and $\omega_{0,2}$ Larmor frequencies of the MFI and MFS coherences, respectively. The Larmor frequencies can be calculated by $\omega_{{m_{a} ,m_{b} }} = \frac{{\mu_{B} B_{0} }}{\hbar }\left[ {g_{a} (m_{a} + m_{b} ) - \delta gm_{a} } \right]$, with $g_{a} = 0.{4998}$ and $g_{b} = - 0.{5}0{18}$ being Lander factors and $\delta g = g_{a} + g_{b} = - 0.{002}$. The retrieval efficiencies of the SWs $\left| {M_{R} } \right\rangle$ and $\left| {M_{L} } \right\rangle$ as well as memory qubit $\left| M \right\rangle$ can be calculated by [14, 16] $\gamma_{R} = \left| {\left\langle {{1_{R} }} \mathrel{\left | {\vphantom {{1_{R} } {1_{R} (t)}}} \right. \kern-\nulldelimiterspace} {{1_{R} (t)}} \right\rangle } \right|^{2}$, $\gamma_{L} = \left| {\left\langle {{1_{L} }} \mathrel{\left | {\vphantom {{1_{L} } {1_{L} (t)}}} \right. \kern-\nulldelimiterspace} {{1_{L} (t)}} \right\rangle } \right|^{2}$ and $\gamma (t) = \left( {\left| {\left\langle {{1_{R} }} \mathrel{\left | {\vphantom {{1_{R} } {1_{R} (t)}}} \right. \kern-\nulldelimiterspace} {{1_{R} (t)}} \right\rangle } \right|^{2} + \left| {\left\langle {{1_{L} }} \mathrel{\left | {\vphantom {{1_{L} } {1_{L} (t)}}} \right. \kern-\nulldelimiterspace} {{1_{L} (t)}} \right\rangle } \right|^{2} } \right)/2$, which are

$$\gamma_{R} (t) = \gamma_{L} (t) = \gamma (t) = \gamma_{0} \left| {\frac{{p_{ - 1} }}{2}{\text{e}}^{{ - \, t/2\tau_{1, - 1} }} {\text{e}}^{{ - i\omega_{ - 1,1} t}} + p_{0} {\text{e}}^{{ - \, t/2\tau_{0,2} }} {\text{e}}^{{ - i\omega_{0,2} t}} } \right|^{2} /N_{f}^{4} ,$$

(4)

where, $\gamma_{0}$ is the zero-delay retrieval efficiency. When the atoms are perfectly prepared into the specific Zeeman level $\left| {m_{a} = - 1} \right\rangle$, i.e., $p_{ - 1} = 1; \, p_{0} = 0$, the retrieval efficiency as a function of storage time t can be derived from Eq. (4), which is $\gamma (t) = \gamma_{0} {\text{e}}^{{ - \, t/\tau_{ - 1,1} }}$. It depends on the lifetime of the SW associated with the MFI coherence, allowing for a long-lived memory for SW qubit. If the atoms are un-polarized ($p_{ - 1} = \, p_{0} = p_{ + 1} = 1/3$), the retrieval efficiency is written as $\gamma (t) = {{\gamma_{0} \left| {\frac{1}{2}{\text{e}}^{{ - \, t/2\tau_{1, - 1} }} {\text{e}}^{{ - i\omega_{ - 1,1} t}} + {\text{e}}^{{ - \, t/2\tau_{0,2} }} {\text{e}}^{{ - i\omega_{0,2} t}} } \right|^{2} } \mathord{\left/ {\vphantom {{\gamma_{0} \left| {\frac{1}{2}{\text{e}}^{{ - \, t/2\tau_{1, - 1} }} {\text{e}}^{{ - i\omega_{ - 1,1} t}} + {\text{e}}^{{ - \, t/2\tau_{0,2} }} {\text{e}}^{{ - i\omega_{0,2} t}} } \right|^{2} } {\left( \frac{3}{2} \right)^{2} }}} \right. \kern-\nulldelimiterspace} {\left( \frac{3}{2} \right)^{2} }}$ according to Eq. (4).

The retrieval efficiency of the SW memory may be measured as $\gamma = P_{S, \, T}^{{}} /\left( {\eta_{T} P_{S}^{{}} } \right)$, where $\eta_{T}$ denotes the detection efficiency in the anti-Stokes channel, $P_{S, \, T}^{{}} = P_{{D_{{S_{{1}} }} , \, D_{{T_{{1}} }} }}^{{}} + P_{{D_{{S_{{2}} }} , \, D_{{T_{{2}} }} }}^{{}}$ is the Stokes–anti-Stokes coincidence probability, $P_{{D_{{S_{{1}} }} , \, D_{{T_{{1}} }} }}^{{}}$ ($P_{{D_{{S_{{2}} }} , \, D_{{T_{{2}} }} }}^{{}}$) is the probability of detecting a coincidence between the detectors $D_{{S_{{1}} }}^{{}}$ ($D_{{S_{{2}} }}^{{}}$) and $D_{{T_{{1}} }}$ ($D_{{T_{{2}} }}$), $P_{S}^{{}} = P_{{D_{{S_{{1}} }} }}^{{}} + P_{{D_{{S_{{2}} }} }}^{{}}$ is the Stokes-detection probability, and $P_{{D_{{S_{1} }} }}^{{}}$ ($P_{{D_{{S_{{2}} }} }}^{{}}$) is the probability of detecting a photon at $D_{{S_{{1}} }}^{{}}$ ($D_{{S_{{2}} }}^{{}}$).

4 Results

For the cases that the excitation probability ${\chi} =1{\% }$ and the laser beam P3 with different powers of $0\;{\mu W}$, $150\;{\mu W}$, and $300\;{\mu W}$ is applied on the atoms, we measured the retrieval efficiency $\gamma$ as a function of the storage time t and shown the results in Fig. 2 a, b, and c, respectively. The black circle dots in Fig. 2a are the measured $\gamma (t)$ for $P_{3} = 0\;{\mu W}$. For this case, the atoms are un-polarized ($p_{ - 1} = p_{0}$). The dashed line in Fig. 2a is the fitting to the data based on $\gamma (t) = {\raise0.7ex\hbox{${\gamma_{0} \left| {\frac{1}{2}{\text{e}}^{{ - \, t/2\tau_{1, - 1} }} {\text{e}}^{{ - i\omega_{ - 1,1} t}} + {\text{e}}^{{ - \, t/2\tau_{0,2} }} {\text{e}}^{{ - i\omega_{0,2} t}} } \right|^{2} }$} \!\mathord{\left/ {\vphantom {{\gamma_{0} \left| {\frac{1}{2}{\text{e}}^{{ - \, t/2\tau_{1, - 1} }} {\text{e}}^{{ - i\omega_{ - 1,1} t}} + {\text{e}}^{{ - \, t/2\tau_{0,2} }} {\text{e}}^{{ - i\omega_{0,2} t}} } \right|^{2} } {\left( \frac{3}{2} \right)^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( \frac{3}{2} \right)^{2} }$}}$ with the parameters of $\tau_{ - 1,1} = 1200\;{\mu s}$, $\tau_{0,2} = 70\;{\mu s}$, $\omega_{ - 1,1} = 2\pi \times 0.0114\;{\text{MHz}}$, $\omega_{0,2} = 2\pi \times 5.716\;{\text{MHz}}$, which yields a 1/e lifetime of 0.15 ms. The yielded parameters $\omega_{ - 1,1} = 2\pi \times 0.0114\;{\text{MHz}}$, $\omega_{0,2} = 2\pi \times 5.716\;{\text{MHz}}$ are in agreement with the calculated results based on $\omega_{{m_{a} ,m_{b} }} = \frac{{\mu_{B} B_{0} }}{\hbar }\left[ {g_{a} (m_{a} + m_{b} ) - \delta gm_{a} } \right]$ with $B_{0} = 4.0771\;{\text{G}}$. According to $\gamma (t) = {{\gamma_{0} \left| {\frac{1}{2}{\text{e}}^{{ - \, t/2\tau_{1, - 1} }} {\text{e}}^{{ - i\omega_{ - 1,1} t}} + {\text{e}}^{{ - \, t/2\tau_{0,2} }} {\text{e}}^{{ - i\omega_{0,2} t}} } \right|^{2} } \mathord{\left/ {\vphantom {{\gamma_{0} \left| {\frac{1}{2}{\text{e}}^{{ - \, t/2\tau_{1, - 1} }} {\text{e}}^{{ - i\omega_{ - 1,1} t}} + {\text{e}}^{{ - \, t/2\tau_{0,2} }} {\text{e}}^{{ - i\omega_{0,2} t}} } \right|^{2} } {\left( \frac{3}{2} \right)^{2} }}} \right. \kern-\nulldelimiterspace} {\left( \frac{3}{2} \right)^{2} }}$, we calculate the ratio of maximum efficiency at short times to the efficiency at times longer than $400\;{\mu s}$, which approaches to 1/9 and is in agreement with the measured data in Fig. 2a. The inset to Fig. 2a clearly shows a decay rapid oscillation of retrieval efficiency which results from the interference between MFI and MFS coherences. The (black) circle dots in Fig. 2b are the measured $\gamma (t)$ for $P_{3} = 150\;{\mu W}$ which still show a decay oscillation (see the insert to Fig. 2b). Such oscillation infers that the atoms are not fully prepared into the Zeeman sublevel $\left| {a, m_{a} = - 1} \right\rangle$. The dashed line is the fitting to the measured data based on Eq. (4) with parameters $p_{ - 1} = 0.7$, $p_{0} = 0.15$ and the same parameters $\tau_{ - 1,1} = 1200\mu s$, $\tau_{0,2} = 70\;{\mu s}$,$\omega_{ - 1,1}$ and $\omega_{0,2}$ as in Fig. 2b. This fitting yields a 1/e lifetime of 0.5 ms. For fully preparing the atoms into the Zeeman sublevel $\left| {a, m_{a} = - 1} \right\rangle$ and then perfectly using MFI coherence to store SW, we increase the power of P3 laser beam to $300\;{\mu W}$. The black circle dots in Fig. 2c are the measured retrieval efficiency $\gamma (t)$ for $P_{3} = 300\;{\mu W}$. One can see that the oscillation disappears in the measured $\gamma (t)$, which infers that only MFI SW is stored and the retrieval efficiency evolves according to $\gamma (t) = \gamma_{0} {\text{e}}^{{ - \, t/\tau_{ - 1,1} }}$. The dashed line is the fitting to the data based on $\gamma (t) = \gamma_{0} {\text{e}}^{{ - \, t/\tau_{ - 1,1} }}$ with the parameter $\tau_{ - 1,1} = 1200\;{\mu s}$, which yields a 1/e memory lifetime of 1.2 ms.

Fig. 2

Retrieval efficiencies of the SW qubit as a function of t for different powers of $P_{3} = 0\;{\mu W}$ (a), $P_{3} = 150\;{\mu W}$ (b), and $P_{3} = 300\;{\mu W}$ (c). The insets to a and b show details of the short-time damped oscillations for the cases that the atoms are un-polarized and imperfectly prepared, respectively.

The blue circle dots in Fig. 3 plots 1/e lifetime of the qubit memory as a function of the power of P₃ for ${\chi} =1{percent }$. As the increase in the power of P₃, the atomic populations in the Zeeman sublevel $\left| {a, m_{a} = - 1} \right\rangle$ increase and then the lifetime increases. Until the power of P3 reach a specific value, which is $300\;{\mu W}$ in the presented work, the atoms will be perfectly prepared in the Zeeman sublevel $\left| {a, m_{a} = - 1} \right\rangle$and the lifetime reaches up to its maximal value (1.2 ms). Also, we noted that when the power of P3 is far beyond $300\;{\mu W}$, the strong interaction between laser beam P3 and the atoms will lead to a significantly decrease in optical depth, which in turn lead to the decrease in the retrieval efficiency.

Fig. 3

Lifetime of the qubit memory M as a function of the power of P₃ for ${\chi} =1{\% }$

For the case that the atoms are perfectly prepared in the Zeeman sublevel $\left| {a, m_{a} = - 1} \right\rangle$ ($p_{ - 1} = 1, \, p_{0} = 0$), the SWs described in Eq. (1) are rewritten as:

$$\left| {1_{R} } \right\rangle = \left| {1^{ - } } \right\rangle_{R} ,$$

(5a)

$$\left| {1_{L} } \right\rangle = \left| {1^{ - } } \right\rangle_{L} ,$$

(5b)

In this case, the SWs are only associated with the single MFI coherence and then the nonvacuum part in Eq. (2) represents atom–photon entanglement state

$$\Phi_{ap} = \left[ {\left| {H_{S} } \right\rangle \left| {1_{R} } \right\rangle + \left| {V_{S} } \right\rangle \left| {1_{L} } \right\rangle } \right]/\sqrt 2$$

(6)

After the retrieval, the atom–photon entanglement state is transformed into the two-photon entangled state $\Phi_{{\text{p - p}}}^{{}} = \left[ {\left| H \right\rangle_{S} \left| H \right\rangle {}_{T} + e^{i(\varphi + \psi )} \left| V \right\rangle_{S} \left| V \right\rangle_{T} } \right]/\sqrt 2$, where $\varphi$ ($\psi$) denotes the phase difference between the Stokes fields (anti-Stokes) fields in arms $A_{R}$ and $A_{L}$ before they overlap at BD2 (BD1). Using the phase compensator (labeled PC in Fig. 1a), we set the phase difference $\varphi + \psi$ to zero.

For demonstrating the atom-photon entanglement, we measure the correlation function $E(\theta_{S}^{{}} ,\theta_{T} )$ _{defined by}

$$E(\theta_{S} ,\theta_{T} ) = \frac{{C_{{D_{{S_{{1}} }} ,D_{{T_{{1}} }} }}^{{}} (\theta_{S} ,\theta_{T} ) + C_{{D_{{S_{{2}} }} ,D_{{T_{{2}} }} }}^{{}} (\theta_{S} ,\theta_{T} ) - C_{{D_{{S_{{1}} }} ,D_{{T_{{2}} }} }}^{{}} (\theta_{S} ,\theta_{T} ) - C_{{D_{{S_{{2}} }} ,D_{{T_{{1}} }} }}^{{}} (\theta_{S} ,\theta_{T} )}}{{C_{{D_{{S_{{1}} }} ,D_{{T_{{1}} }} }}^{{}} (\theta_{S} ,\theta_{T} ) + C_{{D_{{S_{{2}} }} ,D_{{T_{{2}} }} }}^{{}} (\theta_{S} ,\theta_{T} ) + C_{{D_{{S_{{1}} }} ,D_{{T_{{2}} }} }}^{{}} (\theta_{S} ,\theta_{T} ) + C_{{D_{{S_{{2}} }} ,D_{{T_{{1}} }} }}^{{}} (\theta_{S} ,\theta_{T} )}}$$

where, for example, $C_{{D_{{S_{{1}} }} ,D_{{T_{{1}} }} }}^{{}} (\theta_{S} ,\theta_{T} )$ ($C_{{D_{{S_{{2}} }} ,D_{{T_{{2}} }} }}^{{}} (\theta_{S} ,\theta_{T} )$) denotes the coincidence counts between the detectors $D_{{S_{{1}} }}^{{}}$( $D_{{S_{{2}} }}^{{}}$) and $D_{{T_{{1}} }}$( $D_{{T_{{2}} }}$) for polarization angles $\theta_{S}$and $\theta_{T}$. In measurements of the correlation function $E(\theta_{S}^{{}} ,\theta_{T} )$, we vary the polarization angles $\theta_{S}$( $\theta_{T}$) by rotating the polarization orientation of the λ/2 wave-plate before PBS_S (PBS_T). The quality of the atom-photon can be well characterized by CHSH-Bell parameter S , which is written as:

$S = \left| {E(\theta_{S}^{{}} ,\theta_{T} ) - E(\theta_{S} ,\theta_{T}^{^{\prime}} ) + E(\theta_{S}^{^{\prime}} ,\theta_{T} ) + E(\theta_{S}^{^{\prime}} ,\theta_{T}^{^{\prime}} )} \right| < 2$,

In the measurement for, we use the canonical settings $\theta_{S} { = }0^{o}$, $\theta_{S}^{\prime } { = }45^{o}$ , $\theta_{T} { = }22.5^{o}$, $\theta_{T}^{\prime } { = }67.5^{o}$. The measured CHSH-Bell parameter S as a function of storage time is shown in Fig. 4 for the perfect preparation of the atoms ($P_{3} = 300\;{\mu W}$) and ${\chi} =1{\% }$. At $t{ = }0\;{\text{ms}}$, $S = 2.51 \pm 0.01$, which violates the CHSH inequality by 51 standard deviations. At $t\,{ = }\,1.2\;{\text{ms}}$, $S = 2.03 \pm 0.02$, which violates the CHSH inequality by 1.5 standard deviations.

Fig. 4

Bell parameter S as a function of t for ${\chi} =1{\% }$. Error bars represent 1 standard deviation.

The quality of the photon–photon (atom–photon) entanglement can be characterized by the fidelity, which is given by $F = {\text{Tr}}\left( {\sqrt {\sqrt {\rho_{r} } \rho_{d} \sqrt {\rho_{r} } } } \right)^{2}$, where $\rho_{r}$ ($\rho_{d}$) denotes the reconstructed (ideal) density matrix of the two–photon entangled state. From measurements of the Stokes–anti-Stokes coincidences for $t = 1 {\mu s}$ and $\chi = 1\%$, we reconstructed $\rho_{r}$ (Fig. 5), which yields $F = 90.4 \pm 1.6\%$.

Fig. 5

Real and imaginary parts of the reconstructed density matrix $\rho_{r}$

5 Conclusion

In conclusion, we demonstrated a millisecond spin-wave-photon entanglement for the cases that cold atoms are perfectly prepared into the specific Zeeman level. When the cold atoms are imperfectly prepared into the specific Zeeman level, the results show that the lifetimes of the SWs for the imperfect preparation are significantly shorter than that for the perfect preparation. Also, a rapid oscillation will appear in read out when the atoms are not perfectly prepared into the specific Zeeman level. The measured results and the theoretical analysis on them enable one to understand decoherence of SWs and interference between the SWs. The present work may help them to obtain optimal lifetime of the entanglement storage in DLCZ scheme using cold atoms.