Bright and dark diffractive focusing

Abstract

We investigate bright and dark diffractive focusing emerging in the free propagation of specific wave profiles. These general wave phenomena manifest themselves in matter, water, and classical waves. In this article, we lay the foundations for these effects and illustrate their origin in Wigner phase space. Our theoretical studies are supported by experimental demonstrations of dark focusing in water waves. Moreover, by using different phase slits we analyze several aspects of bright and dark focusing for classical and matter waves.

1 Introduction

Focusing is usually associated with an increase of intensity. The other extreme is zero intensity. In this article, we focus on yet another feature of focusing—the focusing of darkness.

The dark diffractive focusing is complementary to the well-known bright diffractive focusing. It arises most prominently for slits with an antisymmetric phase profile. In this article, we develop a novel quantitative criterion that is applicable for the characterization of both bright and dark foci.

1.1 Diffractive focusing

The diffraction in space of plane light waves by a slit and the diffraction in time of a rectangular quantum wave packet of zero momentum are phenomena described by differential equations of the same form. For classical waves, as light and sound, the equation governing the space propagation of the wave is the paraxial Helmholtz equation (PHE). For matter waves, the dynamics of a wave packet is determined by the Schrödinger equation in the absence of a potential. The Helmholtz equation in two dimensions, in the paraxial approximation, and the potential-free Schrödinger equation in one space dimension have the same mathematical form, despite the involved variables having different physical meaning. Whereas the paraxial Helmholtz equation describes the field distribution in two dimensions: the propagation direction and the transverse direction, the Schrödinger equation predicts the evolution in time of a one-dimensional wave packet.

In the paraxial approximation, the scalar field emanating from a slit is determined by the Fresnel diffraction integral [1]. A more general formulation without approximations is based on the first and the second Rayleigh-Sommerfeld diffraction integrals [1, 2]. This formulation will also be used in this article for one-dimensional slits. The time evolution of matter wave packets is obtained by using the Feynman propagator [3]. Based on an initial wave packet $\Psi (x,t=0)$, it determines the shape of the wave packet $\Psi (x,t)$ at a later time t.

It is well-known that wave packets of initial real-valued Gaussian profile always display increasing spatial spreading. In full contrast, waves diffracting from rectangular slits firstly present focusing followed by spreading in time. This effect has been discussed several times for waves of different nature, as optical waves [4, 5], plasmonic waves, surface gravity waves in a water tank [6], and the time-focusing of rectangular wave packets [7].

There are other waves which preserve their shape (non-diffracting) in the propagation direction, as the Bessel light beams [8], or that accelerate in the direction of the transverse coordinate: the Airy wave packets, which were firstly predicted in the context of quantum physics [9] and later experimentally demonstrated with the help of classical waves [10, 11]. Their properties are however beyond the scope of this article.

The diffractive focusing is purely determined by the shape of the initial wave. For instance, wave functions of real-valued Gaussian profile do not display focusing effects in space nor in time. One question that naturally arises is what kind of initial wave functions leads to focusing? Moreover, is there any other type of focusing effect beyond the typical pattern of the Fresnel diffraction?

In this article, we investigate matter, water, and classical wave packets of constant amplitude with an initial phase dependence on the transverse coordinate. This feature results in unexpected focusing effects: an increase of the degree of focusing in some cases, or the emergence of temporary darkness in the middle of the wave packet, corresponding to localized minima in the intensity pattern. We establish the necessary conditions to describe these bright and dark focusing effects and investigate the properties of this new type of focusing from different perspectives.

1.2 Antisymmetric wave functions in physics

In a previous article [5], we have addressed the diffractive focusing of a rectangular wave packet for matter waves and the classical analogy arising in the diffraction from a slit. In this article, we instead focus on antisymmetric wave packets and phase slits.

Wave functions with antisymmetric properties arise in different contexts of classical and quantum physics. Several examples come to our mind: (a) In quantum physics, the second energy eigenfunction of a particle in a rectangular infinite potential well is an antisymmetric function. (b) The odd-numbered energy eigenfunctions of the quantum harmonic oscillator, expressed in terms of Hermite-Gaussian functions, are antisymmetric. (c) Wave functions describing identical fermions are necessarily antisymmetric [12, 13]. In contrast, the wave function describing identical and indistinguishable bosons is symmetric. (d) This is opposed to the classical physics problem of identical coupled resonators. Here the two eigenmodes are symmetric and antisymmetric functions, but the general solution is a superposition of both modes. (e) For a quantum particle in a double-well potential with an energy lower than the potential barrier there are also two eigenmodes: one symmetric and one antisymmetric [12, 13]. Finally, in classical optics we point out (f) the second propagation mode (as well as higher-order even modes) of an electromagnetic wave propagating in a planar waveguide [14], and (g) the second order Hermite-Gaussian laser beam mode [14].

All the functions listed above have in common to be smooth, i.e. they are continuously differentiable. The antisymmetric function on which we focus in the present article is a shifted version of the Haar wavelet [15]. The Haar function, or Haar wavelet is defined in the interval [0, 1] and takes the following form

$$\begin{aligned} f(x)= {\left\{ \begin{array}{ll} 1 &{} \mathrm{if}\quad 0 \le x< 1/2 \\ -1 &{} \mathrm{if}\quad 1/2 \le x < 1 \\ 0 &{} \mathrm{elsewhere}. \end{array}\right. } \end{aligned}$$

In order to define a rectangular wave function with antisymmetric property, we translate the Haar function to the interval $[-1/2, 1/2]$. The resulting function is not differentiable at the edge points $x = -1/2$, $x = 0$, and $x = 1/2$. However, it corresponds to a spatially localized and square-integrable function with constant amplitude and a phase shift of $\pi$ between the half left and the half right. Indeed, by imposing a phase shift of $\pi$ between the left and right half, we transform a symmetric function of rectangular shape into an antisymmetric one. This leads to a destructive interference in the center of the wave packet during its time evolution. The same occurs in the diffraction from a phase slit with the same initial shape. The destructive interference is preserved along the propagation axis.

At first glance, the intensity pattern for a rectangular antisymmetric wave function is divided into two regions with mirror symmetry. However, the width of the central region with very low intensity varies along the time axis, leading to wider and narrower dark regions. We call the later phenomenon dark focusing by analogy and in contrast to the bright focusing familiar from the diffractive focusing of rectangular wave packets or a slit with constant phase. Our study of this phenomenon has been motivated by the experiments that were performed in the context of diffractive guiding, where a similar behavior is displayed in Fig. 2c)of Ref. [16].

In recent years, several articles investigating the splitting of wave packets have appeared. One of them is the production and collision of soliton waves in a parabolic potential well [17]. Others address the dissociation dynamics of molecules like H$_{\mathrm{2}}^{+}$ using laser pulses [18]. In contrast to our studies, these examples rely on the time evolution of non-rectangular packets.

Moreover, we note that the $\pi$-phase shift in the center of an antisymmetric wave packet is also intrinsic to dark soliton solutions of the nonlinear Schrödinger equation which display sudden intensity depressions [19, 20].

1.3 Outline

Our article is divided into six sections. In Sect. 2 we establish the analogy between the free propagation of matter, water, and classical waves in certain regimes with the help of dimensionless variables. We introduce the Feynman propagator to describe the time evolution of such waves. We present the Fresnel diffraction integral governing the propagation of a wave packet that emerges from a rectangular slit. Section 3 is dedicated to a theoretical analysis of bright and dark focusing. We compare and contrast these phenomena by studying the propagation of a rectangular symmetric wave packet and its antisymmetric counterpart. We analyze the characteristics of bright and dark focusing both in space-time and in phase space. In Sect. 4 we present experimental observations of the dark focusing effect in surface gravity water waves generated in a water tank. Section 5 contains an extension of bright and dark focusing to the diffraction of classical waves (acoustic and light waves). For this purpose, we use numerical calculations of the first Rayleigh-Sommerfeld diffraction integral for a variety of phase slits. Beyond the rectangular antisymmetric slit, we present results for slits with other phase values than $\pi$ and slits with triangular symmetric and antisymmetric phase function. The triangular phase slits are the 2D analogue of the 3D axicons used in optics to generate Bessel beams. They can be convergent or divergent. The antisymmetric triangular slit, with a phase difference of $\pi$ between the half left and half right, leads to a kind of dark focusing similar to that of the Haar antisymmetric wave function. In Sect. 6 we summarize the results of the article. Our analysis is supplemented by Appendix A, where we determine the times at which bright and dark foci emerge.

2 Propagation of waves in free space

In the following, we recall an analogy between matter, water, and classical waves, which manifests itself in certain regimes. We introduce the Feynman propagator governing the time evolution of these freely propagating waves. Next, we present the dynamics of a wave profile emerging from a rectangular slit. Thereby, we set the stage for our analysis of bright and dark focusing.

2.1 Matter, water, and classical waves

In quantum mechanics [12, 13], the time evolution of the wave function $\psi (x,t)$ of a free particle of mass m in one dimension is governed by the time-dependent Schrödinger equation

$$\begin{aligned} \mathrm {i}\hbar \frac{\partial }{\partial t} \psi (x,t)=-\frac{\hbar ^2}{2m}\frac{\partial ^2}{\partial x^2}\psi (x,t) \end{aligned}$$

(1)

and determined by the initial condition $\psi (x,0)=\psi _0(x)$. Here $\hbar$ denotes the reduced Planck constant.

In terms of the dimensionless coordinate $\chi \equiv x/W$, time $\tau \equiv t(2\pi \hbar /mW^2)$, and wave function $\Psi \equiv \psi \sqrt{W}$, the Schrödinger Eq. (1) reads

$$\begin{aligned} 4\pi \mathrm {i}\frac{\partial }{\partial \tau } \Psi (\chi ,\tau )=-\frac{\partial ^2}{\partial \chi ^2}\Psi (\chi ,\tau ), \end{aligned}$$

(2)

where W is a characteristic length in the problem under consideration, for example, the width of the slit.

In surface gravity water wave theory, for the narrow-banded waves moving in the x-direction, the instantaneous surface elevation takes the form $h(x,t)=\mathrm {Re}\left\{ a_0 A(x,t)\exp [\mathrm {i}(k_0 x-\omega _0 t)]\right\}$, where $a_0$ denotes the maximal amplitude. Here the carrier wave number $k_0$ and the angular carrier frequency $\omega _0$ are subject to the deep-water dispersion relation $\omega _0^2=gk_0$ with g being the gravitational acceleration. The normalized slowly-varying dimensionless amplitude envelope A(x, t) satisfies the equation [11, 21]

$$\begin{aligned} \frac{\partial ^2 A}{\partial t^2}-2\mathrm {i}\omega _0 \frac{\partial A}{\partial t}=\mathrm {i}g\frac{\partial A}{\partial x}. \end{aligned}$$

(3)

Next, by using the definition of the group velocity $c_g\equiv \omega _0/2k_0$, we introduce the coordinates of the comoving frame [22] $\tau =4\pi \varepsilon ^2 k_0 x$ and $\chi =\varepsilon \omega _0 (x/c_g-t)$, with $\varepsilon \equiv k_0a_0$ being the wave steepness parameter ($\varepsilon \ll 1$). The spatial evolution of the envelope of the surface elevation in the linear regime is governed by the Schrödinger equation in the form

$$\begin{aligned} 4\pi \mathrm {i}\frac{\partial }{\partial \tau }A(\chi ,\tau )=\frac{\partial ^2}{\partial \chi ^2}A(\chi ,\tau ), \end{aligned}$$

(4)

where $\mathrm {i}$ is exchanged by $-\mathrm {i}$ in comparison to Eq. (2). Consequently, for identical initial conditions the corresponding solutions $\Psi (\chi ,\tau )$ and $A(\chi ,\tau )$ are related via complex conjugation.

In optics [1], the Schrödinger equation appears only within the slowly-varying envelope approximation of the Helmholtz equation

$$\begin{aligned} \left( \frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial z^2}\right) u(x,z)+k^2 u(x,z)=0 \end{aligned}$$

(5)

for the position dependence u(x, z) of the linearly polarized electromagnetic wave of the frequency $\omega$. Here $k=\omega /c$ is the corresponding wave vector.

Indeed, for the electromagnetic wave propagating in the z-direction, we can look for the solution of Eq.  (5) in the form $u(x,z)=U(x,z)\exp (\mathrm {i}kz)$, where U(x,z) is a slowly-varying function of z obeying the paraxial equation [1]

$$\begin{aligned} 2\mathrm {i}k\frac{\partial }{\partial z}U(x,z)=-\frac{\partial ^2}{\partial x^2}U(x,z). \end{aligned}$$

(6)

Here we have assumed that the second-order derivative $\partial ^2 U/\partial z^2$ is negligible with respect to $k(\partial U/\partial z)$.

As a result, by introducing the dimensionless coordinate $\chi =x/W$ and the propagation distance $\tau =z\lambda /W^2$, with $\lambda \equiv 2\pi /k$ being the wave length, we arrive again at the dimensionless form of the Schrödinger Eq.  (2) for $U(\chi ,\tau )$.

2.2 Waves emerging from a rectangular slit

The solution

$$\begin{aligned} \Psi (\chi ,\tau )=\int _{-\infty }^\infty \mathrm {d}\chi _0\, G(\chi ,\tau |\chi _0,0) \Psi (\chi _0,0) \end{aligned}$$

(7)

of Eq. (2) at time $\tau >0$ is determined by the propagator [3]

$$\begin{aligned} G(\chi ,\tau |\chi _0,0)\equiv \frac{1}{\sqrt{\mathrm {i}\tau }}\exp \left[ \mathrm {i}\frac{\pi }{\tau }(\chi -\chi _0)^2\right] \end{aligned}$$

(8)

and the wave function $\Psi (\chi ,0)$ at $\tau =0$.

As an elementary example, we now consider the free propagation of the initial wave function

$$\begin{aligned} \Phi _\nu (\chi ,0)\equiv \sqrt{2}\Theta \left[ 1-\left| 4\chi -(-1)^\nu \right| \right] \end{aligned}$$

(9)

as originating from a rectangular slit located between the dimensionless coordinates $\chi =0$ and $\chi =(-1)^\nu /2$ with $\nu =1,2$. Here we have introduced the Heaviside step function

$$\begin{aligned} \Theta (\chi )\equiv {\left\{ \begin{array}{ll}0 &{}\chi \le 0,\\ 1 &{}\chi >0. \end{array}\right. } \end{aligned}$$

(10)

With the help of the propagator $G(\chi ,\tau |\chi _0,0)$, Eq. (8), and the initial wave function $\Phi _\nu (\chi ,0)$, Eq. (9), we determine according to Eq. (7) the propagated wave function

$$\begin{aligned} \Phi _\nu (\chi ,\tau )=&\frac{(-1)^{\nu }}{\sqrt{\mathrm {i}}} \left\{ F\left( \sqrt{\frac{\pi }{\tau }}\chi \right) \right. \nonumber \\&\left. -F\left[ \sqrt{\frac{\pi }{\tau }}\left( \chi -\frac{(-1)^\nu }{2} \right) \right] \right\} \end{aligned}$$

(11)

as expressed in terms of the Fresnel integral [23]

$$\begin{aligned} F(w)\equiv \sqrt{\frac{2}{\pi }}\int _{0}^w\mathrm {d}\xi \, \mathrm {e}^{\mathrm {i}\xi ^2}. \end{aligned}$$

(12)

3 Bright and dark focusing

In the present section, we introduce the phenomena of bright and dark focusing which manifest themselves in the free propagation of particular wave packets.

For this purpose, certain superpositions of the wave functions $\Phi _1(\chi ,\tau )$ and $\Phi _2(\chi ,\tau )$, Eq. (11), are at the focus of our interest. In particular, we consider the function

$$\begin{aligned} \Psi _\pm (\chi ,\tau )=\frac{1}{\sqrt{2}}\left[ \Phi _1(\chi ,\tau )\pm \Phi _{2}(\chi ,\tau )\right] . \end{aligned}$$

(13)

At time $\tau =0$, the real-valued wave function $\Psi _\pm (\chi ,0)$ is composed of two rectangular profiles of length 1/2 without ($+$) and with (−) phase jump of $\pi$ at the coordinate $\chi =0$.

First, we present definitions of bright foci, defocusing, and dark foci. We then analyze the emergence of these features in the free propagation of the initial wave packet $\Psi _\pm (\chi ,0)$. Finally, we provide further insight into these effects with the help of Wigner phase space.

3.1 Bright foci, defocusing, and dark foci

In the following, we define a measure for the focusing of a wave which can be employed both for dark (small intensity) as well as bright regions (large intensity). At first sight, the location of maxima and minima of the intensity seems to be a good criterion to identify the position of bright and dark foci, respectively. However, as we will demonstrate in Sect. 3.3, also an antisymmetric wave with a vanishing intensity at the symmetry axis $\chi =0$ displays focusing effects at the center. For this reason, we introduce in the present section a different measure which closely matches the intensity criterion in many cases.

Our analysis is motivated by the shape of the time-evolved wave function $\Psi _\pm (\chi ,\tau )$, Eq. (13), which is a symmetric $(+)$ or antisymmetric $(-)$ function with regard to $\chi =0$, satisfying the relation

$$\begin{aligned} \Psi _\pm (\chi ,\tau )=\pm \Psi _\pm (-\chi ,\tau ) \end{aligned}$$

(14)

at any time $\tau$. This is due to the fact that the parity of the initial wave packet is conserved during free propagation.

Fig. 1

Schematic sketch of the probability density $\left| \Psi _\pm (\chi ,\tau )\right| ^2$ (red solid line) as function of the transverse coordinate $\chi$ with $\left| \chi \right| \ll 1$, displaying at time $\tau$ (a) a bright focus, (b) defocusing, and (c) a dark focus. For comparison, we present the profile of the probability density (dashed gray line) assumed at slightly larger or smaller times. According to Eq. (15), the probability density $\left| \Psi _\pm (\chi ,\tau )\right| ^2$ at time $\tau$ can be approximated by a parabolic function with curvature $\beta _\pm (\tau )$. a At a bright focus, the curvature $\beta _\pm (\tau )<0$ assumes a local minimum. b For defocusing, the curvature $\beta _\pm (\tau )=0$. c At a dark focus, the curvature $\beta _\pm (\tau )>0$ has a local maximum

Consequently, the probability density $\left| \Psi _\pm (\chi ,\tau )\right| ^2$ is a symmetric function with respect to the center $\chi =0$. Thus, it can be approximated by the parabola

$$\begin{aligned} \left| \Psi _\pm (\chi ,\tau )\right| ^2\simeq \alpha _\pm (\tau )+\frac{1}{2}\beta _\pm (\tau ) \chi ^2 \end{aligned}$$

(15)

for $\left| \chi \right| \ll 1$. Here we have introduced the offset

$$\begin{aligned} \alpha _\pm (\tau )\equiv \left| \Psi _\pm (0,\tau )\right| ^2 \end{aligned}$$

(16)

and the curvature

$$\begin{aligned} \beta _\pm (\tau )\equiv \left. \frac{\partial ^2}{\partial \chi ^2}\left| \Psi _\pm (\chi ,\tau )\right| ^2\right| _{\chi =0}, \end{aligned}$$

(17)

both evaluated at the central position $\chi =0$.

Maxima and minima of $\alpha _+(\tau )$ correspond to large or small intensities of the wave $\Psi _+(\chi ,\tau )$ at the center and could be used to define the location of bright and dark foci. However, due to the antisymmetry of $\Psi _-(\chi ,\tau )$, the function $\alpha _-(\tau )$ vanishes identically. For this reason, we require a more general measure to identify these foci for antisymmetric wave functions. We now introduce a novel criterion that is based on the minima and maxima of the curvature $\beta _\pm (\tau )$. Indeed, minimal and maximal values of $\beta _\pm (\tau )$ correspond to sharply peaked and very narrow regions in the intensity pattern.

More precisely, as illustrated in Fig. 1, we refer to a minimum of the function $\beta _\pm (\tau )<0$ as a bright focus. A maximum of the function $\beta _\pm (\tau )>0$ corresponds to a dark focus. Therefore, it is the sign of $\beta _\pm (\tau )$ in combination with the occurrence of an extremal value which characterizes these special foci.

For $\beta _\pm (\tau )=0$ there is instead a defocusing. Here the quadratic approximation of $\left| \Psi _\pm (\chi ,\tau )\right| ^2$ with regard to $\chi$ presented in Eq. (15) breaks down and higher-order terms have to be taken into account to provide an adequate model of the probability density for $\left| \chi \right| \ll 1$.

As indicated in Fig. 1 and shown in the following, in many cases minima of $\beta _\pm (\tau )$ closely correspond to maxima of the intensity $\alpha _\pm (\tau )$ and vice versa, thus matching our first thoughts.

Fig. 2

Space-time diagram of the probability density $\left| \Psi _\pm (\chi ,\tau )\right| ^2$ as determined by Eq. (13), resulting from an initial wave packet of constant amplitude for $\left| \chi \right| <1/2$ (a) without and (b) with phase jump of $\pi$ at $\chi =0$. a The probability density $\left| \Psi _+(\chi ,\tau )\right| ^2$ displays bright (purple and green ticks) and dark foci (red and orange ticks) close to the central axis $\chi =0$. b The probability density $\left| \Psi _-(\chi ,\tau )\right| ^2$ displays defocusing (purple and green ticks) and dark foci (red and orange ticks) close to the central axis $\chi =0$. In the figure, we have only marked two particular times $\tau$ at which each of these features appears and refer to Fig. 3 for further details

Fig. 3

Profile of the probability density $\left| \Psi _\pm (\chi ,\tau )\right| ^2$ at particular times $\tau$ indicated by ticks in Fig. 2 and arranged as function of the reciprocal time $1/\tau$. a Emerging from a rectangular profile (blue) at time $\tau =0$, we present the last two bright (purple and green) and dark foci (red and orange) for the probability density $\left| \Psi _+(\chi ,\tau )\right| ^2$. b For an initial wave packet with constant amplitude and phase jump of $\pi$, indicated by a blue cross at $\chi =0$, we display the last two dark foci (red and orange) and the occurrence of defocusing (purple and green) as characterized by broad dark regions in Fig. 2. The particular times $\tau _{\mathrm {max},k}^\pm$ and $\tau _{\mathrm {min},k}^\pm$ ($k=1,2,\ldots$) at which these feature emerge are listed in Table 1

Table 1 Numerical values for the times $\tau =\tau _{\mathrm {min},k}^\pm$ and $\tau =\tau _{\mathrm {max},k}^\pm$ at which the curvature $\beta _\pm (\tau )$, Eq. (17), of the probability density $\left| \Psi _\pm (\chi ,\tau )\right| ^2$ displays a local minimum or a maximum at $\chi =0$, respectively, with $k=1,2,\ldots$

3.2 Wave packet with constant amplitude and phase

We now focus on the free propagation of the symmetric wave function $\Psi _+(\chi ,\tau )$, Eq. (13). This particular wave packet originates from a rectangular slit of unit length. In the following, we review the main features that emerge during its time evolution with a slightly different emphasis as in the analysis pursued in Ref. [5].

In Fig. 2a we display the space-time diagram of the time-evolved probability density $\left| \Psi _+(\chi ,\tau )\right| ^2$. At particular times $\tau$, indicated by the colored ticks, we show in Fig. 3a the corresponding profile of the probability density as a function of the transverse coordinate $\chi$.

In particular, for $\tau =0$ the rectangular profile (blue) results from the initial function

$$\begin{aligned} \Psi _\mathrm {+}(\chi ,0)=\Theta \left( 1-\left| 4\chi -1\right| \right) +\Theta \left( 1-\left| 4\chi +1\right| \right) \end{aligned}$$

(18)

according to Eqs. (9) and (13).

At specific times, the probability density $\left| \Psi _+(\chi ,\tau )\right| ^2$ then displays bright (purple and green) and dark (red and orange) foci close to the central position $\chi =0$, as evident from Figs. 2a and 3a. In order to determine these times, we consider the curvature

$$\begin{aligned} \beta _+(\tau )=2\mathrm {Re}\left[ \Psi ^*_{+,\chi \chi }(0,\tau ) \Psi _+(0,\tau )\right] \end{aligned}$$

(19)

as obtained from Eq. (17) by making use of the symmetry $\Psi _+(\chi ,\tau )=\Psi _+(-\chi ,\tau )$ of the wave function. Here $\Psi _{+,\chi \chi }(0,\tau )$ denotes the second derivative of $\Psi _+(\chi ,\tau )$ with regard to $\chi$ evaluated at $\chi =0$.

We display the curvature $\beta _+(\tau )$, Eq. (19), in Fig. 4 by a red solid line in comparison to the probability density $\alpha _+(\tau )$, Eq. (16), at $\chi =0$ shown in blue. Interestingly, a bright focus, that is a local minimum of $\beta _+(\tau )$ with $\tau =\tau _{\mathrm {min},k}^+$, corresponds approximately to a local maximum of the probability density $\alpha _+(\tau )$, where $k=1,2,\ldots$. Analogously, a dark focus, that is a local maximum of $\beta _+(\tau )$ with $\tau =\tau _{\mathrm {max},k}^+$, corresponds approximately to a local minimum of the probability density $\alpha _+(\tau )$.

Fig. 4

Probability density $\alpha _+(\tau )$ (blue), Eq. (16), and curvature $\beta _+(\tau )$ (red), Eq. (17), of the function $\left| \Psi _+\left( \chi ,\tau \right) \right| ^2$ at the center $\chi =0$ as a function of the reciprocal time $\tau ^{-1}$. Here maxima and minima of $\alpha _+(\tau )$ almost coincide with minima and maxima of $\beta _+(\tau )$, respectively, as assumed at times $\tau = \tau _{\mathrm {min},k}^+$ and $\tau =\tau _{\mathrm {max},k}^+$ with $k=1,2,\ldots$. As a consequence, a bright focus is accompanied by a large probability density, while a dark focus corresponds to a small probability density at the center $\chi =0$

We have determined the times $\tau _{\mathrm {min},k}^+$ for a bright focus and $\tau _{\mathrm {max},k}^+$ for a dark focus as detailed in Appendix A. There, we have shown that for small times $\tau$ these foci are approximately located at

$$\begin{aligned} \tau _{\mathrm {min},k}^+\simeq \frac{1}{8k-5} \text \,{and}\, \tau _{\mathrm {max},k}^+\simeq \frac{1}{8k-1}. \end{aligned}$$

(20)

In order to resolve the different foci in Figs. 3a and 4, we have made use of the inverse propagation coordinate $1/\tau$. As a consequence, the foci are approximately equally spaced as evident from Eq. (20).

We also present the numerical values of $\tau _{\mathrm {min},k}^+$ and $\tau _{\mathrm {max},k}^+$ for $k=1,2,3$ in the left two columns of Table 1. Indeed, as illustrated in Fig. 3 for $k=1,2$, at a bright and dark focus we recover the typical behavior of the parabola depicted in Fig. 1.

Moreover, for $k=1$ and $\tau _{\mathrm {min},1}^+\approx 0.268$ we arrive at a probability density of $\alpha _+( \tau _{\mathrm {min},1}^+) \approx 1.67$. Thus, the bright focus appears a bit earlier than the time $\tau _0\approx 0.342$ when the brightest spot with $\alpha _+\left( \tau _0\right) \approx 1.80$ arises. Consequently, a bright focus where the probability density has locally the tightest peak in the region $\left| \chi \right| \ll 1$ matches only approximately a local maximum of the probability density at $\chi =0$. This feature has already been pointed out in Ref. [5].

Finally, we note that at an intermediate time between a bright and dark focus, the probability density $\left| \psi _+(\chi ,\tau )\right| ^2$ displays defocusing with $\beta _+(\tau )=0$, as evident from Figs. 2 and 4. We refrain here from a more detailed analysis of this phenomenon.

3.3 Wave packet with constant amplitude and $\pi$-phase jump

Next, we study the dynamics of the wave function $\Psi _-(\chi ,\tau )$, Eq. (13), describing the free propagation of the initial function

$$\begin{aligned} \Psi _-(\chi ,0)=\Theta \left( 1-\left| 4\chi -1\right| \right) -\Theta \left( 1-\left| 4\chi +1\right| \right) \end{aligned}$$

(21)

according to Eqs. (9) and (13). Here $\Psi _-(\chi ,0)$ has a constant amplitude and a phase jump of $\pi$ at $\chi =0$.

In Fig. 2b, we illustrate the probability density resulting from the propagation of the initial wave packet $\Psi _-(\chi ,0)$. Moreover, we display in Fig. 3b the corresponding profile of the probability density $\left| \Psi _-(\chi ,\tau )\right| ^2$ at particular times $\tau$, indicated by colored ticks in Fig. 2b, and arranged as a function of the reciprocal time $1/\tau$.

Since $\Psi _-(\chi ,\tau )$ is an antisymmetric function, we obtain for all times $\tau$ the value $\Psi _-(0,\tau )=0$ and the second derivative $\Psi _{-,\chi \chi }(0,\tau )=0$ with regard to $\chi$ at $\chi =0$, as evident in Fig. 2b. For this reason, the offset $\alpha _-(\tau )=0$, Eq. (16), of the quadratic approximation in Eq. (15) disappears. Moreover, the curvature $\beta _-(\tau )$, Eq. (17), reduces to

$$\begin{aligned} \beta _-(\tau )=2 \left| \Psi _{-,\chi }(0,\tau )\right| ^2, \end{aligned}$$

(22)

being only determined by the first derivative of the function $\Psi _{-}(\chi ,\tau )$ with regard to $\chi$ at $\chi =0$, where we have made use of the antisymmetry of $\Psi _-(\chi ,\tau )$.

Fig. 5

Probability density $\alpha _-(\tau )$ (blue), Eq. (16), and curvature $\beta _-(\tau )$ (red), Eq. (17), of the function $\left| \Psi _-\left( \chi ,\tau \right) \right| ^2$ evaluated at the center $\chi =0$ as a function of the reciprocal time $1/\tau$. Despite a vanishing probability density $\alpha _-(\tau )$ for all times $\tau$, we are able to identify dark foci that express themselves as local maxima of the function $\beta _-(\tau )$ assumed at the time $\tau =\tau _{\max ,k}^-$ with $k=1,2,\ldots$. However, since $\beta _-\left( \tau _{\min ,k}^-\right) =0$ no bright foci appear during the free propagation of this particular wave packet. Instead defocusing emerges for $\tau =\tau _{\min ,k}^-$

We depict in Fig. 5 the vanishing function $\alpha _-(\tau )$ in blue and the curvature $\beta _-(\tau )$, Eq. (22), in red. Due to the appearance of the absolute value in Eq. (22), the curvature $\beta _-(\tau )$ is always positive. Thus, no bright foci emerge for the probability density $\left| \Psi _-(\chi ,\tau )\right| ^2$.

In order to obtain a deeper insight into the behavior of the function $\beta _-(\tau )$, we consider the first derivative

$$\begin{aligned} \Psi _{-,\chi }(0,\tau )=\frac{2}{\sqrt{\mathrm {i}\tau }}\left[ 1-\exp \left( \frac{\mathrm {i}\pi }{4\tau }\right) \right] \end{aligned}$$

(23)

with regard to $\chi$ at the center $\chi =0$, as derived in Appendix  A.

According to Eqs. (22) and (23) the function $\beta _-(\tau )$ displays local minima and maxima at the times

$$\begin{aligned} \tau _{\mathrm {min},k}^-= \frac{1}{8k} \text\, {and}\, \tau _{\mathrm {max},k}^-\simeq \frac{1}{8k-4}, \end{aligned}$$

(24)

respectively, with $k=1,2,\ldots$. The exact locations of the maxima are presented in Table 1. Indeed, the use of the inverse propagation coordinate $1/\tau$ in Figs. 3b and 5 leads to an approximately equal spacing of these extremal values as a consequence of Eq. (24).

First, we focus on the local minima of $\beta _-(\tau )$. For $\tau =\tau _{\mathrm {min},k}^-$ the function $\beta _-\left( \tau _{\mathrm {min},k}^-\right) =0$. According to Section 3.1, this corresponds to the occurrence of a defocusing.

Moreover, since $\alpha _-(\tau )=0$ for all values of $\tau$, this implies

$$\begin{aligned} \left| \Psi _-(\chi , \tau _{\mathrm {min},k}^-)\right| ^2={\mathcal {O}}\left( \chi ^6\right) \end{aligned}$$

(25)

for $\left| \chi \right| \ll 1$. Indeed, the sixth power of $\chi$ in Eq. (25) is the reason for the emergence of the broad dark regions presented in Fig. 2b, indicated by purple and green ticks. This feature becomes even clearer in Fig. 3b where we show the corresponding profiles of the probability density at the times $\tau _{\mathrm {min},1}^-$ and $\tau _{\mathrm {min},2}^-$.

Next, we turn to the local maxima of the function $\beta _-(\tau )$, Eq. (22), with $\beta _-\left( \tau _{\mathrm {max},k}^-\right) >0$. Accordingly, for $\tau =\tau _{\mathrm {max},k}^-$, the probability density $\left| \Psi _-(\chi ,\tau )\right| ^2$ displays dark foci at $\chi =0$. In Fig. 2b we indicate the times $\tau _{\mathrm {max},1}$ and $\tau _{\mathrm {max},2}$ of the last two dark foci by red and orange ticks and show the corresponding profiles of the probability density in Fig. 3b. At these particular times the dark spots are the tightest and close to the center $\chi =0$ the probability density

$$\begin{aligned} \left| \Psi _-\left( \chi , \tau _{\mathrm {max},k}^-\right) \right| ^2={\mathcal {O}}\left( \chi ^2\right) \end{aligned}$$

(26)

is in lowest order proportional to the second power of $\chi$.

3.4 Bright and dark focusing viewed from phase space

In order to obtain a deeper insight into bright and dark diffractive focusing, we study now the occurrence of these phenomena in Wigner phase space. For this purpose, we make use of the Wigner function [24, 25]

$$\begin{aligned}&W_{\pm }(\chi ,\eta ,\tau )=\nonumber \\&\quad \int _{-\infty }^\infty \mathrm {d}\xi \, \mathrm {e}^{2\pi \mathrm {i}\eta \xi }\Psi _\pm \left( \chi -\frac{\xi }{2},\tau \right) \Psi ^*_\pm \left( \chi +\frac{\xi }{2},\tau \right) \end{aligned}$$

(27)

corresponding to the wave packet $\Psi _\pm (\chi ,\tau )$, Eq. (13), with constant amplitude for $-1/2\le \chi \le 1/2$ and without ($+$) and with (−) phase jump of $\pi$ at $\chi =0$. Here, we have introduced the dimensionless momentum $\eta =p W/(2\pi \hbar )$ as determined by the momentum p and the characteristic length W of the problem in correspondence to the units presented in Sect.  2.

According to Eq. (13), the wave packet $\Psi _\pm (\chi ,\tau )$ can be expressed as a superposition of functions $\Phi _1(\chi ,\tau )$ and $\Phi _2(\chi ,\tau )$. Consequently, also the Wigner function $W_{\pm }(\chi ,\eta ,\tau )$, Eq. (27), can be decomposed into a sum

$$\begin{aligned} W_{\pm }(\chi ,\eta ,\tau )=W_\mathrm {d}(\chi ,\eta ,\tau )\pm W_\mathrm {i}(\chi ,\eta ,\tau ) \end{aligned}$$

(28)

of two phase space distributions

$$\begin{aligned} W_\mathrm {d}(\chi ,\eta ,\tau )\equiv \frac{1}{2}\left[ W_{11}(\chi ,\eta ,\tau )+W_{22}(\chi ,\eta ,\tau )\right] \end{aligned}$$

(29)

and

$$\begin{aligned} W_\mathrm {i}(\chi ,\eta ,\tau )\equiv \frac{1}{2}\left[ W_{12}(\chi ,\eta ,\tau )+W_{21}(\chi ,\eta ,\tau )\right] , \end{aligned}$$

(30)

where

$$\begin{aligned}&W_{\nu \mu }(\chi ,\eta ,\tau )=\nonumber \\&\quad \int _{-\infty }^\infty \mathrm {d}\xi \, \mathrm {e}^{2\pi \mathrm {i}\eta \xi }\Phi _\nu \left( \chi -\frac{\xi }{2},\tau \right) \Phi _{\mu }^*\left( \chi +\frac{\xi }{2},\tau \right) \end{aligned}$$

(31)

for $\nu ,\mu =1,2$.

For $\nu =\mu$, the function $W_{\nu \mu }(\chi ,\eta ,\tau )$, Eq. (31), denotes the Wigner function corresponding to the wave function $\Phi _\nu (\chi ,\tau )$, Eq. (11). Thus, the phase space distribution $W_\mathrm {d}(\chi ,\eta ,\tau )$, Eq. (29), is the sum of the Wigner functions corresponding to the wave functions $\Phi _1(\chi ,\tau )$ and $\Phi _2(\chi ,\tau )$.

Fig. 6

Phase-space distributions (a) $W_\mathrm {d}(\chi ,\eta ,0)$, Eq. (32), and (b) $W_\mathrm {i}(\chi ,\eta ,0)$, Eq. (33). According to Eq. (28), their sum ($+$) and difference (−) yield the Wigner function $W_\pm (\chi ,\eta ,0)$ at time $\tau =0$. a Analogous to the wave function $\Psi _\pm (\chi ,0)$, Eq. (13), emerging from a rectangular slit, the phase-space distribution $W_\mathrm {d}(\chi ,\eta ,0)$ at time $\tau =0$ is restricted to the domain $-1/2\le \chi \le 1/2$. b In contrary, the phase-space distribution $W_\mathrm {i}(\chi ,\eta ,0)$ is restricted to the domain $-1/4\le \chi \le 1/4$. For this reason, the Wigner functions $W_+(\chi ,\eta ,0)$ and $W_-(\chi ,\eta ,0)$ look identical for $\left| \chi \right| >1/4$ as shown in Fig. 7a, b

For $\nu \ne \mu$, the function $W_{\nu \mu }(\chi ,\eta ,\tau )$ expresses the interference of the wave functions $\Phi _\nu (\chi ,\tau )$ and $\Phi _\mu (\chi ,\tau )$ in phase space at time $\tau$. Thus, the phase-space distribution $W_\mathrm {i}(\chi ,\eta ,\tau )$, Eq. (30), is determined by the interference of the wave functions $\Phi _1(\chi ,\tau )$ and $\Phi _2(\chi ,\tau )$.

We now determine the explicit forms of the phase distributions $W_\mathrm {d}(\chi ,\eta ,\tau )$ and $W_\mathrm {i}(\chi ,\eta ,\tau )$ at the initial time $\tau =0$. For this purpose, we insert the wave function $\Phi _\nu (\chi ,0)$, Eq. (9), in Eq. (31) and evaluate the integral for $\mu =\nu =1,2$. By making use of Eqs. (29) and (30), respectively, we arrive at the expressions

$$\begin{aligned}&W_\mathrm {d}(\chi ,\eta ,0)=\nonumber \\&\quad \frac{1}{\pi \eta }\left\{ \Theta \left( \frac{1}{8}-\left| \chi +\frac{3}{8}\right| \right) \sin \left[ 4\pi \eta \left( \chi +\frac{1}{2}\right) \right] \right. \nonumber \\&\quad -\left. \left[ \Theta \left( \frac{1}{8}-\left| \chi +\frac{1}{8}\right| \right) -\Theta \left( \frac{1}{8}-\left| \chi -\frac{1}{8}\right| \right) \right] \sin \left( 4\pi \eta \chi \right) \right. \nonumber \\&\quad -\left. \Theta \left( \frac{1}{8}-\left| \chi -\frac{3}{8}\right| \right) \sin \left[ 4\pi \eta \left( \chi -\frac{1}{2}\right) \right] \right\} \end{aligned}$$

(32)

and

$$\begin{aligned}&W_\mathrm {i}(\chi ,\eta ,0)=\frac{2}{\pi \eta }\cos \left( \pi \eta \right) \nonumber \\&\quad \times \left\{ \Theta \left( \frac{1}{8}-\left| \chi +\frac{1}{8}\right| \right) \sin \left[ 4\pi \eta \left( \chi +\frac{1}{4}\right) \right] \right. \nonumber \\&\quad \left. -\Theta \left( \frac{1}{8}-\left| \chi -\frac{1}{8}\right| \right) \sin \left[ 4\pi \eta \left( \chi -\frac{1}{4}\right) \right] \right\} . \end{aligned}$$

(33)

In Fig. 6, we display the phase space distributions (a) $W_\mathrm {d}(\chi ,\eta ,0)$ and (b) $W_\mathrm {i}(\chi ,\eta ,0)$ at time $\tau =0$. First, we notice that the function $W_\mathrm {d}(\chi ,\eta ,0)$ is composed of two identical patterns as located in the domains $-1/2\le \chi \le 0$ and $0\le \chi \le 1/2$. Indeed, the phase distribution $W_\mathrm {d}(\chi ,\eta ,0)$ is composed of two Wigner functions corresponding to a slit located between $-1/2\le \chi \le 0$ and $0\le \chi \le 1/2$ as expressed by the wave functions $\Phi _1(\chi ,0)$ and $\Phi _2(\chi ,0)$, Eq. (9). In contrary, the phase space distribution $W_\mathrm {int}(\chi ,\eta ,0)$ emerging from the interference of these wave functions only possesses a non-vanishing contribution in the domain $-1/4\le \chi \le 1/4$. Moreover, its pattern resembles the one shown in the left or right half of Fig. 6a, but contains additional oscillations in the direction of the dimensionless momentum $\eta$.

According to Eq. (28), the two phase space distributions $W_\mathrm {d}(\chi ,\eta ,0)$ and $W_\mathrm {i}(\chi ,\eta ,0)$ compose the Wigner function $W_\pm (\chi ,\eta ,0)$. We display these particular Wigner functions at the initial time $\tau =0$ in Fig. 7a, b.

Fig. 7

Time evolution of the Wigner functions $W_+(\chi ,\eta ,\tau )$ (left column) and $W_-(\chi ,\eta ,\tau )$ (right column). a At time $\tau =0$, positive and negative contributions of $W_+(\chi ,\eta ,0)$ interfere and form a rectangular profile of the probability density. c At $\tau =\tau _{\mathrm {max},1}^+$ negative parts of $W_+(\chi ,\eta ,\tau )$ dominate at the center $\chi =0$ and give raise to a dark focus. e For $\tau =\tau _{\mathrm {min},1}^+$ positive parts of $W_+(\chi ,\eta ,\tau )$ dominate in the central region $\chi =0$, giving raise to a bright focus. b At time $\tau =0$, positive and negative contributions of the Wigner function $W_-(\chi ,\eta ,0)$ interfere and form a rectangular profile of the probability density, except of the central position $\chi =0$ where $\left| \Psi _-(0,0)\right| ^2=0$. d At a later time $\tau =\tau _{\mathrm {min},1}^-$ positive and negative parts of $W_-(\chi ,\eta ,\tau )$ are approximately equally distributed at each position in the central region $\left| \chi \right| \ll 1$, leading to a defocusing. f At time $\tau =\tau _{\mathrm {max},1}^-$ negative parts of $W_-(\chi ,\eta ,\tau )$ instead dominate in the center and lead to the appearance of a dark focus. These particular times are listed in Table 1

First, we notice that both functions $W_\pm (\chi ,\eta ,0)$ are identical in the domain $\left| \chi \right| >1/4$ where the phase space distribution $W_\mathrm {i}(\chi ,\eta ,0)$ does not yield a contribution. Moreover, we observe in Fig. 7 a that the Wigner function $W_+(\chi ,\eta ,0)$ indeed corresponds to a rescaled version of the pattern displayed in the left half of Fig. 6a. In addition, we note that the Wigner function $W_+(\chi ,\eta ,0)$ is positive close to the center $\chi =0$ and $\eta =0$ as depicted in red. On the other hand, the Wigner function $W_-(\chi ,\eta ,0)$ displayed in Fig. 7b is dominated by negative values close to the center $\chi =0$ and $\eta =0$ as depicted in blue.

Next, we recall that the probability density can be extracted as marginal of the Wigner function [25]. In dimensionless coordinates this relation reads

$$\begin{aligned} \left| \Psi _\pm (\chi ,\tau )\right| ^2=\int _{-\infty }^\infty \mathrm {d}\eta \ W_\pm (\chi ,\eta ,\tau )\,. \end{aligned}$$

(34)

Interestingly, as shown in Fig. 7a, b by the blue curves, the marginals $\left| \Psi _+(\chi ,0)\right| ^2$ and $\left| \Psi _-(\chi ,0)\right| ^2$ are identical except of the point $\chi =0$, where the function $\Psi _-(\chi ,0)$ vanishes while $\Psi _+(\chi ,0)$ has a positive value.

We now analyze the emergence of bright and dark foci in terms of the Wigner function. For this purpose, we recall that dynamics of the Wigner function is governed by the quantum Liouville equation [25]. Consequently, the free evolution of the Wigner function $W_\pm (\chi ,\eta ,0)$ corresponds to the phase space transformation

$$\begin{aligned} W_{\pm }(\chi ,\eta ,\tau )=W_{\pm }\left( \chi -\eta \tau ,\eta ,0\right) \end{aligned}$$

(35)

as induced by a shift of the argument $\chi$ which is determined by the product of the momentum $\eta$ and the time $\tau$.

First, we focus on the time evolution of the Wigner function $W_+(\chi ,\eta ,\tau )$ displayed in the left column of Fig. 7. At the time $\tau =\tau _{\mathrm {max},1}^+$ a dark focus arises as shown as in Fig. 7c. Here the negative contributions to the Wigner function play a stronger role close to the center $\left| \chi \right| \ll 1$. On the other hand, as displayed in Fig. 7e a bright focus at time $\tau =\tau _{\mathrm {min},1}^+$ arises due to the absence of negative contributions to the Wigner function close to the central region $\left| \chi \right| \ll 1$. The particular times at which these foci arise are listed in Table 1.

Second, we turn to the dynamics of the Wigner function $W_-(\chi ,\eta ,\tau )$ presented in the right column of Fig. 7. At time $\tau =\tau _{\mathrm {min},1}^-$ defocusing occurs as depicted in Fig. 7d. Here, close to the center $\chi =0$ the probability density $\left| \Psi _-(\chi ,\tau )\right| ^2$ is governed by a sixth power in $\chi$ as demonstrated in Eq. (25). This particular dependency arises because positive and negative contributions to the Wigner functions almost cancel in the region $\left| \chi \right| \ll 1$. On the other hand, at the time $\tau =\tau _{\mathrm {max},1}^-$ positive and negative contributions to $W_-(\chi ,\eta ,\tau )$ only cancel very close to the center $\chi =0$, while otherwise positive contributions dominate giving raise to a dark focus.

In conclusion, the illustration of the quantum dynamics in Wigner phase space allowed us to obtain a deeper understanding of bright and dark focusing. However, it is remarkable that the Wigner functions $W_+(\chi ,\eta ,\tau )$ and $W_-(\chi ,\eta ,\tau )$ display very different phenomena although these functions are closely related, as demonstrated in the present section.

4 Dark focusing with surface gravity water waves

As demonstrated in Sect. 2, surface gravity water waves behave in a certain regime analogous to matter and classical waves. This analogy has proven to be useful in the study of various effects which are familiar from optics and quantum mechanics [11, 16, 21, 26,27,28]. In the present section, we benefit again from the similarity of the wave dynamics in these systems and demonstrate an experimental observation of dark focusing with surface gravity water waves.

First, we introduce our experimental setup for measuring the propagation dynamics. Next, we show the initial wave profile and the methods to extract the evolution of the amplitude envelope. Finally, we present our measurements and the occurrence of a dark focus in water waves.

4.1 Experimental setup

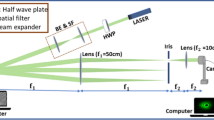
In order to measure the propagation dynamics of surface gravity water waves pulses and the dark/bright focusing phenomena, we have conducted a series of experiments in a $5\,\mathrm{m}$ long, $0.4\,\mathrm{m}$ wide, and $H=0.2\,\mathrm{m}$ deep laboratory wave tank (see Fig.  8). The wave maker is programmed to excite a wave packet with a desired programmable envelope of different slit shapes by a computer-controlled wedge that is partly immersed in the water and moves up and down. The carrier wave number $k_{0} \approx 23\,\mathrm{m^{-1}}$ satisfies the deep-water condition $k_{0}H>\pi$ [29]; the wave dissipation can be neglected. To avoid any effect of residual reflections from the beach located at the far end of the test section, measurements are performed at distances between $0.3\, \mathrm{m}$ to $4.2\, \mathrm{m}$ from the wave maker. We note that while surface gravity water waves are nonlinear in their nature, the effects of nonlinearity are not relevant for the propagation distance considered in the laboratory set-up. Only by increasing the fetch to much longer propagation distances they could become notable.

Fig. 8

Experimental setup for generating surface gravity water wave packets. The wave maker (right) is computer controlled and can generate different types of surface gravity water wave envelopes which propagate freely. Their elevation is measured using the capacitance type wave gauges (center) and an absorbing beach (left) is placed to avoid reflections

The instantaneous water surface elevation is measured by four wave capacitance-type wave gauges [30] mounted on a bar parallel to the tank side walls. The bar with the gauges is fixed to an instrument carriage that can be shifted along the tank.

4.2 Methods

In order to mimic the antisymmetric state $\Psi _-(\chi ,\tau )$, Eq. (21), we prepare a temporal rectangular water wave packet of width $t_{0}$ with a sign flip at $t=0$. At the wave maker it has the form

$$\begin{aligned} A_-(x=0, t) \equiv {\left\{ \begin{array}{ll}-1, &{} -\frac{t_{0}}{2}< t< 0 \\ 1, &{} 0< t < \frac{t_{0}}{2} \\ 0, &{} \text{ otherwise }\end{array}\right. } \end{aligned}$$

(36)

and the temporal surface elevation at the origin

$$\begin{aligned} h(t,0) \equiv \mathrm {Re}\left[ a_0 A_-(x=0,t) \mathrm {e}^{\mathrm {i}\omega _{0}t}\right] \end{aligned}$$

(37)

is prescribed by the wave maker at $x=0$, where $\omega _0$ is the carrier frequency, $a_{0}$ is the maximal amplitude, and $A_-$ the normalized amplitude envelope. The propagation dynamics of the surface gravity water wave is then governed by Eq. (4).

In order to extract the amplitude envelope at a different position, we make use of wave gauges that are shown in Fig. 8. These wave gauges measure the real part of the wave function. The Hilbert transform is applied to obtain the imaginary part and thus allows us to obtain the evolution of the envelope. Similar as in Ref. [21] we have utilized the toolbox function “hilbert” [31] of Matlab for this purpose. For further details on the Hilbert transform we refer to Ref. [32].

4.3 Measurements

We study experimentally and numerically the case of an initially rectangular profile with phase jump of $\pi$ at $\tau =0$ as given by Eq. (36). We recall from Sect. 2 that the evolution of the complex amplitude envelope $A_-(\chi ,\tau )$ is analogous to the dynamics of the wave function $\Psi _-(\chi ,\tau )$ analyzed in Sect. 3.3. To ease the comparison of both cases, we make use of the dimensionless units introduced in Sect. 2.

The experiments are performed with a carrier frequency of $\omega _{0}=15\, \mathrm{rad/s}$, an initial amplitude of $a_{0}=3\, \mathrm{mm}$, and width of $t_{0}=5.18\, \mathrm{s}$. Thus, satisfying both deep water and linear propagation conditions.

Fig. 9

Profile of the absolute square $\left| A_{-}(\chi ,\tau )\right| ^2$ of the complex amplitude envelope at particular times $\tau$ marked in Fig. 2, arranged as function of the reciprocal time $1/\tau$. These specific profiles arise for an initial wave packet with constant amplitude and phase jump of $\pi$ at $\chi =0$. The particular times $\tau _{\mathrm {max},k}^-$ and $\tau _{\mathrm {min},k}^-$ ($k=1,2,\ldots$) are listed in Table 1 and indicate the emergence of defocusing and a dark focus, respectively. a Experimental envelopes given via Hilbert transform for the corresponding experimental locations $x=1.2\, \mathrm {m}, 1.9\, \mathrm {m}, 3.4\,\mathrm {m}, 3.8\,\mathrm {m}$ (shown as inverse of $\tau _{\mathrm {min},2}^{-}$, $\tau _{\mathrm {max},2}^{-}$, $\tau _{\mathrm {min},1}^{-}$, $\tau _{\mathrm {max},1}^{-}$). b Simulations performed numerically via the split step Fourier transform algorithm for a finite slit with the same characteristics as given in the experiment

The experimental curves are shown in Fig. 9a and the corresponding simulations in Fig. 9b. We note that the simulations were performed under conditions similar to the experimental ones i.e. with a finite amount of oscillations due to a limitation given by the finite carrier frequency. We display the two dark foci (orange and red) and the occurrence of defocusing (green and purple) characterized by broad dark regions. The particular times $\tau _{\mathrm {max},k}^-$ and $\tau _{\mathrm {min},k}^-$ ($k=1,2,\ldots$) at which these feature emerge are listed in Table 1.

Fig. 10

Double logarithmic plot of two experimental profiles that are presented in Fig. 9a for $\tau =\tau _{\mathrm {min},1}^-$ and $\tau =\tau _{\mathrm {max},1}^-$ in the domain $0.076<\chi <0.176$. For small values $\left| \chi \right| \ll 1$ we expect a power-law dependence $\left| A_-(\chi ,\tau )\right| ^2\sim \left| \chi \right| ^s$ of the absolute value squared of the amplitude envelope as determined by the power s. With the help of a linear fit, we obtain (a) for $\tau =\tau _{\mathrm {min},1}^-$ (black) the slope $s=6.03\pm 0.34$ and (b) for $\tau =\tau _{\mathrm {max},1}^-$ (blue) the slope $s=2.07\pm 0.12$

Furthermore, we study the dependence

$$\begin{aligned} \left| A_-(\chi ,\tau )\right| ^2\sim \left| \chi \right| ^s \end{aligned}$$

(38)

with regard to the power s in the domain $\left| \chi \right| \ll 1$. According to Eqs. (25) and (26), there is characteristic power $s=6$ for defocusing in contrary to $s=2$ corresponding to the leading order at a dark focus. For the experimental data, we present in Fig. 10 the dependence of $|A_-\left( \chi ,\tau \right) |^2$ on $\chi$ in a double logarithmic plot. Here we have used the particular values $\tau =\tau _{\mathrm {min},1}^-$ (black curve) and $\tau =\tau _{\mathrm {max},1}^-$ (blue curve), respectively. The power law Eq. (38) is examined for both curves in the region $0.076<\chi <0.176$. a For defocusing at $\tau =\tau _{\mathrm {min},1}^-$, we identify a slope of $s=6.03\pm 0.34$ which is in agreement with the expected sixth power presented in Eq. (25). b For a dark focus at $\tau =\tau _{\mathrm {max},1}^-$, the slope $s=2.07\pm 0.12$ instead confirms the parabolic dependence shown in Eq. (26).

5 Bright and dark focusing of classical waves with phase slits

In this section we investigate the properties of diffraction patterns of scalar waves, for several cases of initial wave functions at the slit with non-constant phase value. We define a complex wave function where the amplitude is constant in the slit, but the phase is either piecewise constant (Haar wavelet), or has a linear dependence on the slit coordinate x. We use the general formulation of diffraction based on the Rayleigh-Sommerfeld integrals, as they provide more accurate results for acoustic and light waves than the Fresnel integral, when comparing to experimental measurements [5]. However, the predictions for the location, maxima and width of bright and dark focusing regions agree with the results based on the Fresnel integral. Only for small values of the normalized coordinate $z\lambda /W^{2} < 0.1$ the lobes in the intensity pattern differ considerably.

First, we discuss the intensity and phase diffraction patterns obtained for a Haar phase slit with a width of a few wavelengths, using the Rayleigh-Sommerfeld scalar diffraction theory. Second, we generalize our analysis to phase slits with a linear dependence on the transverse coordinate. We study the triangular phase slits with symmetric and asymmetric profiles, in analogy to the three-dimensional axicon used to generate Bessel beams. Finally, we present results for the divergent phase slit, where the triangular phase profile is mirrored relative to the x-axis. Despite the differences in the theoretical treatment we find a good correspondence with time diffraction patterns of matter waves.

The diffraction pattern of a two-dimensional aperture or a slit illuminated by a plane scalar wave of wavelength $\lambda$ and wave number $k = 2\pi /\lambda$ can be obtained either by the first, or by the second Rayleigh-Sommerfeld (RS) diffraction integral [2, 33], respectively.

$$\begin{aligned} \left\{ \begin{aligned} U_{RS}^{(I)}({\mathbf {P}})&= -\frac{1}{2\pi }\int _{{\mathcal {A}}} dS\, \frac{\partial U_{0}(Q)}{\partial {\mathbf {n}}}\, \frac{e^{iks}}{s} \\ U_{RS}^{(II)}({\mathbf {P}})&= \frac{1}{2\pi }\int _{{\mathcal {A}}} dS\, U_{0}(Q)\, \frac{\partial }{\partial {\mathbf {n}}}\left( \frac{e^{iks}}{s}\right) . \end{aligned} \right. \end{aligned}$$

(39)

$Q(\xi ,\eta ,0)$ is a point inside a plane aperture denoted by ${\mathcal {A}}$ and ${\mathbf {n}}$ is a unit vector perpendicular to the aperture. P(x, y, z) is a space point in the diffraction region where the field is calculated. The distance between P and Q is denoted by $s = PQ$. $U_{0}(Q)$ is the scalar field at the aperture, assumed to be identical to the field propagating in free space without diffracting screen. Both integrals achieve similar results, but in the calculations presented below we have only used the first integral.

For classical waves a slit is defined as a two-dimensional aperture of finite width W in one dimension (x-coordinate) and infinite in the other (y-coordinate). This slit is translation invariant along the y-axis and thus, we can restrict the calculation of the integrals to one dimension. We set the slit aligned with the y-axis. When the illuminating field is a plane wave, the first RS integral takes the following form [33]:

$$\begin{aligned} U_{RS}^{(I)}(x, z) = \frac{k}{2\pi }\int _{- W/2 + x}^{W/2 - x} d(\xi - x)\ U_{0}(\xi ) H_{0}^{(1)}(\beta ) . \end{aligned}$$

(40)

Here $\beta = k\sqrt{(\xi - x)^{2} + z^{2}}$ and $H_{0}^{(1)} = J_{0} + iY_{0}$ are Hankel functions of the first kind and order 0. $J_{0}$ and $Y_{0}$ are the respective Bessel functions of first and second kind. $\xi$ denotes the x coordinate inside the slit domain. In Ref. [33] the field at the aperture was normalized to 1.0 and no phase factor with spatial dependence was used. However, modifying the initial field by imposing an amplitude and a phase with dependence on the coordinate $\xi$ does not affect the form of the integrals.

5.1 Slits of constant amplitude and Haar phase

In diffraction problems of scalar waves by a slit, the field at the aperture is often assumed to be identical to the free space propagating field and its phase is constant. We can impose an amplitude dependence on the transverse coordinate of the slit $\xi$, or a non-constant phase. We restrict our discussion to cases where the amplitude remains constant in the aperture, but the phase has a discrete jump $\Delta \phi = 2\phi _{0}$ between the two halves of the slit. The scalar field at the origin of the propagation axis takes the form $U_{0}(\xi ) = A_{0}\exp (\pm i\phi _{0})$, where $A_{0}$ is constant. The phase constant $\phi _{0}$ can have any value between 0 and $2\pi$. For the sake of simplicity we can set a negative phase ($-\phi _{0}$) for $-W/2< \xi < 0$ and a positive phase ($\phi _{0}$) for $0< \xi < W/2$. The amplitude is a real function of $\xi$, which is set constant and equal to 1.0 in the present discussion.

The profiles of the amplitude and phase are presented in Fig. 11a. The intensity, on-axis profile and phase of the diffraction pattern for an antisymmetric slit with phase difference $\Delta \phi = \pi$ and width $W = 12\lambda$ are presented in Fig. 11b–d. The dark focusing already discussed in Sect.  3 for matter waves is also clearly visible. The main difference is the number of bright lobes close to the axis origin. Unlike in the Fresnel diffraction, the number of lobes on the RS diffraction patterns is finite and related to $W/\lambda$. On the other hand, the intensity on axis has a small, but non-zero value as in the Fresnel diffraction pattern. We attribute this deviation to errors in the numerical integration.

When the slit width is only a multiple of a few wavelengths, i. e. $W/\lambda \sim m$, the intensity profile close to the slit, calculated using the first RS integral, has an oscillatory behaviour with a number of lobes equal to m. This is in contrast to the assumption of a constant field amplitude at $z = 0$. However, this is not only confirmed by other calculation methods but also experimentally verified for optical waves [5]. It is the result of scattering and resonance imposed by the boundary of the narrow slit. In wider slits the intensity approaches 1.0 and the number of small oscillations decrease in amplitude and increases in the same step of m (see Fig. 11b). By contrast, in the Fresnel diffraction the number of oscillations in the intensity profile increases to infinity as one approaches $z = 0$.

The differences in the dark focusing between the intensity maps of the matter wave diffraction and the Rayleigh-Sommerfeld diffraction can be quantitatively analyzed by comparing the position of the maxima and minima of the second derivative along the symmetry axis (z-axis). For a direct comparison with the results of Sect. 3 we define the normalized coordinates $\chi = x/W$ and $\tau = z\lambda /W^{2}$. The results are illustrated in Fig. 12. The second derivative with regard to $\chi$ of the intensity pattern in Fig. 11a was evaluated numerically along the $\tau$-axis. Profiles of the intensity at the $\tau$ values of first two maxima and minima listed in Table 1 are presented in Fig. 12a. A visual inspection finds clear similarities with the profiles of Fig. 3b. However, when we mark the positions of these maxima and minima in the second derivative of the intensity, denoted by $\beta _{-}^{\mathrm{RS}}(\tau )$ and presented in Fig. 12b, an increasing deviation is perceived along the inverse coordinate ($1/\tau$) between the actual maxima and minima and the corresponding values of Table 1. For instance, the curvature at $\chi = 0$ of the last profile in Fig. 12a (plotted in magenta) is in contrast to the nonzero curvature of the blue profile. The deviation is explained by the fact that intensity patterns of the Rayleigh-Sommerfeld diffraction present always a finite number of lobes, and thus bright or dark focus regions. By contrast, in the Fresnel diffraction the number of lobes, either of maxima, or minima increases to infinity as one approaches the slit.

The results of the intensity pattern for different values of $\phi _{0}$ are presented in Fig. 13. There are two cases where the intensity pattern presents a mirror symmetry along the propagation axis. For $\phi _{0} = \pi /2$ the phase difference between the left and the right half of the field at the slit is $\Delta \phi = \pi$. The intensity pattern is divided into two separated bright regions. If the phase difference is $\Delta \phi = 2n\pi$, with n integer, the field intensity corresponds exactly to that of the classical diffraction pattern associated with the bright focusing. For intermediate values of the phase jump, either $0<\phi _{0}<\pi /2$, or $\pi /2<\phi _{0}<\pi$ the intensity pattern becomes asymmetric along the z-axis (see Fig. 13). This property can be exploited in light beam steering close to the slit. The same phase difference applied to matter wave packets would also produce an asymmetry in the time evolution of the spreading packet.

Fig. 11

Antisymmetric phase slit with (a) a phase jump of $\Delta \phi = \pi$. The phase function is the shifted and scaled Haar wavelet. The intensity (b), intensity along the symmetry axis (c), in logarithmic scale and phase (d) of the diffraction pattern for a slit of width $W = 12\lambda$. The on-axis intensity presents a small but non-zero oscillatory behavior along z (c). Based on the symmetry properties of the first RS integral, the antisymmetric slit should produce a zero value on the symmetry axis, as for the Fresnel integral. Thus, we attribute this deviation to numerical errors in the quadrature calculation

Fig. 12

Intensity profiles (a) and second derivative of the intensity along the symmetry axis (b) of scalar waves diffracted by a slit, calculated using the Rayleigh-Sommerfeld diffraction theory. The second derivative of the Rayleigh-Sommerfeld intensity, denoted by $\beta _{-}^{\mathrm{RS}}(\tau )$ along the symmetry axis (b), was calculated numerically from the same data set used in Fig. 11. Intensity profiles corresponding to 5 different values of $1/\tau$ are plotted in (a) (with colors orange, green, red, blue and magenta). The first 4 profiles correspond to the first two values $\tau ^-_{\mathrm{\max ,k}}$ and $\tau ^-_{\mathrm{\min ,k}}$ of $\beta _{-}(\tau )$ in Table 1 with $k=1,2$. The last profile (magenta) corresponds to the second minimum of $\beta _{-}^{\mathrm{RS}}(\tau )$, located at $\tau \approx 0.0555$ and marked by a solid vertical line of the same color in (b). The positions of the other 4 profiles are marked in (b) by vertical dashed lines. Whereas the first maximum and the first minimum of the curvature $\beta _{-}^{\mathrm{RS}}(\tau )$ of the intensity, corresponding to the farthest dark focal region, match well with the values of Table 1, the positions of the following maxima and minima deviate considerably

Fig. 13

Field intensity maps as function of phase constant $\phi _{0}$. The phase difference between the left and the right side of the slit is $\Delta \phi = 2\phi _{0}$. Non-integer values of $\Delta \phi /\pi$ lead to asymmetric intensity patterns along the symmetry axis. For $\phi _{0} = \pi /2$ and $\phi _{0} = \pi$ there is symmetry. These cases correspond to dark and bright focusing patterns, respectively

5.2 Slits with symmetric and antisymmetric linear phase profile: analogy with the Bessel beam

There are other ways to produce an apparent splitting in the intensity diffraction pattern, by defining other initial wave functions. The Haar phase profile is the most simple one. However, if we impose a phase difference of $\pi$ between the right and the left side of the field in the slit, the resulting diffraction pattern also presents dark focusing, for phase profiles with linear dependence on x. We discuss first the case of a symmetric linear phase profile, that is, the phase slit has a triangular shape. We define a slit centered at $x = 0$ with the phase defined as a linear function of $\xi$, but with symmetric and constant gradient. The maximum phase value is in the center ($x = 0$) and denoted by $\phi _{0}$. The phase at the boundaries of the slit is 0. We must emphasize that a one-dimensional wave function with a phase linearly dependent on the coordinate x and constant gradient corresponds to a wave packet with momentum. For classical waves, the linear phase dependence is equivalent to a refraction. Thus, with a triangular phase the left wave packet has a positive and the right one has a negative momentum. The diffraction in space of both sides of the wave function is equivalent to the collision of two wave packets in time.

The triangular phase profile is the one-dimensional analogue of the axicon prism used to generate Bessel beams [8]. The field at the slit is composed of two waves with constant amplitude evolving in space with opposite propagation direction. The result is a narrow field profile along the z-direction, similar to the Bessel beams field profile, despite being only one-dimensional (Fig. 14a). An increasing value of $\phi _{0}$ leads to a tighter focusing, increasing the intensity maximum.

When the right and the left sides of the initial wave are dephased by $\pi$ (Fig. 15), the evolving intensity pattern splits into two well-separated bright branches and a central dark region where dark focusing arises. The intensity pattern is similar to that of the Haar phase function. However, the distance of the region where the dark focusing occurs with regard to $z = 0$ differs. When the peak phase $\phi _{0}$ increases, the focusing is faster and the distance to $z = 0$ decreases (see Fig. 15b–e).

Fig. 14

Slit with (a) constant amplitude and symmetric triangular phase profile. $\phi _{0}$ is the maximum of profile. Intensity maps (b)–(e), for phase slits with various values of $\phi _{0}$. The degree of focusing increases with $\phi _{0}$. The triangular phase profile is the 2D analog of the axicon. For large slits the transverse intensity profile approaches that of the Bessel beam and the focal region extends along the z-axis

Fig. 15

Slit with (a) asymmetric phase profiles. The left linear segment of a symmetric triangular profile is shifted by $\pi$ resulting into an asymmetric function. Intensity maps (b)–(e), for various slits with asymmetric triangular profile. The phase difference at $x=0$ is $\Delta \phi = \pi$. A dark region is formed close to $z\lambda /W^{2} \approx 0.1$ in the symmetry axis. This region moves down with increasing $\phi _{0}$. A requirement for this effect is a phase jump of $\pi$ between both slit sides

A further example of the impact of the phase function on the intensity maps is presented in Fig. 16. This corresponds to the two-dimensional version of a divergent axicon, where the middle point of the slit has a phase minimum. Thus, the triangular phase profile points downwards. This wave function leads to divergent waves in the diffraction pattern, as the half left and the half right plane waves have initial momenta pointing in opposite direction. This is especially evident if the phase maximum $\phi _{0}$ has a large value, or equivalently, the gradient increases (see Fig. 16 b–d).

Fig. 16

Phase slit with (a) symmetric and linear phase function. Intensity maps (b)–(d) for various slits. This type of phase function leads to divergent waves. It is the 2D analogue of the divergent axicon. In this example the maximum for $\phi _{0}$ is $\pi$. The increasing gradient of the linear phase determined by the constant $\phi _{0}$ leads to waves with increasingly divergent intensity

We can conclude that the dark focusing can occur not only for phase slits with Haar phase profile, but also in antisymmetric phase slits with a phase jump of $\pi$. Moreover, symmetric phase slits with divergent triangular profile also produce a dark region in the center of the intensity diffraction pattern. Though, this requires large gradients of the linear phase function.

6 Conclusions and outlook

To the best of our knowledge, we have investigated for the first time the dark focusing of matter, water, and classical waves. We have established a quantitative measure for the definition of bright and dark foci and have analysed the mathematical properties of these closely related features.

For this purpose, we have made use of phase slits of rectangular shape without and with phase jump of $\pi$ at the center, the latter corresponding to the Haar wavelet. We have compared the localization of intensity maxima and minima and the corresponding hill and valley widths which emerge during free propagation. Moreover, we have analyzed and illustrated the emergence of bright and dark foci in Wigner phase space.

Our theoretical studies were complemented by an experimental observation of dark foci in the propagation of surface gravity water waves. Moreover, we have shown that dark focusing is not only a feature of real-valued wave functions, but also appears for other wave functions. In particular, we have studied the diffraction of classical waves from antisymmetric phase slits with a linear dependence on the transverse coordinate and a phase difference of $\pi$ between the half left and half right.

Dark focusing is not only the low-intensity counterpart of the bright focusing, rather it has its own characteristics. For instance, it emerges at different locations of the propagation coordinate than the bright focusing and is connected to minimal valley widths. We note that dark focusing not only arises for antisymmetric, but also for symmetric wave packets. However, due to the vanishing intensity at the center, the dark focusing is more prominent in the first case.

In addition, we have demonstrated that also defocusing can occur which leads to broad dark regions. Interestingly, this phenomenon is connected to a very particular power law which governs the dependence of the intensity on the transverse coordinate.

In order to obtain a deeper insight into these focusing effects, we have made use of Wigner phase space. In our analysis, we have revealed the intimidate connection between a freely propagating wave packet with and without a phase jump at its center. In fact, both situation only differ by the sign in front of the interference term contributing to the Wigner function. We have shown, that it is the absence or presence of negative contributions to the Wigner function close to the center of the transverse coordinate which result in a bright or a dark focus. Indeed, the free time evolution of the Wigner function corresponds to a shearing of phase space. As a result, at very particular times negative contributions to the Wigner function play a more dominant role in the central region and give raise to these diffraction phenomena.

Experimental measurements of surface gravity water waves generated in a water tank verify our theoretical predictions. With the help of an antisymmetric slit in time, we have indeed observed the emergence of a dark focus. Moreover, we have demonstrated the particular power law that is connected with defocusing and the broad dark regions that show up in the propagation of this particular wave profile. Our results indicate that the dark focusing as well as the bright focusing are universal phenomena in classical and quantum physics for wave functions of constant amplitude.

The extension of the diffraction of scalar waves, characterized by a rectangular antisymmetric profile, to phase slits with intermediate values of the phase between 0 and $2\pi$ allows us to understand how the value of the phase difference influences the symmetry of the diffraction pattern and how the transition between bright and dark focusing occurs.

When the initial wave function has a constant amplitude, but the phase profile is linear and not piecewise constant, other diffractive effects arise. When the phase profile is an isosceles triangle, with the maximum in the middle point of the coordinate axis, the bright diffractive focusing is boosted along the propagation axis. The maximum in the intensity pattern also increases with an increasing value of the phase maximum. On the other hand, the point of highest intensity approaches the origin of diffraction. Moreover, the diffraction pattern of a triangular phase slit corresponds to the 2D analog of the 3D field intensity generated by an axicon. In the case where the middle point of the slit has a phase minimum, the diffraction pattern becomes increasingly divergent with increasing gradient of the phase profile.

These results are of relevance in many fields of physics where wave packets evolve freely in space. Then the dark focusing manifests itself most prominently for wave packets that have initially an antisymmetric profile. In particular, the dark focusing of classical waves can be exploited in the Talbot effect of one-dimensional gratings and Fresnel phase zone plates.

In this article, we have limited our analysis to wave functions with only two segments, either symmetric, or antisymmetric. The extension to wave functions that display repeated profile segments and are generated by finite periodic phase slits may be explored in the context of the Talbot effect. In most cases, the Talbot effect is studied by using one-dimensional amplitude slits. Here phase slits introduce an additional degree of freedom. Recently, it has been demonstrated by calculations and experiments that a plasmonic wave can be guided using a periodic array of slits in the propagation direction [16]. However, beyond amplitude slits, the effects introduced by phase slits remain to be investigated. Moreover, non-periodic multilayer slits have been used to focus electromagnetic waves of short wavelength (X-rays and extreme UV) in one dimension [34]. These gratings are a special version of the Fresnel zone plates called Multilayer Laue Lens [35]. A phase slit where the phase segments are adequately tailored could as well be used as a one-dimensional focusing lens.

Appendix A: Appearance of bright and dark foci

In this Appendix, we determine the times at which bright foci, dark foci, and defocusing occurs for the freely-propagating wave packet $\Psi _\pm (\chi ,\tau )$, Eq. (13), originating from a rectangular profile ($+$) without and (−) with phase shift of $\pi$ at the center $\chi =0$.

For this purpose, we recall the wave packet $\Phi _\pm (\chi ,\tau )$ which originates at time $\tau =0$ from a rectangular slit located between the dimensionless coordinates $\chi =0$ and $\chi =(-1)^\nu /2$ with $\nu =1,2$. According to Eq. (11), the propagated wave packet takes the form

$$\begin{aligned} \Phi _\nu (\chi ,\tau )=&\frac{(-1)^{\nu }}{\sqrt{\mathrm {i}}} \left\{ F\left( \sqrt{\frac{\pi }{\tau }}\chi \right) \right. \nonumber \\&\left. -F\left[ \sqrt{\frac{\pi }{\tau }}\left( \chi -\frac{(-1)^\nu }{2} \right) \right] \right\} . \end{aligned}$$

(41)

The behavior of $\Phi _\nu (\chi ,\tau )$ close to $\chi =0$ is governed by the first and second partial derivative with regard to $\chi$. Indeed, making use of the explicit form of the Fresnel integral F(w), Eq. (12), yields the first partial derivative

$$\begin{aligned} \Phi _{\nu ,\chi }(\chi ,\tau )=&(-1)^{\nu }\sqrt{\frac{2}{\mathrm {i}\tau }}\nonumber \\&\times \left\{ \mathrm {e}^{\frac{\mathrm {i}\pi }{\tau }\chi ^2}-\mathrm {e}^{\frac{\mathrm {i}\pi }{\tau }\left[ \chi -\frac{(-1)^\nu }{2}\right] ^2}\right\} \end{aligned}$$

(42)

with regard to $\chi$. Moreover, the second partial derivative with regard to $\chi$ reads

$$\begin{aligned}&\Phi _{\nu ,\chi \chi }(\chi ,\tau )=\left( -1\right) ^{\nu }\sqrt{\frac{2}{\mathrm {i}\tau }}\frac{2\mathrm {i}\pi }{\tau }\nonumber \\&\quad \times \left\{ \chi \mathrm {e}^{\frac{\mathrm {i}\pi }{\tau }\chi ^2} -\left( \chi - \frac{(-1)^\nu }{2}\right) \mathrm {e}^{\frac{\mathrm {i}\pi }{\tau }\left[ \chi - \frac{(-1)^\nu }{2}\right] ^2}\right\} . \end{aligned}$$

(43)

By making use of the definition

$$\begin{aligned} \Psi _\pm (\chi ,\tau )=\frac{1}{\sqrt{2}}\left[ \Phi _1(\chi ,\tau )\pm \Phi _2(\chi ,\tau )\right] , \end{aligned}$$

(44)

Eq. (13), we are now in the position to analyze the properties of the wave packet $\Psi _\pm (\chi ,\tau )$ close to the central position $\chi =0$.

First, according to Eq. (41) we obtain the values

$$\begin{aligned} \Psi _+(0,\tau )=\sqrt{\frac{2}{\mathrm {i}}}F\left( \sqrt{\frac{\pi }{4\tau }}\right) \end{aligned}$$

(45)

and

$$\begin{aligned} \Psi _-(0,\tau )=0 \end{aligned}$$

(46)

at the center $\chi =0$ as a function of the time $\tau$. Here we have made use of the antisymmetry $F(-w)=-F(w)$ of the Fresnel integral defined by Eq. (12).

Second, the first derivatives

$$\begin{aligned} \Psi _{+,\chi }(0,\tau )=0 \end{aligned}$$

(47)

and

$$\begin{aligned} \Psi _{-,\chi }(0,\tau )=-\frac{2}{\sqrt{\mathrm {i}\tau }}\left( 1-\mathrm {e}^{\frac{\mathrm {i}\pi }{4\tau }}\right) \end{aligned}$$

(48)

with regard to $\chi$ at $\chi =0$ result from Eqs. (42) and (44).

Third, according to Eqs. (44) and (43) the second derivatives of $\Psi _\pm (\chi ,\tau )$ with regard to $\chi$ read

$$\begin{aligned} \Psi _{+,\chi \chi }(0,\tau )=\frac{2\mathrm {i}\pi }{\tau }\sqrt{\frac{1}{\mathrm {i}\tau }}\mathrm {e}^{\frac{\mathrm {i}\pi }{4\tau }} \end{aligned}$$

(49)

and

$$\begin{aligned} \Psi _{-,\chi \chi }(0,\tau )=0 \end{aligned}$$

(50)

at $\chi =0$.

As demonstrated in the following, Eqs. (45)–(50) allow us to determine the times at which bright foci, dark foci, and defocusing appears for the probability density $\left| \Psi _\pm (\chi ,\tau )\right| ^2$ close to the symmetry axis $\chi =0$.

1.1 Slit with constant amplitude and phase

First, we study the appearance of these features during the propagation of the wave packet $\Psi _+(\chi ,\tau )$, Eq. (44), originating from a rectangular slit with constant amplitude and phase.

According to Eq. (15), the probability density

$$\begin{aligned} \left| \Psi _+(\chi ,\tau )\right| ^2\simeq \alpha _+(\tau )+\frac{1}{2}\beta _+(\tau ) \end{aligned}$$

(51)

displays a parabolic dependence for $\left| \chi \right| \ll 1$. Here the offset of the parabola

$$\begin{aligned} \alpha _+(\tau )=2\left| F\left( \sqrt{\frac{\pi }{4\tau }}\right) \right| ^2, \end{aligned}$$

(52)

as expressed in terms of the Fresnel integral F(w), Eq. (12), can be obtained with the help of Eqs. (16) and (45).

Moreover, according to Eqs. (17) and (47), the curvature of the parabola

$$\begin{aligned} \beta _+(\tau )=2\mathrm {Re}\left[ \Psi ^*_{+,\chi \chi }(0,\tau ) \Psi _+(0,\tau )\right] . \end{aligned}$$

(53)

is determined by the value $\Psi _+(0,\tau )$ and the complex conjugate of the second partial derivative $\Psi ^*_{+,\chi \chi }(0,\tau )$ at $\chi =0$. By inserting Eqs. (45) and (49) and making use of the explicit form of the Fresnel integral F(w) given by Eq. (12), we express Eq. (53) as

$$\begin{aligned} \beta _+(\tau )=\frac{8\pi }{\tau \sqrt{\pi \tau }}\int _{0}^{\sqrt{\frac{\pi }{4\tau }}}\mathrm {d}\xi \, \sin \left( \xi ^2-\frac{\pi }{4\tau }\right) . \end{aligned}$$

(54)

In order to determine the times $\tau _{\mathrm {min},k}^+$ and $\tau _{\mathrm {max},k}^+$ at which bright and dark foci appear, we calculate according to Sect. 3.1 the minima and maxima of the function $\beta _+(\tau )$, Eq. (54). Our numerical results are enumerated by the index $k=1,2,\ldots$ and presented in Table 1. Moreover, we note that defocusing occurs at the zeroes of $\beta _+(\tau )$.

Next, we derive approximate analytical expressions for $\tau _{\mathrm {min},k}^+$ and $\tau _{\mathrm {max},k}^+$ which are valid for small times $\tau \ll 1$. For this purpose, we recast Eq. (54) in the form

$$\begin{aligned} \beta _+(\tau )=&\frac{8\pi }{\tau \sqrt{\pi \tau }}\left[ \cos \left( \frac{\pi }{4\tau }\right) \int _{0}^{\sqrt{\frac{\pi }{4\tau }}}\mathrm {d}\xi \, \sin \left( \xi ^2\right) \right. \nonumber \\&\left. -\sin \left( \frac{\pi }{4\tau }\right) \int _{0}^{\sqrt{\frac{\pi }{4\tau }}}\mathrm {d}\xi \, \cos \left( \xi ^2\right) \right] . \end{aligned}$$

(55)

In the domain $\tau \ll 1$ we can approximate the Fresnel integrals

$$\begin{aligned} \int _{0}^{\sqrt{\frac{\pi }{4\tau }}}\mathrm {d}\xi \,\sin \left( \xi ^2\right) \simeq \int _{0}^{\infty }\mathrm {d}\xi \,\sin \left( \xi ^2\right) =\sqrt{\frac{\pi }{8}} \end{aligned}$$

(56)

and

$$\begin{aligned} \int _{0}^{\sqrt{\frac{\pi }{4\tau }}}\mathrm {d}\xi \,\cos \left( \xi ^2\right) \simeq \int _{0}^{\infty }\mathrm {d}\xi \,\cos \left( \xi ^2\right) =\sqrt{\frac{\pi }{8}} \end{aligned}$$

(57)

in Eq. (55) by using infinity as the upper bound of integration. Inserting Eqs. (56) and (57) then yields the approximation

$$\begin{aligned} \beta _+(\tau )\simeq \frac{2\pi }{\tau }\sqrt{\frac{2}{\tau }}\left[ \cos \left( \frac{\pi }{4\tau }\right) -\sin \left( \frac{\pi }{4\tau }\right) \right] , \end{aligned}$$

(58)

or, equivalently,

$$\begin{aligned} \beta _+(\tau )\simeq \frac{4\pi }{\tau \sqrt{\tau }}\cos \left( \frac{\pi }{4\tau }+\frac{\pi }{4}\right) . \end{aligned}$$

(59)

For small values $\tau \ll 1$, the location of the maxima and minima of $\beta _+(\tau )$ approximately corresponds to those of the cosine in Eq. (58). Accordingly, we obtain with $k=1,2,\ldots$ the approximate expressions

$$\begin{aligned} \tau _{\mathrm {min},k}^+\simeq \frac{1}{8k-5} \end{aligned}$$

(60)

for the minima, and

$$\begin{aligned} \tau _{\mathrm {max},k}^+\simeq \frac{1}{8k-1} \end{aligned}$$

(61)

for the maxima of $\beta _+(\tau )$, Eq. (53), valid for small times, that is for $k\gg 1$. Here $\tau _{\mathrm {min},k}^+$ denotes the time of a bright focus and $\tau _{\mathrm {max},k}^+$ the one of a dark focus, being located at $\chi =0$ and emerging during the free propagation of the wave function $\Psi _+(\chi ,\tau )$, Eq. (44), originating from a rectangular slit.

1.2 Slit with constant amplitude and $\pi$-phase jump

Next, we perform an analogous analysis for the freely-evolving wave packet $\Psi _-(\chi ,\tau )$, Eq. (44), emerging from a slit with constant amplitude and a $\pi$-phase jump at $\chi =0$. Also here we make use of a quadratic approximation of $\left| \Psi _-(\chi ,\tau )\right| ^2$ close to the symmetry axis $\chi =0$. According to Eqs. (16) and (47), the offset of the parabola

$$\begin{aligned} \alpha _-(\tau )=0 \end{aligned}$$

(62)

for all times $\tau$ due to the antisymmetry of the wave function $\Psi _-(\chi ,\tau )$ with regard to $\chi$.

By making use of Eqs. (46) and (50), we can show that the curvature of the parabola

$$\begin{aligned} \beta _-(\tau )=2 \left| \Psi _{-,\chi }(0,\tau )\right| ^2, \end{aligned}$$

(63)

Eq. (17), is only determined by the first derivative of the function $\Psi _{-}(\chi ,\tau )$ with regard to $\chi$. By inserting Eq. (48) into Eq. (63), we arrive at the exact expression

$$\begin{aligned} \beta _-(\tau )=\frac{16}{\tau }\left[ 1-\cos \left( \frac{\pi }{4\tau }\right) \right] \end{aligned}$$

(64)

or, equivalently,

$$\begin{aligned} \beta _-(\tau )=\frac{32}{\tau }\sin ^2\left( \frac{\pi }{8\tau }\right) . \end{aligned}$$

(65)

According to Sect. 3.1, the times at which bright and dark foci occur are governed by the minima and maxima of the function $\beta _-(\tau )$, Eq. (65). First, we emphasize that $\beta _-(\tau )\ge 0$ for $\tau >0$. Thus, minima of $\beta _-(\tau )$ are assumed at the times

$$\begin{aligned} \tau _{\mathrm {min},k}^-=\frac{1}{8 k} \end{aligned}$$

(66)

with $k=1,2,\ldots$, where $\beta _-(\tau _{\mathrm {min},k}^-)=0$. For this reason, there are no bright foci during the propagation of the wave packet $\Psi _-(\chi ,\tau )$. Instead, according to Sect. 3.1, defocusing occurs at $\tau =\tau _{\mathrm {min},k}^-$.

On the other hand, we numerically determine the times $\tau =\tau _{\mathrm {max},k}^-$ when the function $\beta _-(\tau )$, Eq. (65), displays local maxima. We present the corresponding values in Table 1. Since $\beta _-(\tau _{\mathrm {max},k}^-)>0$, the time $\tau =\tau _{\mathrm {max},k}^-$ indicates the emergence of a dark focus.

In addition, for small times $\tau \ll 1$ we find an approximate analytical expression at which a maximum of $\beta _-(\tau )$ occurs. Indeed, the maximum of the sine function in Eq. (65) emerges at

$$\begin{aligned} \tau _{\mathrm {max},k}^-\approx \frac{1}{8 k-4}, \end{aligned}$$

(67)

where $k=1,2,\ldots$. For $k\gg 1$, Eq. (67) provides a good estimation of the time at which a dark focus appears as demonstrated in Table 1.