Flexible control of laser transverse modes using a Fox-Smith mirror

Abstract

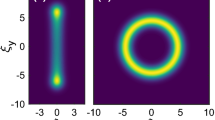
The Fox-Smith mirror (FSM) has long been used in a three-mirror laser cavity arrangement for forcing the laser oscillation on a single-longitudinal mode. However, its transverse properties are very little studied, and we report three interesting transverse features. First, the FSM gives the possibility to change the order p of the oscillating radial Laguerre–Gaussian LG_p0 mode by adjusting the microscopic position of one of its mirrors. These results help for understanding non-interpreted experimental observations of interferometric control of the oscillating transverse mode reported by Smith in 1965. Second, we have shown that otherwise values of FSM parameters allow an equal FSM reflectivity of LG₀₀ and LG₀₁ (doughnut) modes. This would in effect give, to a laser using a FSM as rear mirror, a simultaneous oscillation of these two transverse modes giving rise to a shape-invariant flat-top laser beam. The latter having the interesting property to keep its uniform transverse intensity profile as it propagates inside and outside the laser cavity. Third, we have shown that the beam emerging from the FSM output through its beam splitter can be an Optical Bottle Beam by an adequate choice of parameters.

Appendix: Reflectivity and transmission of the Fox-Smith mirror for plane waves

We will present in this Appendix an elegant method for calculating the reflectivity $R_{{{\text{FS}}}}$ and the transmission $T_{{{\text{FS}}}}$ of the Fox-Smith mirror which can be called as round-trip method. The latter does not need to sum up all the different reflected waves so forming a geometric series such as in Fabry–Pérot interferometer calculations [13, 15]. The Fox-Smith mirror shown in Figs.

Fig. 12

Fox-Smith mirror showing the incident field $E^{{\text{I}}}$, the reflected field $E^{{\text{R}}}$, the internal field E(t) before and E(t + Δt) after a round-trip between mirrors M₁ and M₂. with $\Delta t = 2(d_{1} + d_{2} )/c$

12 and

Fig. 13

Fox-Smith mirror showing the incident field $E^{{\text{I}}}$, the transmitted field $E^{{\text{T}}}$, the internal field E(t) given by Eq. (14)

13 has one input port (field $E^{{\text{I}}}$) and two output ports (fields $E^{{\text{R}}}$ and $E^{{\text{T}}}$).

Let us consider a plane wave characterised by the electric field $E^{{\text{I}}}$ incident on the Fox-Smith mirror, and let $E^{{\text{R}}}$ the electrical field associated with the reflected waves (Fig. 12).

The beam splitter (BS) split the input plane wave into a proportion (in intensity) K in the reflection and (1−K) in its transmission, respectively. Consequently, the reflectance r and the transmittance $\tau$ (ratio of amplitudes) of the beam splitter are given by $r = \sqrt K$ and $\tau = \sqrt {1 - K}$. Taking into account the phase shift (Fig. 2) introduced by the beam splitter we can write that the field E(t + Δt) after a round-trip inside the FS mirror as follows:

$$ E(t + \Delta t) = \left( {e^{i\pi /2} } \right)^{2} E(t)r^{2} e^{ - i\varphi } + \tau E^{I} , $$

(13)

where $\varphi = 2k(d_{1} + d_{2} )$ and $\Delta t = 2(d_{1} + d_{2} )/c$.

Equation (13) involves the dynamic of the electrical field over a round-trip inside the Fox-Smith mirror. The steady-state is defined by $E(t + \Delta t) = E(t)$, and allows to express the field E(t) as follows:

$$ E = \frac{{\tau E^{{\text{I}}} }}{{1 + r^{2} e^{ - i\varphi } }}. $$

(14)

1.1 Reflectivity of the Fox-Smith mirror

The reflected field $E^{{\text{R}}}$ corresponds to the field E having made a round-trip between the beam splitter and mirror M₁, transmitted through BS, namely:

$$ E^{{\text{R}}} = \tau Ee^{{ - i2kd_{1} }} . $$

(15)

By combining Eqs. 14 and 15 we obtain the reflectance $r_{{{\text{FS}}}}$ of the Fox-Smith mirror:

$$ r_{{{\text{FS}}}} = \frac{{E^{{\text{R}}} }}{{E^{{\text{I}}} }} = \frac{{(1 - K)e^{{ - i2kd_{1} }} }}{{1 + Ke^{ - i\varphi } }}. $$

(16)

Finally, the reflectivity $R_{{{\text{FS}}}} = r_{{{\text{FS}}}} \times r_{{{\text{FS}}}}^{*}$ of the Fox-Smith mirror enlighten by plane waves is written as follows

$$ R_{{{\text{FS}}}} = \frac{{(1 - K)^{2} }}{{1 + K^{2} + 2K\cos (\varphi )}} = \frac{{(1 - K)^{2} }}{{(1 - K)^{2} + 2K[1 + \cos (\varphi )]}} $$

Finally by setting $F = 4K/(1 - K)^{2}$ we obtain

$$ R_{{{\text{FS}}}} { = }\frac{1}{{1 + F\cos^{2} \left( {\frac{\varphi }{2}} \right)}} $$

(17)

1.2 Transmission of the Fox-Smith mirror

Figure 13 shows the different quantity for calculating the transmitted field $E^{T}$ for reference purpose. The field $E_{1}$ shown in Fig. 13 corresponds to the field E having travelled the distance $(2d_{1} + 2d_{2} )$ and undergoing a reflection on the beam splitter.

As a consequence, one can write:

$$ E_{1} = Ee^{{ - i2kd_{1} }} re^{i\pi /2} e^{{ - i2kd_{2} }} = irEe^{ - i\varphi } $$

(18)

Then the transmitted field $E^{{\text{T}}}$ can be expressed as follows:

$$ E^{{\text{T}}} = re^{i\pi /2} E^{{\text{I}}} + \tau E_{1} = iE^{{\text{I}}} \left[ {r + \frac{{\tau^{2} re^{ - i\varphi } }}{{1 + r^{2} e^{ - i\varphi } }}} \right]. $$

(19)

Finally from the transmittance $t_{{{\text{FS}}}} = E^{{\text{T}}} /E^{{\text{I}}}$, we express the transmission $T_{{{\text{FS}}}} = t_{{{\text{FS}}}} \times t_{{{\text{FS}}}}^{*}$ (ratio of intensities):

$$ T_{{{\text{FS}}}} = (i)\left[ {r + \frac{{\tau^{2} re^{ - i\varphi } }}{{1 + r^{2} e^{ - i\varphi } }}} \right] \times ( - i)\left[ {r + \frac{{\tau^{2} re^{ + i\varphi } }}{{1 + r^{2} e^{ + i\varphi } }}} \right], $$

$$ T_{{{\text{FS}}}} = r^{2} \left[ {\frac{{1 + (r^{2} + \tau^{2} )e^{ - i\varphi } }}{{1 + r^{2} e^{ - i\varphi } }}} \right] \times \left[ {\frac{{1 + (r^{2} + \tau^{2} )e^{ + i\varphi } }}{{1 + r^{2} e^{ + i\varphi } }}} \right]. $$

Since $\left( {r^{2} + \tau^{2} } \right) = 1$, then we obtain:

$$ T_{{{\text{FS}}}} = \frac{{2r^{2} [1 + \cos (\varphi )]}}{{1 + r^{4} + 2r^{2} \cos (\varphi )]}}. $$

(20)

By adding $\left( {2r^{2} - 2r^{2} } \right)$ to the denominator of Eq. (20), and taking into account the definition of parameter F, we finally obtain:

$$ T_{{{\text{FS}}}} = \frac{{F\cos^{2} (\varphi /2)}}{{1 + F\cos^{2} (\varphi /2)}}. $$

(21)

Note that we find obviously $\left( {R_{{{\text{FS}}}} + T_{{{\text{FS}}}} } \right) = 1$.