Negative resonant modes in a hyperbolic metamaterial slot cavity

Abstract

We show that negative resonant modes with an inverse relationship between the wavelength and the cavity length can be excited in a hyperbolic metamaterial slot cavity (HMMSC) in addition to positive resonant modes. The observed negative resonant modes in an HMMSC are in sharp contrast to that observed in a metal slot cavity. We analyze the dynamics of the excited negative resonant modes in the visible spectrum regime as HMMSC parameters vary.

Appendix

We derive the dispersion relation by calculating the transfer matrix for each of the interfaces of the layered HMMs. Transfer matrix for a dielectric–HMM interface is given by:

$$\begin{aligned} \begin{array}{l} {\mathrm {M} _{\mathrm{H},\mathrm{d}}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{\mathrm{M} _{11} }} & {} {{\mathrm{M} _{12} }}\\ {{\mathrm{M} _{21} }} & {} {{\mathrm{M} _{22}}} \end{array}} \right] ,\\ \\ {\mathrm {M} _{11}} = \frac{{{k} _{x}^{2} }}{{{k}_{0}^{2}}} + \frac{{{\varepsilon} _{y} {k} _{y}^{2} }}{{{\varepsilon} _{x} {k} _{0}^{2} }} - i\frac{{{\varepsilon} _{y} {k} _{y} }}{{{\varepsilon} _{x} {\kappa} _{d} }}, {\mathrm{M} _{11} = \mathrm{M} _{22}} ,\\ {\mathrm{M} _{12}} = \frac{{{k} _{x}^{2} }}{{{k}_{0}^{2}}} + \frac{{{\varepsilon} _{y} {k} _{y}^{2} }}{{{\varepsilon} _{x} {k} _{0}^{2} }} + i\frac{{{\varepsilon} _{y} {k} _{y} }}{{{\varepsilon} _{x} {\kappa} _{d} }}, {\mathrm{M} _{12} = \mathrm{M} _{21}} , \end{array} \end{aligned}$$

(3)

and for HMM–dielectric interface is given by

$$\begin{aligned} \begin{array}{l} { \mathrm{N} _{\mathrm{d},\mathrm{H}}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{ \mathrm{N} _{11} }} & {}{{ \mathrm{N} _{12} }}\\ {{ \mathrm{N} _{21} }} & {}{{ \mathrm{N} _{22} }} \end{array}} \right] ,\\ \\ { \mathrm {N} _{11}} = {\left( {\frac{{{k} _{x}^{2} }}{{{k}_{0}^{2}}} + \frac{{{\varepsilon} _{y} {k} _{y}^{2} }}{{{\varepsilon} _{x} {k} _{0}^{2} }}} \right) } ^{ - 1} + {i}\frac{{{\varepsilon} _{x} {\kappa} _{d} }}{{{\varepsilon} _{y} {k} _{y} }}, { \mathrm{N} _{11} = \mathrm{N} _{22} },\\ { \mathrm{N} _{12}} = {\left( {\frac{{{k} _{x}^{2} }}{{{k}_{0}^{2}}} + \frac{{{\varepsilon} _{y} {k} _{y}^{2} }}{{{\varepsilon} _{x} {k} _{0}^{2} }}} \right) } ^{ - 1} - {i}\frac{{{\varepsilon} _{x} {\kappa} _{d} }}{{{\varepsilon} _{y} {k} _{y} }}, { \mathrm{N} _{12} = \mathrm{N} _{21} }. \end{array} \end{aligned}$$

(4)

In Eqs. (3) and (4), ${k}_{y}$ is the y-component of wavevector inside HMM and ${\kappa} _{d}$ is the wavevector inside dielectric host, which are related by equations

$$\begin{aligned} \begin{array}{l} {\kappa} _{d} = \sqrt{{k} _{x}^{2} - {\varepsilon }_{dh} {k} _{0}^{2} } ,\\ \frac{{{k} _{x}^{2} }}{{{\varepsilon} _{y} }} + \frac{{{k} _{y}^{2} }}{{{\varepsilon} _{x} }} = {k} _{0}^{2} , \end{array} \end{aligned}$$

(5)

where ${\varepsilon }_{dh}$ is the dielectric constant of host matrix. Transfer matrices for propagation through an HMM and dielectric of lengths t and g, respectively, become

$$\begin{aligned} \begin{array}{l} {\mathrm {D} _\mathrm {H}} = \left[ {\begin{array}{*{20}{c}} {{e} ^{ - i{k} _{y} t} } & {}0\\ 0 & {}{{e} ^{i{k} _{y} t} } \end{array}} \right] ,~~~ {\mathrm {D} _\mathrm {d}} = \left[ {\begin{array}{*{20}{c}} {{e} ^{{\kappa} _{d} g} } & {}0\\ 0 & {}{{e} ^{ { - \kappa } _{d} g} } \end{array}} \right] . \end{array} \end{aligned}$$

(6)

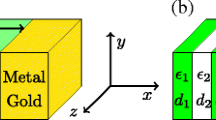
Thus the overall transfer matrix for the HMM slot cavity shown in Fig. 1a is

$$\begin{aligned} \begin{array}{l} \mathrm {S }= \left[ {\begin{array}{*{20}{c}} {{\mathrm{S} _{11}} } & {}{{\mathrm{S} _{12} }}\\ {{\mathrm{S} _{21}} } & {}{{\mathrm{S} _{22} }} \end{array}} \right] ,\\ \quad = {\mathrm{N} _{\mathrm{d},\mathrm{H}} \mathrm{D} _\mathrm{H} \mathrm{M} _{\mathrm{H},\mathrm{d}} \mathrm{D} _\mathrm{d} \mathrm{N} _{\mathrm{d},\mathrm{H}} \mathrm{D} _\mathrm{H} \mathrm{M} _{\mathrm{H},\mathrm{d}}}. \end{array} \end{aligned}$$

(7)

The quantities M, N, and D are found from Eqs. (3), (4), and (6), respectively. Now, applying the boundary condition [13]

$$\begin{aligned} {\mathrm {S}_{11} = 0}, \end{aligned}$$

(8)

and solving for ${k}_{x}$ and ${k}_{y}$, the mode index is determined for particular set of parameter values, i.e., g, ${\varepsilon} _{x}$, ${\varepsilon} _{y}$, and ${\varepsilon} _{dh}$ at a desired wavelength.