1 Introduction

While higher order transverse modes are often suppressed in lasers to obtain a pure fundamental output beam, they have become of increasing interest over the past few years, as their unique properties have found various applications, e.g., in the field of microscopy [1,2,3], in the telecommunication sector [4,5,6] or for quantum experiments [7,8,9]. Higher order transverse modes can be generated with a high degree of purity outside of a laser cavity, using for example spatial light modulators [10, 11] or diffractive optical elements [12, 13]. However, if transverse modes are generated within a laser cavity, e.g., by a modulation of the spatial loss [14], phase [15], or gain [16] distribution, they will experience a frequency shift, which depends on their mode order [17]. As a result of this frequency shift, the interference of multiple transverse laser modes will cause fast spatio-temporal dynamics in the intensity distribution of the output beam. If the modes are phase-locked with each other, a transverse mode-locked (TML) laser with a periodically scanning output beam is realized [18, 19]. The scanning frequency of such TML lasers only depends on the transverse mode spacing of the laser and can, therefore, achieve high spot resolving rates in the multi-GHz regime [20]. Since transverse mode locking was suggested [18] and demonstrated [19] for the first time in a He-Ne laser, it has also been realized in semiconductor [21] and solid state lasers [22, 23]. Furthermore, the simultaneous locking of longitudinal and transverse modes has been demonstrated [24,25,26]. Even though Haug et al. [27] showed that by locking two Laguerre-Gaussian (LG) modes a time varying spot size could be achieved, the so far presented TML lasers [19, 21,22,23] have concentrated solely on the locking of Hermite-Gaussian (HG) modes with higher mode orders limited to a single spatial dimension. As a result, the generated TML laser beams were limited to an oscillation on a straight line in the same direction as the higher order transverse modes. Thus, the transverse mode locking based on other mode sets like the LG or Ince-Gaussian modes is of great interest, as these mode sets feature alternative symmetries that can enable new oscillation patterns for TML lasers. However, as most free-space lasers favor the operation in an HG mode set [17], the intra-cavity excitation of TML laser beams based on other modes sets can be difficult.

Therefore, as an alternative approach, we demonstrate the cavity-external conversion of a TML laser beam from an HG mode set into a beam with an LG mode set using a cylindrical lens mode converter [28]. As a result, the linear oscillation of the spot was converted into a circular rotation, extending the spatio-temporal dynamics of the laser beam from a one-dimensional to a two-dimensional motion. The circular trajectory of the converted beam enables new applications for TML lasers, e.g., for fast and accurate distance measurements in two-photon fluorescence microscopy [29].

2 Theoretical background on transverse mode-locking and mode conversion

If multiple Hermite-Gaussian modes \(HG_{m,n}\) of a laser, with the mode orders m and n in the horizontal and vertical direction, respectively, are superposed with each other, they will generate a periodic spatio-temporal output pattern, repeating itself with the frequency of the transverse mode spacing \(\nu _T\). In the ideal case of a TML laser beam with a Poissonian modal power distribution of HG modes with higher mode orders limited to the vertical direction (\(m = 0\)) and a linear phase relation between the contributing modes, the spatio-temporal intensity distribution of the beam can be described by [18]

$$\begin{aligned} I(\xi _x,\xi _y,t) = \frac{1}{\pi } \exp {(-\xi _x^2 - (\xi _y-\xi _0 \cos (2\pi \nu _T t))^2)}, \end{aligned}$$
(1)

where \(\xi _x = \sqrt{2}x/w_x\) and \(\xi _y = \sqrt{2}y/w_y\) represent the normalized spatial coordinates in the horizontal and vertical direction, respectively. The terms \(w_x\) and \(w_y\) are the fundamental mode sizes in the corresponding directions, within the plane of observation. The spatio-temporal intensity distribution described by Eq. 1 forms a Gaussian-shaped spot that performs a harmonic oscillation along a straight vertical line with the frequency \(\nu _T\). The normalized oscillation amplitude of the spot depends on the average mode order \({\bar{n}}\) of the modal power distribution and is given by \(\xi _0 = \sqrt{2{\bar{n}}}\). To visualize the periodic motion of the spot an animation of an ideal TML beam calculated for a Poissonian HG mode set with \({\bar{n}} = 21\) and \(m = 0\) is shown in the supplementary material (Animation 1a). In the corresponding time-averaged intensity distribution the oscillations are averaged out, resulting in a straight vertical line as can be seen in Fig. 1a).

Fig. 1
figure 1

Numerically calculated, time-averaged intensity distribution of a TML laser beam based on a HG modes and b LG modes. Both beams were calculated assuming a Poissonian modal power distribution with an average mode order of \({\bar{n}} = 21\) or \({\bar{l}} = - 21\), respectively, and a linear phase relation between the contributing modes

Full size image

For the mode conversion of such a TML laser beam from an HG mode set into an LG mode set we used the mode converter presented by Beijersbergen et al. [28]. The converter is based on the idea that each HG mode can be decomposed into a defined number of diagonal HG modes, i.e., HG modes oriented under \(45^\circ \) with respect to the principal axis of the original HG mode. If the phase difference between the diagonal HG modes obtained from such a modal decomposition is changed from \(\varDelta \phi = 0\) to \(\varDelta \phi = \pi /2\) the modal interference results in an LG mode. Thus, to convert an HG into an LG mode a phase difference of \(\pi /2\) has to be introduced between the contributing diagonal HG modes. This phase shift is achieved by introducing an additional Gouy phase shift between the diagonal modes via a defined astigmatic beam section which is created by two cylindrical lenses of identical focal length in the mode converter. To act as a mode converter the cylindrical lenses have to be oriented under an angle of \(45^\circ \) with respect to the principal axes of the incident HG mode. Furthermore, the distance between the cylindrical lenses has to be [28]

$$\begin{aligned} d = \sqrt{2} f_{CL}, \end{aligned}$$
(2)

with \(f_{CL}\) corresponding to the focal lengths of the cylindrical lenses. Finally, the mode size of the incident HG beam has to be matched to the mode converter. Therefore, the fundamental mode size at the beam waist has to be [28]

$$\begin{aligned} w_0 = \sqrt{\left(1+\frac{1}{\sqrt{2}}\right)\cdot \frac{\lambda }{\pi }\cdot f_{CL}}, \end{aligned}$$
(3)

in the unfocused direction of the cylindrical lenses, with \(\lambda \) corresponding to the average wavelength of the laser beam. Using this mode converter any given \(\hbox {HG}_{m,n}\) mode can be converted into a specific \(\hbox {LG}_{l,p}\) mode with the azimuthal index \(l = m-n\) and the radial index \({p = \text {min}(m,n)}\), and vice versa.

As the mode conversion only depends on the relative phase differences between the contributing modes, the mode-matching conditions (Eqs. 2 and 3) and, thus, the converter alignment are independent of the mode orders m and n of the mode to be converted. Therefore, the mode converter can be used to simultaneously convert all contributing modes of a TML laser beam.

To predict the spatio-temporal dynamics of such a converted TML laser beam, we have numerically calculated the time-dependent superposition of multiple LG modes. In accordance with the ideal HG TML beam presented in Fig. 1a) the modal power was Poisson-distributed and centered at an average mode order of \({\bar{l}} = - 21\), with \(p = 0\), while the modal phases were set to be zero. As a result, a Gaussian-shaped spot oscillating on a circular trajectory was obtained from the calculations. To visualize the circular motion of the converted TML beam, an animation of the time-dependent spatial intensity distribution is shown in the supplementary material (Animation 1b). The circular trajectory of the oscillating spot can also be seen in the corresponding time-averaged intensity distribution shown in Fig. 1b). In a direct comparison with the time-averaged intensity distribution of the corresponding unconverted HG TML beam (Fig. 1a) it becomes apparent that the normalized radius \(\rho _0\) of the converted LG TML beam is smaller than the normalized oscillation amplitude \(\xi _0\) of the unconverted beam. This difference, is a result of the beam projections onto the principal axes of the mode converter: as the unconverted HG TML beam is oriented under an angle of \(45^\circ \) with respect to the axis of the cylindrical lenses, the oscillation amplitude of the two projections is reduced by a factor of \(1/\sqrt{2}\) compared to the oscillation amplitude \(\xi _0\) of the HG TML beam. In front of the mode converter, the two projections are in phase, resulting in a linear oscillation under \(45^\circ \) as observed for the unconverted beam. However, when the beam passes through the mode converter the phase between the two projections is shifted by \(\pi /2\). As a result the two projections are no longer in phase and the output beam oscillates on a circular trajectory with a normalized radius of \(\rho _0 = \xi _0 / \sqrt{2} = \sqrt{{\bar{n}}}\). In terms of the LG mode indices the normalized radius would then be given by \(\rho _0 = \sqrt{\left| {\bar{l}}\right| }\). These considerations are in accordance with the transverse dimensions of the LG modes which scale with a factor of \(\sqrt{2p+\left| l\right| +1}\) compared to the fundamental mode [30]. We verified our hypothesis by numerically calculating the ratio of \(\rho _0\) and \(\xi _0\) for a series of LG TML and HG TML beams with \({\bar{l}} = -{\bar{n}}\) (solid blue line in Fig. 4d). Furthermore, a comparison of the predicted ratio of \(\rho _0 / \xi _0 = 1/\sqrt{2}\) with the experimental results will be presented in Sect. 4.2.

3 Method and experimental setup

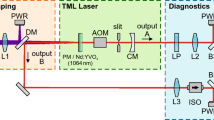
A schematic of the experimental setup used for the mode conversion of the TML laser beam is shown in Fig. 2.

Fig. 2
figure 2

Schematic of the experimental setup for the modal conversion of a TML laser beam. The setup consists of a transverse mode-locked laser (TML laser), optical lenses (L1, L2, and L3), a mode converter consisting of two cylindrical lenses (CL1 and CL2) placed in a distance d to each other, a beam splitter (BS), a neutral density filter (ND), a CCD-camera (CCD), and a photodiode (PD)

Full size image

The TML laser setup was similar to the setup described in our previous publication [20]. A plano-concave two-mirror laser cavity was chosen, with a \(1\,\)mm long, 1 at.\(\%\) doped Nd:\(\hbox {YVO}_4\) crystal as active gain medium. The laser crystal was pumped at a wavelength of 808 nm with a vertical line-shaped pump focus, limiting the laser oscillation in the horizontal direction to a single mode order while enabling the simultaneous oscillation of multiple mode orders in the vertical direction. The amplitude of the cavity-internal laser light at 1064 nm was modulated using an acousto-optic modulator (AOM). By matching the transverse mode spacing \(\nu _T\) of the pumped laser cavity to the effective optical modulation frequency of the AOM (\(82.2\,\)MHz) transverse mode-locking of the laser in the vertical direction was obtained. The oscillation amplitude \(\xi _0\) of the generated TML laser beams was controlled via the cavity alignment and a cavity internal slit, limiting the beam profile in the vertical direction. The average applied pump power was \(6\pm 1\,\)W and resulted in an average output power in the range of \(4\,\)mW up to \(20\,\)mW, which was strongly dependent on the laser alignment and oscillation amplitude \(\xi _0\). Due to the line-shaped pump focus an asymmetric thermal lens was induced in the laser crystal, such that a slightly astigmatic fundamental mode was measured for the HG TML beam in the plane of the laser crystal, with a fundamental mode size of \(w_{x} = 383 \pm 13\,\mu \)m and \(w_{y} = 423 \pm 3\,\mu \)m in the horizontal and vertical direction, respectively.

To convert the TML laser beam from the HG mode set into an LG mode set the mode converter described in Sect. 2, based on two cylindrical lenses (CL1 and CL2), was used. To satisfy Eq. 2 the two cylindrical lenses, which both had a focal length of \(f_{CL} = 50\,\)mm, were placed in a distance of \(d = 70.7\,\)mm to each other. Furthermore, the lenses were rotated by \(45^\circ \) with respect to the principal axis of the incident TML beam. In accordance to Eq. 3, the fundamental mode size of the incident TML beam was adjusted to be \(w_0 = 170\,\mu \)m at the beam waist in the unfocused direction of the cylindrical lenses, using the lens L1 [31]. The second lens L2 was used to adjust the size of the converted TML beam to the detection setup described below.

To measure the time-averaged intensity distribution of the beam a CCD-camera was used, while the spatio-temporal intensity distribution of the beam was measured with a photodiode on a two-dimensional translation stage. For the measurements the beam was split into two beams using a beam splitter (BS) with a transmission of \(10\%\) and a reflectivity of \(90\%\). However, the optical path length from the second lens of the mode converter to the CCD-camera and the photodiode was the same. Therefore, the beam size measured in the plane of the CCD-camera was equal to the beam size measured in the plane of the photodiode. The fundamental mode size in the plane of the CCD-camera was measured to be \(w_{x} = 296 \pm 4\,\mu \)m and \(w_{y} = 312 \pm 3\,\mu \)m in the horizontal and vertical direction, respectively. The time-averaged as well as spatio-temporal intensity distributions of the unconverted TML beam were measured in a similar fashion directly behind the TML laser; the corresponding setup is described in detail in our previous publication [20]. For a better comparability of the measurements obtained for the converted and unconverted TML beams the normalized coordinates \(\xi _x\) and \(\xi _y\) will be used throughout Sects. 4.1 and 4.2 of this publication.

To investigate the quality of the converted TML beam the beam profile was measured at different positions along the optical axis. Therefore, the CCD-camera depicted in inset A of Fig. 2 was replaced by the focusing lens L3 and a CCD-camera on a translation stage (Fig. 2, inset B). With this setup the time-averaged intensity distribution of the LG TML beam could be measured over a total propagation distance of \(28\,\)cm, reaching from \(z=-5.4\,\)cm to \(z=22.6\,\)cm with the focal plane at \(z=0\,\)cm. The propagation distance from the focal plane to the end of the translation stage of \(22.6\,\)cm was more than 16 times larger than the Rayleigh length \(z_R = 1.37\pm 0.15\,\)cm of the fundamental mode, enabling both the measurement of the near- (\(z=0\,\)cm) and far-field (\(z \gg z_R\)) [17].

4 Results and discussion

To demonstrate the successful mode conversion of TML beams, HG TML beams with different oscillation amplitudes \(\xi _0\) (i.e., different average mode orders \({\bar{n}}\)) have been converted from an HG mode set to an LG mode set with the above-described cylindrical lens mode converter. For each of the beams with \({\bar{n}} = 18, 21, 25\), and 30 the time-averaged and spatio-temporal intensity distributions have been measured before as well as after the conversion. The qualitative changes of the TML beams due to the mode conversion were the same and independent of their mode order. This can be seen when comparing the time-dependent spatial intensity distributions of the measured beams, which are visualized in Animation 2, provided in the supplementary material. A detailed discussion of the measurements for the unconverted and converted TML beams is presented in Sects. 4.1 and 4.2, respectively. In addition, in Sect. 4.3 a quality analysis of the converted TML beams, based on the measured evolution of the beam profile during propagation, is presented. For the sake of simplicity, the representative examples shown in Sects. 4.1, 4.2 and 4.3 concentrate on the TML beam with an average mode order of \({\bar{n}} = 21\) and \({\bar{l}} = -21\), respectively. However, the same qualitative observations were valid for all of the measured TML beams.

4.1 Unconverted TML beam based on an HG mode set

In accordance with the theory presented in Sect. 2 the laser spots of the unconverted TML beams performed a harmonic oscillation in the transverse plane of the laser as described by Eq. 1. As a result, the time-averaged intensity distributions of the measured beams formed straight vertical lines, as can be seen in the representative example shown in Fig. 3a).

Fig. 3
figure 3

a and b Show the measured time-averaged and spatio-temporal intensity distribution of the unconverted TML beam with an average mode order of \({\bar{n}} = 21\), respectively. The dashed white line in b represents a cosine function that was fitted to the center of mass of the spatio-temporal intensity distribution. The blue bars in c represent the corresponding reconstructed modal power distribution of the unconverted HG TML beam, while the solid green line indicates the reconstructed phases of the contributing modes. The uncertainty interval for the modal power coefficients and the modal phases are represented by the black error bars and the width of the green line, respectively

Full size image

The periodic oscillations of the TML beams, however, are displayed by the corresponding spatio-temporal intensity distributions shown for example in Fig. 3b). To determine the normalized oscillation amplitudes \(\xi _0\) of the beam trajectories, a cosine function was fitted to the center of mass of the TML beams (dashed white line in Fig. 3b). For all of the measured TML beams the obtained normalized oscillation amplitudes were in a good agreement with the theoretical prediction based on the average mode orders \({\bar{n}}\) of the beams. In case of the beam with an average mode order of \({\bar{n}} = 21\) for example the measured oscillation amplitude was \(\xi _0 = 6.40\pm 0.28\) compared to a theoretical value of 6.48.

In contrast to the ideal HG TML beam described by Eq. 1, the oscillating spots of the measured TML beams changed their size and shape during the oscillation. This can for instance be seen when directly comparing the calculated time-dependent intensity distribution of an ideal HG TML beam (Animation 1a), with the time-dependent intensity distribution of the measured HG TML beam (Animation 1c). We have recently shown that these variations of the spot size and shape were caused by deviations of the modal power distribution from a Poisson distribution as well as by higher order terms of the modal phases [20]. As the modal power distributions and modal phases of the incident HG TML beams were passed on to the LG TML beams during the conversion process, they had a significant influence on the spatio-temporal dynamics of the converted beams. In order to investigate the influence of the modal power distribution and modal phases of the incident HG TML beams on the spatio-temporal intensity distributions of the converted LG TML beams a modal reconstruction of the HG TML beams was performed.

A variety of different schemes have been developed to obtain a modal decomposition of single-frequency multi-mode laser beams [32,33,34,35,36,37,38]. For TML laser beams, where the modes oscillate at different frequencies, we have recently demonstrated [20] that a numerical reconstruction method based on the SPGD algorithm [35,36,37] can be used to reconstruct the modal power distribution and the modal phases of the beam. We used the same algorithm here to reconstruct the modal power and phase distributions of the unconverted HG TML beams. For each beam the results of ten independent reconstructions were averaged and the standard deviations of the coefficients were calculated as uncertainties. Considering the random nature of the reconstruction algorithm, the low standard deviation of the reconstructed coefficients of less than \(0.8\%\) of the total power verified that the algorithm had converged close to the global optimum. The reconstructed modal power distribution and the modal phases of the TML beam shown in Fig. 3a and b, are displayed in Fig. 3c. If the reconstructed amplitude and phase coefficients were considered in the calculations of the spatio-temporal intensity distribution of the unconverted beam (Animation 1e) a good agreement with the measured spatio-temporal intensity distribution (Animation 1c) was achieved, confirming the successful reconstruction of the beam parameters. For the four beams presented within this manuscript an average mode order of \({\bar{n}} = 18, 21, 25,\) and 30 was reconstructed, respectively.

In Sect. 4.2 the reconstructed modal power coefficients and modal phases will be used to explain deviations of the spatio-temporal intensity distribution between a measured and an ideal LG TML beam, i.e., a TML beam based on a Poissonian modal power distribution of LG modes in the azimuthal direction and with a linear phase relation between the contributing modes.

4.2 Converted TML beam based on an LG mode set

Using the cylindrical lens mode converter described in Sect. 3 the HG mode set of the TML beams was converted into an LG mode set. For each LG TML beam the time-averaged intensity distribution and the spatio-temporal intensity were measured using the diagnostic setup depicted in Fig. 2.

Due to the mode conversion the linear motion of the oscillating laser spots was changed into a motion along a circular trajectory, as can be seen in the time-dependent intensity distributions of the measured LG TML beams, which are visualized in Animation 2, provided in the supplementary material. To measure the circular trajectory of the oscillating laser spots the time-averaged intensity distribution of the LG TML laser beams was used.

Fig. 4
figure 4

a Shows the measured time-averaged intensity distribution of the converted TML laser beam based on an LG mode set with an average mode order of \({\bar{l}} = - 21\). b + c show the projections of the spatio-temporal intensity distribution onto the x- and y-axis, respectively. The dashed white lines represent cosine functions which were fitted to the center of mass of each distribution. The red circles in d represent the normalized trajectory radius \(\rho _0\) of the four different converted LG TML beams plotted versus the oscillation amplitude \(\xi _0\) of the respective unconverted HG TML beams. The blue line corresponds to the theoretical ratio of \(\rho _0/\xi _0 = 1/\sqrt{2}\)

Full size image

As a representative example the time-averaged intensity distribution of the LG TML beam with \({\bar{l}} = -21\) is shown in Fig. 4a, and the normalized radius of the circular trajectory was measured to be \(\rho _0 = 4.66 \pm 0.17\), which is close to the theoretically predicted radius of \(\sqrt{\left| {\bar{l}}\right| } = 4.58\). The normalized radii \(\rho _0\) of all measured LG TML beams are plotted versus the normalized oscillation amplitude \(\xi _0\) of the original HG TML beams in Fig. 4. In the same figure the ratio of \(\rho _0/\xi _0 = 1/\sqrt{2}\), which was predicted by the theory presented in Sect. 2, is marked by a solid blue line. As can be seen, the measurements are in a good agreement with the predicted ratio and, therefore, confirm the theory presented in Sect. 2 that \(\rho _0 = \sqrt{\left| {\bar{l}}\right| }\).

The periodic motion of the laser spots in the transverse plane can be observed in the measured spatio-temporal intensity distributions of the LG TML beams. As a representative example the projections of the spatio-temporal intensity distribution of the LG TML beam with \({\bar{l}} = -21\) onto the t-y- and t-x-plane, are shown in Fig. 4b and c, respectively. By fitting two cosine functions to the center of mass of the projections the normalized oscillation amplitudes in the x- and y-direction were measured to be \(\rho _{x} = 4.82 \pm 0.31\) and \(\rho _{y} = 4.29 \pm 0.28\), respectively. The relative phase offset \(\varDelta \varphi = 1.67 \pm 0.05\) between the two projections was close to \(\pi /2\), resembling a circular clockwise motion of the laser spot. Furthermore, the oscillation frequency was measured to be \(82.2\pm 0.7\,\)MHz matching the transverse mode spacing of the TML laser. With the above measured parameters the motion of the laser beam in the transverse plane is completely described by [39]

$$\begin{aligned} \begin{pmatrix} x\\ y\end{pmatrix} = \begin{pmatrix} \rho _x \cos {(2 \pi \nu _T t)}\\ \rho _y \cos {(2 \pi \nu _T t + \varDelta \varphi )}\end{pmatrix}. \end{aligned}$$
(4)

In case of the beam shown in Fig. 4a–c Eq. 4 describes a slightly elliptic trajectory, whose mayor axis is rotated by about \(21^\circ \) with respect to the x-axis. However, due to the relatively large diameter of the photodiode of \(100\,\mu \)m, the uncertainties of the measurements are too large to provide a reliable measure for the ellipticity of the LG TML beam. Therefore, a more precise analysis and discussion of the ellipticity of the LG TML beams will be provided in Sect. 4.3, based on the time-averaged intensity distributions measured with the CCD-camera which had a higher spatial resolution of \(5.5\,\mu \)m.

As described in Sect. 2, the spot of an LG TML beam converted from an ideal HG TML beam, i.e., with a Poissonian modal power distribution and a linear phase relation between the modes, will also be a Gaussian-shaped spot. As a visualization the numerically calculated time-dependent intensity distribution for such an ideal LG TML beam with \({\bar{l}} = -21\) is shown in Animation 1b provided in the supplementary material. A snapshot of the calculated intensity distribution at the time \(t=0\,\)s is shown in Fig. 5a.

Fig. 5
figure 5

Time-dependent intensity distributions of the LG TML beam with an average mode order of \({\bar{l}} = - 21\): a calculated for an ideal beam with a Poissonian modal power distribution and a linear phase relation between the modes, b measured by the photodiode and c calculated based on the modal power distribution and phase relations reconstructed for the original HG TML beam in Sect. 4.1

Full size image

The weak tail of intensity trailing the calculated Gaussian-shaped spot in Fig. 5a was caused by the response function of the photodiode, which was included in the calculations via convolution to increase the comparability between the measured and calculated data. As a crosscheck, the tail vanished, if the response function of the photodiode was not considered in the calculations.

The spot shape of the measured LG TML beam with \({\bar{l}} = -21\), shown in Animation 1d and in Fig. 5b, however, deviated from a Gaussian shape as it was stretched along its circular trajectory. In a direct comparison with the numerical calculations of the ideal LG TML beam it becomes apparent that the observed stretching significantly exceeded the expected stretching due to the response function of the photodiode.

We have observed a similar stretching of the laser spot for HG TML laser beams in our previous work [20], where we demonstrated that the changes of the spot size and shape were caused by deviations of the modal power and phase distribution from that of an ideal HG TML beam. It is noteworthy, however, that in contrast to the HG TML beams the spot size and shape of the LG TML beams were constant over time. In case of HG TML beams the laser spots moved up and down along a straight line and were stretched at the center of the oscillation and squeezed at the outer turning points (see Animation 1c). In case of the LG TML beam the spot changed its direction of motion constantly while moving along a circular trajectory. Therefore, the shape and size of the stretched spot remained unchanged, while the orientation was rotated according to the direction of motion.

To investigate the origin of the above described stretching, we included the reconstructed modal power and phase distribution of the incident HG TML beam (see Sect. 4.1) in the calculation of the time-dependent intensity distribution of the LG TML beam. The corresponding animation and a snapshot of the time-dependent intensity distribution are presented in Animation 1f and Fig. 5c, respectively. The calculations based on the reconstructed parameters resemble the measured laser spot in size and shape, confirming that the deformation of the spot was due to deviations of the modal power and phase distribution of the incident HG TML beam. The quality of the spot shape would, therefore, benefit from an improved mode control of the incident HG TML beam, e.g., by optical gain shaping techniques [16], or by a compensation of the relative modal phases of the HG TML beam.

4.3 Beam profile under propagation

In case of an ideal LG TML beam the beam profile remains circular under propagation, while the beam radius changes along the optical axis. However, in the case of an LG TML beam measured in an experiment, deviations of the mode converter alignment and imperfection of the incident HG TML beam will affect the beam quality. In our experiments for example an increased misalignment of the mode converter resulted in an increased ellipticity

$$\begin{aligned} \epsilon = (r_{\max }-r_{\min })/r_{\max }. \end{aligned}$$
(5)

of the beam profile, where \(r_{\max }\) and \(r_{\min }\) correspond to the largest and smallest radius of the measured beam profile, respectively. Therefore, the ellipticity of the beam profile was used as a measure for the quality of the converted LG TML beams. Note, however, that it was not sufficient to simply measure the beam profile in a single plane, because even a strongly astigmatic beam could have a nearly circular beam profile at distinguished positions. Instead, the time-averaged intensity distributions of the LG TML beams were measured at multiple positions along the optical axis, using the setup shown in inset B of Fig. 2. The intensity profiles of the LG TML beams were then optimized via the mode converter alignment for a low ellipticity of the beam in the near- and far-field.

The change of the measured time-averaged intensity distribution under propagation of the above presented beams is visualized in Animation 3, provided in the supplementary material. As a representative example Fig. 6a and b show the time-averaged intensity distributions of the TML beam with \({\bar{l}} = -21\) measured in the focal plane (\(z = 0\,\) cm) and in the far-field (\(z = 22.6\,\) cm), respectively.

Fig. 6
figure 6

a and b Show the measured time-averaged intensity distributions of the converted TML beam in the focal plane (z = \(0\,\) cm) and at a distance of z = \(22.6\,\)  cm, respectively. Note, that the scale of (b) is 15.8 times larger than the scale of (a). The black dashed lines serve as a reference and represent circles with a radius of \(223\,\mu \)m and \(3751\,\mu \)m, respectively, corresponding to the average radii measured for (a) and (b)

Full size image

 Starting at the focal plane the beam radius increased by a factor of \(16.8 \pm 0.8\) from 223 up to \(3751\,\mu \)m over a propagation distance of \(22.6\,\)cm. This result was in a good agreement with the predicted broadening of \(\sqrt{1+(z/z_R )^2} = 16.5\) calculated for the fundamental mode with a corresponding Rayleigh length of \(z_R = 1.37\pm 0.15\,\)cm. Furthermore, the measured beam quality factor of \(M^2_{exp} = 22.7 \pm 1.2\) matched with a value of

$$\begin{aligned} {M^2_{theo} = 2{\bar{p}}+\left| {\bar{l}}\right| +1 = 22 \pm 1}, \end{aligned}$$

predicted by theory for Laguerre-Gaussian modes [40].

Despite a careful alignment of the mode converter a remaining average ellipticity of \(\epsilon = 6\%\) was measured for the different LG TML beams. Note, however, that for each beam the ellipticity changed with propagation and the ellipticity could range from 1 up to \(10\%\) at different positions along the optical axis. Additionally, an inhomogeneous distribution of the beam intensity on the circular beam profile was observed. Especially in the vicinity of the focal plane a concentration of the intensity at specific positions of the spatial beam profile was measured (see Animation 3 and Fig. 6a).

The reduced beam quality, i.e., the ellipticity and inhomogeneity of the measured beam profiles, was most likely related to inefficiencies of the mode conversion process resulting in additional unwanted LG modes that oscillated at the same frequencies as the targeted LG modes. Due to the degenerate frequencies the interference between the targeted and unwanted LG modes was temporally stable and changed the spatial profile of the converted LG TML beams [41].

A reduced efficiency of the mode conversion process could be either caused by deviations of the mode converter alignment, i.e., the focal length and position of the cylindrical lenses (see. Eq. 2), or by deviations of the incident beam from the mode matching condition (see Eq. 3) [41]. For our setup the uncertainty of the focal length of the cylindrical lenses (\(\pm 1\%\)), the uncertainty of the position of the cylindrical lenses (\(\pm 3\%\)), and the uncertainty of the mode matching of the incident HG TML beam (\(\pm 8\%\)) had to be considered. The largest contribution to the uncertainty of \(\pm 8\%\) was given by the mode matching of the incident HG TML beam, due to its astigmatism. Thus, to reduce the uncertainty in future work, we would compensate the astigmatism of the input beam before the mode conversion, e.g., using an anamorphic prism pair [42].

Additionally, it can be observed in Animation 3, that the beam continuously rotated its orientation in the transverse plane by about \(180^\circ \) when propagating through its beam waist. While such a rotation is atypical for a stigmatic or a simple astigmatic beam [43], it is well known for beams with general astigmatism [44]. General astigmatism occurs, if a beam passes through a non-orthogonal optical system, which was the case in our setup if the two cylindrical lenses were not oriented at exactly the same angle.

5 Summary and outlook

We demonstrated the conversion of transverse mode-locked (TML) laser beams from an HG mode set to an LG mode set using a cylindrical lens mode converter. As a result, the linear motion of the oscillating laser spot was translated into a two-dimensional motion along a circular trajectory. The normalized radius \(\rho _0\) of the converted LG TML beams was dependent on the average mode order \({\bar{l}}\) by \(\rho _0 = \sqrt{\left| {\bar{l}}\right| }\) which was numerically and experimentally verified in compliance with theory.

Apart from a remaining average ellipticity of about \(\epsilon = 6\%\) the beam profiles remained circular over the complete propagation distance from the near- to the far-field. For applications that require a reduced ellipticity, we suggested that the astigmatism of the incident HG TML beam should be compensated in front of the mode converter to improve the mode matching for the conversion process.

The conversion of the HG TML laser beam to an LG mode set enables new scanning patterns for future applications. For example a circular scanning trajectory makes TML lasers viable for fast and precise distance measurements in the field of microscopy [29]. To achieve the high peak intensities that are required, e.g., for two-photon microscopy, a simultaneous longitudinal and transverse mode-locked laser beam [25] could be used as input for the conversion process. Furthermore, the modal conversion of HG TML laser beams could be of interest for sub-diffraction limited imaging based on STED [1] or Minflux [45], as our first numerical calculations have demonstrated that a beam with an \(\hbox {LG}_{0,1}\) mode profile, oscillating on a circular trajectory, could be generated if a multi-trace HG TML beam (e.g., HG\((m=1,{\bar{n}}=21)\)) [20] is converted (see Animation 4 in the supplementary material). Finally, LG modes provide a high overlap with the LP mode set of optical step-index fibers [46] and could, therefore, provide mode matching between transverse mode-locked free-space and fiber lasers or amplifiers [26].