Low-temperature and low-pressure effective fluorescence lifetimes and spectra of gaseous anisole and toluene

Abstract

Fluorescence spectra and lifetimes of anisole and toluene vapor in nitrogen have been measured at conditions below ambient (257–293 K and 100–2000 mbar) upon excitation with 266-nm laser light to expand the applicable range of anisole and toluene laser-induced fluorescence (LIF) for conditions below room temperature that occur in expanding flows and cases with strong evaporative cooling. Anisole fluorescence spectra broaden with decreasing pressure while fluorescence lifetimes decrease simultaneously. This is consistent with a more pronounced effect of internal vibrational redistribution on the overall fluorescence signal and can be explained by significantly reduced collision rates. In the case of toluene, the transition from photo-induced heating to photo-induced cooling was observed for the first time for 266 nm. The data confirm predictions of earlier work and is particularly important for the advancement of the available photo-physical (step-ladder) models: since those transitions mark points where the molecules are already thermalized after excitation (i.e., no vibrational relaxation occurs during deactivation), they are important support points for fitting empirical parameters and allow analytical determination of the ground state energy transferred to the excited state. The data enable temperature and/or pressure sensing, e.g., in accelerating cold flows using laser-induced fluorescence of both tracers.

1 Introduction

Laser-induced fluorescence (LIF) of organic gas-phase tracer species has been widely used to measure temperature, composition, and density of various kinds of flows, often with the purpose of light-sheet based imaging [1]. While concentration and density measurements take advantage of local signal intensities [2], temperature measurements are often based on ratiometric measurements of signal intensities detected in separate spectral regions of the fluorescence emission bands [3,4,5,6]. A similar approach can also be used for the analysis of molecular interactions, when collisional quenching (and thus, e.g., local O₂ partial pressure) can be detected through modifications in the fluorescence spectra [7,8,9,10,11]. A less frequently applied technique exploits the dependence of the fluorescence lifetime on temperature, pressure or bath-gas composition for quantitative measurements [12, 13]. While the effective fluorescence lifetime is proportional to the fluorescence quantum yield, it can be measured directly without knowledge of the tracer concentration.

The use of these effects for quantitative measurements requires detailed knowledge of the underlying spectroscopic properties under the respective environmental conditions. Most applications studied so far have focused on the application of tracer LIF at room temperature or above, e.g., for the analysis of fuel/air mixing in combustion systems and extensive data bases as well as modeling approaches have been developed for these conditions as discussed in the following sections. For temperatures below room temperature that are practically relevant, e.g., in expanding flows, in engines at cold start, or in sprays with strong evaporative cooling, the underlying spectroscopic data are missing and thus, the applicability of existing photophysical models is not validated. In this paper, this deficiency is addressed with studying fluorescence properties of two relevant species, anisole and toluene, in sub-ambient conditions and comparing the results with the state-of-the art model understanding.

The application of tracer-LIF to challenging environments such as internal combustion engines or supersonic flows requires careful choice of the best-suited fluorescence tracer and spectroscopic approach. Besides the dependence of the tracers photophysical properties on temperature, pressure, and bath-gas composition, factors such as evaporation properties (i.e., for spray analysis [14,15,16]), high-temperature stability [17], environmental impact (especially, in the case of large-scale experiments [11, 18,19,20]), interaction with the reactive system (auto-igniting fuel/air mixtures [21]) and physical limits (attainable vapor pressure, onset of self-quenching [22]) must be considered for a proper choice of tracer. Applications to super- or transonic flow experiments [5, 11, 19, 20, 23, 24] pose several challenges: first, due to gas-dynamic cooling, temperatures drop well below standard conditions where so far little photophysical data on typical tracers are available. Second, the environmental impact of the tracers used must be limited as large amounts are required for full-scale experiments ruling out the application of toxic species, i.e. nitric oxide, which would be a more obvious choice for cold gas flows as demonstrated in the literature [8, 25, 26]. Aromatics such as anisole and toluene are promising candidates for tracer LIF in such flows, because they, first, can easily be excited by standard laser wavelengths such as emitted by KrF excimer lasers (248 nm) or the 4th harmonic of Nd:YAG lasers (266 nm) [27]. Second, they exhibit large fluorescence quantum yields [28, 29] that enable application at low tracer concentration and that compensate for their limited vapor pressure at low temperature.

Toluene is an established and well-studied fluorescence tracer for various applications [30]. In contrast, anisole has gained attention more recently. Its advantages include an increased per-molecule signal level that enables improved signal-to-noise ratios in many applications despite its lower vapor pressure compared to toluene [4, 15]. However, most efforts studying photophysical properties of anisole [17, 31,32,33] and toluene [13, 23, 32, 34,35,36,37] have been carried out for room temperature or above and photophysical data at low temperature and low pressure are scarcely available.

Low-temperature conditions outside the previously explored range occur frequently in transonic nozzle flows, e.g., where spatial temperature and pressure gradients are present in which our own LIF measurements have been limited to qualitative analysis [11, 20] so far. In the past, Combs et al., presented a thorough photophysical analysis of naphthalene vapor [24] for measuring flow properties in cold supersonic wake flows [38]. Using toluene LIF, Gamba et al. [5] measured temperature in supersonic flows with complex compressibility effects with a two-color detection scheme. However, since their spectral calibration data were only available above room temperature, the complete temperature range could not be covered. Estruch-Samper et al. [6] encountered the same problem while applying a similar technique in a hypersonic gun tunnel but used linear extrapolation of their above room-temperature data for toluene. Also, concentration measurements in cold supersonic flows required sophisticated calibration techniques [5, 23]. The data provided in this paper close these gaps for anisole and toluene.

Practical applications of tracer-LIF have often been supported by empirical data fits [28, 32, 39] or semi-empirical models [31, 40,41,42] that predict the fluorescence quantum yield for the given conditions. Both require measured data for validation in the respective temperature range. Measurements within an increased parameter range thus provide critical boundary conditions for the validation of existing models [29, 31, 42] and expand their valid range. Also, because of reduced collision rates, processes such as intramolecular vibrational energy redistribution, which are usually insignificant compared to rapid vibrational relaxation [43], are easier to study in low-density and low-temperature environments. The current state of model development is described in Sect. 2 also highlighting the importance of extending the existing datasets to regions of lower temperature and pressure regions.

The primary goal of this work is to provide spectrally resolved fluorescence intensities and fluorescence lifetimes, representing fluorescence quantum yields, for anisole and toluene in so far scarcely or not available ranges of temperature (257–293 K) and pressure (100–2000 mbar). Such data expand the applicable range of anisole and toluene LIF and also support the advancement of the most recent fluorescence quantum yield models toward the low-temperature and low-pressure regime.

2 Photophysics

The fluorescence signal of organic tracer species depends on the tracer number density n_tr, the incident laser intensity I_laser, the tracer’s absorption cross-section σ_abs and fluorescence quantum yield (FQY) ϕ_fl. For aromatic tracers, σ_abs is a function of temperature T and pressure p, whereas ϕ_fl additionally depends on the partial pressure p_q of the respective quenching species q present in the gas such as oxygen [44], other organic molecules [9], or excited state molecules of the tracer itself [22].

$$S_{{{\text{fl}}}} \propto n_{{{\text{tr}}}} I_{{{\text{laser}}}} \sigma_{{{\text{abs}}}} \left( {T,p} \right)\phi_{{{\text{fl}}}} \left( {T,p,p_{{\text{q}}} } \right).$$

(1)

After excitation from the ground state S₀ to the first excited state S₁, single-ring aromatics like anisole and toluene can fluoresce in the ultraviolet spectral range (S₁→S₀). The fluorescence is in strong competition with rapid non-radiative deactivation of the excited state through intersystem crossing (ISC) to the triplet state T₁, internal conversion (IC) to highly vibrationally excited states in S₀, and collisional quenching, while undergoing vibrational relaxation (VR) within the S₁ state due to collisions with bath gas molecules. Intramolecular vibrational energy redistribution (IVR) can often be neglected in denser gases where VR is dominant because of high collision rates.

The quantum yield of a fluorophore is defined as the ratio of the rate of spontaneous emission of light k_fl to the total deactivation rate k_tot with the latter being the sum of the rate constants for each individual deactivation channel (cf. Fig. 1). The rate constants for intersystem crossing k_ISC and internal conversion k_IC often are combined to the single non-radiative rate constant k_nr. The rate constant for collisional quenching is the product of the quenching rate k_q and the tracer concentration (here in the form of p_q). The ratio of the rate constants can further be expressed as the ratio of their reciprocals, the excited state lifetime τ_fl and the experimentally accessible effective lifetime τ_eff, respectively [1].

$$\phi_{{{\text{fl}}}} = \frac{{k_{{{\text{fl}}}} }}{{k_{{{\text{tot}}}} }} = \frac{{k_{{{\text{fl}}}} }}{{k_{{{\text{fl}}}} + k_{{{\text{ISC}}}} + k_{{{\text{IC}}}} + \sum k_{{\text{q}}} p_{{\text{q}}} }} = \frac{{k_{{{\text{fl}}}} }}{{k_{{{\text{fl}}}} + k_{{{\text{nr}}}} + \sum k_{{\text{q}}} p_{{\text{q}}} }} = \frac{{\tau_{{{\text{eff}}}} }}{{\tau_{{{\text{fl}}}} }} \propto \tau_{{{\text{eff}}}} .$$

(2)

Fig. 1

Jablonski diagrams showing the principle of a photo-induced heating, b photo-induced cooling after increasing temperature, and c photo-induced heating after increasing pressure based on the findings of Benzler et al. [32] and Baranowski et al. [46] for anisole at elevated temperatures

Step-ladder models as first described by Freed and Heller [45] and implemented, e.g., by Thurber et al. [40] for ketones describe the successive vibrational relaxation in the initially optically excited energy levels of the fluorophore and is competition with fluorescence emission and non-radiative deactivation processes using kinetic rate expressions. Implementations consist of a procedural model function that traverses all occupied vibrational energy levels in S₁ during VR (cf. Fig. 1a): after excitation to a certain energy level E_initial in S₁, the contribution of each subsequent energy level to $\phi_{{{\text{fl}}}}$ during thermalization is calculated from the balance of all competing deactivation channels, while each step corresponds to the mean time between collisions. The rate constants used for quantifying this kinetic scheme are either parameterized (energy-dependent) equations or scalar fit parameters that are determined from fitting the model function to measured fluorescence data. The starting point, E_initial, is determined from the laser energy E_laser, the ground-state thermal energy level E_therm,0 and the S₀–S₁ band gap E₀ (Eq. 3).

$$\begin{array}{*{20}c} {E_{{{\text{initial}}}} = E_{{{\text{laser}}}} + E_{{{\text{therm}},0}} - E_{0} .} \\ \end{array}$$

(3)

The thermal energy levels E_therm are calculated from the vibrational frequency modes (Eq. 4).

$$E_{{{\text{therm}}}} = \mathop \sum \limits_{i = 1}^{n} \frac{{\omega_{i} }}{{\exp \left( {{\raise0.7ex\hbox{${hc\omega_{i} }$} \!\mathord{\left/ {\vphantom {{hc\omega_{i} } {kT}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${kT}$}}} \right) - 1}}.$$

(4)

Based on these relations, attempts to model the FQY or fluorescence lifetime have been made. Thurber et al. [40] have presented a phenomenological step-ladder model describing the FQY of acetone. Rossow [42] adapted this stepladder model for toluene between 350 and 900 K and 1–30 bar. Faust et al. [39] developed an empirical model for toluene predicting the FQY for a range of temperature (T = 296–1025 K and 296–977 K, respectively), pressure (p = 1–10 bar) and bath-gas composition ($p_{{{\text{O}}_{2} }}$ = 0–210 mbar) by measuring fluorescence lifetimes upon picosecond laser excitation at 266 nm.

Faust et al. [28] also developed an empirical model for anisole using data obtained at similar conditions. Wang et al. [31] adapted a more physical step-ladder model to anisole using experimental normalized FQY data for p = 2–40 bar and T = 473–873 K and different bath-gas compositions. Benzler et al. [32] investigated the effective fluorescence lifetime of anisole for temperatures between 296 and 475 K at low pressure (< 1 bar). They observed a switch-over of the fluorescence lifetime from increasing to decreasing with pressure occurring between ambient temperature and 355 K and explained it with the transition from photo-induced heating (PIH) to photo-induced cooling (PIC).

Photo-induced heating (Fig. 1a) occurs if the initially populated vibrational energy level E_initial after laser excitation of the fluorophore exceeds the thermal energy level E_therm,1, i.e., the most populated energy level of the thermal distribution in the excited state. Energy exchange (radiative or non-radiative) with the environment occurs while the excited molecule thermalizes to E_therm,1. Photo-induced cooling (Fig. 1b) occurs if E_initial is below E_therm,1 and the molecule extracts heat from the environment while relaxing through the vibrational energy levels. These effects were initially observed for naphthalene by Beddard et al. [47] and, later thoroughly described and analyzed by Wadi et al. [48]. As the non-radiative deactivation rate k_nr increases with increasing vibrational energy, τ_eff is lower for higher excess energies for both tracers, anisole [31] and toluene [42]. Increasing pressure (Fig. 1c) leads to faster vibrational relaxation to E_therm,1 due to increased collision rate. This means that τ_eff increases with increasing pressure in the case of PIH (k_nr is higher at E_initial compared to E_therm,1) and decreases in the case of PIC (k_nr is lower at E_initial compared to E_therm,1).

Baranowski et al. [46] followed-up on the findings of Benzler et al. [32] by systematically varying the excitation wavelength (λ = 256–270 nm) while measuring the fluorescence lifetime of anisole for moderate temperatures (T = 335–525 K) and pressures (p = 1–4 bar) above ambient conditions. By observing a vanishing pressure dependence (i.e., the tipping point where PIC switches to PIH) for a specific temperature and given excitation wavelength, they could improve the predictions of E_initial by approximating the portion of E_therm,0 actually transferred to S₁ using the spectral overlap of the excitation wavelength with ab initio calculated absorption spectra. To this end, they exploited that at the tipping points, excitation occurs directly to the thermal energy level so that E_initial equals E_therm,1. Hence, they were able to calculate the effective ground-state thermal energy Ē_therm,0 from a straight-forward energy balance (Eq. 5) to support their assumptions.

$$\begin{array}{*{20}c} { \overline{E}_{{{\text{therm}},0}} = E_{{{\text{therm}},1}} - E_{{{\text{laser}}}} + E_{0} .} \\ \end{array}$$

(5)

However, there still exist uncertainties in the simulation of the absorption spectra at elevated temperatures due to unknown spectroscopic simulation parameters. Knowledge of additional tipping points, therefore, is crucial to validate the assumptions and further increase the accuracy of the predictions. One could also imagine using Ē_therm,0 as additional fit parameter.

The work of Benzler et al. [32] also suggests that in the case of toluene, the PIH–PIC transition temperature for the commonly used excitation wavelength of 266 nm is below ambient conditions as the pressure dependence of the signal drops until his lowest measured temperature of 296 K. However, confirmation of this prediction has been lacking so far.

3 Experiment

3.1 Continuous flow cell

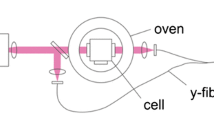
A liquid-cooled flow cell with four-way optical access was utilized for all experiments presented here (Fig. 2). The cell consists of the 150-mm long cylindrical test section with an inner diameter of 10 mm. Laser light enters and exits the cell through windows at its far ends while fluorescence can be collected through two side windows perpendicular to the light propagation direction in the center of the cell providing a large numerical aperture (NA ≈ 0.4). An insulated outer jacket (inner diameter 40 mm) allows to circulate liquid coolant around all surfaces of the test section except the windows. Therefore, all windows are mounted retracted within the jacket to minimize heat losses. Threaded retainers made from low heat-conduction plastic press the windows against o-ring seals that are supported by an inner metal ring. This permits inward and outward pressure loads for operation at below and above ambient pressure while enabling easy removal for cleaning purposes. The retainers feature tube connectors for providing a constant flush gas flow of dry N₂ to avoid condensation of atmospheric water on the outer window surfaces if the cell is operated below ambient temperature. Optionally, secondary windows can be mounted in the retainers to prevent water condensation. The temperature is measured by two thermocouples inserted approximately 2 mm into the flow through the inlet and exit lines, respectively.

Fig. 2

Liquid-cooled flow cell with four-way optical access. Inner diameter along the laser light propagation direction is 10 mm, the absorption path length is 150 mm. Thermocouples are inserted through the sample-gas inlet and outlet so that their tips reach into the inner cell volume

The sample-gas feed system consists of two mass flow controllers (MFCs) and a bubbler (Fig. 3). One MFC feeds the carrier gas (N₂) through a bubbler containing the tracer while the other provides a bypass flow (N₂) for dilution. The bubbler is cooled to the same temperature as the cell ensuring that the dew point temperature of the mixed gas flow is below the cell temperature to prevent condensation. The ratio of bypass-to-bubbler gas flow was 4:1, meaning that the tracer partial pressure was always below 20% of its vapor pressure at any given temperature. This results in a maximum tracer number density (at the highest temperature and pressure investigated) of < 1.3 × 10¹⁶/cm³ for anisole and < 1.1 × 10¹⁷/cm³ for toluene and a lowest tracer number density (at the lowest temperature and pressure) of < 5.0 × 10¹³/cm³ and < 6.8 × 10¹⁴/cm³, respectively. A pre-cooler installed directly on top of the cell compensates for ambient heat added on the way ensuring minimal temperature variation inside the cell. In all cases, the coolant is provided by the same compressor-cooled circulating chiller (Huber Minichiller 300, cooling power 300 W at 15 °C and 70 W at − 20 °C) with an operating temperature range from room temperature down to − 20 °C. The total gas mass flow rate was 1000 sccm resulting in a flow velocity of approximately 0.3 up to 6 m/s. Thus, the complete cell volume is exchanged at least every second even in the worst (i.e., the highest density) case.

Fig. 3

Simplified flow diagram of the sample-gas feed system

The pressure prior and after the flow cell is adjusted with needle valves. The first valve upstream of the flow cell is set to ensure that the pressure in the feed system before entering the cell and is above 2.5 bar monitored by a pressure transducer (Keller, 35 X HTC, 0 − 15 bar, accuracy 0.5% of full scale). Maintaining this pressure ensures that ambient oxygen cannot enter the system even if small leaks exist. Two parallel needle valves downstream of the flow cell are required to set the cell pressure over the complete investigated range of 100–2000 mbar. The pressure in the flow cell is measured at the cell exit using a capacitance manometer (MKS, Baratron 722B, 0–5000 mbar, accuracy 0.5% of reading). Prior to the experiments, the low-pressure section has been helium leak tested. The temperature is calculated from the arithmetic mean of the two thermocouples (type K, calibrated using the triple-point method) readings in the gas inlet and exit lines (Fig. 2). This approximation has been validated to be within the measurement error by inserting an additional thermocouple directly into the measurement plane through a stainless-steel dummy instead of one of the detection windows. Experiments were performed at five set-point temperatures with a repeatability of < 0.05 K (95% confidence interval).

3.2 Optical setup

3.2.1 Fluorescence lifetime measurements

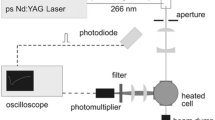
The effective fluorescence lifetime was measured by time-correlated single photon counting (TCSPC, [49]) that has been applied to tracer-LIF-related studies before [12, 13]. The TCSPC system (see Ref. [12] for details) consists of a mode-locked high repetition rate (1–20 MHz) picosecond fiber laser (Fianium, FemtoPower UVP266-PP-0.1, 266 nm, 5 nJ/pulse, 20 ps), a fast photomultiplier tube (PMT) (Hamamatsu, R3809U50, 150 ps rise time), and a TCSPC board (Becker & Hickl, SPC-130). Short excitation pulses are required because of the short fluorescence lifetimes of anisole [28, 32]. Because of the single-photon detection principle of TCSPC, experiments at very low signal levels are possible. This enables measurements with the low tracer partial pressures prevailing at the low temperatures. In addition, measurements can be carried out at low laser fluence, which prevents self-quenching by laser-excited molecules, according to the mechanism described by Fuhrmann et al. [22] for toluene. Hence, limiting the number of excited molecules by either reducing the tracer concentration or the laser fluence eliminated any measurable non-linearities in the LIF signals vs. concentration. In our case, the laser fluence was < 0.6 µJ/cm² which is well below their established minimum 5 mJ/cm² where no non-linearities were observable at any conditions. We confirmed the linearity of the signal by systematically varying the bypass ratio from 4:1 down to 0 for both tracers.

The optical setup is shown in Fig. 4: the laser beam is directed centrally through the flow cell and fluorescence is detected through one of the quartz windows by the PMT mounted perpendicular to the beam propagation direction. A bandpass filter (Semrock, BP292, 292 nm, 14 nm FWHM) centered close to the peak wavelength of the fluorescence spectrum of both tracers (Fig. 5b) is used in front of the PMT to block residual ambient and laser stray light. For both tracers, Faust et al., established that the measured fluorescence lifetime was independent of the spectral integration window [28, 39]. Reflective UV-grade neutral-density (ND) filters (Thorlabs, NDUV, OD 0.3–3.0) are used to limit the photon count rate so that only after every 10th–200th pulse a photon is detected avoiding pile-up effects [49] caused by more than one photon per laser pulse reaching the detector. The cavity in front of the laser inlet and outlet windows was deep enough to prevent interaction with moist room air by purging without an additional window, while the optical path to the PMT could be completely enclosed to ensure sufficient flushing by dry N₂.

Fig. 4

Optical setup for simultaneous measurement of fluorescence spectra and fluorescence lifetimes

Fig. 5

a Typical TCSPC signal, IRF, and fit using the convolve-and-compare method. b Transmission bands of the BP292 bandpass filter and an ND filter with an optical density of 0.3 (Thorlabs, NDUV03A) for reference measured in a UV–Vis spectrophotometer (Varian, Cary 400 Scan) compared to spectra of toluene and anisole vapor in N₂ at near-ambient conditions

The fluorescence lifetime τ_eff is determined by the convolve-and-compare method [50]. To this end, the temporal fluorescence signal trace is modeled by the convolution (operator ∗) of the instrument response function ($S_{{{\text{IRF}}}}$) of the TCSPC system with a mono-exponential decay (Eq. 6). $S_{{{\text{IRF}}}}$ corresponds to the elastically scattered light measured without the bandpass filter while flushing the flow cell with pure N₂.

$$\begin{array}{*{20}c} {S_{{{\text{fl}}}} \left( t \right) = A\left( {S_{{{\text{IRF}}}} \left( t \right)* {\text{exp}}\left( { - \frac{t}{{\tau_{{{\text{eff}}}} }}} \right)} \right) + B S_{{{\text{IRF}}}} \left( t \right). } \\ \end{array}$$

(6)

The second term in Eq. (6) accounts for potential residual laser stray light. The scaling factors A and B as well as τ_eff are determined by fitting the model function to the temporal signal trace. The noise floor is subtracted from signal (< 5 counts per channel) and S_IRF (< 10 counts) to avoid artifacts during the convolution and preventing the need for an additional fit parameter for a constant offset. Example fits are shown for toluene at near ambient conditions in Fig. 5a, with the residuals between the model function and the measured data presented below the graph. Each measurement is repeated at least three times.

3.2.2 Fluorescence spectra

Fluorescence spectra are measured following excitation with the same laser system operating at 2 MHz. Two off-axis parabolic mirrors (Fig. 4) image the fluorescence signal onto the entrance slit of a spectrometer (Horiba, iHR320, 320 mm focal length, 1200 groves/mm grating) with the spectrum in the exit plane dispersed on a CCD detector (Horiba, Syncerity CCD, 256 × 1024 pixels). The entrance slit opening is set to 100 µm while the exposure time (mechanical shutter) is varied from 1 to 10 s depending on the signal level. The intensity is integrated over the 256 vertical pixels. Note, that the spectra we measured for this work have not been smoothed. This was unnecessary since the integration time was chosen so that the signal level was at the maximum of the instrument’s dynamic range so that signal noise is nearly imperceptible.

In a post-processing step, a previously recorded dark spectrum taken with the same exposure time (laser off) is subtracted. Outliers are removed prior to averaging individual spectra by interpolation between neighboring pixels. Spectra are then corrected for the wavelength-dependent transmission characteristics and detection sensitivity of the complete system, which was determined using an intensity-calibrated laser-driven light source (Energetiq EQ-99); the wavelength axis was calibrated using known atomic line emissions from a Hg(Ar) pen-ray lamp (LOT). The spectral resolution of the setup with the aforementioned settings was measured to be 0.27 nm (FWHM of they 296.7-nm Hg line). To compare the measured fluorescence spectra with previously published data recorded at lower resolutions, the spectra were downsampled by convolution with a Gaussian function (Fig. 6), with a FWHM determined by minimizing the least-squares error to the literature data. Especially in the case of toluene, our spectra then agree well with those of Koban et al. [34]. Agreement with the spectra of Faust et al. [28], however, is not so good, which may be attributed to their significantly lower spectral resolution of ~ 3 nm of the streak camera system used in their work.

Fig. 6

Measured a toluene and b anisole fluorescence spectra at close-to standard conditions next to literature data from Koban et al. [34] and Faust et al. [28]. For better comparability, the new high-resolution (0.26 nm indicated by arrows) spectra were downsampled by convolution with a Gaussian with an FHWM of ~ 2.35 nm

Each individual spectrum in Fig. 6 and in the following chapter is normalized by its integral value between 275 and 360 nm. The ordinates of each plot are then scaled arbitrarily so that y = 1 corresponds to the maximum intensity of each test series, thus maintaining the relative intensity of the graphs to each other. The spectral interval for the normalization was chosen so that laser stray light (visible in low-intensity measurements, cf. Fig. 12a on the left-hand side) would not distort the graphs ratio to each other.

4 Results

4.1 Anisole

As shown in Fig. 7a, for anisole, τ_eff decreases in the low-pressure region (< 600 mbar) with decreasing pressure thus exhibiting PIH behavior at all temperatures investigated. This is in good agreement with Benzler et al. [32] who found that E_initial > E_therm,1 for excitation at 266 nm and temperatures from ambient to about 400 K. For higher pressures (> 800 mbar), τ_eff decreases slightly supposedly due to increased nitrogen bath gas quenching. A similar effect on the fluorescence lifetime has been observed by Cheung et al. [41]for 3-pentanone. At all temperatures, anisole fluorescence lifetimes exhibit a similar temperature dependence (Fig. 7b) decreasing by 10% over the investigated temperature range of about 35 K.

Fig. 7

a Pressure dependence of the effective fluorescence lifetimes of anisole for a range of temperatures below ambient. b Relative (normalized by the room temperature value) effective fluorescence lifetime showing the temperature dependence for the investigated pressure range. Error bars represent the statistical error of repeated measurements. Lines (spline fits) were added to guide the eye

Normalized fluorescence spectra for anisole are shown in Fig. 8 for the lowest (a) and highest (b) investigated pressure. In both cases, an increase in temperature causes a slight broadening of the spectra, which is most prominent in the sharper spectral features at shorter wavelengths. Additionally, a slight shift of the spectral centroid to longer wavelengths is visible (cf. Fig. 9). The spectral centroid λ_c can be interpreted as the center of the area below each intensity curve and is calculated according to the following equation:

$$\begin{array}{*{20}c} {\lambda_{{\text{c}}} = {\raise0.7ex\hbox{${\smallint \lambda S\left( \lambda \right){\text{ d}}\lambda }$} \!\mathord{\left/ {\vphantom {{\smallint \lambda S\left( \lambda \right){\text{ d}}\lambda } {\smallint S\left( \lambda \right){\text{ d}}\lambda }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\smallint S\left( \lambda \right){\text{ d}}\lambda }$}} .} \\ \end{array}$$

(7)

Fig. 8

Temperature-dependent normalized anisole fluorescence spectra for a the lowest (100 mbar) and b for the highest measured pressure (2000 mbar). Arrows indicate the spectral resolution

Fig. 9

Wavelength of the centroid of the anisole fluorescence spectra calculated for the region from 275 to 360 nm as a a function of pressure and b a function of temperature. Lines (spline fits) were added to guide the eye

One needs to be careful to not confuse shifts of the spectral centroids with a shift of the fluorescence spectra. Rather, the spectral features at shorter wavelengths become weaker compared to those at longer wavelengths so that only normalized spectra appear to shift. The shift of the anisole fluorescence spectral centroid with increasing temperature can be explained by considering the anharmonicity of S₀ and S₁: the increase of ground state energy at increased temperature results in a population of higher vibrational levels in S₁. If one considers only that more energy is available, one expects a shift to shorter wavelengths. However, it follows from the Franck–Condon principle that transitions are particularly strong that link similar vibration levels ν′ in S₁ and ν′′ in S₀. As a result of an increase in anharmonicity from S₀ to S₁, the well depth (dissociation energy) in S₁ is smaller than in S₀, and E(ν′) is converging faster than E(ν′′). This and the Franck–Condon principle then cause that an increase in E(ν′) (e.g., by temperature increase) is associated with a shift of the spectral centroid to longer wavelengths. The shift to the short wavelength by increasing p is caused by the same effect since anisole shows PIH behavior so that collisions reduce E(ν′′). For more details, see, e.g., Uy et al. [51].

Somewhat unexpectedly, as shown in Figs. 8 and 10 for the lowest and highest temperatures investigated, a reduction in total pressure broadens the spectral features. This behavior can be explained by considering that for a molecule undergoing slow VR (long τ_eff), fluorescence occurs from several levels along the vibrational energy cascade (cf. Fig. 1a). A rapidly thermalized (short τ_eff) molecule, in contrast, emits light from a narrower distribution of energy levels around E_therm,1.

Fig. 10

Pressure-dependent normalized anisole fluorescence spectra for a the lowest (257 K) and b for the highest measured temperature (292 K). Arrows indicate the spectral resolution

Kimura et al. [52] observed this effect by evaluating highly time-resolved fluorescence spectra for naphthalene. Spectra measured just after (1 ns) excitation, well before the estimated mean collision time (~ 6 ns), exhibited a broadband structure while spectra measured after several collisions (up to 120 ns) were much finer structured. They concluded, that in the first case only sub-nanosecond IVR was responsible for the broader energy distribution of emitting vibrational energy levels, while in the second case, molecules have already thermalized to a narrow energy distribution around E_therm,1.

In the case of anisole, the mean time between collisions at room temperature has been estimated to 0.82 and 0.03 ns at 100 and 2000 mbar, respectively, by calculating the Lennard–Jones frequency using the coefficients from Wang [31] and assuming a bubbler efficiency of 75% (actual anisole vapor pressure divided by saturation vapor pressure). This means, that especially in the low-pressure case, only few (< 15) collisions occur during the fluorescence lifetime compared to the high-pressure case (> 380). This explains the much broader spectral structure of the former as IVR has a larger effect on the vibrational energy distribution compared to the external (collision-driven) VR.

4.2 Toluene

As shown in Fig. 11a, for toluene, τ_eff increases monotonously with pressure in the low-pressure region (< 600 mbar) for T ≤ 274 K but decreases for 292 K. This implies that the transition from PIC to PIH occurs between 292 and 283 K as predicted when extrapolating the results of Benzler et al. [32]. For both cases τ_eff decreases slightly for higher pressures (> 800 mbar) due to increasing nitrogen quenching. Contrary to anisole (cf., Fig. 7b), the temperature dependency of τ_eff (Fig. 11b) differs significantly for different pressures. Whereas τ_eff decreases ~ 26% at 2 bar, it only drops ~ 10% at 100 mbar over the investigated temperature range of 35 K while exhibiting a more non-linear behavior.

Fig. 11

a Pressure dependence of the effective fluorescence lifetimes of toluene for a range of temperatures below ambient. b Relative (normalized by the room temperature value) effective fluorescence lifetime showing the temperature dependence for the investigated pressure range. Error bars represent the statistical error of repeated measurements. Lines (spline fits) were added to guide the eye

Toluene fluorescence spectra are shown as a function of temperature (Fig. 12) and pressure (Fig. 13), for the lowest (panels a) and the highest (panels b) pressure and temperature, respectively. It is apparent, that the spectra are nearly invariant to changes in pressure. At the lowest temperature (Fig. 13a), however, the fine structure of the spectrum is more pronounced compared to the room temperature spectrum (Fig. 13b). The spectral intensity centroid remains nearly constant except for the low-temperature (i.e., below about 280 K) and low-pressure (i.e., below about 800 mbar) cases where it red-shifts by up to 1.5 nm (Fig. 14). Unfortunately, scattered laser light (Figs. 12a and 13a, left-hand side of the spectrum) affects the calculation of the centroids especially at those low-signal conditions. The absence of a significant low-pressure broadening compared to anisole can be explained by the much longer fluorescence lifetimes (Fig. 11) and, therefore, more dominant VR and insignificant contribution of IVR to the temporally integrated fluorescence signal.

Fig. 12

Temperature-dependent normalized toluene fluorescence spectra for a the lowest (100 mbar) and b for the highest measured pressure (2000 mbar). Arrows indicate the spectral resolution

Fig. 13

Pressure-dependent normalized anisole fluorescence spectra for a the lowest (257 K) and b for the highest measured temperature (292 K). Arrows indicate the spectral resolution

Fig. 14

Wavelength of the centroid of toluene fluorescence spectra calculated for the region from 275 to 360 nm as a a function of pressure and b a function of temperature. Lines (spline fits) were added to guide the eye

4.3 Implications for temperature measurements

Quantitative LIF measurement techniques generally exploit that the absorption and fluorescence properties of the fluorophore, or rather the combination of both, can be related to a physical property (temperature, pressure, concentration, bath gas composition) [1]. Two-color detection schemes are often used to measure the spectral change of the fluorescence signal by spectrally separating it onto two detectors. This method is popular [30], since it allows for directly imaging a dependent variable (i.e., the ratio of both detector signals) using a relatively simple setup (single light source with two cameras with different optical filters). However, it requires at least a single-point calibration to account for differences in detection efficiency of both detection channels. This often proves difficult for experiments that only allow calibration under controlled conditions at rest. This applies, e.g., in cases where optical accesses shift spatially due to thermal expansion under operating conditions as we encountered in previous experiments [11]. Fluorescence-lifetime-based methods, on the other hand, measure the fluorescence decay time which can be detected independently of the variable sensitivity of the detection hardware. This makes them especially attractive for challenging environments [12, 13] if spatial resolution is not required or achieved otherwise (e.g., by scanning the laser beam).

To evaluate the suitability of the data for temperature measurements relying on the two measurement schemes discussed above (spectral and lifetime-based), the sensitivity of either was calculated for atmospheric pressure as an example. For the lifetime-based scheme, we assumed that fluorescence lifetime is measured, while the properties of interest are interpolated from the tabulated lifetime data. For the spectral method, we used the single-color excitation (266 nm) and two-color detection scheme employed by Kranz et al. [53] for anisole and Gamba et al. [5] for toluene to calculate the signal ratio based on their respective spectral filter sets. Since Gamba et al. used two independent optical paths, each camera was equipped with its own filter, a 280-nm (± 5 nm) bandpass and a 305-nm longpass (colored glass), respectively (Fig. 15b). Their choice was based on previous work, where the suitability of different filter sets based on sensitivity and signal-to-noise ratio was considered [23]. In the case of Kranz et al., the optical paths of both channels partly overlap until the light is separated by a dichroic beam splitter (310-nm cut-off wavelength) before it reaches the cameras individual filters, a 280-nm (± 10 nm) and a 320-nm (± 20 nm) bandpass. Additionally, each camera is equipped with a 266-nm longpass filter to block scattered laser light. The resulting filter curves (Fig. 15a) have been calculated from the manufacturer’s (Semrock) datasheets.

Fig. 15

Spectra and filter curves for a hypothetical two-color detection scheme to measure temperature based of the optical filter sets used by a Kranz et al. [53] for anisole and b Gamba et al. [5] for toluene

The resulting signal ratios R = S_blue/S_red for are shown in Fig. 16 for a (a) temperature variation at p = 1000 mbar and (b) pressure variation at T = 274 K. For better comparison to the evolution of the fluorescence lifetime data, both R and τ_eff are normalized their ambient value and are further referred to as the normalized dependent variable Γ. The dashed lines in Fig. 16a represent second-order exponential functions that have been fitted to Γ. These have been used to calculate the sensitivity shown in Fig. 16b defined as the absolute normalized change of Γ over the normalized change of the temperature.

Fig. 16

a The experimentally-accessible independent variable Γ normalized to ambient conditions of a temperature series at 1000 mbar and b the according sensitivities of the hypothetical measurement schemes calculated from a second-order exponential fit (shown as dashed lines in a)

The lifetime-based method outperforms the spectral method in the case of toluene regarding its sensitivity, especially in the higher temperature region. In the lower temperature region, however, the sensitivities are similar. For anisole, the spectral method yields a higher sensitivity also showing a positive trend with decreasing temperature. In all cases, one would have to consider the achievable signal level of each method. For the spectral method, e.g., one may opt for a different filter pair to trade off some sensitivity for increased signal-to-noise ratio which is especially important for ratiometric methods [30]. For measurements in steady-state applications where averaging does introduce only minor statistical error, one may choose the opposite.

5 Conclusions

Effective fluorescence lifetimes (Table 1) and higher resolution (0.27 nm) fluorescence spectra of anisole and toluene vapor in nitrogen have been studied for 266-nm excitation in a temperature range below ambient (257–293 K) for various pressures (100–2000 mbar), thus extending the available datasets for these common aromatic tracer-LIF species to conditions prevalent, e.g., in trans-/supersonic flow experiments. The measured dataset enables thermometry or even pressure sensing (if temperature can be established otherwise, e.g., by laser-induced thermal acoustics [54]) under such conditions using either fluorescence lifetime-based or spectral (single-color or two-color-ratio) LIF schemes. We found that thermometry using toluene LIF with a lifetime-based measurement scheme could compete with the sensitivity achieved with a commonly applied spectral ratiometric method. It is important to note that the lifetime-based measurement scheme, contrary to the spectral-method, does not require a single-point calibration making it particularly useful in applications where controlled reference-conditions cannot be achieved easily. Furthermore, this method allows measurements with a single light source and single detector independent of tracer concentration without the need of ratioing (i.e., introducing additional error), which is highly useful to measure temperature or pressure in, e.g., mixing flows.

Table 1 Effective fluorescence lifetimes of toluene and anisole for the complete parameter set

The transition from photo-induced cooling (PIC) to photo-induced heating (PIH) behavior was observed for toluene between 283 and 292 K, confirming predictions from literature [32]. As this transition marks the point where the initial energy after excitation equals the thermal energy in the S₁ state (E_initial = E_therm,1), no vibrational relaxation occurs during deexcitation since the molecule is already thermalized. This enables the calculation of the averaged ground state energy Ē_therm,0 transferred from S₀ to S₁ for the given excitation wavelength from a straight-forward energy balance [46]. Baranowski et al. [46] recently identified the (usually) unknown Ē_therm,0 is a major cause of uncertainty in stepladder models. Hence, these points are crucial for model validation and development.

For anisole, a broadening of fluorescence spectra correlating with decreasing fluorescence lifetimes with total pressure was observed while for toluene the spectra remained nearly invariant to pressure. This is consistent with the literature [52] identifying sub-nanosecond intramolecular vibrational energy redistribution (IVR) as the responsible mechanism, which is more dominant at conditions where fewer collisions with bath gas molecules occur (i.e., in the case of short excited state lifetimes, low density, and low temperatures). Published stepladder fluorescence models [40,41,42] neglect IVR since they were parameterized for above-ambient conditions. Our findings imply that accounting for IVR will be crucial for advancing these models to below-ambient conditions.

Appendix

All measured effective fluorescence lifetimes measured for both tracers are summarized in Table 1. At the present time we are preparing to launch an online database dedicated to sharing and visualizing published and unpublished spectroscopic data for gas-phase tracer-LIF applications [55] to which the data including the fluorescence spectra will be uploaded.