1 Introduction

In 2018, the DynPT project was started [1, 2], co-funded by the EU and the participating member states within the EMPIR research programme. One of the goals of the project is the investigation of methods for dynamical calibration of pressure transducers (pressure sensors), like they are used in manufacturing, automotive engines [3], and safety testing of ammunition [4]. Typical pressure pulses are a few milliseconds long with peak amplitudes of several 100 MPa. One of the contributions by Physikalisch-Technische Bundesanstalt (PTB) is the characterization of a drop-weight apparatus for the generation and interferometric monitoring of short, high-amplitude pressure pulses (Fig. 1), with the goal of providing calibration services for dynamic pressure up to 800 MPa. The initial setup was constructed within the framework of an earlier project [5].

Fig. 1
figure 1

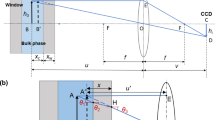
The PTB drop-weight apparatus for dynamic calibration of pressure transducers. Top: a steel ball (12 cm in diameter) drops from a maximum height of 1 m onto a steel piston inserted into a pressure cell. A vibrometer sends a laser beam through the pressure cell and receives the retroreflected beam for interferometric analysis of the index of refraction of the hydraulic fluid. Bottom: the pressure cell with its cylindrical bearing for the piston, the Kapton retaining string, the two slots for piezoelectric pressure transducers, and the volume between two sapphire windows giving optical access to the hydraulic fluid

Full size image

Currently, the calibration of pressure transducers typically is performed in a static [6] or in a quasistatic [7] way. The customer’s transducer (device to be calibrated) is connected to a vessel filled with a gas or a liquid. Static pressures or sudden pressure steps (quasistatic) are applied, with an amplitude that is precisely known. The response of the customer’s transducer is recorded and compared to the applied pressure, to give the calibration curve of the transducer. A typical target uncertainty for the calibration curve is 1% or better. This means that the pressure applied must be known (traceable) with respect to the unit of pressure in the international system of units (SI) with even lower uncertainty, to leave room for the additional sources of uncertainty affecting the transfer to the device to be calibrated.

Anecdotal evidence states that different pressure transducers calibrated to the same static standard can exhibit strongly different dynamic behavior. It is therefore of interest to investigate whether a dynamic calibration might mitigate this difference. Several groups are working towards this goal, see for example [2, 8,9,10,11,12,13]. A particular challenge is the transfer of SI traceability from static pressure, where well established primary standards are available, to dynamic pressure, where work on providing standards with the required characteristics (pressure range, frequency range, uncertainty) is still in progress.

Several principles have been used to construct devices for the non-destructive generation of strong pressure pulses, i.e., stronger than can in general be reached by shock tubes [14, 15]. They include, for example, fast opening valves [7], the use of a commercial drop-weight apparatus [16], a drop-weight apparatus designed for secondary calibrations using two piezoelectric sensors [8, 17], a drop-weight apparatus measuring pressure via the monitoring of the deceleration of the piston [9, 18, 19], an air gun [16], a pressure-tank setup [10], or optical absorption spectroscopy [11]. Diamond anvil cells [20], well known for the very high pressures they can exert on small samples, necessarily need to be small-volume devices, too small to permit attaching a customer’s transducer (typical sensor casings use M10 or M12 threads).

The distinguishing characteristics of the drop-weight setup discussed here is that the pressure measurement is performed with a laser heterodyne interferometer, via the pressure-dependent index of refraction of the hydraulic fluid compressed by the impacting weight [21, 22]. In principle, this makes dynamic pressure directly traceable to static pressure. In a first step, one applies a series of well-known static pressures to the cell and measures the corresponding change in optical path length, which is closely proportional to the change in index of refraction. In a second step, one can use this relation between pressure and optical path length also for pressure pulses, making use of the fact that the change in index of refraction is instantaneous on the scale of the development of the millisecond pressure pulse. In this way, any dynamic pressure pulse shape can be measured interferometrically and scaled to the SI-traceable static pressure via the statically determined relation between pressure and optical path length. In principle, this provides an ideal input for the modeling of the dynamical properties of the transducer itself [23].

The best choice of hydraulic fluid is a tradeoff between a number of material parameters. Here we report on the results of experiments with three different hydraulic fluids: sebacate, glycerol, and water. In all three cases, a difference between static and dynamic pressure curves is found. This can be traced back to the different thermodynamic processes at work in the static case (isothermal) and in the dynamic case (mostly adiabatic). It had been expected that some difference would exist [21]. Here we show the magnitude of the effect and what it means for the prospect of using the apparatus for dynamic calibration of pressure transducers.

2 Transferring static to dynamic traceability

The idea behind the direct transfer of static to dynamic traceability for pressure measurements is as follows [21]. In a first step a series of static pressures is applied to an optically transparent hydraulic medium, for instance sebacate. This pressure is measured with a first sensor that has been calibrated by applying static pressure in a traceable calibration device. The fluid in the cell forms part of the optical path in one arm of a laser interferometer. Under pressure, the density of the fluid changes, and therefore its index of refraction. This pressure dependent change in optical path length is detected by the interferometer. With a series of static pressures, the dependence of index of refraction on pressure can be determined.

When in the same general setup a pressure pulse is applied the interferometer measures the dynamic change of the optical path length during the pulse. Using the relation between index of refraction and pressure determined previously one can rescale the axis from optical path length to pressure. In this way, the static calibration of the pressure sensor used for the first (static) part of the experiment is transferred to the sensor used in the second (dynamic) part (which could be the same or a different sensor).

The Clausius–Mossotti equation provides a relation between the density \(\varrho\) of a medium and its index of refraction \(n_{\mathrm {fl}}\):

$$\begin{aligned} n_{\mathrm {fl}}^2=\frac{1+2\varrho k}{1-\varrho k} \end{aligned}$$
(1)

with

$$\begin{aligned} k=\frac{N_{\mathrm {A}} \beta }{3\varepsilon _0 M_{\mathrm {mol}}}. \end{aligned}$$
(2)

Here \(\beta\) is the molecular polarizability, \(N_{\mathrm {A}}\) the Avogadro constant, \(M_{\mathrm {mol}}\) the molar mass, and \(\varepsilon _0\) the permittivity of vacuum.

For isothermal processes, like in the static pressure calibration mode of the apparatus, the density change is related to the pressure change by the isothermal compressibility \(\kappa _{T}\):

$$\begin{aligned} \frac{\mathrm{d}\varrho }{\varrho }=\kappa _{T} \mathrm{d}p. \end{aligned}$$
(3)

For the dynamic case, the heat of compression must be taken into account, with the adiabatic compressibility \(\kappa _{S}\) [24]

$$\begin{aligned} \frac{\mathrm{d}\varrho }{\varrho }=\kappa _{S} \mathrm{d}p =\left( \kappa _{T} - \alpha \frac{\partial T}{\partial p} \right) \mathrm{d}p. \end{aligned}$$
(4)

Here \(\alpha\) is the coefficient of thermal volume expansion at constant pressure.

3 Experimental setup

3.1 The main hardware

The experimental setup is based on a commercial drop-weight apparatus, specially modified for use in a dynamic pressure standard (Fig. 1). A steel ball (diameter 12 cm, mass 7 kg) is held by an electromagnet and can be dropped on command. After a free fall from an adjustable height of up to 1 m it hits a steel piston that slides inside a cylindrical bearing at the top of a pressure cell filled with a hydraulic fluid. Two side channels lead to piezoelectric pressure transducers. Two sapphire windows on opposite sides of the pressure cell provide an optical access to the fluid. Light from a commercial laser vibrometer [25] (wavelength 633 nm) passes through the windows and the fluid, is retroreflected outside the cell, passes through the cell a second time, and travels back into the vibrometer for heterodyne interferometric analysis. The vibrometer (model Polytec OFV 505 with controller OFV-5000, velocity decoder VD-09, and distance decoder DD-900) calculates the one-way optical distance to the retroreflector (i.e., the spatial integral over the index of refraction along the laser path, divided by 2). This output as well as the signal amplitude are recorded during the experiments.

In addition, two pizeoelectric sensors are installed in the two slots in the cell. Both of them were calibrated at PTB using a pressure-step device with a fast-opening valve [7]. These sensors are read out in parallel to the vibrometer signals. In a future use of the drop-weight device for sensor calibration, one or both slots would be used to mount the device(s) to be calibrated.

When the ball hits the piston it compresses the fluid up to a maximum pressure at minimum volume, after which the system bounces back. The ball ascends and then falls back again, where it is blocked from hitting the piston a second time by a tray that initially rests below the piston and rapidly moves upwards after the impact of the ball onto the piston. Figure 2 shows a typical pressure curve, as registered by the interferometric measurement and by one of the piezoelectric sensors, for sebacate as the hydraulic fluid. The term “change of optical path length” refers to the difference of the observed path length from that at ambient pressure.

Fig. 2
figure 2

Pressure vs. time and change of optical path length for the fast pressure pulse during impact of the dropping ball (sebacate, drop height 1 m)

Full size image

A key advantage of the setup is that the exact shape of the pressure pulse does not matter. Whatever that shape is, it is followed by the optical path change (Fig. 3). There is a small pressure-dependent hysteresis of about 0.4% (at 300 MPa), in that the optical path length for the falling edge of the pressure pulse is slightly smaller than for the increasing edge. This has to be taken into account in the analysis of measurement uncertainty.

Fig. 3
figure 3

Change of optical path length as a function of the dynamic pressure measured by a piezoelectric transducer, for sebacate as the fluid. The inset gives an indication of the small hysteresis between the sections for increasing and for decreasing pressure

Full size image

The change in optical path length is about 2 mm for the largest drop height and sebacate as a fluid, or about 3000 wavelengths of the 633 nm light. In an auxiliary experiment, it was investigated whether the interferometer is fast enough to handle the large slew rate during the pressure pulse. The retroreflector was replaced by a \(45^\circ\) mirror and more optical components (mirrors, beamsplitter), so that after a first pass through the cell the interferometer beam is routed around the cell back into the vibrometer, instead of through the cell. In this way, the slew rate is halved. Except for this factor of 2, no change to the signal was observed at the 0.3% level, which is about half the hysteresis between the data traces for the increasing and the decreasing edge of the pressure pulse (Fig. 3). This indicates that the vibrometer is fast enough to track the changes in index of refraction even in the standard double-pass configuration. At the same time, it gives an impression of the reproducibility of individual curves, because the single- and double-pass measurements were performed three weeks apart.

Special care has to be taken with the filling of the cell to avoid trapping air bubbles, especially near corners. A judicious technique involving tilting of the cell and use of a syringe filled with fluid is applied. A look through the optical windows can serve as a partial quality control. For best results, de-gassed fluids should be used [26].

3.2 Piston movement and the “squid” effect

A high-speed camera was focused on the top of the piston. Movies with up to 125,000 frames per second showed the details of the piston movement during and after the impact of the falling ball. Using markers glued to the piston an automatic routine extracted the position of the piston from the video frames, with sub-pixel resolution (Fig. 4).

Fig. 4
figure 4

Motion of the top of the piston, as determined by inspection of the video frames taken with a high-speed camera, for the case of sebacate. When the ball hits the piston the latter is not pushed into the fluid smoothly but repeated elastic collisions “hammer” it in. The small ripple on the position curve for larger times is attributed to the finite resolution of the sub-pixel video extraction algorithm

Full size image

During the pressure pulse phase, the overall motion of the piston follows a half-sine shape (Hooke’s law). A closer inspection of the beginning of the pressure pulse reveals that the ball is not pushing the piston into the fluid in a smooth motion. Instead, upon first impact, the piston is projected into the fluid by the elastic collision. Due to its much smaller mass it separates from the ball and travels faster into the fluid than the ball (Fig. 4). This motion is strongly impeded by the increasing pressure in the fluid, so that after a short while the falling ball has caught up with the piston and collides with in again. This repeats in quick succession until no more separation of ball and piston can be seen in the video frames. So one could say that the piston is not pushed into the fluid but hammered in. The whole process happens within the first 0.5 ms of a pulse that is typically 4 ms \(\ldots\) 6 ms long. Even for the largest drop height of the ball, the initial velocity of the piston is below 10 m/s. This is far below the speed of sound in all materials involved so that shock wave formation is not an issue.

The step-like character of the piston movement is not visible in the output signal of the piezoelectric sensors because of the presence of acoustic resonances in the narrow channels leading from the main volume of the cell to the pressure sensors. The observed frequencies (at around 10.5 kHz for sebacate) correspond to the resonance frequency of an organ pipe of the same length, closed at one end. This identification is supported by two findings. Firstly, the oscillation frequencies observed in the signals of the two sensors are in a ratio of 1.11, which is exactly the inverse ratio of the lengths of the channels leading to the sensors. Secondly, the oscillation frequency changes for the three fluids in accordance with their different speeds of sound. For water the oscillation frequency is 11 kHz, whereas for glycerol it is 14 kHz. Since the oscillations are not of concern for the intended use of the apparatus as a calibration facility (they can easily be suppressed by placing a thin sheet of rubber or felt on top of the piston), the details of those oscillations have not been investigated further.

In the initial experiments the Kapton retaining string (Fig. 1) was not used. Therefore, at the end of the pressure pulse the piston was free to propagate upwards above its resting position with the kinetic energy it had acquired on the way up. It overshot about a centimeter before returning to its resting position in an overdamped motion. During this phase, the signal amplitude received at the vibrometer dropped to zero shortly after the pressure pulse. This phenomenon was investigated with the help of the high-speed camera. A light source was place in front of one cell window, and the fast camera, looking through the other window, focused to approximately the center of the cell.

Initially, the fluid is transparent and remains so until just after the pressure pulse is over, i.e., when the ball has separated from the piston on the way up. It is shortly after this time of separation that—coming from the channel leading to the piston—a “dark cloud” penetrates the optical volume (Fig. 5), causing the vibrometer signal to drop to zero. The visual effect is similar to ink being injected from above, like from a squid trapped inside the cell.

Fig. 5
figure 5

Four frames of a video (120,000 frames per second) showing the blocking of the path of the vibrometer laser beam once the piston is overshooting its resting position. The bottom frame corresponds to the beginning of the phase where the path clears again but where several smaller “defects” remain for a minute or more. The second frame was taken 0.467 ms after the first, the next 1.367 ms later, and the last one another 6.425 ms later

Full size image

The explanation is not absorption but scattering. When the piston is above its resting position, i.e., when the total volume below the piston is larger than it was initially, a hole is created in the fluid [27] that turbulently propagates into the volume between the windows and scatters the light out of the straight optical path. Part of this scattered light can be seen in the video as quickly moving spots of light reflected off the inner wall of the cell.

To avoid this cavitation-like effect a small ring was fixed around the top of the piston and two Kapton strings attached to it from below (Fig. 1). The piston can still freely enter the fluid but is held back on the way up once it reaches its resting position. With the strings in place, no more cavitation can be seen for either of the three fluids examined here. High-speed movies with a fine rectangular grid imaged through the pressure cell do not reveal optically relevant turbulence within the fluid during the pressure pulse. However, in the case of glycerol a small transient lensing effect can be seen shortly after the pulse. For sebacate, no optical indication of a phase transition is evident, as expected given that the maximum pressure reached here is much lower than the 1180 MPa transition pressure of sebacate [28]. Likewise, for water as a hydraulic fluid the phase transition to ice VI at pressures above 620 MPa [29] cannot be reached.

The “squid effect” might also be at play, possibly unnoticed, in other drop-weight devices or even other dynamic-pressure devices. Although it occurs only after the pressure pulse is over, there are lingering effects of turbulence and persistent gas bubbles, particularly in sebacate. One could imagine that the shape of a subsequent pressure pulse might be affected by this mixed state of the fluid if the waiting time is too short [26]. We have found that one needs to wait a minute or more for the visible perturbations to clear away. One could envision that there might be bubbles permanently getting stuck in the small ducts leading to the piezoelectric pressure sensors, potentially changing their effective response [26]. This might need to be taken into account for devices that calibrate a pressure sensor by comparison to a second, reference sensor.

3.3 Energy loss

For sebacate, the 7-kg ball dropping from a height of 1 m bounces up again to about 92 cm. Therefore, only 8% of the initial potential energy of 69 J is lost in the process, indicating that the overall process of compression and relaxation is mostly adiabatic. This is consistent with the net mechanical work performed on the fluid, as calculated by integrating the product of volume displaced by the piston and pressure.

If all of the “missing” energy for the largest drop height would have been converted into heat within the sebacate it would warm up by about 1.6 K. Given that the dimensions of the fluid-filled structures are rather small, surrounded by thick metal walls, this small amount of heat is dissipated quickly. Also, the cell itself will not heat up appreciably. Therefore, a subsequent drop of the weight will not be affected by the heat deposited during the previous drop.

However, this does not mean that no thermal effects occur. Based on the data in [30] one can estimate a transient temperature rise of about 30 K during a compression to 400 MPa. This has consequences for the quantitative analysis, see Sect. 5 below.

3.4 Cell expansion and window movement

To investigate the effect of cell expansion under pressure, in particular window movement, the vibrometer was focused on the entrance facet of the closer optical window so that it measured its movement along the laser beam direction during impact of the falling ball. A second vibrometer placed on the other side of the sebacate-filled cell measured the displacement of the other window. The sum of the displacements gives the expansion of the sebacate-filled cell as a function of time during the pressure pulse, showing an almost perfectly linear relation with a slope of \(0.201\,\upmu\)m/MPa (Fig. 6).

Fig. 6
figure 6

The outward motion of the windows under pressure is proportional to measured pressure, with only a 1% hysteresis between rising and falling edge of the pressure pulse

Full size image

With Young’s modulus for bulk steel, \(E\approx 200\) GPa, one obtains an estimate for the expected geometric length change \(l\times p/E=57\,\upmu\)m for the cell with an optically relevant length of the fluid of \(l=34\) mm and a pressure of \(p=300\) MPa. This is in good agreement with the experimental observation of \(60\,\upmu\)m.

There is only a small hysteresis of less than 1%, as seen from the residuals of the linear fit curve (Fig. 6). It might be due to thermal expansion of the cell due to the heat pulse associated with the compression of the liquid. For the purposes of interest here, we can ignore the small oscillations (about 40 nm amplitude) on the residuals.

Since the cell expansion under pressure also appears in the static calibration curve for optical path length vs. pressure, the hysteresis has no effect for the traceability from static to dynamic pressure. This, however, assumes that cell expansion is basically instantaneous, which appears reasonable given that the speed of sound in steel is 5 m/ms and that the cell is only centimeter-sized.

In principle, the cell expansion needs to be taken into account when converting from pressure to index of refraction because the expansion is linear in pressure whereas the Clausius–Mossotti relation is non-linear (see Sect. 2). However, the effect only makes a contribution of order p/E with respect to the pressure-induced change in index of refraction of the fluid. Even for a pressure of 400 MPa, p/E is only \(2\times 10^{-3}\). It is therefore neglected here for the time being but eventually should be included in an uncertainty budget.

Thermal expansion of the cell is of order \(0.34\,\upmu\)m/K, based on literature data for steel. Since the average thermal effect on the cell is not more than 1.6 K (Sect. 3.3) and the maximum repetition rate is less than one ball drop per minute, thermal expansion of the cell can be neglected on average. The transient heating of the fluid of several 10 K during the pressure pulse does not have much of an effect here, either; even under the unrealistic assumption of perfect and instantaneous heat transfer from fluid to cell body the thermal expansion of the cell would amount to not more than 1% of the optical path change.

4 Static calibration

To obtain the dependence of index of refraction on the static pressure the setup was modified. The piston was removed and a high-pressure line installed in its place; it sealed the cell tightly. The other end of the line was attached to the output of a pressure generator with a mechanical spindle. Initially, this was a hand-operated model. However, turning the handle was adding too many vibrations to the setup, including pressure spikes the vibrometer could not follow completely. Instead, an electric motor with a reduction gear was attached to the pump. When running at full speed, the motor turned the pump such that the pressure increased from ambient to 400 MPa over the course of 2 h. This pressure was measured with a strain-gauge based sensor (HBM model P2VA1/5000bar) statically calibrated against the national standard at PTB. The vibrometer output was monitored in parallel.

In Fig. 7 the results of the static calibration are collected for sebacate, glycerol, and water (dashed lines). Because of the slow pressure increase the compression of the fluid corresponds to isothermal conditions.

Fig. 7
figure 7

Relation between pressure and change of optical path length for the case of sebacate, glycerol, and water (dashed lines: static pressure applied; solid lines: dynamic pressure applied)

Full size image

5 Dynamic measurement

The solid lines in Fig. 7 denote the pressure curves for the dynamic case. Except for the maximum pressure reached, these curves are independent of drop height. When plotting the curves for different drop heights on top of each other they visually overlap completely.

For the same optical path change the pressure in the static (isothermal) case is lower than in the dynamic (adiabatic) case. Since the optical path length is related to molecular density (Clausius–Mossotti relation), it means that the heat of compression in the dynamic case increases the pressure in the fluid compared to the same density in the static (isothermal) case. For water, the difference is less than 1%, for sebacate about 20%. As a consequence, the direct transfer of static traceability to dynamic measurements is not possible. Instead, one has to correct for the difference of isothermal and adiabatic behaviors using material parameters. This is discussed further below.

From a look at Fig. 7 one could gain the impression that water should be the best choice of fluid because the difference between isothermal and adiabatic behavior is very small; also, there is a wealth of data on the thermodynamic properties of water as a function of pressure and temperature that can be used to obtain the correction factor. However, the damping of the organ pipe resonances is low so that they extend all the way to the pressure maximum and beyond. The low viscosity of water makes it hard to seal the piston in its bearing while still allowing it to slide more or less freely under the impact of the ball. During the compression phase, water squirts out of the seal; this loss of water makes it necessary to refill the cell after only a few ball drops, a very time-consuming procedure and impractical in everyday use. In addition, the cell leakage means that only small dynamic pressures can be applied because of the risk of driving the piston too far into the cell where it might damage the cell. And finally, even after just a few hours, there are visible corrosion effects within the cell and on the piston. Overall, water is not a suitable fluid for the intended purpose.

Compared to sebacate, glycerol has the advantage of a smaller difference between isothermal and adiabatic response. There is more data on the properties of glycerol available; however, with glycerol being hygroscopic, the water content needs to be taken into account, as a parameter that is hard to control. Furthermore, the pulses are noticeably non-symmetric. For example, there is a hysteresis of 4.7% near 200 MPa, compared to only 1.4% for sebacate; this hysteresis decreases for higher pressures (like in Fig. 3).

In Fig. 8 the pressure curves for the static and the dynamic case have been plotted again for sebacate as the hydraulic fluid. In addition, the upper solid line (blue) shows the result of a “correction” or rescaling applied to the dynamic pressure curve to take account of the difference between the isothermal and the adiabatic process. To derive the rescaling factor r, one considers the ratio of optical path changes for the two processes:

$$\begin{aligned} r=\frac{n_{\mathrm {iso}}-n_0}{n_\mathrm {adi}-n_0}, \end{aligned}$$
(5)

with \(n_0\) being the index of refraction at ambient pressure. The indices of refraction can be expressed in terms of densities, using the Clausius–Mossotti equation (1). With a first approximation step

$$\begin{aligned} \sqrt{\frac{1-k\varrho _0}{1-k\varrho _{\mathrm {iso}}}}\approx 1, \end{aligned}$$
(6)

which is correct to within 3% for the experimental parameters here, and similarly for \(\varrho _\mathrm {adi}\), one arrives at

$$\begin{aligned} r\approx \frac{\sqrt{1+2k\varrho _{\mathrm {iso}}}-\sqrt{1+2k\varrho _0}}{\sqrt{1+2k\varrho _\mathrm {adi}}-\sqrt{1+2k\varrho _0}}. \end{aligned}$$
(7)

Using the approximation \(\sqrt{a+\epsilon }-\sqrt{a}\approx \epsilon /2\sqrt{a}\) for \(\epsilon \ll a\), one obtains

$$\begin{aligned} r\approx \frac{\exp (\kappa _{T}\Delta p)-1}{\exp (\kappa _{S}\Delta p)-1}, \end{aligned}$$
(8)

where \(\Delta p\) stands for the difference between final and initial pressure of the adiabatic compression. The exponents are small, so the exponential can be expanded to first order, giving a very simple equation for r:

$$\begin{aligned} r_\mathrm {approx}=\frac{\kappa _{T}}{\kappa _{S}}. \end{aligned}$$
(9)
Fig. 8
figure 8

Comparison of pressure and change in optical path length for the case of sebacate. The upper solid line (blue) is derived from material constants given in the literature and explained in the main text

Full size image

A more rigorous approach starts from Eq. (4). The partial derivative \(\partial T / \partial p\) has been examined by Ardia [31]. He approximates his experimental results by the polynomial

$$\begin{aligned} \left\{ \frac{\partial T}{\partial p}\right\} =a+bT+cp+dT^2+ep^2+fTp, \end{aligned}$$
(10)

where the coefficients \(a\ldots f\) have the numerical values \(0.0775689, -0.000070866, 0.00011502, 1.82827\times 10^{-8}, -2.3313\times 10^{-7},\mathrm {and\ }-1.9837\times 10^{-8}\) when T, the starting temperature for the adiabatic compression, is given in \({}^\circ\)C and the pressure p in MPa. No measurement uncertainty is available for these parameters.

Integration of Eq. (4) for an adiabatic process starting at pressure \(p_\mathrm {start}\) and ending at pressure \(p_\mathrm {end}\) is straightforward, when \(\alpha\) is assumed constant (for lack of better knowledge):

$$\begin{aligned} \varrho _\mathrm {end}&=\varrho _\mathrm {start}\exp [(\kappa _{T}(p_\mathrm {end}-p_\mathrm {start})]\exp (-x)\end{aligned}$$
(11)
$$\begin{aligned}&=\varrho _{\mathrm {iso}}\exp (-x), \end{aligned}$$
(12)

where

$$\begin{aligned} x= & {} \alpha \left[ (a+bT+dT^2)(p_\mathrm {end}-p_\mathrm {start}) \right. \nonumber \\&\left. +(c+fT)(p_\mathrm {end}^2-p_\mathrm {start}^2)/2+e(p_\mathrm {end}^3-p_\mathrm {start}^3)/3 \right] . \end{aligned}$$
(13)

The densities \(\varrho _{\mathrm {iso}}\) and \(\varrho _\mathrm {adi}=\varrho _\mathrm {end}\) can be inserted into the Clausius–Mossotti relation and then Eq. (5) to obtain the full formula for the rescaling factor r. For the conditions here, the approximation Eq. (9) matches the full formula (5) to within better than 2%.

The dynamically measured curve in Fig. 8 (lower solid line) is multiplied by this \(p_\mathrm {end}\)-dependent factor r, to give the upper solid line (blue). It falls on top of the statically measured curve, even though the process is not fully adiabatic (see Sect. 3.3) and knowledge of material parameters is not complete. The agreement demonstrates that one can account for the complete difference observed between the static and the dynamic pressure curves by correcting for the difference between isothermal and adiabatic compressibility of the hydraulic fluid. This correction can be applied either way, depending on the intended purpose. Here it was used to trace back from dynamic to static pressure, thus providing a validation of the method.

6 Conclusion

We have examined the effect of adiabatic and isothermal pressure increases on the index of refraction of three different fluids. In the process, important insights into the operation of a drop-weight apparatus were obtained, with possible consequences for other devices, in particular regarding the effects of cavitation. The operation and signal generation in our own device is now fully understood.

As a side benefit, the literature values for thermodynamic properties of sebacate (an important hydraulic fluid) were cross-validated (Fig. 8) by making use of the Clausius-Mossotti relation between density and index of refraction.

The difference between the static and the dynamic curves (Figs. 7, 8) can be explained by the difference between an isothermal and an adiabatic process. This means that for the pressures and timescales used here a dynamic calibration of the pressure transducers is not necessary: a static calibration gives the same result. Or in other words, a dynamic calibration would not bring benefits in terms of a more precise calibration for sensors used in a dynamic mode (on the time scale of a few milliseconds). This is not surprising, since it is known that the resonance frequencies of the transducers for dynamic pressure used here (Kistler model 6215 and Kistler model 6213BK) are much higher than the highest Fourier frequencies contained in the temporal shape of the half-sine pressure pulse generated by the falling ball (approximately 250 Hz). The higher frequencies represented by the oscillations like those illustrated in Fig. 4 cannot be used to probe higher Fourier frequencies of the sensor response because they do not appear in the optical signal, as discussed above.

Because of the large difference between the static (isothermal) and the dynamic (adiabatic) behavior of the hydraulic fluid it will not be possible to use the apparatus as originally planned, i.e., as a realization of a direct transfer of static to dynamic traceability. A correction will have to be applied, based on the mathematical model (Eq. 4) and literature data for the material constants.

The next step in the project will be an evaluation of the measurement uncertainty that might be attained with the drop-weight device when the adiabatic-isothermal correction is applied. It will be interesting to see whether this uncertainty comes out low enough to be of interest for a calibration service.

Furthermore, one could envision using the apparatus to determine material constants for compressibility under isothermal and adiabatic conditions over a wide pressure range.