1 Introduction

Spectral broadening and pulse compression of ultrashort pulses from high-peak power lasers (10 MW–GW) are typically performed in gas-filled capillaries, photonic bandgap or Kagome-type hollow core photonic-crystal fibers (HC-PCF) [1]. Especially, spectral broadening in gas-filled hollow core fibers has been proven a powerful tool for the temporal compression of high-average and peak power lasers, yielding, for example, a 16-fold compression to 88 fs at > 100 W of average power by spectral broadening in a single argon-filled Kagome HC-PCF in the normal dispersion regime in combination with a chirped mirror compressor [2]. By choosing an appropriate combination of gas and pressure, HC-PCFs can, furthermore, be operated in the anomalous dispersion regime [3], where the generation of < 10 fs pulses has been demonstrated in a two-stage Kagome-fiber system seeded by a Kerr-lens mode-locked thin-disk oscillator [4]. Despite providing an efficient measure for temporal pulse compression with excellent beam quality, fiber-based spectral broadening is alignment sensitive and couples pointing-drifts to laser power fluctuations. Additionally, fibers show increased susceptibility to damage at high-average and peak powers. Moreover, photoionization in gas-filled HC-PCFs might limit their use in high-average power systems at high repetition rates [5, 6].

Lately, a new spectral broadening method relying on a waveguide-like periodic assembly consisting of focusing elements (concave dispersive mirrors) and nonlinear media was suggested and demonstrated [7,8,9,10]. Both, all-bulk and gas-filled geometries were successfully realized in high-average and peak power regimes, pushing the broadened spectrum to sub-10 fs Fourier limit and pulse durations to sub-30 fs in a highly robust and simple manner [11,12,13,14,15]. As one of the main advantages of this concept, the sign of the overall net dispersion and its profile including higher order dispersion terms can be readily engineered in the quasi-waveguide. To date, such multi-pass cells (MPC) have mainly been operated in the zero- or normal dispersion regime. However, the advantages of MPC-based spectral broadening become increasingly interesting at high peak power levels in combination with operation in the anomalous dispersion regime where self-compression, Raman soliton self-frequency shifting, supercontinuum generation and other highly nonlinear effects are expected to come into play [16].

Only recently, self-compression in an all-bulk Herriott-type MPC has been demonstrated in a fiber amplifier-seeded OPCPA system delivering 63 fs pulses with 19 µJ at 125 kHz repetition rate and a wavelength of 1550 nm [17]. The MPC was operated in the anomalous dispersion regime using a 2-mm fused silica (FS) plate as broadening medium, exhibiting a slightly negative group velocity dispersion (GVD) of − 28 fs2 at 1550 nm. However, the absence of suitable materials with negative GVD prohibits a similar approach at 1 µm wavelength where high-power ytterbium (Yb)-based lasers are readily available.

Here, we show that self-compression can be realized in an all-bulk multi-pass geometry driven directly by a powerful thin-disk oscillator. The MPC is operated in the net negative dispersion regime. The dispersion is provided by the anomalously dispersive mirror coating which slightly overcompensates the normal dispersion of the broadening substrate. The demonstrated output peak power of 140 MW and pulse duration of 31 fs with an overall efficiency of more than 85% clearly competes with the soliton self-compression demonstrated in gas-filled Kagome fibers [4]. Importantly, it paves a way towards exploiting various nonlinear soliton propagation regimes at unprecedentedly high peak power and pulse energy levels.

2 Experimental setup and results

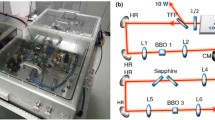
The experimental setup is sketched in Fig. 1. The driving laser is a high-power Kerr-lens mode-locked thin-disk Yb:YAG oscillator emitting 136 W average power at 10.6 MHz with 12.8 μJ pulse energy and a pulse duration of 300 fs resulting in 38 MW peak power [18]. The oscillator output is mode matched to a Herriott-type MPC by a beam expander. The MPC comprises a pair of complementary dispersive 2-inch mirrors with 300 mm radius of curvature placed on a common optical axis at a distance of 532 mm. Beam injection and extraction are realized by placing a small scraper mirror in front of one of the cell mirrors. The configuration utilized in this work allows a total number of 46 passes through the 6.35-mm-thick, anti-reflective-coated FS window which is used as a nonlinear medium. To maintain a high quality of the spatial beam profile, a low initial nonlinear phase shift of ~ 0.4 rad per pass was chosen by placing the FS window at a distance of ~ 180 mm from one of the MPC mirrors.

Fig. 1
figure 1

Schematic of the setup. The oscillator output is sent to a commercially available Galilean beam expander for matching the focus size and position to the subsequent Herriott-type MPC. The MPC comprises two complementary dispersive 2-inch mirrors with 300 mm radius of curvature (F1, F2) and a 6.35 mm fused silica (FS) window placed ~ 180 mm from one of the MPC mirrors

Full size image

The dispersive MPC mirrors are designed to have a group delay dispersion of − 150 fs2 at 1030 nm, slightly overcompensating the linear material dispersion of the FS window which is ~ 120 fs2 at this wavelength. However, even with employing a complementary dispersive mirror design, the GDD curve of the mirrors shows significant residual oscillations in the wavelength range from 890 to 1070 nm (Fig. 2). Measurements beyond 1070 nm could not be performed reliably due to the limited responsivity of the utilized silicon photodetector. Upon propagation in the MPC, new frequency components are generated by self-phase modulation (SPM) in the FS window. Due to the operation in the net anomalous dispersion regime, the newly generated frequency components consecutively get temporally compressed by chirp removal. The output pulses are compressed to 31 fs. The Fourier-transform limit (FTL) is ~ 28 fs retrieved from the output spectrum measured by an optical spectrum analyzer (Fig. 3). Importantly, these pulse durations can be achieved without necessitating the use of any additional dispersive optics. The main pulse was found to carry more than 45% of the total pulse energy resulting in a peak power of 140 MW.

Fig. 2
figure 2

Group delay dispersion (GDD) measurements of the utilized MPC mirrors. The measurements were performed on a reference pair of flat 1-inch mirrors. The dashed green lines display the GDD of the two individual sample mirrors. The solid black line displays the arithmetic mean GDD of the two measured complementary curves with a resulting GDD of ~ − 150 fs2 at 1030 nm wavelength. The red line shows the GDD curve for which best agreement between simulation and experiment was found

Full size image
Fig. 3
figure 3

Temporal characterization of the self-compressed MPC output at full input power. a Spectral phase and intensity, compared to reference measurement with an optical spectrum analyzer (OSA); b temporal phase and intensity compared with the Fourier-transform limit (FTL) of the spectrum; c measured SHG-FROG trace, and d reconstructed FROG trace with < 0.0074 error on a 512 × 512 grid. For the temporal characterization measurement, a small fraction of the full power beam was extracted using a broadband AR-coated wedge

Full size image

3 Theory and simulation

Since up to now self-compression has predominantly been studied in fibers, it is instructive to take a closer look at the involved soliton dynamics in the all-bulk case. In analogy to optical fibers, one can define a soliton order in MPCs [17]. Soliton dynamics can then be observed for soliton orders \(N=\sqrt{{L}_{\mathrm{d}}/{L}_{\mathrm{SPM}}} >1.\) Here \({L}_{\mathrm{d}}=\left|{T}_{0}^{2}/{\beta }_{2}\right|\) is the dispersion length where \({T}_{0}\) is the input pulse duration and \({\beta }_{2}\) is the total GVD of the fiber. To account for the discrete, non-negligible mirror dispersion in MPCs, one can replace \({\beta }_{2}\) in the preceding formula by \({\beta }_{2}^{\mathrm{eff}}={\beta }_{2}^{\mathrm{mat}}+GDD/{l}_{\mathrm{mat},}\) where \({\beta }_{2}^{\mathrm{mat}}=18.97 {\mathrm{fs}}^{2}/\mathrm{mm}\) is the GVD of the broadening medium material, \(GDD\) is the group delay dispersion (GDD) introduced by one reflection from the utilized MPC mirror and \({l}_{\mathrm{mat}}=6.35 \mathrm{mm}\) is the thickness of the broadening medium. The influence of SPM is described by \({L}_{\mathrm{SPM}}=c{A}_{e\mathrm{ff}}/{\omega }_{0}{n}_{2}{P}_{\mathrm{peak}}\), where \(c\) is the speed of light, \({A}_{\mathrm{eff}}\) is the effective beam area, \({\omega }_{0}\) is the optical angular frequency, \({n}_{2}\) is the nonlinear refractive index and \({P}_{\mathrm{peak}}\) is the input peak power. For the system presented here, the input pulse duration is \({T}_{0}\)= 300 fs and \({\beta }_{2}^{\mathrm{eff}}\)= − 3.39 fs2/mm, yielding a dispersion length \({L}_{\mathrm{d}}\)= 26.55 m. To calculate the characteristic length for self-phase modulation, we employ \({A}_{\mathrm{eff}}=\pi \cdot {w}_{\mathrm{eff}}^{2}\) using the effective beam radius which is approximated by \({w}_{\mathrm{eff}}=\frac{w\left({z}_{1}\right)+w\left({z}_{1}+{l}_{\mathrm{mat}}\right)}{2}=242 \mu m,\) where \(w(z)\) is the spot size parameter of a Gaussian beam corresponding to the eigenmode of the MPC and \({z}_{1}=86\mathrm{ mm}\) is the distance of the nonlinear medium to the focal plane of the MPC. Assuming a nonlinear refractive index \({n}_{2}\)= (2.46 \(\times \hspace{0.17em}{10}^{-20})\) m2/W at a central wavelength of 1030 nm [19], this results in a characteristic length \({L}_{\mathrm{SPM}}=\)(32.90 ×\(\hspace{0.17em}{10}^{-3}\)) m and a soliton order \(N=28.41.\) The achievable compression ratio and optimal compression distance in fibers have been shown to scale with \(N\) and \(1/N\), respectively [20]. Choosing a large soliton order for our experiments allowed us to achieve a large temporal compression factor of almost 10, albeit, at the expense of a reduced fraction of the energy contained in the main pulse.

For a more detailed understanding of the temporal evolution of the pulse upon propagation through the MPC, simulations were carried out by numerically solving the nonlinear Schrödinger equation using an adaptive step-size implementation of the fourth-order Runge–Kutta in the interaction picture [21]. The simulations were performed on a one-dimensional grid spanning 16 ps in time and using \({2}^{14}\) points, corresponding to a frequency resolution of 0.062 THz. To account for the discrete nature of the quasi-waveguide, each consecutive pass in the MPC was modeled by propagating the pulse through a 6.35-mm-long block of fused silica material and subsequently applying the dispersion curve of the MPC mirror to the pulse. This allows us to closely match the simulation to the experimental conditions where the nonlinear interaction takes place in a net-positive dispersion environment.

For the simulation, we assumed a sech2 temporal input pulse shape, 300 fs initial pulse duration at 1030 nm central wavelength and an input pulse energy of 12.8 µJ at 10.6 MHz pulse repetition rate. The nonlinear interaction inside the fused silica material was modelled by setting \({A}_{\mathrm{eff}}=\left(188.6 \times {10}^{-5}\right){\mathrm{ m}}^{2}\) and \({n}_{2}=\)(2.46 × \({10}^{-20})\) m2/W at a central wavelength of 1030 nm as described above. The wavelength-dependent refractive index of fused silica was calculated using the Sellmeier equation with the coefficients given in [22]. Furthermore, Raman contributions and self-steepening were included according to [16] with the Raman coefficient set to \({f}_{R}=0.18\). The properties of the dispersive cell mirror coating were approximated by − 140 fs2 GDD, and − 800 fs3 third-order dispersion at 1030 nm wavelength and 99.7% reflectivity corresponding to the red curve in Fig. 2. We were able to qualitatively reproduce the temporal and spectral shape (Fig. 4a, b). The predicted pulse duration and bandwidth agree well with the measured ones albeit, with the power loss into the pedestal being slightly overestimated by the simulation. The simulated temporal shape clearly identifies self-compression as the prevalent effect for the pulse shortening inside the MPC. The spectral and temporal evolution inside the MPC (Fig. 4c, d) shows that for the large soliton order > 25 precise tuning of the nonlinear interaction length is required, where excessive propagation through the broadening medium results in a fragmentation of the main pulse structure into multiple pulses.

Fig. 4
figure 4

Simulation of the self-compression inside the MPC using an adaptive step-size implementation of the fourth order Runge–Kutta method in the interaction picture to solve the nonlinear Schrödinger equation a spectrum and b time domain representation of the MPC output when operated at 136 W input power. c Spectrum and d time domain evolution vs. number of passes through the FS medium inside the MPC. The red line indicates the number of passes used in this experiment

Full size image

4 Discussion

In our earlier work [11], numerical simulations have indicated that, for a similar MPC, a nonlinear phase-shift exceeding 0.6 rad per pass through the broadening medium results in spectral inhomogeneity and a severe deterioration of the beam profile quality, typically manifesting in a characteristic ring pattern around the main beam [23]. When operating the MPC in the net positive dispersion regime, the maximum nonlinear phase shift per pass is given by the nonlinear phase shift in the first pass through the broadening medium and can easily be adjusted by choosing suitable input beam parameters. When operating the MPC in the self-compression regime, the nonlinear phase shift per pass will increase with each pass through the broadening substrate. In the experiments presented here, adjusting the nonlinear phase shift in the first pass through the broadening medium to ~ 0.4 rad resulted in a clean Gaussian beam profile at the output of the MPC with no noticeable differences observable between operation at low and high input power (5 W and 119 W, correspondingly, Fig. 5a and b). When focused down, the Gaussian shape of the beam is maintained with no ring structure appearing (Fig. 5c). Figure 4d indicates that within the accuracy of the simulation, the temporal pulse shape only changes significantly within the last three roundtrips (six passes through the FS window). Consequently, only these few passes exhibit a nonlinear phase shift exceeding 0.4 rad, where a maximum phase shift of < 1.4 rad is reached solely in the last pass through the FS window. Since most of the nonlinear spectral broadening is homogeneously distributed over many passes (cf. Fig. 4c), the slightly increased phase shift within the last few passes appears to be insufficient to cause nonlinear spatial effects. This is further supported by the measurement of the M2 parameter where inhomogeneous broadening would result in a varying q-parameter across the spectrum leading to an overall reduction in beam quality [24]. The measured M2 factor is 1.16 in both sagittal and tangential planes (Fig. 5d) which is well comparable to the M2 factor of the Yb:YAG oscillator of 1.08, indicating reasonable homogeneity of the beam.

Fig. 5
figure 5

Beam quality measurement of the MPC output operated in the self-compression regime (using RayCi CinCam beam profiler). a Collimated beam at 5 W average output power. b Collimated beam at 119 W average output power. c Attenuated beam profile of a focus created by lens with f = 200 mm focal length at full power (the Si-based beam profiler is only sensitive in the range 266–1100 nm). The 1/e2 beam diameter in the focus is 150 µm. d M2 measurement according to ISO 11146-2

Full size image

Measurements of the long-term average power stability (recorded over 1 h) yield a normalized root-mean-square (RMS) deviation of 0.2% at 119 W mean average power (Fig. 6a) which is similar to the average power stability of the driving oscillator. Positional- and angular beam stability measurements of over 1 h were taken after a warm-up period of 30 min with the collimated beam and in the focal plane of a lens with 200 mm focal length, correspondingly (Fig. 6b, c). The low value of the angular beam stability of below 6 µrad compares well with typical driver laser RMS (< 5 µrad) and is comparable to commercial lasers [25].

Fig. 6
figure 6

a Average power stability measured over 1 h with 1 Hz sampling frequency. b Positional and c angular beam stability over 1 h The angular beam stability was measured in the focal plane of a f = 200 mm lens. All measurements were taken after ~ 30-min thermalization of the MPC

Full size image

5 Conclusion

In summary, we have demonstrated self-compression in an all-bulk Herriott-type multi-pass cell in the near infrared. By operating the MPC in the anomalous dispersion regime via tailored dispersive mirrors, an output peak power of 140 MW at a pulse duration of 31 fs with over 45% of the pulse energy in the main peak could be achieved. This corresponds to an increase in peak power by more than a factor of three and a temporal compression by almost a factor of ten in a single broadening stage. Additionally, one-dimensional simulations were carried out where the temporal shape and bandwidth of the output could be reproduced. Despite the strong B-integral (> 1.2 rad) accumulated by the pulse during the last roundtrip, excellent beam quality was measured. The high overall throughput of > 85% in combination with the all-bulk multi-pass geometry facilitates further investigation of nonlinear effects such as Raman soliton self-frequency shift and supercontinuum generation.