1 Introduction

High-intensity lasers have been used in the last thirty years for a wide range of applications from basic research to societal applications. Such machines, that range from table-top commercial sources to building-size facilities, are nearly all based on the chirped-pulse amplification technique that employs an oscillator and several stages of amplification located between stretcher and compressor stages. The beam shape is characterized by a linearly polarized Gaussian to super-Gaussian near field fluence distribution and Gaussian-like focus. In such systems, wavefront aberration effects are usually problematic because of the many optical components and large beam sizes, and they have to be kept under control to maximize the in-focus intensity.

Many applications employing high-intensity laser beams would benefit from tailored spatial intensity distributions in the far field (FF) that do not follow the standard Gaussian shape. While simple distortions can be achieved using adaptive optics to add low-order wavefront (WF) modifications, complex shapes require the use of phase masks in the near field (NF). Those can be either random to spread the laser energy over an area several orders of magnitude larger than the diffraction limit [1], or more elaborated designs, generating vertices in the laser field which carry orbital angular momentum (OAM) and lead to structured light in the FF [2]. In particular, focus intensity distributions with a ring-like shape could find a large series of applications with high-intensity lasers, making use of the OAM during the interaction [3,4,5]. This type of beam is already used in a variety of other fields, e.g., particle trapping, optical communication, microscopy and astronomy [6,7,8,9,10,11,12,13,14,15,16,17,18].

The simplest beams featuring a ring-shaped focal fluence contain a single optical vortex in the center of the beam. For example, this is the case for the Laguerre–Gaussian laser beam of radial index 0 and azimuthal index 1 (\(\mathrm{LG}_0^1\)) or modified versions, where the NF intensity distribution is altered to a supergaussian profile to extract energy more efficient from laser amplifiers. Several theoretical studies showed the desirable features of the donut-like spatial intensity distribution for different high-intensity laser applications, for example schemes of particle acceleration, including the transfer of OAM, the generation of microscopic solenoidal magnetic fields of high strength or new geomeries of laser wakefield in underdense plasmas [3, 4, 19,20,21]. However, the success of experimental studies were limited due to the deterioration of the intensity pattern in the FF [22]. A high sensitivity of Laguerre–Gaussian-like beams to low-order off-axis WF aberrations compared to regular, OAM-free beams is suspected to be the reason for this.

The reaction of these modes to aberrations has been studied extensively for optical communications in terms of mode cross-talk caused by air turbulence [12,13,14,15,16, 23, 24]. However, these studies were performed in a statistical manner and do not quantify the resulting energy distribution in the FF. Furthermore, in high-intensity laser systems, air turbulence effects are a matter of laboratory environment, while static and on-shot WF aberrations are dominant [25]. If the FF distribution of a Laguerre–Gaussian-like beam is more sensitive to off-axis WF deformations, a regular adaptive optics control loop may not be able to correct for these defects anymore. A better understanding of the influence of different aberrations on OAM beams is, therefore, necessary to define the beam quality requirements for improving high-energy, high-intensity laser systems to deliver usable ring-shaped foci onto the target.

In this article, we present a quantitative numerical and experimental study on the visibility of aberrations on beams with OAM, deriving visibility criteria in the sense of the Seidel or Zernike aberration formalism. After shortly introducing Laguerre–Gaussian-like modes in the frame of high-intensity lasers, we show that the ring contrast is much more appropriate to describe the aberration effects on a beam with OAM than the standard Strehl ratio used traditionally to quantify the quality of a laser beam. To verify our findings, we experimentally set up a test bench with a spiral phase element (SPE) and a deformable mirror to add arbitrary aberrations, measured by a WF sensor. Observing the far field, we verify the expected high sensitivity of the ring distribution to off-axis aberrations for the first time, which until now was underestimated.

2 General description of laser modes with orbital angular momentum

The overall angular momentum of an electromagnetic (EM) wave is composed of the spin angular momentum and the OAM \(\mathbf {L}\). The OAM of an EM wave, propagating along \(\mathbf {z}\) in cylindrical coordinates, is defined as

$$\begin{aligned} \mathbf {L}(t) = \epsilon _0 \int \rho \cdot \left( \mathbf {r}-\mathbf {r}_0\right) \times \mathbf {S}(\mathbf {r}, t) \,\mathrm {d}\rho \mathrm {d}\theta \mathrm {d}z , \end{aligned}$$
(1)

where \(\mathbf {r}\) is the position vector, \(\mathbf {r}_0\) a point on the beam axis and \(\mathbf {S}(\mathbf {r},t)\) the Poynting vector of the EM field [26]. As \(\left( \mathbf {r}-\mathbf {r}_0\right) \times \mathbf {S}\) is always perpendicular to the direction of propagation, \(\mathbf {L}\) becomes zero for any beam with a continuous WF and an intensity distribution that both do not vary in transverse direction. This is, for example, the case for the most ubiquitous fields like plane waves and beams with a Gaussian amplitude distribution, which are naturally generated by laser cavities. This explains why the OAM of a field has received little attention in the last century.

However, there exist self-similar solutions to the wave equation which exhibit OAM and that have become available, thanks to various beam shaping and holographic techniques [27]. One of the simplest beams with OAM is described as the Laguerre–Gaussian Mode \(\mathrm{LG}_0^1\) [25]:

$$\begin{aligned} E_{(0,1)}(r,\theta ,z)&\propto \frac{r\sqrt{2}}{\omega (z)} \cdot \mathrm {exp}\left[ -\frac{r^2}{\omega ^2(z)} + i \phi (r,\theta ,z) \right] , \nonumber \\ \phi (r,\theta ,z)&= \theta + k\frac{r^2}{2R(z)} -kz+\varPhi (z). \end{aligned}$$
(2)

Here, \(\omega (z)\) is the beam waist, R(z) the radius of curvature and \(\varPhi (z)\) the Gouy phase. The phase term \(i\theta\), characterizing the case \(l=1\) for the \(\mathrm{LG}_p^l\) modes, is responsible for the helical wavefront, which is exhibited by \(\mathrm{LG}_p^l\) modes with \(l \ne 0\) in general and leads to a non-canceling \(\left( \mathbf {r}-\mathbf {r}_0\right) \times \mathbf {S}\) in (1). The \(\mathrm{LG}_0^1\) mode is also known as “donut” mode because of the hollow shape of the intensity distribution that is used in lots of applications. Note that this description of the field amplitude is valid for various polarization states of the \(\mathrm{LG}_0^1\) mode, that include radially, linearly and azimuthally polarized beams, while linearly polarized beams are always favored at high-intensity lasers for technical reasons. In addition, the interest for the self-similar property can be easily understood as the beam-generation location is not necessarily the plane of the application, between which a significant amount of diffraction can happen.

However, laser beams used in high-intensity high-energy lasers require a top-hat intensity profile in the NF in general to optimize the energy extraction from the amplifiers. This can be accomplished with the use of a serrated aperture that is relay imaged through the system, where diffraction artifacts are removed with spatial filters [28].

For this reason, a pure \(\mathrm{LG}_0^1\) mode is not an appropriate solution when high-intensity laser beams with OAM are desired. Alternatively, one can define a modified \(\mathrm{LG}_0^1\) beam optimized for such application, that features a NF with a high-energy fill factor and a “donut” shape in the FF. The generation of the modified \(\mathrm{LG}_0^1\) beam is then obtained after a dedicated SPE is employed together with the serrated aperture to introduce OAM on the beam.

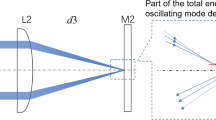
In Fig. 1, the calculated intensity distributions of both a regular Laguerre–Gaussian mode and a modified mode with homogeneous NF are shown. A NF aperture of \(10 \, \text {mm}\) has been chosen and the beam-waist matched to fit 99.5% of the energy through the aperture. For the Laguerre–Gaussian beam, this results in a waist of \(2.5 \,\text {mm}\). The beam is then numerically propagated to the focal plane of a lens with \(1 \,\text {m}\) focal length, assuming a wavelength of \(1 \, {\upmu }\text {m}\). The normalized intensity distributions in the FF do not vary significantly. In the following, the magnitude of the aberration will be given in the pupil of the beam as defined in Fig. 1. For that matter, it should be noted that the NF intensity distribution of the modified \(\mathrm{LG}_0^1\) mode is more appropriate for this comparison study as the visibility of aberrations is defined for uniformly illuminated pupils.

Fig. 1
figure 1

The NF (top row) and FF intensity distributions (bottom row) of the \(\mathrm{LG}_0^1\) mode (left) and the modified \(\mathrm{LG}_0^1\) mode (right). The intensity modulation of the top-hat beam is the diffraction effects introduced by the SPE. The dotted line represents the optical aperture that is defined as the area where 99.5% of the energy is located

Full size image

3 Formulation of tolerance criteria

The quality of optical systems can be described in various ways. First attempts used geometrical optics for derivation and experiments were conducted using incoherent light sources. Lord Rayleigh later took diffraction at round apertures into account. His description of the visibility of aberrations led to the conclusion that two plane waves are only to be distinguished in the FF of a lens if the distances of the main maxima of each corresponding diffraction disc were greater than or equal to the distance between the maximum of a single disk and its first minimum in radial direction [29].

Since then, the quality of an optical system could be described as “diffraction limited” if the aberrations were small. Otherwise, the diffraction limit would be outrun by the aberration of the system. This tolerance criterion can be applied to all kinds of aberration. For a purely spherical WF deformation, this leads to a tolerance threshold of \(\lambda /4\), which is the famous Rayleigh criterion. For arbitrary WF deformations, using the same quality condition, Marechals criterion can be applied, where the root mean square (RMS) of the aberration has to be lower than \(\lambda /14\) [30].

A more quantitative assessment of the previous statement has been introduced with the Strehl ratio, a widely accepted criterion for the beam quality, defined as

$$\begin{aligned} \text {Strehl ratio} = \frac{\text {Max. intensity reached}}{\text {Max. intensity possible}}. \end{aligned}$$
(3)

Here, any system with a Strehl ratio greater than 0.8 is considered “visually corrected” [31]. Unfortunately these criteria cannot be applied to a beam with OAM, as the Strehl ratio does not define the quality of the focal ring, nor the visibility of the aberrations. Therefore, other quality conditions have to be found.

Generalized Strehl-ratio One way is to generalize the Strehl ratio from 3 to

$$\begin{aligned} \text {Gen. Strehl ratio} = \frac{\text {Max. intensity reached}}{\text {Max. aber free intens.}}. \end{aligned}$$
(4)

This quality factor can be used to formulate a tolerance criterion, allowing e.g. \(20 \,\)% of deviation. The ratio, therefore, has to be within 0.8 and 1.2. However, this criterion can only be used for a beam with OAM if the WF deformations are cylindrically symmetric, as other aberrations would affect not only the intensity of the focal ring, but also its transverse geometry (see Fig. 2).

Fig. 2
figure 2

Measured FF distributions of a modified Laguerre–Gaussian beam with \(0.15 \, \lambda\) PtV of spherical aberration (left) and \(0.2 \, \lambda\) PtV of normal astigmatism (right) in the Zernike base. Normal astigmatism generates two intensity maxima on the \(45^{\circ }\) axis, contrary to its \(0^{\circ }\) symmetry

Full size image

Ring-contrast To take the geometry of the FF into account, another condition can be obtained by measuring the variation of the peak intensity around the ring in the FF via the following iterative algorithm: First, the center of the ring is estimated, e.g., as the center of gravity. Second, the positions of the maximum intensity for a number of lineouts in different radial directions are determined. Third, a circle is fit to these points and its origin is used to repeat the cycle. Usually, this method converges after only a few iterations. As the center of the ring is detected, the maximum intensity can be determined for radial lineouts in a higher angular resolution. Note that the positions of the maximum intensity not necessarily follow a circular shape. An example for this is given in Fig. 3.

By measuring the ratio of the minimum intensity to the peak intensity around the ring (from now on referred to as ring contrast) and requiring it to be greater than 0.8, a quality condition for general WF deformations is set. As this is sensitive to the geometry of the ring, it provides a much stronger criterion for the visibility on beams with OAM (see Fig. 3).

Fig. 3
figure 3

Measured FF distribution of a modified Laguerre–Gaussian beam with \(0.1 \, \lambda\) of normal astigmatism (equals \(0.2 \, \lambda\) PtV) in the Zernike base with the positions of maximum ring intensity drawn in green (left) and the corresponding ring intensity over the angle (right)

Full size image

4 Experimental measurements

Having defined quantitative criteria for beam quality, we have conducted an experiment that aimed at estimating the sensitivity of beams with OAM like the modified Laguerre–Gaussian beam to aberrations. Aberrations can be defined following the Zernike polynomial or Seidel formalism and we studied their visibility numerically, which we ultimately compared to experimental data gathered on a metrology test bench.

Experimental setup The goal of this experimental setup is to create a beam with quantitatively well defined WF, then add an OAM of \(l=1\) to it and measure the variation in maximum intensity and ring contrast of the farfield. This has to be done for several low-order aberrations of varying amplitudes.

To accomplish this, the setup shown in Fig. 4 was chosen. A continuous-wave fiber laser at 1053 nm was used as a light source. The beam is collimated by a lens after free propagation to reduce the number of elements in order to keep the static aberrations at a minimum. A serrated aperture (A) defines the image plane, which is relay imaged through a spatial filter onto a deformable mirror (DM). A bimorph, piezoelectric mirror with 31 actuators and an aperture of 60 mm, manufactured by NightN, was used. The beam is then relay imaged into a camera box, containing cameras for the NF and the FF, as well as a Shack–Hartmann sensor (SHS).

Using this setup, the WF in the camera box can be modified freely without OAM. Then the SPE (in form of phase mask) is inserted right before the aperture and the farfield with OAM can be measured. The recorded NF without SPE is shown in Fig. 5. Some intensity dropoff in the outer ranges on the top and left of the beam can be observed, which is about \(20\,\)% of the average intensity. The dark spot at (\({-2}\,\text {cm}\),\({-1}\,\text {cm}\)) is generated by a surface damage of the lens L4.

Fig. 4
figure 4

The experimental setup for adding arbitrary aberrations to a beam with a deformable mirror (DM) and measuring the WF and the FF

Full size image
Fig. 5
figure 5

The measured NF in the setup shown in Fig. 4

Full size image

Recording of data We decided to study astigmatism, coma, trefoil and spherical aberration, as these aberrations are often observed in laser systems. Defocussing is not considered, as it is not expected to deteriorate the geometry of the ring intensity due to its self-similar diffraction. For the other aberrations, the definition of the Zernike polynomials is used, while the normalization is chosen such that the radial term \(R^m_n(1) = 1\) (see Table 1).

Table 1 The names and polynomials of the investigated aberrations in the Zernike base
Full size table

The Zernike base does suit the problem well as the lower-order terms in the coma and spherical aberration will, according to the displacement theorem [32], keep the position of the best focus at the position of the aberration free focus.

For each of the aberrations, amplitudes from 0 to \(0.3\, \lambda\) in steps of \(25\, m\lambda\) are applied to the beam without OAM. The WF is measured with the SHS and averaged over 40 single measurements to compensate for air turbulence in the surrounding environment. Then, 200 images of the focal spot are recorded to have statistic information about the influence of the turbulences. The same is done for the FF with OAM.

Validation of the experimental setup To validate our test bench, we first checked the setup for self-consistency and performed a series of measurements on known beams to confront our results to those found in optics handbooks afterwards.

To validate the self-consistency of the setup, we removed the SPE, used the DM to correct the static aberrations of the system and recorded the NF, the FF and the WF in the camera box. The FF then was additionally estimated by Fourier-transforming the complex wave function on the aperture of the system, which itself can be obtained from the measured WF and NF intensity distribution. The result is presented in Fig. 6. The deviation is within \(\pm 2.5\,\)% of the maximum normalized intensity, which can occur due to aberrations in the FF beam line in the camera box and effects from air turbulence effects that were not averaged out successfully.

In the next step of validation, the Strehl ratio was calculated for all measured FFs, using the average maximum intensity measured for a the flat WF. Figure 7 shows the measured Strehl ratio and aberration visibility threshold for single aberrations, introduced by the DM, as compared to our numerical estimates and the visibility thresholds according to Born and Wolf.

Fig. 6
figure 6

The focal spot (bottom left) is calculated from the measured NF intensity distribution (top left) and the WF (top right). Subtracting the observed normalized FF intensity from the calculated normalized FF intensity, the relative difference can be determined (bottom right)

Full size image

As a first validation observation, the negative quadratic dependence of the experimental Strehl ratio on the aberration amplitude becomes apparent, which matches predictions from theoretical calculations [32]. A more quantitative validation can be obtained from the measurement of the aberration visibility threshold. According to Sect. 3, a Strehl ratio of 0.8 can be tolerated. Comparing the threshold amplitudes, where the curves hit 0.8, with values from Born and Wolf [32] (see Fig. 8), it is obvious that the measured tolerances are higher than the theoretical ones. A reason for this is the assumption of Born and Wolf to have a homogeneous intensity distribution over a circular aperture in the NF, whereas the top-hat beam used for the measurement is less sensitive to aperture edge effects (see Fig. 5).

Using the recorded WF and a homogeneous NF intensity, the tolerance threshold can also be estimated for a real top-hat distribution. These values are much closer to those found in the literature, while still overestimating them by \(8.5\%\) (coma) to \(14.5\%\) (spherical), with astigmatism (\(10.6\%\)) and trefoil (\(12.3\%\)) being in between. As coma and the spherical aberration do feature the biggest slopes in the outer areas of the beam, which are measured with the least precision due to the low intensity, their amplitudes are determined with least precision as well. Therefore, this overestimation indicates a systematic error of 10–13%. A possible reason is a misalignment of the WF sensor, where a shift of about 0.6 mm of the lens array relative to the camera chip would be sufficient to reach this error.

Fig. 7
figure 7

The measured Strehl ratio of the OAM-free beam over the strength of astigmatism, coma, trefoil and spherical aberrations. The amplitudes, where the curves reach a value of 0.8, are the measured tolerance thresholds. The tolerances from Born and Wolf [32] as well as the calculated tolerance thresholds with a homogeneous NF intensity are drawn for comparison

Full size image
Fig. 8
figure 8

The measured tolerances of the OAM-free beam over the strength of all four aberrations, including the calculated tolerances with a homogeneous NF intensity, marked as “Calc. (hom. NF)”, and the values from literature [32]

Full size image

As a conclusion of this validation step, we have found a good agreement between our numerical and experimental values for the visibility threshold of the aberration. The measurement tends to systematically overestimate the tolerance to the aberration by up to 10%. Knowing this, the following measurements will be assumed to be valid within these limits.

Measurement results for beams with OAM At this point, similar evaluations can be conducted with the measured modified Laguerre–Gaussian beam. The first tolerance criterion would be the generalized Strehl ratio to be greater than 0.8, as discussed in Sect. 3. Here, the maximum intensity is assumed to be the average maximum intensity of the modified Laguerre–Gaussian beam at the flat WF. The curves of the generalized Strehl ratio are shown in Fig. 9. It is obvious that this criterion is not suitable for the aberrations that vary in azimuthal direction as the quality indicator grows larger than one with raising aberration amplitude. Furthermore, this does not indicate a better beam quality, as the higher peak intensity corresponds to energy concentration in a few spots along the ring (see Fig. 10). Knowing this, the generalized Strehl-ratio criterion can still be used for the spherical aberration.

Fig. 9
figure 9

The measured generalized Strehl ratio of the beam with OAM over the strength of astigmatism, coma, trefoil and spherical aberrations. The amplitudes, where the curves reach a value of 0.8, are the measured tolerance thresholds

Full size image
Fig. 10
figure 10

The measured exposure-averaged focus of the aberrated modified Laguerre–Gaussian beam at \(0.2\,\lambda\) of astigmatism, coma, trefoil and spherical aberrations (from left to right)

Full size image

The second tolerance criterion uses the ring contrast as quality indicator. While the optimum value is 1, the measured ring contrast has already slightly dropped due to residual WF errors that cannot be corrected with the DM or arise from turbulences in the air. To still be able to determine a realistic tolerance threshold, the ring contrast is not required to be greater than 0.8 but \(80\,\)% of the maximum measured value. The resulting curves are shown in Fig. 11. Different to the last criterion, the spherical aberration appears to be insensitive to this criterion, while it is quite restrictive against the other aberrations. Less than \(50\, \text {m} \lambda\) of astigmatism is allowed until the threshold is reached.

In combination with the measured FF distributions, this leads to the conclusion that the ring contrast is sensitive enough for judging the quality of the ring focus for off-axis aberrations.

Fig. 11
figure 11

The measured ring contrast of the beam with OAM over the strength of astigmatism, coma, trefoil and spherical aberrations. The amplitudes, where the curves reach \(80\,\)% of the optimum value, are the measured tolerance thresholds

Full size image

With those criteria, a full set of tolerance conditions is measured. The values are collected in Table 2. As the Strehl ratio appeared to be overestimated mainly due to the inhomogeneous NF distribution, the tolerance threshold of the Spherical aberration was additionally calculated for a homogeneous NF.

Table 2 Measured tolerance thresholds of a modified Laguerre–Gaussian beam for the investigated aberrations. For the spherical aberration, the threshold was additionally calculated using the recorded WFs and a homogeneous NF distribution to remove the influence of the inhomogeneous illumination of the pupil
Full size table

5 Comparison with aberrations in the seidel sense

The visibility of the aberrations on beams with OAM can also be studied numerically for Seidel aberrations. The used aberrations were defined in cylindrical coordinates the following way (Table 3).

Table 3 The names and polynomials of the investigated aberrations in the simulation [25, 32]
Full size table

Other than scaling, the used definitions differ from the Zernike base only in a defocus term (astigmatism, spherical aberration) or a tilt term (coma). According to the displacement theorem, moderate amounts of defocusing or tilt of the WF lead to a shift of the three dimensional intensity distribution in space [32]. To accommodate this effect, the simulation routine performs a scan around the focal plane in the direction of propagation and the quality indicators are computed at the plane of the optimum focus. At this location, the intensity distribution corresponds to the distribution in the focal plane if the Zernike aberrations were used. Therefore, the amplitudes found in the simulation can be scaled to match the Zernike base listed in Table 1. The resulting tolerance thresholds are compared with our measurements in Fig. 12 and Table 4.

Fig. 12
figure 12

The measured and (scaled) simulated tolerance thresholds for the modified Laguerre–Gaussian beam for the investigated aberrations in the Zernike base

Full size image
Table 4 The (scaled) simulated and measured tolerance thresholds for the modified Laguerre–Gaussian beam for the investigated aberrations in the Zernike base
Full size table

For astigmatism and coma, the measured values match the simulation within the measurement uncertainty, although the experimental thresholds again seem to be slightly systematically overestimated. The simulated threshold for the spherical aberration, in the sense of the generalized Strehl ratio, falls slightly outside the error bar of the measurement. However, overestimation in the regime of the Strehl ratio has already been observed for the Gaussian focal spot and mainly backtracked to an inhomogeneous intensity distribution in the NF. Using the measured WF and a homogeneous NF distribution, the calculated threshold of \(0.191\, \lambda\) is closer to the simulation (see also Table 2).

6 Discussion and conclusion

The work at hand is a numerical and experimental study of the influence of the aberrations on beams with OAM with an emphasis on the modified Laguerre–Gaussian beam, because of its potential interest for application in laser–plasma interaction. The experimental setup allows a head-to-head comparison of a beam with OAM and without OAM, as switching is just done by removing the SPE from the beam. In the last step, the measured tolerances of the modified Laguerre–Gaussian mode, listed in Table 2, shall be compared with the measured tolerances of the OAM-free beam, which is shown in Fig. 8. The comparison is shown in Fig. 13. The plot shows that the visibility of the spherical aberration is more or less the same for both types of beams, as determined using the generalized Strehl ratio. On the opposite, the modified Laguerre–Gaussian beam seems much more sensitive to off-axis aberrations. While the aberration visibility for a top-hat beam is relatively independent of the type of aberration at about \(\lambda /4\), the modified Laguerre–Gaussian beam can tolerate aberration amplitudes of \(\lambda /30\), \(\lambda /15\) and \(\lambda /10\) for astigmatism, coma and trefoil, respectively. This difference is the strongest for astigmatism, whose threshold is only \(15\%\) of that of the OAM-free beam.

Fig. 13
figure 13

The measured tolerances of the beam with and without OAM for low-order aberrations in the Zernike base (see Table 1)

Full size image

These values must be put in the context of the beam quality of high-intensity high-energy lasers, where the beam wavefront is distorted by the finite quality of the optical elements and other perturbation sources like thermal effects. This clearly shows that a beam with OAM cannot be treated like a regular laser beam during transportation, as even well corrected systems in a traditional sense might already outrun these tolerance criteria by several times for Laguerre–Gaussian-like beams. Nevertheless, these results are an important step in the understanding of the creation and transport of beams with OAM and can be used to setup the specifications for the optical elements, correction and detection systems employed in a laser facility aiming at working with beams with OAM.

As a conclusion, we have conducted an estimate of the visibility of low-order aberration on beams with OAM based on numerical simulations confirmed by experimental measurement on a dedicated test bench. A beam with well-defined aberrations using adaptive optics has been generated in an experimental setup. For astigmatism, coma, trefoil and spherical aberrations in the Zernike base, images of the focal plane have been recorded for different strengths of WF deformations.

These data have been evaluated using a generalized Strehl ratio and the ring contrast as quality criteria to determine tolerance thresholds. Based on this, we believe that we have conducted a study that delivers values with an accuracy of \(10\%\).

Following this, it is clear that the “donut-like” focus of a modified Laguerre–Gaussian beam is extremely sensitive to off-axis WF deformations. The most critical aberration is astigmatism, allowing less than \(75\, \text {m} \lambda\) PtV of deformation on the beam. A possible application of this result, is the use of SPEs that introduce OAM as a beam quality test plate for applications that have high beam quality requirements. Because the SPE makes the beam shape much more sensitive to low-amplitude aberrations, those residual aberration are made more visible and easier to detect and measure. This way, the beam quality could be improved beyond the state of the art of what is currently available with use of closed-loop adaptive-optics systems.