Abstract
We propose and demonstrate a novel method for temperature determination using dual-comb spectroscopy and a novel analysis technique, “Rotational-state Distribution Thermometry: RDT.” We obtained the spectral profile of a vibration–rotation band of 12C2H2 using dual-comb spectroscopy at room temperature. The line-center absorbance was determined for each transition by fitting the line profile to a Gaussian function. A model function that relates the rotational temperature of the molecule to the distribution of the line-center absorbance was introduced; the gas temperature was determined by fitting the distribution to the model function. The determined temperature agrees to within 0.6 K with the cell-wall temperature measured with a platinum resistance thermometer. In addition, using the spectral profile obtained in this study, we compare the present analysis with two conventional methods for determining the gas temperature; one is based on the line-center absorbance ratio, and the other on the Doppler width. The present method takes full advantage of the supreme characteristics of dual-comb spectroscopy and has the potential to offer fast and precise thermometry.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Non-contact, fast, and precise gas thermometry is desired for various applications such as industrial and environmental evaluations. Laser spectroscopy is a powerful tool for undertaking such measurements. Several spectroscopic methods have been reported for measuring gas temperatures [1,2,3,4,5,6]. Gas thermometry using molecular absorption spectra is one of the mainstream spectroscopic thermometry techniques; because the absorption profile of a molecule is determined by the Boltzmann factor kT, it provides information regarding the thermodynamic temperature.
Two approaches are familiar to the thermometry community when it comes to determining thermodynamic temperature using spectroscopy; one uses the Doppler width of an absorption profile [7, 8] and the other uses the line-center absorbance ratio [9,10,11,12]. In particular, thermometry using the Doppler width has been enthusiastically studied in the field of temperature standards because of its preciseness.
The above-mentioned studies use a continuous-wave (CW) laser, or lasers, for the spectroscopy. CW lasers have high spectral-purity and are ideal as light sources for observing molecular response in spectroscopy. Meanwhile, it is necessary to precisely control the frequency of the CW laser. High experimental skill is required and the data acquisition is time consuming.
In contrast, fast thermometry can be expected using a coherent broadband light source such as an optical frequency comb for spectroscopy. Recently, the temperature of H2O gas was successfully measured with a supercontinuum-based absorption spectrometer in a rapid compression machine [13]. There have also been reports of gas temperature measurements using a frequency comb [14, 15] and a two-dimensional dispersive spectrometer based on a virtually imaged phased array (VIPA) [16].
Dual-comb spectroscopy (DCS) [17, 18] is an attractive spectroscopic tool that enables us to observe multiple absorption profiles of molecular gas precisely in a short time. Since the comb signals are directly linked to the frequency standard, compatibility with thermodynamic thermometry is expected to be good. DCS has been extensively employed in molecular spectroscopy [19, 20], such as coherent anti-Stokes Raman spectroscopy [21], and environmental gas monitoring [22]. Very recently, the temperatures of H2O and CO2 in gas turbine exhaust were measured using DCS [23]. However, as yet there has been no detailed discussion of how to determine the temperature from the absorption profile obtained by DCS.
In this paper, we use DCS to acquire the absorption profile of the entire \({\nu _1}+{\nu _3}\) band of 12C2H2 in a room temperature environment. Then, we propose and demonstrate a novel method, namely “Rotational-state Distribution Thermometry (RDT)”, for determining the temperature by efficiently utilizing the line-profile information. Furthermore, we compare the present results with those obtained by employing two conventional techniques and the present data.
2 Experimental setup
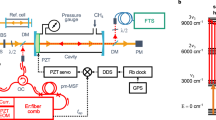
Figure 1 shows the experimental setup we used to record the wide band spectrum of acetylene in the 1.5 µm region with DCS. We summarize it briefly here since the principle of the dual-comb spectrometer has been described in detail elsewhere [24].
We prepared two optical frequency combs generated by mode-locked erbium-doped-fiber lasers with repetition rates of about 48 MHz as a signal and a local comb. The repetition rates of the signal and local combs differ slightly as follows: \({f_{{\text{rep,S}}}}\;{\text{and}}\;{f_{{\text{rep,L}}}}={f_{{\text{rep,S}}}} - \Delta {f_{{\text{rep}}}},\) respectively. The optical pulse train of the signal comb passes through a sample, and that of the local comb is used as a local oscillator to retrieve the spectroscopic signal carried on the signal comb by the multi-heterodyne technique. After passing through the sample cell, the beam of the signal comb overlaps that of the local comb at a polarizing beam splitter (PBS). The combined beam is divided into two beams using a half-wave plate and another PBS. After the second PBS, the transmitted and reflected beams generate opposite-phase beat signals according to the polarization. These signals are balanced-detected with two InGaAs photodiodes to reduce common-mode noise. The detected beat signal of the local and signal beams repeatedly provides time-domain interferograms at every time interval of (Δfrep)−1, which are then sampled by a 14-bit digitizer and transferred to a PC. The interferograms are averaged over 10,000 times with a coherent averaging technique [25] and then transformed into a transmission spectrum using a fast Fourier transform (FFT) algorithm. In this work, we set Δfrep at 93 Hz.
The modes of both the signal and local combs are phase-locked to a common 1.54-µm CW laser. The carrier-envelope offset frequencies are phase-locked to an RF reference synthesizer. These two phase-locks reduce the relative linewidth of the two combs to less than 1 Hz, which enables us to reduce Δfrep and thus increase the Nyquist-condition-limited spectral span in a one-shot measurement.
We used a White-type multiple-pass cell with a path length of 304 cm as the sample cell (see Fig. 1). The cell is filled with acetylene at a pressure of 60 Pa measured with a piezoelectric transducer gauge. The cell temperature is measured with a platinum resistance thermometer (PRT).
3 Analytical procedure of rotational-state distribution thermometry (RDT)
We determined the gas temperature from the observed absorption spectrum using the following procedure.
First, we derived the line-center absorbance of each rotation–vibration transition of acetylene by fitting the observed spectrum. According to Lambert–Beer’s law, the transmittance spectrum of a gas can be expressed as:
where αmax is the line-center absorbance, \(G(\tilde {\nu },{\tilde {\nu }_0})\) is a peak normalized Gaussian function [26]:
\({\tilde {\nu }_0}\) is the wavenumber of the transition at the line center, and \(\Delta {\tilde {\nu }_{\text{D}}}\) is the half-width at half-maximum (HWHM) of the Doppler broadened spectral line. Here, we use wavenumber \(\tilde {\nu }=\nu /c\) in place of frequency \(\nu ,\) where c is the speed of light. In this study, the pressure width is at most 1.2 × 10−4 cm−1 (HWHM) for a pressure of 60 Pa [27] and is negligible compared with the Doppler width of 7.9 × 10−3 cm−1 (HWHM) calculated from the cell-wall temperature. Therefore, we considered the spectral linewidth to be dominated by the Doppler broadening and used the Gaussian function \(G(\tilde {\nu },{\tilde {\nu }_0})\) in Eq. (1). \(I(\tilde {\nu })\) and \({I_0}(\tilde {\nu })\) are the intensities of the transmitted and incident radiation at the optical wavenumber \(\tilde {\nu },\) respectively. There are a number of absorption lines corresponding to rotational transition (J′ ← J, J: the quantum number for the rotational angular momentum) in the observed band. We deal with the P-branch (J − 1 ← J) and R-branch (J + 1 ← J) transitions simultaneously by introducing a conventional index m, which is:
Therefore, the line-center absorbance of the transition indexed by m are expressed as αmax(m), which is determined by fitting the observed transmittance spectrum to Eq. (1).
Second, we determine the molecular temperature from the obtained αmax(m). The line-center absorbance can be rewritten as:
using the line strength S(m) defined by Eq. (5) in Ref. [28], where N is the molecular number density, and L is the cell length. The line strength S(m) is given by the following formula:
where \({\varepsilon _0}\) is the electric constant, h is Planck’s constant, kB is the Boltzmann constant, \({\tilde {\nu }_m}\) is the mth transition wavenumber, E(m) is the lower state energy of the mth transition, Trot and Tvib are the rotational and vibrational temperatures, respectively, g I is the nuclear spin degeneracy of the lower state (g I = 1 for even J and 3 for odd J in the ground vibrational state), Q is the total partition function, and µV is the vibrational transition dipole moment. The function F(m) is the Herman–Wallis factor, which accounts for the additional m-dependence caused by the rotation-vibration interaction [28, 29]. It can be approximated as follows when m is as small as in this study \((|m|\; \leqslant 26)\):
The coefficient c1 was determined in Ref. [30], and the value was − 0.453(72) × 10−3. Equation (5) is essentially the same as Eq. (5) in Ref [28] if the expression of the dipole moment is switched to the cgs-Gauss system by removing the factor (4πε0)−1 as discussed in [30]. Since S(m) is a function of m and depends on T, we can determine T by fitting the obtained αmax(m) to Eq. (4).
In this study, the energy difference \(hc{\tilde {\nu }_m}\) is much larger than kBT since the temperature is around 300 K (kBT/hc ~ 200 cm−1). Then the term \([1 - \exp ( - hc{\tilde {\nu }_m}/{k_{\text{B}}}{T_{{\text{vib}}}})]\) in Eq. (5) is nearly equal to unity. The total partition function Q can be written as the product of a rotational partition function Qrot and a vibrational partition function Qvib as follows,
It is noted that the total partition function Q is constant for all transitions of a rotation–vibration band. Consequently, Eq. (4) can be summarized as the following equation when we assume that the molecules in the cell are in thermal equilibrium, i.e., T = Trot = Tvib;
where β(T, NL, µV) is a constant factor independent of m (or J), and \(\tilde {B}\) is the rotational constant of the ground vibrational state.
Finally, we determined the gas temperature T by fitting the experimentally observed line-center absorbance αmax(m) to Eq. (8) with T and β as adjustable parameters. We call this procedure “Rotational-state distribution thermometry (RDT).”
4 Experimental results
In the present study we recorded the \({\nu _1}+{\nu _3}\) band of 12C2H2 at 1.52 μm. We repeated the measurement nine times and thus obtained nine independent data sets. First, we determined the line-center absorbance of each rotation-vibration transition of acetylene by fitting the observed transmittance spectrum to Eq. (1). Figure 2a shows a transmittance spectrum recorded with our dual-comb spectrometer. We observed 51 transitions from P(25) to R(25). The cell-wall temperatures measured with the PRT and the gas pressure were 22.9(1) °C, i.e., 296.04(10) K, and 60(1) Pa, respectively, where the numbers in parentheses are the estimated uncertainties in units of the last digits quoted. We show a magnified spectrum around the R(13) transition in Fig. 2b as an example. The black dots and the red curve show the observed spectrum and calculated spectrum using Eq. (1), respectively.
Transmittance spectrum of the 12C2H2 \({\nu _1}+{\nu _3}\) vibration band at a room temperature of 22.9 °C (296.04 K). a Observed spectrum. The left and right groups consist of the P- and R-branch transitions, respectively. The small numbers under the absorption lines show the rotational quantum numbers J of the lower states of the transitions. b Observed (black dots) and calculated (red curve) spectra of the R(13) transition
As a result of this fitting, we determined the line-center absorbance αmax (m) for each transition. Figure 3 shows the obtained αmax(m) with the uncertainty of this fitting (black dots and error bars).
Absorption intensity αmax(m) obtained from the observed transmittance (black dots) and that calculated by fitting αmax(m) to Eq. (8) (blue curves) and the residual of the fit (black diamonds). The temperature determined by the fitting is 296.26(90) K
Second, we determined the molecular temperature by employing a weighted least-square fitting of the obtained αmax(m) to Eq. (8). The fitted result is shown in Fig. 3 (blue curves). We used 49 transitions from P(25) to R(25) to determine the gas temperature except for the P(24) and R(0) transitions because of their low signal-to-noise ratio (SNR). The four blue-curves correspond to the even and odd J values of the P-branch and of the R-branch, respectively, and are plotted separately to show that the observed αmax(m) is well fitted by Eq. (8). Most of the fitted values agree well with the observed αmax(m) within their individual uncertainties estimated from the errors obtained by the line-profile fitting.
Table 1 lists the temperatures determined by the above-mentioned analysis for nine spectral data sets. They agree with the cell-wall temperature measured with the PRT within 0.6 K.
5 Discussion
5.1 Comparison of three methods for determining the gas temperature using spectra obtained with DCS
To show the good compatibility of RDT combined with the absorption spectrum acquired with DCS, we compared the gas temperatures we determined with our method with those obtained using two conventional methods.
The first conventional method uses the Doppler widths of the respective absorption lines. In this approach, first we determined the Doppler widths \(\Delta {\tilde {\nu }_{\text{D}}}\) of the transitions by fitting the observed transmittance spectrum to Eq. (1). For each transition, the temperature and its uncertainty were obtained from the value of \(\Delta {\tilde {\nu }_{\text{D}}}\) and its fitting error. The conclusive gas temperature was determined as a weighted mean of the temperatures calculated for 49 (or 50 depending on the data set) transitions with sufficient SNR for the line fitting.
The second conventional analysis technique uses the line-center absorbance ratio of the transition pairs. In this approach, as with the proposed method, we first determined the line center absorbances αmax for the transitions with sufficient SNR by fitting the observed transmittance spectrum to Eq. (1). The 49 or 50 transitions correspond to 1176 or 1225 transition pairs, respectively. Then we individually determined the temperature and its uncertainty derived from the error of the line-center absorbance for each transition pair. The conclusive gas temperature was determined as a weighted mean of the temperatures for all transition pairs.
Figure 4 shows the differences between temperatures determined by the three methods and the PRT temperature, using nine data sets acquired by DCS. In RDT, the variation of the mean value was significantly small and the differences from the PRT temperature were within the measurement uncertainty for all data sets. In contrast, in the analysis using Doppler width, the determined temperature tends to be higher than the PRT temperature and fluctuates for each data set. It is obviously a disadvantage of applying the Doppler width method to DCS spectra. The number of data points for each line acquired by DCS is significantly less than that acquired by spectroscopy using a CW laser, and thus it is difficult to determine the Doppler widths precisely by DCS. In the analysis using the line-center absorbance ratios of the transition pairs, the conclusive uncertainty and the variation of the center values were slightly larger than with RDT. Further investigation is needed to understand these phenomena. Nevertheless, from these results, RDT seems to be an excellent and compatible method for determining the gas temperature from the absorption spectrum acquired by DCS.
5.2 Uncertainty induced by the approximations in the model function
We discuss the uncertainty induced by the approximations used in the model function Eq. (8) for determining the gas temperature with RDT. In Eq. (8) we neglected the population in excited vibrational states, the centrifugal correction to the rotational energy, and the higher order terms of the Herman–Wallis factor.
The uncertainty of the first order coefficient of the Herman–Wallis factor [30] corresponds to the temperature uncertainty of 5 mK at 296 K. The higher order contributions are negligible for the lines of J less than 26 [30]. The uncertainty of the B constant of the rotational energy corresponds to 0.7 µK at 296 K. Centrifugal distortion constants up to the fourth order have been reported [31]. The temperature determined by the rotational energy up to fourth order term was 33 mK higher than that determined by the rotational energy in the rigid-rotor approximation. From these results, we determined that the impacts of the approximations of the Herman–Wallis factor and the rotational energy are much smaller than the error of RDT (1 K level). Therefore, the employed approximations do not affect the temperature determination in the measurement precision of this work. However, we may need to consider these factors if we need to determine the temperature more precisely.
5.3 Required measurement time for RDT
In this work, the observed interferograms were averaged over 10,000 times (measurement time of 110 s) to reduce the white noise mainly originating from the laser intensity noise. We investigated the determined temperature fluctuation with respect to the averaging number (measurement time) and confirmed that the fluctuation is sufficiently suppressed by averaging more than 5000 interferograms (measurement time of 55 s). We expect that the measurement time can be shortened while maintaining the precision by optimizing the pulse amplification and spectral broadening of the comb to suppress the laser intensity noise.
6 Conclusion
We proposed a novel RDT method based on a model function that includes temperature and rotational quantum number as variables and demonstrated its capability by determining the gas temperature from the vibration-rotation band of acetylene obtained by DCS. RDT has the property of a primary thermodynamic thermometry since this model function consists of only Boltzmann’s constant kB, Planck’s constant h, and molecular constant B, other than the above-mentioned variables. By comparison with the two conventional methods used for thermodynamic thermometry, we showed that RDT has good compatibility with DCS, which can acquire a broad and precise spectrum in a short time. We expect that the uncertainty of RDT may be reduced in future by, for example, improving the temporal stability of the comb spectrum, and preparing a precise temperature field. If this is realized, the combination of RDT and DCS will be an excellent tool for non-contact, fast, and precise thermodynamic thermometry, which has the potential to be widely used for scientific, industrial, and metrological applications.
References
X. Pan, P.F. Barker, A. Meschanov, J.H. Grinstead, M.N. Shneider, R.B. Miles, Temperature measurements by coherent Rayleigh scattering. Opt. Lett. 27, 161–163 (2002)
J.P. Singh, F.Y. Yueh, Multiplex CARS for simultaneous measurement of temperature and CO2 and H2 concentrations in a combustion environment. Appl. Opt. 30, 1967–1975 (1991)
G.A. Raiche, J.B. Jeffries, Laser-induced fluorescence temperature measurements in a dc arcjet used for diamond deposition. Appl. Opt. 36, 4629–4635 (1993)
M. Tamura, J. Luque, J.E. Harrington, P.A. Berg, G.P. Smith, J.B. Jeffries, D.R. Crosley, Laser-induced fluorescence of seeded nitric oxide as a flame thermometer. Appl. Phys. B 66, 503–510 (1998)
B. Williams, M. Edwards, R. Stone, J. Williams, P. Ewart, High precision in-cylinder gas thermometry using laser induced gratings: quantitative measurement of evaporative cooling with gasoline/alcohol blends in a GDI optical engine. Combust. Flame 161, 270–279 (2014)
J. Kiefer, P. Ewart, Laser diagnostics and minor species detection in combustion using resonant four-wave mixing. Prog. Energy Combust, Sci. 37, 525–564 (2011)
K. Akihama, T. Asai, S-branch CARS applicability to thermometry. Appl. Opt. 29, 3143–3149 (1990)
F.Y. Yueh, E.J. Beiting, Simultaneous N2, CO, and H2 multiplex CARS measurements in combustion environments using a single dye laser. Appl. Opt. 27, 3233–3243 (1988)
C.J. Borde, Base units of the SI, fundamental constants and modern quantum physics. Philos. Trans. R. Soc. Lond. A 363, 2177–2201 (2005)
C. Daussy, M. Guinet, A. Amy-Klein, Y. Djerroud, K. Hermier, S. Briaudeau, C.J. Bordé, C. Chardonet, Direct determination of the Boltzmann constant by an optical method. Phys. Rev. Lett. 98, 250801 (2007)
K.M.T. Yamada, A. Onae, H.-L. Hong, H. Inaba, H. Matsumoto, Y. Nakajima, F. Ito, T. Shimizu, High precision line profile measurements on 13C acetylene using a near infrared frequency comb spectrometer. J. Mol. Spectrosc. 249, 95–99 (2008)
L. Castrillo, E. Moretti, M.D. Fasci, G. De Vizia, L. Casa, Gianfrani, The Boltzmann constant from the shape of a molecular spectral line. J. Mol. Spectrosc. 300, 131–138 (2014)
T. Werblinski, S. Kleindienst, R. Engelbrecht, L. Zigan, S. Will, Supercontinuum based absorption spectrometer for cycle-resolved multiparameter measurements in a rapid compression machine. Appl. Opt. 55, 4564–4574 (2016)
T. Udem, J. Reichert, R. Holzwarth, T.W. Hansch, Absolute optical frequency measurement of the cesium D-1 line with a mode-locked laser. Phys. Rev. Lett. 82, 3568–3571 (1999)
D.J. Jones, S.A. Diddams, J.K. Ranka, A. Stentz, R.S. Windeler, J.L. Hall, S.T. Cundiff, Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 288, 635–639 (2000)
G. Klose, F.C. Ycas, D.L. Cruz, S.A. Maser, Diddams, Rapid, broadband spectroscopic temperature measurement of CO2 using VIPA spectroscopy. Appl. Phys. B 122, 1–8 (2016)
F. Keilmann, C. Gohle, R. Holzwarth, Time-domain mid-infrared frequency-comb spectrometer. Opt. Lett. 29, 1542–1544 (2004)
I. Coddington, N. Newbury, W. Swann, Dual-comb spectroscopy. Optica 3, 414 (2016)
P. Giaccari, J.-D. Deschênes, P. Saucier, J. Genest, P. Tremblay, Active Fourier-transform spectroscopy combining the direct RF beating of two fiber-based mode-locked lasers with a novel referencing method. Opt. Express 16, 4347 (2008)
B. Bernhardt, A. Ozawa, P. Jacquet, M. Jacquey, Y. Kobayashi, T. Udem, R. Holzwarth, G. Guelachvili, T.W. Hänsch, N. Picqué, Cavity-enhanced dual-comb spectroscopy. Nat. Photonics 4, 55 (2010)
T. Ideguchi, S. Holzner, B. Bernhardt, G. Guelachvili, N. Picqué, T.W. Hänsch, Coherent Raman spectro-imaging with laser frequency combs. Nature 502, 355–358 (2013)
C. Cossel, E.M. Waxman, F.R. Giorgetta, M. Cermak, I.R. Coddington, D. Hesselius, S. Ruben, W.C. Swann, G.-W. Truong, G.B. Rieker, N.R. Newbury, Open-path dual-comb spectroscopy to an airborne retroreflector. Optica 4, 724 (2017)
P.J. Schroeder, R.J. Wright, S. Coburn, B. Sodergren, K.C. Cossel, S. Droste, G.W. Truong, E. Baumann, F.R. Giorgetta, I. Coddington, N.R. Newbury, G.B. Rieker, Dual frequency comb laser absorption spectroscopy in a 16 MW gas turbine exhaust. Proc. Comb. Inst. 36, 4565–4573 (2017)
S. Okubo, K. Iwakuni, H. Inaba, K. Hosaka, A. Onae, H. Sasada, F.-L. Hong, Ultra-broadband dual-comb spectroscopy across 1.0–1.9 µm. Appl. Phys. Express 8, 082402 (2015)
W.C. Coddington, N.R. Swann, Newbury, Coherent linear optical sampling at 15 bits of resolution. Opt. Lett. 34, 2153–2155 (2009)
C.H. Townes, A.L. Schawlow, Microwave spectroscopy. (McGraw-Hill Co., New York, 1955)
K. Iwakuni, S. Okubo, K.M. Yamada, H. Inaba, A. Onae, F.-L. Hong, H. Sasada, Ortho-para-dependent pressure effects observed in the near infrared band of acetylene by dual-comb spectroscopy. Phys. Rev. Lett. 117, 143902 (2016)
M. Kusaba, J. Henningsen, The \({\nu _{\text{1}}}+{\nu _{\text{3}}}\) and the \({\nu _{\text{1}}}+{\nu _{\text{2}}}+\nu _{4}^{1}+\nu _{5}^{{ - 1}}\) combination bands of 13C2H2 line strengths, broadening parameters, and pressure shifts. J. Mol. Spectrosc. 209, 216–227 (2001)
R. Herman, R.F. Wallis, Influence of vibration–rotation interaction on line intensities in vibration–rotation bands of diatomic molecules. J. Chem. Phys. 23, 637–646 (1955)
S. Okubo, K. Iwakuni, K.M.T. Yamada, H. Inaba, A. Onae, F.-L. Hong, H. Sasada, Transition dipole-moment of the ν1 + ν3 band of acetylene as measured by dual-comb Fourier-transform spectroscopy. J. Mol. Spectrosc. 340, 10–16 (2017)
A. Madej, A.J. Alcock, A. Czajkowski, J.E. Bernard, S. Chepurov, Accurate absolute reference frequencies from 1511 to 1545 nm of the \({\nu _{\text{1}}}+{\nu _{\text{3}}}\) band of 12C2H2 determined with laser frequency comb interval measurements. J. Opt. Soc. Am. B 23, 2200–2208 (2006)
Acknowledgements
We thank Professor Sasada for valuable comments.
Funding
Japan Science and Technology Agency (JST) the ERATO MINOSHIMA Intelligent Optical Synthesizer (IOS) Project; Exploratory Research for Advanced Technology (JPMJER1304); Grants-in-Aid for Scientific Research (KAKENHI); Japan Society for the Promotion of Science (JP) (JP16K05009).
Author information
Authors and Affiliations
Corresponding author
Additional information
We dedicate this article to Dr. Atsushi Onae who has passed away unexpectedly during the preparation of this manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shimizu, Y., Okubo, S., Onae, A. et al. Molecular gas thermometry on acetylene using dual-comb spectroscopy: analysis of rotational energy distribution. Appl. Phys. B 124, 71 (2018). https://doi.org/10.1007/s00340-018-6933-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00340-018-6933-x