A quantum cascade laser-based Mach–Zehnder interferometer for chemical sensing employing molecular absorption and dispersion

Abstract

We employ a novel spectroscopic setup based on an external cavity quantum cascade laser and a Mach–Zehnder interferometer to simultaneously record spectra of absorption and dispersion of liquid samples in the mid-infrared. We describe the theory underlying the interferometric measurement and discuss its implications for the experiment. The capability of simultaneously recording a refractive index and absorption spectrum is demonstrated for a sample of acetone in cyclohexane. The recording of absorption spectra is experimentally investigated in more detail to illustrate the method’s capabilities as compared to direct absorption spectroscopy. We find that absorption signals are recorded with strongly suppressed background, but with smaller absolute sensitivity. A possibility of optimizing the setup’s performance by unbalancing the interferometer is presented.

1 Introduction

Mid-infrared (Mid-IR) absorption spectroscopy of liquids finds a wide range of applications in chemical sensing due to its simplicity, speed and outstanding selectivity. More recently, quantum cascade lasers (QCL) were employed successfully to replace notoriously weak thermal emitters as Mid-IR sources. In particular, external cavity (EC) QCLs proved to be an ideal match for many liquid sensing applications owing to their large spectral tuning range of typically 200 cm⁻¹ [1,2,3,4,5,6,7,8,9]. To date, the vast majority of measurements are performed using direct absorption spectroscopy, in which the laser beam’s intensity is recorded after passing through the sample or being totally reflected at its surface. Since this technique relies on recording small changes of the laser intensity, its sensitivity is ultimately limited by fluctuations of the laser power and noise from the detection system.

As of today, documented advantages of EC-QCL based systems over Fourier transform infrared spectrometers with thermal light sources are mainly increased ruggedness made possible by an enlarged optical path [10]. For example, recently an EC-QCL was successfully employed for the determination of protein secondary structures and protein folding in water using an optical path of 38 µm instead of 8 µm as required in FTIR spectrometry [10]. The so far achieved sensitivities of fully room temperature operated EC-QCL based systems compare well with those documented with high-end FTIR spectrometers which, however, employ liquid nitrogen cooled MCT detectors [11, 12].

For gas phase measurements, monolithic distributed feedback (DFB) QCLs have already been established as reliable light sources void of mechanical imperfections limiting the performance of EC-QCLs, albeit of a far reduced tuning range. Nevertheless, considering the narrow ro-vibrational transitions in small gas molecules, a range of new measurement approaches expanding on direct absorption spectroscopy have been demonstrated to feature important advantages in terms of ruggedness as well as sensitivity [13, 14]. Some of these novel approaches exploit molecular dispersion, rather than absorption, to decouple the recorded quantity (phase or frequency) from the laser intensity [15, 16]. For liquids, these developments are yet pending. Linewidths of tens of cm⁻¹, the accordingly required lasers with tuning ranges beyond those achievable with DFB-QCLs, highly absorbing matrices and generally less well defined samples preclude a direct technology transfer from gas- to liquid spectroscopic sensing.

We present a novel, alternative approach to direct absorption spectroscopy for liquid samples that simultaneously and independently senses a sample’s absorption and dispersion (refractive index). This is made possible by employing an interferometric principle of operation in a Mach–Zehnder type optical setup. Although single wavelength (integrated) Mach–Zehnder interferometers (MZI) are widely employed for (bio-)chemical sensing, especially in the visible spectral range [17, 18], a report on directly recording a liquid sample’s absorption and dispersion spectrum in the Mid-IR using a MZI is, to the best of our knowledge, yet pending. The reader is, however, pointed to infrared spectroscopic ellipsometry [19] and dispersive Fourier transform spectroscopy [20, 21, 22] that were used in (far-) infrared spectroscopic measurements of the complex dielectric function, mostly in reflection measurements.

We derive simple expressions relating the signals recorded in our setup to refractive index and absorption. Based on theory and experimental results we discuss distinct differences between direct absorption spectroscopy and our setup and how they can be exploited to extend the scope of QCL-based Mid-IR spectroscopy.

2 Setup

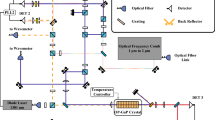
The setup is depicted schematically in Fig. 1. It is based on a free space MZI illuminated by an EC-QCL. A sample—and a reference liquid cell are introduced into the arms of the MZI, making the setup analogous to dispersive Fourier transform spectroscopy. The MZI is adjusted to equal optical path lengths in the two arms. To minimize fringing, all transparent optics, except for the liquid cells, are placed in the beam path in Brewster’s angle and the light is p—polarized, resulting in the rhombic shape of the interferometer.

Fig. 1

Experimental setup. Light from the EC-QCL enters the Mach–Zehnder-type interferometer through a beam splitter and passes the reference- or the sample liquid cell. The intensity I_des of the destructively interfering fields leaving the MZI is measured by two mercury–cadmium–telluride detectors and is a measure of the sample’s absorption. Destructive Interference is ensured by regulating I_des to its minimum by tilting a BaF₂ window in the sample beam path. The position sensitive photo diode facilitates the measurement of tilt, yielding the sample’s refractive index

The two interfering partial beams leaving the interferometer to the right in Fig. 1 (one from the reference arm and one from the sample arm of the interferometer) are recorded at a thermoelectrically cooled MCT detector, while a BaF₂-window is tilted to adjust the phase φ_rel between them to π, i.e. to best possible destructive interference. The window is twice as thick as the beam splitters which compensates for dispersion picked up by the reference (upper) beam in Fig. 1 within the beam splitters’ substrate. With no or equal samples in the liquid cells, the partial beams’ amplitudes are equal, resulting in full destructive interference and no signal from the MCT-detector. Equal amplitudes are ensured by both beams being once transmitted and reflected at beam splitters of equal beam splitting ratios.

The basic principle of operation is as follows: When the sample liquid cell is filled with an absorbing species, the amplitudes of the interfering fields differ. Hence, destructive interference will be incomplete and a detectable signal is recorded that is a measure of the sample’s absorption. At the same time, dispersion in the sample will cause a change in the relative phase of the two fields which needs to be compensated by the BaF₂ window’s tilt. By reading the tilt, the sample’s refractive index is recorded. The tilt of the window is measured via the position of a reflected HeNe-laser beam on a two zone photodiode. Optionally, the constructively interfering output of the MZI can be recorded by a second MCT detector and used to reference the destructively interfering signal to the laser power.

3 Theory

3.1 Basic equations

The signal I_des recorded at the detector is modelled as the coherent superposition of two plane wave electric fields E_s and E_ref of intensities I_s and I_ref, relative phase ${\varphi _{{\text{rel}}}}$ and equal frequency. E_s and E_ref are defined as the fields on the detector that were transmitted and reflected, respectively, at the first beam splitter of the MZI. This yields

$$\begin{array}{*{20}{c}} {{I_{{\text{des}}}}={{\left| {{E_{\text{s}}}+{E_{{\text{ref}}}}} \right|}^2}={I_{\text{s}}}+{I_{{\text{ref}}}}+2\sqrt {{I_{\text{s}}}{I_{{\text{ref}}}}} \cos \left( {{\varphi _{{\text{rel}}}}} \right).} \end{array}$$

(1)

During the experiment, the relative phase is set to π by tilting the BaF₂ window. In a symmetric interferometer with equal samples in both arms, ${\varphi _{{\text{rel}}}}$ does not change while scanning the wavelength and the window’s tilt is constant. When the sample cell is loaded with a sample other than the reference, dispersion in the sample causes a spectrally varying additional phase φ that needs to be actively compensated by tilting the window to set ${\varphi _{{\text{rel}}}}=\pi$. This phase φ, recorded via the window’s tilt, is a measure of the sample’s refractive index n_s as compared to the reference n_ref and is given as

$$\begin{array}{*{20}{c}} {\varphi =2\pi \frac{{d \times \left( {{n_{\text{s}}} - {n_{{\text{ref}}}}} \right)}}{\lambda }.} \end{array}$$

(2)

Herein, the film thickness d was assumed equal for both cells. As can be seen from (2), the recorded phase is directly proportional to the sample’s refractive index and hence, for diluted samples, its concentration c.

In the configuration described above, the intensities I_s and I_ref are equal, except for absorption in the sample (decadic absorption is used throughout).

$$\begin{array}{*{20}{c}} {{I_{\text{s}}}={I_{{\text{ref}}}}{{10}^{ - A}}={I_0}{T_{{\text{ref}}}}RT{{10}^{ - A}}} \end{array}$$

(3)

Herein, I₀ is the laser intensity, T_ref the transmission of the reference and $R=1 - T$ the reflectivity of the beam splitters. Combining (1) and (3) and setting ${\varphi _{{\text{rel}}}}=\pi$ yields

$$\begin{array}{*{20}{c}} {{I_{{\text{des}}}}\left( A \right)={I_{{\text{ref}}}} \times {{\left( {1 - {{10}^{ - A/2}}} \right)}^2}.} \end{array}$$

(4)

For calibration purposes using Beer’s law it is useful to write out A explicitly from (4).

$$\begin{array}{*{20}{c}} {A=\varepsilon \times c \times d= - 2{{\log }_{10}}\left( {1 - \sqrt {\frac{{{I_{{\text{des}}}}}}{{{I_{{\text{ref}}}}}}} } \right)} \end{array}$$

(5)

3.2 Discussion of interferometric signals

When recording I_des to measure concentrations or absorptions, some pronounced differences to direct absorption spectroscopy need to be taken into account. Most of them stem from the interferometric setup being sensitive to the amplitude of the transmitted E-field (‘amplitude spectroscopy’), while direct absorption measures its power (‘power spectroscopy’) [22]. This behaviour is indicated by the square root of the fraction I_des/I_con in the logarithm in (5) rather than the fraction of two intensities (as is the case in direct absorption spectroscopy). The differences between amplitude- and power spectroscopy can be seen in the graphs of I_s (direct absorption signal, compare (3)) and I_des (Fig. 2) as a function of A as well as from Taylor series expansion of I_des in A around ${A_0}=0$.

Fig. 2

Graphs of absorptive signals recorded in direct absorption spectroscopy (I_s) and the Mach–Zehnder interferometer (I_des) as well as their sensitivities ${\text{d}}I/{\text{d}}A$

$$\begin{array}{*{20}{c}} {{I_{{\text{des}}}}={I_{{\text{ref}}}} \times \left[ {0+0A+\frac{{\ln {{\left( {10} \right)}^2}{A^2}}}{4} - \frac{{\ln {{\left( {10} \right)}^3}{A^3}}}{8}+ \cdots } \right]} \end{array}$$

(6)

One important feature of the interferometric signal is that it is background free, i.e. ${I_{{\text{des}}}}\left( 0 \right)=0$ (no constant term in (6)). However, as indicated by the vanishing linear term of (6), its sensitivity ${\text{d}}{I_{{\text{des}}}}/{\text{d}}A$ is zero too. The sensitivity increases with A until a maximum is reached at $A=2\ln \left( 2 \right)/\ln \left( {10} \right) \approx 0.6$, with a shallow role off towards larger A. This behaviour is in strong contrast to the direct absorption signal I_s, which has its largest magnitude (background) and largest sensitivity at $A=0$, decreasing with A.

Due to the vanishing sensitivity at small A the MZI should in general not be operated with equally intense reference and sample beams. By increasing I_ref relative to I_s, the sensitivity can be strongly enhanced. This can be implemented by using beam splitters of different splitting ratios or—when dealing with samples featuring broadband background absorptions—by simply using a sample liquid cell of larger film thickness as compared to the reference. The latter approach potentially increases the method’s sensitivity due to increased film thickness, but imbalances the optical path lengths in the interferometer, which requires additional care when interpreting the recorded spectra of I_des and φ. A generalized theory for unbalanced interferometers is derived in the Appendix.

For large absorptions $A>1$, the sensitivity of the interferometric signal is much larger than the quickly decreasing sensitivity ${\text{d}}{I_{\text{s}}}/{\text{d}}A$ of the direct absorption signal. This makes the technique an interesting candidate when high concentrations need to be measured at good precision or for strongly absorbing solvents such as water. Also, the good sensitivity for large A yields a significantly larger dynamic range of I_des as compared to direct absorption spectroscopy.

Just like in conventional FTIR spectroscopy, I_des needs to be referenced to the laser power and the absorption of the reference sample, i.e. to I_ref. In comparison to direct absorption spectroscopy, however, referencing is much less critical because the interferometer inherently references the sample beam to the reference beam. Drifting laser power solely scales I_des (and retrieved A and c), but does not add constant errors to it, as is the case for power spectroscopy. A detailed comparative discussion of LODs in the presence of detector noise, shot noise and laser intensity noise is given in Sect. 6.

The simultaneously recorded refractive index is independent from laser power and provides additional robustness towards laser power fluctuations. For diluted samples, refractive index spectra scale linearly with concentration and show highly characteristic features in the Mid-IR, making them a useful tool for chemical analysis.

4 Experimental

4.1 Spectra acquisition and instrumentation

The optical setup was described above. For all measurements presented herein, two close to identical beam splitters with a 50/50 splitting ratio were employed. The liquid cells’ film thickness was 1.9 mm. Uncoated BaF₂ windows were employed as windows for the liquid cells. With the liquid cells filled with the same sample, the optical path length in the two arms was found to be equal on the order of the wavelength used. This was confirmed by scanning the wavelength over approximately 200 cm⁻¹ without changing the BaF₂-window’s tilt and recording the destructive signal. The absence of spectral oscillations in the recorded interferometric signal indicates equal optical path lengths. The modulation efficiency M of the interferometer, defined as the contrast between constructively and destructively interfering signals, $M={I_{{\text{con}}}}\left( {A=0} \right)/{I_{{\text{des}}}}\left( {A=0} \right)$, exceeded 23 dB throughout the experiments (fringes from the liquid cells not taken into account). It was limited by slightly different intensities of the reference—and sample beam as well as imperfect overlapping of the beams at the detector.

To record spectra of I_des and φ, a simple program on a personal computer was used to tune the EC-QCL’s wavelength across the desired range stepwise. At each step, the BaF₂-window, mounted in a piezo-motor driven kinematic mount (Newport Agilis), was tilted in a closed loop to minimize the signal I_des at the MCT detector. The closed loop differential controller was implemented in software to step the window’s angle by a given value for a predefined number of times. Each step’s direction was determined by the change in destructive signal upon the previous step to move towards smaller I_des. The smallest recorded value of I_des as well as I _con and its corresponding tilt-signal was stored.

The EC-QCL, developed and manufactured at Fraunhofer IAF Freiburg, provided a tuning range from 1080 to 1370 cm⁻¹ in pulsed mode with an average power of 250 mW within a 120-ns pulse at 1200 cm⁻¹ [23]. Spectra were recorded by tuning the EC-QCL in steps of 0.4 cm⁻¹ at a rate of 0.2 steps/s. The acquisition speed was limited by the slow closed loop for tilting the window, especially the actuator, which was by no means optimized towards speed. I_des as well as the attenuated second output of the interferometer, I_con, was measured by thermoelectrically cooled MCT-detectors (PVI-10.6, Vigo Systems S.A.) which were read out by a boxcar integrator at the laser repetition frequency of 9 kHz (limited by the maximum frequency of the gated integrator) and averaged over 300 pulses. I_con was used to reference I_des to the laser power and the reference absorption spectrum by calculating I_des/I_con. This is only valid for small absorptions and sufficient to demonstrate the characteristics of the interferometric setup within the context of this work. For a rigorous calibration, a separately recorded spectrum of I_ref must be used to calculate A from I_des using (5).

Reference absorption spectra were recorded on a Bruker Vertex 80v-FTIR spectrometer.

4.2 Chemicals and samples

Samples of acetone in cyclohexane at varying concentrations were prepared from reagent grade chemicals. Methanol added to some of the samples was of the same grade.

5 Experimental results

5.1 Simultaneous measurement of absorption- and refractive index spectra

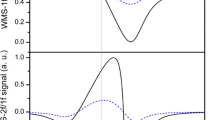
The simultaneously measured spectra of I_des/I_con and the BaF₂ window’s tilt of 2.4 mmol/L acetone in cyclohexane are depicted in Fig. 3. The spectra were smoothed using a Savitzky–Golay filter to remove fringes that could be assigned to the liquid cells. Inverse fast Fourier transformation of the raw spectra revealed multiple etalons of round trip optical path lengths between 4.5 and 7.5 mm, well separated from the signal spanning out from DC to 0.2 mm (FWHM of studied absorption profile is 8 cm⁻¹). The BaF₂ window’s tilt resembles the sigmoid anomalous dispersion profile of the refractive index. Kramers Kronig transformation yields an expected change in refractive index (peak to trough) of $\Delta {n_{{\text{max,min}}}} \approx 7 \times {10^{ - 5}}$, corresponding to a phase difference of 6°, around the molecular resonance.

Fig. 3

Smoothed absorptive signal (solid line) and tilt of the BaF₂ window (dashed line) of 2.4 mmol/L acetone in cyclohexane. Note that I_des is normalized to a small fraction of I_con, explaining I_des/I_con > 1

5.2 Dilution series of acetone in cyclohexane

Absorption spectra of different concentrations of acetone in cyclohexane were recorded. To demonstrate that no second detector is required to derive a reference for normalization, the interferometric spectra presented in Fig. 4 were normalized as $\left( {{I_{{\text{des}}}} - {I_{{\text{des}}}}\left( {c=0} \right)} \right)/{I_{{\text{des}}}}\left( {c=0} \right)$. ${I_{{\text{des}}}}\left( {c=0} \right)$ was recorded for pure cyclohexane in the sample- and reference position. Although this signal should be zero according to the theory derived above, due to limited modulation efficiency, ${I_{{\text{des}}}}\left( {c=0} \right)$ represents a background spectrum that was found to be a good measure for ${I_{{\text{ref}}}}$.

Fig. 4

Top; absorptive signal $\left( {{I_{{\text{des}}}} - {I_{{\text{des}}}}\left( {c=0} \right)} \right)/{I_{{\text{des}}}}\left( {c=0} \right)$ for varying concentrations of acetone in cyclohexane. Bottom; absorptive signal at absorption maximum (1214 cm⁻¹) against peak absorption A = c × 0.0359 L/mmol

The normalized spectra of the recorded intensity I_des in Fig. 4 qualitatively exhibit the expected behaviour of the interferometric signal discussed above with the sensitivity clearly increasing for larger concentrations, i.e. larger absorption A. After converting concentration to absorption via $A=c \times 0.0359\,\,{\text{L/mmol}}$, the parameters a₁ and a₂ of the function ${I_{{\text{des}}}}={a_1} \times \left( {1+{{10}^{ - \left( {A+{a_2}} \right)}} - 2 \times {{10}^{ - (A+{a_2})/2}}} \right)$ were fitted to the signal at the absorption maximum (Fig. 4, bottom). a₂ represents an offset absorption that resembles the small imbalance in the intensities of the reference- and sample beam.

5.3 Increased reference intensity

As discussed above, the absorptive signal exhibits its smallest sensitivity dI_des/dA when the intensities of the reference and the sample beam are equal (A = 0) and increases as the two are unbalanced (increasing A, compare Fig. 2). To demonstrate the effect of unbalancing the signal and reference intensity, varying amounts of a spectrally flat absorber (methanol) were added to a sample of 3 mmol/L acetone in cyclohexane and their interferometric spectra were recorded with cyclohexane as a reference (Fig. 5, top left). The absorption spectrum of 3 mmol/L acetone in cyclohexane, recorded on an FTIR spectrometer, was used to replace the wavenumber axis of the interferometric spectra by an absorption axis (compare Fig. 5). The so derived curves of I_des/I_con versus A were analysed by fitting second-order polynomials to them. The fitted coefficients are given in Table 1. The coefficient K₁, representing the sensitivity of the absorptive signals for small A, is increased by a factor of seven by reducing the intensity of the sample beam by 11 percent. At the same time, the background-signal (K₀) is increased by a factor of five, giving rise to a trade-off between background intensity and sensitivity. As discussed in detail in Sect. 6, this trade-off must be made based on the sources of noise in the system.

Fig. 5

Top, left: interferometric spectra of 3 mmol/L acetone in cyclohexane for decreasing intensities I_s in the sample arm of the interferometer. Top, right: absorption spectrum of the same sample from an FTIR spectrometer used to assign a value of absorption to any wavenumber within the range indicated by the grey area (e.g. A₁ for ν₁). Bottom: normalized destructive signal versus sample absorption for different intensities I_s and I_ref

Table 1 Fitted parameters of ${I_{{\text{des}}}}/{I_{{\text{con}}}}={K_0}+{K_1}A+{K_2}{A^2}$ for the curves shown in Fig. 5

Fig. 6

Estimated LODs of the interferometric—and a direct absorption measurement. For details, see text

Fig. 7

Estimated uncertainties of an interferometric phase and refractive index measurement of 1 Hz bandwidth. Assumptions equal to Fig. 6, see text

As discussed above, the noticeable offset of I_des/I_con for ${I_{\text{s}}}={I_{{\text{ref}}}}$ and $A=0$ in Fig. 5 arises from the limited modulation efficiency M and the slightly differing intensities in the two interferometric arms (Fig. 7).

6 Modelling limits of detection

Experimental shortcomings of the current setup (fringes, poor phase adjustment, limited ruggedness) prohibit a direct experimental assessment of figures of merit as compared to established direct absorption spectroscopy (e.g. FTIR). Here, we give a comparative discussion based on the equations presented above and a noise model including shot noise, detector noise and power noise of the light source. For the Mach–Zehnder interferometer, noise associated with the interferometric phase is considered negligible, as can be expected for a rugged design and well-optimized feedback loop that keeps the phase at π. For both, direct absorption and interferometric measurements, fringes are indistinguishable from absorption (and dispersion) in the equations and effect the measurements equally.

The noise equivalent power (NEP), given in WHz^−1/2, overlying the recorded signals, is modelled as

$$\begin{array}{*{20}{c}} {{\text{NEP}}=\sqrt {{\text{NEP}}_{{{\text{det}}}}^{2}+P_{{{\text{shot}}}}^{2}+P_{{{\text{PN}}}}^{2}} } \end{array}$$

(7)

Herein, P_shot, NEP_det and P_PN are shot noise, the noise equivalent power of the detector and power noise from the laser (or other light source), respectively. Shot noise is given as

$$\begin{array}{*{20}{c}} {{P_{{\text{shot}}}}=\sqrt {h\nu {P_{{\text{sig}}}}\left( {A=0} \right)} } \end{array}$$

(8)

with h representing Planck’s constant and ν the optical frequency. The power of the detected light P_sig is given by (compare (4))

$$\begin{array}{*{20}{c}} {{P_{{\text{sig,int}}}}={P_0}RT{{\left( {1 - {{10}^{ - \frac{{A+{A_{{\text{off}}}}}}{2}}}} \right)}^2}} \end{array}$$

(9)

for the interferometric signal and by

$$\begin{array}{*{20}{c}} {{P_{{\text{sig,dir}}}}={P_0}{{10}^{ - A}}} \end{array}$$

(10)

for direct absorption, with P₀ representing the laser power. A_off represents an intentionally introduced imbalance between the intensities of the destructively interfering fields (compare Sect. 5.3). P_PN is derived by considering the effect of normally distributed laser power noise of power P_N on the recorded signals P_sig for A = 0.

$$\begin{array}{*{20}{c}} {{P_{{\text{PN,dir}}}}={P_{\text{N}}}} \end{array}$$

(11)

$$\begin{array}{*{20}{c}} {{P_{{\text{PN,int}}}}={P_{\text{N}}}RT{{\left( {1 - {{10}^{ - \frac{{{A_{{\text{off}}}}}}{2}}}} \right)}^2}} \end{array}$$

(12)

NEP_det, often specified inversely as detectivity D^*, usually scales with the power of light to be detected. Typical NEP_det for Mid-IR detectors are on the order of 10⁻⁶ Hz^−1/2 of the saturation power. Assuming an amplification chosen to match the highest expected signals, NEP _det is given as

$$\begin{array}{*{20}{c}} {{\text{NE}}{{\text{P}}_{{\text{det,dir}}}}=a \times {P_{{\text{sig,dir}}}}\left( {A=0} \right)=a{P_0}} \end{array}$$

(13)

$$\begin{array}{*{20}{c}} {{\text{NE}}{{\text{P}}_{{\text{det,int}}}}=a \times {P_{{\text{sig,int}}}}\left( {{A_{{\text{max}}}}} \right).} \end{array}$$

(14)

From here on, we assume A_max = 0.2 (corresponding to ${P_{{\text{sig,int}}}}={10^{ - 2}}{P_0}$) for the strongest interferometric signal. a is assumed 10⁻⁶ Hz^−1/2.

To calculate limits of detection (LOD), we employ

$$\begin{array}{*{20}{c}} {{\text{LOD}}=3 \times \frac{{{\text{NEP}}}}{{{\text{d}}{P_{{\text{sig}}}}/{\text{d}}A(A=0)}}} \end{array}$$

(15)

The sensitivities dP_sig/dA read

$$\begin{array}{*{20}{c}} {\frac{{{\text{d}}{P_{{\text{sig,int}}}}}}{{{\text{d}}A}}\left( A \right)={P_0}\ln \left( {10} \right)RT \times \left( {{{10}^{ - \frac{{A+{A_{{\text{off}}}}}}{2}}} - {{10}^{ - \left( {A+{A_{{\text{off}}}}} \right)}}} \right)} \end{array}$$

(16)

$$\begin{array}{*{20}{c}} {\frac{{{\text{d}}{P_{{\text{sig,dir}}}}}}{{{\text{d}}A}}\left( A \right)= - {P_0}\ln \left( {10} \right){{10}^{ - A}}.} \end{array}$$

(17)

The so estimated LOD of the interferometric absorption measurement for three different offset absorptions A_off as well as the LOD of the direct absorption measurement are plotted in Fig. 6 against the laser intensity noise P_N. For small P_N, signals are detector noise limited and independent from P_N. With an offset absorption A_off = 0.1, the interferometric measurement yields slightly smaller LODs due to the reduced detector noise associated with the reduced dynamic range of the detector. As P_N increases, the interferometric measurement yields smaller LODs. This is due to the interferometric referencing of the light from the sample arm of the interferometer to the reference arm, which cancels common mode noise. As A _off increases, the increased sensitivity ${\text{d}}{P_{{\text{sig,int}}}}/{\text{d}}A$ yields lower LODs in the detector noise limited regime, but higher LODs for increased laser power noise. This is explained by incomplete destructive interference in the unbalanced interferometer and hence only partial removal of power noise.

Assuming no additional noise sources for the interferometric phase, LODs for the refractive index can be estimated based on the noise floor of the signal

$$\begin{array}{*{20}{c}} {{P_{{\text{sig,int}}}}\left( \varphi \right)={P_0}RT\left[ {1+{{10}^{ - (A+{A_{{\text{off}}}})}} - 2 \times {{10}^{ - \frac{{A+{A_{{\text{off}}}}}}{2}}}\cos \left( \varphi \right)} \right],} \end{array}$$

(18)

since this signal’s minimum with respect to φ defines the refractive index (see (2)). An estimate of LODs equivalent to (15) using the sensitivity dP_sig,int/dφ is prohibited by the vanishing sensitivity at φ = 0. Instead, we propagate the error NEP of the P_sig,int measurement to the measurement of phase by solving ${\text{NEP}}={P_{{\text{sig,int}}}}\left( {\Delta \varphi } \right) - {P_{{\text{sig,int}}}}\left( 0 \right)$ for Δφ setting A = 0.

$$\begin{array}{*{20}{c}} {\Delta \varphi =\arccos \left( {1 - \frac{{{\text{NEP}} \times \sqrt {BW} }}{{2{P_0}RT \times {{10}^{ - {A_{{\text{off}}}}/2}}}}} \right)} \end{array}$$

(19)

The measurement uncertainty Δφ and resulting Δn are plotted in Fig. 7 against laser power noise P_N using the same parameters for NEP as in Fig. 6, a bandwidth BW of 1 Hz, a liquid film thickness of 1.9 mm and a wavelength of 8.3 µm. For a comparison, refractive index and phase can be referenced to absorption using Kramers–Kronig transformation and assuming an isolated Gaussian absorption profile of peak absorbance A. For this profile, Kramers–Kronig transformation yields an anomalous dispersion profile spanning, from top to bottom, ${n_{\hbox{max} }} - {n_{\hbox{min} }}=A/d \times 1.86 \times {10^{ - 3}}{\text{m}}{{\text{m}}^{ - 1}}$, or ${\varphi _{\hbox{max} }} - {\varphi _{\hbox{min} }}=A \times 80^\circ /AU$. For the Mach–Zehnder interferometer, this comparison yields a much better performance of absorptive measurements, which is a result of the vanishing sensitivity dP_sig,int/dφ at φ = 0.

7 Conclusions

In this contribution, we introduced an interferometric setup that facilitates the simultaneous measurement of absorption and refractive index spectra of liquid samples. We discussed the theory relating the recorded signals to absorption and dispersion and presented proof of principle measurements supporting theoretical predictions.

For the absorptive signal, the theoretical considerations and experimental data demonstrate important differences to direct absorption spectroscopy. Spectra are recorded close to background free and are inherently referenced to the sample (e.g. solvent or matrix) introduced into the reference position. Although the sensitivity, i.e. change of recorded signal with absorption or concentration, is reduced as compared to direct absorption spectroscopy, this does not imply higher limits of detection (LOD). The latter depend on the noise floor, which, assuming the same sources of noise, is very different for the two techniques. While the reduced sensitivity (smaller signals) makes interferometric absorption measurements more prone to detector noise, they are much less susceptible to intensity noise due to the reduced levels of background intensity at the detector. This is of particular interest for external cavity laser based spectroscopy, since these lasers are known for intensity noise associated with mode hops [10, 24]. A trade-off between sensitivity and immunity to intensity noise can be made by unbalancing the intensities of the reference and sample beam.

So far, an experimental investigation of these interesting properties was hampered by fringes in the sample cells as well as the slow actuator and feedback loop for the phase adjustment. Using wedged and/or anti reflection-coated windows could reduce the fringes. Adjustment of the phase can be greatly speeded up by using one of the interferometer’s mirrors on a piezo element as the phase actuator [25].

Appendix: Generalized theory

The interferometer can be imbalanced in two ways. The intensities I_ref and I_s can differ (compare Sect. 5.3) or the film thickness of the liquid cells can be unequal.

The former situation can be easily described by the equations derived above by describing the difference between I_ref and I_s via an offset absorption ${A_0}=\log \left( {{I_{{\text{ref}}}}/{I_{\text{s}}}} \right)$, which modifies (3) to

$$\begin{array}{*{20}{c}} {{I_{\text{s}}}={I_{{\text{ref}}}} \times {{10}^{ - \left( {A+{A_0}} \right)}}} \end{array}$$

(20)

A₀ can be a constant or vary spectrally, depending on the mechanism creating the imbalance of intensities.

Unequal film thicknesses ${d_{{\text{ref}}}} \ne {d_{\text{s}}}$ result in differing intensities of I_s and I_ref because of absorption by the matrix and differing optical path lengths in the two liquid films. Increased matrix absorption enters the equations above just like A₀ in (20) and is given as ${A_{{\text{matrix}}}}={\alpha _{{\text{matrix}}}} \times \left( {{d_{\text{s}}} - {d_{{\text{ref}}}}} \right)$, with α being the decadic absorption coefficient. The optical path lengths are given as

$$\begin{array}{*{20}{c}} {{l_{{\text{opt,s,ref}}}}={n_{{\text{s,ref}}}} \times {d_{{\text{s,ref}}}}} \end{array}$$

(21)

The difference between the two path lengths yields the phase φ (compare (2)) as

$$\begin{array}{*{20}{c}} {\varphi =\frac{{2\pi }}{\lambda } \times \left[ {{n_{{\text{ref}}}}\left( {{d_{\text{s}}} - {d_{{\text{ref}}}}} \right)+\left( {{n_{\text{s}}} - {n_{{\text{ref}}}}} \right){d_{\text{s}}}} \right]} \end{array}$$

(22)

The extended form of (22) illustrates that φ is composed of a background spectrum resembling the refractive index of the reference and a sample spectrum.