1 Introduction

Palladium is one of the high-value platinum metals present in nuclear power plant radioactive waste, occurring in quantities comparable to that available from natural reserves [1]; however, they are presently unable to be utilized due to the co-presence of the long-lived radioactive isotopes 107Pd (17%). To date, techniques to selectively remove this radioactive isotope have not been established on a commercial scale. As the isotope shifts in palladium are only approximately 50 MHz [2], it is not feasible to selectively ionize isotopes using narrow linewidth lasers; however, two effective techniques exist for selective ionization. The first is based on a proposal by Balling and Wright [1] using circularly polarized lasers, in which only odd-mass number isotopes having nonzero nuclear spin and thus having hyperfine structure are able to be excited due to optical transition selection rules. The feasibility of this scheme as applied to platinum group metals is reported by Chen [3], implemented by Yamaguchi and Sasao [4, 5], and further developed in our previous paper [6]. The second technique, resonant ionization mass spectrometry (RIMS) [7, 8], obtains selectivity of ionized isotopes via a narrow slit and accelerating fields, such as the RISIKO separator system as applied to palladium [9]. Comparison between the efficiencies and costs of both techniques are essential before commercial-scale projects can be undertaken.

We have developed our apparatus employing the first technique, that is, exploiting transition rules for selective excitation [10]. Resonant excitation to autoionizing states is a promising means to obtain efficient ionization after such mass-selective excitation. Autoionizing Rydberg states come about due a characteristic in the spin–orbit interaction of Pd, where the ion Pd II has two ground states of different ion core configurations, namely 4d 9(2D5/2) at 67241.3(8) cm−1 and 4d 9(2D3/2) at 70779.8(8) cm−1 [11]. Any states existing between the two ground states are autoionizing, and the ion yield is over an order of magnitude higher than excitation to the ionization continuum [12].

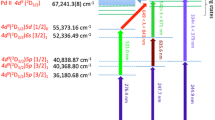
The conventional Pd odd-mass selectivity excitation scheme excites via intermediate states having a 2D5/2 core [3–6], as shown as configuration (a) in Fig. 1. For this scheme, selectivity is obtained via (0-1-0) transition rules, that is, the first level is J = 0, the first intermediate state is J = 1, and the second intermediate state is J = 0. If circularly polarized light of the same chirality is used for the first- and second-step excitation, then only isotopes with odd-mass number (and thus having nonzero spin) can be excited, as the first basis-setting transition then requires ∆m J  = ±1 for the second transition. Alternatively, cross-linear polarization can be used that satisfies the same selection rules [6].

Fig. 1
figure 1

Two-step selective excitation scheme, with a third step to autoionizing Rydberg states; a the conventional (0-1-0) scheme using circularly polarized light for selectivity; b the proposed (0-1-1) scheme using linearly polarized light for selectivity. The frequency of the third excitation laser (ω3) is swept over the ranges indicated to map autoionizing Rydberg states converging to Pd II 4d 9(2D3/2). Energies and level designations are from NIST Atomic Spectra Database [11]

Full size image

To improve ionization efficiency, we propose an excitation scheme via intermediate states having a 2D3/2 core, shown as configuration (b) in Fig. 1. This excitation scheme works via (0-1-1) selection rules, using linearly polarized light (∆m J  = 0) which forbids excitation of even-mass number isotopes from the first to the second intermediate state (when ∆J = 0, \(\Delta m_{J} 0{ \nLeftrightarrow }\) 0).

2 Experiment

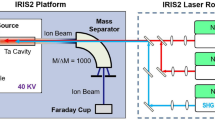
We use the same excitation lasers and optics as described in detail previously [6], although the lasers are now tuned to different frequencies for the newly devised (0-1-1) scheme. To briefly summarize, we use an electron beam source (ULVAC EGK-3) directed into a crucible of Pd, producing a Pd vapor collimated by two 10-mm-diameter apertures. We monitor the evaporation rate with a thickness meter (Inficon Q-Pod) and can deduce the atomic density in the interaction region (typically of order 1010 cm−3).

A single excimer laser (Lambda Physik Compex 103) simultaneously pumps three dye lasers (Lambda Physik FL3002 × 2, Lumonics HD500), producing pulses of width 20 ns and repetition rate of 10 Hz. Wavelengths are recorded using a wavemeter (Coherent WaveMate Deluxe) calibrated using an optogalvanic neon gas cell.

The first dye laser at 495.4 nm is frequency doubled in a BBO crystal to produce the first excitation wavelength (λ1) of 247.7 nm, exciting Pd atoms from the ground state into the 4d 9(2D3/2)5p 2[3/2]1 state, which is optimally tuned by maximizing fluorescence to the 4d 9(2D3/2)5 s 2[3/2]1 state, detected at 330.3 nm by a photomultiplier tube (Hamamatsu R955) through a monochromator (Jasco: CT-25C). The second laser at 835.6 nm excites Pd atoms from 4d 9(2D3/2)5p 2[3/2]1 to 4d 9(2D3/2)6 s 2[3/2]1, tuned by maximizing the decay emission to 4d 9(2D3/2)5p 2[5/2]2 at 739.4 nm. The third laser is inserted colinear to the second laser with a dichroic mirror, counter-propagating to the first laser, and is swept over the entire range between the ionic ground states of Pd II.

Photoions are produced in a field-free region to reduce frequency shift effects and are subsequently horizontally repelled by a set of three electrodes charged with a time-delayed high-voltage pulse (switched on 1.8 μs after photoionization) in a Wiley–McLaren configuration [13] in order to separate mass isotopes in a 1-m time-of-flight mass spectrometer, with mass resolution (m/∆m) of 600. The relative amounts of Pd isotopes are detected using a 2-stack microchannel plate (Hamamatsu F4655-11). Statistical fluctuations in the observed signal are averaged over several hundred laser shots on a 500-MHz storage oscilloscope. Ion current is calculated from the area under the voltage–time curve, via the input impedance of the oscilloscope.

The ion current is observed as a function of ω3 to determine resonant transition frequencies of autoionizing Rydberg levels. Intensity variations in the third laser over the range of the frequency scan, measured by sampling a portion of the beam using a photodetector, are normalized in post-processing to determine relative transition intensities. Four different dye solutions are required to span the entire frequency range, so several overlapping peaks are selected and compared to ensure congruous intensity scaling between each dye.

3 Results and discussion

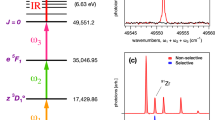
Selectivity of odd-mass number isotopes using our proposed 2D3/2 core intermediate states scheme is shown in Fig. 2. In these demonstrative experiments, we use natural samples in which isotope 107Pd (the radioactive isotope of interest in selectivity schemes) is not present. However, as 105Pd and 107Pd have the same nuclear spin (I = 5/2), both isotopes are expected to behave identically in the separation process. For comparison, we show the observed signal when the first two excitation lasers do not have their polarization axes aligned, and all isotopes are observed in ratios that are expected in natural abundance [14]. When the polarization axes of the excitations lasers are aligned, complete selectivity is achieved, with only odd-mass number isotopes ionized. It is of note that the selection process does not alter the amount of odd-mass number isotopes that are ionized in comparison with when all isotopes are ionized.

Fig. 2
figure 2

Observed isotopes of Pd II; polarization axes of the two (linearly polarized) excitation lasers are not aligned and all isotopes of Pd are observed (102Pd: 1.1%, 104Pd: 10.7%, 105Pd: 28.9%, 106Pd: 25.2%, 108Pd: 21.5%, 110Pd: 12.8%); polarization axes are aligned, only odd-mass number isotopes are excited and subsequently ionized, with <0.3% of even-mass number isotopes ionized

Full size image

One important distinction between this transition-rule mass-selective method and that using ion mass selection (RIMS) is that the former has strict limitations on the fluence of the first laser, in that it must be below the threshold for two-photon ionization, as described previously [6]. Conversely, an advantage to the former is that only isotopes of interest are excited and thus overall yield is not limited by ion current, whereas in the RIMS method ion–ion Coulombic repulsion imposes a limit on selectivity with increased ion current.

We have investigated the autoionizing Rydberg series by scanning the third laser (ω3) over the entire range between the two ionization potentials to find the most efficient transition, as shown in Fig. 3. Peak positions are calculated by fitting a Lorentzian to experimental data points, with peak center uncertainty of ±0.1 cm−1. Spectral lines are listed in Table 2.

Fig. 3
figure 3

High-resolution Rydberg spectrum observed from the intermediate state Pd I 4d 9(2D3/2)6 s 2[3/2]1; ○ ionic ground state of Pd II 4d 9(2D5/2) having value of 67241.3 cm−1; × ionic ground state of Pd II 4d 9(2D3/2) having value of 70780.40 cm−1. Guidelines and integers indicate principal quantum numbers of Rydberg series. Arrows indicate peaks arising from the sequence (ω1 → ω3 → ω2)

Full size image

The most efficient autoionization state was found to be at 67668.39(10) cm−1, corresponding to a third-step laser wavelength of 652.244(5) nm. The proposed 2D3/2 core scheme with autoionization to this Rydberg level has an ion current over 130 times larger than the conventional 2D5/2 core scheme [3, 4, 15–17] when ω3 is tuned to the corresponding maximal ion current Rydberg level of this scheme occurring at 69055.51(30) cm−1. Comparison of ion current between both schemes as a function of fluence of ω3 is shown in Fig. 4.

Fig. 4
figure 4

Observed ion current in the two different odd-mass isotope selectivity schemes. using the conventional 2D5/2 core scheme; × using the proposed 2D3/2 core scheme

Full size image

Peaks due to ionization via the sequence (ω1→ω3→ω2) have been identified at (67340.855, 70106.338, 70163.113, 70375.986, 70416.395, 70523.647, 70649.190) cm−1, where experimentally measured peaks differ from the NIST spectra database [11] by <0.20 cm−1. Although ion current is substantially lower (transitions are to the continuum rather than autoionizing Rydberg states), it is important that these peaks are identified as ionization is via intermediate states equally allowed for both odd and even mass isotopes.

The energies of the Rydberg states E(n) can be approximated by the extended Ritz formula [18, 19]:

$$E\left( n \right) = {\text{I}}.{\text{P}}. - \frac{{R_{Pd} }}{{\left[ {n - \delta \left( n \right)} \right]^{2} }}$$
(1)

where

$$\delta \left( n \right) = \delta_{0} + \frac{{\delta_{2} }}{{\left( {n - \delta_{0} } \right)^{2} }}$$
(2)

where I.P. is the ionization energy of Pd I, R Pd is the mass-corrected Rydberg constant of Pd I (109736.75 cm−1), and both δ0 and δ2 are the energy-dependent quantum defects that account for the shielding of the nucleus by the core electrons.

For assignment of the energy levels, we use the J c K coupling scheme [20] which is appropriate for Pd I. Selection rules for the transition from the 4d 96 s state indicate eight Rydberg series are expected, five of which are autoionizing: 4d 9(2D3/2)np[1/2]0, 4d 9(2D3/2)np[3/2]1, 4d 9(2D3/2)np[1/2]1, 4d 9(2D3/2)np[5/2]2, and 4d 9(2D3/2)np[3/2]2. Of these, only 4d 9(2D3/2)np[1/2]1 and 4d 9(2D3/2)np[3/2]1 are in common with those observed when exciting Pd I electrons from a d state: This can be either via direct excitation from the 4d 10 ground state with VUV radiation, as is reported in Baig et al. [21] in which the np Rydberg series (n = 8–17, δ = 3.02) were observed, or alternatively, these two series are also observed in our earlier study from the 4d 95d intermediate state [22]. The co-incidence of the two np series in [22] allows us to assign two of the five observed series in this work.

We calculate the principal quantum number by extrapolating to lower-lying levels and matching to identified levels [11], and tentatively assign the observed series. The lowest member of the series assigned to 4d 9(2D3/2)np[3/2]2 has the largest ion current and exhibits fine-structure splitting about the predicted position of 67664.30 cm−1, suggesting interaction with some local perturbation. Similarly, we note energy level splitting around (68,500, 69,050, 69,400, and 69,700) cm−1, and we observe distorted profiles in a series of broad linewidth spectral lines that suggest a strong interaction with a resonance around 69,700 cm−1. However, further analysis on the origin of these interactions is difficult without knowledge of spectroscopic data [11] on two-electron excited states of palladium.

The energy of Pd II 4d(2D3/2) is determined to be 70780.6(1) cm−1 from least squares fitting of Eq. 1 to experimentally observed data. This ionization potential can be compared to the range reported in literature, which are 70779.8(8) cm−1 [21], 70780.9(10) cm−1 [12], and 70780.38(8) cm−1 [22]. By least squares fitting, we also determine the quantum defects of the observed Rydberg series, as shown in Table 1. Residuals of the fits to Eq. 1 are shown in Fig. 5.

Table 1 Fitting coefficients (± 1 standard deviation) to the extended Ritz formula; δ 0 and δ 2 are the energy-dependent quantum defects
Full size table
Table 2 Observed energy levels (± 0.1 cm−1) tentatively assigned to five Rydberg series, effective quantum number (n*), and ion current yield relative to the largest transition at 67668.18(10) cm−1
Full size table
Fig. 5
figure 5

Residuals of least squares fit to extended Ritz formula of observed peaks in ion current, tentatively assigned to Rydberg series. Solid line extended Ritz formula of Eq. (1); ◆ 4d 9(2D3/2)np[3/2]1; 4d 9(2D3/2)np[5/2]2; □ 4d9(2D3/2)np[1/2]1; ○ 4d 9(2D3/2)np[3/2]2; + 4d 9(2D3/2)np[1/2]0

Full size image

4 Conclusion

We have demonstrated an increase in efficiency of over 130 times in odd-mass-selective ionization using a newly proposed three-step excitation scheme when compared to the current art, with a odd-mass isotope selectivity of 99.7(3)%. This new excitation scheme has as the first two steps parallel linearly polarized lasers instead of circularly polarized lasers, and has greater yield efficiency as these intermediate states share the same core state as the third step to autoionizing Rydberg states. We have observed five autoionizing Rydberg series by scanning the third-step laser over the entire range between the two ionization potentials of palladium and by using fits to the extended Ritz formula have derived the energy of Pd II 4d(2D3/2) to be 70780.6(1) cm−1 and determined the quantum defects of these Rydberg series. We have made the first report of relative transition efficiencies to these autoionizing Rydberg states from the 6 s intermediate state, a critical step toward development of practical implementation of even- to odd-mass separation schemes. The most efficient autoionization state is at 67668.18(10) cm−1, corresponding to a third-step laser wavelength of 652.244(5) nm. The second-most efficient state (having a yield of 86% of the most efficient) is at 69642.97(10) cm−1, corresponding to a third-step laser wavelength of 577.818(5) nm.