Ultracold metastable helium: Ramsey fringes and atom interferometry

Abstract

We report on interference studies in the internal and external degrees of freedom of metastable triplet helium atoms trapped near quantum degeneracy in a $1.5 \,\upmu {\mathrm{m}}$ optical dipole trap. Applying a single $\pi /2$ rf pulse we demonstrate that 50% of the atoms initially in the $m=+1$ state can be transferred to the magnetic field insensitive $m=0$ state. Two $\pi /2$ pulses with varying time delay allow a Ramsey-type measurement of the Zeeman shift for a high precision measurement of the $2\,^3S_1$–$2\,^1S_0$ transition frequency. We show that this method also allows strong suppression of mean-field effects on the measurement of the Zeeman shift, which is necessary to reach the accuracy goal of 0.1 kHz on the absolute transition frequencies. Theoretically the feasibility of using metastable triplet helium atoms in the $m=0$ state for atom interferometry is studied demonstrating favorable conditions, compared to the alkali atoms that are used traditionally, for a non-QED determination of the fine structure constant.

1 Introduction

The helium atom has a long history as testing ground for fundamental atomic physics. With two electrons, helium is a three-body system and the nonrelativistic Schrödinger equation cannot be solved exactly. Level energies are therefore more difficult to calculate than for atomic hydrogen showing a more stringent test of atomic physics theory. Calculations of level energies and transition frequencies have pushed our understanding of atomic physics since the twenties of last century. A major breakthrough occurred in the nineties with the advent of variational calculations in a double basis set in correlated form for the electrons, adding relativistic and quantum electrodynamics (QED) terms in orders of the fine structure constant $\alpha$ and the reduced electron to helium mass ratio $\mu /M_{\rm He}$ [1, 2]. As nonrelativistic calculations can now be performed to virtually arbitrary precision, measurements of level energies nowadays are sensitive to QED and nuclear size effects. As these effects are strongest for S-states and small principle quantum number n, the $n\,^{1,3}S$ states are theoretically the most promising to test QED. In particular the $n=2$ states are important for high-resolution spectroscopy as these also show long lifetimes, 7800 s for the $2\,^3S_1$ state and 20 ms for the $2\,^1S_0$ state (natural linewidth 8 Hz), while the $2\,^3P$ state has, for an allowed electric dipole transition, a relatively long lifetime of 98 ns (natural linewidth 1.6 MHz). A helium level scheme is shown in Fig. 1.

Fig. 1

Level scheme, lifetimes and transition wavelengths for low-lying $n\,^{1,3}L_J$ states of helium ($n<4$). The $2\,^3S_1$ and $2\,^1S_0$ states are metastable and can be populated in a dc discharge. The $2\,^3S_1$ state is the ground state of orthohelium and is the starting point of experimental work in this paper

Transition frequencies in helium can nowadays be measured more accurately than calculated, where the theoretical limitation is in the calculation of high-order QED terms. This hampers extraction of the charge radius of the helium nucleus (the alpha-particle for $^4\hbox {He}$ and the helion for $^3\hbox {He}$) from transition frequencies with an accuracy that can compete with other experiments. However, in calculating transition isotope shifts between $^4\hbox {He}$ and $^3\hbox {He}$, QED terms cancel to a large extent, allowing very accurate extraction of the difference in the (squared) nuclear charge radii of the alpha-particle and the helion. This is particularly interesting in relation to the proton size puzzle [3,4,5]. To help solving the proton size puzzle, Lamb shift measurements have recently been performed in muonic $^4\hbox {He}^+$ and $^3\hbox {He}^+$ ions, from which results are expected soon. The projected accuracy of the muonic helium experiments is around 0.5 am (0.03% relative accuracy in the nuclear charge radius) [4]. For electronic helium and assuming point nuclei, Pachucki and Yerokhin [6] have performed QED calculations of the isotope shift with an accuracy of 0.7 and 3.9 kHz for, respectively, the $2\,^3S_1$–$2\,^1S_0$ transition at 1557 nm and the $2\,^3S_1$–$2\,^3P$ transition at 1083 nm. These QED limited accuracies allow extraction of the squared nuclear charge radius difference with an accuracy that will be similar to values deduced from the muonic helium experiments if the experimental accuracy of the isotope shift is of similar or higher accuracy. Presently, for the $2\,^3S_1$–$2\,^1S_0$ transition, the accuracy is 2.4 kHz [7] while for the $2\,^3S_1$–$2\,^3P$ transition the isotope shift accuracy is 3.2 kHz [8, 9]. Surprisingly, a four standard deviation difference exists between the nuclear charge radius difference extracted from both measurements.

The possibility to accurately calculate level energies and wavefunctions has allowed confrontation with several other experimental results. Radiative lifetimes of the $2\,^3S_1$ and $2\,^1P_1$ states have been measured in cold clouds of helium atoms initially prepared in the metastable $2\,^3S_1$ state of $^4\hbox {He}$ [10, 11], showing good agreement with theory. Also molecular potentials for two metastable helium atoms can be calculated very accurately in some cases. This has allowed a stringent test of quantum chemistry calculations from a measurement of the s-wave scattering length a between two $m=+1$ atoms in the metastable $2\,^3S_1$ state, $a_{\mathrm{theory}}=7.567\,(24)$ nm [12, 13], while $a_{\mathrm{exp}}=7.512$ (5) nm [14]. Examples of other confrontations between experiment and theory for cold collisions between metastable helium atoms can be found in Ref. [15].

Helium atoms in the metastable $2\,^3S_1$ state (He*) are also very interesting from the perspective of atomic matter wave physics. Being light, superposition states with different momenta spatially separate fast and detection of He* atoms can be performed on a microchannel plate (MCP) detector with high efficiency [15]. Actually one of the first experiments on atom interferometry (Young’s double slit experiment) was performed with a beam of He* atoms [16]. Transversal Bragg scattering experiments in a well-collimated beam of He* atoms were performed around the turn of the century in Eindhoven [17]. Recent experiments include measurement of the Hanbury Brown Twiss effect for bosons [18] and fermions [19], the Hong-Ou-Mandel effect for matter waves [20] and realization of Wheelers delayed choice experiment for single massive particles [21].

In this paper we present recent results on interferometry in the internal and external degrees of freedom with He* atoms. First we discuss interference experiments to prepare $^4\hbox {He}$* atoms in a superposition of the $m = +1, 0$ and $-1$ states. This is realized by a $\pi /2$ rf pulse transferring 50% of the $m = +1$ atoms, trapped in a dipole trap, to the $m = 0$ state and 25% to the $m = -1$ state. By performing a $\pi /2-\pi /2$ pulse sequence we deduce the value of the magnetic field in our setup by measuring Ramsey-type oscillations between the states. This is crucial to correct for the Zeeman shifts in the $2\,^3S_1$–$2\,^1S_0$ transitions in $^3\hbox {He}$, which has hyperfine structure and no $m = 0$ states. Furthermore, we show that this method allows a mean-field shift free measurement of the Zeeman shift, which is necessary to reach the absolute transition frequency accuracy goal of 0.1 kHz.

The second part of the paper focuses on the use of He* atoms in atom interferometry. We discuss the fundamental advantages of using helium for atom interferometry in general and for determining an accurate value of the fine structure constant. These advantages relate to the metastability of the atoms allowing efficient detection, the very small second-order Zeeman shift for $m=0$ atoms, the 1083 nm laser wavelength, and the low mass, allowing macroscopic (${\sim }1\,\hbox {m}$) wavepacket separation.

2 Spectroscopy

In an earlier publication we have measured the transition frequency of the $2\,^3S_1$–$2\,^1S_0$ transition in $^3\hbox {He}$ and $^4\hbox {He}$ with 1.5 kHz resp. 1.8 kHz accuracy [7]. The 2.3 kHz accuracy in the isotope shift, together with the 0.7 kHz theoretical accuracy in the point-nucleus isotope shift [6], has allowed a determination of the difference in the squared nuclear charge radius of 1.028 (11) $\hbox {fm}^2$ [6]. With the present knowledge of the charge radius of the alpha-particle, i.e., 1.681 (4) fm [22], this provided an evaluation of the helion charge radius with the same accuracy. However, the 0.5 am projected accuracy of the nuclear charge radii for both isotopes determined from muonic helium [4] constitutes a factor 4 smaller (0.0026 $\hbox {fm}^2$) error in the difference in squared nuclear charge radii. Our goal for a new measurement is at least to match this accuracy in order to compare the values of the squared nuclear charge radii for muonic and ‘normal’ matter with similar accuracy. For this to happen we need to measure the absolute frequencies of the $^4\hbox {He}$ and $^3\hbox {He} \,2\,^3S_1$–$2\,^1S_0$ transition at 1557 nm with sub-kHz accuracy. A 0.2 kHz accuracy in the experimental isotope shift together with the 0.7 kHz accuracy in the theoretical isotope shift for point nuclei already allows an accuracy of 0.0033 $\hbox {fm}^2$ in the squared nuclear charge radius difference. If theory would be at the same 0.2 kHz accuracy (which seems feasible [23]), the squared nuclear charge radius difference would be at the 0.001 $\hbox {fm}^2$ level, better than anticipated with the muonic experiments and so providing crucial input to solve the proton size puzzle.

Aiming for a 0.1 kHz accuracy in the experimental transition frequency for both $^4\hbox {He}$ and $^3\hbox {He}$ several challenges have to be met. Looking at the error budget of our previous experiment [7] one major error source is the ac Stark shift as a result of the optical dipole trapping potential. This we will solve by working in a magic wavelength crossed dipole trap. At 319.8 nm the polarizabilities of the $2\,^3S_1$ and $2\,^1S_0$ states cancel [24]. We have generated 2 W narrowband radiation at this wavelength, more than enough to trap our atoms and have demonstrated trapping and Bose–Einstein condensation in a 319.8-nm dipole trap [25]. Our lock of the 1557-nm spectroscopy laser to the femtosecond frequency comb was a second error source. This we resolved by phase-locking a narrowband 1557-nm laser to an ultrastable laser (linewidth <2 Hz) using a frequency comb to bridge the 15 nm wavelength difference between both lasers. A third challenge is Zeeman shifts due to the presence of a small (earth-)magnetic field. $m=+1$ and $m=-1$ Zeeman states of the $2\,^3S_1$ state shift by ${\pm }$2.8 MHz/Gauss. While for $^4\hbox {He}$ one could work with atoms in the $m=0$ state, that shows a negligible second-order Zeeman shift (2.3 and $3.2\,\hbox {mHz}/\hbox {G}^2$ for, respectively, the $2\,^3S_1$ and $2\,^1S_0$ states [26]), $^3\hbox {He}$ does not allow this and one has to measure the magnetic field with sufficient accuracy and rely on sequential $\sigma ^-$ excitation (from $F=3/2, m_F=+3/2$) and $\sigma ^+$ (from $F=3/2, m_F=-3/2$) excitations with opposite Zeeman shift to find the zero B-field transition frequency.

In Sect. 2.1 we give a short overview of our experimental setup, in Sect. 2.2 we discuss how we populate the $m=0$ state for $^4\hbox {He}$, and in Sect. 2.3 we discuss the present status of our Zeeman shift measurement, based on two $\pi /2$ pulses, including a full theoretical discussion of the frequency-degenerate three-level cascade system interacting with resonant rf radiation.

2.1 Experimental setup

The main parts of our experimental setup have been described in Ref. [7]. In short, we use a liquid-nitrogen cooled dc discharge to excite helium atoms into the metastable triplet state. The He* atomic beam, with a most probable velocity of 1100 m/s, is collimated and slowed to allow trapping in a magneto-optical trap (MOT), where the atoms are transferred to a cloverleaf magnetic trap and further cooled toward BEC by evaporative cooling. About $10^6$ atoms in the $m=+1$ state are transferred to a 1557-nm (sufficiently detuned from the transition) crossed dipole trap. A small magnetic field is used to keep the atoms in the spin-polarized $m=+1$ state as atoms in the $m=0$ state show fast Penning ionization [15]. $m=-1$ states are populated by rapid adiabatic passage using a magnetic field sweep [7, 27]. In this way we can transfer nearly 100% of the atoms to $m=-1$. We detect the number of atoms as well as the temperature by either absorption imaging (on an InGaAs photodiodes camera) or by time-of-flight to a microchannel plate (MCP) detector mounted 17 cm below the trap. Ultracold $^3\hbox {He}$ atoms are laser cooled and trapped using a separate laser system and further cooled toward quantum degeneracy by sympathetic cooling with $^4\hbox {He}$ atoms [28, 29].

We detect the relative population of the magnetic substates $m=+1$, $m=0$ and $m=-1$ by a Stern–Gerlach technique, where we release the atoms from the dipole trap and apply a magnetic field gradient. The substates separate in space and are observed using absorption imaging. We have determined the magnetic field strength during our experiment by inducing transitions from $m=+1$ to $m=0$ and $m=-1$ as a function of rf frequency for a $40\,\upmu \hbox {s}$ pulse and measuring the spin-flip ratio (see Fig. S1 of Ref. [7]). Using this method and observing the resonance frequency over extended periods of time (to measure a linear trend) we were able to deduce the Zeeman shift with 0.5 kHz accuracy, which should be improved to the 0.1 kHz level.

2.2 rf excitation of m=0 states

For spectroscopy of $^4\hbox {He}$ it is advantageous to work with $m=0$ atoms in-stead of $m=+1$ atoms due to the absence of magnetic field shifts. It is not trivial to populate only the $m=0$ state. Two Raman laser pulses slightly detuned from the $2\,^3S_1$–$2\,^3P_0$ transition [20] can be used and close to 100% transfer efficiency can be obtained at the cost of a separate laser system. A simpler and robust method is to apply an rf pulse as discussed in the next subsection.

2.2.1 Theory of resonant three-level Rabi oscillations

$^4\hbox {He}$ has no nuclear spin, which causes the quadratic Zeeman shift to be extremely small. At the small fields that we typically work at (of the order of a few Gauss) it is completely negligible so to excellent approximation $^4\hbox {He}$ in the $2\,^3S_1$ state is a symmetric three-level system with a splitting given by the linear Zeeman shift. The special case of a cascaded multi-level system is a system of multiple symmetric Zeeman levels. This system has a very interesting symmetry: coupling together two levels with an rf field automatically couples the other levels as well in a stepwise (cascaded) fashion.

For the state vector

$$\begin{aligned} |{\psi }\rangle = C_+ |{m=+1}\rangle + C_0 |{m=0}\rangle + C_- |{m=-1}\rangle \end{aligned}$$

(1)

the Hamiltonian, in the rotating wave approximation and neglecting the z-component of ${\varvec{B}}_{\mathrm{rf}}$, is

$$\begin{aligned} H = g_J \mu _B {\varvec{S}} \cdot {\varvec{B}}(t) = \hbar \begin{pmatrix} \omega _0 &{} \frac{\varOmega }{\sqrt{2}} e^{-i \omega t} &{} 0 \\ \frac{\varOmega }{\sqrt{2}} e^{i \omega t} &{} 0 &{} \frac{\varOmega }{\sqrt{2}} e^{-i \omega t} \\ 0 &{} \frac{\varOmega }{\sqrt{2}} e^{i \omega t} &{} - \omega _0 \end{pmatrix}. \end{aligned}$$

(2)

Here ${\varvec{B}}(t) = {\varvec{B}}_0 + {\varvec{B}}_{\mathrm{rf}}(t)$, $\omega$ is the rf frequency, $\omega _0 = g_J \mu _B B_0 / \hbar$ the Larmor frequency and $\varOmega$ the effective Rabi frequency, defined as $\varOmega ^2=\varOmega _R^2 + \delta ^2$, with $\varOmega _R = g_j \mu _B |B_{\mathrm{rf}}|/2 \hbar$ the on-resonance Rabi frequency and $\delta$ the detuning from resonance.

The populations in the substates then follow from the coupled equations, derived from the time-dependent Schrödinger equation:

$$\begin{aligned} i \frac{\hbox {d}C_+}{\hbox {d}t}= & {} \omega _0 C_+(t) + \frac{\varOmega }{\sqrt{2}} \exp (-i \omega t) C_0(t) \end{aligned}$$

(3)

$$\begin{aligned} i \frac{\hbox {d}C_0}{\hbox {d}t}= & {} \frac{\varOmega }{\sqrt{2}} \exp (i \omega t) C_+(t) + \frac{\varOmega }{\sqrt{2}} \exp (- i \omega t) C_-(t) \end{aligned}$$

(4)

$$\begin{aligned} i \frac{\hbox {d}C_-}{\hbox {d}t}= & {} \frac{\varOmega }{\sqrt{2}} \exp (i \omega t) C_0(t) - \omega _0 C_-(t). \end{aligned}$$

(5)

These equations can be solved analytically. For the case of zero detuning ($\omega =\omega _0$), where $\varOmega =\varOmega _R$, and when the atoms start out spin-polarized ($m=+1$):

$$\begin{aligned} |C_+(t)|^2= & {} \cos ^4 \left( \frac{\varOmega _R t}{2} \right) \end{aligned}$$

(6)

$$\begin{aligned} |C_0(t)|^2= & {} \frac{1}{2} \sin ^2 \left( \varOmega _R t \right) \end{aligned}$$

(7)

$$\begin{aligned} |C_-(t)|^2= & {} \sin ^4 \left( \frac{\varOmega _R t}{2} \right) . \end{aligned}$$

(8)

This result is shown in Fig. 2. It is thus possible to transfer 50% of the atoms to $m=0$, while 100% can be transferred to $m=-1$.

Fig. 2

Normalized population of the $m=+1$ (blue line, full), $m=0$ (black, dotted) and $m=-1$ (red, dashed) substates according to Eqs. 6, 7 and 8. A $\pi /2$ pulse transfers 50% of the atoms to $m=0$, a $\pi$ pulse transfers all atoms to $m=-1$

2.2.2 Results on three-level Rabi oscillations

Both for the experiments on spectroscopy and atom interferometry it is important to use metastable $^4\hbox {He}$ atoms in the $m=0$ substate. Figure 2 shows that a $\pi /2$ pulse ($t=\pi /(2 \varOmega _R)$) is expected to transfer 50% of the atoms in the $m=+1$ state to $m=0$. In the experiment we prepared $10^6$ atoms, either slightly above the transition to BEC or primarily in a BEC, in the $m=+1$ state at an earth-magnetic field strength of about 0.5 Gauss. An rf pulse was then applied for a varying time and the population in the three magnetic substates was measured by absorption imaging after expansion in a magnetic field gradient. In Fig. 3 we show results for the case of a BEC as this provides the best contrast in absorption imaging 8 ms after switching off the trap. As it is difficult to normalize the different pictures we have normalized to the total number of atoms at all measurement times. Poisson noise in the atom number then introduces an up to 10% error in the normalized population of the different m states.

Figure 3 clearly shows that Eqs. 6, 7 and 8, with a Rabi frequency $\varOmega _R= 2 \pi \times$ 23.348(3) kHz, represent the measurements very well in general. The signal-to-noise stays the same, but a change in the Rabi frequency is apparent for long Rabi pulse lengths. This is possibly caused by transient behavior of the rf amplifier system, but currently not limiting for creating $\pi /2$ and $\pi$ pulses for which we use the shortest Rabi pulse length available (${\sim }10$ and ${\sim }20\,\upmu \text {s}$, respectively). A $\pi$ pulse transfers all atoms to the $m=-1$ state while for a $\pi /2$ pulse we find equal numbers of atoms in each of the spin-stretched states as expected. However, there is a clear deficit of atoms in the $m=0$ state. Where 50% is expected only about 25% is observed. This is illustrated in the left part of Fig. 4, which shows an image of the three magnetic substates after a $\pi /2$ pulse on a BEC and 8 ms expansion time. We attribute this deficit of $m=0$ atoms to Penning ionization within the expanding $m=0$ cloud. Being strongly dependent on density [15] we tested this by preparing a thermal cloud with about a factor 10 lower density. Indeed we see (right part of Fig. 4b) that after the same expansion time now the number of $m=0$ atoms remaining for imaging is much larger relative to the number of atoms in $m=1$ and $m=-1$ and of the order of 50%.

Fig. 3

Relative populations of the $m=+1$ (blue triangles), $m=0$ (black dots) and $m=-1$ (red diamonds) state of He* as a function of pulse length, for atoms starting in the $m=+1$ state at $t=0$. The error bars are largest near a population of 50% and zero at 0 and 100% as a consequence of normalization

Applying a magnetic field gradient after the $\pi /2$ pulse pushes the $m = {\pm }1$ state atoms out of the dipole trap, leaving a pure $m = 0$ cloud of quantum degenerate $^4\hbox {He}$*. This can be used for atom interferometry (see Sect. 3), but also provides a new possibility for spectroscopy in $^4\hbox {He}$. Although Penning ionization losses do not allow sufficient time to perform spectroscopy in a Bose - Einstein condensate, we have observed the $2\,^3S_1 \, m=0$–$2\,^1S_0 \, m=0$ transition in a thermal cloud near quantum degeneracy. This allows for a Zeeman shift free measurement of the transition frequency in $^4\hbox {He}$, especially if future measurements are performed in an optical lattice where Penning ionization losses are suppressed.

2.3 $m=1$ Zeeman shift measurements

Although it is in principle best to work with $m=0$ atoms, Penning ionization limits the lifetime of such a cloud. Moreover, for $^3\hbox {He}$ there is no $m=0$ state. It is therefore mandatory to investigate ways to measure the magnetic field strength with sufficient accuracy. In the following subsection we discuss Ramsey spectroscopy as a means to measure the magnetic strength by observing the Larmor precession after creation of a three-level superposition state with a $\pi /2$ pulse and waiting as long as possible before introducing the second $\pi /2$ pulse. As we work with a magnetic field $B_0$ of the order of 0.5 G, this causes oscillations in the order of microseconds (Larmor frequency ${\sim }1.5\,\hbox {MHz}$) and allows an accurate measurement of the magnetic field strength via $\omega _0 = g_J \mu _B B_0 /\hbar$.

In between the two rf pulses mean-field interactions between the different Zeeman substates may play a role as these cause shifts of the chemical potential and therefore also of the transition frequency. These effects and their mitigation therefore need to be addressed, which is done in Sect. 2.3.2.

2.3.1 Theory of Ramsey spectroscopy

To generate a Ramsey signal the rf field is switched on for a time $\tau$, after which the spins precess freely for a time $\Delta T$, and then the rf field is switched on again for a time $\tau$. To describe this theoretically we need the time evolution operator for free precession $U_{\mathrm{free}}(\Delta T)$ and for an rf pulse $U_{\mathrm{Rabi}}(\tau )$. The wavefunction after a Ramsey measurement is then

$$\begin{aligned} |{\psi (t + t_{\mathrm{seq}})}\rangle = U_{\mathrm{Rabi}}(\tau ) U_{\mathrm{free}}(\Delta T) U_{\mathrm{Rabi}}(\tau ) |{\psi (t)}\rangle , \end{aligned}$$

(9)

where $t_{\mathrm{seq}} = 2 \tau + \Delta T$. The initial phases for both rf pulses should be the same for all free evolution times $\Delta T$.

To measure the population of the different magnetic substates with good signal-to-noise, $\tau = \pi /(2 \varOmega _R)$ (a $\pi /2$ pulse) is used. Scanning $\Delta T$, oscillations should be observed with frequency given by the Larmor frequency.

The analytic form of the time evolution operator for the $\pi /2$ pulses with zero detuning have simple forms:

$$\begin{aligned} U_{\mathrm{Rabi}}\left(\frac{\pi }{2 \varOmega _R}\right) = \begin{pmatrix} \frac{1}{2} &{} - \frac{ i}{\sqrt{2}} &{} - \frac{1}{2} \\ - \frac{i}{\sqrt{2}} &{} 0 &{} - \frac{i}{\sqrt{2}} \\ - \frac{1}{2} &{} - \frac{ i}{\sqrt{2}} &{} \frac{1}{2} \end{pmatrix}. \end{aligned}$$

(10)

From Eq. 9 an analytical expression for the populations of the different spin components after a Ramsey measurement with $\pi /2$ pulses can be deduced which is very similar to the case of a single $\pi /2$ pulse (with $C_+$ and $C_-$ interchanged, and $\omega _0$ instead of $\varOmega _R$):

$$\begin{aligned} |C_+(\Delta T)|^2= & {} \sin ^4 \left( \frac{\omega _0 \Delta T}{2} \right) , \end{aligned}$$

(11)

$$\begin{aligned} |C_0(\Delta T)|^2= & {} \frac{1}{2} \sin ^2 \left( \omega _0 \Delta T \right) , \end{aligned}$$

(12)

$$\begin{aligned} |C_-(\Delta T)|^2= & {} \cos ^4 \left( \frac{\omega _0 \Delta T}{2} \right) . \end{aligned}$$

(13)

2.3.2 Mean-field effects on the Zeeman shift

In the Ramsey spectroscopy experiment, set up to measure the Zeeman shift, we have not yet considered the fact that mean-field interactions between the different magnetic substates have an effect on the phase evolution of the individual states. We incorporate these effects to the total energy for the individual m states (expressed as the chemical potential $\mu$ for trapped Bose–Einstein condensates), and they can be directly used as a modification of the free evolution operator $U_{\mathrm{free}}$ introduced in the previous section.

In order to fully describe the problem, we use the Gross-Pitaevskii (GP) description of the three BECs that are present once we apply a $\pi /2$ Rabi pulse. For a state i out of the three states i, j, k (constituting the $m = +1, 0, -1$ states), the wavefunction $\psi _i$ is described by the GP equation

$$\begin{aligned} \left( -\frac{\hbar ^2 \nabla ^2}{2m} + V_{\text {int}} + N_i g_{i,i} \vert \psi _i \vert ^2 + N_j g_{i,j} \vert \psi _j \vert ^2 + N_k g_{i,k} \vert \psi _k \vert ^2 \right) \psi _i = \mu _i \psi _i, \end{aligned}$$

(14)

where $V_{\text {int}}$ is the internal energy of the state and $N_i$ the atom number in state i. The interaction parameter $g_{i,j}$ is defined as

$$\begin{aligned} g_{i,j} = \frac{2 \pi \hbar ^2 a_{i,j}}{M}, \end{aligned}$$

(15)

where $a_{i,j}$ is the s-wave scattering length between states i and j. From Fig. 1 of Ref. [30] we extract scattering lengths if we ignore the imaginary part related to Penning ionization or degenerate collisions ($0,0 \rightarrow -1,+1$ or vice versa): $a_{0,0} \approx 120$ $a_0, a_{1,1}=a_{-1,-1}=a_{0,1}=a_{0,-1} \approx 140$ $a_0, a_{1,-1} \approx 60$ $a_0$ (with $a_0$ the Bohr radius). Of these three scattering lengths, only $a_{1,1}$ is known from experiments to be 142.0(1) $a_0$ [14, 15]. As the interaction strengths $g_{i,j}$ scale linearly with the scattering lengths, we find $g_{0,0} \approx \frac{6}{7} g_{1,1} \approx 2 g_{1,-1}$.

In the Thomas-Fermi approximation the kinetic term in the GP equation is neglected with respect to other energies, and the problem simplifies to the scalar expression

$$\begin{aligned} V_{\text {int}} + N_i g_{i,i} \vert \psi _i \vert ^2 + N_j g_{i,j} \vert \psi _j \vert ^2 + N_k g_{i,k} \vert \psi _k \vert ^2 = \mu _i. \end{aligned}$$

(16)

From $\psi _i = \sqrt{n_i({\mathbf {r}})/N_i}$ we deduce

$$\begin{aligned} \mu _1= & {} V_{\text {int}}^1 + g_{1,1} (n_1 + n_0) + n_{-1} g_{1,-1}, \end{aligned}$$

(17)

$$\begin{aligned} \mu _0= & {} V_{\text {int}}^0 + g_{1,1} (n_1 + n_{-1}) + g_{0,0} n_0, \end{aligned}$$

(18)

$$\begin{aligned} \ \mu _{-1}= & {} V_{\text {int}}^{-1} + g_{1,1} (n_{-1} + n_0) + n_1 g_{1,-1}. \end{aligned}$$

(19)

The internal energies all contain the same Stark shift from the optical dipole trap (as this is a scalar shift). It is therefore omitted from this calculation. The Zeeman shift is included as a linear shift. Defining the $m = 0$ state as reference energy for the Zeeman shift, $V_{\text {int}}^0 = 0$ and $V_{\text {int}}^{\pm 1} = \pm \hbar \omega _0$, where $\omega _0$ is the Larmor frequency. The energies $V_{int}$ would be the only relevant energies in the free evolution operator $U_{\mathrm{free}}$ as introduced in the previous section, and now they can be replaced by the full chemical potential $\mu$ of each state. As long as the timescale of interest is shorter than the Penning ionization timescale (which leads to atom number loss), the chemical potentials fully describe the phase evolution of the three components of the Bose–Einstein condensate.

When applying a perfect $\pi /2$ pulse, $n_1 = n_{-1} = n/4$ and $n_0 = n/2$, where n is the initial density of the BEC. In that case

$$\begin{aligned} \mu _1= & {} \hbar \omega _0 + \frac{n}{4} (3 g_{1,1} + g_{1,-1}), \end{aligned}$$

(20)

$$\begin{aligned} \mu _0= & {} \frac{n}{2}(g_{1,1} + g_{0,0}), \end{aligned}$$

(21)

$$\begin{aligned} \mu _{-1}= & {} - \hbar \omega _0 + \frac{n}{4} (3 g_{1,1} + g_{1,-1}) \end{aligned}$$

(22)

and the differential phases become

$$\begin{aligned} \mu _1 - \mu _{-1}= \,& {} 2 \hbar \omega _0, \end{aligned}$$

(23)

$$\begin{aligned} \mu _1 - \mu _0= \,& {} \hbar \omega _0 + \frac{n}{4} (g_{1,1} + g_{1,-1} - 2 g_{0,0}) \approx \hbar \omega _0 - \frac{n}{14} g_{1,1}. \end{aligned}$$

(24)

To get an order of magnitude estimate of these effects on the chemical potential of the individual states, we calculate the mean-field energies $E_{\text {mf}}^m$ of the m states for a typical BEC density of $10^{13} \ \text {cm}^{-3}$. We get

$$\begin{aligned} E_{\text {mf}}^{\pm 1}= \,& {} \frac{n}{4} (3 g_{1,1} + g_{1,-1}) \approx h \times 2.0 \ \text {kHz}, \end{aligned}$$

(25)

$$\begin{aligned} E_{\text {mf}}^0= \,& {} \frac{n}{2}(g_{1,1} + g_{0,0}) \approx h \times 2.2 \ \text {kHz}, \end{aligned}$$

(26)

which are typically ${\sim }0.1$% of the Zeeman shift experienced by the states. At first sight this is problematic when trying to measure the Zeeman shift beyond the kHz level. However, the mean-field energy drops out as common mode when considering the phase evolution between the $m = +1$ and $m = -1$ states if the densities are equal. In terms of sensitivity, we can calculate the resulting frequency shift $\Delta E_{\text {mf}}$ for a fractional population difference $\Delta n / n$ between the two states at the typical experimental density of $10^{13} \ \text {cm}^{-3}$ :

$$\begin{aligned} \Delta E_{\text {mf}} = \frac{\Delta n}{n} \times h \times 1.3 \ \text {kHz}. \end{aligned}$$

(27)

If we can get the populations to be stable within a few percent the shift is ${<}0.1$ kHz. Also, from a practical point of view this method only involves the $m = {\pm }1$ states, which are much better imaged than the $m = 0$ state (see Sect. 3).

To summarize, at our typical BEC densities of $10^{13} \ \text {cm}^{-3}$, the mean-field energy of the individual states is around $h \times 2 \ \text {kHz}$ and an order of magnitude larger than the accuracy goal of the optical transition frequency measurement. However, when applying the Ramsey measurement method the mean-field energies of the $m = +1$ and $m = -1$ states result in a common phase evolution and they can cancel to a shift of ${\sim }0.1$ kHz if both states are equally populated within 10% of each other using a $\pi /2$ pulse. From the results shown in Fig. 4 this seems doable.

Fig. 4

Absorption images taken after a $\pi /2$ pulse in case of Bose–Einstein condensate (left) and a thermal cloud (right). The pictures and the integrated column density below it are taken 8 ms after switching off the dipole trap. This causes the thermal cloud to expand much faster diminishing Penning ionization losses. The expected relative populations of the three magnetic substates are thus recovered

2.3.3 Ramsey spectroscopy experimental results

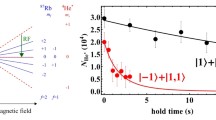
Extending the experiments to the Ramsey scheme, we applied two $\pi /2$ pulses according to the scheme of Eq. 9. The results are shown in Fig. 5, which shows the normalized (to the sum of the population of the $m=+1$ and $m=-1$ states) number of $m=+1$ atoms after the second $\pi /2$ pulse (with statistical error bars as in Fig. 3, while now ${\sim }$50 ns timing noise in the $\pi /2$ pulse delay as well as magnetic field noise somewhat increase the error at all delay times). We were able to observe up to 80 oscillations after a $\pi /2$ pulse preparation of the superposition state. The origin of the observed decoherence is presently unkown. It cannot be due to Penning ionization as this does not cause decoherence and also does not occur yet at the 50 $\upmu$s timescale. A possible source may be experimental rf amplifier noise. On the other hand, as every shot takes about 15 s we suspect the observed decoherence may also be due to slow drifts and shot-to-shot variations in the magnetic field strength.

Fig. 5

Relative populations of the $m=+1$ state of He* as a function of pulse delay between two $\pi /2$ pulses, for atoms starting in the $m=+1$ state at $t=0$. Below an expanded part for short and long time delay showing that the oscillations remain visible up to 45 $\upmu$s. The red line is a fit to the signal applying Eqs. 11 and 13

3 Atom interferometry

Macroscopic separation of atomic wave packets allows stringent tests of basic quantum mechanics and sensitive sensing of forces when wave packets are split and combined to form an atom interferometer. For the most sensitive experiments cold atoms are used, either from a MOT or BEC. We aim to build an atom interferometer for ultracold helium atoms in the metastable triplet state, optically trapped close to Bose–Einstein condensation at a temperature of ${\sim }0.2\,\upmu \hbox {K}$.

3.1 Metastable helium for atom interferometry

Cold atom interferometers generally use alkali atoms. The workhorse is Rb but Cs atoms are also used. Recently first results on Sr have been published [31]. In Table 1 a comparison of some atomic properties of these atoms is presented that shows why He* is a good candidate for several studies.

Table 1 Atomic data for atoms used in cold atom interferometry

Despite the experimental complexity of working with atoms in a metastable state, He* has several advantages. From the experimental point of view, He* allows efficient detection of atoms, as a function of time and position, on an MCP detector [15]. Secondly, the required wavelength for manipulating the atoms and splitting the wavepacket, often requiring high laser power, is 1083 nm, a wavelength where high power fiber amplifiers and narrow band fiber lasers are commercially available. The required power for generating flat wavefronts over large dimension for wavepacket splitting is therefore readily available. A very important advantage of using He* atoms (in the $m=0$ state) is the five orders of magnitude lower sensitivity to stray magnetic fields compared to Rb and Cs (see Table 1). This small second-order Zeeman shift originates from the absence of hyperfine structure and, as a consequence, very large energetic distance to nearby other $m=0$ states that mix in at second order. Because of this low sensitivity no elaborate magnetic shielding is required, in contrast to the alkalis. A disadvangae of using $m=0$ atoms is Penning ionization, which implies that low densities have to be used.

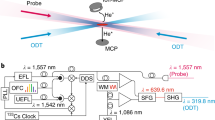
Although the low mass will not help in reducing systematic shifts there is still a large advantage in using low mass atoms that relates to the large recoil velocity. This allows easy wavepacket separation over macroscopic distances with only a few photon recoils. To illustrate this we compare the recent large 0.54 m wavepacket splitting obtained with Rb in the 10 m fountain in Stanford [34]. This was realized after 1.04 s ballistic flight following 45 consecutive Bragg pulses providing $90 \hbar k$ wavepacket splitting. We estimate that we can realize a 1 m wavepacket splitting after 0.5 s in a fountain of no more than 1.6 m height applying one 12th order Bragg pulse generated using a 2-W fiber amplifier. An experimental setup dedicated to atom interferometry was designed in our laboratory to demonstrate such a large superposition state (see Fig. 6).

Fig. 6

Experimental setup for atom interferometry and measurement of the fine structure constant. Enlarged parts show the designed geometry for the fountain (left) and detection of the atomic beam (right). For details see text

We have designed this setup analogous to the setup described in Sect. 2, with a vertical geometry for the atom interferometer. We will work with evaporatively cooled atoms, close to or below the temperature for BEC, initially trapped in a horizontal 1557-nm crossed dipole trap. We then intend to transfer the atoms to a vertical one-dimensional optical lattice at 1083 nm. Bragg diffraction will both be used to launch the atoms and for wavepacket splitting to realize an atom interferometer. Figure 6 shows we intend to detect the different vertical momentum states on an MCP detector after horizontal displacement by a push beam.

Apart from demonstrating the 1-m wavepacket splitting, with a possible test of atom neutrality as application [35], we aim for a measurement of the fine structure constant by measuring the one-photon recoil velocity analogous to the Rb experiment in Paris [36]. He* has additional advantages here as well [37]. The fine structure constant can be deduced from the relation

$$\begin{aligned} \alpha ^2 = \frac{2R_{\infty }}{c}\frac{h}{m_e}= \frac{2R_{\infty }}{c}\frac{M_X}{m_u}\frac{m_u}{m_e}\frac{h}{M_X}. \end{aligned}$$

(28)

The Rydberg constant $R_{\infty }$ is presently known with 0.006 ppb accuracy, the electron mass in atomic units $m_e/m_u$ with 0.03 ppb accuracy [38] and the atomic masses $M_X/m_u$ for X = Rb, Cs and He with resp. 0.08, 0.07 and 0.016 ppb accuracy [32]. As the most precise measurement of h / M today is for Rb, i.e., 1.3 ppb [36], a factor of ten improvement in this measurement will already hit the limit set by the knowledge set by Rb mass (measured in a Penning ion trap). Helium provides more room at the bottom in challenging the presently most accurate determination of $\alpha$, i.e., by applying QED to the measurement of the g-factor of the electron [39]. Comparing an improved measurement of the fine structure constant from photon recoil measurements, almost independent of QED theory, with g-factor results (that require the most advanced high-order QED calculations [40]), may provide the most stringent test of QED theory possible in the near future.

3.2 Characterization of the Zeeman slower using an ITO window

The experimental setup shown in Fig. 6 is presently being built. In an initial experiment demonstrating slowing in our Zeeman slower, we used a vacuum window with an indium tin oxide (ITO) coating on the vacuum side. ITO is a conductive layer, transmitting in our case ${>}$ 80% of the circularly polarized light entering the Zeeman slower. ITO is known to release an electron after impact of a metastable helium atom [41] albeit with an unknown efficiency hampering quantitative measurements. As indicated in Fig. 6 we detect the detached electrons on a channeltron electron multiplier (CEM) detector (with exposed front side at +100 V), mounted 20 cm upstream from the vacuum window just above the 1083-nm Zeeman slower laser beam. Chopping the atomic beam with a rotating slit in a chopper wheel, mounted at the entrance of the first part of the Zeeman slower, allows measurement and optimization of the velocity distribution of the atomic beam. Results are shown in Fig. 7 demonstrating with high signal-to-noise that one can detect the He* atomic beam and measure its velocity.

Fig. 7

Channeltron signal showing released electrons from the ITO window in case of a He* beam that is slowed to various final velocities varying the current in the second part of the Zeeman slower. The first peak, caused by high energy XUV photons from the He* plasma source, provides a t=0. Slowed atoms with a average velocity of 290 m/s appear after 7 ms when switching on only the first part of the Zeeman slower (ZS1 only), while lower velocities corresponding to later arrival times appear for increasing currents applied to the second part of the Zeeman slower

From the time delay between the light peak, caused by XUV photons from the source, and the time the atoms arrive, the most probable velocity of the atomic beam is measured to be 1100 m/s, which agrees with earlier measurement in another setup [41]. The width of the peaks depends on the rotation velocity and the width of the slit in the chopper wheel. By ramping up the current in the second part of the slower, the end velocity is tuned. The slowed atomic beam peaks in Fig. 7 correspond to a velocity of 290, 120, 90 and 60 m/s, in good agreement with calculations at the applied currents and the −250 MHz detuning of the Zeeman slower beam. The small peak in between the unslowed and slowed atom peaks in Fig. 6 is caused by atoms that drop out of the slowing process in the first part of the Zeeman slower. Due to transverse divergence of the atomic beam, the atomic flux at the ITO window after slowing to 50 m/s (the capture velocity of a He* MOT) is very small. To measure the flux and optimize the number of slowed atoms we tweaked the transversal collimation stage, which makes a quantitative comparison with the unslowed beam difficult. In the optimization procedure the measured most probable velocity actually reduces to 900 m/s demonstrating that the collimation stage also acts as a velocity selector. Because the slowed atoms cover a large area on the ITO window, the position of the CEM detector directly influences the amount of electrons that can be detected. Lowering the CEM to face more of the window drastically changes the amplitude ratios of the slowed and unslowed beams, where a practical limit was set at the point where it starts to clip the slowing light beam. We also observe a small reduction in the base line due to saturation of the CEM detector, which was used in current mode.

The ITO window thus allows for direct detection of the slowed atomic beam in a way that does not interfere with the rest of the experiment, an advantage made possible by the high internal energy of the metastable atoms.

4 Conclusions and future prospects

We have shown progress toward measuring the transition isotope shift of the $2\,^3S_1$–$2\,^1S_0$ transition at 1557 nm with an accuracy that may compete with the muonic helium Lamb shift experiment underway in Switzerland. We demonstrated that we can efficiently transfer our trapped atoms to the magnetic field insensitive $m=0$ state and demonstrated the suitability of $m=0$ atoms for both spectroscopy and atom interferometry. Densities below $10^{12}$ cm$^{-3}$ are needed in order to neglect Penning ionization losses at time scales < 1 s. In the interferometry experiment this implies fast expansion of the cloud after transfer to the $m=0$ state.

For the spectroscopy experiment we can use both $m=0$ and $m=1$ atoms. We can measure the transition in a thermal $m=0$ gas close to the BEC transition where Doppler broadening increases the linewidth by only a factor of two and the lifetime is sufficiently large while Zeeman shifts are absent. However, to compare and look for systematic effects we will also use $m=1$ atoms in a BEC (a BEC of $m=0$ atoms has only a lifetime of ${\sim }10 \hbox {ms}$). An $m=1$ BEC shows a long (${\sim }10\,\hbox {s}$) lifetime also at high density while the earth magnetic field strength may be measured with sufficient accuracy. The mean-field shift of ${\sim }2$ kHz in the magnetic field measurements is a systematic shift which is an order of magnitude larger than the accuracy goal of 0.1 kHz (and is therefore a systematic effect on the measurement of a systematic effect). The Ramsey-type measurement as proposed and demonstrated in this paper provides a way to negate this effect to allow for a 0.1 kHz accurate measurement of the absolute optical transition frequency. As we will soon turn to full operation of the magic wavelength trap [25], the ac Stark shift will no longer be the dominant systematic effect. It should be noted that for $^3\hbox {He}$, where a magnetic field insensitive measurement is impossible, the accuracy of the Zeeman shift correction will be the limiting factor in the final accuracy. Our proposed Ramsey-type measurement is currently the most promising way to suppress this systematic uncertainty. Ultimately we could work with a three-dimensional magic wavelength lattice with single atoms trapped in the Lamb-Dicke regime at the nodes. This would provide an ideal geometry to perform the experiment with $m=0$ atoms, without ac Stark, mean-field, recoil and Doppler shifts, and approaching the 8 Hz natural linewidth.

The large recoil velocity, the extremely small second-order Zeeman shift, and unique spatial and temporal detection possibilities make metastable helium an excellent candidate for atom interferometry. For the fine structure constant measurement we showed the high potential to measure the recoil velocity accurately using Bragg diffraction and atom interference. The high accuracy of the helium mass promises a QED test at the 0.01 ppb level by comparison of a measured $\alpha$ with a value of $\alpha$ calculated from g-factor measurements, if systematic effects can be controlled well enough.