1 Introduction

Vertical external cavity surface-emitting lasers (VECSELs) have received substantial attention over the last years. They exhibit excellent beam quality and high output power. VECSELs cover a wide spectral range on the IR, which can be extended by intra-cavity frequency mixing [1, 2]. They can operate in pulsed mode [3] and be used for emission of terahertz radiation [4].

A typical optically pumped VECSEL structure is composed of a highly reflective distributed Bragg reflector (DBR), an active region consisting of the quantum wells (QWs) separated by spacers and enclosed by a window layer. A major part of the pump radiation is absorbed by the spacer layers in the active region [5]. Even more pump radiation is absorbed in thicker active regions allowing for higher pumping efficiency to be achieved [6]. For long absorption paths, larger number of OWs is desirable to shorten the carrier diffusion length [6]. Also, due to the logarithmic gain dependency on the carrier concentration, the increased number of QWs leads to lowering of the threshold concentration. However, QWs introduce strain into the heterostructure lattice, which increases with their number. When the critical layer thickness for a QW is exceeded, the strain might relax by generating misfit dislocations.

The dislocations are the origin of non-radiative recombination centers, increasing the threshold excitation power and even suppressing the lasing. In order to predict the input/output characteristics correctly, theoretical models, including carrier recombination rates, must be used to compute the thermal and spectral absorption/gain dependences [7]. However, the lattice strain/relaxation, which affects the power characteristics, is difficult to factor into the calculations as it depends not only on the structure design (i.e., chemical composition and number of QWs) but also on the growth parameters (temperature, growth rate). The optimal number of QWs, i.e., an acceptable balance between the strain/relaxation in VECSEL structures, can only be determined experimentally.

The relation between the threshold and maximum power on the number of QWs was predicted by the Kuznetsov et al. [8]; however, until today it has not been shown experimentally. It is probably because of the difficulty in preparation of the samples differing only in the number of QWs. The precise control of the VECSEL heterostructure is a challenge since any minor variation in the individual layer thickness translates to a substantial spectral shift of the Fabry–Perot mode. Even in the case of large-scale VCSEL production, the wavelength variation is in the range of 10 nm [9].

In order to prevent the misfit dislocation generation, the strain-compensating layers are typically introduced within the microcavity. Specifically for InGaAs-based QWs, thin GaAsP layers are placed in the proximity of the QW, in the center of the separating barriers, or fill up the full space between the QWs [8, 10, 11]. This procedure allowed for achieving a high-power emission [11, 12] and was outside the scope of our work.

Due to the simplicity of the lasing action excitation, the surface-emitting VECSELs are interesting subjects for the quantitative research of the impact of dislocations on the laser parameters. These structures with non-strain-compensated active regions are of interest because of their straightforward design, possibility of precise epitaxial growth control, simple strain control by the number of QWs and the relatively high achievable output power [13]. To meet this aim, i.e., determine quantitatively the impact of strain relaxation on emission properties, in this paper, a unique set of VECSEL-like structures purposively prepared without strain compensating was investigated. The analyzed structures—called from now on VECSELs—differ only in the thickness of their active regions and the number of QWs. All other parameters concerning structure design, emission parameters, gain/Fabry–Perot tuning and growth conditions were constant. Due to laboriousness of the growth rate calibration and its day-to-day variation, the Fabry–Perot resonance and the QW emission tuning can be controlled with a limited precision, resulting in random tuning of the FP mode and the gain maximum [14–17]. Thus, the fabrication of the large number of VECSEL structures with fixed tuning has not been undertaken up till now. Furthermore, in this work we aimed to quantify the acceptable strain/relaxation balance, i.e., to determine the maximum number of QWs allowing for highest power emission.

In Section 2, the design of the VECSEL, its growth conditions and the achieved growth accuracy are described. In Section 3, the measurement techniques and laser setup are detailed. Section 4 is devoted to a short presentation of the model used for the analysis. In Section 5, the results for VECSELs with active regions of different lengths and with different numbers of QWs are presented and discussed. The last section contains a summary and conclusions.

2 Experiment

2.1 VECSEL design and fabrication

The VECSEL structures were designed to emit at 980 nm. The distributed Bragg reflector (DBR) consisted of 29.5 pairs of AlAs/GaAs with a calculated reflectance of 99.99 %. The periodic active region was deposited directly on the DBR. Compressive-strained quantum wells were placed at each antinode of the standing wave in the active region. The QWs were designed to exhibit the peak of room-temperature photoluminescence (PL) at ~970 nm, thereby taking into account the thermal redshift that occurs under high-power pumping. In order to precisely control the strain, deliberately there were no strain-compensating layers grown in the active regions. The GaAs spacers between the QWs act as pump absorbers. A 150-nm-thick Al0.5Ga0.5As layer was applied as a window layer additionally protected against oxidization by a 10-nm-thick GaAs cap layer. Details of the VECSEL structures concerning microcavity data and QW numbers are presented in Section 4.

The structures were grown on a (001) GaAs substrate using molecular beam epitaxy (MBE) in a RIBER 32P chamber. The MBE reactor was equipped with cracking cells for group V elements and standard Knudsen cells for group III spaces. The temperature was measured with a narrow spectral line Ircon Modline pyrometer operating at 930 nm. The growth temperature was 530 °C and kept constant during the whole epitaxial process. The epitaxial growth of VECSEL structures was preceded by the optimization both of the active region containing QWs and the DBR structures consisting of 15 pairs of AlAs/GaAs. Precise determination of the growth rate enabled corrections to subsequent test processes and led to a reproducible growth of VECSEL structures with variable numbers of QWs distributed uniformly in subsequent antinodes of the standing waves in microcavities: 4QW, 8QW, 12QW and 16QW.

2.2 Accuracy of epitaxial growth

VECSEL laser fabrication requires highly accurate control of the growth rate since for optimum operation an alignment of the peak gain and Fabry–Perot (FP) resonance is needed. Figure 1 shows calculated data describing the relationship between, on the one hand, the optimal temperature for VECSEL laser operation and deviation from the desired microcavity length (bottom axis) and, on the other hand, the wavelength detuning Δλ FP-PL between the Fabry–Perot resonance wavelength λ FP and the photoluminescence/gain peak λ FP (upper axis). The data were calculated assuming a spectral shift of 0.3 and 0.1 nm K−1 for the photoluminescence/gain peak and FP resonance, respectively. These values had been determined earlier for our structures. The GaAs refractive index was assumed to be n = 3.52 at 980 nm. For instance, when, due to a growth inaccuracy of 2 %, the microcavity FP resonance is blueshifted (thinner than desired microcavity) at ambient temperature with respect to the gain maximum (i.e., Δλ FP-PL < 0), as shown in Fig. 1, the VECSEL structure should be cooled by about 59 °C to a very low temperature of −39 °C for optimal laser operation.

Fig. 1
figure 1

Dependences of the change in optimal operation temperature, at which λ FP = λ PL on the deviation from the desired thickness of the microcavity (left axis) and spectral shift, at room temperature, between the microcavity Fabry–Perot resonance and the gain maximum (right axis). The refractive index for GaAs of 3.52 (for 980 nm), a microcavity peak shift rate of 0.1 nm K−1 and photoluminescence/gain peak shift rate of 0.3 nm K−1 were assumed for the calculations. λ FP—FP resonance wavelength, λ PL—photoluminescence/gain peak, Δλ FP-PL—the detuning between λ FP and λ PL

Full size image

On the other hand, when the microcavity is 2 % thicker than the designed value (i.e., Δλ FP-PL > 0), the laser operation temperature should be increased by 136 °C. In both cases, the temperature readjustment range is far too large. Based on above example, it seems that an acceptable value for layer thickness deviation is around 1.0 %, whereas the epitaxial limit for growth rate deviation in a standard MBE chamber is 0.5 %. This accuracy is due to the limited long-term stability of molecular fluxes and their repeatable calibration. One should notice that 0.5 % precision translates to 0.6-nm variation in GaAs barrier thickness which corresponds to two monolayers. To reach a deviation of 0.5 %, a time-consuming calibration procedure of the growth rate was applied. First, an in situ reflection high-energy electron diffraction (RHEED) technique was used and then a number of test heterostructures were grown and tested ex situ using high-resolution X-ray reflectometry (HR XRR) as well as high-resolution diffractometry (HR XRD). Special care was taken to assure the day-to-day reproducibility of the growth conditions. We measured the oscillations of the specular beam in the RHEED patterns from 2 × 4 reconstructed surfaces for GaAs and AlAs alloys carefully and repeatedly. The 20 oscillations observed during 90 s were analyzed to precisely determine the growth rate (see Fig. 2). Since the oscillation period corresponds exactly to a single monolayer, the growth rate was estimated to be 0.96 ML/s for GaAs and 0.98 ML/s for AlAs. However, when the shutter of the effusion cell is open, the flux of molecules is high at first, then decreases and finally stabilizes during ~150 s for Ga and ~100 s for Al (inset figures). In consequence, an average growth rate established during the time of RHEED oscillation measurements is higher than over longer periods. Except for the QWs and the GaAs cap layer, all layers of the VECSEL structure take few minutes to grow, so an additional ex situ verification of growth rates is needed. For this purpose, a set of test DBR heterostructures was prepared. The measurement of these heterostructures was taken ex situ by HR XRR as well as HR XRD. For high precision, the thicknesses of the layers derived first from reflectometric profile by fitting the model to the experimental data (Fig. 3a) were further used as input data for HR XRD analysis (Fig. 3b). This procedure permitted us to exclude the errors due to the possible flux drift during the DBR growth. The obtained precise growth rates for binary alloys of which the deposition times were longer than those needed to stabilize fluxes were: rGaAs = 0.93 ML/s and rAlAs = 0.96 ML/s, i.e., lower by 3 and 2 %, respectively, than those obtained from RHEED data.

Fig. 2
figure 2

Intensity oscillations of a specular beam in the RHEED pattern from 2 × 4 reconstructed surfaces for GaAs (a) and AlAs (b) alloys. Insets present the term dependences of Ga (a) and Al (b) fluxes

Full size image
Fig. 3
figure 3

Experimental (dark line) and calculated (gray line) X-ray reflectivity (a) and diffraction (b) curves for the DBR structure

Full size image

3 Characterization techniques and laser setup

The overall assessment of the quality and accuracy of as-grown VECSEL wafers is made by analyzing their optical properties. For this purpose, reflectance (R) and photoluminescence (PL) measurements are commonly used. Complementary results from these two experimental techniques reveal any possible discrepancies between the design and the real structure obtained through epitaxial growth.

Reflectance measurements were taken using so-called bright configuration of the experimental setup. The light of a broadband source (quartz–tungsten–halogen lamp) was formed by optical elements into a quasi-parallel light beam which struck the surface of the wafer under examination from an angle of 90°. The light reflected by the VECSEL structure was dispersed by a 0.46-m spectrometer (Jobin–Yvon HR460) equipped with a grating of 600 lines mm−1, and detected using an analog Ge detector. The measured signal was amplified using a standard synchronous lock-in technique. The reflectance spectra showed a broad stop band with characteristic dips which mark the absorption of the incident light within the QW active region and the spectral position of the cavity resonance.

The QW gain region was also examined through an analysis of its photoluminescence spectra. As an excitation source for PL measurements, a low power (<8 mW) He–Ne laser was used. Our measurement system allows for registration of both surface- and edge-emitted PL signals. The latter we investigated using the microprobe photoluminescence (µPL) technique. The excitation beam was focused to a diffraction-limited spot size of about 1 µm on the cleaved edge of the structure using a long-working-distance microscope objective with magnification 20×. The position of the structure under analysis was controlled by a 2-D translation stage with 0.1-μm spatial resolution. The PL signal was collected in backscattering mode using the same objective lens and then dispersed by means of the spectrometer described above. As a signal detector, we used a Si multichannel charge-coupled device (CCD) cooled to 146 K. All measurements were taken at room temperature. The QW emission spectrum observed perpendicularly to the wafer surface was modified significantly by the microcavity resonance and was unaffected when the signal was collected from the edge of the wafer. In consequence, the PL signal taken through the surface of the structure indicated the spectral position of the cavity resonance while the edge emission showed the pure QW emission.

An X-ray analysis of the strain built into the structures was carried out by reciprocal space mapping the 004 and -2-24 reciprocal space points for [0 1 1] and [0 −1 1] directions, respectively, using Cu Kα1 (λ ~ 1.54056 Å) radiation. The X’Pert PRO diffractometer was equipped with a hybrid 4 × Ge(400) monochromator and three-bounce Ge(220) analyzer. The reflection intensity was measured using a proportional detector. 004 reciprocal space maps were made for each structure and the perpendicular lattice constants determined. Taking these values into account, the parallel lattice constants were also calculated, using asymmetrical -2-24 reciprocal space maps. This permitted to establish the degree of strain relaxation, which is defined as the difference between parallel lattice constant of the layer and the lattice constant of the substrate divided by the difference between undistorted lattice constant of the layer and the lattice constant of the substrate.

$$R_{\text{relax}} = \frac{{a_{{{\text{L}}^{*} }} - a_{\text{S}} }}{{a_{\text{L}} - a_{\text{S}} }} \cdot 100\;\%$$
(1)

where \(a_{{{\text{L}}^{*} }}\) is the layer lattice constant parallel to the interface, a L is the undistorted layer lattice constant and a S is the substrate lattice constant.

In addition to X-ray investigation, the structural relaxation was also visualized by spatially resolved PL intensity mapping. For the image registration, an infrared-sensitive CCD camera was connected to an optical microscope, and for the PL excitation, a strongly unfocused high-power 808-nm pump laser was used. An edge-pass filter was inserted in front of the camera to block the laser light dispersed on the sample surface. Bright PL images with high contrast dark areas (lines, ovals) are registered. The dark areas are associated with defects since the density of non-radiative recombination centers increases in the defects proximity.

As a final evaluation of the wafer quality, the lasing properties of 3 × 3 mm chips separated from the samples by cleavage were tested. The VECSEL emission properties depend not only on the structure design and epitaxial growth quality but also on the chip’s heat management [17]. Heat extraction can be achieved by either capillary bonding of an adequate transparent heatspreader [18–20] or so-called flip-chip technology, i.e., a chip is soldered with the epi-layers facing downwards directly onto a heat sink and the substrate is totally removed [21]. Although the flip-chip technology permitted for record high-power emission exceeding 100 W [11], here for the heat extraction we have tested as-grown structures capillary bounded to a diamond heatspreader. The flip-chip technique requires the soldering of the epitaxial structure which after the removal of the substrate is only few micrometer thick. Such a thin structure is prone to the strain which is introduced by the solder. Since in this paper we concentrate on the structural relaxation of strain originating from the mismatched QW, the additional source of strain could obscure the processes under investigation. Moreover, the VECSEL structures prepared for the transparent heatspreader application can be tested without any preliminary preparation. The QW region grown on DBR can be easily accessed in PL experiment. In wafers prepared for flip-chip, on substrate the QW region is grown before the DBR which is opaque for PL signal. In consequence, the crucial feature of the wafer the PL and Fabry–Perot resonance tuning cannot be verified.

The as-grown samples were glued with a thermal conductive paste directly to a copper heatsink, while the diamond bounded structures were tightly screwed in a specially prepared copper holder [22]. A thin indium foil was used to improve the thermal contact between the semiconductor chip and the copper. On the opposite side, 300-μm-thick transparent diamonds acted as intracavity heatspreaders dissipating effectively the heat from the active region. Regardless of the heat extraction schema, the laser chips were mounted in a simple linear resonator. A high-power fiber-coupled laser diode bar emitting at 808 nm was used for optical pumping. The maximum deliverable pump power was 27 W. The pump laser beam was directed at the VECSEL chip at an angle of 30° from the optical axis of the VECSEL cavity. The dielectric mirrors of the curvatures in the range 90–100 mm and the transparency 1–4 % were chosen for maximum power emission. The length of the cavity could be changed within few millimeters, to match the mode size to the size of the pump beam spot. The laser chip was mounted on a heat sink and thermally stabilized by a thermoelectric cooler (i.e., Peltier element). A water-cooling system was used to remove excess heat from the heat sink. A Thorlabs PM100 laser power meter equipped with Thorlabs S130C photodiode power sensor was used to measure the output power. Details of the setup are provided in Fig. 4.

Fig. 4
figure 4

VECSEL cavity scheme (upper) and photograph of the setup (bottom)

Full size image

4 Model used for the analysis

A self-consistent model was used to calculate the VECSEL output power characteristics. The model has been already validated, and it has proved satisfactory agreement with experimental characteristics [23, 24]. This model consists of four closely connected modules for temperature, gain and optical field calculations, which are reported in Ref. [25–27] and for carrier transport described in the next subsection.

4.1 Carrier transport model

Our model assumes a cylindrical symmetry of the considered device, so the calculations are done in the cylindrical coordinate system (r, z). Since the structure of an optically pumped VECSEL contains an active region with several QWs separated by relatively long barrier layers, the exponential character of the absorption of pumping radiation results in non-homogeneous excitation of the QWs. Therefore, to determine the carrier density in each QW it is necessary to consider carrier transport in the vertical direction along the whole active region. On the other hand, our simulations show that the carrier transport in the radial direction can be neglected for pumping beams with diameters of tens and more of microns for arsenide compounds with diffusion coefficient of the order of magnitude of ~10 cm2 s−1. In this case, the radial carrier distributions are determined rather by the pumping beam profile and carrier losses due to recombination processes. Such an assumption causes that the problem of solving a 2D diffusion equation in the (r, z) for the carriers in the active region may be replaced by the problem of solving a number of independent 1D equations in the z direction for successive values of the r coordinate. This greatly simplifies numerical calculations.

The model assumes that the laser active region consists of alternate QW and barrier layers and QWs are reduced to points and act as carrier absorbers. To calculate the carrier density distribution along this active region for the given r value, the following 1D diffusion equation with no carrier drift contribution is solved for each barrier [28, 29]:

$$D\frac{{{\text{d}}^{2} n}}{{{\text{d}}z^{2} }} - \frac{n}{\tau } + G = 0$$
(2)

where D is the ambipolar diffusion coefficient, n is the carrier density, z is the vertical coordinate and τ is the carrier lifetime:

$$\frac{1}{\tau } = A + Bn + Cn^{2}$$
(3)

in which A, B, C are monomolecular, bimolecular and Auger recombination coefficients, respectively. G in Eq. (2) stands for the carrier generation rate expressed as:

$$G = \frac{{q_{\text{a}} \alpha_{\text{p}} \lambda_{\text{p}} }}{hc}\exp \left( { - \alpha_{\text{p}} z} \right) \equiv G_{0} \exp \left( { - \alpha_{\text{p}} z} \right)$$
(4)

where λ p is the pumping wavelength, α p is the absorption coefficient for pumping radiation, h is the Planck constant, c is the speed of light in vacuum and q a is the surface power density of pumping radiation entering the active region. The analytical solution of Eq. (2) for the jth barrier is:

$$n\left( z \right) = C_{1}^{\left( j \right)} \sinh \left( {\frac{z}{{\sqrt {D\tau } }}} \right) + C_{2}^{\left( j \right)} \cosh \left( {\frac{z}{{\sqrt {D\tau } }}} \right) + \frac{{G_{0} \tau }}{{1 - \alpha_{\text{p}}^{2} D\tau }}\exp \left( { - \alpha_{\text{p}} z} \right)$$
(5)

where C (j)1 and C (j)2 are certain constants. Solutions for the individual barriers were connected at QWs using the following boundary conditions. First, the carrier density was assumed to be continuous at each QW, which gave the following condition (for jth QW between jth and (j + 1)th barriers at z = z (j)QW ):

$$C_{2}^{{\left( {j + 1} \right)}} - C_{2}^{\left( j \right)} = \left( {C_{1}^{\left( j \right)} - C_{1}^{{\left( {j + 1} \right)}} } \right)\tanh \left( {\frac{{z_{\text{QW}}^{\left( j \right)} }}{{\sqrt {D\tau } }}} \right)$$
(6)

Carrier losses in the jth QW could be calculated using the steady-state carrier balance equation:

$$D\left( {\left. {\frac{{{\text{d}}n}}{{{\text{d}}z}}} \right|_{{z_{\text{qw}}^{\left( j \right) + } }} - \left. {\frac{{{\text{d}}n}}{{{\text{d}}z}}} \right|_{{z_{\text{qw}}^{\left( j \right) - } }} } \right) = d_{\text{QW}}^{\left( j \right)} \left( {A_{\text{qw}}^{\left( j \right)} \left( {n_{\text{qw}}^{\left( j \right)} } \right) + B_{\text{qw}}^{\left( j \right)} \left( {n_{\text{qw}}^{\left( j \right)} } \right)^{2} + C_{\text{qw}}^{\left( j \right)} \left( {n_{\text{qw}}^{\left( j \right)} } \right)^{3} + L_{\text{st}}^{\left( j \right)} } \right)$$
(7)

where terms on the left-hand side represent the carrier flux at, respectively, the left and right edge of the jth QW. The symbol d QW designates the QW thickness and n QW is the carrier density in the QW, which can be determined by finding the quasi-Fermi levels and calculating the density integrals. L st in Eq. (7) is the component responsible for stimulated emission losses [30]:

$$L_{\text{st}}^{\left( j \right)} = \frac{{q_{\text{e}} \lambda_{\text{e}} }}{hc} \cdot \frac{{\left| {E_{\text{qw}}^{\left( j \right)} } \right|^{2} }}{{\left| {E_{\text{air}} } \right|^{2} }} \cdot n_{\text{R,qw}}^{\left( j \right)} \cdot g_{\text{qw}}^{\left( j \right)}$$
(8)

where q e is the surface power density of emitted radiation, λ e is the emitted wavelength, E qw and E air are electric fields at the QW and the air cavity, respectively (|E qw|2 and |E air|2 are equal to corresponding light intensities) and n R,qw and g qw are the refractive index and material gain of the QW, respectively.

4.2 Model parameters

Table 1 lists the material parameters used in carrier transport, thermal and optical models at temperature T = 300 K, for pump wavelength λ p = 808 nm and emission wavelength λ e = 980 nm. Spectral and temperature dependences of the parameters can be found in the references given in the table. The values of monomolecular recombination coefficients A have been determined separately for each active region to fit the experimental results. Parameters and relations for the gain calculations can be found in the reference [31].

Table 1 Material parameters used in carrier transport, thermal and optical calculations at T = 300 K, λ p = 808 nm, λ e = 980 nm
Full size table

5 Results and discussion

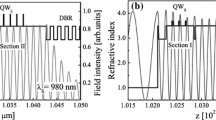
The measured reflectance and photoluminescence spectra for test structures (#s_DBR and #s_MQW) and four as-grown VECSELs: #s4–#s16 are displayed in Table 2 and for selected structures of #s4 and #s16 are presented in Fig. 5. Three dips in the high reflectivity plateau of #s16 observed at 940, 977 and 1020 nm appeared because the free spectral range of the 17λ/2-thick microcavity is smaller than the DBR stop band (Fig. 5b). Taking into account the scattering of the spectral position of the FP resonance, the microcavity thickness deviation was less than 1.0 % between the structures. The spectral detuning between resonance and gain maxima was almost equal for all the lasers analyzed. This was the indispensable feature that permitted us to compare the lasing properties.

Table 2 Measured spectral parameters for DBR, MQW and n × QW-VECSEL
Full size table
Fig. 5
figure 5

Reflectivity and PL spectra for 4QW-VECSEL (a) and 16QW-VECSEL (b). Edge photoluminescence signal (line) indicates the gain peak, whereas the surface photoluminescence peaks (symbols) correspond to the microcavity resonances

Full size image

The analyzed VECSEL structures were lattice mismatched in respect of the GaAs substrate and partially relaxed. Relaxation is achieved by the generation of misfit dislocations (MDs). Higher MD density indicates more intense relaxation, which takes place in structures with thicker mismatched lattice material. This was observed in the PL images of the VECSEL structures under an optical microscope (see Fig. 6). We interpret the dark lines as faults caused by grouping of MDs, while the bright points are Ga-related surface defects. The dark line density is higher for structures with higher numbers of QWs, i.e., for structures with thicker In0.18Ga0.82As material. To determine the structural relaxation degree quantitatively, two maps for each sample were made using HR XRD. As reference, the separately grown DBR and MQWs structures were examined. The results for two chosen structures are shown in Fig. 7: #s4 (a) and #s16 (b) and summarized for all samples in Fig. 8.

Fig. 6
figure 6

Surface images of 50 × 40 μm for VECSELs observed under microscope: #4s, 4QW-VECSEL (a), #s8, 8QW-VECSEL (b), #s12, 12QW-VECSEL (c), #s16, 16QW-VECSEL (d)

Full size image
Fig. 7
figure 7

Recipocal space maps taken for 4QW-VECSEL (left side) and 16QW-VECSEL (right side). The relaxation is 0.15 for 4QW-VECSEL and 0.33 for 16QW-VECSEL

Full size image
Fig. 8
figure 8

Relaxation of structure lattice vs QW number measured using reciprocal space maps

Full size image

In Fig. 7, the arrow indicates the peak position of the GaAs substrate/buffer. The straight line is for guidance and lies on the main and satellite peaks originating from the VECSEL’s periodic structure. The peak of the GaAs substrate in #s16 VECSEL is shifted more from the line position of the satellite peaks than in the case of #s4-VECSEL structure. The positions of the substrate and satellites determine the relaxation level, which in the case of the 16 QW-VECSEL structure (0.33) is more than double that of the 4 QW-VECSEL structure (0.15). The results for other structures are shown in Fig. 8.

A relaxation level of 0.1 (10 %) for AlAs/GaAs DBR structure seems to be relatively high, see Fig. 8. However, the total thickness of AlAs material in our structure was about 2.5 μm. It was about five times larger than the critical layer thickness (CLT, d c ≈ 500 nm) for AlAs grown on GaAs substrate, determined using the Mathews–Blakeslee formula [43]. This suggests that such high structural relaxation degree indeed takes place.

For In0.18Ga0.82As grown on GaAs substrate, the CLT is about 37 nm. In #s_MQW, the total thickness of In0.18Ga0.82As material was 96 nm. This means that it exceeded almost threefold. The relaxation degree determined from the reciprocal space maps was 0.013 (1.3 %) (not shown in the text). The same structure of #s_MQW consisting of 12 QWs and deposited on 10.0 %-relaxed DBR structure increased the relaxation to 0.27 (27.0 %). The MQW containing 4 QWs has total thickness of In0.18Ga0.82As material (4 × 8 nm = 32 nm) lower than the CLT (37 nm). It allows to claim that the structure is fully strained (0.0 % relaxation). Its deposition on 10.0 %-relaxed DBR structure increased, however, the relaxation to 0.15 (15.0 %). It means that for the partially strained/relaxed structure of In0.18Ga0.82As QWs deposited on the DBR structure with the same compressive strain, the total relaxation is not the sum of the individual relaxations, as shown in Table 2 and Fig. 8. A possible explanation can be derived from assumption that the interfaces act as lattice perturbations, i.e., as planar defects. If the defect density in a material is higher, more relaxation will occur in thinner layers than in material with lower defect density. The interfaces accelerate lattice relaxation and may appear even at material thicknesses smaller than CLT. As shown in Fig. 8, the dependence of relaxation on the number of QWs can be described using the linear equation R relax = 0.0145 × N QW + 0.104, where the R relax is relaxation and N QW is the number of QWs. This dependence is true only for samples grown under the epitaxial conditions described in this paper.

Further, the dependence of lattice strain/relaxation on lasing parameters was studied. The comparison of power characteristics measured and simulated is presented in Fig. 9 for as-grown samples and in Fig. 10 for diamond bounded ones.

Fig. 9
figure 9

Power characteristics for the as-grown structures heat conductive past glued to a heatsink. All data taken for 60 μm spot diameter and 2 % transmittance of the mirror with 90 mm curvature radius. Symbol b is the factor in the monomolecular recombination coefficient for the InGaAs/GaAs material system: A = b × 108(T/300)4 s−1

Full size image
Fig. 10
figure 10

Power characteristics for the structures bounded with a diamond heatspreader in a copper holder. All data taken for 200 μm spot diameter and 4 % transmittance of the mirror with 100 mm curvature radius. Symbol b is the factor in the monomolecular recombination coefficient for the InGaAs/GaAs material system: A = b × 108(T/300)4 s−1

Full size image

Because the heat dissipation in as-grown samples is very weak, the maximum emission power could be registered for the pump spots and matched mode diameters as low as 60 μm. For those samples, any attempt to increase the spot size resulted in decrease in the emitted power due to premature thermal rollover. In opposition, the diamond heat spreader permitted to increase the pump spot and mode diameter to the 200 μm. The increase in the emission capability permitted also to increase the output coupler transmission from 2 to 4 %, which overall resulted in the 20-fold increase in the maximum emission power from 20 mW to the value above 4.7 W.

The measured emission characteristics are compared with the numerical simulations for the structures with and without the heat spreader. In the calculations, the monomolecular recombination coefficient A was used as the fitting parameter and both lasers based on the same structure (with and without the heat spreader) were modeled assuming the same value of A. The good agreement between the experimental and numerical data for each heterostructure regardless of the heat dissipation schema proves the reliability of the achieved data.

The values of the monomolecular recombination coefficient increase with the number of QWs and equal from 1.0 × 108 to 1.54 × 108 s−1 for 4 QW and 16 QW, respectively. This indicates that longer active regions and greater number of QWs are characterized by stronger defect recombination, which is due to the observably larger relaxation and higher misfit dislocation density. The highest power was measured for the #s12 and #s16 heterostructures. This is understandable since a larger number of QWs provide larger gain for discussed number of QWs and thus permit for the higher output coupling. However, in case of #s16 A the larger coefficient limits this advantage. The low power registered for #s4 heterostructure bounded with a diamond heat spreader is due to insufficient gain provided by 4QWs. The largest power of 1.3 W for this heterostructure was registered when the output coupler transmission was reduced to 1 %.

The obtained results are universal, because the monomolecular recombination coefficient as a function of the QW number is clearly related to lattice relaxation (Fig. 11).

Fig. 11
figure 11

Monomolecular recombination coefficient A versus relaxation level: A = (3R relax + 0.52) × 108 s−1

Full size image

This finding can be used to simulate the power characteristics of lasers in InGaAs/GaAs material systems assuming that relaxation ranging from 0.1 to 0.33 regardless of QW number and stoichiometry. The key factor is the defect density in InGaAs/GaAs material system. The defect density is the same in structures with the same relaxation values, assuming that all of them relax via misfit dislocations with a Burger’s vector of 60°. This in turn means that in VECSELs with high number of QWs if the strain relaxation could be kept on the low level, the output power would be higher. No strain relaxation can be achieved using layers adjacent to QW with the opposite type of strain. The compressive strain of InGaAs/GaAs QW is commonly compensated by tensely strained GaAsP layers [44].

In Figs. 9 and 10, for each VECSELs there are power characteristics calculated under assumption of low strain relaxation (as in #s4, A = 1.0 × 108 s−1) and the strain relaxation referring to QW number (A > 1.0 × 108 s−1). The output power calculated at A = 1.0 × 108 s−1 is higher than power calculated (and measured) for VECSELs with higher strain relaxations. The maximum powers are higher by 6, 10 and 27 % for #s8, #s12 and #s16 VECSELs, respectively. In other words, using the strain compensation technique (GaAsP layers in adjacent to gain region) the output power for #s16 VECSEL could be increased by almost 30 %. Further increase in output power can take place if the strain relaxation of DBR structures is reduced, as well. For AlAs/GaAs DBR strain relaxation is 10 %. We also hypothesize that the strain relaxation in DBR accelerates the relaxation of the gain region. If relaxation in DBR is attenuated, the strain relaxation in resonant periodic gain region can be significantly reduced [comparing 12 QWs deposited on GaAs (1.3 %) and on DBR structure (27 %)]. It could be considered as an alternative means to the strain compensation technique. We have achieved partial success in this area—we showed that AlAs/GaAs DBR mirror with 15 periods can be obtained without any dislocation lines on HR XRD topograms [45].

It is worth emphasizing that the agreement between the simulations and experimental results was achieved based on the sole assumption that the structures differ only in the level of relaxation. All other parameters affecting the output power characteristics were kept constant. This enabled the precise monomolecular recombination coefficient for InGaAs/GaAs material systems to be determined.

6 Conclusion

In this study, VECSEL structures with non-strain-compensated active regions were analyzed to explore the influence of strain built into their periodic gain structure on power characteristics. The unique set of VECSELs structures differed only in the thickness of their active regions and in the number of their QWs has been investigated for the first time. All other parameters concerning structure design and growth conditions were the same. Precise control of the growth rate was ensured by in situ RHEED observation and ex situ verification using XR XRR measurements, which supplied the results for HR XRD analysis. A two-step control process allowed us to fabricate VECSEL structures with microcavities of different lengths and fixed spectral detuning between gain and Fabry–Perot resonance peaks. The structures differed therefore only in the strain introduced by lattice-mismatched InGaAs QWs. We assumed that the structure relaxed only through the generation of misfit dislocations with a Burger’s vector of 60°, which form non-radiative recombination centers. The inclusion of MD density in the simulation by adjusting the monomolecular recombination coefficient produced good agreement between the simulated and experimental data. The results show that the power characteristics worsened mainly due to carrier non-radiative recombination on misfit dislocations. Taking output power as a criterion, the optimal QW number was found to be 12 and the maximal tolerable relaxation value 0.27 for our InGaAs/GaAs VECSEL structures. The relationship established by this study between the monomolecular recombination coefficient and material relaxation can be useful in simulations of various optical device designs based on InGaAs/GaAs material systems.

We have evidenced that MDs present in DBR structure accelerate the strain relaxation in MQW active region. The attenuation of DBR relaxation could significantly reduce or annihilate the strain relaxation in resonant periodic gain region. It might be done by DBR growth optimization.