Multi-μJ harmonic emission energy from laser-driven plasma

Abstract

We report on simultaneous efficiency and divergence measurements for harmonics from solid targets generated by the relativistic oscillating mirror mechanism. For a value of the normalized vector potential of $a_{\mathrm{L}}\simeq 1.5$, we demonstrate the generation of 30 μJ high-harmonic radiation in a $17\pm 3$ mrad divergence cone. This corresponds to a conversion efficiency of $\gtrsim$10⁻⁴ in the 17–80 nm range into a well-confined beam. Presuming phase-locked harmonics, our results predict unprecedented levels of average power for a single attosecond pulse in the generated pulse train. Results of PIC simulations raise the prospect of attaining efficiencies of a few percent at higher laser intensities.

Introduction

In the emerging field of attosecond science, a key ingredient in every experimental technique has been the availability of an attosecond light source [1]. To date, most of these sources are based on high-order harmonic generation (HHG) in gaseous media. However, due to intrinsic processes associated with this generation mechanism, there is a maximum laser pulse intensity that can be used with the consequence of limiting their brightness and severely restricting the scope of applications [2, 3]. Techniques like the loose-focusing [4–7] or the double optical gating [8] have been implemented to enhance the XUV flux and exploit higher laser energies from modern laser systems. More recently using these techniques, a tabletop source delivering 2.6 GW power in a single attosecond pulse was reported [9]. Nevertheless, mainly due to impractical setups required, the prospects to further increase the XUV pulse energy by efficiently exploiting state-of-the-art multi-10-TW and PW class laser systems appear to be bleak. An alternative nonlinear medium, the plasma–vacuum interface, holds the promise of surmounting this limitation and substantially increasing the number of photons carried away even in single attosecond bursts [10]. It is more attractive for two main reasons; it provides higher conversion efficiencies, and it does not exhibit a limit to the maximum laser intensity that can be used. Thus, the plasma medium for the conversion of short optical pulses into attosecond pulses via harmonic generation appears to be particularly suitable for use with very high-power laser systems that are currently or will become available in the near future. The harmonic emission emanating from the interaction of intense laser pulses with solid-density plasma is due to two main mechanisms. For relatively low laser intensities, the so-called coherent wake emission mechanism (CWE) dominates [11, 12]. Under these circumstances, it has been recently demonstrated that the harmonic emission leads to temporal bunching with attosecond pulse durations [13, 14]. At higher intensities, the relativistic oscillating mirror (ROM) mechanism becomes dominant [15–17]. The delimitation between the two mechanisms is usually based on the normalized vector potential $a_{\mathrm{L}}$ value, which in terms of the focused laser intensity $I_{\mathrm{L}}$ and laser wavelength $\lambda _{\mathrm{L}}$ is given by $a_{\mathrm{L}}^{2}=I_{\mathrm{L}}\lambda _{\mathrm{L}}^{2}/[1.38\times 10^{18}\,\hbox{W cm}^{-2}\,\upmu {\mathrm{m}}^{2}]$. Under ideal conditions regarding the laser pulse characteristics, the ROM mechanism prevails when $a_{\mathrm{L}}$ is larger than unity, while for $a_{\mathrm{L}}\lesssim 1,$ the CWE mechanism is considerably more efficient. In the transitional range, the two processes can coexist and which one of the two dominates depends sensitively on the gradient of the plasma density profile [18, 19]. Due to its superior properties and predominance at high intensities, the basis for the generation of single attosecond light pulses [20] using this source will most probably be the ROM mechanism.

One of the most important quantities of interest associated with every nonlinear medium is the efficiency with which the laser pulse energy is converted to XUV light, i.e., to higher harmonics of the fundamental laser frequency and consequently to attosecond pulses. According to predictions based on particle-in-cell (PIC) simulations, under ideal conditions, the conversion efficiency of solid targets dramatically increases with laser intensity and for $I_{\mathrm{L}}\ge 1.0\times 10^{18}\,\hbox{W cm}^{-2}$ significantly surpasses the corresponding conversion efficiency of gas targets [10, 16]. In view of the outmost importance of having a source providing intense attosecond pulses, these theoretical predictions have to be experimentally verified. An accurate conversion measurement in the case of harmonic emission from solid targets is far from trivial even for the ROM mechanism. The reason is the commonly large solid angle of the emission due to tight laser beam focusing compared to the pencil-like XUV beam produced by the gas targets. More importantly, instabilities occurring at the plasma–vacuum interface can cause rippling of the critical surface resulting in the scattering of the emission into a large solid angle up to $2\pi$ [21–23]. The generation of ROM harmonics with divergence corresponding to the harmonic wavelength, i.e., less than the original laser beam was accomplished only since the availability of high-contrast ultrashort laser pulses using double plasma mirrors [17]. It is therefore essential that the efficiency measurement is accompanied by a simultaneous determination of the beam divergence. In the past, a number of efficiency measurements mainly for individual harmonics and for different spectral ranges have been reported [13, 18, 21, 24–26]. The solid angle of the emission in these reports was mostly estimated without concurrent determination of the actual emission cone. More recent work has addressed the issues of divergence and XUV efficiency and their dependence on the initial density scalelength prevailing at the plasma–vacuum interface [19, 27, 28].

Here, we report simultaneous (in the same laser shot) measurements of efficiency and XUV emission cone in a spectral range of practical relevance. Furthermore, we demonstrate ROM harmonic generation even at modest laser energies in the form of a well-collimated XUV beam. In contrast to the ideal conditions assumed in simulations, in practice, the laser pulse produced by the laser system usually deviates substantially from the ideal form thus modifying the course and outcome of the interaction. Under realistic operating conditions of our laser with respect to pre-pulse level, pulse contrast and phase front quality, we find that an increase in the laser pulse intensity affects adversely the generation of ROM harmonics yielding at first a rather complicated spectrum while for even higher intensities, the harmonic emission is quenched. This is attributed to the laser pulse characteristics that determine to a great extent the steepness of the density ramp at the plasma–vacuum interface. As has been already reported [19, 27, 29], the initial density gradient scalelength $L$ has a profound influence on the spectral and spatial properties of the harmonic emission. In our experiment, we were able to observe “beaming” of the harmonic emission and a reproducible spectrum, only when we attenuated the laser beam energy to the level that the pre-pulse effects were switched-off. For simultaneous ROM harmonic generation and optimum beaming, the integrated conversion in the Al filter spectral window was measured by absolutely calibrated diodes. As we are primarily interested in the generation of intense attosecond pulses, our measurements focus on the efficiency of a broad spectral range defined by an appropriate filter. At reduced laser intensities, the measured conversion efficiency compares reasonably well with 1D-PIC and more satisfactorily with 2D-PIC simulations results.

Experimental results

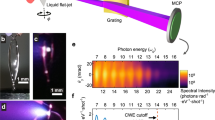
In our experiments, we used the ATLAS laser system that was operated at reduced output to deliver pulses of $\tau _\mathrm{L}=28$ fs duration with energy of up to a maximum of $E_\mathrm{L }=280\,\hbox { mJ}$. A schematic of the experimental setup is shown in Fig. 1.

Fig. 1

Schematic of the experimental setup for the simultaneous measurements of the divergence and efficiency. Inset The laser focal spot and the encircled energy as a function of radius

The beam was focused by a $90^{\circ }$ off-axis parabola mirror onto the fused silica targets at $45^{\circ }$ angle of incidence. The 3-μm full-width-half-maximum (FWHM) diameter focal spot contained 34 % of the laser pulse energy, whereas 63 % was encircled within the 7 μm diameter of the first Airy-minimum (see inset in Fig. 1). The later values are used to calculate the average laser intensity, which was varied in the range of $\langle I_{\mathrm{L}}\rangle =4 \times 10^{18}-1.5 \times 10^{19}\,\hbox{W cm}^{-2}\, (a_{\mathrm{L}}= 1.4{-}2.6)$. For this laser system, the third-order autocorrelation trace reveals a contrast of $\sim$10⁻⁷ on the 10 ps scale and of the order of $\sim$10⁻⁴ on the 1 ps scale. The harmonics in the specular direction propagated toward a 75-mm-diameter MCP detector which was situated behind Al filter foils at a distance of 750 mm from the target. It is to be noted here that only in case of beaming when the size of the XUV beam is smaller than the solid angle subtended by the MCP of 100 mrad, it would be possible to observe the whole XUV profile. Once beaming was achieved, the absolutely calibrated IRD-AXUV diode was inserted in front of the MCP to intercept the XUV beam. Thus, beaming was ensured in each shot in which the XUV diode signal was recorded. The harmonic spectrum was investigated by a Hitachi flat-field grating spectrometer [30] at two different positions. To obtain spectra compatible with the MCP records, the MCP detector was disassembled and the spectrometer was mounted in direct view of the source with only an Al filter at its entrance slit. To allow for in situ optimization of spectrum during the divergence measurements, the spectrometer was mounted in the alternative arrangement as shown in Fig. 1. The harmonics were reflected into the spectrometer by a removable Au mirror. First, the harmonic spectrum was optimized by gradually varying the laser energy with the target surface in focus, and afterward, beaming and conversion were measured.

Figure 2 shows the spectrum recorded within the Al transmission spectral window (17–80 nm) for three increasing laser energies on target.

Fig. 2

a–c Harmonic spectra for the indicated laser pulse energy. Upper row raw spectrometer data. Lower row line-outs after vertical binning. For $E_{\mathrm{L}}=140\,\hbox{mJ}$ in (b), the short wavelength range is plotted to show the substructure observed. d Composite (17–40 and 40–80 nm range) and absolutely calibrated spectrum at the lowest intensity corresponding to $E_{\mathrm{L}}=80\,\hbox{mJ}$. Red line spectrometer record. Blue-shaded line with the Al filter transmission (green line) deconvolved spectrum

All the spectra extend clearly into the ROM regime as the frequency cutoff for the CWE mechanism is at 40 nm. Whereas for the lowest energy of $E_{\mathrm{L}}=80\,\hbox{mJ}$ the emitted spectrum exhibits a regular and reproducible structure (Fig. 2a), for the intermediate energy of $E_{\mathrm{L}}=140\,\hbox{mJ},$ it becomes strongly modulated with a complicated substructure in the short wavelength range reminiscent to the one discussed in Ref. [31]. For the maximum laser energy of $E_{\mathrm{L}}=280\,\hbox{mJ},$ the spectrum is rather irregular and irreproducible with possible admixture of line emission (see Fig. 2c). This is attributed to the interplay between pre-pulse level and pre-plasma formation. As it is pointed out by Dollar et al. [32], small changes in the pre-pulse intensity can cause substantial variation in the scalelength of the produced density profile. It is to be noted that by attenuating the laser beam, the contrast did not change significantly; therefore, the pre-pulse level and the corresponding pre-plasma size were reduced as well. It appears that for the lowest energy value, the pre-pulse is at a low enough level as not to form a pre-plasma before the arrival of the main pulse. This suggests that the interaction occurs in a plasma with a relatively steep density gradient similar to the conditions encountered when a double plasma mirror is used to reduce the pre-pulse level [17, 19]. In contrast, the observed spectral structure of the harmonics for the intermediate and maximum energies appears to be a signature of the interaction taking place in a preformed plasma of increasing scalelength. The spectrometer at a single shot could record only a limited spectral range. In order to cover the complete emission spectrum, records were taken at $E_\mathrm{L }=80\,\hbox{mJ}$ at different grating positions and subsequently combined. An example of a readily reproducible full range spectrum at this laser energy is shown in Fig. 2d. As can be seen, despite the low laser intensity on target corresponding to an $a_{\mathrm{L}}\approx 1.5$, harmonics due to the ROM mechanism are produced extending down to 17 nm, corresponding to the L-edge of the Al filter used.

The regularity of the harmonic spectrum closely correlates to the beaming of the XUV emission. This is depicted in Fig. 3a, b, where the MCP records for the maximum and lowest laser intensity used are shown. For the irregular spectrum observed at the highest intensities, the corresponding XUV beam exhibits no directionality but rather a diffuse pattern (Fig. 3a). It was only when the spectrum was optimized so as to consist of regularly spaced harmonics that beaming could be observed on the MCP as shown in Fig. 3b. Although the observed beamed harmonics show an elliptical distribution, the observed structure was reproducible exhibiting a FWHM beam divergence of ${\varTheta }_{\mathrm{XUV}}=17\pm 3$ mrad along the minor axis of the elliptical shape. This is in excellent agreement with previous observations under similar conditions [17, 27]. Note that the divergence of the laser beam ${\varTheta }_{\mathrm{L}}\simeq 370$ mrad is an order of magnitude higher, and at the same distance from the source, it would produce a footprint almost four times the size of the MCP detector. The pointing stability of the beamed harmonics was comparable with its divergence. As can be seen from the comparison of the two different records in Fig. 3b, c, the observed elliptical footprint of the harmonics and the associated orientation of the asymmetry are from shot-to-shot fairly reproducible. This points to the conclusion that it should correlate to the spatial properties of the laser pulse. A plausible explanation is the spatiotemporal coupling (STC) of the laser beam [33]. It is to be noted here that the laser focus shown in the inset of Fig. 1 appears quite round and no laser beam aberration is evident. However, as discussed in the report by Pretzler et al. [34], a slight misalignment of standard pulse stretcher and/or compressor setup (not observable with standard diagnostic techniques) can have a measurable effect on the pulse front tilt before it can be detected as an elongation of the focus. The effect is similar to the one described in a recent proposal in which STC and the resulting wavefront rotation can be exploited to generate single attosecond pulses [35].

Fig. 3

MCP single-shot records clearly showing beaming of the harmonic emission for the lowest laser energy. a, b XUV beam footprints for the maximum $E_{\mathrm{L}}=280\,\hbox{mJ}$ and minimum $E_{\mathrm{L}}=80\,\hbox{mJ}$ laser energy used. The corresponding spectra are given in Fig. 2c, a. c MCP image with the XUV diode inserted. d Reproduction of the XUV footprint pattern by 2D interpolation

By inserting the IRD diode in front of the MCP (see Fig. 1), the conversion efficiency was measured under conditions of clean beaming, i.e., when a well-defined XUV beam footprint was observed on the MCP. The size of the diode (10 mm square) was smaller than the footprint of the XUV beam, and its position was carefully controlled with the help of the shadow casted on the MCP image. Each time that the XUV diode signal was recorded, the corresponding footprint of the XUV profile was also seen on the MCP image albeit partially obscured by the diode holder (see Fig. 3c). In order to deduce the fraction of the beam profile seen by the diode and its intensity, the part of the MCP not seen due to the shadow was interpolated as shown in Fig. 3d. The diode measured the total charge due to XUV signal intercepted after it was transmitted through the filter in front of the diode. Based on the charge recorded by the diode and taking into account the transmission of the Al filter, the QE and the fraction intercepted by the diode, and the relative spectral efficiency of the CCD in the spectrometer, a calibration factor for the corresponding spectra at $E_{\mathrm{L}}=80\,\hbox{mJ}$ could be determined [36]. By integrating the absolutely calibrated power spectrum, a total XUV energy of $E_{\mathrm{XUV}}\approx 30~\upmu \hbox {J}$ in the transmission window of the Al filter was deduced. The laser to XUV conversion efficiency is thus calculated as $\eta _{\mathrm{XUV}}=E_{\mathrm{XUV}}/E_{\mathrm{L}}$. Averaging the results of 10 single shot energy/efficiency records, a value of $\eta _{\mathrm{XUV}}\simeq (3.7\pm 1.0)\times 10^{-4}$ for $\lambda =17$–80 nm was obtained. This is comparable or even higher than that of gas harmonics [3–6].

Comparison with simulations

The experimental results are now compared to predictions of the 1D-PIC code LPIC [15] and 2D-PIC code LAPINE [37]. At first, the scaling of the efficiency with the laser pulse energy in the experimentally measured spectral range (17–80 nm) has been studied using the 1D-PIC code (see Fig. 4a). It exhibits a strong dependence on the normalized vector potential of the form $\eta _{\mathrm{XUV}}\propto a_{\mathrm{L}}^{3.5}$. It is important to mention that the exact parameters of the interaction, like scalelength of the pre-plasma, are expected to strongly influence the efficiency of the ROM process. Since the scalelength of the pre-plasma is unknown, 1D-PIC simulations for different scalelengths have been performed for the laser intensity and pulse duration used in the experiments (see Fig. 4b). Interestingly, the dependency on the scalelength predicted by the 1D-PIC simulations does not show a reduction of the efficiency toward longer scalelengths. Furthermore, the experimentally determined efficiencies are about a factor of 5 lower than the ones predicted by the 1D-PIC simulations. The lack of multi-dimensionality in the simulations can explain the discrepancy. The plasma surface in a 1D simulation is intrinsically smooth, and effects of turbulence and instabilities are not included. In Ref. [38], 3D-PIC simulations are reported for two values of the scalelength. The results, in agreement with our measurements, clearly show that in case of long scalelength, turbulence develops, which destroys the directionality of the XUV beam. To access the effect of the geometry of the interaction in our experiment, we have performed 2D-PIC simulations using the code LAPINE [37]. The focal spot is approximated by a Gaussian spatial profile having an intensity FWHM diameter of $3\,\upmu \hbox{m}$. The other parameters used are exactly the same as in the 1D simulations. As seen in Fig. 4b where the integrated energy within the 100 mrad cone is shown, there is a maximum efficiency for an optimum scalelength of $L\simeq 0.2\lambda$. This optimum scalelength value is in very good agreement with the value reported by Dollar et al. [32]. Additionally, the absolute value of the efficiency for this scalelength agrees within the error with the measurement. The angular pattern of the emission as obtained from the 2D-PIC simulations for two scalelengths is shown in Fig. 4c, d. The harmonic intensity in false color is mapped out in the $\widehat{k}_{y}-\widehat{k}_{z}$ plane with $\widehat{k}_{y}^{2}+\widehat{k}_{z}^{2}=\widehat{k}^{2}=q^{2}$ and $q$ the harmonic order. It is seen that for $L/\lambda =0.2$ most of the beam is within the cone of observation whereas for $L/\lambda =1.0$ a large fraction of the emitted harmonic radiation propagates outside this cone. These results explain the difference in the footprint observed for the two cases depicted in Fig. 3a, b and indicate that there is an optimum scalelength for an XUV beam with high directionality and maximum intensity. Also, they clarify the discrepancy in the absolute value and dependence of the efficiency on scalelength between 1D and 2D simulation results (see Fig. 4b).

Fig. 4

PIC simulations for the harmonic conversion efficiency in the 17–80 nm spectral range. a Efficiency versus $a_{\mathrm{L}}$ for a plasma scalelength of $L=\lambda /8$. The dashed line is a fit to the simulation results. b Efficiency versus plasma scalelength for $a_{\mathrm{L}}=1.5$. The squares and triangles are 1D-PIC and the rhombus 2D-PIC simulation results. The triangles represent 1D-PIC results with higher number of particles in the cells while the solid line is to guide the eye. The experimental value is also indicated as a horizontal line and its uncertainty as a shaded balk. c, d 2D-PIC simulation results depicting in relative units and logarithmic scale the intensity of the harmonic emission in the $\widehat{k}_{y}-\widehat{k}_{z}$ plane for two scalelength values. The dotted lines represent the cone subtended by our detector in the specular direction (see Fig. 1)

Discussion and conclusions

In the present experiment, the laser pulse contains approximately ten cycles under its Gaussian envelope. Assuming that the emitted harmonics are phase locked, in the time domain, a train of attosecond pulses would form separated by one laser period. Due to the strong instantaneous nonlinearity of the harmonic generation process, not all cycles would produce attosecond pulses, roughly only half of them [20]. This is conformed with the number of attosecond pulses in the train obtained by inverse Fourier transform assuming constant harmonic phase of the spectrum in Fig. 2d. The same calculation reveals that the experimental spectrum can support attosecond pulses of $\tau _{\mathrm{XUV}} \sim 100$ as duration. Assuming that the measured XUV energy of $30\,\upmu \hbox {J}$ is equally distributed over the five pulses comprising the attosecond pulse train, the average energy of the individual attosecond pulse is $E_{\mathrm{as-pulse}}\simeq 6 \,\upmu \hbox {J}$. The estimated power into a beam with divergence of ${\varTheta }_{\mathrm{XUV}}\approx 17$ mrad is then $P_{\mathrm{as-pulse}}\simeq 60\,\hbox { GW}$, which presumably makes these pulses intense enough for application in pump–probe-experiments. However, this assertion will have to be experimentally verified using techniques for the temporal characterization of attosecond pulses like those described in Ref. [13] or Ref. [39].