A compact solution for ion beam therapy with laser accelerated protons

Abstract

The recent advancements in the field of laser-driven particle acceleration have made Laser-driven Ion Beam Therapy (L-IBT) an attractive alternative to the conventional particle therapy facilities. To bring this emerging technology to clinical application, we introduce the broad energy assorted depth dose deposition model which makes efficient use of the large energy spread and high dose-per-pulse of Laser Accelerated Protons (LAP) and is capable of delivering homogeneous doses to tumors. Furthermore, as a key component of L-IBT solution, we present a compact iso-centric gantry design with 360° rotation capability and an integrated shot-to-shot energy selection system for efficient transport of LAP with large energy spread to the patient. We show that gantry size could be reduced by a factor of 2–3 compared to conventional gantry systems by utilizing pulsed air-core magnets.

Introduction

Radiation therapy plays a major role in cancer treatment by not only providing local tumor control, but also a cost-effective way to improve quality of life of late stage cancer patients. In developed countries, more than 50 % of all cancer patients undergo radiation therapy during the course of their treatment while the total number of patients is increasing every year. Currently, compact medical linear accelerators, producing photon and electron beams with energies up to 20 MeV, are the most common way to deliver radiation doses to tumor volumes. The accelerator and the components for beam delivery and formation are mounted on an iso-centric gantry with 360° rotation angle. This allows a flexible choice of irradiation field direction according to clinical requirements for individual patients, i.e., irradiating the tumor while sparing critical organs in the beam path. However, due to the characteristic depth dose profile of photons and electrons (maximum dose close to the entrance and subsequently decreasing dose with increasing penetration depth) it is difficult to prevent damaging healthy tissues around deep seated tumors. The use of charged particle beams (protons or heavier ions) may provide superior dose conformity in tumor volumes while better sparing normal tissues and organs at risk [1, 2] since they deliver low dose at entrance and maximum dose near the end of their range [3, 4] (see Fig. 1). Currently, radiation therapy, by photons and electrons, provides ∼60 % treatment success. However, it is estimated that at least 10–20 % of all radiotherapy patients may benefit from Ion Beam Therapy (IBT) [5, 6].

Fig. 1

a Single-field-uniform-dose scheme; the depth dose profiles (green) are shown as a function of penetration depth in water, displaying a pristine Bragg peak corresponding to a proton beam with energy spread of ∼1–3 %. A flat-top SOBP (red) is achieved by non-linear superposition of these energy- and intensity-modulated Bragg peaks. The SOBP has an acceptable ±3–5 % dose uniformity within the tumor region bounded by the proximal (near) and distal (far) edges of tumor region, depending upon the beam entrance. More complex depth dose regimes than single-field-uniform-dose are also commonly practiced with beams entering from two or more directions; b shows two SOBPs (dashed blue) matched in the middle of the tumor region, while c shows overlapped SOBPs (dashed blue). The first variant cover larger extent of tumor widths and can also be achieved by matching slanting SOBPs, and the latter variant delivers a higher peak to entrance dose ratio. In con-IBT, a combination of these schemes is used for patient treatment plans with higher order of complexity to optimize tumor conformity and normal tissue sparing

In IBT, large conventional accelerators (cyclotrons or synchrotrons) are deployed to produce particle beams with high energies (e.g., 70–250 MeV protons), which are necessary to deliver doses at clinically relevant depths (of up to 30 cm). These beams are then transported via magnetic transfer lines to several treatment rooms and delivered to patients preferably via a 360° rotatable gantry system. However, at these high energies, particle beams become highly rigid and beam transport by conventional iron-core magnets require big and heavy transfer lines and beam gantries. Existing IBT iso-centric gantries therefore are massive and large (e.g., for protons: above 100 tons, ∼7–11 m diameter and ∼9–12 m in length) and must be supported by enormous and massive architectural complexes and support structures which house and rotate the whole gantry systems around the patient table with high precision. This all adds up to the complexity and cost of IBT facilities [7] with capital investments easily exceeding 100 million Euros. This is the main reason for limiting IBT implementation to few large centers and hindering the wide spread of particle therapy around the world.

In order to reduce the size and cost of IBT systems, several novel technologies are under investigation such as high field superconducting synchrocyclotron systems, which even may be mounted onto a rotating gantry [8], combination of cyclotron and linear accelerators [9], non-scaling fixed-field alternative gradient accelerator concepts [10, 11], dielectric-wall accelerators [12] and laser particle acceleration mechanisms [13–17]. However, recent huge advancements in the field of laser-driven particle acceleration have made Laser-driven Ion Beam Therapy (L-IBT) a very promising and attractive alternative to conventional IBT (con-IBT) facilities [15–18]. By replacing conventional accelerators with table top high power laser systems may considerably reduce the size and cost of IBT facilities. Moreover, laser pulses can be guided to target assemblies inside several treatment rooms by compact optical lines with mirrors making heavy magnetic transfer lines obsolete. Nonetheless, apart from actual accelerator and transfer-lines, the size of the gantry is still a limiting factor and the size and cost reduction of IBT facilities through laser-driven accelerators can only be capitalized on if the size and weight of the associated gantry systems can be reduced.

The properties of laser-driven beams, e.g., ultra-intense particle bunches with large energy spread and divergence, are different from conventional beams. Therefore, new methods and techniques for beam transport, irradiation field formation and treatment planning [19–21], along with beam-monitoring, dosimetry and dose-controlled irradiation [22–26] are required. Moreover, determination of radio-biological effects induced by ultrashort intense particle bunches [26–32] is necessary. In addition to laser particle accelerator development, a parallel oncology-focused research and development is essential to bring this highly promising technology to the clinics.

In this paper we present a depth dose deposition model optimized for L-IBT and an energy-selective compact 360° iso-centric gantry design with efficient capturing of divergent bunches and integrated energy filtering system. The pulsed nature of the laser accelerated ion beam generation has allowed us to utilize air-core high field pulsed magnet systems over iron-core magnets for our gantry design. Pulsed magnets can achieve higher magnetic field strengths at a comparatively smaller size, but a beamline system consisting of pulsed magnets has never been deployed before. Our proposed design for laser-driven beams results in a substantial reduction in size by a factor of 2–3, and hence weight, compared to the most compact con-IBT gantry systems for coasting beams.

Laser particle accelerator

In laser-driven ion acceleration, a highly focused ultra-intense laser pulse (with peak light intensity of 10¹⁹ W cm⁻² or higher) interacts with thin (∼μm) solid density targets. The most commonly used and best understood mechanism to accelerate ion beams by lasers is Target Normal Sheath Acceleration (TNSA) [13, 33]. In this robust acceleration mechanism, first the light field generates a plasma plume in the laser focal region. The electrons in the plasma are accelerated by the laser field, pass through the target and exit it at the rear side. These electrons form a negatively charged sheath that extends up to the Debye length (μm to nm scale depending on laser and target parameters) which generates a quasi-static acceleration field for positively charged ions on the target rear side which is of the order of TV/m. The accelerated ion bunches are pulsed and have an exponential energy spectrum and large energy-dependent divergence angles, with an upper limit for repetition frequency coming from the high power laser systems which extends from 10 Hz for ultrashort pulse durations (<50 fs) to few pulses per minute for long pulse (∼700 fs) laser systems. Although, several ion species can be accelerated through laser-matter interactions, we focus our work on Laser Accelerated Protons (LAP) since protons are much more often used than heavier ions in con-IBT [34]. The maximum proton energies currently published could reach up to ∼70 MeV [35] by a long pulsed laser system of few 100 Terawatt power and are not yet sufficient for most radiation therapy purposes. However, scaling models show higher energies are reachable with increased laser power [36–38] and/or new target geometries [39]. Also, several laser particle acceleration mechanisms are under investigation which could be more efficient yet experimentally much more demanding than TNSA, such as laser-piston regime [40], radiation pressure acceleration [41, 42] and breakout afterburner regime [43, 44], which could provide higher-energy ion beams with potentially better beam quality (i.e., lower-energy spread with better collimation). Nevertheless, with the development of next generation Petawatt (1,000 Terawatt) laser systems, protons with much higher energies are expected to be reached in the near future. However, in this paper we have used a scaled TNSA spectrum for input parameters as worst case scenario to design the beamline.

Laser-driven ion beam therapy will be different from con-IBT in several ways [45]. For instance, due to the pulsed nature of high power laser systems, with low repetition rates of a few laser pulses per second, the accelerated proton bunches are also pulsed with bunch durations of nsec range and with up to ∼10¹² protons per bunch depending upon laser parameters [28, 46]. Such intense bunches can attain pulsed peak dose rate values up to 10¹⁰ Gy/s which exceeds con-IBT mean values of 15–30 Gy/s through quasi-continuous beam by many orders of magnitude. Therefore, L-IBT poses a whole new set of challenges on both physical and biological levels. Laser-driven irradiation technology with all the necessary main components (such as high power laser system and laser target to produce the particle beam, and also beam transport and monitoring as well as dose delivery technique) has already been developed to perform in-vitro cell [26–32] and small animal [24, 26] irradiation with low energy LAP within radiobiological experiments. These recent promising results encourage a go-ahead with further L-IBT solutions.

Laser-driven versus conventional IBT dose delivery

In most sophisticated con-IBT, pencil-like monoenergetic beams with energy spread of $\Updelta E/E$ ∼1–3 % with decreasing energy and intensity are superimposed to deliver uniform doses to the tumor region via a spread out Bragg peak (SOBP) (Fig. 1) [4, 47]. Nevertheless, a clinically relevant SOBP of certain width and at certain depth requires a broad energy window to scan the complete depth of the tumor. The inherent laser acceleration process suggests LAP beams with therapeutic energies would be far from monoenergetic, but with high bunch intensities (particle number) and large divergences. As a consequence, the broad energy spectrum may already contain the required energy windows for SOBPs with sufficient amounts of protons to deliver enough dose for treatment purposes over a short time, i.e., by reasonable low number of bunches. However, capturing divergent protons and efficient energy selection system is necessary for any L-IBT solution.

Uniform doses in clinical settings with LAP bunches can be delivered either by filtering out quasi-monoenergetic ($\Updelta E/E$ ∼5–10 %) protons from a predicted therapeutic broad LAP spectrum and superimpose multiple filtered bunches akin to con-IBT [19, 48] or to achieve a SOBP by a single filtered broad energy bunch in combination with shaping the energy spectrum by physical wedges [49]. Such proposed schemes were based on a compact beamline with a primary collimator in front of a magnetic chicane filter [19, 48]. Due to the very small opening angle (0.6°) of the primary collimator, used to limit diverging LAP bunches, such beamline uses a mere of ∼0.02 % of all protons in a bunch for dose delivery [50], while depositing huge numbers of protons in beam dumps and producing a high level of secondary (background) radiations. Such collimator-based beamlines are highly inefficient [51] reducing the per bunch dose. The advanced treatment planning technique optimized for LAP beams proposed by Schell [20] and Hofmann [21] could be a good way to go, but the presented method of dose delivery is, however, based on the before mentioned collimator-based beamline.

For L-IBT to be competitive with con-IBT, any successful scheme must make efficient use of the high number of protons available in each LAP bunch, as repetition rates of high power lasers are limited to few pulses per second. The demand on short treatment times of below 10 min thus requires the clinically relevant total dose to be delivered by not more than a few thousand bunches. Spatial and energy-dependent filtering must therefore be optimized for throughput to keep proton numbers high. As this up to now requires to capture and transport strongly divergent pulsed proton bunches of broad energy spread, both the method to deposit a homogeneous dose distribution in the tumor volume and the gantry design have to reflect these constraints.

Scaling of existing data

Currently, there is no experimental data available for LAP in the full therapeutic energy range which could be used as realistic input parameters for our depth dose deposition model and beamline design. However, for this study, we have exploited and scaled available data from the Dresden laser acceleration source (DRACO), which is a 10 Hz 150 TW ultrashort (∼30 fs) pulsed laser system [52]. We have averaged proton energy spectra of five bunches (shown in Fig. 2a as green line) and then scaled it to the energy range required for therapy, using a similar approach presented in ref. [46]. An exponential fit to the averaged data is made, which can be described by:

$${\text d}N/{\text d}E =N_0 {\text e}^{-E/E_0}$$

(1)

Fig. 2

a Shows an averaged energy spectrum is shown as green-line (top energy axis) measured at the DRACO laser system with an exponential fit shown as dashed yellow-line (top energy axis). The scaled function predicts a proton spectrum over therapeutic range and is shown as dashed red-line (bottom energy axis), while the blue-line shows the spectrum (bottom energy axis) of a proton bunch generated through Monte Carlo code. b Shows the energy-dependent half-angle divergence observed in experiments (shown as solid cyan-line), extrapolated to therapeutic energies (shown as dashed cyan-line) and with an added constant of 2° for the safety margin (shown as blue-line)

where N ₀ = 2 × 10¹¹ MeV⁻¹ and E ₀ = 2.33 MeV (shown in Fig. 2a as yellow dashed line). For scaling this spectrum to therapeutic energy range both proton energies E observed in experiments and the characteristic slope parameter are increased by a factor of 250/14 = 17.86 while conserving the total number of protons available for acceleration. Thus after scaling N ₀ drops to 1 × 10¹⁰ MeV⁻¹ with E ₀ = 46.73 MeV, yielding a scaled function for higher energies, shown in Fig. 2a as red dashed line.

Laser-driven proton sources exhibit energy-dependent large divergences, which decreases with increasing proton energies within a bunch. For realistic scaling, this angular dependence of LAP spectra has to be accounted for. The half-angle divergences observed in experiments can be defined by a power fit as:

$$\theta(E)= a E^{k}$$

(2)

with a = 19.48 and k =  −0.15. We have extrapolated Eq. 2 to 250 MeV, showed as dashed cyan line in Fig. 2b. To provide a safety margin on beamline parameters, we have added a constant of 2° to this fit to compensate any fluctuations or deviation that might occur in future experiments, which is a very conservative approach as divergences of LAP beams are expected to decrease for higher energies. The scaled angular energy dependence can now be defined by Eq. 2 with a = 20.98 and k =  −0.13, which is shown in Fig. 2b as blue line. These scaled functions, in Fig. 2a, b, were then used to generate LAP bunches for simulation inputs by a Monte Carlo code.

Fig. 3

a Shows TNSA like scaled exponential function for energy spectrum of laser accelerated protons. The top horizontal axis displays the range in water for protons with corresponding energies given on the bottom axis. The tumor position is marked by a red bar, while the “useful energy window” corresponding to the tumor range is hatched in blue. b Shows a comparison between depth dose profiles of two LAP shots with (1) a broad energy band of $\Updelta E/E_0\approx 22$ % corresponding to the “useful energy window" in (a), and (2) a narrow energy band of $\Updelta E/E_0\approx 1.3$ % similar to single Bragg peaks used in con-IBT

Broad energy assorted depth dose deposition model

In our dose model, SOBPs are realized by the superposition of depth dose profiles of individual LAP bunches with varied energy bandwidths. In the following, this technique is referred to as Broad Energy Assorted depth Dose deposition (BEAD). As one laser pulse is required on the target to generate one LAP bunch, we call it as one shot. In order to understand BEAD, let us consider a tumor to be irradiated (see Fig. 3). The energy windows selected to create a SOBP within the tumor region must lie within the energy range set by the minimum energy E _min corresponding to the depth of the proximal edge of the tumor and the maximum energy E _max corresponding to the depth of the distal edge. The energy window thus defined by $\Updelta E=E_{\rm max}- E_{\rm min}$, with centered nominal energy of E _n  = (E _max + E _min)/2, can be referred as “useful energy window” within the initial spectrum. If this $\Updelta E/E_n$ band could be filtered out, its depth dose profile is neither a flat-top SOBP nor a pristine Bragg peak, but displays a peak and bounded plateau situated within the tumor region (see Fig. 3b). In the following, we conservatively assume that a single shot does not deliver the clinically relevant dose of 2 Gy to the tumor, and for the purpose, multiple shots could be superimposed.

Figure 4 is a schematic representation of a single-field-uniform-dose regime with our BEAD model by superimposing several individually filtered LAP shots. The first LAP shot (shot1) was filtered with $\Updelta E_{\rm shot1}/E_{n(\rm shot1)}=21.4\,\%$, required to produce a baseline dose profile covering the entire tumor depth. The second LAP shot (shot2) was delivered with a narrowed energy window, $\Updelta E_{\rm shot2}$, as compared to shot1 while increasing nominal energy as $E_{n(\rm shot2)}\rightarrow E_{\rm max}$ to fill the shallow dose region toward the distal edge. This implies E _min for the next consecutive shots to be greater than the previous shot, such as E _min(shot1) < E _min(shot2) < E _min(shot3)⋯ < E _{min(shot-last)}. The shot2 with $\Updelta E_{\rm shot2}/E_{n\rm (shot2)}=18.5\,\%$ was superimposed on shot1. Due to the exponentially decreasing energy spectrum, shots with $E_n\rightarrow E_{max}$ and smaller $\Updelta E$ windows contain lesser number of protons thus multiple deposition of shots would be needed to flatten the cumulative dose profile. For this reason, shot3 with $\Updelta E_{\rm shot3}/E_{n\rm (shot3)}=8.60\,\%$ and shot4 with $\Updelta E_{\rm shot4}/E_{n\rm (shot4)}=6.0\,\%$ were deposited twice. The last shot (shot5) was deposited eight times, because of relatively smaller $\Updelta E_{\rm shot5}/E_{n\rm (shot5)}$ of 3.60 % containing lesser particles, to achieve a flat-top SOBP.

Fig. 4

Shows the flat-top SOBP (red) as it evolves due to superimposing energy-filtered individual LAP shots (blue), see text for the detailed description

The flatness (or dose homogeneity) of the resultant SOBP could be enhanced by decreasing the difference in the energy windows between two consecutive shots $\Updelta E_{n21}=E_{n\rm (shot2)}-E_{n\rm (shot1)}$, while the total number of shots, N _LAP required would also increase, which would directly translate into longer treatment times. Thus, for a specific treatment plan, there is a trade-off between required flatness and treatment time. In our example, N _LAP = 14 were needed for a normalized SOBP within an acceptable uniformity of ±4 %, using five different $\Updelta E/E_n$ settings. We found $\Updelta E/E_n=22-3\,\%$ bands were sufficient to produce a normalized SOBP of ∼5 cm width at depths of 5–25 cm. The N _LAP required to scan the complete depth of the tumor for a prescribed dose depends on three sets of factors:

• 1. LAP bunch properties, such as characteristic slope of the spectrum, divergence angles and total number of protons per energy range.

• 2. Tumor aspects, such as width, depth and required uniformity in delivered dose.

• 3. Beamline (gantry) parameters, such as energy acceptance, capture and transport efficiencies per energy range.

The first set could be considered predetermined due to the features of laser particle accelerators, while the second set could be considered fixed due to the clinical requirements. While we have focused on the third set and aimed to design a compact beamline (gantry) capable of capturing, filtering and transporting desired $\Updelta E/E_n$ ranging from 22 to 3 % bands at any required E _n , with maximum possible transport efficiency η(E _n ).

Gantry design

The magnetic rigidity (Bρ), described as Bρ = momentum/charge, states that higher magnetic field strength B is required for higher-energy protons to follow a compact bending radius ρ which in turn determines the size of any gantry in question. The maximum magnetic field strength B _max achievable by conventional resistive magnets is limited by saturation of the magnetization of the iron-core to a value of B _max ∼1.9 T. However, pulsed magnets are air-core designs powered by pulsed energy supplied by capacitor banks (for more see ref.[53]). By eliminating the core saturation issue, B _max achievable with pulsed magnets is mainly limited by the peak current provided by the power supply and by the mechanical strength of the construction materials needed to hold intense magnetic pressures. A 90° bending conventional iron-core magnet limits ρ to ∼1.13 m for 200 MeV protons, but if pulsed magnets could be constructed with field strengths of B _max ∼8 T, it could be possible to reduce ρ down to ∼0.27 m.

The pulsed nature of laser systems and hence the pulsed LAP bunches allowed us to consider pulsed magnets for our gantry design. Due to the higher magnetic fields achievable by pulsed magnets, we were able to reduce the size of our gantry to 1.7 m in radius and ∼3.0 m in length which is about two times smaller in height and about three times shorter in length than compact conventional iso-centric gantries being deployed in con-IBT facilities. Also, due to the missing iron-core, pulsed magnets are much lighter in weight than conventional magnets.

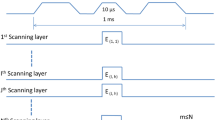
The magnetic fields in pulsed magnets usually have a rise time in the range of few 100 μs with pulse durations of the order of ms, thus fields can be considered constant during ns LAP bunches traversing through them. Pulsed solenoids have already been successfully deployed to capture and collimate LAP bunches in experiments [46, 54]. These studies demonstrate a good control over the magnetic-field-pulsing mechanism synchronized with laser pulses. With currently achievable proton energies, such experiments required only low magnetic field values; however, realizing higher field strengths is possible through present day technologies.

Our concept L-IBT solution is comprised of a laser source outside the treatment room, capable to channel laser pulses into several rooms. A laser-target assembly is considered to be mounted inside a 360° rotatable iso-centric gantry. Laser pulses enter the gantry along the axis through the iso-center and are deflected into the laser-target chamber, where laser interacts with target to generate accelerated proton bunches perpendicular to the patient table (see Fig. 5 for the complete setup). All magnets considered are air-core designs powered by a system capable to pulse each magnet at 10 Hz synchronized with the laser pulses, which would provide a full control over the magnetic field strengths in individual magnets of the beamline for each LAP bunch traversing through them

Fig. 5

Schematic representation of 360° iso-centric gantry concept for particle therapy with LAP, including a radiation protection cave housed around the patient table. A Monte Carlo generated LAP bunch with energy spectrum shown in Fig. 2a was tracked through our double-achromatic beamline design, as shown by the color spread inside the picture and described by the colored energy scale. The beamline elements are drawn on the tracks to illustrate their positions, with working parameters listed at the bottom. A water phantom underneath the exit window represents the setup used for the depth dose simulations in Geant4

A pulsed power solenoid, with aperture radius of 2.75 cm is used to couple laser-target assembly and beamline. The solenoid acts as an axially symmetric chromatic focusing lens and efficiently captures divergent protons to make a well-defined beam (for details see [46, 51, 54–56]). Its field strength can be selectable (0 < B _o < 40 T) for each bunch so that protons with one optimized energy E _opt are collimated, while protons with E ≫ E _opt experience a much lower force inside the solenoid and continue to diverge while protons with E ≪ E _opt experience a much greater force and diverge after focusing strongly, which also provide a coarse first-step energy selection. The beam is collimated around E _opt so that to match it to the following dipole bending magnet.

A fine energy filtering system has been devised and incorporated in our gantry design. This Integrated Shot-to-shot Energy Selection System (ISESS) is based on a 90° bending sector magnet SM1 and a quadrupole triplet QT1 with two physical apertures. Energy dispersion in SM1 allows energy selection as a function of magnetic field B _SM1. The beam diameter at this point is large due to the aperture size of the solenoid which was necessary for maximum capture efficiency; therefore, fine energy selection is not possible with SM1 only. For fine-tuned selection, a pulsed quadrupole triplet (QT1) follows SM1 which acts as a strong chromatic focusing lens. The magnetic gradients are tuned to focus protons with E _opt at 15 cm after QT1. Aperture A2 with fine variable opening radius R _A2 is placed to effectively filter protons around E _opt with the bandwidth $\Updelta E/E_{\rm opt}$, where the bandwidth directly depends on R _A2. A second quadrupole triplet (QT2) after A2 recaptures the filtered bunch, and the second 90° bending sector magnet (SM2) bends the beam toward the patient table. This magnetic arrangement allows for canceling the dispersion introduced earlier for energy selection in the SM1 to zero, hence achieving a doubly achromatic transport beam line. A third quadrupole triplet QT3, followed by conventional physical collimators, is introduced after SM2 which in principle could be used to re-shape the filtered bunch to desired field sizes of 1–6 cm in diameter at iso-center. The patient table is considered to be enclosed by a radiation protection cave. The patient table can be moved precisely to scan the beam across the tumor volume to apply multiple laterally adjacent fields to homogenize dose over larger volumes.

Particle transport through the gantry design

The scaled spectrum and angular dependence functions (Fig. 2, explained in Sect. 4) have been used to generate LAP bunches for the particle tracking simulations via a Monte Carlo code. These Monte Carlo LAP bunches were then transported through the gantry setup in general particle tracer (GPT) version 3.0 code [57]. Two sets of simulations have been performed. In the first set, the capability of the ISESS to filter $\Updelta E/E_{\rm opt}$ bandwidths is investigated as the radius R _A2 of aperture A2 was varied from 12 to 1 mm. The magnetic field values in each of the magnets were optimized for a single E _opt. Figure 6a shows the simulation results with E _opt set to 148 MeV by fixing optimized magnetic field values in each magnetic element. ISESS was able to filter a bell-shaped spectrum out of the input bunch spectrum with a peak at the selected E _opt, while the bunch was transported through the beamline from laser-target chamber to the patient table with high efficiency. The filtered bandwidth $\Updelta E/E_{\rm opt}$ decreased from 25 % at R _A2 = 12.0 mm to 4.1 % at R _A2 = 2.0 mm with almost constant transport efficiency of η(E _opt) ≈ 22 %. However, below R _A2 = 2.0 mm η(E _opt) dropped quickly, due to chromatic aberrations, to 5 % for $\Updelta E/E_{\rm opt}=1.4\,\%$ at R _A2 = 1.0 mm. Nevertheless, a satisfactory control over $\Updelta E/E_{\rm opt}$ as function of R _A2 was established over the desired bandwidth range of 3–22 %.

Fig. 6

A Monte Carlo generated LAP bunch with scaled energy spectrum (blue) was transported through the gantry in GPT simulations. a Shows results with ISESS set to deliver E _opt = 148 MeV with five R _A2 settings were used for five consecutive LAP bunches. The filtered $\Updelta E/E_{\rm opt}$ width at the exit window for each R _apt setting is shown, while b shows the filtered spectrum through ISESS at fixed R _A2 = 3.0 mm while E _opt values are varied through selecting optimized magnetic field strengths for each magnetic element of the beamline

The second set of simulations was performed to establish a control to select desired value of E _opt [MeV] at the exit window. Normally, 1–1.5 mm range steps are used in con-IBT to scan the complete depth of the tumor which would require ∼0.5 MeV controllable energy steps. This translates to a requirement of a controllable step change in magnetic field values in each magnet with an accuracy of 10⁻² T, which is achievable with present day technology and thus assumed as incremental change in E _opt. One Monte Carlo generated LAP bunch was transported for fixed R _A2 aperture size with B fields optimized for E _{opt_1}, while for a second consecutive LAP bunch, B field strengths were reduced such that now protons with E _{opt_2} (<E _{opt_1}) would be transported. Figure 6b shows the results of five simulations with R _A2 = 3.0 mm for transporting LAP bunches with E _opt optimized for five different values, shown in the figure.

These two sets of simulation results established the control over the whole spectrum for selecting any desired energy window per pulse, thus showing the capability and functionality of the presented compact gantry design to implement the BEAD scheme.

BEAD through the gantry design

Depth dose profiles of individually filtered LAP bunches and superimposed dose distributions from multiple filtered shots were simulated in a 10 × 10 × 30 cm³ water phantom using the Geant4 simulation code [58]. Particle positions and velocities at the exit window of the gantry from GPT simulations were taken as input to the Geant4 simulations. We were able to reproduce the SOBP shown in the BEAD (single-field-uniform-dose) example in Fig. 4. The SOBP was achieved by superimposing multiple LAP shots with five different optimized beamline settings of $\Updelta E/E_{\rm opt}$ for E _opt = E _n as given in the initial example. The simulated depth dose profiles in the water phantom are shown in Fig. 7a. It took N _LAP = 19 shots to reach a normalized SOBP, within uniformity of ±3 %. This is more than the expected 14 shots as discussed in Sect. 5, and this slight increase in shot number is due to the change in spectral shape of filtered shots.

Fig. 7

a Shows LAP shot depth dose profiles (blue) filtered through ISESS with five different settings. A total of N _LAP = 19 shots were required to be superimposed to reach SOBP (red) of 5.4 cm width, within uniformity of ±3 %. b Shows an opposing irradiation scheme using the BEAD regime. The depth dose profile (blue), resulted from dose profiles of individual filtered LAP shots (dashed blue), overlapped inside the tumor region from opposing directions to achieve a flat-top SOBP (red). Only 3 filtered LAP shots per field were required to deliver uniform dose by SOBP of ∼8 cm width

To deliver a clinically relevant uniform dose of 2 Gy, to a water equivalent tumor volume of 1 l, the normalized scheme mentioned above is needed to be implemented multiple times. For this, we have roughly estimated that ∼600 laser-shots would be required, provided a laser-driven proton source with a pulse-to-pulse dose fluctuation of <±5 %. At 10 Hz repetition rate this would translate in a treatment time of about 1 min.

Figure 7b shows individual filtered LAP shots superimposed in the middle of the phantom to achieve uniform SOBP in an opposing irradiation scheme. The number of filtered shots required per field depends on the tumor width and depth, and it was found that only 1–2 filtered shots per field would be sufficient to achieve normalized flat-top SOBPs of up to 4 cm of width and 3–8 filtered shots per field for wider SOBPs of 4–10 cm. An opposing irradiation scheme in combination with the single-field-uniform-dose scheme could be utilized for better conformity with multiple entry positions with higher order of treatment plan complexity.

Discussion

We have developed a depth dose deposition model for broad energy LAP bunches and a compact gantry design, based on pulsed magnets as a L-IBT solution. In addition we have shown the control scheme for filtering these bunches and delivering uniform SOBP at the patient site via the gantry design. One common critique of L-IBT is the lack of dose control compared to standard accelerators. Recently, an unprecedented relative dose uncertainty of below 10 % has been achieved during cell-irradiation experiments with laser-driven protons [26], which was previously reported as 28 % [28], which demonstrates the potential of high intensity lasers to control shot-to-shot fluctuations. Our gantry concept allows fixing the energy window of filtered bunches through ISESS; thus, shot-to-shot fluctuations may only influence the flux delivered while the spectral width for each bunch could be kept almost constant. If we consider a fairly large error of ±30 % per shot, following reference [51], this would then increase the treatment time by a factor of three, which is still below the acceptable limit of 10 min, which may relax 10 Hz constraint on laser systems. Also, for shot-to-shot fluctuations and to get enough particles, one has to avoid operating at the maximum proton cutoff energy of the exponential spectrum of the laser accelerator. Instead, it would be desirable to have the maximum proton cutoff energy at ∼300 MeV. Online dose control per bunch is essential to monitor the shot-to-shot dose fluctuations and has been successfully used in experiments with LAP [23, 25, 26, 28].

Laser-driven IBT requires additional space for monitoring and control equipment, as does a con-IBT facility. Therefore, the suggested dimensions of our gantry, with a height of 1.7 m and a length of ∼3.0 m (Fig. 5), may increase by 35–50 %, nevertheless, is still a considerable reduction in size compared to conventional gantries. In addition, the pulsed power sources itself can considerably contribute to the overall size of the system as to the energy budget. Here, a setup allowing for recovery of field energy by resonant circuits would help to keep this contribution to a minimum. With the overall size and weight reduction of a pulsed gantry design compared to conventional gantry designs, all these contributions would be greatly outweighed by the considerable amount of infrastructural investment that might be saved.

The large energy-dependent divergence with wide energy spectrum, typically observed in TNSA regime, has provided a worst case scenario for designing the energy selection system and the transport beamline. If in future, another acceleration mechanism (as mentioned in Sect. 2) could be established with improved beam parameters, such as lower divergence angles and reduced energy spread, this would lower the constraints on the beamline, such as lower acceptance values for beamline elements, increase transport efficiency and decrease particle waste. Thus, such features would only compliment the proposed beamline making our gantry concept compatible with any future advancement in laser particle acceleration.

As laser-driven proton beams are produced in quasi-neutral plasma bunches of protons, ions and electrons, beam filtering with radiation protection must be integrated into any L-IBT system. In our design, we have considered these issues. Initial particle selection happens in the solenoid that collects the LAP bunches, which is thus oriented perpendicular to the iso-line as seen in Fig. 5 away from the patient. The dispersive bending magnets, SM1 and SM2, are accompanied by the beam dumps D1 and D2, respectively. Both beam dumps are necessary in order to shield the secondary radiation produced via interactions of out-filtered particles. Again, our design foresees that any unwanted radiation does not directly face toward the patient table. As an extra protection, any secondary radiation from these beam dumps would be blocked by the radiation protection cave walls around the patient area. The amount of secondary radiation would depend on the input proton spectrum along with co-moving electrons from future laser acceleration experiments. The radiation protection and the design of particle dumps for laser accelerated beams are not trivial; however, according to ref. [50] a 6 to 7 cm thick multilayer shielding material should be enough to prevent leakage doses. For a detailed study of radiation protection, we refer to future publications, as it may influence the detailed geometry and size of a final gantry design.

Conclusion and outlook

In this paper, we have presented a solution for IBT with LAP bunches based on a novel concept for dose deposition with broad energy bands—BEAD and a compact pulsed power gantry system with integrated energy selection—ISESS. The main advantage of our L-IBT solution compared to previous approaches is that it combines high collection efficiency and high transport efficiency with greatly relaxed demands on the energy spread of the LAP bunch. In fact, the L-IBT scheme presented here utilizes the broad energy spread commonly observed in laser-driven proton acceleration as it deposits dose in SOBPs by superimposing the dose of proton bunches with variable energy windows. Therefore, our proposed solution works well with standard laser-driven TNSA which is well understood and can be controlled to a high level but is also compatible with new laser acceleration mechanisms, such as radiation pressure acceleration etc., which could potentially deliver proton bunches with smaller energy spread and better collimation.

While our BEAD scheme shows that L-IBT can be competitive to con-IBT in terms of treatment time, the use of pulsed magnets for the treatment greatly reduces the size and weight of the gantry and in turn all related infrastructure. Although our demands on maximum magnetic field strength are moderate, the realization of a fully pulsed gantry system at a continuous 10 Hz pulse rate is a challenge, both in terms of magnet design and in design of the pulsed power system. However, the great reduction in overall cost expected from a compact gantry design makes the effort of developing it a worthwhile endeavor.