Abstract
In this paper, the first experimental demonstration of the optical correlation spectroscopy lidar (OCS-lidar) is proposed. It is a new active remote sensing methodology to measure range-resolved atmospheric gas concentrations, based on broadband laser spectroscopy and light amplitude modulation. As a first step, a numerical study is performed for OCS-lidar measurements to optimize the accuracy of the range-resolved gas concentration measurement. Then, we demonstrate the ability of the OCS-lidar methodology to monitor the water vapor in the planetary boundary layer using the 4ν 720-nm absorption band. In addition to this first experimental proof, two different experimental configurations are proposed. The amplitude modulation, related to the optical correlation spectroscopy, is operated either at the emission with an active amplitude modulator before the backscattering process, or with passive optical filters on the laser backscattered light. For both configurations, range-resolved gas concentration measurements, achieved with a micro-pulse ground-based OCS-lidar, are presented. An extended discussion presents the mixing-ratio accuracy, which reaches ±1,000 ppm at a 2,000-m range for a range resolution of 200 m. The differences between the two experimental configurations are also discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Natural and anthropogenic atmospheric gases, such as CO2, CH4, VOCs and water vapor, are nowadays well recognized to play an important role in the Earth’s radiative budget and in air pollution [1]. Hence, monitoring techniques have been developed by applying laser spectroscopy to precisely assess their concentration as a function of time and space. In this context, laser-based remote sensing measurements, such as lidar measurements, have been used in numerous situations, in which differential absorption spectroscopy measurements were carried out to retrieve atmospheric gas concentrations. Integrated [2, 3] or range-resolved trace gas concentrations have hence been assessed over a wide variety of ranges, within the planetary boundary layer (PBL) [4] up to global planetary measurements [5–8]. Gas mass flux measurements have been also achieved when combined with wind field measurements [9]. In addition, leak localization [10] and safety measurements for hazardous gas have been performed and are now commonly used [11, 12].
Meanwhile, advances in optics and laser technology have been made, allowing measurements with higher sensitivity and accuracy. Among these recent advances, we may mention novel research achievements on remote sensing of greenhouse gases, by using a broadband laser source instead of a narrowband laser. Examples of these new advances are the broadband differential absorption lidar [13–19] and the optical correlation spectroscopy lidar (OCS-lidar) methodology, introduced by B. Thomas et al. [20]. The OCS-lidar methodology is a new differential absorption spectroscopy method based on pioneer work performed on gas correlation lidar [21]. The OCS-lidar has been extensively described in theoretical papers [20, 22] for methane remote sensing. In these papers, it is shown that OCS-lidar differs from the standard differential absorption lidar (DIAL) and also from the wavelength modulation spectroscopy (WMS) [23].
In this contribution, we present the first experimental OCS-lidar achievement and its application to water vapor remote sensing in the PBL, which is new. Another novelty of this work is the presentation of two experimental configurations, depending on whether the optical correlation spectroscopy is achieved with passive or active optical components.
Water vapor concentration measurements using lidar have become a standard, especially for free troposphere soundings [24–28]. In this paper, the OCS-lidar measurement is performed on water vapor in the PBL as an experimental proof of this methodology, rather than achieving another study on a possible new water vapor lidar instrument. As well known, the water vapor content exhibits low fluctuations in the PBL within several hours, which eases the measurement interpretation. The experimental results show that the water vapor concentration can be successfully monitored in the PBL, by using a ground-based micro-pulse OCS-lidar system in the 4ν 720-nm water vapor absorption band. This spectral range [29] has been chosen because it corresponds to an absorption spectral band, available to the laser emission and also to the light detector spectral range. Moreover, around 720 nm, in the PBL, other atmospheric gases will not significantly absorb the laser light, so that the influence of possible interfering species will be fully negligible.
The paper is organized as follows. In Sect. 2, the principle of the OCS-lidar methodology is detailed and the possibility of achieving two OCS-lidar experimental configurations is hence highlighted. Then, an OCS-lidar numerical simulation is for the first time performed for water vapor concentration measurements. In Sect. 3, the corresponding experimental setups are presented for each experimental configuration, by detailing their own characteristics. The first OCS-lidar experimental proofs are then presented in Sect. 4 for both experimental configurations, and differences between these two configurations are also discussed. The paper ends with a conclusion and outlooks.
2 OCS-lidar methodology and numerical model
In this section, we first briefly recall the OCS-lidar principle to fix our notations while presenting the corresponding formalism to be used in the next sections. Then, a numerical simulation is performed for OCS-lidar water vapor concentration retrievals. This approach is used to properly set some of the OCS-lidar experimental parameters, such as the broadband laser central wavelength and the amplitude modulation functions. Therefore, it helps optimizing the accuracy on the retrieved water vapor concentration.
2.1 The OCS-lidar principle
The OCS-lidar methodology consists in retrieving range-resolved trace gas concentrations from the difference in optical absorption experienced by two lidar signals. More precisely, at a wavelength λ, the power spectral density P 0(λ) of a broadband laser pulse is spectrally shaped to correlate with the trace gas absorption cross section, giving rise to the correlated OCS-signal (subscript C), while a second broadband laser pulse is spectrally shaped to be non-correlated (subscript NC). This spectral shaping of a broadband laser pulse is achieved by amplitude modulation functions, hereafter noted M C(λ) and M NC(λ) for the correlated and the non-correlated functions, respectively. The presence of the atmospheric gas presence is then retrieved using the two OCS-lidar signals. At a range r from the lidar receiver station, the measured optical power P i (r) is given by the OCS-lidar equation, based on the well-known lidar equation [30, 31]
where the subscript i refers to either correlated (C) or non-correlated (NC). The atmospheric backscatter coefficient β(r, λ) is range and wavelength dependent while T(r, λ) corresponds to the atmospheric transmission. As in conventional lidar systems, K(r) represents the geometrical overlap function, which depends on the receiver and laser specifications, as well as on the range r. Finally, η(λ) represents the detector quantum efficiency which is wavelength dependent. In Eq. (1), an integral is performed over an effective wavelength spectral range Δλ, defined from the effective width of the amplitude modulation function; therefore, the OCS-lidar methodology does not require a spectrally resolved detector. From the two OCS-lidar signals P C and P NC, a calculus detailed in B. Thomas et al. [20] is then performed to retrieve absolute range-resolved atmospheric gas concentrations, with statistical and systematical error assessment. It is important to note that this OCS-lidar methodology does not require a permanent gas calibration as in regular optical correlation spectroscopy [32]. Moreover, the multiplication being a commutative operator, it can be seen from Eq. (1) that the amplitude modulations M C(λ) or M NC(λ) can be applied either before or after the backscattering process occurring in the atmosphere. It follows that two experimental OCS-lidar configurations can be achieved:
-
OCS-lidar in AME-configuration (for amplitude modulation at the emission), in which the broadband laser pulse is shaped before its emission in the atmosphere.
-
OCS-lidar in AMR-configuration (for amplitude modulation at the reception), where amplitude modulation functions Mi(λ) are applied after the atmospheric backscattering process.
These two experimental OCS-lidar configurations are detailed in Sect. 3 and in Figs. 5 and 7.
2.2 Simulation of OCS-lidar measurement
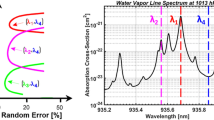
As a preliminary stage for the Sect. 3 experiment, we here perform a numerical simulation using the OCS-lidar methodology for water vapor concentration retrievals to optimize the precision on the retrieved concentration. We use the numerical model developed in B. Thomas et al. [20] to generate OCS-lidar signals. This numerical model has four main inputs: the water vapor absorption cross-section spectrum plotted in Fig. 1, calculated by using a temperature- and pressure-dependent Voigt spectral line profile based on the HITRAN database [33], the two amplitude modulation functions M C(λ) and M NC(λ), also presented in Fig. 1, and the laser power density P 0(λ). We hence generated the two OCS-lidar signals P C and P NC corresponding to the given range-resolved water vapor mixing-ratio to be seen in Fig. 3c (green squares), using lidar parameters under standard urban atmospheric conditions [34] and including the random detector noise in our numerical simulation. It should be noted that the numerical model is the same for the AME- and the AMR-configuration, since both configurations follow the same formalism detailed in Sect. 2.1. However, some input parameters may be different, since, as to be seen in Sect. 4, the experimental equipments differ from one configuration to another.
Amplitude modulation function M C(λ) (red dash line) and M NC(λ) (blue line) together with the water vapor absorption cross-section spectrum derived from the HITRAN database [32]
Calculated normalized weighted water vapor transmission T H2O as a function of the central wavelength λ M of the amplitude modulation function M(λ M , λ) and for a 4,000-m optical pathway. As M(λ M , λ) is shifted toward higher wavelengths, T H2O(λ M ) reaches a minimum because of higher values of the H2O absorption cross section in the 720-nm spectral region
The generated OCS-lidar signals, to be seen in Fig. 3a, are then used as inputs for our concentration retrieval algorithm. The concentration retrieval algorithm is based on a Taylor expansion of the transmission T(r, λ) leading to a third-order polynomial equation, whose solution allows to retrieve the water vapor mixing-ratio at a range r from the lidar receiver. It avoids using the ratio of P C(r) to P NC(r) signals, as usually performed in differential absorption spectroscopy [20].
To improve the precision on the retrieved water vapor concentration, the laser power density P 0(λ) and the amplitude modulation functions M C(λ) and M NC(λ) have to be properly adjusted.
The central wavelength λ 0 of P 0(λ) as well as the M C(λ) and M NC(λ) functions are set to maximize the difference in optical transmission due to the presence of water vapor between the two OCS-lidar signals. In order to do so, we use the normalized weighted transmission T H2O(r, λ M ), defined in Eq. (2), where λ M is the central wavelength of a Gaussian amplitude modulation function M(λ M , λ):
As an example of this optimization procedure, Fig. 2 shows T H2O(r, λ M ) resulting on a 4,000-m optical pathway for a water vapor mixing-ratio of 8,000 ppm as a function of λ M . Since T H2O(λ M ) depends on the water vapor absorption cross section, over a Δλ spectral width, the minimum value of T H2O(λ M ) defines the optimized M C(λ). Similarly, the local maximum defines the optimized M NC(λ). Using similar procedures, we optimized the spectral width of M C(λ) and M NC(λ) functions, as well as the central wavelength λ 0 of the laser power density, to increase the accuracy on the retrieved water vapor mixing-ratio.
As expected, in Fig. 3b, the ratio of both OCS-lidar signals shows that the correlated signal undergoes a higher extinction than the non-correlated one. Based on the previous M C and M NC optimization procedure, additional numerical simulations are performed to evaluate the expected range-dependent precision on the retrieved water vapor concentration profile. For an input water vapor mixing-ratio of 6,000 ppmv (50 % relative humidity at 10 °C, green squares), our OCS-lidar numerical simulation shows that the difference in extinction between the two OCS-lidar signals P C(r) and P NC(r) reaches 10 % at a 4,000-m lidar optical pathway (i.e., at a 2,000 m range). The model input mixing-ratio and the retrieved water vapor mixing-ratio are shown in Fig. 3c. The retrieved water vapor mixing-ratio undergoes statistical fluctuations due to the detector noise. The plotted error bars represent the standard deviation, which increases with range r. As a conclusion of this section, within the OCS-lidar methodology, our numerical results show that, for water vapor mixing-ratio retrievals, the sensitivity reaches 200,000 ppm.m at a 2,000-m range, corresponding to a detection limit of 1,000 ppm with a 200-m spatial resolution when using micro-energy-pulses.
3 OCS-lidar experimental setup
In this section, the first OCS-lidar experimental setup is presented as well as its specifications. In particular, we detail our chosen broadband laser source and the experimental setup for both AME- and AMR-experimental configurations.
3.1 The laser source
The spectral stability of the laser source is essential since the OCS-lidar methodology is based on optical correlation; otherwise, the retrieved gas concentration may undergo a higher statistical error. In our experiment, the emitted laser pulse is generated by an optical parametric amplifier pumped by a Ti-Sa laser having a 100-femtosecond pulse duration and a 10−4 radian beam divergence at the exit of a 3× beam expander. Each fs-laser pulse emits 63 μJ with a 1 kHz repetition rate. The pulse-to-pulse laser intensity fluctuations and possible spectral drifts from the laser source have been measured for three hours, as presented in Fig. 4. The laser power density spectrum has a central wavelength λ 0 set to (714.0 ± 0.2) nm and a (15 ± 1) nm FWHM spectral width. Our numerical simulation shows that such low laser spectral fluctuations are required and induce a 5 % statistical error on the retrieved water vapor mixing-ratio (up to 2,000 ppm); this error becomes fully negligible at higher water vapor mixing-ratios.
Upper graph: laser power density spectrum P 0(λ) (a) Five measurements are presented with a 1-h delay between each measurement; each spectrum is an average over 1,500 laser pulses. Bottom graph: laser power as a function of time showing the laser intensity fluctuations for 3 h, for a 1-s integration time, with a (63 ± 1) mW mean laser power (b)
3.2 Amplitude modulation and detection scheme in the AME-configuration
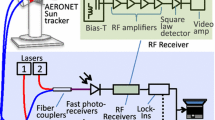
As shown in Fig. 3 where the setup for the AME-configuration is presented, each laser pulse is spectrally shaped by an amplitude modulator, alternatively generating the amplitude modulation functions M C(λ) and M NC(λ). The backscattered photons are collected with a 30-cm-diameter f/4 Newtonian telescope, then focused on a light detector D (Hamamatsu photomultiplier tube R7400-U20). OCS-lidar signals P C(r) and P NC(r) are alternatively measured since each pulse propagating into the atmosphere is specifically designed to be correlated or non-correlated with the atmospheric gas absorption cross section. The two OCS-lidar signals are hence measured with a single detector D. The OCS-lidar signals are then sampled by a Transient Recorder (Licel, 12 bits, 40 MHz sample rate) in an alternate mode allowing to record the P C(r) and P NC(r) signals on two different memories.
The amplitude modulation functions M C(λ) and M NC(λ) are alternatively generated by an acousto-optical programmable dispersive filter (AOPDF) [35], which provides versatile amplitude modulations functions having a 1-nm spectral resolution and controllable with a computer interface. Moreover, both M C(λ) and M NC(λ) functions have been optimized following the procedure depicted in Sect. 2.2. Figure 6 shows the power density spectrum once it has been modulated, as formally described by the \(P_{0} (\lambda ) \times M_{C} (\lambda )\) and \(P_{0} (\lambda ) \times M_{NC} (\lambda )\) functions. To avoid nonlinear effects in the AOPDF crystal, the maximum input energy is limited to 30 μJ.
3.3 Amplitude modulation and detection scheme in the AMR-configuration
In the AMR-configuration, the optical correlation is achieved at the lidar receptor, as shown in Fig. 7 where the experimental setup in the AMR-configuration is presented. The AMR-configuration is closed to a low-spectral-resolution differential absorption spectroscopy scheme which uses a broadband laser source instead of a spectrally extended light source (white light continuum, spectroscopic lamp, natural light source) or a narrow band laser. Amplitude modulation at the reception has also been performed by Edner et al. [21] and Minato et al. [19]. However, in these cases, the modulation is performed thanks to a gas cell containing the target gas instead of optical filters as in our case. Moreover, in the OCS-lidar concentration retrieval methodology, the low optical extinction approximation is not applied. In the AMR-experimental configuration, the broadband laser pulse with power density spectrum P 0(λ) does not undergo any spectral modification before being sent into the atmosphere. The amplitude modulation is there operated once the photons are backscattered by the atmosphere. The backscattered light is collimated and then separated with a 50-50 beam splitter (Thorlabs BSW11) in two optical pathways (detection channels). On each detection channel, optical interference filters (Thorlabs FB71010 and FB72010) are used to achieve the optical correlation, the transmissions of these optical filters acting as the M C(λ) and M NC(λ) amplitude modulation functions. The interference filter bandwidths and their transmission have been chosen by using the numerical simulation results presented in Sect. 2, and the transmission of these interference filters are presented in Fig. 1. In the AMR-configuration, the OCS-lidar signals P C(r) and P NC(r) are measured thanks to two Hamamatsu photomultiplier tubes R7400-U20 (D C and D NC) placed on each detection channel. The resulting OCS-lidar signals are sampled with two transient recorders (Licel, 12 bit, 20 and 40 MHz sample rate).
Unlike the AME-configuration, where the amplitude modulation is performed at the emission, the laser pulse energy can here be higher and each laser pulse contributes to both P C(r) and P NC(r) OCS-lidar signals with only half intensity, since a 50/50 beam splitter is used. As the backscattered light splits into two different detection channels, any difference between the light collection efficiency over the range of both channels, written as K(r) in Eq. (1), would lead to a bias in the retrieved concentration as well. Hence, the difference between the two overlap functions has to be significantly lower than the difference of water vapor optical absorption undergone by the two OCS-lidar signals (see Fig. 2). Such alignment of both channels has been checked and is presented in Sect. 4.
Moreover, the optical efficiency η(λ) introduced in Eq. (1) between the two channels may differ and cause systematic error on the retrieved concentration if considered as identical for the two detection channels. In order to avoid this difficulty, each optical component of each channel has been accurately specified. The transmission coefficient of the beam splitter at 45° has hence been measured with a UV–VIS–NIR spectrograph with less than 0.1 % error. The transmission coefficient exhibits a 5 % variation between 700 and 740 nm. Secondly, the quantum efficiencies of both detectors have been measured as a function of the wavelength: Within our spectral range Δλ, the two quantum efficiencies differ one to another up to 10 %.
4 Experimental results on OCS-lidar
In this section, the first experimental OCS-lidar signals are proposed in the AME and AMR OCS-lidar configurations. This being a case study to realize an experimental proof of the OCS-lidar methodology, we focus on the measurement of atmospheric water vapor concentrations in the troposphere. These first measurements have been performed during nighttime, at ground level in the Lyon PBL. Range-resolved water vapor mixing-ratio measurements are presented and discussed in both configurations. The detection limit is also studied.
4.1 Water vapor mixing-ratio measurements in the AME-configuration
Before the OCS-lidar measurement itself, a bias control experiment is first performed to ensure that the two OCS-lidar signals probe the same atmospheric volume and do not undergo any range-dependent bias. For that purpose, we first apply the same amplitude modulation on the broadband laser pulse, that is, M C(λ) = M NC(λ). Under such circumstances, using Eq. (1), it is clear that at a range r, P C(r) should be equal to P NC(r). Figure 8a shows the resulting range-corrected OCS-lidar signals, and the ratio of these two signals is displayed in Fig. 8b with error bars, induced by the statistical fluctuations of the OCS-lidar signals.
Control bias experiment in the AME-configuration, performed at Lyon on December 19, 2012, at 19 h UTC. a Range-corrected OCS-lidar signals P A (blue) and P B (red) sampled on the two channels A and B of the transient recorders with a 40-m range resolution. b Ratio of both OCS-lidar signals with respective error bars, derived from the statistical fluctuations of the OCS-lidar signals for a ground-level relative humidity and temperature of 85 % and 280 K, respectively
Then, the amplitude modulations functions derived in Sect. 3.2 have been applied to the broadband laser pulse to achieve the optical correlation. OCS-lidar signals P C(r) and P NC(r), presented in Fig. 9a, have been acquired with a 1-kHz repetition rate over a time average of 5 min. The ratio P C/P NC, presented in Fig. 9b, decreases with r as expected in a differential absorption measurement technique. Such a behavior reveals the water vapor content of the atmosphere, with a range-dependent water vapor mixing-ratio to be seen in Fig. 9c. Error bars on the retrieved water vapor mixing-ratios are evaluated thanks to a Monte Carlo simulation on the OCS-lidar numerical simulation based on the signal-to-noise ratio of experimental OCS-lidar signals. The mixing-ratio detection limit is evaluated from this error bar taken at 2σ. This approach leads to a range-dependent sensitivity equal to 3 × 105 ppm.m at a 2-km range. The water vapor profile starts at (9,250 ± 70) ppm at a range of 260 m, then strongly decreases down to (2,000 ± 500) ppm at a 1,200 m range, and finally slightly varies up to (4,000 ± 1,200) ppm. At a 2-km range, the mixing-ratio is (3,500 ± 1,400) ppm.
OCS-lidar water vapor measurement in the AME-configuration performed at Lyon on December 19 at 19 h UTC. a Range-corrected OCS-lidar signals, due to the water vapor presence P C(r) exhibits a higher extinction when compared to P NC(r). b The ratio P C/P NC is no longer constant with r, as it was in the control experiment. c Retrieved water vapor mixing-ratio profile obtained using the retrieval algorithm. The relative humidity observed with a standard hydrometer at ground level was equal to 85 % and the temperature was 280 K, corresponding to a water vapor mixing-ratio of 8,400 ppm at ground level
4.2 Water vapor mixing-ratio measurements in the AMR-configuration
Performing the bias control experiment corresponding to M C(λ) = M NC(λ) is much more complex in the AMR-configuration since in this configuration, the detector is composed of two optical channels, as detailed in Sect. 3. To ensure that the correlated and the non-correlated channels are properly set, lidar measurements have been carried out without any interferential filters, that is, M C(λ) = M NC(λ) = 1. The corresponding range-corrected signals and their ratio are displayed in Fig. 10, which is equivalent to Fig. 8, but for the AMR-configuration.
Control bias experiment in the AMR-configuration, performed at Lyon on November 6 at 22 h UTC. a Range-corrected OCS-lidar signals P A (blue) and P B (red) are obtained with two detection channels (A and B) with a 40-m range resolution. b Ratio of both OCS-lidar signals with respective error bars, derived from the statistical fluctuations of the OCS-lidar signals for a ground-level relative humidity of 76 % and a 283 K temperature
Then, the amplitude modulations functions derived in Sect. 3.3 have been applied to the broadband laser pulse to achieve the AMR-configuration, using the same measurement duration, location and pointing as those described for the AME-configuration. The amplitude modulations functions M C(λ) and M NC(λ) used in this experiment are identical to those displayed in Fig. 1. The corresponding OCS-lidar signals, the range-dependent P C/P NC ratio and the retrieved water vapor mixing-ratio profile are presented in Fig. 11. As expected, the correlated signal P C(r) undergoes a higher extinction than the non-correlated signal P NC(r), and, consequently, the ratio P C(r)/P NC(r) decreases with range r. Errors bars retrieved from the Monte Carlo numerical simulation lead to a sensitivity of 2 × 105 ppm.m at a 2-km range. The retrieved water vapor mixing-ratio profile starts at (7,850 ± 55) ppm at a 260-m range and drops around (4,000 ± 300) ppm from 500 to 1,000 m. It then reaches a minimum of (1,250 ± 650) ppm at a 1,400-m range before increasing after 1,600 m up to (7,500 ± 1,000) ppm.
OCS-lidar water vapor measurement in the AMR-configuration performed at Lyon on November 5 at 22 h UTC. a Range-corrected OCS-lidar signals; due to the water vapor presence, P C(r) exhibits a higher extinction when compared to P NC(r). b The ratio P C/P NC is no longer constant with r, as it was in the control experiment. c Retrieved water vapor mixing-ratio profile obtained using the retrieval algorithm. Ground-level relative humidity and temperature are respectively equal to 76 % and 283 K, corresponding to a water vapor mixing-ratio of 9,200 ppm at ground level
4.3 Discussion
In both configurations, sources of statistical signal fluctuations are due to shot noise, detection noise and background noise. These sources of noise limit the measurement range to a maximum of 2 km. The signal-to-noise ratio depending on the range is, however, two times higher in the AMR than in the AME-configuration due to the AOPDF acceptance energy, limited to 30 micro-joules. Above this threshold, the laser energy would generate white light in the paratellurite crystal TeO2 of the AOPDF, which reduces significantly the effective transmission of the crystal, as well as decreasing the amplitude modulation quality. Moreover, at such energies, the Kerr effect [36] may induce a change in the refractive index of the AOPDF crystal, which could cause an unwanted increase in the laser beam divergence before the propagation of the laser pulse in the atmosphere. These two effects (white light generation and Kerr effect) increase with higher input laser power, and in our case, for a 3-mm-diameter beam section, we measured a threshold of 1 GW under which these effects are fully negligible.
The preliminary bias control experiment, operated by applying the same amplitude modulation functions, ensures that systematic errors are negligible when compared with the statistical fluctuations of the OCS-lidar signals. In both configurations, this control experiment also ensures that the signal acquisition process and trigger system are not a source of bias. For the specific case of the AMR-configuration, this control experiment also helps to check that the two detection channels experience the same geometrical overlap function.
The two different experimental configurations AMR and AME achieve water vapor measurement in the PBL with the OCS-lidar methodology. The OCS-lidar signals taken on two different days lead to water vapor mixing-ratio that are in the same range. Our measurements show water vapor mixing-ratios varying from 9,250 ppm (RH = 93 %) at a 250-m range (corresponding to a 35-m altitude), down to 1,250 ppm (RH = 10 %) at a range of 1,500 m (corresponding to a 210-m altitude). The water vapor mixing-ratio increases at a 1,800-m range, which most likely corresponds to the water evaporation process above the 100-m-wide Rhône river.
These first experimental results show that the retrieved water vapor mixing-ratio profiles are comparable and in both cases correspond to realistic relative humidity profiles described by standard atmosphere. Moreover, near ground level, comparison between in situ hydrometer at ground level and OCS-lidar measurements at the lower altitude (≈30 m) shows similar concentrations values within 15 %. It shows that the OCS-lidar methodology is able to monitor water vapor mixing-ratios in the PBL. When comparing the main advantages/drawbacks of each configuration, it clear that the AMR-configuration has a higher signal-to-noise ratio due to the use of a higher laser energy. However, it should be noted that this configuration raises a much more complex detection setup and the corresponding sources of supplementary biases have to be checked. An accurate knowledge of the spectral response of each optical component and a very accurate alignment of the two detection channels are hence required. In addition, the backscattered photons, once they have been collected by the telescope and parallelized by using a lens, still exhibit a non-negligible divergence of around 5 × 10−2 radian, which may slightly broaden interferential filter transmissions toward shorter wavelengths. Except for field measurements in which high temperature variations are involved, the modification of the spectral behavior of the interferential filter due to temperature gradients should be negligible since the spectral drift due to temperature gradients is only equal to 0.025 nm per °C. In the AME-configuration, the sources of bias on the retrieved mixing-ratio are from that point of view minimized, since the emission and the reception are performed with the same equipments for both the correlated and the non-correlated signals. Despite the fact that the AOPDF limits the laser energy, it offers a great versatility: Any amplitude modulation, including multiple transmission peaks or gaps, can be faithfully shaped within the spectral resolution of the AOPDF, equal to 1 nm in the visible spectral range (1.8 nm in the infrared spectral region).
5 Conclusion and outlooks
In this paper, for the first time, we experimentally demonstrate the ability of OCS-lidar methodology to measure the water vapor content in the lower atmosphere. This is the first experimental achievement of the femtosecond broadband OCS-lidar methodology with a ground-based micro-pulse lidar. This paper is hence in the logical follow-up of the theoretical and numerical study published by B. Thomas et al. [20], who first explored the potentiality of combining two well-known spectral techniques, namely optical correlation spectroscopy (OCS) and lidar.
It has been shown that for experimentally achieving the OCS-lidar methodology, two experimental configurations are possible, namely the AME-configuration, where the amplitude modulations functions are applied before the backscattering process occurs (i.e., at the emission, AME stands for amplitude modulation at the emission), and the AMR-configuration, where the modulation achieving the optical correlation spectroscopy is performed at the reception (AMR stands for amplitude modulation at the reception). These two configurations have been presented and tested for water vapor mixing-ratio measurements. In the AME-configuration, we used an active AOPDF to achieve the amplitude modulation before the laser pulse be sent into the atmosphere, while, in the AMR-experimental configuration, passive interferential filters have been introduced in the lidar detector to achieve the spectral correlation. These first OCS-lidar measurements exhibit water vapor mixing-ratios varying from 1 000 to 10 000 ppm. The accuracy on the retrieved water vapor mixing-ratios varies with the range r from the lidar receiver and with the water vapor content. In the AME-configuration, it reaches 40 % at a 2-km range for a 3,500 ppm water vapor mixing-ratio. In the AMR-configuration, this accuracy reaches 15 % at a 2-km range for a 7,500 ppm water vapor mixing-ratio. Such accuracies, performed with a 250-m range resolution, can be reached because measurements are performed in the planetary boundary layer where a high content of molecules and particle matter favors absorption and scattering processes. In the higher part of the atmosphere, where a lower water vapor content and a lower particle matter mixing-ratio are present, the OCS-lidar methodology could be applied but in the near-infrared spectral range, the water vapor absorption band should be considered to balance the lower water vapor mixing-ratio.
In order to reduce the statistical error on the retrieved mixing-ratio, the laser energy should be increased. This limitation due to the AOPDF is related to nonlinear effects which occur in response to a very high intensity; therefore, the energy threshold can be raised, on the one hand, by increasing the pulse duration with a pulse stretcher leading to a lower instantaneous power and, in the other hand, by increasing the section of the laser beam to lower the intensity. More complex amplitude modulations can be operated with the AOPDF; for example, by combining more than two different amplitude modulation functions, multiple gases could be simultaneously monitored as long as they present sufficiently high absorption bands within the spectral width of the broadband laser source. In addition, this versatility would enable to greatly decrease the bias due to the possible presence of interfering gases, by adapting the amplitude modulation functions to reduce their extinctions.
In regard to these numerous possible outlooks, we believe that the OCS-lidar methodology offers great possibilities for atmospheric trace gases remote sensing. However, as it is brand new, many developments and improvements in terms of sensitivity and accuracy still have to be performed.
References
IPCC (2007) ed. by S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis, K.B. Averyt, M. Tignor, H.L. Miller. Cambridge University Press, Cambridge United Kingdom (2007)
H. Riris, K. Numata, S. Li, S. Wu, A. Ramanathan, M. Dawsey, J. Mao, R. Kawa, J.B. Abshire, Appl. Opt. 51, 8296 (2012)
G. Ehret, C. Kiemle, M. Wirth, M.A. Amediek, A. Fix, S. Houweling, Appl. Phys. B 90, 593 (2008)
P. Gaudio, M. Gelfusa and M. Richetta, Proceedings of SPIE 8534 (2012)
M. Guo, X. Wang, J. Li, K. Yi, G. Zhong, H. Tani, Sensors 12, 16368 (2012)
A.J. Cogan, H. Boesch, R. J. Parker, L. Feng, P. I. Palmer, J.-F. L. Blavier, N. M. Deutscher, R. Macatangay, J. Notholt, C. Roehl, T. Warneke, D. Wunch, J Geol. Res. Atm. 117 (2012)
C. Kiemle, M. Quatrevalet, G. Ehret, A. Amediek, A. Fix, M. Wirth, Atmos. Meas. Tech. 4, 2195 (2011)
S. Ismail, G. Koch, N. Abedin, T. Refaat, M. Rubio, U. Singh, IEEE Aerosp. Conf. Proc. 1–9, 1527 (2008)
A.K. Chambers, M. Strosher, T. Wooton, J. Moncrieff, P. McCready, J. Air Waste Manage. Assoc. 58, 1047 (2008)
A. Fix, G. Ehret, A. Hoffstadt, H. Klingenberg, C. Lemmerz, P. Mahnke, M. Ulbricht, M. Wirth, R. Wittig, W. Zirnig, ILRC 2004(561), 45 (2004)
B. Gu, Z. Fang, Opt. Elec. Mat. Appl. II 529, 487 (2012)
J. Wang, Manuf. Sci. Technol. 383, 2907 (2012)
S. Penchey, V. Pencheva, S. Naboko, Compte Rendus de l’Academie Bulgare des Sciences 56, 669 (2012)
G.M. Krekov, M.M. Krekova, A.Y. Sukhanov, Atmo. Ocea. Opt. 22, 346 (2009)
E. M. Georgieva, W. S. Heaps and W. Huang, Proceedings of SPIE, 8182 (2011)
X.T. Lou, C.T. Xu, S. Svanberg, G. Somesfalean, Appl. Phys. B 109, 453 (2012)
X.T. Lou, G. Somesfalean, S. Svanberg, Y.G. Zhang, S.H. Wu, Opt. Exp. 20, 4927 (2012)
X.T. Lou, G. Somesfalean, B. Chen, Y.G. Zhang, H.S. Wang, Z.G. Zhang, S.H. Wu, Y.K. Qin, Opt. Lett. 35, 1749 (2010)
A. Minato, M.A. Joarder, S. Ozawa, M. Kadoya, N. Sugimoto, Jap. J. Appl. Phys. 38, 6130 (1999)
B. Thomas, A. Miffre, G. David, J.P. Cariou, P. Rairoux, Appl. Phys. B 108, 689 (2012)
H. Edner, S. Svanberg, L. Unéus, W. Wendt, Opt. Lett. 9, 493 (1984)
B. Thomas, G. David, C. Anselmo, E. Coillet, A. Miffre, J-P. Cariou and P. Rairoux. J Mol. Spec., Submitted (2013)
S. Schilt, L. Thevenaz, P. Robert, Appl. Opt. 42, 6728 (2003)
V. Wulfmeyer, H. Bauer, P. Di Girolamo, C. Serio, Rem. Sens. Env. 95, 211 (2005)
B. Hennemuth, A. Weiss, J. Bosenberg, D. Jacob, H. Linne, G. Peters, S. Pfeifer, Atmos. Chem. Phys. 8, 287 (2008)
S. Ismail, R.A. Ferrare, E.V. Browell, S.A. Kooi, J.P. Dunion, G. Heymsfield, A. Notari, C.F. Butler, S. Burton, M. Fenn, T.N. Krishnamurti, M.K. Biswas, G. Chen, B. Anderson, J. Atmos. Sci. 67, 1026 (2010)
D.N. Whiteman, D. Venable, E. Landulfo, Appl. Opt. 50, 2170 (2011)
A.R. Nehrir, K.S. Repasky, J.L. Carlsten, Opt. Exp. 20, 25137 (2012)
R. Shermaul, J. Mol. Spectrosc. 208, 32 (2001)
C. Weitkamp, (Springer, Berlin, New-York 2005)
R. M. Measures: laser remote sensing, fundamentals and applications (Krieger Ed. 1992)
J.P. Dakin, M.J. Gunning, P. Chambers, Z.J. Xin, Detection of gases by correlation spectroscopy. Sens. Actuators, B 90, 124–131 (2003)
L.S. Rothman, J. Quant. Spectrosc. Radiat. Transf. 60, 665 (1998)
J.H. Seinfeld, S.N. Pandis, J (Wiley, New York, 1998)
D. Kaplan, P. Tournois, J. Phys. IV France 12, 69 (2002)
M. Melnichuk, L. T. Wood, Phys. Rev. A 82 (2010)
Acknowledgments
The authors would like to thank Leosphere and Région Rhône-Alpes for research grants and EZUS for comprehensive administration of the project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Thomas, B., David, G., Anselmo, C. et al. Remote sensing of atmospheric gases with optical correlation spectroscopy and lidar: first experimental results on water vapor profile measurements. Appl. Phys. B 113, 265–275 (2013). https://doi.org/10.1007/s00340-013-5468-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00340-013-5468-4