On numerical integration with high-order quadratures: with application to the Rayleigh–Sommerfeld integral

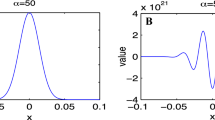
Abstract

The paper focusses on the advantages of using high-order Gauss–Legendre quadratures for the precise evaluation of integrals with both smooth and rapidly changing integrands. Aspects of their precision are analysed in the light of Gauss’ error formula. Some “test examples” are considered and evaluated in multiple precision to $\approx$200 significant decimal digits with David Bailey’s multiprecision package to eliminate truncation/rounding errors. The increase of precision on doubling the number of subintervals is analysed, the relevant quadrature attribute being the precision increment. In order to exemplify the advantages that high-order quadrature afford, the technique is then used to evaluate several plots of the Rayleigh–Sommerfeld diffraction integral for axi-symmetric source fields defined on a planar aperture. A comparison of the high-order quadrature method against various FFT-based methods is finally given.

Appendix: High-order quadrature program

The FORTRAN program used to evaluate the integrals is listed below. The high-order Gauss–Legendre weights and abscissae are read from data-statements in the cquad subroutine or, as here, read from a file in the main program and put in the wtsabs common block that is shared with cquad.

Note that it basically evaluates the integral, $\int_{x\rm {min}}^{x\rm{max}} \hbox{fun}(x)\,\hbox{d}x$, over M equal subintervals using weights and abscissae that are “read-in” from a file by the calling program and made available to the cquad subroutine via the common block, wtsabs.¹

To evaluate the R–S integral, which is 2-dimensional, the integrand function, $fun1(\user2{r}_{\mathbf{0}},r,\theta )$, in general, depends on $\theta$ and must be integrated numerically over this polar angle (and including any $\theta$-dependence in $u(r,\theta$)). This gives a result, $fun(\user2{r}_0,r)$, which is then integrated over the radial distance, $0\le r\le \infty$ and so cover the whole aperture plane as shown schematically in (36).

$${\rm i.e.}\; u({\user2{r}_{\mathbf{0}}}) = \int\limits_0^a\,{\rm d}r{\underbrace{\int\limits_0^{2\pi }\!\!{\rm d}\theta \;{fun1}({\user2{r}}_{\mathbf{0}},r, \theta )}}_{{fun}({\user2{r}}_{\mathbf{0}},r)}$$

(36)

Here the programmer is alerted to the fact that, if the same quadrature is used for both the $\theta$- and $r$-integrations, then it is recursively called. Most modern compilers will recognise this and take appropriate action, but there are some compilers that do not—and accordingly produce “non-sensical” output as all of both quadrature evaluations were done in the same quadrature ‘memory space’. In such cases the solution is to compile two cquad quadrature subroutines, differing only in their calling names, and to call them appropriately in the calling program(s). This forces the compilation of a distinct subroutine for each quadrature.