1 Introduction

Early diagnosis of breast cancer is essential in reducing women's death risks. If the cancer is diagnosed early, it can be treated more effectively. Malignancy can now be diagnosed using a variety of approaches, including laboratory testing that uses body fluids to assess the amounts of specific hormones or substances that indicate malignancy. An alternate way is to examine tumors by tissue sample under a microscope and runs tests on it before reporting the diagnosis [1]. Other testing methods involve imaging tests like mammography, Positron Emission Tomography (PET), and ultrasound, which are common modalities for cancer detection. Mammography is an imaging procedure for diagnosing breast illness that uses a low dosage of X-rays, whereas ultrasonography uses high-pitched sound frequencies. Despite this, those approaches have a 10% false-negative screening testing rate [2]. At the same time, X-rays may not be permitted to diagnose pregnant women, because it may harm their bodies [3]. Alternative studies on screening technologies are Magnetic Resonance Imaging (MRI), which utilizes an electromagnetic field and a powerful magnetic field to detect the tumor. Gadolinium is a chemical tracer that improves the image quality developed by MRI. However, compared to mammogram testing for cancer, the MRI technique has a higher probability of false convictions and does not differentiate between cancerous cells [4]. The current detection methods are on tissue biopsies, which are inspected under a microscope by a pathologist to look for malignant cells. However, the diagnosis will take 1 or 2 weeks.

The structural difference between malignant and benign cancerous cells is the ratio of fibrous tissue to fat deposits and the number of interstitial liquids that helps to define the electrical properties of cell conductivity and permittivity [5]. The dielectric properties of cancerous cells are greater than those of normal cells. The increase in dielectric property is due to the higher water content in the breast layers. Subsequently, there will be more scattering of microwaves [6]. The dielectric measurement is carried out using a cancer cell line, which is equivalent to cancer cells. This measurement will be helpful for testing and diagnosing directly on the human body itself. The dielectric constant and conductance properties of every cancer cell line are unique. As a result, the electrical properties of different types of cells can be used to classify them. Some approaches, like microwave detection and characterization, rely on the material's conducting characteristics. The reflection coefficient is used in one technique, whereas the resonance frequency is used in the other. The reflection coefficient can be determined using the coaxial probe method by measuring at the waveguide's open end [7]. The resonating frequency approach is a different way to distinguish between different cells; changes in resonant frequencies are used to determine performance as a function of material qualities. Furthermore, the excitation frequency method is better than the coefficient of reflection method [8].

Nowadays, the scope is toward metamaterial antennas in sensing technologies. Metamaterial is an artificial material framed by changing the electromagnetic properties of natural materials [9]. Split Ring Resonator (SRR) metamaterial-based patch antenna is used for wireless communications. The different layers of SRR are suitable for improving an antenna's bandwidth [10]. When the metamaterial-based sensor comes into contact with the test material, there are changes in the electromagnetic field. The field variations produce resonant frequencies and variations in the intensity of the response signal [11]. The metamaterial detects melanoma using two liquid rods and a square indium antimony film [12].

The skin reflectance spectra are evaluated as part of the identification process. This is done by placing the metamaterial by casting a horizontal light on the skin in the 1–1.5 THz range. Then, the resonance frequency is determined. Generally, the sensor will resonate at a particular frequency of 1.398 THz. In the involvement of aberrant cells, a change in the resonant frequencies was identified. A noticeable change has taken place in aberrant cells [12]. A metamaterial with multi-microfluidic conduits is used to detect fluids in low amounts.

A bow-tie structure is the metamaterial's basic unit cell. The sensor works by injecting the sample into microfluidic channels and measuring the transmission coefficient's significance [13]. Likewise, a complimentary electric LC resonator is to develop a microfluidic detector for monitoring solution’s dielectric constant. They placed the detector through its paces on ethanol–water combinations of different water levels. For each specimen, the transmission coefficient, frequency response, and maximal absorption are calculated and recorded to calculate the dielectric constant. Additionally, for any faults that may arise due to the solution's in-homogeneity, the number of cells per unit of volume must be stable throughout all times, which is impossible to do [14].

The SRR microwave detectors are often resonant at a frequency of higher rates, resulting in noise, which can be minimized by expanding the SRR element's size. The Defected Ground Structure (DGS) is a typical approach for reducing circuit size, lowering circuit resonance frequency, and making the circuit fabricate easily. DGS structure carved from the metallic ground of a microwave-printed circuit board (PCB). DGS is incorporated into a microstrip, and the current dispersion on the ground changes, causing the capacitance and inductance to vary [15]. DGS was used as a filter to manage antenna oscillations and remove surface wave disturbance [16]. Furthermore, DGS can be employed in the position of sensor design.

The detector can also be used with liquids by placing tubes on top of DGS and infusing liquids with a syringe [17]. The primary objective of this study is to create a less expensive and quicker approach for identifying and differentiating various cancer cell lines depending on their electrical characteristics (such as conductance and dielectric constant). MCF7, MDA-MB-231, and HS578T are the three cancer cell lines are studied. The electrical characteristics of cancerous cell lines are employed in the simulated design to ensure that it is functional and accurate [18].

2 Procedures and materials

The fractal antenna has a fractal structure with a mixture of capacitors and inductors. For different frequency resonance, this fractal structure can be modified to attain the result. Fractal antennas are used for the compact design, since it has a new boundary structure, the path length will be increased, which guides the reduction of frequency. It gives better results such as bandwidth, miniaturization, gain, and complicated structure [40, 41].

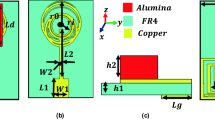
The proposed metamaterial sensor antenna consists of a single Split Ring Resonator (SRR) on the top region of the substrate and a third iterated Minkowski curve is acted as Defected Ground Structure (DGS) in the ground region. The SRR is a pair of enclosed loops with gaps at opposite ends. The metal ring includes one or even more small gaps. Various shapes of SRR structure rings are shown in Fig. 1 [18]. A magnetic field creates a current flowing through a transmitting ring when it passes through it. The gaps between the rings generate higher capacitive values that the capacitive reactance equals inductive reactance in magnitude, and the resonance occurs. Because the space works as a capacitance area, SRR is an ideal candidate for a sensor [35]. Accordingly, any substance placed in the gap will produce a frequency shift. Because every substance will have its own dielectric constant and conductivity, the change in frequency can assist in determining the type of material [19]. The proposed design's compactness, comparably low price, and ease of manufacturing make the SRRs widely utilized as sensors.

Fig. 1
figure 1

Split Ring Resonator design

Full size image

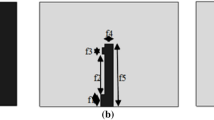
In contrast to dipole antennas, the metamaterial fractal antenna’s tendency is to resonate at a low-frequency range. Fractal patterns could be as tiny as 0.1 λ, but a diameter of about 0.5 λ is about to have in dipole [20]. The construction of the Minkowski fractal is done by dividing the single line segment into eight parts, as shown in Fig. 2. To bend the curve from first order to second order, the construction is lowered to half of its initial value size and duplicated in two pairs. The second iteration is divided into eight parts to form a third iteration. This process is repeated to form further iterations [22]. The Minkowski curve is utilized as DGS to lower the frequency response; it will enhance the detection sensitivity and raise the capacitance between the bottom and the tracker. By lowering the frequency, losses and noises can be reduced [23,24,25,26].

Fig. 2
figure 2

Iterations of Minkowski fractal curves

Full size image

A microstrip feed line is coupled with the SRR to form the sensor feed. The testing sample must be positioned between the transmission network and the SRR gap. Beginning with the first order of the Minkowski curve and progressing up to the third order, obtained results were investigated throughout the designing stage. High orders are avoided, since they lower the curve size and make it difficult to produce due to the restricted resolution of PCB etching machines. The first thing is to focus on the Minkowski fractal orders that will produce the strongest magnetic and electrical fields all around sampling site, and then, they will enhance the capacitance and hence increase the sensor's sensitivity. The orders of the first–third iteration with their E-field and H-field results are shown in Fig. 3.

Fig. 3
figure 3

E-field and H-field results for the third iteration

Full size image

2.1 Layout and construction of SRR

The proposed design of the metamaterial sensor works at a frequency of 15.42 GHz, which may be reduced to resonate at a lower frequency. Given that the frequency is inversely proportional to the size, the resonating frequency resulted in a high range of frequencies [23, 25]. The SRR's frequency response can be calculated using an LC circuit

$$f=1/(2\pi \sqrt{L}C),$$
(1)

where C and L are the capacitance and inductance of the resonator. The inductance of the resonator can be obtained using the equation

$$L={\mu }_{0}{R}_{m}\left(ln\left(\frac{8{R}_{m}}{h+w}\right)-0.5\right),$$
(2)

where μ0 is the free space permeability, w is the width of the SRR model, ℎ is the height of the SRR, and Rm is the mean radius of the SRR ring. The mean radius Rm is calculated using the following formula:

$${R}_{m}=R+\frac{w}{2},$$
(3)

where R is the SRR ring’s radius. The split ring's total capacitance, C, was created by combining the surface and gap capacitance in a parallel way, as expressed below

$$C={C}_{gap}+{C}_{surf},$$
(4)

where Cgap is the capacitance of the gap and Csurface is the capacitance of the SRR ring surface. These two parameters can be formulated using the formula given below

$${C}_{gap}={\varepsilon }_{0}\left|\frac{wh}{g}+\frac{2\pi h}{ln\left(\frac{2.4h}{w}\right)}\right|$$
(5)
$${C}_{surf}=\frac{2h\varepsilon }{\pi }ln\left(\frac{4R}{g}\right).$$
(6)

From Eqs. (5) and (6), g is the length of the gap, ε is the free space's permittivity and the substrate material's permittivity. The permittivity ε of substrate material is demonstrated as given below

$$\varepsilon ={\varepsilon }_{0}{\varepsilon }_{r},$$
(7)

where εr is the relative permittivity of the substrate. The dimensional value of the parameters used in the proposed SRR resonance frequency calculation is listed in Table 1. Table 1 shows the parameters which are included in the design of SRR.

Table 1 Dimensions of SRR design
Full size table

2.2 Mathematical design of Minkowski fractal as a defective ground structure

To lower the SRR's resonant frequencies and to enhance the sensor's sensitivity, the Minkowski curve is acted as a Defective Ground Structure (DGS), and its circuit configuration is shown in Fig. 4. Minkowski curve is constructed based on the recursive procedure.

Fig. 4
figure 4

(a, b) Design of SRR of top region of the proposed antenna. (c) RLC circuit of Minkowski curve as DGS. Wd width of the defected ground circle, Rd radius of the defected ground circle, Sw substrate width, SL substrate length, R resistor of Minkowski curve, L inductor of Minkowski curve, C capacitor of Minkowski curve

Full size image

The fractal geometry is employed to develop the smaller device. In a standard ring, the surface current (Js) is employed to flow along the length of the top of the ring path; however, in a fractal, the path length is doubled, resulting from declining frequency. Compared to other fractal topologies like Koch and Serpinski fractal, the proposed approach on Minkowski fractal curve produces higher performance in terms of downsizing, gain, and bandwidth [36,37,38]. The resonance frequency of the defective ground is calculated using the following approach in Eq. (8):

$${f}_{DGS}\approx \frac{{c}_{o}}{2{S}_{s}\sqrt{\mathrm{\epsilon r}}},$$
(8)

where c0 is the speed of the light and ϵr is the medium's permittivity surrounding the defected ground structure; in this case, it is a vacuum equal to 1, and Ss is the length of the Minkowski curve slot. The first iteration is a single baseline, as illustrated in Fig. 5a.

Fig. 5
figure 5

(a) First iteration of the Minkowski curve; (b) top view of combined second and third iteration antenna design; (c) SRR and DGS—equivalent circuit

Full size image

The beginning element for the first iteration is a line segment of length 'A.' For the first iteration, each horizontal and vertical segment comprises one-third (A/4) of the lengths of a reference line. The second and third iteration portions comprise A/8 and A/12 of a line segment's length (Fig. 5 b). Rotation, scaling and translation are just a few of the fractal kinds that may be created using the iteration process. The iteration phase modifications are written by the following equations [31]:

$$W\left(\begin{array}{c}x\\ y\end{array}\right)= \left(\begin{array}{cc}\frac{1}{r} cos\varnothing & \frac{-1}{s}sin\varnothing \\ \frac{1}{r} sin\varnothing & \frac{1}{s} cos\varnothing \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}e\\ f\end{array}\right),$$
(9)

where s and r are scaling factors in the x- and y-axes, ϕ is the rotation angles, and f and e are the linear translations in both the x and y-axes. An iterative functional structure can be used to create Minkowski fractals is given in Eq. (10) [31]

$$W\left(A\right)= \bigcup_{n=1}^{N}{W}_{N}\left(A\right).$$
(10)

The designed Minkowski fractal geometry has a particular resonating frequency of 0.787 GHz. The total inductance and capacitance should determine the integrated design's resonant frequencies. Equation (4) can be used to find the capacitance of the SRR ring, and Eq. (2) can be used to find the inductance. The inductance of the DGS can be approximated as follows to get the inductance of the perturbed Hilbert curve under the constraint of (WT/H) < 1, where H is the depth of the substrate and WT is the breadth of the metal track of the DGS

$${L}_{DGS}= \frac{60{S}_{T}}{{C}_{0}}\mathrm{ln}\left(\frac{8H}{{W}_{T}}+ \frac{{W}_{T}}{4H}\right),$$
(11)

where H is the height of the metal track of the defected ground structure. The side length of the DGS can be estimated by the parameter ST as given below

$${S}_{T}= \frac{{L}_{DGS}- {W}_{S}{L}_{S }\left({2}^{n}+1\right)}{{W}_{T}},$$
(12)

where ST is the side length of the defective ground structure, WS is the width of the slot, and Ls is the length of the slot in the defected ground structure. The parameters employed for constructing DGS are listed in Table 2.

Table 2 Parameters utilized for designing the Minkowski curve
Full size table

As a result, the inductance value used to calculate the capacitor value of the Minkowski curve is as follows:

$${C}_{DGS}= \frac{1}{4{\pi }^{2}{L}_{DGS}{{f}_{DGS}}^{2}}.$$
(13)

By combining DGS and SRRs’ equivalent circuits in parallel, the capacitances of the system are equivalent to the simultaneous sum of SRR capacitance and the Minkowski curve capacitor, as seen in Fig. 8c. The DGS and SRR have capacitance values of 0.51 pF and 0.003271 pF, respectively. 0.51327 pF is the entire capacitance value. In the same way, the total inductance is equal to the sum of the Minkowski curve and SRR inductance. The DGS and SRR inductances are 0.01659 µH and 0.0364 µH, respectively. 0.01136 µH is the equivalent inductance. The resistance of DGS is 434.89 Ω. Next, the LC circuit formula determines the overall design's resonant frequencies, as shown in Eq. (1). The proposed design is then resonated at a frequency of 2.084 GHz.

3 Results and discussion

The simulation design of the proposed structure and SRR are done using HFSS software. The return loss (S11) dB of the simulated proposed metamaterial sensor antenna is resonated at the frequency of 15.42 GHz, which is shown in Fig. 6.

Fig. 6
figure 6

Return loss S11 parameter for SRR cell

Full size image

The unit cell design of SRR with its boundary constraints and its activation ports in HFSS software to generate unit cells can be seen in Fig. 7 (wave port model).

Fig. 7
figure 7

Unit cell—SRR (a), E-field (b), and H-field (c) assigned wave port-1 and (d) assigned wave port 2

Full size image

Likewise, the structure of the third-order Minkowski curve from the mathematical model was replicated using a simulation tool as a unit cell to test its functionality. The metamaterial sensor antenna is shown in Fig 8a, 3D gain plot is shown in Fig 8b, the maximum achieved is 2.38 dB, and the radiation pattern of the proposed antenna is two dimensional pattern is shown in Fig. 8c.

Fig. 8
figure 8

(a) Sensor Design. (b) Gain plot of simulated sensor antenna design. (c) Radiation pattern of proposed antenna design

Full size image

The third-order Minkowski fractal ground and the SRR are integrated to obtain the complete optimized design. Two different ports of the microstrip transmission line are being used to drive the finished design, as shown in Fig. 8a. The Minkowski fractal curve is placed in the ground structure to optimize the frequency modulation of the resonator.

The SRR model is placed on the top of the substrate, and the substrate has a breadth of 19.5 mm and a length of 29 mm. The width of the transmission feed on the side of the substrate is 3.62 mm, and the height of the substrate is 1.6 mm. These dimensions result in an input impedance of 50.15 Ω, comparable to the coaxial line impedance [37,38,39]. The two ports, and one on every transmission feed line end, are being used to stimulate the sensor.

The S11 vs frequency curve for the optimized parameters is shown in Fig. 9 for the final design in which the antenna is resonated at a particular frequency of 2.31 GHz with a return loss of − 36.9745 dB is obtained. Different iterations of Minkowski curves and the design of ground without DGS were explored to examine the variety of resonant frequencies and their response. The designs are examined without any samples. Figure 9b clearly shows the transmission coefficient S11 parameter for the first-, second-, and third-order Minkowski curve antenna design. It is evident that as the order of the fractal ground improves, the resonance frequency falls.

Fig. 9
figure 9

(a) Simulated S11 parameter of sensor antenna design. (b) S11 parameter for different orders of Minkowski. (c) Simulated S11 parameter for breast cancer cell lines

Full size image

The gain achieved for sensor antenna design is 2.38 dB. Figure 8 shows the gain plot of the sensor antenna design applicable to detect or sense human breast cancer cells [40, 41]. The third order was used for its low resonant frequencies to eliminate loss and reduce the possibility of inaccuracy. Considering that the third-order transmission is efficient, the results must be steady and less impacted by grid disturbances.

4 Electrical characteristics of cancer cells measured with simulated proposed antenna

The cancer cell types are placed in the gap of the designed sensor design, and it is simulated. The fabricated metamaterial sensor antenna is shown in Fig. 10. A spherical-shaped radius of 1.05 mm of the breast cancer cell is placed in the space of the sensor model. The electrical characteristics of human cancer cells were derived from [6].

Fig. 10
figure 10

Fabricated sensor antenna design: (a) top view and (b) bottom view

Full size image

Table 3 shows the conductivity and dielectric constant for every cell line considered in the simulations. The obtained results for change in conductivity and dielectric constant for three types of breast cancer cell lines: HS578-T, MCF-7, MDA-MB-231, and vacuum in terms of return loss result are illustrated in Fig. 9c. The final antenna design resonated at a particular frequency of 2.31 GHz with a return loss of − 36.9745 dB when the model is called vacuum.

Table 3 Conductivity and dielectric constant values for cancer cell lines
Full size table

The testing of breast cancer cell lines is done in antenna design. Various cancer cell lines will have their responses developed and compared to the simulated results. FR-4 Epoxy material is used as substrate material for fabricating antenna with a height of 1.60 mm and 3.687 as dielectric constant. The sensor ports are bonded with Sub Miniature version A (SMA) connections (Table 4).

Table 4 Simulated testing results of proposed antenna with cancer cell lines
Full size table

The VNA must first calibrate to eliminate methodological errors to obtain sensing performance. The ensure error detection and correction in transmitted and reflected waves in both the forward and reverse directions; the calibration was carried out using two ports. Following VNA calibration, the antenna's two terminals were attached to the VNA's two ports. The sensor is placed, so that it is enclosed by air, since any material that makes contact with it will impact the sensor's response. Human cancer cells are HS578-T, MCF-7, MDA-MB-231, and also vacuum’s measurement is taken. S11 parameters are measured and noted.

Figure 11b compares simulated and measured output for antenna design. The simulated result of the designed antenna is resonated at 2.31 GHz with a return loss of − 36.9745 dB, and the fabricated antenna resonated at 2.31 GHz frequency with a return loss of − 31.7545 dB. Nanomaterial catalysts may also be incorporated in diagnosing the electrical characteristics of cancer cells in the further experimentation [42,43,44,45,46,47]. The comparison of the obtained results of the proposed antenna with the reference antenna is done and it is given in Table 5.

Fig. 11
figure 11

(a) Measured output of final antenna design and (b) simulated and measured output of final antenna design

Full size image
Table 5 Comparative analysis of proposed antenna with related design
Full size table

From the above comparison table of reference antenna with the proposed antenna, antenna size is minimized, simulated and measured results of the return loss which is better for medical applications. Bidirectional form of radiation and gain of 2.38 dB is more suitable for detection cancer using electrical characteristics of cancer cell lines.

5 Conclusions

In this research work, metamaterial sensor antenna with Split Ring Resonator (SRR) on the top region and Minkowski fractal curve as a Defected Ground Structure (DGS) is numerically studied. The measured results of the fabricated antenna for return loss are also done. The combination of SRR with Minkowski fractal design has given better results to perform the antenna as metamaterial sensor in investigating with the electrical characteristics of cancer cell line. The simulated investigation were made by the designed antenna with the electrical characteristics of cancer cell lines is also tested. The proposed antenna is analyzed in terms of return loss, gain, and radiation pattern. The antenna resonated for the frequency of 2.31 GHz at − 36.97 dB return loss and maximum gain of 2.38 dB with the bidirectional radiation pattern. The simulated results of an antenna were resonated for frequencies of 2.35, 2.42, and 2.52 GHz for different dielectric constants and conductivity of cancer cell lines like MDA-MB-231, MCF-7, and HS758-T. The proposed sensor was assessed using three breast cancer cell lines to ensure its performance and selectivity. In future, the designed antenna may be tested with the nanomaterial catalysts for better results with the electrical characteristics of cancer cell lines for real-time future testing with the human body.