1 Introduction

Aerogels are lightweight porous materials with densities typically in the range of 0.003–0.5 g/cm3 [1, 2] and depending on their pore size, can be classified as microporous or mesoporous materials [2, 3]. Aerogels come in many varieties and formulations and are often utilized for their extreme low thermal conductivity and low refractive index making aerogels popular materials for thermal [4, 5], optical [6, 7], and many acoustic [8,9,10,11,12,13,14] applications. In recent years, aerogels have emerged as the material of choice for anechoic applications and interest in aerogels is continuously growing. Due to the high tortuosity of the aerogel structure, these materials have demonstrated superior behavior as sound absorbers compared to other materials [8,9,10, 15, 16]. Most of the published literature, however, explores the experimental use of aerogels for sound applications mostly in the audible range (0–4000 Hz) and is thus very limited in scope [9, 10, 15, 17]. Some studies have explored higher frequency ranges including the ultrasound region (> 20 kHz) [8, 17,18,19,20,21,22,23], where the main interest has been developing acoustic metamaterials [24, 25]. Progress in optimizing material properties for these applications is hindered by the lack of a reliable model that can predict the response of these materials in different environments and can be addressed to some extent by the work presented here.

Aerogels are also gaining traction as the material of choice for many biomedical applications, such as neuronal scaffold, dental implants, and vascular implants to name a few [26,27,28,29,30]. Given that aerogels have a high acoustic impedance mismatch (compared to soft tissue in the body), ultrasonic detection can be reliably utilized for noninvasive rapid detection of aerogels in vivo which is made possible by the acoustic signature of these implants [30,31,32,33]. This was demonstrated for the first time experimentally in 2013 [32] and serves as the inspiration for the work presented here.

The summary provided above attempts to capture the versatile nature of aerogels and the many applications that they have been developed for to date. In many cases, whether embedded in an aqueous or non-aqueous environment, rapid and non-invasive detection and tracking of aerogels is an important part of the conversation and sound-based techniques offer a clear advantage over other techniques such as those that rely on ionizing radiation [31]. Diagnostic techniques that exploit non-ionizing radiation (NIR) are preferred and sound-based techniques are among the most popular ones [34].

The study of wave propagation is a complicated process because of complex intrinsic and extrinsic aerogel properties. This may lead to difficulty in acquisition and interpretation of data from acoustic measurements [17]. The difficulty is often due to the varying size of the pores, their distribution, and the density, stiffness, and surface roughness of the aerogel structure. These all affect the wave propagation in different ways [17, 35]. A computational approach to investigating wave–aerogel interaction allows for control over these parameters and the ability to study one parameter at a time in a manner that is not necessarily possible experimentally and forms the foundation of the work presented here. In spite of a clear need, the existing/published computational frameworks have not explored wave simulations in aerogels and only limited work has been done on detecting structural defects in silica aerogels. Our work addresses this need.

Nonlinear wave equations are the preferred method of choice for simulating wave propagation in heterogenous media [36, 37]. Some of the tools that have been used here include Field II [38], SimSonic [39], and mSound [40]. Field II and SimSonic are only capable of linear acoustic simulations and mSound is a relatively new tool with limited amount of published data and literature on it. k-wave, being one of the readily available wave solvers, is easy to use and can be widely adopted. It uses pseudo-spectral time domain method to derive the solutions to discretized wave equations in a spatial domain [36, 37, 41] which allows for high numerical accuracy [36, 37] without a significant computational demand. As an example, k-wave has been successfully applied to study ultrasound propagation in skull [42,43,44], aerated inhomogeneous medium, such as lungs [45], as well as microfiber flaw detection in carbon fibers [46]. Silica aerogels have been the focus of prior computational analysis by our group with an emphasis on developing a genetic algorithm to reconstruct defects in silica aerogels and how they affect thermal behavior of the aerogels [47].

The motivation behind the work presented here is to achieve real time visualization of wave interactions with aerogels in two different media (aqueous and non-aqueous) using k-wave tool, and by recording the regions of maximum and minimum pressure at the interfaces. Our earlier work demonstrated that aerogels show interesting acoustic properties in response to ultrasound waves and give rise to distinct B-mode when used as implants in biological media [32, 33]. We have successfully applied through transmission technique to study the acoustic behavior of aerogels while accounting for different intrinsic (density, pore geometry, speed), as well as extrinsic (frequency, scanning angle) material properties.

2 Methods

2.1 Preparation of crosslinked silica aerogels and imaging

Polyurea crosslinked silica aerogel (PCSA) monoliths were prepared using sol–gel techniques and critical point drying as discussed in detail in previous publications, where a detailed synthesis method has been provided [48,49,50,51,52]. Aerogels prepared by this method had bulk densities in the range of 100–500 kg/m3. After synthesis, samples were prepared for scanning electron microscopy (SEM). The SEM images were utilized for creating a template of the aerogel structure and will be discussed in Sect. 2.3 in further details. High resolution images were acquired using a Hitachi S-4700 (Santa Clara, CA, USA) scanning electron microscope (SEM). To achieve better contrast, samples were first sputter-coated with a 10 nm layer of AuPd. The acquired SEM images were then transferred to ImageJ open-source software (ver:1.53q) and further analyzed. Table 1 summarizes all the parameters and symbols used in this study.

Table 1 Summary of all the symbols and parameters used in the study
Full size table

2.2 Simulation framework: designing a computational domain to replicate air and water

Defining the computational domain: A two-dimensional computational domain of grid size 3032 × 1496 with a cell dimension of 3.5 × 10–4 cm along x and y axis was created which led to a spatial resolution of 2 × 0.8 cm along axial (x axis) and lateral (y axis) directions, respectively. The size of the domain was determined by a convergence test and designed to minimize the computational load. More details on convergence test and accuracy of simulations are provided in Sect. 4. The domain property was initially set up to mimic the conditions of an aerogel in air and then separately the conditions of an aqueous environment (water). This was achieved by presetting the values for density (ρ), speed of sound (v), attenuation (αo) and, non-linearity factor (B/A) specific to the chosen medium. The values chosen are summarized in Table 2 and reflect the values that are accepted in literature and determined in an earlier publication [43]. All the simulations were carried out using k-wave, MATLAB tool that ran using Nvidia Grid RTX8000-4Q GPU at the University of Memphis. The 1st order wave equations that the simulations are based on are provided below [36, 37]:

Table 2 Acoustic parameters defined for air and water
Full size table
$$\frac{\partial \mathbf{u}}{\partial t}= -\frac{1}{{\rho }_{o}}\nabla P,$$
(1)
$$\frac{\partial \rho }{\partial t}= -\left(2\rho + {\rho }_{O}\right)\nabla .\mathbf{u}-\mathbf{u} . \nabla {\uprho }_{\mathrm{O}},$$
(2)
$$P={c}_{o}^{2}\left(\rho +{\varvec{d}}. \nabla {\rho }_{o}+\frac{B {\rho }^{2}}{2A {\rho }_{o}}-L\rho \right).$$
(3)

Defining the wave source: The domain size defined above corresponded to a maximum supported frequency of ~1 MHz frequency. The maximum frequency was calculated using the expression suggested in the literature [36, 37]. With this frequency, source was constructed to replicate a time varying plane wave at a burst cycle of 3, and source strength of 1 MPa, as shown in Fig. 1a. The position of the source was defined at the top end of the computational domain for axial propagation. The source was defined as airborne or waterborne depending on the type of medium being investigated.

Fig. 1
figure 1

Schematic diagram representing a setup and relative placement of source, sensor, and aerogel. b Relative angle of incidence of wave with respect to the aerogel indicated by θo. c Schematic representation of wave interaction with aerogel at different angles of incidence, where i and ii represent 0º and non-zero angles. d Amplitude recording of incident and transmitted waves for measurement of transmission loss for a given source frequency. e Sample wave intensity recording of incident, reflected, and transmitted wave

Full size image

For simulations regarding normally (perpendicular to boundary) propagating wave, source was set up as shown in Fig. 1a, such that the propagating wave interacts with aerogel at θ = 0, as shown in Fig. 1c (i). The relative position of the source was then varied from θ = 0 to θ = 30° in increments of 5°, as shown in Fig. 1b, c (ii). This allowed us to investigate the effect of increasing angle of incidence on the wave propagation behavior. In addition, the frequency of the Source was varied from 0.5 to 1 MHz to investigate the effect of frequency on propagation of the wave in different media.

2.3 Modeling aerogel structure and defining the acoustic properties

The SEM images acquired earlier served as a template to build the desired aerogel pore structure model in 2D. Using ImageJ, SEM images were binarized and thresholding was applied to create pore geometry of different classes. A “1” value corresponds to a material with no pores, while a setting of “8” indicates highly porous and non-uniform material. Geometry values beyond 8 were also evaluated and it was determined that values above 8 had no effect on transmission loss values; therefore, that data are not reported here. To mimic ultra-low-density aerogels, bulk density values (ρag) between 50 and 200 kg/m3 were investigated [8, 9]. The ρag value was increased by 10 kg/m3 in each step starting at 50 until 200 kg/m3 was reached. For each ρag value, the speed of propagation (v) was calculated using the equation below, known as the scaling law of density [53]:

$$v \propto {\left({\rho }_{\mathrm{ag}}^{ }\right)}^{\beta },$$
(4)

where β represents the scaling factor. Experimentally determined values of v and ρag for aerogels suggest a β value of the order of 1.2 [33, 53]. The assigned values of density gave speed of propagation in the range of 109–577 m/s, details provided in Table 3. Nonlinearity factor (B/A) for aerogels was not readily available and was assigned a value of 400. This value was chosen to reflect a highly non-linear medium and to prevent k-wave from defaulting to a linear wave simulation [43, 54]. These aerogels were then positioned at the midpoint of the computational domain with a thickness of 0.4 cm in y direction. The values that were used for this computational work are summarized in Table 3. The range of the parameters explored are presented in Table 4.

Table 3 Classification of aerogels with the defined acoustic parameters
Full size table
Table 4 Variation of different parameters done for wave propagation simulations
Full size table

2.4 Setup for acoustic measurements

The interaction of an ultrasound wave with aerogels of different densities under both aqueous and non-aqueous conditions was quantified using the following steps:

  1. (a)

    Visual representation of pressure distribution was arrived at by measuring the maximum pressure in each grid point.

  2. (b)

    Transmission loss was measured from the amplitude of incident and transmitted waves

  3. (c)

    Absorption was calculated from the intensity value of incident, reflected, and transmitted waves.

To successfully carry out the above-mentioned steps, two separate sensors were defined and strategically placed at different locations. Sensors were either defined to include all the grid points in the computational domain, or, were confined to the region that identified the parameter of interest, as explained in the section below. All grid points in the computational domain recorded maximum pressure exerted by the propagating wave which gave a pressure distribution map over the entire grid.

To be able to identify and record the wave that has traveled through the aerogel bulk, a through-transmission technique [56] of measuring the amplitude of the waves was adopted. This was achieved by placing two sensors (Sensor-1 and Sensor-2) on each side of the aerogel, vertically, as shown in Fig. 1a. Time series pressure data were converted into amplitude signal in frequency domain and graphed as a function of frequency (Fig. 1d). The maximum amplitude of incident and transmitted wave, Ao and At (Fig. 1d) was recorded by Sensor 1 and 2 (Fig. 1a) to calculate the transmission loss. The equation used is given below [17, 19]:

$$\mathrm{Loss}= -10\mathrm{Log }\left(\frac{{A}_{\mathrm{t}}}{A\mathrm{o}}\right).$$
(5)

Absorption measurements were done by repositioning Sensor-1, such that it is moved away from the aerogel boundary and is placed closer to the top of the computational domain. The intensity of incident wave (Ii) reflected wave (Ir) and transmitted wave (It) were recorded by Sensors-1 and 2 (Fig. 1a) to obtain intensity graph, as shown in Fig. 1e. The standard equation used for the calculation of absorption is given by Eq. 3 [23]:

$$\mathrm{Absorption}=1-\frac{{I}_{\mathrm{r}}}{{I}_{\mathrm{i}}}-\frac{{I}_{\mathrm{t}}}{{I}_{\mathrm{i}}}.$$
(6)

To explain the loss and the absorption characteristics, the acoustic impedance (Z) of medium and aerogel was first calculated from the density and speed values (Eq. 4). Next, the reflection coefficient at the interface of air–aerogel (\({r}_{\mathrm{a}-\mathrm{ag}}\)) and water–aerogel (\({r}_{\mathrm{w}-\mathrm{ag}}\)) was calculated, per Eq. 5 [23]:

$$Z=v . \rho ,$$
(7)
$${r}_{\mathrm{a}-\mathrm{ag}}(\mathrm{air})=|\frac{{Z}_{\mathrm{a}}-{Z}_{\mathrm{ag}}}{{Z\mathrm{a}}_{ }+{Z}_{2}}|, {r}_{\mathrm{w}-\mathrm{ag}}(\mathrm{water})=\left|\frac{{Z}_{\mathrm{w}}-{Z}_{\mathrm{ag}}}{{Z\mathrm{w}}_{ }+{Z}_{2}}\right|.$$
(8)

3 Results

3.1 Effect of aerogel density on wave amplitude

Nonlinear acoustic wave simulations were carried out for aerogels with densities in the range of ρag = 50–200 kg/m3. The simulations were performed by modeling the aerogel structure either suspended in air or submerged in water. The pressure maps were obtained by recording the maximum pressure at each grid point. Amplitude spectra across the aerogel in a vertical manner (as indicated by the arrow in Fig. 1b) were recorded using the line sensors and the calculation of transmission loss was performed using maximum value in the amplitude spectrum. To identify the trend of the transmission loss, the reflection coefficient was calculated using Eq. 8. Results are discussed in the sections below and are summarized in Table 5 (in air) and Table 6 (in water).

Table 5 Impedance, reflection coefficient, and loss calculated for different combinations of density and speed for aerogel in air
Full size table
Table 6 Impedance, reflection coefficient, and loss calculated for different combinations of density and speed values for aerogel in an aqueous environment
Full size table

3.1.1 Aerogel–air

Figure 2a–d Shows the representative pressure maps for aerogels with densities ρag = 50, 100, 150 and 200 kg/m3, respectively, while surrounded by air. For the sake of brevity, in between values of ρag are not shown in the table. Before interaction with aerogel, the propagating US wave in air exerts smaller than 1 MPa pressure which can be seen in Figs. 2a–d, indicated with the green shaded area. As the wave approaches the air–aerogel boundary (indicated by the red arrow in all four images—BT) the pressure increases to 2 MPa for a narrow region inside the structure indicated by the red streak (peak pressure band) in Fig. 2a, b, c, d. The region of higher pressure inside the structure appears to increase as the density increases which is attributed to high reflection coefficient. The lower boundary (BB—represented by yellow arrow) is distinctly visible for aerogel with ρag = 50 kg/m3 and starts to fade as the density increases. This is associated with the amplitude of the wave decreasing.

Fig. 2
figure 2

Pressure maps representing interaction of incoming wave with aerogels of densities a 50, b 100, c 150, and d 200 kg/m3, in air. Upper and lower boundaries are shown with red and yellow arrows, respectively. The gradual decrease of aerogel structure visibility as the density increases is clearly visible from these pressure maps

Full size image

Figures 3a–d shows the amplitude spectra for aerogels with densities ρag = 50, 100, 150 and 200 kg/m3 recorded using Sensors 1 and 2 positioned above and below the aerogel, as indicated in Fig. 1a. Transmission loss was calculated using Eq. 5. For densities 100, 150, and 200 kg/m3 this value increased 2.6, 3.6, and fourfold, respectively, when compared to the loss calculated for aerogel with density ρag = 50 kg/m3. The reflection coefficient calculated using Eq. 8 shows a similar trend, such that it increases as the density of the aerogel increases (Table 5). The maximum value of ra-ag was obtained for an aerogel density of 200 kg/m3 which was 0.94. This suggests that at this density, over 90% of the incoming soundwave is rejected, when compared to only 25% when the aerogel has a density of only 50 kg/m3.

Fig. 3
figure 3

Amplitude recorded using Sensor 1 and Sensor 2 for aerogels of increasing density a 50, b 100, c 150, and d 200 kg/m3 suspended in air. The signal recorded by the Sensor 2 decreases with an increase in ρag as indicated by the Loss value

Full size image

The impedance values for air and aerogel were calculated using Eq. 7 and results are summarized in Table 5. Given that Za and Zag values are of similar magnitude, it is expected that reflection coefficients will be small.

3.1.2 Aerogel–water

The same analysis that was performed when a monolith of aerogel was placed in air, was repeated for aerogels of the same densities (ρag = 50, 100, 150, and 200 kg/m3) but this time in an aqueous environment. Figures 4a–d shows the pressure maps for this scenario, where the upper and lower boundaries of the aerogel are indicated using the red (BT) and the yellow arrows (BB), respectively. As can be seen, the aerogel boundaries are not as pronounced in an aqueous environment as they were in air (Fig. 4 compared to Fig. 2). In this case, the peak pressure band occurs external to the aerogel, at the liquid–aerogel boundary showing that US waves propagating in liquid are not able to penetrate the aerogel for densities ρag = 50, 100, and 150 kg/m3 (Figures. 4a, b, and c, respectively). Figure 4d, however, shows a slight penetration of the US wave into the aerogel giving rise to some visibility of the aerogel structure. Once again, loss and reflection coefficient were calculated using Eqs. 5 and 8, respectively, and results are summarized in Table 6.

Fig. 4
figure 4

Pressure maps for aerogels with densities a 50, b 100, c 150, and d 200 kg/m3, in an aqueous environment. Red arrows indicate the upper boundary, while the yellow arrows indicate the lower boundary of the aerogel

Full size image

The impedance values for aerogel (Zar) and water (Zw) were again calculated using Eq. 7 and results show a significantly large difference in values, with Zw greater by a factor of 300.0, 60, 25, and 13 for densities 50,100, 150, and 200 kg/m3, respectively. Since reflection coefficient is proportional to the impedance value, the high impedance of water will dominate the observed trend, such that the reflection coefficient is no longer strongly dependent on density values.

The amplitude spectra for an aqueous environment (Fig. 5) were prepared in the same manner, as shown in Fig. 3. The loss decreased as a function of density, which can be explained when the reflection coefficient is taken into consideration (Table 6).

Fig. 5
figure 5

Amplitude recorded using Sensor 1 and Sensor 2 for aerogels of increasing density a 50, b 100, c 150, and d 200 kg/m3 in aqueous conditions. The signal recorded by Sensor 2 increases with an increase in ρ as indicated by decreasing loss value

Full size image

To better understand the relationship between loss and reflection coefficient, calculations were performed for more density values (in increments of 10 kg/m3) and shown in Fig. 6. When aerogels are in air, for smaller reflection coefficients, loss amount is also less indicating that most of the wave can penetrate the aerogel monolith. As the reflection coefficient increases, the degree of loss also significantly increases, gradually, to the point, where very little of the sound wave can enter the bulk of the aerogel monolith. In an aqueous environment, however, the trend is reversed and suggests substantial attenuation due to the presence of water.

Fig. 6
figure 6

Dependance of transmission loss on reflection coefficient as a function of medium. Increase in loss appears to be more gradual for air than for water

Full size image

3.2 Effect of porosity on wave amplitude

To understand the effect of the different aerogel pores on scattering, and the amplitude of the propagating wave, we varied the pore structure from ‘1’–‘8’ as mentioned in Sect. 2.3 (while keeping all other parameters constant) and performed simulations similar to Sect. 3.1. Both aqueous and non-aqueous conditions were explored, and results are discussed below.

3.2.1 Aerogels suspended in air

Figure 7 shows the pressure maps obtained for an aerogel of density 150 kg/m3 as a function of pore variation of ‘1’, ‘3’, and ‘6’ along with the corresponding amplitude spectra in non-aqueous conditions. For structure ‘1’ (Fig. 7a) the pressure map is uniform without much scattering of the waves. The amplitude spectrum (Fig. 7b) shows a loss of approximately 40 dB. As pore structure is changed to ‘3’, the pressure map distribution is no longer uniform (Fig. 7c). The region of peak pressure band appears at the top boundary of the aerogel as a red streak (indicated by the red arrow). This led to a 0.75-fold increase in loss at a value of 71 dB as recorded by the amplitude spectra in Fig. 7d. Another change in pore structure to ‘7’ caused the region of peak pressure to become less prominent (Fig. 7e) and the loss value to fall to 40 dB (Fig. 7f).

Fig. 7
figure 7

Pressure maps and amplitude spectra representing the effect of scattering on loss values due to change in pore structure, in non-aqueous environment. a, c, and d represent pressure maps for pore geometries ‘1’, ‘3’ and ‘5’. b, d, and f are the corresponding amplitude spectra for each pore geometry

Full size image

3.2.2 Aerogel submerged in water

Figure 8 shows the pressure maps for three different pore structure (‘1’, ‘5’, and ‘7’) with the corresponding amplitude spectra in an aqueous condition. For a pore structure ‘1’ (Fig. 8a) the pressure map is uniform due to no scattering of the waves, and the aerogel structure (indicted between the red and yellow arrows) appears at very low pressure compared to the aqueous environment. The amplitude spectrum (Fig. 8b) shows a loss of approximately 91 dB. As pore structure is changed to ‘5’, the pressure distribution is no longer uniform (Fig. 8c). The small region of peak pressure band appears at the top boundary of the aerogel as a red streak. This change in geometry led to a 0.29-fold increase in at a value of 118 dB (Fig. 8d). Further change in pore geometry to ‘7’ led to the decrease in loss value to 106 dB.

Fig. 8
figure 8

Pressure maps and amplitude spectra representing the effect of scattering on loss values due to change in pore structure, in non-aqueous environment. a, c, and d represent pressure maps for pore geometries ‘1’, ‘5’ and ‘7’. b, d, and f are the corresponding amplitude spectra for each pore geometry

Full size image

Figure 9 summarizes loss dependency of wave propagation with all the different pore geometries studied. The peak value of loss occurs at different pore geometry when the medium is changed keeping all the other parameters same. The presence of water influences the scattering of the wave differently. The loss is high in the presence of water and low in air.

Fig. 9
figure 9

Effect of pore presence on loss for aerogels in air and in water. A highly non-linear relationship can be observed in both cases with an overall lower loss value for air, as expected

Full size image

3.3 Effect of angle of incidence on loss

For this section, simulations were done by varying the angle of incidence (θ) of the wave, as shown in Fig. 1b, andc, to explore the possible effect of angular difference on loss measurements. This was done by studying the relationship between loss, and angle of incidence keeping a constant density, ρag = 150, in Fig. 10. The loss value was calculated for each angle of incidence (θ = 5, 10, 15, 20, 25 and 30ο) for both aqueous and dry environments. Figure 10a, andb shows change in loss value as a function of reflection coefficient calculated for both aqueous (10b) and non-aqueous (10a) conditions for different angles of incidence. Results indicate that loss appears independent of angle of incidence for a non-aqueous environment (Fig. 10a), for all reflection coefficients.

Fig. 10
figure 10

Measurement of loss in aerogel as a function of angle of incidence θ = 0–30° and reflection coefficient (r) in (a) air and (b) water

Full size image

In an aqueous environment the overall loss is substantially higher compared to the non-aqueous case, as expected. At a reflection coefficient value of 0.92, loss shows a strong angle dependency. This might be due to generation of shear waves which might have contributed to the loss values.

3.4 Effect of source frequency on loss

The simulations for this section were carried out by varying the source frequency from 0.5 to 1 MHz. Figure 11a, andb shows the frequency dependency of loss for increasing aerogel densities, studied both in an aqueous (Fig. 11b) and non-aqueous (Fig. 11a) medium. Loss is observed to increase with increasing frequency. The loss is highest for ρag = 200 kg/m3 throughout the frequency range of 0.5–1 MHz, and lowest for ρag = 50 kg/m3. These results are in line with published experimental work [17]. The simulations were repeated for aerogels in aqueous environment (Fig. 11b). The results indicate a loss dependency on frequency similar to what was observed in non-aqueous conditions. However, unlike the previous case, the loss is lowest for ρag = 200 kg/m3 throughout the frequency range, and highest for ρag = 50 kg/m3. This can be attributed to higher reflection coefficient for ρag = 50 kg/m3 aerogels and vice versa. The presence of aqueous environment also contributes to overall high loss which is expected. It can also be observed that the frequency dependency is not as strong as in non-aqueous medium.

Fig. 11
figure 11

Effect of frequency on loss measured for aerogels with densities 50, 100, 150, and 200 kg/m3 in (a) air and in (b) water, in the range of 0.5–1 MHz

Full size image

3.5 Absorption as a function of wave frequency

The absorption measurements for different aerogel densities (ρag = 50–200 kg/m3) were calculated from the reflected and transmitted intensity of the wave (Fig. 1a, e) in the frequency range of 0.5–1 MHz. From Fig. 12a, the absorption in non-aqueous medium is observed to increase with an increase in frequency for all ρag values. Low density aerogels (ρag = 50 kg/m3), show overall high absorption (~1 at 1 MHz of frequency) and minimal frequency dependency. High-density aerogels (ρag = 200 kg/m3) show low absorption compared to low density aerogel but a strong frequency dependency. In an aqueous environment (Fig. 12b), the absorption for aerogel is high for ρag = 200 kg/m3 and low for ρag = 50 kg/m3, and a strong frequency dependency is seen for all the densities. This was similar to the transmission loss measurements seen in earlier simulations. Interestingly, the absorption value for aerogel submerged in water was found to be negative. This is attributed to a high reflection coefficient value which cause the wave reflecting at the aerogel boundary to superimpose (overlap) with the incident wave. This makes the intensity of reflected wave higher than the incident wave and gives rise to a negative value of absorption (from Eq. 3).

Fig. 12
figure 12

Absorption of aerogel in the frequency range of 0.5–1 MHz. a Aerogel suspended in air, b aerogel in an aqueous environment. The overall absorption for aerogel densities in the range of 50–200 kg/m3 is higher in air than in water

Full size image

4 Discussion

For the first time, k-wave tool was applied to the study of ultrasound wave propagation in a multilayer medium consisting of air/water and monolithic aerogel. Nonlinear wave equations were utilized to simulate wave propagation in a heterogeneous media consisting of aerogels with pores filled with either air or water. Our results indicate that the B/A factor does not affect the outcome and this discovery is in line with previously published literature [43]. The accuracy of the results obtained from the simulations using k-wave was ensured by increasing the spatial discretization (grid size), which increases the Points Per Wavelength (PPW) value and reduces the phase errors in simulations [36, 37]. Typically, it is recommended that more than 15 PPW is used for nonlinear wave equations in heterogeneous media [36]. A PPW value of 32 was used in this investigation. To determine the optimal grid size a convergence test was performed which showed the loss value converging towards a stable value at 32 PPW, as shown in Fig. 13.

Fig. 13
figure 13

Parameter convergence test to determine the optimal size of computational domain with set grid points. The convergence test shows simulations becoming stable after 32 PPW

Full size image

Our results are consistent with earlier publications that have investigated experimentally the acoustic loss behavior in silica aerogels with bulk density values similar to the range considered here (0.05–0.2 g/cm3). Aerogels of a higher density (0.2 g/cm3) show greater loss compared to those of a lower density [9, 10] for frequencies < 400KHz. Our investigation of acoustic loss in aerogels has extended the frequency range from 0.5 MHz to 1 MHz. Our k-wave simulation of the ultrasound wave–aerogel interaction also provides meaningful results when aerogels are embedded in different environments, i.e., air versus liquid. Experimentally it has been shown that aerogels in air have a lower attenuation than when they are in an aqueous bath, [22] which is consistent with our model’s prediction.

Extrinsic material properties such as frequency and angle of wave propagation were also studied in detail. For different geometries, acoustic properties can vary greatly, as shown in this study. For a pore-less structure, the loss seems to be very low, and increases with the introduction of pores. The presence of pores causes US waves to bounce back and forth within the aerogel structure, and energy is, therefore, dissipated in the form of heat. This leads to a high attenuation by the aerogel. In the frequency range 0.5–1 MHz, transmission loss showed an overall increasing trend as the frequency increased and is consistent with related published work [57, 58].

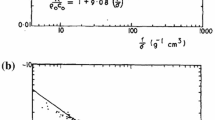
The position of the source, either airborne or waterborne, played an important factor in wave propagation. Airborne source can transmit an acoustic wave efficiently for aerogel densities that are extremely low (~ 50 kg/m3), while the water borne sources need a denser aerogel. This is evident from the theoretical calculations of impedance value for aerogel and medium (either air or water) shown in Fig. 14. It can be seen that aerogel matches the impedance of air at 3 × 10–3 MRayl, and water at 1.6 MRayl. The lowest aerogel density tested in our study had an impedance value of 5 × 10–3 MRayl (ρag = 50) and highest 0.1 MRayl (ρag = 200). The model predicted a loss value of 16 dB for aerogel/air and a loss value of 21dB for aerogel/water which is what would be expected. Finally, wave propagation at different angles of incidence had little impact on the interaction with aerogel. For aerogels with densities 100 and 150 kg/m3, a source propagating at 0° had more attenuation as opposed to the source that radiated at 30°.

Fig. 14
figure 14

a Theoretical value of acoustic impedance measurement for aerogel using scaling law and impedance of air and water, where the red line represents impedance of water and blue line represents air. b Expanded view of the 0–50 kg/m3 region showing the intersection point of impedance of aerogel with that of air

Full size image

5 Conclusion and summary

Simulating propagation of sound waves in aerogels was successfully accomplished using k-wave. This technique was applied to aerogels with ρag values in the range of 50–200 kg/m3 and ɸ in the range of 0–70%, surrounded either by air or an aqueous environment to mimic physiologically relevant conditions. Computational results obtained here are in line with some of the experimental data previously reported for the frequency range 0–0.4 MHz while also expanding the range to 0.5–1 MHz. The influence of density, angle of incidence, pore size, and medium was quantified by through-transmission loss measurements. Acoustic wave propagation in aerogel was affected the most by the medium and affected the least by the angle of incidence. The method described in this work can be adopted for a large number of applications and can play an important role in optimization of parameters for use of aerogels in acoustic applications. Future studies will include investigating the US response of aerogels in different physiological environments, mimicking the tissue inhomogeneity and different anatomic layers. Future work will also include 3D simulations which will better simulate the wave–aerogel interaction and wave propagation.