A semiclassical approach to the magnetotransport in quasi-1D electron systems

Abstract

The issue of the magnetotransport in any quasi one-dimensional (quasi-1D) electron system has not hoarded so much attention as the magnetotransport in two-dimensional (2D) system. At most, at the beginning of the realization of those systems, some experimental studies and phenomenological models were developed. However, it is an interesting subject that can throw light on the physical mechanisms determining the transport properties of low-dimensional electron systems. In our previous paper, Hidalgo (Eur Phys J Plus 137:1–-14, 2022), we described in detail a semiclassical global approach to the quantum Hall and Shubnikov-de Haas phenomena in a 2D system for both, the integer and fractional quantum Hall effects (IQHE and FQHE), and not only in semiconductors quantum wells but also in graphene. Here, we focus on the magnetotransport in a quasi-1D electron system following also a semiclassical approach, i.e., taking into consideration the Landau-type density of states for such system and its implication in the conductivity.

1 Introduction

We have recently published a semiclassical approach for the analysis of the quantum Hall effect, integer and fractional, and the Shubnikov-de Haas (SdH) phenomena in different two-dimensional electron systems (2D): semiconductor quantum-wells and graphene [1], (additional references therein). Here, also using a semiclassical approach, we try to address the issue of the transport properties in the quasi-1D electron systems. We show that it has an analogous origin, based on two main facts: the quantization of the density states of the 1D system on account of the confinement of electrons and the application of a magnetic field, and the Fermi level fixed by the environment of the 1D system.

Since decades ago, the development of the semiconductors technology has provided physical realizations of such systems, as shown in the early references [2, 3], or more recently [4, 5], (based on Si metal-oxide field effect transistors) [6,7,8] (based on III–IV heterostructures), or [9], (based on graphene). In addition, all these structures are fabricated through different techniques, [10]. Then, any quasi-1D electron system is embedded in a higher dimensionality structure: to get it a confinement potential has to be applied over a 2D material, and in turn, this 2D system is located in the interface of a heterostructure, and/or obtained with a gate voltage over a 3D system (for example, an HEMT or MOSFET structures).

The former experimental results related to such systems were obtained by Fang and Stiles in the first part of the eighties of the past century [11, 12]. Their results corresponded to measurements of the resistance as a function of the gate voltage and an applied magnetic field around 15 T. The most significant and amazing feature of their results was the appearance of plateaux in the resistance, but not necessarily matched to integer or fractional values of ${h}/{e}^2$ (being h the Planck constant and e the electron charge) unlike 2D electron systems, where they are always matched to them [1].

Therefore, as mentioned above, a suitable confinement potential applied to a 2D electron system provides a quasi-1D system. In addition, due to that potential, quantized energy spectra emerges. A subsequent application of a magnetic field entails a shifting in the energy spectra (see below).

Landauer was who first analysed theoretically the conductance in wires, in 1D electron systems [13], later widespread by Büttiker [14, 15], broadening them to more complex electron systems. Other additional explanations have been established, based on the Kubo linear response formula or in the non-equilibrium Green function technique [16, 17]. However, the Landauer–Büttiker theoretical approach is the most extensively used for the analysis of the phenomenon.

Here, we present a different approach that want to show how a semiclassical approach is able to account for the observations of plateaux in the conductivity of quasi-1D electron systems. Then, after determining the density of states of such systems when also a magnetic field is applied, we calculate the Drude conductance, which already shows those plateaux.

The structure of the paper is the following: once obtained the density of states for the quasi-1D system, with and without the application of a magnetic field, Sect. 2, we determine the electron density, and from it the conductance, (and its inverse the resistance), Sect. 3, where the plateaux are clearly displayed. Finally, in Sect. 4 we sum up conclusion of the work.

2 Density of states of a quasi 1D electron system

When over some 2D electron system a quasi-1D confinement potential is applied, V(y), the movement of the electron will be limited to one direction (the wire direction), which in our case we will assume to be the x direction. If, additionally, we suppose that a magnetic field is applied in the z direction

$$\begin{aligned} \vec {B}=(0,0,B), \end{aligned}$$

(1)

the general Hamiltonian for every electron can be expressed by the following equation [18]:

$$\begin{aligned} H=\frac{\left( \vec {p}+e\vec {A} \right) ^2}{2m^*}+V(y), \end{aligned}$$

(2)

where e is the electron charge, $m^*$ is the effective mass of the electron and $\vec {A}$ is the vector potential. Then, we solve the Schrödinger equation choosing the most appropriate gauge for the 1D system, the Landau gauge, that is

$$\begin{aligned} \vec {A}=(-By,0,0), \end{aligned}$$

(3)

and involving a parabolic confinement potential

$$\begin{aligned} \ V(y)=\frac{\alpha }{2}y^2, \end{aligned}$$

(4)

where $\alpha$ determined its intensity. In addition, in all below, we consider periodic boundary conditions in the x-direction.

Thus, under all these conditions, the eigenfuntions of the Hamiltonian correspond to the product of plane waves, given by the harmonic oscillator functions and expressed as a function of the Hermite polynomials. Then, the solutions are

$$\begin{aligned} \psi _{nk}=\frac{1}{\sqrt{L}}e^{ikx} \frac{1}{\sqrt{\pi }2^n n! l_{qw}}H_n\left( \frac{y-y_k}{l_{qw}}\right) e^{-\left( \frac{(y-y_k)^2}{2l_{qw}} \right) }, \end{aligned}$$

(5)

L represents in our problem the length of the quantum wire, and $y_k$ is given by

$$\begin{aligned} y_k=\frac{\omega _c\hbar k}{m^* \Omega ^2}=\frac{1}{\sqrt{\left( 1+\beta \right) }}kl_{qw}^2, \end{aligned}$$

(6)

where $\omega _c$ is the cyclotron frequency

$$\begin{aligned} \omega _c=\frac{eB}{m^*}, \end{aligned}$$

(7)

and

$$\begin{aligned} \Omega =\sqrt{\left( 1+\beta \right) }\omega _c \end{aligned}$$

(8)

where $\beta$ is the a-dimensional parameter

$$\begin{aligned} \beta =\frac{\alpha }{m^*\omega _c^2}=\frac{\omega _0^2}{\omega _c^2}, \end{aligned}$$

(9)

and we have used the relation

$$\begin{aligned} \alpha =m^* \omega _0^2 \end{aligned}$$

(10)

$\omega _0$ represents the frequency related to intensity of the confinement applied. On the other hand

$$\begin{aligned} l_{qw}=\left( 1+\beta \right) ^{-\frac{1}{4}}l_B, \end{aligned}$$

(11)

being $l_B$ the magnetic length

$$\begin{aligned} l_B=\sqrt{\frac{\hbar }{eB}}. \end{aligned}$$

(12)

Thus, the eigenvalues obtained for the Hamiltonian, Eq. (1), are given by the relation:

$$\begin{aligned} E_{nk}=\hbar \Omega \left( n+\frac{1}{2} \right) +\frac{\hbar ^2k^2}{2m_{qw}}, \end{aligned}$$

(13)

where n is a natural number, n=0,1,2..., and ${m}_{qw}$ a re-normalized mass defined by the expression, [19]

$$\begin{aligned} m_{qw}=\frac{1+\beta }{\beta }m^*. \end{aligned}$$

(14)

When the confinement potential is high, in particular at limit approaching to infinite, the re-normalized trends to the effective mass, ${m}^*$, of the electron in the 2D dimensional system.

We see that the energy levels correspond to Landau-type levels, where $\Omega$ now plays the role of the cyclotron frequency in the 2D and 3D systems. From Eqs. (5) and (11), we see that the effect over the energy spectra of a quasi-1D system of the application of a magnetic field are limited to a shifting of it.

In summary, from Eq. (13), we can establish that the confinement potential leads to a energy spectrum characterized by Landau-type energy levels, aside from the additional dependence with the wave number, k, what entails a dispersion relation corresponding to that of a free particle in the wire direction, but now with re-normalized mass ${m}_{qw}$. Therefore, we can determine a group velocity given by

$$\begin{aligned} v_{nk}=\frac{1}{\hbar }\frac{\partial E_{nk}}{\partial k}=\frac{\hbar k}{m_{qw}}. \end{aligned}$$

(15)

If the potential of confinement were not so simple as the parabolic one, Eq. (4), the relationship between the group velocity and the wave number would be more complex. However, the method and general conclusions detail below would be fully applicable.

Once we know the energy spectrum, we have now to obtained the density of states. Here, we will follow a similar procedure as we did in [1].

In the present case, we draw from the expression for the density of states of a 1D electron system, given by

$$\begin{aligned} g_0^{1D}=\frac{1}{\pi \hbar }\left( \frac{m^*}{2 E} \right) ^\frac{1}{2}, \end{aligned}$$

(16)

in which we have already taken into account the spin degeneration, Fig. 1a.

Fig. 1

Density of states of any 1D electron system, Eq. (16) (a). Superimposed to it the density of states of a quasi-1D system, Eq. (17), is shown (b), assuming a parabolic confinement potential, Eq. (4). For the simulation, we have considered an electron effective mass of 0.0624 $m_0$ and a constant width $\Gamma$=0.025 eV, with $g^*$ to be zero

Considering now the Landau-type energy levels, Eq. (11), Eq. (16), and using the Poisson sum formula, [20, 21], we can determine the expression for the density of states of a quasi-1D electron system, also under the application of a magnetic field (a detailed deduction of it is detailed in the added Appendix):

$$\begin{aligned} g_\textrm{1D}(E)=g_0^\textrm{1D}\left[ 1+2\sum _{p=1}^{\infty }A_{\Gamma ,p}A_{S,p}cos\left( 2\pi p\eta \right) \right] , \end{aligned}$$

(17)

where the term $A_{\Gamma ,p}$ is associated with the width of the Landau-type levels, arisen due to the interaction of electrons with defects and impurities. For the sake of simplicity, in this work, we assume a Gaussian shape for every energy level, with constant width $\Gamma$, i.e.,

$$\begin{aligned} A_{\Gamma ,p}=e^{\left( -\frac{1}{2}\frac{p^2\Gamma ^2}{\hbar ^2\Omega ^2} \right) }. \end{aligned}$$

(18)

The other additional term in the sum, the Zeeman term, has the expression

$$\begin{aligned} A_{S,p}=\textrm{cos}\left( p \pi \frac{g^*m^*}{2 m_0}\right) , \end{aligned}$$

(19)

and takes into account the effect of the magnetic field over the spin of electrons. ${m_0}$ is the free electron mass and ${g^*}$ is the generalized gyromagnetic factor, that in this work we assume to be 2.

Finally, in Eq. (17)

$$\begin{aligned} \eta =\frac{E}{\hbar \Omega }-\frac{1}{2}. \end{aligned}$$

(20)

In Fig. 1b, it is shown the density of states of a quasi-1D electron system superimposed to the density of states of a 1D system, Fig. 1a. For the simulation, we have considered an electron effective mass of 0.0624 ${m_0}$ and a constant width $\Gamma$=0.025 eV. (In this case, $g^*$ has been assumed to be 0.)

3 The conductance model

Once obtained the density of states of the quasi-1D electron system, we can determine its conductance.

Because the wave number, k, is a good quantum number to describe the system, Eq. (13), that means that, assuming applicable the semiclassical approach, we can use the Drude conductance for the transport of electrons in the quasi-1D dimension. Therefore, the expression for the conductance, if the length of the quantum wire is L, will be

$$\begin{aligned} G_\textrm{1D}=\frac{\sigma }{L}=\frac{e^2 n\tau }{L m_{qw}}, \end{aligned}$$

(21)

where ${m}_{qw}$ is given by Eq. (14), $\tau$ is the relaxation time, and n the electron density in the quasi-1D electron gas that, using Eq. (17), has the expression:

$$\begin{aligned} n &= \int _{0}^{E_F}f^0(E)g_\textrm{1D} (E)\textrm{d}E\nonumber \\ &= n_0+\frac{2m_{qw}\Omega }{h}\sum _{p=1}^{\infty } \frac{1}{\pi \sqrt{p}}A_{\Gamma ,p}A_{S,p}A_{T,p}\textrm{sin}\left( 2\pi p\eta _F \right) \end{aligned}$$

(22)

where ${f}^0(E)$ is the Fermi–Dirac distribution function and, from Eq. (20)

$$\begin{aligned} \eta _F=\frac{E_F}{\hbar \Omega }-\frac{1}{2}, \end{aligned}$$

(23)

being ${E_F}$ the Fermi level, related to the density of electrons of the 1D system through the equation:

$$\begin{aligned} E_F=\frac{h^2 n_{0}^2}{8m^{*}}, \end{aligned}$$

(24)

${n}_{0}$ represents the electron density of the 1D electron gas.

At very low temperatures, the term associated with the temperature in the sum of the Eq. (22), $A_{T,p}$, can be approximated by

$$\begin{aligned} A_{T,p}=\frac{z}{\textrm{sinh}(z)}, \end{aligned}$$

(25)

with $z=2\pi p\frac{kT}{\hbar \Omega }$.

Because the relationship between conductance and resistance is

$$\begin{aligned} R_\textrm{1D}=\frac{1}{G_\textrm{1D}} \end{aligned}$$

(26)

Then, from Eq. (21), we have

$$\begin{aligned} R_\textrm{1D}=\frac{L m_{qw}}{e^2n\tau }. \end{aligned}$$

(27)

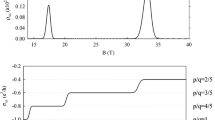
We mentioned above that the first measurements made on quantum wires were those by Fang and Stiles [11]. Thus, our first attempt with the model was to reproduce those results. In Fig. 2, we show the simulation obtained for the conductance and the resistance, as obtained with Eqs. (21) and (27), respectively. The plateaux are clearly seen at integer values of $2e^{2}/h$. The reference parameters used for these simulations were the following: an effective mass of of $0.0624m_{0}$, a magnetic field of 8 T, $\Gamma$ = 0.012 eV, $g^*$ = 2, T = 0.2 K and $\tau$ = $2.2 \times 10^{-14}$ s. If a different value for the intensity of the magnetic field were assumed the plateaux would shift.

Fig. 2

Simulation with the model of the conductance and its inverse, the resistance, for a quasi-1D electron system. The plateaux are clearly see at integer values of ${e}^{2}/h$. The reference parameters used for these simulations were the following: an effective mass of of 0.0624 ${m}_{0}$, a magnetic field of 8 T, $\Gamma$=0.012 eV, ${g}^*$=2, T=0.2 K and $\tau$ = $2.2 \times 10^{-14}$ s

At the very beginning several measurements of the conductance also appeared in the bibliography, exploring different experimental conditions [22,23,24,25]. Thus, in Fig. 3, we show the simulation obtained with the model for the conductance for several confinement energies, ${E}_0=\hbar \omega _0$, where $\omega _0$ is obtained from Eq. (10). It is observed that the conductance keeps the same shape although shifted respecting to the gate voltage axis. On the other hand, in Fig. 4 is shown the influence of the temperature over the plateaux, that are dimmer and dimmer as the temperature increases.

Fig. 3

Conductance for different confinement energies, from ${E}_0$=0.1–0.15 eV. The general parameters used in this simulation are the same as in Fig. 2

Fig. 4

Dependence of the conductance as a function of the gate voltage with temperature. From left to right, the conductance shown correspond to that at 1 K, 10 K, 20 K and 30 K, respectively. The rest of the fixed parameters used in the simulation are the same as in Fig. 2

4 Summary and conclusion

In this paper, we have described a semiclassical approach to the magnetotransport effects observed in quantum wires, a quasi-1D electron system, following a similar focus to that describes in [1] for the QHE and SdH phenomena in a 2D-dimensional electron system. We have found that the onset of the quantization phenomenon in the conductance, the plateaux, is a consequence of the Landau-type shape of the density of states. However, in the quasi-1D system, the quantization is not so defined and good as observed in a 2D electron system, because the quality of the plateaux is inherently conditioned by the profile of the density of states, Fig. 1b.

We hope that this semiclassical approach, very easy to implement and handle in any study, may be an useful tool in the understanding of the conduction mechanisms in the quasi-1D electron system.

In a forthcoming paper, we will try to extend the semiclassical approach described in this work and in [1] for addressing the magnetotransport properties of multilayers graphene and topological insulators.

Appendix: determination of the density of states, Eq. (17)

To determine the density of states for the electrons in the quasi-1D system, Eq. (15), we have first to get an expression for the density of every Landau-type energy level. Then, if we assume not broadening of them by the interaction with impurities and structural defects, it can be written as

$$\begin{aligned} g(x)=\frac{1}{\pi \hbar }\sqrt{\frac{m^*}{2\hbar \Omega x}}\delta \left( x-\frac{E}{\hbar \Omega }\right) , \end{aligned}$$

(28)

where $\delta$ is the Dirac distribution function. This equation allows us to use the Poisson sum rule

$$\begin{aligned}{} \sum _{n=-\infty }^{\infty }g(n+\frac{1}{2}) & =\int _{-\infty }^{\infty }g(x)\textrm{d}x\nonumber \\ & \quad +2\text {Re}\left\{ \sum _{p=1}^{\infty }\left( -1 \right) ^p \int _{-\infty }^{\infty }g(x)e^{\left( 2\pi px i \right) \textrm{d}x}\right\} , \end{aligned}$$

(29)

to express the entire density of states, given by

$$\begin{aligned} g_{1D}(E)=\frac{1}{\pi \hbar }\sqrt{\frac{m^*}{2E}}\left\{ 1+2 \sum _{p=1}^{\infty }\ \textrm{cos}\left[ (2\pi p \left( \frac{E}{\hbar \Omega }-\frac{1}{2}\right) \right] \right\} \end{aligned}$$

(30)

Moreover, if, additionally, we now take into account the effect of the magnetic field over spin of the electrons, instead of Eq. (26) we have to use the following expression for the density of every Landau-type energy levels:

$$\begin{aligned} g(x)=\frac{1}{\pi \hbar }\sqrt{\frac{m^*}{2\hbar \Omega x}}\delta \left( x-\left( \frac{E}{\hbar \Omega }{\mp } \frac{g^*}{4}\frac{m^*}{m_0}\right) \right) \end{aligned}$$

(31)

That substituting in Eq. (27) provides the equation

$$\begin{aligned} g_{1D}(E)=\frac{1}{\pi \hbar }\sqrt{\frac{m^*}{2E}}\left\{ 1+2 \sum _{p=1}^{\infty }\ \textrm{cos}\left[ 2\pi p \left( \frac{E}{\hbar \Omega }-\frac{1}{2}\right) \right] \textrm{cos}\left( p \pi \frac{g^*}{2}\frac{m^*}{m_0}\right) \right\} \end{aligned}$$

(32)

i.e.,

$$\begin{aligned} g_{1D}(E)=\frac{1}{\pi \hbar }\sqrt{\frac{m^*}{2E}}\left\{ 1+2 \sum _{p=1}^{\infty }\ A_{S,p}\textrm{cos}\left[ 2\pi p \left( \frac{E}{\hbar \Omega }-\frac{1}{2}\right) \right] \right\} \end{aligned}$$

(33)

Finally, taking into account the effect of the impurities over the width of the Landau-type levels, and assuming, for example, that this leads to a Gaussian broadening, the density of states of every Landau-type level can be written as

$$\begin{aligned} g(x)=\int _{-\infty }^{\infty }\frac{1}{\pi \hbar }\sqrt{\frac{m^*}{2\hbar \Omega x}}\delta \left( x-\left( \frac{E}{\hbar \Omega }{\mp } \frac{g^*}{4}\frac{m^*}{m_0}\right) \right) \left[ \frac{\sqrt{2\pi }\hbar \Omega }{\Gamma } \right] e^{\left\{ -\frac{2 \pi ^2x^2(\hbar \Omega )^2}{\Gamma ^2}\right\} } \end{aligned}$$

(34)

In addition, once introduced this expression in Eq. (27), an additional term, Eq. (16), appears inside the sum for the entire density of states of the quasi-1D electron system, arriving to Eq. (15).