1 Introduction

Spintronic relates the electron spin, charge current, and heat currents [1]. The interconversion between two of the three quantities mentioned will play an important role in energy conversion applications in the future. A branch of the spintronic is the spin caloritronics, which couple the spin currents with the heat currents, and its rapid development was due to the discovery of the spin Seebeck effect (SSE) [2], which has the potential to reduce power consumption in spintronic devices [3, 4]. The SSE refers to the generation of a flow of spin angular momentum, known as spin current, in a magnetic material due to the application of a temperature gradient. However, it is not possible to measure a spin current directly; therefore, it is necessary to inject this current in an adjacent conducting material with large spin–orbit interaction, such as Pt or Pd, through the inverse spin Hall effect (ISHE), the spin current is converted in a transverse charge current [3, 5, 6]. The spin current density flowing into the conducting material, also known as normal metal (NM), generates a transverse charge current density (\({\overrightarrow{J}}_{\mathrm{c}}\)) given by \({\overrightarrow{J}}_{\mathrm{c}}={\theta }_{\mathrm{SH}}(2e/\hslash ){\overrightarrow{J}}_{\mathrm{s}}\times \widehat{\sigma }\), where \({\theta }_{\mathrm{SH}}\) and \(\widehat{\sigma }\) are the spin Hall angle and the spin polarization vector parallel to the magnetization vector \(\overrightarrow{M}\), respectively, \(\hslash\)/2e guarantees the correct dimensions of the spin current density (\({\overrightarrow{J}}_{\mathrm{c}}\)) [7,8,9]. The SSE can be observed in two different configurations, longitudinal (LSSE) and transversal (TSSE), the difference lies in the direction of the spin current with respect to the temperature gradient (\(\nabla T\)), in the first case, the spin current is parallel to the \(\nabla T\); while in the other case it is perpendicular[4]. One important consideration in the experimental investigation of SSE is to get rid of unwanted contributions from magneto-thermoelectric effects, such as anomalous Nernst effect (ANE), which can be achieved using magnetic insulator materials. In this case, the spin current induced by the thermal gradient, is carried by magnons instead of charge carriers that transport the spin current in metals. Many SSE experiments are based on the ferrimagnetic yttrium iron garnet Y3Fe5O12 (YIG) material [10] because it exhibits two wanted properties: (i) it is insulator; (ii) it has the smallest known Gilbert damping parameter, \(\alpha \sim {10}^{-5}\). The Gilbert damping parameter causes the magnetization to spiral towards the direction of the magnetic field up to reach equilibrium, with a decay characteristic time of the precession amplitude depending on the material properties. Thus, a low damping parameter can be useful for high-frequency microwave applications [6]. Nowadays, the spinel ferrites have attracted attention for current generation due to the fact that they can be prepared from low-cost materials [11], they have a less complex crystal structure compared to YIG [12], and to exhibit Gilbert damping parameter around \(\sim\)(\({10}^{-2}-{10}^{-3}\)) [10, 13]. Also, the quite strong magnetocrystalline anisotropy observed in some ferrites can be used to tune the preferred orientation of the magnetization vector, thus affecting the results obtained by the SSE experiment [14]. On the other hand, since the ferrites have different compositions and can be prepared by different methods, the reported values of the SSE coefficient are widely spread. For example, the value of the Seebeck coefficient for slab ferrites previously reported were (Mn, Zn)Fe2O4 (0.071 mV/K) [15], Ba2Zn2Fe12O22 (0.11 mV/K) [14], Ni–Zn ferrites (0.025 mV/K) [16]; while the reported values for some ferrites thin films were NiFe2O4 (0.030–0.58 mV/K) [17, 18], CoFe2O4 (0.0941 mV/K) [12]. In recent years, it has been reported the room temperature observation of SSE in a normal spinel zinc ferrite (ZFO) in slab shapes. These ferrites presented a soft weak ferromagnetic behavior, with a magnetization of 1.2 emu/g, suggesting a partially inverted spinel structure, producing a nonzero magnetization compared with the ideal ZFO [16, 19]. Despite its weak ferromagnetism, an unexpected LSSE response was obtained with a spin Seebeck coefficient of about 28 nV/K. These results suggested that the LSSE response was originated from the surface magnetization of the ZFO slabs, which could explain the considerable value of the LSSE thermopower despite the negligible saturation magnetization [19]. Then the LSSE measurements in the zinc ferrites thin films might help to clarify the origin of the observed effect. Therefore, in this paper, we study the influence of the substrate and the magnetic anisotropies on the spin Seebeck effect, to better understand the spin’s thermopower origin in a weak ferromagnetic film, ZnFe2O4. The paper is organized into the following sections: Sect. 2 presents the experimental details of the techniques used, specifying the sample preparation, the description of the experimental setup for the ferromagnetic resonance technique, and the longitudinal spin Seebeck effect. In Sect. 3, the main results are discussed, comparing the LSSE response in a zinc ferrite thin film growth on different substrates, also, the spin current density generated by the SSE was studied. Finally, the conclusions are presented in Sect. 4.

2 Experimental procedure

2.1 Preparation of thin films

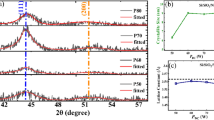
ZFO thin films were grown on different substrates, Si (111), SrTiO3 (100), and MgO (100) using a RF magnetron sputtering system, under an atmosphere of Ar/O2 and a substrate temperature of 500 °C. The thin films had a thickness of approximately 90 nm, which was measured by a Bruker DektakXT profilometer. The method of preparation of the samples from the ceramic target to thin films is detailed in [20].

2.2 Characterization of thin films

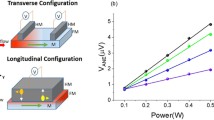
The crystal structure of the target as well as of the thin films was analyzed using X-ray diffraction (XRD), which was performed on a Malvern-PANalytical Modelo Empyrean 2012 diffractometer with CuKα radiation with wavelength λ = 0.154 nm. On the other hand, the ferromagnetic resonance (FMR) technique was performed to study the magnetic properties in thin films such as the anisotropy fields and relaxation mechanisms. The fixed frequency was 9.5 GHz and the samples were placed in the middle of a rectangular microwave cavity at room temperature. Figure 1a shows a schematic illustration of the in-plane precession of the magnetization vector (\(\overrightarrow{M}\)) around the effective magnetic field (\(\overrightarrow{H}\)), driven by a perpendicular microwave field. The resonance field was obtained as a function of the azimuthal angle (\({\varphi }_{\mathrm{H}}\)) to study what type of symmetry and magnetic anisotropy was presented in each sample. Additionally, the damping parameter was obtained by measuring the FMR linewidth \(\Delta H\) as a function of the microwave frequency.

Fig. 1
figure 1

a Schematic illustration of the sample studied by ferromagnetic resonance (FMR) technique. b Schematic illustration of the LSSE experimental setup to generate the perpendicular spin current and the planar view showing the Ag electrodes to measure the VSSE voltage

Full size image

For the SSE measurement, we used the LSSE configuration, which is the most straightforward manner to acquire the spin Seebeck response in insulator materials [10]. Before describing the experimental set-up, as shown in Fig. 1b, it is necessary to take into account that the sample used is a bilayer made of zinc ferrite as a ferromagnetic insulator (FM), and a paramagnetic metallic layer (NM) with strong spin–orbit coupling, in this case, it was used Pt. Thus, the experimental setup consisted of the following:

  1. i.

    Apply a temperature gradient across the thickness of the sample, it is applied parallel to the surface normal (z-direction). Two Peltier elements with a surface dimension of 4 \(\times\) 4 mm2 were connected in series, but in opposition, so that one surface of the sample (Pt side) was heated while the other surface (substrate side) was cooled. A thermocouple was used to measure the temperature difference \(\Delta T\) across the sample.

  2. ii.

    At the same time, an external magnetic field (\(\overrightarrow{H}\)) is applied parallel to the sample surface (y-direction). Therefore, the magnetic field and the temperature gradient are both perpendicular to the electric field generated along the Pt layer (x-direction).

  3. iii.

    To each sample, a Pt (\(\sim\) 4 nm) layer was deposited by DC sputtering. Ag electrodes were attached to the ends of the Pt layer for measuring the voltage directly with a nanovoltmeter.

Finally, to correlate the magnetic response with the Seebeck signal, a Vibrating Sample Magnetometer (VSM Microsense model EV7) was used to measure the magnetization in the material.

3 Results and discussion

The X-ray diffraction pattern for the powder sample was analyzed using the FullProf program by employing the Rietveld refinement technique. The Rietveld method gives structural details, such as the lattice parameter, cation distribution, asymmetry, and type of structure using a least squares approach to compare the peaks of X-ray diffraction patterns obtained experimentally with those calculated from a structural model. The experimental data match with that of the calculated as well as ICSD collection code: 85,869. The XRD pattern exhibited a normal spinel structure for ZFO bulk, i.e. all the Fe ions are forced to occupy the octahedral sites (B); while the Zn ions fill tetrahedral sites (A). Also, it was found a lattice parameter of 8.44 Å and Fd-3 m space group. Rietveld refinement parameters such as the goodness of fit (\({\chi }^{2}\)), profile reliability index (Rp), and weighted profile reliability index (Rwp) reached a minimum value of 2.6, 38.2, and 13.4, respectively. A schematic illustration of the crystallographic structure obtained from the refined data was drawn using the program VESTA and it is shown in the inset of Fig. 3.

In the case of the thin films, they presented lattice constants close to bulk and were derived from the observed Bragg diffraction peaks. Fig. 2a–c shows the XRD patterns of the ZnFe2O4 thin films on Si (111), MgO (100), and STO (100), respectively, and Fig. 2d shows the experimental and the Rietveld refined XRD pattern for the ZFO target. The lattice mismatch between the substrate and the film was around 3.9%, 4.1% and 4.5% for the films grown under Si, MgO, and STO, respectively.

Fig. 2
figure 2

a–c XRD patterns of ZnFe2O4 thin films on Si (111), MgO (100), and STO (100), respectively. d Rietveld refined XRD patterns for the ZFO target. The circles represent experimental data, and the solid line represents Rietveld’s refined data.

Full size image

According to works performed by other authors, a large lattice mismatch can induce some magnetic anisotropies such as the strain and magnetocrystalline anisotropies in thin films, especially the perpendicular magnetic anisotropy [21, 22]. Therefore, it is necessary to study de magnetic anisotropies of the zinc ferrite thin films to confirm this.

The magnetization of the films was compared with the nominal value of the bulk sample [19]. For this purpose, we performed in-plane magnetization measurements at room temperature by VSM. The results shown in Fig. 3 indicated that the ZFO thin films presented a magnetic response of about 8.0 \({\mu }_{\mathrm{B}}\), which is much larger when compared with the magnetization of the bulk sample of 0.05 \({\mu }_{\mathrm{B}}\).

Fig. 3
figure 3

Room temperature in-plane magnetic hysteresis loops of ZFO thin films on different substrates. The inset shows the crystallographic structure of ZFO obtained using the program VESTA

Full size image

This enhancement in the magnetization suggests that Fe ions migrate to A sites so that a partial transformation of the ferrite is occurring; i.e. the norm spinel structure from bulk ZFO is converted into an inverse spinel structure during the fabrication process of the ZFO thin film. This behavior can be attributed to the fact that not all the zinc ions occupy tetrahedral sites due to the zinc ferrite-manufacturing process when the sample is rapidly cooled at a high temperature [23]. Therefore, the ferromagnetic interaction between Fe ions increases by the migration of these ions to tetrahedral sites [19, 20, 24,25,26,27]. Previously, these samples were analyzed by X-ray photoelectron spectroscopy, this studio showed the existence of a partial inversion when the material was fabricated in thin film. Therefore, the cation distribution would be attributed to an increase in the saturation magnetization in ZFO thin films, this means that possibly the exchange interaction between A and B sites (JAB) will govern the magnetic properties instead of the BB interaction [20].

To gain insight into the magnetization dynamics of the samples, ferromagnetic resonance (FMR) measurements were performed. So, for each sample, the experimental data obtained from the in-plane (IP) angular dependence of the ferromagnetic resonance field, were fitted to a model that takes into account the magnetic free energy of the system, similar to that employed in [28, 29]. From this fitting model, it was possible to extract some physical parameters, such as the saturation magnetization and the anisotropy fields.

The results showed a fourfold symmetry for the samples deposited on MgO and STO, while a twofold symmetry was observed in the sample deposited on Si. Figure 4a–c shows the resonance field (\({H}_{\mathrm{R}}\)) measured as a function of the azimuthal angle (\({\varphi }_{\mathrm{H}}\)) for the ZnFe2O4 thin films on Si, MgO, and STO substrates, respectively. The measurements show that the samples grown on MgO and STO have a small uniaxial contribution superimposed on a fourfold crystalline anisotropy. The effective magnetization (Meff), the perpendicular (Hut), longitudinal uniaxial (Hul), and cubic (Hc) anisotropy fields were extracted from the fitted curves (red solid line). All samples exhibited a large perpendicular magnetic anisotropy, which may be a consequence of the presence of the tensile strain and the lattice mismatch between the film and the substrate, according to [21, 30].

Fig. 4
figure 4

a–c In-plane angular dependence of the ferromagnetic resonance field (HR) for the thin films of ZFO/Si, ZFO/MgO, and ZFO/STO, respectively. The black spheres are the experimental data and the red solid lines are the theoretical fits

Full size image

On the other hand, a coplanar waveguide (CPW) spectrometer was used to estimate the intrinsic Gilbert damping (\(\alpha\)), via the dependence of the FMR linewidth (\(\Delta H\)) with the frequency (not shown here). Considering the linear approximation \(\Delta H=(4\pi \alpha /\gamma )f+ {\Delta H}_{0}\), where the first term gives the Gilbert damping and \({\Delta H}_{0}\) reflects the contribution of the magnetic inhomogeneities.

The Gilbert damping parameter for ZFO90/Si, ZFO90/MgO, and ZFO90/STO was estimated to be 0.022, 0.026, 0.035, respectively, which had the same order of magnitude as the reported damping constant for typical spinel ferrites [31, 32] and are comparable with the Gilbert damping in other systems such as NiFe and Tm3Fe5O12 [33, 34]. More details of the investigation of the twofold and fourfold anisotropies in these ferrites can be found elsewhere [35]. Then, taking into account only the lower damping parameter, the highest LSSE voltage is expected to be provided by the sample grown on Si.

To confirm the above hypothesis, we investigated the LSSE signal of our thin films, which is the most straightforward manner to measure the SSE in insulators [10]. The initial measurements were made in the Pt/ZFO90/Si sample.

Initially, a temperature gradient was applied in parallel with the surface normal of the thin film, along the + z and − z-directions. Subsequently, the magnetic field \(\overrightarrow{H}\) was applied along the y direction. So the spin current that is generated in the ZFO material is injected into the Pt layer and is transformed into a charge current (\({I}_{\mathrm{ISHE}}\)) through the inverse spin Hall effect. Therefore, to detect the SSE voltage (\({V}_{\mathrm{ISHE}}=R\times {I}_{\mathrm{ISHE}}\)), on the edges of the Pt film, were placed two silver-painted electrodes, this voltage was measured with a nanovoltmeter directly. Figure 5a shows the \({V}_{\mathrm{ISHE}}\) voltage detected between the Ag electrodes as a function of the magnetic field, for the Pt/ZFO90/Si sample when it is subjected to various temperature differences \(\Delta T\) between the surfaces of the sample. By reversing the \(\nabla T\) direction, the voltage signal is also reversed, as shown in Fig. 5b for different values of \(\Delta T\), indicating that the \({V}_{\mathrm{ISHE}}\) signal is attributed to the longitudinal spin Seebeck effect [15, 36]. Figure 5c shows the linear variation of SSE voltage with the temperature difference \(\Delta T\), when a \(\nabla T\) is applied in two opposite directions. As expected, the inversion of the direction of the temperature gradient changes the sign of the voltage signal. Although large values in the anisotropy fields were obtained, they did not modify the shape and magnitude of the LSSE voltage hysteresis loop measured as a function of the external magnetic. These results suggest that there is not a large strain anisotropy to significantly influence the LSSE response for the samples, in agreement with the results reported for other ferrites, NiFe2O4 [22].

Fig. 5
figure 5

a, b Variation with the magnetic field of the \({V}_{\mathrm{SSE}}\) measured on the Pt layer for different values of \(\Delta T\). c Variation of the voltage with \(\Delta T\) when the temperature gradient is applied along the + z and − z

Full size image

As mentioned previously, the spin current injected into Pt is converted into charge current due to ISHE, which leads to the emergence of an electric field given by \(\overrightarrow{E}=\beta \left({\overrightarrow{J}}_{\mathrm{s}}\times \widehat{\sigma }\right)\), onde \(\beta\) is the coefficient of normal metal. The electric field along the electrodes can be written as \(E={S}_{\mathrm{FM}}\nabla T\) [37,38,39], where \({S}_{\mathrm{FM}}\) is the Seebeck spin coefficient with a unit of V/K.

The measured electric potential difference is given by \({V}_{\mathrm{ISHE}}=E{w}_{\mathrm{Pt}}\mathrm{cos}\phi\), where \({w}_{\mathrm{Pt}}\) is the distance between electrodes and \(\phi\) is the angle between the \({\overrightarrow{J}}_{\mathrm{c}}\) and \(\overrightarrow{H}\).

Writing \(\nabla T=\Delta T/{t}_{\mathrm{FM}}\), (where \({t}_{\mathrm{FM}}\) is the thickness of the material) the potential difference due to LSSE becomes \({V}_{\mathrm{ISHE}}={S}_{\mathrm{FM}}\left(\frac{{w}_{\mathrm{Pt}}}{{t}_{\mathrm{FM}}}\right)\Delta T\mathrm{cos}\phi\). However, it is important to take into account the thermal conductivity (\(\kappa\)) along the sample and the thickness of the substrate and the FM layer as the temperature difference applied to the sample is not equal to the temperature difference in the FM [35, 36].

Neglecting the interfacial resistances, the potential difference measured between the ends of the sample becomes [36] \({V}_{\mathrm{ISHE}}={S}_{\mathrm{FM}}\left(\frac{{w}_{\mathrm{Pt}}{\kappa }_{\mathrm{Sub}}}{{{\kappa }_{\mathrm{Sub}}t}_{\mathrm{FM}}+{{\kappa }_{\mathrm{FM}}t}_{\mathrm{Sub}}}\right)\Delta T\mathrm{cos}\phi\). Considering the substrate as the Si and the FM layer as the ZFO, using \({\kappa }_{\mathrm{Si}}=148\) W/mK, \({\kappa }_{\mathrm{ZFO}}=8\) W/mK [40, 41], \(\phi =0^\circ\) (\({\overrightarrow{J}}_{\mathrm{c}}\perp \overrightarrow{H})\), \({w}_{\mathrm{Pt}}=4\) mm, \({t}_{\mathrm{ZFO}}=90\) nm, \({t}_{\mathrm{Sub}}=0.5\) mm, we get \({S}_{\mathrm{ZFO}}\approx 0.003\) μV/K. On the other hand, due to the \({V}_{\mathrm{ISHE}}\) reflects the behavior of the magnetization, it is possible suggesting that the measured voltages are originated from the magnetism of the ZFO films, in the same way as other investigations [12, 39].

Figure 6 shows the magnetic field dependence with the SSE voltage for the ZFO films on MgO and STO. \({\Delta V}_{\mathrm{SSE}}\) vs \(\Delta T\) showed a linear dependence, where the red solid lines are the theoretical fits. Using a known value of thermal conductivity for MgO and STO (\({\kappa }_{\mathrm{MgO}}=44.2\) W/mK, \({\kappa }_{\mathrm{STO}}=12\) W/mK), \({t}_{\mathrm{Sub}}=5\) mm and \({w}_{\mathrm{Pt}}=10\) mm for both samples, the spin Seebeck coefficients extracted were \({S}_{\mathrm{ZFO}}\approx 0.03\) μV/K and \({S}_{\mathrm{ZFO}}\approx 0.11\) μV/K for Pt/ZFO/MgO and Pt/ZFO/STO, respectively. Also, we notice in Fig. 6a, c that to reach the same value of \({V}_{\mathrm{SSE}}\) (\(\sim\) 3 V\(\upmu\)), a higher temperature gradient is needed in STO90/ZFO than in MgO90/ZFO. This may be due to two reasons: (i) the Gilbert damping derived from the fitting of the data measured by FMR, which was higher for the sample growth on STO than for the film on MgO, or; (ii) due to the higher thermal conductivity of MgO in comparison with the thermal conductivity of STO.

Fig. 6
figure 6

a, c Magnetic field dependence of SSE signal for Pt/ZFO90/MgO and Pt/ZFO90/STO. b, d correspond to voltage variation with \(\Delta\)T for Pt/ZFO90/MgO and Pt/ZFO90/STO, respectively

Full size image

Finally, for each sample, the values of the spin current density were estimated, using the equation \({J}_{\mathrm{s}}=\hslash /2e {\theta }_{\mathrm{SH}}{J}_{\mathrm{c}}\) [7]. Figure 7 shows the dependence of charge current density and spin current density with \(\Delta T\) for all samples. For the case of the Pt/ZFO90/Si film, the electric resistance after connecting the electrical contacts to measure \({V}_{\mathrm{SSE}}\) was 1.7 k\(\Omega\). Considering the thickness of Pt with 4 nm, the \({\theta }_{\mathrm{SH}}\) for the Pt is \(\sim\) 0.07 [40, 41], the sample dimension was 16 mm2, we have that applying a \(\Delta T\) = 11 K, a voltage of 2.37 mV was generated, which leads to \({J}_{\mathrm{c}}\approx\) 87.13 A/m2, which implies \({J}_{\mathrm{s}}=6.09\frac{\hslash }{2e}\) A/m2.

Fig. 7
figure 7

Dependence of charge current density and spin current density with \(\Delta\)T for Pt/ZFO/Si, Pt/ZFO/MgO, and Pt/ZFO/STO as indicated

Full size image

Similarly, \({J}_{\mathrm{c}}\) and \({J}_{\mathrm{s}}\) were calculated for the films grown on MgO and STO, in this case, the resistance and dimensions were R = 1.20 k\(\Omega\) and 10 mm \(\times\) 5 mm for both materials, which correspond to a value of the resistivity of 2.4 \(\times\) 10–6 \(\mathrm{\Omega m}\). This value is around of order of magnitude that was previously reported in Pt films of similar thicknesses [44]. The values of \({J}_{\mathrm{s}}\) were similar for the samples grown on STO and MgO, which can be directly related to the similarity between the fourfold symmetry obtained by FMR, and the damping parameter for the two films. According with Qiu et al. [45], the magnitude of the voltage induced by the LSSE is sensitive to the FM/NM interface. So, it is possible to guarantee a large LSSE voltage in a FM/NM system with a good crystalline interface, but if an amorphous layer is formed at the top surface of the magnetic film, the LSSE voltage can decay steeply [46, 47]. However, The LSSE voltage is also influenced by magnetocrystalline anisotropy [47]. So, if the cubic or uniaxial anisotropy field increases, then the LSSE voltage decreases, suggesting that the spin Seebeck effect can be tuned by manipulating the anisotropy of the material.

By comparing the spin Seebeck coefficients with the thermal conductivities of the substrates, we found that the \({S}_{\mathrm{FM}}\) of thin films is highly sensitive to the thermal conductivity of the magnetic layer and substrate. Both quantities are inversely proportional. However, a low thermal conductivity does not imply low spin current densities, which was evidenced by the spin current densities calculated for the Pt/ZFO/MgO and Pt/ZFO/STO samples, which presented similar values of \({J}_{\mathrm{s}}\). With this result, we suspect that the type of anisotropies, twofold and fourfold in the sample plays an important role in the generation of spin currents. Although the \({S}_{\mathrm{FM}}\) for the Pt/ZFO/MgO thin film was similar to that coefficient obtained for the bulk sample around 28 nV/K [19]; the spin Seebeck coefficient of Pt/ZFO/STO was an order of magnitude greater than the one obtained for the bulk. For this reason, it is necessary paying special attention to the growth conditions to adjust structural characteristics that allow for improving the SSE response. On the other hand, in the ZFO bulk, the saturation magnetic field for the SSE signal (\({H}_{\mathrm{SSE}}^{\mathrm{Sat}}\)) was higher than 2 kOe [19], whereas in the ZFO thin films, the values of \({H}_{\mathrm{SSE}}^{\mathrm{Sat}}\) were achieved with 600 Oe. This change in the magnitude of \({H}_{\mathrm{SSE}}^{\mathrm{Sat}}\) can be associated with the presence of a notable perpendicular magnetic anisotropy in the thin films, as shown in Fig. 4, either due to the induced surface strain or the shape anisotropy in the bilayer system FM/NM, our results are in agreement with the other results [47, 48].

4 Conclusion

In summary, it was possible to detect a LSSE voltage in ZnFe2O4 (ZFO) thin films grown on Si, MgO, and STO. The spin Seebeck coefficients extracted from the data for the thin films are highly sensitive to the thermal conductivity of the thin film and the substrate. Therefore, it is important to pay more attention to the growth of the magnetic layer, and the choice of substrate, before measuring the Seebeck response in a material. Even though the ZFO thin films presented an enhanced magnetic response compared to its bulk counterpart, the LSSE response cannot be only attributed to the magnetism of the material itself, as we mentioned previously, the lattice mismatch and the presence of anisotropies can change significantly the magnitude of LSSE voltage; also, the type of substrate plays an important role in the spin Seebeck coefficient calculated. Therefore, we conclude that the significant difference in the magnetic and LSSE response between the thin films and bulk material makes thin films attractive as a material of study for the spin current generation in the SSE, like other ferrites that are opening new paths to engineering the LSSE dispositives.