Abstract
During flight, vibrations potentially cause aerodynamic instability and noise. Besides muscle control, the intrinsic damping in bird feathers helps to reduce vibrations. The vanes of the feathers play a key role in flight, and they support feathers’ aerodynamic function through their interlocked barbules. However, the exact mechanisms that determine the damping properties of the vanes remain elusive. Our aim was to understand how the structure of the vanes on a microscopic level influences their damping properties. For this purpose, scanning electron microscopy (SEM) was used to explore the vane’s microstructure. High-speed videography (HSV) was used to record and analyze vibrations of feathers with zipped and unzipped vanes upon step deflections parallel or perpendicular to the vane plane. The results indicate that the zipped vanes have higher damping ratios. The planar surface of the barbs in zipped vanes is responsible for aerodynamic damping, contributing 20%–50% to the whole damping in a feather. To investigate other than aerodynamic damping mechanisms, the structural and material damping, experiments in vacuum were performed. High damping ratios were observed in the zipped vanes, even in vacuum, because of the structural damping. The following structural properties might be responsible for high damping in feathers: (i) the intact planar surface, (ii) the interlocking of barbules, and (iii) the foamy inner material of the barb’s medulla. Structural damping is another factor demonstrating 3.3 times (at vertical deflection) and 2.3 times (at horizontal deflection) difference in damping ratio between zipped and unzipped feathers in vacuum. The shaft and barbs filled with gradient foam are thought to increase the damping in the feather further.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The flight of birds is believed to have originated from dinosaurs’ jumping, gliding, and eventually flapping powered flight [1]. Through evolution, birds have transformed the challenging act of flight into a complex mode of locomotion [2]. Aerial locomotion was accompanied by numerous anatomical and physiological adaptations [3]. These avian adaptations include wing stroke efficiency, the fusion of skeleton parts, and strong yet lightweight feathers [3, 4]. In addition, the bird feathers are linked to the musculoskeletal and soft tissues and can create efficient aerodynamic force [5].
During flapping, wings undergo continuous oscillations [6]. Unwanted oscillations can negatively influence the performance of dynamic systems, such as giant reeds [7], wings of dragonflies [8] and damselflies [9], and insect antennae [10]. In oscillations, damping alters the response of the system and results in stability and enhanced controllability [11]. The loss factor is the ratio of the loss modulus to the storage modulus and represents a system's viscoelasticity and damping capacity. For small damping ratios, the loss factor is twice the damping ratio [12]. The loss factor is in the range of 0.03–0.07 for the bending of the shaft of swan feathers [13] and 0.896 ± 0.238 for the shafts of pigeon feathers [14]. The damping ratios of pigeon feather shaft regions gradually decreased from the base to the tip from 0.268 to 0.034 [15].
A typical primary feather consists of a shaft and vanes. The shaft has a rigid outer cortex and an inner foam-like medulla [16]. The vanes consist of numerous barbs aligned parallel to each other but at a certain angle to the shaft [17]. The architecture of the vane is closely linked with advancements in aerial locomotion [18]. The barb angle variations [19, 20] and length [3] were assumed to be responsible for the vanes’ morphology. Two regions along the barb were observed by Robert Hooke [21], and details of barbules were described [19]: the distal part with hooks that interlock with grooves on the proximal part.
Previous research has studied the properties and mechanisms related to the interlocking of the zipped barbs and their potential application [14, 22,23,24,25,26]. The barb’s interlocking is reversible and can be quickly re-established after separation, and the separation force of the hooklets was investigated [22]. The robustness and flaw-tolerance of the barb-barbule structure were explained by an analytical model [23]. It was assumed that the membranous flaps of overlapping barbules of feathers are impervious to air [27]. The vane’s permeability is based on the effect of barb dimensions and the degree of their mechanical interlocking [28]. Damping of feather vibrations could be affected by the vanes supported by reversible hooklets, cooperative effects of neighboring hooklets groups, and overlapping barbules [29].
In this study, the damping behavior and the underlying damping mechanisms of the zipped and unzipped vanes were examined at two types of deflection under atmospheric conditions, to show the functional significance of zipping structures in damping. Air is considered a viscous media in our experiments. Therefore, the energy dissipation of feathers vibrating in air occurs due to the viscous airflow caused by the vibrating structure [30]. Experiments were also carried out in vacuum, to decrease the effect of the friction between feathers and air and the associated aerodynamic damping. Three damping mechanisms were discussed based on the feather morphology and obtained experimental data.
2 Materials and methods
2.1 Feather preparation and morphology observations
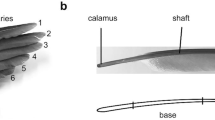
The outermost primary feathers (Fig. 1A, Nos. 1–5) of an adult male rock pigeon (Columba livia) were taken from the Zoological Institute of Kiel University, Germany. An iPhone X camera (Apple, California, USA) and a scanning electron microscope (SEM) Hitachi S-4800 (Hitachi, Chiyoda, Japan) were used to explore the hierarchical structure of the feathers (Fig. 1). For SEM, the middle section of the vanes was sectioned, glued, and mounted on an SEM stub, coated with 8 nm gold–palladium using a sputter coater EM SCD500 (Leica, Wetzlar, Germany), and examined at an acceleration voltage of 3.0 kV.
Morphology of the primary flight feathers. A Wing of the pigeon with numbered primary feathers. B Primary flight feather (PFF No.1) is composed of the shaft and asymmetric vanes (upper image). Lower image represents unzipped vanes after air gun treatment. C Hooked barbules are interlocking with the neighboring barbs within the vane. D Hooklets at the tip of the barbules interlocking with the barbules. E The damping oscillation of the feather specimen was measured by two excitations and release vertically (upper panel) perpendicularly to the vane and horizontally in the plane of the vane (lower panel). The right image shows the simplified cross section of the feathers shaft (dot) with zipped vanes (full line) and unzipped vanes (dotted line) under 2 deflections
2.2 Damping test at the atmospheric pressure and in the vacuum condition
Damping tests were performed at ambient conditions (room temperature of 18 °C–20 °C and relative humidity of 40%–45%). The specimens (primary feathers Nos.1–5) were fixed at the calamus with the vane oriented horizontally. The feather oscillations were excited by a step deflection of 10 mm in horizontal (parallel to the vanes, from the leading edge to the trailing edge, x-axis) or vertical (perpendicular to the vanes, from the ventral to the dorsal side, y-axis) direction. The tips of the feathers were marked using a small white paint point (the mass could be ignored compared to the mass of the feathers) to increase the tracking efficiency. The vanes' unzipping was performed by treating the feather with an air gun for 1 min with a pressure of 1.7 atm (Fig. 1B).
Damping tests in vacuum were performed inside a glass bell at 10 mbar pressure, to decrease the effect of air friction. Oscillations of the feathers fixed at their calamus on a 3D micro-manipulator were excited by the 10 mm tip deflection.
The decaying vibrations were recorded using a high-speed digital video (HSV) camera (I-Speed 3, Olympus, Tokyo, Japan) focused on the tip of the feathers with a focal plane parallel to the oscillation plane at 3000 fps, shutter time of 0.667 µs, and resolution of 1280 × 1024 pixels.
The tracking data (horizontal position X and vertical position Y) were extracted by Tracker (OSP, Massachusetts, USA) and plotted in the orthogonal coordinate system (Fig. 2). Fast Fourier Transform (FFT) in Origin software (OriginLab, Massachusetts, USA) was performed for determination of the fundamental frequencies in X- and Y-directions separately. Damping ratios were obtained using the fitting procedure in Origin software (OriginLab, Massachusetts, USA).
It is challenging to predict orders of frequencies and mode shapes that do not have uniform cross-section areas or constant elastic moduli [31]. A related aspect of flutter in airflows was described. Feathers may exhibit several oscillation modes and abruptly switch from one mode to another [32]. The first main frequencies of the vibrations in horizontal (fx) and vertical (fy) directions in the air and vacuum were determined to simplify the analysis. The equation for under-damped vibrations was employed to define vibrations of the first main (fundamental) frequency. The displacement X and the decay time t satisfy the under-damped condition according to the following equation [33]:
where β is the damping coefficient, A is the initial amplitude, e is Euler’s number, ω is the frequency, and φ is the phase angle. The damping coefficient β was obtained by curve fitting with initial boundary conditions for A being the peak value of the oscillation, ω being the frequency gained by FFT analysis, and φ initially set to zero. To compare the present data with results gained from earlier studies, the damping coefficient was converted to the damping ratio ζ using the equation below:
For statistical analysis, two-way ANOVA was used for normalized data, including the Turkey test for multiple comparisons by the software SigmaPlot 12.0 (SPSS Inc, Chicago, USA).
3 Results
3.1 Morphology
The primary feathers are shown in Fig. 1A. In the primaries, the shaft is surrounded by the zipped asymmetrical vanes (Fig. 1B). A feather with unzipped vanes after treatment with the air gun is shown in Fig. 1B. Barbules and hooklets could be visualized using SEM. The barbs are arranged at some angle towards the tip. They are interlocked with the adjacent barbs via the overlapping barbules in a uniform direction (Fig. 1C). The barbules can be subdivided into two distinct regions, the distal part that branches out at the tip having hooklets and the proximal one towards the base (Fig. 1D) The hooklets overlap at the adjacent barb and keep neighboring barb in parallel (Fig. 1D). The simplified cross section of the feathers shaft (dot) with zipped vanes (full line) and unzipped vanes (dotted line) under 2 deflections is presented in the right image (Fig. 1E).
3.2 Damping behaviors
Damping tests were conducted to investigate the damping property of the feathers with both zipped and unzipped vanes at ambient conditions (atmospheric pressure) and in vacuum. In the air, the shapes of the trajectories, excursion amplitudes, and the directionality of the vibrations varied depending on the zipping state of the vanes and initial deflection direction (Fig. 2A–D). The vibrations of feathers in the vacuum differed in their tip trajectory shapes and amplitude decay speed (Fig. 2E–H). The oscillations of the primary feathers with the zipped vanes and unzipped vanes in the atmosphere and the vacuum are shown in Figs. 3, 4. The oscillations of all feathers decayed in an under-damped regime. The oscillations in vacuum decayed slower.
3.3 Vibration frequency
The frequency spectra were obtained using FFT of the X(t) and Y(t) curves. To simplify the analysis, the first main frequencies of the vibrations in horizontal (fx) and vertical (fy) directions at ambient atmospheric conditions and the vacuum condition are summarized in Tables 1 and 2.
In the atmosphere, the feathers with zipped vanes had significantly lower fundamental vibration frequencies f(x) and f(y) than the unzipped vanes at both horizontal (P < 0.001) and vertical deflections (P < 0.001). The possible reasons for the higher vibration frequencies of the unzipped vanes could be the effective rigidity and its distribution, which may affect the vibration modes and damping ratios. In zipped feathers, the innumerable barbules and hooklets interact during vibrations. Since the hooklets interlocking and overlap of barbules are influenced by the external force, the sliding, unzipping and new hooking may change the temporary microstructure.
In vacuum, only under vertical deflection, the frequencies of vibration f(x) and f(y) of the zipped vanes were significantly lower than that of the unzipped vanes (P = 0.021 and P = 0.041, correspondingly). f(x) was significantly different between the two deflection directions (P = 0.013 and P < 0.001, for feathers with zipped/unzipped vanes). The possible reason for the absence of a significant difference between zipped and unzipped vanes at horizontal deflection in vacuum could be the following. The influence of the barbs’ interlocking in vertical deflections still works, even though the hooks were partly unzipped. These barbs overlapping and interlocking hinder the barb separation (vane extension) but allow the vane compression. This overlapping barb property could affect the effective feather stiffness and distribution at horizontal deflection.
3.4 Damping in air
For comparative aspects, the damping characteristics of the vanes were analyzed using the damping ratios determined for the first natural frequency. Under vertical deflections, the damping ratios of feathers with the zipped vanes were ζx = 0.368 ± 0.068 and ζy = 0.477 ± 0.213, and the values of unzipped vanes were ζx = 0.297 ± 0.042, ζy = 0.248 ± 0.092. Under horizontal deflection, the damping ratios of the zipped vanes were ζx = 0.628 ± 0.110 and ζy = 0.272 ± 0.026, while with the unzipped vanes were ζx = 0.330 ± 0.083 and ζy = 0.219 ± 0.044 (Fig. 5).
For vibrations in the horizontal direction, the highest damping ratio ζx was observed in feathers with zipped vanes under horizontal deflection (P < 0.001). At vertical deflections, ζx decreased by 20%, and ζy decreased by 50% after unzipping. At horizontal deflections, the ζx decreased by 48%, and ζy decreased by 20% after unzipping. There was no difference in the damping ratio between zipped and unzipped vanes under vertical deflection (P = 0.295). In the feathers with zipped vane, a significant difference was found between the two deflection directions (P < 0.001). In contrast, no difference was present in the damping ratio between the two deflections in the feathers with unzipped vanes (P = 0.758).
For vibrations in the vertical direction, significant differences in the damping ratios ζy were found in zipped and unzipped vanes under vertical deflection (P < 0.001). In zipped vanes, damping ratios for the two deflection directions showed a statistically significant difference (P = 0.002). However, no statistically significant difference was found in the unzipped feathers.
In summary, the zipped vanes had a higher damping capacity along the direction of deflections. For both ζx and ζy from unzipped vanes, no significant difference was found between the two deflection directions. The unzipping changed the damping of vanes under two deflections by affecting their integrity, partly weakening the hooklets-mediated interactions between barbs and reducing the coupling between vibrations perpendicular and parallel to the vane plane.
3.5 Damping in vacuum
In vacuum, the damping ratios of feathers with the zipped vanes under vertical deflections were ζx = 0.216 ± 0.051 and ζy = 0.341 ± 0.049, and the values for unzipped vanes were ζx = 0.096 ± 0.009, ζy = 0.075 ± 0.013. Under horizontal deflection, the damping ratios of feathers with zipped vanes were ζx = 0.353 ± 0.140 and ζy = 0.252 ± 0.097, whereas those of feathers with unzipped vanes were ζx = 0.131 ± 0.012 and ζy = 0.135 ± 0.005 (Fig. 6).
First, in both ζx and ζy, the damping ratios of the zipped vanes were significantly higher than those of unzipped vanes (P < 0.001). Respectively, at vertical deflections, ζx decreased 66%, and ζy decreased 79% after unzipping. At horizontal deflection, the decrease was 63% in ζx and 46% in ζy. Second, in zipped vanes, both damping ratios ζx and ζy at horizontal and vertical deflection were higher than ζx and ζy by perpendicular deflection (vertical and horizontal, correspondingly) (P < 0.001, P = 0.001). Third, in unzipped feathers, the damping ratio ζy at horizontal deflection was higher than ζy at vertical deflection (P = 0.014; P < 0.001).
In vacuum conditions, the contributions of the structural and material damping of the zipping structure of vanes are distinguishable. Compared to vacuum conditions, feather oscillations decay faster and have higher damping ratios in the atmosphere.
4 Discussion and conclusion
Our results show that the feathers with zipped vanes have a higher damping capacity in the atmosphere and vacuum in comparison to those with unzipped vanes. The damping ratios of the feathers at deflections within the vane plane and perpendicular to it are different. The mechanisms contributing to damping are the following:
-
I.
Aerodynamic damping. Aerodynamic damping is related to the effect of the air on vibrating structures [34]. Feathers are practically air-impermeable during flight [35], and the airflow interacting with feathers could aerodynamically dampen their vibrations [34]. The intact planar shape and the air-valved hooked structure in the zipped vane help to enhance the damping ratios of feathers. This could help explain why the feather damping in the air decreases from 20 to 50% after unzipping. In addition, the feathers with intact zipped vanes had lower fundamental frequencies at both deflections. However, in vacuum, there is no difference between zipped and unzipped vanes at horizontal deflection. The influence of the barbs’ interlocking in vertical deflections still works, even if the hooks are partly unzipped. Such overlapping and interlocking of barbs hinder the barb separation (vane extension) but allow the vane compression.
-
II.
Structural damping. Structural damping is another factor demonstrating a 3.3 times and 2.3 times difference in damping ratio between zipped and unzipped feathers in vacuum (0.278 vs. 0.085 at vertical deflections, 0.303 vs. 0.133 at horizontal deflections, the corresponding mean values). Under feather deformation, the barbules and hooklets undergo relative displacements. The barbules and hooklets are assumed to encounter moving, sliding, anchor-breaking, twisting, uncoupling, and recoupling: all these actions lead to energy dissipation. The resulting friction leads to energy dissipation and, consequently, to structural damping. Besides, the extension of a zipped vane is irregular because of the collective effect in hooklets’ separation [22], which facilitates the oscillation energy transfer from natural frequency to higher harmonics. The energy dissipation is typically higher at higher frequencies.
-
III.
Material damping. Material damping, as an inherent energy dissipation mechanism during material deformation, is another source of feather damping. The most efficient is the material damping in the basal part of the shaft medulla, since the damping ratio measured in vacuum is lower than the damping ratio measured for the base of a feather shaft. The interior part of the barbs is filled with gradient foams [18]. This foam structure undergoes plastic deformation, which contributes to energy dissipation, similar to the damping in the shaft medulla [15]. However, the contribution of the material damping is the lowest if compared to the two mechanisms mentioned above.
Future studies may investigate other sources of damping, such as acoustic vibration, i.e., the transfer of vibrations to the surrounding feathers and tissues (skin, bones). Sound is classified as pressure waves generated by vibrating structures [36]. The sound damping related to the zipping structure is also an interesting mechanism that may contribute to the overall damping of the feather.
In conclusion, our research suggests that the interlocking in the zipped vanes increases the damping ratio of feathers and transfers oscillations perpendicular to the vane into oscillations parallel to the vane plane. This effect shortens the decay time and dampens the oscillations by friction. The damping capability in the vanes can potentially contribute to the bird's flight efficiency. The zipped vanes features can inspire efficient, lightweight aerospace materials with tailored damping properties. The vibration behavior and damping ratio of artificial wings or other parts in unmanned aerial vehicles could be adjusted by varying the number of zipped structures.
Higher damping in the zipped vanes of primary feathers, compared to unzipped ones, is confirmed in the atmospheric and vacuum conditions. Possible damping mechanisms and their relation to feather morphology are discussed. In ambient condition, the planar surface and the interlocked one-way barbs in the vane improves its aerodynamic damping. The experiments in vacuum showed that the vane microstructure significantly contributes to its high damping due to the cooperative effect of overlapping barbs in zipped vanes helping the energy dissipation. Finally, the shaft and barbs filled with the gradient foam are thought to improve the damping in the feather further.
The magnified mimic vanes mode could be printed and matched in a 3D printer. It is possible to adjust the hooked and overlapped layers to control the damping properties and develop flexible damping structures. These bioinspired composites could improve the stability of flapping robots or other shock absorption applications with energy conservation and make less noise.
Data availability statement
The data supporting this study’s findings are available from the corresponding author upon request.
Change history
17 March 2023
Missing Open Access funding information has been added in the Funding Note.
References
D.E. Alexander, On the wing. Insects, pterosaurs, birds, bats, and the evolution of animal flight (Oxford University Press, Oxford, UK, 2015)
J. Clarke, Feathers before flight. Science 340, 690–692 (2013)
T.J. Feo, D.J. Field, R.O. Prum, Barb geometry of asymmetrical feathers reveals a transitional morphology in the evolution of avian flight. Proc. R. Soc. B. 282, 20142864 (2015)
H. Bragulla, R.M. Hirschberg, Horse hooves and bird feathers: two model systems for studying the structure and development of highly adapted integumentary accessory organs - the role of the dermo-epidermal interface for the micro-architecture of complex epidermal structures. J Exp Zool B Mol Dev Evol 298(1), 140–151 (2003)
T.L. Hieronymus, Flight feather attachment in rock pigeons (Columba livia): covert feathers and smooth muscle coordinate a morphing wing. J. Anat. (2016). https://doi.org/10.1111/joa.12511
C.H. Greenewalt, The wings of insects and birds as mechanical oscillators. Proc. Amer. Phil. Soc. 104(6), 605–611 (1960)
O. Speck, H.S. Spatz, Damped oscillations of the giant reed Arundo donax (Poaceae). Am. J. Bot. 91, 789–796 (2004)
H. Rajabi, A. Shafiei, A. Darvizeh, J.H. Dirks, E. Appel, S.N. Gorb, Effect of microstructure on the mechanical and damping behaviour of dragonfly wing veins. R. Soc. Open Sci. 3, 160006 (2016)
C. Lietz, C.F. Schaber, S.N. Gorb, H. Rajabi, The damping and structural properties of dragonfly and damselfly wings during dynamic movement. Commun. Biol. 4, 737 (2021)
H. Rajabi, A. Shafiei, A. Darvizeh, S.N. Gorb, V. Dürr, J.H. Dirks, Both stiff and compliant: morphological and biomechanical adaptations of stick insect antennae for tactile exploration. J. R. Soc. Interface 15(144), 20180246 (2018)
C.W. De Silva, Vibration: fundamentals and practice (CRC Press, Boca Raton, USA, 1999)
C. Hansen, Foundations of vibroacoustics (CRC Press, Boca Raton, USA, 2018)
R.H.C. Bonser, P.P. Purslow, The Young’s modulus of feather keratin. J. Exp. Biol. 198, 1029–1033 (1995)
J.L. Gao, J.K. Chu, L. Guan, H.X. Shang, Z.K. Lei, Viscoelastic characterization of long-eared owl flight feather shaft and the damping ability analysis. Shock Vib. 2014, 709367 (2014)
K. Deng, A. Kovalev, H. Rajabi, C.F. Schaber, Z.D. Dai, S.N. Gorb, The damping properties of the foam-filled shaft of primary feathers of the pigeon Columba livia. Sci. Nat. (2022). https://doi.org/10.1007/s00114-021-01773-7
Z.Q. Liu, D. Jiao, M.A. Meyers, Z.F. Zhang, Structure and mechanical properties of naturally occurring lightweight foam-filled cylinder: the peacock’s tail coverts shaft and its components. Acta Biomater. 17, 137–151 (2015)
R.O. Prum, Development and evolutionary origin of feathers. J. Exp. Zool. 285, 291–306 (1999)
T.N. Sullivan, A. Pissarenko, S.A. Herrera, D. Kisailus, V.A. Lubarda, M.A. Meyers, A lightweight biological structure with tailored stiffness: the feather vane. Acta Biomater. 41, 27–39 (2016)
A.R. Ennos, J.R.E. Hickson, A. Roberts, Functional morphology of the vanes of the flight feathers of the pigeon Columba livia. J. Exp. Biol. 198, 1219–1228 (1995)
R.O. Prum, S. Williamson, Theory of the growth and evolution of feather shape. J. Exp. Zool. 291, 30–57 (2001)
R. Hook, Micrographia: or some physiological descriptions of minute bodies made by magnifying glasses with observations and inquiries thereupon (Royal Society, London, UK,1665)
A. Kovalev, A.E. Filippov, S.N. Gorb, Unzipping bird feathers. J. R. Soc. Interface 11, 20130988 (2013)
Q. Chen, S.N. Gorb, A. Kovalev, Z. Li, N. Pugno, An analytical hierarchical model explaining the robustness and flaw-tolerance of the interlocking barb-barbule structure of bird feathers. Europhys. Lett. 116, 24001 (2016)
J. Zhao, J. Zhang, Y. Zhao, Z. Zhang, P. Godefroit, Shaking the wings and preening feathers with the beak help a bird to recover its ruffled feather vane. Mater. Design 187, 108410 (2020)
L.Y. Matloff, E. Chang, T.J. Feo, L. Jeffries, A.K. Stowers, C. Thomson, D. Lentink, How flight feathers stick together to form a continuous morphing wing. Scicence 367, 293–297 (2020)
Y. Wang, Z. Mu, Z. Zhang, W. Song, S. Zhang, H. Hu, Z. Ma, L. Huang, D. Zhang, Z. Wang, Y. Li, B. Zhang, B. Li, J. Zhang, S. Niu, Z. Han, L. Ren, Interfacial reinforced carbon fiber composites inspired by biological interlocking structure. Science 25(4), 104066 (2022)
J. Dyck, The evolution of feathers. Zoolog. Scr. 14(2), 137–154 (1985)
T.N. Sullivan, M. Chon, R. Ramachandramoorthy, M.R. Roenbeck, T. Hung, H.D. Espinosa, M.A. Meyers, Reversible attachment with tailored permeability: the feather vane and bioinspired designs. Adv. Funct. Mater. 27, 1702954 (2017)
K. Deng, H. Rajabi, A. Kovalev, C.F. Schaber, Z.D. Dai and S.N. Gorb, The role of vanes in the damping of bird feathers. J. Bionic Eng. JBEN-D-22–00204. Accepted (2022) https://doi.org/10.1007/s42235-022-00329-3
M. Bao, H. Yang, H. Yin, Y. Sun, Energy transfer model for squeezed-film air damping in low vacuum. J. Micromech. Microeng. 12, 341–346 (2002)
C.J. Clark, A.M. Mountcastle, E. Mistick, D.O. Elias, Resonance frequencies of honeybee (Apis mellifera) wings. J. Exp. Bio. 220, 2697–2700 (2017)
C.J. Clark, D.O. Elias, M.B. Girard, R.O. Prum, Structural resonance and mode of flutter of hummingbird tail feathers. J. Exp. Bio. 216, 3404–3413 (2013)
S.S. Rao, Mechanical vibrations, in New Jersey. (USA, 2010)
A. Akay, A. Carcaterra, Damping mechanisms, in Active and passive vibration control of structures. ed. by P. Hagedorn, G. Spelsberg-Korspeter (CISM International Centre for Mechanical Sciences, Springer, Vienna, 2014), pp.259–299
W. Mueller, G. Patone, Air transmissivity of feathers. J. Exp. Biol. 201, 2591–2599 (1998)
J.L. Gao, J.K. Chu, H.X. Shang, L. Guan, Vibration attenuation performance of long-eared owl plumage. Bioinspired Biomim. Nanobiomaterials 4, 187–198 (2015)
Acknowledgements
The authors would like to thank Dr. Oleksii Vodka (National Technical University, Ukraine) for separating the vibration modes. They also thank the members of the Department of Functional Morphology and Biomechanics at Kiel University and the Institute of Bioinspired Structure and Surface Engineering at Nanjing University of Aeronautics and Astronautics.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was financially supported by Sino-German Center for Research Promotion (Grant no. GZ1154 to SNG and ZDD).
Author information
Authors and Affiliations
Contributions
SNG designed and coordinated the study; KD, AK, HR, CFS, and SNG designed the experiment; KD performed the experiment, carried out the statistical analysis, and wrote the manuscript; All authors analyzed the data, discussed the results, edited the manuscript, and gave final approval for publication.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Deng, K., Schaber, C.F., Kovalev, A. et al. Aerodynamic vs. frictional damping in primary flight feathers of the pigeon Columba livia. Appl. Phys. A 129, 121 (2023). https://doi.org/10.1007/s00339-023-06395-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00339-023-06395-6