1 Introduction

Nanotechnologies that enable sub-hundred-nanometer-scale engineering have been evolving to meet the demands of cutting-edge technologies, such as advanced semiconductor manufacturing and emerging quantum science applications. The most typical is nanolithography, which is categorized into photolithography employing deep/extreme ultraviolet light, electron-beam direct-write lithography, and so on. Focused-ion-beam (FIB) etching/milling, in which a high-energy gallium ion beam sputters atoms from the sample surface, is another important technique. Recently, an interference laser ablation processing technique using ultrafast lasers with visible/near-infrared wavelength was proposed to treat free-standing nanofilms with thicknesses of less than 100 nm [1,2,3,4]. This technique has the potential to complement conventional nanotechnologies and lead a new frontier in material engineering, because such thin samples tend to suffer from cracking and damage owing to beam irradiation in FIB systems.

Electron phase plates used for phase contrast imaging or beam shaping in electron microscopy are nanostructures that have attracted increasing attention in the past decade [5, 6]. They are created by machining non-metallic nanofilms to ensure low-loss transmission of an electron beam. To generate an electron vortex beam [7, 8], a type of shaped beam, a metal diffractive plate was first fabricated by FIB micromachining [9]. Subsequently, holographic transmission gratings with a support layer of approximately 100 nm thickness were developed using state-of-the-art FIB machining to improve the efficiency of vortex beam generation [10, 11]. However, these methods require skilled operators in addition to expensive equipment and thus are challenging for other groups to replicate. By contrast, interference laser ablation can instantaneously process a nanofilm into a binary phase grating via single-shot laser irradiation. The efficient generation of electron vortices using a free-standing (no support layer) grating made of 35 nm thick silicon was reported in [2].

Membrane-based nanomechanical devices, which have potential applications in quantum technology [12,13,14], are also important nanostructures with geometries similar to a two-dimensional grating. For example, two-dimensional photonic-crystal slabs with relatively simple multi-hole structures in reference [15] were fabricated by complex nanolithography consisting of patterning, etching, and depositing. The thickness of their slabs was 200 nm, and the radius of the required hole was 293 nm, which is within the applicable range of the laser ablation technique. The introduction of simpler processing methods would be highly beneficial, as employing nanolithography to fabricate small batches of nanostructures as required in the laboratory is burdensome.

Ultrafast laser processing has been actively studied over the past three decades [16], whereas little attention seems to have been focused on targeting nanofilms. Near-field laser ablation using the tip-enhancement effect enables processing of gold nanofilms with a resolution of \(\sim 10\) nm [17], making it an extreme direct writing method using light; however, this technique has the difficulty of processing large areas. The interference laser processing technique can yield relatively large patterning areas of tens of square micrometers with a minimum processing size of \(\sim 100\) nm [3]. To apply this technique to actual nanostructure fabrication, as mentioned above, it is necessary to achieve processing of various two-dimensional patterns, as well as a simple stripe pattern via two-beam interference. In this study, we demonstrate laser ablation processing of nanofilms using a multi-beam interference optical system. Furthermore, multipleshot laser processing is performed to achieve dense multi-hole drilling beyond the interference period of light, and the results are presented.

2 Experimental methods and setups

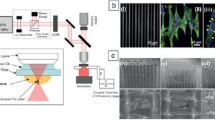
We previously demonstrated an optical system for two-beam laser interference processing based on a Mach–Zehnder interferometer [2, 3]. That configuration is suitable for creating binary holograms but is difficult to extend to multi-beam interference processing. In addition, the need to precisely overlap two bifurcated laser pulses with a pulse duration of \(\sim 300\) fs both spatially and temporally poses a drawback for long-time operation. We, therefore, adopted a single-arm optical system using a diffractive optical element (DOE), which is common in multi-beam interference systems [18,19,20,21]. Figure 1 shows a conceptual drawing of the setup. An input laser beam enters the DOE and is split into several diffracted beams. These beams then pass through a convex lens. All but the first-order diffracted beams are blocked by a spatial filter (SF) at the focal plane of the lens. The first-order diffracted beams are imaged on the surface of a sample by an objective lens. Since the two lenses constitute a 4f system, namely bi-telecentric lenses, an interference fringe pattern is formed in an area that reflects the aperture shape of the DOE.

Fig. 1
figure 1

Conceptual drawing of multi-beam interference laser processing in the experiment. The first-order diffracted beams from the diffractive optical element (DOE) are focused on the surface of the sample by a 4f system (lens and objective). A spatial filter (SF) eliminates the other diffracted beams

Full size image

In the experiment, a reflection-type spatial light modulator (SLM; SLM-200, Santec corporation) was used as the DOE. The size, pitch, and number of pixels of the SLM were 7.8 µm, 8 µm, and \(1920\times 1200\) pixels, respectively. A schematic of the optical setup is shown in Fig. 2. The input laser beam was a frequency-doubled femtosecond laser with a center wavelength of 521 nm, a pulse energy of 15.5 µJ, and a pulse duration of \(\sim 300\) fs. The beam had an M square factor of \(\mathrm {\textit{M}}^{2}\sim 1.3\) with a \(1/e^{2}\) beam size of \(\sim 10\) mm. A motorized variable attenuator (VA) was used to control the input laser pulse energy delivered to the following optics. The first-order diffracted beams were transported onto the sample surface through a 4f system consisting of a lens with a focal length of 1 m (L1) and a plan achromatic objective with a focal length of 2.5 mm and a numerical aperture of 0.8 (L2). Hence, the magnification of the 4f system was 1/400. The first-order diffraction angle was set to avoid vignetting on the pupil of L2. All but the first-order diffracted beams were eliminated by the SF. The polarization of the laser was controlled by half and quarter wave plates (WPs). A shortpass dichroic mirror (DM) combined the laser processing optics with epi-illumination optics for observing the sample.

Fig. 2
figure 2

Schematic of the experimental optical setup: VA motorized variable attenuator, SLM spatial light modulator used as the DOE, L1andL2 lenses with focal lengths of 1 m and 2.5 mm, respectively; WPs half and quarter wave plates, SF spatial filter, DM dichroic mirror, BS beam splitter

Full size image

The samples used in the experiment were specimen-holding membrane windows for use in transmission electron microscopy (manufactured by Norcada, Canada). A schematic is shown in Fig. 3. A silicon-nitride (\(\mathrm {Si_{3}N_{4}}\)) layer, which is a typical material for nanostructure fabrication, was formed on a supporting silicon substrate with a size of approximately 2.9 mm. The substrate was back-etched to form nine \(100\times 100\) µm\(^{2}\) windows, resulting in free-standing prepared nanofilms of \(\mathrm {Si_{3}N_{4}}\). During the laser processing, incident laser pulses were focused on an area less than 100µm in diameter of one of the membrane windows. Three thicknesses, 5 nm, 10, and 100 nm, were prepared. The sample was mounted on a three-axis piezo-motorized linear stage with a closed-loop resolution of 1 nm.

Fig. 3
figure 3

Schematic of nanofilms used in the experiment, which are commercial specimen-holding membrane windows for use in transmission electron microscopy. Images are not drawn to scale; the thickness of the silicon-nitride (\(\mathrm {Si_{3}N_{4}}\)) layer was much thinner than that of the silicon substrate

Full size image

3 Results of multi-beam interference processing

We first conducted multi-beam interference processing via a single-shot operation. Four types of phase modulation patterns were applied to the SLM in the experiment, as shown in Fig. 4a. The phase difference between the areas indicated in black and white is \(\pi\). For two-beam interference processing, the grating spacing of the pattern was 400 µm. For three-, four-, and six-beam interference processing, the lattice spacings were 380, 540, and 450 µm, respectively, as indicated in the insets. The yellow-colored areas were tiled with a random phase pattern to give the aperture effect. The SLM functioned as a two-dimensional binary phase grating with an aperture diameter of 5 mm. Thus, each incident beam formed a spot of 12.5 µm on the sample.

Fig. 4
figure 4

a Phase modulation patterns applied to the SLM. Yellow-colored areas correspond to a random phase pattern. b Calculated Fraunhofer diffraction spots. Red circles indicate diffracted beams passing through the spatial filter. c Calculated interference fringes on the sample surface. Images are for two-, three-, four-, and six-beam interference processing, from left to right. Scale bars represent 2 µm

Full size image

Figure 4b shows the calculated Fraunhofer diffraction of the phase modulation patterns, corresponding to the optical intensity distribution in the focal plane of L1. The spots circled in red indicate the first-order diffracted beams that were selected to pass through the SF.

The expected intensity distributions at the sample plane were calculated and are shown in Fig. 4c. A stripe fringe with spacing of 500 nm was obtained for the two-beam interference. The three- and four-beam interferences yielded multi-spot fringes with a threefold rotational symmetry with spacing of 560 nm and a fourfold rotational symmetry with spacing of 700 nm, respectively. The six-beam interference produced sixfold rotationally symmetric triangular spots with the narrowest spacing of 630 nm.

We applied the multi-beam interference processing to \(\mathrm {Si_{3}N_{4}}\) nanofilms with a thickness of 10 nm. The incident laser beam was linearly polarized and its direction was horizontal at the DM. Figure 5 shows scanning electron microscope (SEM) images of the sample processed with the two-, three-, four-, and six-beam interferences, from left to right. The black areas in the image indicate that the nanofilm was removed. The grating/lattice spacings were \(502\pm 7\) nm, \(565\pm 8\) nm, and \(704\pm 12\) nm for the two-, three-, and four-beam interferences, respectively, which are in good agreement with the calculations. For the six-beam interference, the pattern was consistent with the rightmost image in Fig. 4c except for the rotation by 30°.

The result of the four-beam processing showed that the holes near the periphery were approximately circular in shape, whereas those near the center were rectangles approximately 580 nm \(\times\) 470 nm in size (horizontal \(\times\) vertical). There are two possible causes for the creation of the rectangular shape. The first is the polarization-dependent reflectivity of the sample surface; the ablation thresholds differ depending on whether the irradiated femtosecond laser is p- or s-polarized [22]. The second is the polarization-dependent formation of the focused light field; the field distribution at the focal plane is elongated in the polarization direction in the high-NA condition [23]. By changing the polarization of the incident laser, the shape of the rectangle could be modified. The measured aspect ratios of the rectangles were 1.17 and 0.87 for horizontal and vertical polarizations, respectively, and 1.03 for circular polarization, while the lattice spacing had no change horizontally or vertically.

Fig. 5
figure 5

Scanning electron microscopy images of processed silicon-nitride nanofilms with a thickness of 10 nm. Images are results for two-, three-, four-, and six-beam interference laser processing, from left to right. Scale bars represent 1 µm

Full size image

Four-beam interference processing was then performed on nanofilms of three different thicknesses at various incident laser pulse energies. Figure 6a–c show the results for nanofilms with thicknesses of 5, 10, and 100 nm, respectively. The left side of each figure shows the result when the incident pulse energy was near the processing threshold. The SEM images in Fig. 6c were blurred because the 100-nm-thick nanofilm was more easily charged than the others. The incident laser beam shape was not flat-topped; therefore, when the pulse energy was reduced, the periphery was not laser ablated and the processed area was smaller. Such near-threshold conditions, however, made the hole diameter smaller, which was advantageous for multi-hole drilling, as shown in the next section. In the result shown on the left in Fig. 6b, the hole diameter ranged from 90 to 280 nm. Here, note that although the processing threshold was lower for the thick nanofilm from the results in Fig. 6c, it was not easy to discuss the relationship between the thickness and the threshold because the measured threshold changed by a few tens of percent for each optics adjustment.

Fig. 6
figure 6

Results of four-beam interference processing of silicon-nitride nanofilms with thicknesses of a 5 nm, b 10 nm, and c 100 nm. Incident laser pulse energies used are shown in the upper left of each figure. Scale bars represent 1 µm

Full size image

4 Results of dense multi-hole drilling

To demonstrate dense multi-hole drilling, we conducted four-beam interference processing on 10-nm-thick nanofilms with a quadruple-shot operation. A schematic of the process is shown in Fig. 7. The lattice spacing \(\Lambda\) was 700 nm in the case of single-shot operation. By slightly modifying the phase modulation depth in the center of the modulation pattern projected onto the SLM, the diffraction efficiency changed in space, and thus the laser profile was brought closer to a flat top. The hole diameter d ranged from 100 to 220 nm, which was sufficiently small to drill another hole between the holes. The drilling points were changed vertically and horizontally by \(\Lambda /2\) in three additional processes, aiming to increase the hole density by a factor of four.

Fig. 7
figure 7

Schematic diagram of the procedure for performing high-density multi-point hole drilling. Four-beam interference processing is performed four times while shifting the laser irradiation position by \(\Lambda /2\), where \(\Lambda\) represents the hole spacing obtained by single-shot processing. Typical hole diameters ranged from 100 to 220 nm when the incident laser pulse energy was 0.32 µJ

Full size image

The results of the quadruple-shot processing are shown in Fig. 8. The right side of each figure is an enlargement of the center of the left side. The incident pulse energy was 0.32 µJ. It can be seen that no cracks were verified in the SEM images obtained. The processed area was enlarged compared to the case of single-shot operation (left side of Fig. 6b), whereas the shape of the processed area was distorted and far from circular. The manipulation of the laser profile to flat top probably introduced non-uniformity in the laser intensity distribution.

Two different methods were employed for moving the drilling points. The first involves moving the sample using the piezo-motorized linear stage, as shown in Fig. 8a. The use of a closed-loop controlled stage with a resolution as fine as 1 nm allowed precise control of the drilling points. The directions between the stage movement and the lattice axes of the drilled holes were slightly inconsistent, causing distortion in the arrangement of the holes. The second involves changing the phase of the interference fringes on the sample surface by altering the modulation pattern displayed on the SLM, as shown in Fig. 8b. This was accomplished by shifting the check pattern shown in Fig. 4a by 540 µm in the horizontal and vertical directions. Whereas this method provided higher parallelism, the minimum step size was limited to \(\sim 20\) nm by the pixel size of the SLM. The response time of the SLM was \(>10\) ms, while the driving speed of small steps of the stage was considered to be several kHz, although this is not stated in the specifications. Thus, the stage method was faster than the SLM method in terms of processing speed in quadruple-shot operation.

Fig. 8
figure 8

Scanning electron microscopy (SEM) images of processed 10-nm-thick nanofilms by quadruple-shot processing. a Result of hole drilling while moving the sample \(\Lambda /2\) using a piezo-motorized linear stage. Red square boxes show examples of sets of four drill holes. b Result of hole drilling while shifting the beam position by \(\Lambda /2\) using a spatial light modulator. Each right figure is an enlargement of the center of the corresponding left figure. Scale bars represent 1 µm for the left and 500 nm for the right

Full size image

The result of the stage method shows that the hole shape for each shot was approximately the same, as indicated by the red square boxes in Fig. 8a. Thus, the influences of deflection and tilt of the sample surface on the hole shape were found to be negligible. This is because the depth of focus of the interference spots reached several tens of micrometers. By contrast, the results of the SLM method showed different diameters for each hole. This was probably due to insufficient optimization of the phase modulation depth and/or unexpected polarization manipulation by the liquid crystal elements. It was recognized that ensuring a stable and consistent incident laser condition for each process is essential for near-threshold laser processing.

5 Discussion and conclusions

The 5 nm thick membrane shown in Sect. 3 is the thinnest sample we have reported so far. As no cracks or damage were found on it, we believe that thinner materials, e.g., atomic layer materials [24, 25], can be treated with laser ablation processing. The processing of thicker samples with thicknesses of tens to one hundred nanometers is also interesting in relation to the dependence on the laser wavelength used. The use of near-infrared wavelengths results in a steep cross-section of created nanostructure due to the high nonlinearity of the laser ablation process [4], whereas shorter wavelengths in the visible and ultraviolet regions with lower nonlinearity are expected to result in mortar-shaped ablation holes. We hoped that the processing results of the 100-nm-thick film would provide some information about the steepness dependence on the wavelength, but as mentioned above, this was difficult to achieve with SEM. It would be reasonable to evaluate the surface topography of the laser-processed film with an atomic force microscope, which has a high affinity for optics, and to integrate it with the presented laser processing system in the future.

In multi-hole drilling, the key to achieving further densification lies in reducing and homogenizing the hole diameters. The SEM images in Fig. 8 show that there was room for additional drilling at the periphery of the processed area where the hole diameter was a minimum of \(\sim 80\) nm. Thus, denser multi-hole drilling with a lattice spacing of \(\Lambda /4\) or more is possible if an 80-nm hole diameter is achieved uniformly over a wide processing area. In actual laser interference applications, such as photolithography, various techniques have been proposed and established to form clean interference fringes by highly uniforming the intensity distribution and wavefront of the incident laser beams [26, 27]. This can be accomplished by replacing the present focusing optics with a reflective system or prism-based optics that can reduce aberrations and expand the processing area.

In conclusion, we demonstrated multi-beam interference processing of nanofilms made of silicon-nitride using a femtosecond laser. The nanofilms, with thicknesses of 5–100 nm, which could not be readily treated by FIB, were laser-processed without cracks. The obtained geometry of the nanostructures reflected the intensity distribution of the interference fringes formed on the sample surface. Laser processing with quadruple-shot operation was also conducted to achieve dense multi-hole drilling beyond the interference fringe pitch. The obtained multi-point holes were arranged with a half period compared to those by single-shot operation. It is expected that the hole density can be further increased by optimizing the incident laser optics. The demonstrated method will be instrumental in the fabrication of actual nanostructures such as electron phase plates and membrane-based opto-/electro-mechanical devices. The ability to machine a few-nanometers-thick material may lead to practical applications for emerging nanomaterials, including atomic layer materials.