1 Introduction

Ultrashort-pulsed laser (USP) sources nowadays provide pulse energies up to several mJ and they find application in many fields of laser materials processing [1,2,3]. However, their potential often remains unused since the processing quality and efficiency may be reduced due to a too high fluence. Ultrashort-pulsed laser material ablation is a nonlinear process as it scales nonlinearly with the fluence. The optimum fluence indicates the position, where the volume ablation rate per energy is maximized [4]. However, the provided peak fluence is typically orders of magnitude higher than the optimum fluence.

To make full use of the provided pulse energy, beam shaping with a phase-only spatial light modulator (SLM) enables tailoring the intensity profile to optimize the amount of deposited energy, inter alia, by distributing the light field over a large area. The process is highly efficient, since almost no losses occur. Furthermore, new phase masks can be dynamically applied to adapt for new processing geometries. Beam shaping with the SLM finds application in laser materials processing [5] and there are reports employing a liquid crystal SLM for high average power lasers [6].

Besides a direct modulation of the wave front, phase-only beam shaping enables arbitrary intensity distributions in the target plane. Iterative algorithms like the Gerchberg–Saxton algorithm are often used to calculate the required phase masks [7]. Those phase masks are calculated as a diffuser that redirects the light. Thus, each region of the phase mask equally contributes to the target image. It is, however, not possible to control the full complex light field with a single phase-only element. While the amplitude can be constrained in the target plane, the wave front remains uncontrolled and phase vortices occur, which result in a speckle pattern overlaying the tailored target structure [8].

Fig. 1
figure 1

Methods for beam shaping: a phase-only beam shaping exhibits speckle, b averaging of independent phase masks can be used to get a uniform beam profile, c amplitude and wave front need to be controlled to fully shape the target structure

Full size image

Since speckle strongly impair the shaped intensity pattern and thereby the processing result, methods for uniform beam shaping in laser materials processing are required. Several methods have been proposed, all of which have their advantages and disadvantages. In this paper we study two main approaches: averaging of independent phase masks, and amplitude and wave front shaping by employing two SLM planes.

In the case of averaging, several phase masks designed for the same target structure but with different speckle patterns can be sequentially applied on the SLM to obtain a uniform result [9,10,11]. Thereby, the optical homogeneity scales with \(\frac{1}{\sqrt{N_{\text {PM}}}}\), where \(N_{\text {PM}}\) is the number of independent phase masks [12]. Furthermore, shift averaging of a single hologram completely averages out speckle [13].

If, however, each individual pulse needs to be speckle-free, averaging is not an option. A single phase mask may be used to get uniform results if only a small fraction of the light field is used to shape the target distribution [14, 15]. Since this method is highly inefficient, it is inappropriate for laser material ablation. Another option to achieve uniform beam profiles is adaptive beam shaping with an encoded phase grating [16, 17]. The target pattern is effectively cut from the remaining light by imaging the SLM plane with a 4f configuration and applying a phase grating to spatially separate the target image from the remaining light in the Fourier plane. While this method provides excellent results, only the separated portion can be used.

To this end, two consecutive SLMs can be used to control the full complex light field [18,19,20,21,22], namely amplitude and wave front, and by this make full use of the available light. To apply this method to high energy lasers, the fluence has to remain below the damage threshold of the device and therefore the energy has to be distributed over a large area on the SLM. In prior work, we developed a setup that meets those requirements [22].

Even though averaging and amplitude and wave front shaping give similar results in optical homogeneity, the ablation process on the material is different. For a fully controlled light field, an already homogeneous intensity profile interacts with the material whereas in the other case each single profile is overlaid with a speckle pattern and the homogeneity is only created by averaging.

For practical applications in laser materials processing it is important to know which method should be used. We analyze and evaluate both methods with respect to the resulting quality and efficiency of the ablated profiles. Both methods are implemented in the same setup to maintain the same experimental conditions. To obtain a direct mapping of the tailored beam in the ablation process, we work with the amorphous metal Heraeus AMLOY VIT105 which provides homogeneous and isotropic material characteristics since it exhibits no grain structure. Based on the analysis of two fundamentally different methods for achieving a uniform profile, we give suggestions which method should be applied depending on the requirements.

The paper is structured in the following way: in Sect. 2, we outline the method of amplitude and wave front shaping for high-energy lasers. Thereby, we present the experimental setup which can be adapted to accommodate both methods. Information about the used laser source and the amorphous metal sample with the ablation threshold follow thereafter. Sect. 3 shows the ablation profiles resulting from both methods. Here, we gradually analyze the results on different criteria, categorized within quality, efficiency, and feasibility, to finally conclude the paper based on this analysis.

2 Methods

To achieve a certain amplitude distribution, phase-only beam shaping with the SLM typically applies a phase mask which is calculated with the Gerchberg–Saxton algorithm. Figure 1 exemplarily shows this for a rectangular target structure. Figure 1a indicates that this results in a speckle pattern which can be averaged out with several independent phase masks as Fig. 1b shows. While averaging still works with this basic configuration, amplitude and wave front shaping (Fig. 1c) requires a more sophisticated setup. For this reason, our experimental setup is designed for amplitude and wave front shaping but it can easily be adapted to perform averaging. We will thus first outline the concept of amplitude and wave front shaping and present the experimental setup for this method before we continue with the adaptions for averaging.

2.1 Experimental setup

Amplitude and wave front shaping

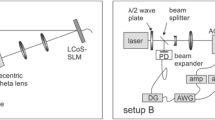
Two SLM planes are employed to create a uniform beam profile. Based on the desired intensity pattern in the target plane, the complex light field is backpropagated to the second plane of the SLM. Shaping this amplitude and wave front distribution will result in the target pattern. Thereby, the first plane of the SLM is used to shape the amplitude on the second plane of the SLM. The corresponding phase mask is calculated with the Gerchberg–Saxton algorithm. The resulting intensity pattern exhibits speckle but with that method the amplitude itself can be controlled on the second plane of the SLM. The target wave front is well-known from the backpropagated light field and the second plane of the SLM is now capable of applying the proper wave front. A phase mask is applied that compensates for the arriving wave front and likewise applies the proper wave front to shape the full complex light field [18,19,20,21,22]. Figure 2a shows the setup in transmission. To avoid high peak fluences on the plane of the second SLM, the setup is designed in a 4-f-like configuration with a tube lens \(f_1\) between the two planes. Furthermore, an additional variable lens term \(f_2\) is part of the second SLM’s phase mask and controls the magnification of the target structure. This enables target structures of arbitrary scale while the illuminated area on the second SLM stays constant.

Fig. 2
figure 2

Experimental setup plotted in transmission for a amplitude and wave front shaping, and b for averaging. c Shows a 3D image of the setup in case of amplitude and wave front shaping. It can be adapted to averaging by removing the lens \(f_1\) and applying a plane wave front on the first SLM plane

Full size image

The target structure is finally imaged with a lens \(f_3\) into the target plane. An additional benefit of the 4-f-like setup is the vanishing \(0{\text {th}}\) order of non-diffracted light since it is inherently defocussed on the second SLM and in the target plane. We additionally introduce an adaptable defocus in the target plane since this enables some modifications of the numerical aperture (NA).

In our experimental implementation, we work with one liquid crystal SLM (Meadowlark P1920-1064) that is split in two individual areas as Fig. 2c shows. While a relatively long focal length can be chosen for \(f_3\) to image the target structure on a camera (IDS UI-1240LE-M-GL), it can be exchanged with a short focal length lens (\(f_3 = 50\,\text {mm}\) (Thorlabs LA1255-B) or \(f_3 = 18\,\text {mm}\) (Thorlabs LSM02-BB)) to focus on the surface of the sample and ablate material. The distance between the second SLM’s plane and the imaging lens can be chosen freely as long as the target structure is calculated on-axis. Since the NA changes with the applied lens term on the second SLM as a consequence of magnification control, we add a positive defocus of a quarter of the used focal length to keep the NA high.

Averaging

To maintain the same experimental conditions for averaging of individual phase masks, the same setup is used. A plane wave front is applied to the first plane of the SLM to use it as a mirror. Additionally, the lens between the two SLM planes has to be removed. The remaining elements build the typical setup for phase-only beam shaping as can be seen in Fig. 2b. By providing different starting conditions for the Gerchberg–Saxton algorithm, independent phase masks are calculated. The target structure thereby appears in the focus of the lens \(f_3\). It is shifted slightly off-axis to separate it from the \(0{\text {th}}\) order of non-diffracted light. Based on the results in [11], we use 40 different phase masks to get a smooth averaged profile.

2.2 Laser parameter

The laser system Cepheus (Photon Energy) emits \(12\,\text {ps}\) pulses at a wavelength of \(\lambda = 1064\,\text {nm}\). The repetition frequency is set to its minimum at \(20\,\text {kHz}\) where the laser system provides the highest pulse energy (\(150\,\upmu \text {J}\)). Inappropriate coating of the tube lens and high losses at the backplane of our SLM strongly reduce the laser power such that we measured \(55\,\upmu \text {J}\) on the surface of the material. Those are technical limitations of our used system and no general constraints. The reflectivity of our SLM’s aluminium mirror is \(85\,\%\) whereas dielectric mirrors are available which achieve a reflectivity \(>95\,\%\). The same applies for the anti-reflection coating of the tube lens. Based on measurements of shaped rectangles in [22], the total efficiency is \(73\,\%\) for amplitude and wave front shaping, whereas phase-only beam shaping results in \(81\,\%\) on-axis and \(69\,\%\) off-axis if those two losses are excluded. This shows that both methods are almost comparable in their optical efficiency. To work with comparable laser fluences for both methods, we reduced the laser power in the case of averaging slightly since the tube lens was removed from the setup.

We made ablation experiments with 500 and 1000 pulses. In both cases, we apply 40 different phase masks for averaging. For 1000 pulses, a new phase mask is applied after 25 pulses. In the case of 500 pulses, either 12 or 13 pulses are applied until a new phase mask is loaded to end up with 500 pulses in total. To provide similar conditions for amplitude and wave front shaping, we added regular pauses even though no new phase masks needed to be loaded on the SLM. Similar to averaging, a pause of \(1\,\text {s}\) was added after 25 pulses for 1000 pulses. In case of 500 pulses, a pause of \(1\,\text {s}\) was added after 50 pulses.

Fig. 3
figure 3

a Recorded intensity profile of the used ultrashort pulsed (USP) laser source in front of the SLM (\(w_0 = 2.5\,\text {mm}\)). The asymmetric mode profile affects the homogeneity of the beam shaped output. For comparison an intensity image of a snowflake shaped with this laser mode (b) and a snowflake shaped with a mode-filtered \(\text {TEM}_{00}\) mode (\(w_0 = 3.1\,\text {mm}\)) c are shown for amplitude and wave front shaping

Full size image

It is worth mentioning that the mode profile of our laser source is relatively bad. A recorded image can be seen in Fig. 3a. Based on this recording, we fitted a beam width of \(w_0 = 2.5\,\text {mm}\). While phase-only beam shaping with phase masks based on a diffuser mask should not exhibit any dependence on the mode profile, our method is more sensitive to deviations from an ideal Gaussian input. Comparing camera images recorded with a high-quality mode-filtered Gaussian beam reveals a reduction in homogeneity as can be seen in Fig. 3b, c.

2.3 Material parameter

To achieve a direct mapping of the shaped beam profile within the ablation process, we use the Zirconium-based amorphous alloy Heraeus AMLOY VIT105. We specifically chose this material because it does not exhibit a grain structure which otherwise would locally affect the ablation result and probably limit the achieved quality from a material’s perspective.

The ablated samples are cleaned in an ultrasound bath to remove residuals around the ablation area. We use the confocal laser scanning microscope Olympus LEXT OLS 4000 to perform depth and size measurements.

Fig. 4
figure 4

Determination of the ablation threshold according to Liu [23]. Each measurement was performed three times (\(n = 3\))

Full size image

In preceding experiments, we determined the ablation threshold of the amorphous metal VIT105 according to Liu [23]. Therefore, we conducted two different measurement series: one within our setup with the lens for ablation experiments (\(f_3 = 50\,\text {mm}\) and \(w_0 = 2.5\,\text {mm}\)) and another series with a lower NA (\(f=100\,\text {mm}\) f-\(\theta \)-lens, Rodenstock F-Theta-Ronar, \(w_0 = 1.5\,\text {mm}\)) outside the setup (compare Fig. 4). The latter experiments serve as a reference since the relatively high NA in the first case makes it difficult to get precise results due to the low slope resulting from the small hole diameters. The ablation threshold is around \(0.15\,\frac{\text {J}}{\text {cm}^2}\) for 1000 pulses with a pause of \(1\,\text {s}\) after 25 pulses. The reference measurements gave \(F_{\text {th}} = 0.18\,\frac{\text {J}}{\text {cm}^2}\) and \(F_{\text {th}} = 0.22\,\frac{\text {J}}{\text {cm}^2}\) for 100, and respectively 10 pulses. Those values match well with the determined ablation threshold for 1000 pulses.

3 Results and discussion

In the following section, we present ablation results and evaluate them with respect to quality (roughness and homogeneity, shape accuracy, \(0{\text {th}}\) order of non-diffracted light, influence of the laser fluence), efficiency, and feasibility.

Fig. 5
figure 5

Comparison of ablation results with 500 and 1000 pulses for phase-only beam shaping, averaging, and amplitude and wave front shaping (\(f_3 = 50\,\text {mm}\)). Camera images and simulated intensity distributions are added on the left side for comparison. In case of phase-only beam shaping and averaging, the \(0{\text {th}}\) order of non-diffracted light can be seen on the bottom on the left side

Full size image

Figure 5 shows ablation profiles and the corresponding intensity images. In the upper left corner the target structure can be seen. The laser fluence is \(F = 3\cdot F_{\text {th}}\) (\(F_{\text {th}} = 0.15\,\frac{\text {J}}{\text {cm}^2}\) and calculation with a pulse energy of \(55\,\upmu \text {J}\), where \(80\,\%\) of the light shapes the target structure). For speckled profiles in the case of averaging, this value accounts for the mean fluence even though individual speckle peaks may be far above that value. The first row shows phase-only beam shaping results with a single phase mask. The overlaying speckle pattern mirrors in the ablated profile which makes it difficult to recognize the initial target structure. The \(0{\text {th}}\) order of non-diffracted light appears in the lower left corner beside the target structure. The second row shows the averaging results for 40 different phase masks. The smooth ablated profiles show that speckle can be averaged out well even though each single pulse exhibits a strong speckle pattern. A simulated intensity profile and the corresponding camera recording can be seen in the left column. The images for the camera recordings are generated with a \(300\,\text {mm}\) lens and are thereafter projected to the target structure’s size where the ratio between the two focal lengths gives the scaling. The ablated profiles for amplitude and wave front shaping can be seen in the third row. Similar to averaging, this method gives smooth results. Again, the simulated intensity profile and a camera recording of the beam are shown in the left columns.

3.1 Quality

Roughness and homogeneity

To compare the homogeneity of the ablated structures, we evaluated the roughness \(R_a\) along the outer circle’s line as average of the profile height deviations from the mean line [24]. In case of averaging, we measured \(R_a^{\text {avg}}(500\text { pulses}) = 0.7\,\upmu \text {m}\) and \(R_a^{\text {avg}}(1000\text { pulses}) = 1.8\,\upmu \text {m}\). In comparison, amplitude and wave front shaping results in \( R_a^{\text {A} \& \text {WF}}(500\text { pulses}) = 1.2\,\upmu \text {m}\) and \( R_a^{\text {A} \& \text {WF}}(1000\text { pulses}) = 1.8\,\upmu \text {m}\). While the line roughness for both methods is relatively comparable, it more than doubles after averaging with 1000 instead of 500 pulses. In both cases 40 different phase masks are applied but averaging happens faster for a lower number of pulses and this provides a smoother surface. We also expect the roughness for a uniformly shaped beam profile to marginally increase with a higher number of pulses since the prevalent roughness from 500 pulses tends to strengthen with further pulses being applied.

The ablation profile in case of amplitude and wave front shaping is very sensitive to small inhomogeneities in the profile. A slight deviation from the targeted structure not only reproduces with every single pulse but also affects the incoupling of new pulses due to an increased roughness/inhomogeneity in the surface structure. This may cause strengthened deviations in the final ablation profile. Comparing the intensity image of the camera measurement with the ablated profiles shows that slightly weaker illuminated areas result in less ablation or a thinner width of the ablated circle. Furthermore, the outer ring of the smiley shape was intentionally set slightly brighter than the inner part. This still can be recognized in the case of averaging whereas this nuance disappears for amplitude and wave front shaping.

Shape accuracy

Besides homogeneity, there is a clear difference in the sharpness resulting from both methods. The contours for amplitude and wave front shaping are sharper and show clear edges even though both experiments were performed in the same setup with the identical beam diameter and optical elements. 20 averaged line profile along the outer circle in Fig. 6 stress this observation. Radial slices of the outer ring are shown as mean edge contour: averaging results in a less steep and deep but broader profile. Here, the resolution is limited to the diffraction limit of the optical system, namely the beam diameter and the focal length of the imaging lens. If however, the amplitude is shaped beforehand, this step already selects only the relevant frequencies which are required to shape the target structure. This affects the resolution and provides sharper edges and thus finer details. This is an inherent effect of the pre-shaped amplitude whereas phase-only beam shaping is restricted to the initial light distribution on the SLM plane.

Fig. 6
figure 6

Mean edge contour of the outer circle. The profile shows a sharper slope and a clear edge for amplitude and wave front shaping. Apart from that, the amount of ablated material is equal for both methods

Full size image

\(\mathbf{0}^{\mathbf{th}}\) Order of non-diffracted light

Due to the 4-f-like configuration for amplitude and wave front shaping, the \(0{\text {th}}\) order of non-diffracted light is defocussed on the plane of the second SLM. Since here only the wave front is adjusted to obtain the proper analytical solution, there appears no focused \(0{\text {th}}\) order of non-diffracted light, neither while working in the focus, nor while working in the defocus. Phase-only beam shaping only enables shifting the target structure off-axis to separate the \(0{\text {th}}\) order of non-diffracted light away from the shaped profile or applying an additional lens term to work in the defocus.

The marked optical axis in Fig. 5 denotes the position of the \(0{\text {th}}\) order of non-diffracted light. It is focussed for phase-only beam shaping and averaging whereas it is vanished for amplitude and wave front shaping.

Influence of laser fluence

Fig. 7
figure 7

Dependence of the ablation result on the laser fluence: the first image in the upper row shows the simulated ablation profile for amplitude and wave front shaping on basis of the recorded intensity image in Fig. 3b with the fluence set to \(F = 1.6\cdot F_{\text {th}}\). The color map here is normalized to the maximum ablation depth. The two images on the right show averaged profiles with differing laser fluence. The lower row illustrates the results for amplitude and wave front shaping in dependence of the chosen laser fluence. To shape the complex structure of a snowflake with the limited laser power, we used a micro scanner objective \(f_3 = 18\,\text {mm}\). All measurements are done with 500 pulses (50 pulses with \(1\,\text {s}\) in between). A median filter with a kernel size of \(3\times 3\,\text {px}\) was applied to the recorded depth shapes to suppress outliers from low-signal areas. The threshold fluence is \(F_{\text {th}} = 0.15\,\frac{\text {J}}{\text {cm}^2}\) and we assume that \(80\,\%\) of the measured laser power shape the target structure

Full size image

The nonlinear ablation process in ultrashort-pulsed laser material interaction can be approximated logarithmically [25]. This indicates that the chosen laser fluence is a relevant parameter to tune the homogeneity and flatness of the ablation profiles. As Häfner et al. [11], the quality of averaging improves with higher fluences since intensity fluctuations from the speckle profile have less impact on the ablation profile. Besides this difference in homogeneity and apart from the ablation depth itself, there appear no local deviations in flatness as the upper row in Fig. 7 indicates. Inhomogeneities in the intensity profile for amplitude and wave front shaping however strongly reduce the flatness of the ablated results especially close to the threshold fluence. While the ablated snowflake in Fig. 7 for \(F = 2.8\cdot F_{\text {th}}\) gives a uniform ablation profile, the weaker illuminated outer parts (compare the camera recording in Fig. 3) start to disappear for \(F = 1.6\cdot F_{\text {th}}\). The same effect can be observed in the simulated ablation profile for \(F = 1.6\cdot F_{\text {th}}\). Deviations in the resulting intensity profile are rather enhanced for low fluences but they tend to disappear for higher fluences with respect to the threshold fluence.

3.2 Efficiency

Judging efficiency with respect to the amount of ablated material gives comparable results for both methods. Even though the ablated volume per applied energy is similar, averaging requires regular pauses for switching with the result that only a fraction of the emitted pulses can be used, leading to a reduced duty cycle. Here, two different systems have to be synchronized: the ultrashort pulsed laser typically emits pulses with a repetition frequency \(f_{\text {rep}}\) of several tens of \(\text {kHz}\) for materials processing, whereas typical frame rates \(f_{\text {s}}\) of a liquid crystal SLM are around several \(\text {Hz}\). \(\tau \) gives a measure for the non-instantaneous response of the liquid crystals until a new phase mask is loaded.

The duty cycle is given by:

$$\begin{aligned} \begin{aligned} \text {DutyCycle} =&\frac{N_{\text {t}}}{f_{\text {rep}}/f_{\text {s}}\cdot N_{\text {PM}}\cdot \left\lceil \frac{N_{\text {t}}/N_{\text {PM}}+f_{\text {rep}}\cdot \tau }{f_{\text {rep}}/f_{\text {s}}}\right\rceil } \\&\text {for } N_{\text {t}}\ge N_{\text {PM}} > 1, \end{aligned} \end{aligned}$$
(1)

where \(N_{\text {t}}\) is the total number of pulses needed for the desired depth, and \(N_{\text {PM}}\) is the number of applied phase masks. The brackets \(\lceil \,\rceil \) in the equation indicate the ceil-operation. Figure 8 sketches the relative distances for the corresponding number of pulses. The denominator in Eq. 1 counts the total number of pulses provided by the laser during the machine time. This involves the number of passing pulses within the SLM’s response time \(f_{\text {rep}}\cdot \tau \) plus the number of pulses which shall be applied to a single phase mask \(N_{\text {t}}/N_{\text {PM}}\). Due to the fixed frame rate of the SLM, we can not directly take this sum but we have to find the next greater multiple of the number of pulses within the SLM’s time frame \(f_{\text {rep}}/f_{\text {s}}\). This gives the total number of pulses for a single phase mask. Multiplied with the number of phase masks \(N_{\text {PM}}\) we can calculate the duty cycle.

Fig. 8
figure 8

Sketch of the relative distances for the corresponding number of pulses

Full size image

This duty cycle multiplied with the optical efficiency gives the total efficiency of the setup.

Fig. 9
figure 9

Duty cycle as a function of the number of phase masks: appropriate system parameters and a carefully chosen number of applied phase masks enable a high duty cycles even for low frame rates

Full size image
Fig. 10
figure 10

Duty cycle as a function of the number of pulses: a high pulse number, in general, increases the duty cycle but an unfavorable number might lead to a strong drop of the duty cycle due an increased dead time

Full size image

Contrary to a naive guess, the total efficiency does not monotonically decrease with an increasing number of applied phase masks (compare Fig. 9) nor monotonically increase with an increasing number of applied pulses (compare Fig. 10). This is a result of the fixed frame rate of the SLM leading to a large dead-time if the time where a single phase mask is displayed can only be used partially for processing. Therefore, the number of used phase masks should be chosen such that the argument of the ceil-operation is close but still below an integer value.

As typical frame rates of commercially available liquid crystal SLMs are about \(60\,\text {Hz}\), the total efficiency is significantly reduced for a high number of phase masks. Typical response times, i.e. rise/fall times, -defined as the time a change from \(10\,\%\) to \(90\,\%\) takes and vice versa - for liquid crystal SLMs in the near infrared range from a few milliseconds to a few tens of milliseconds. Note that after the response time has elapsed the SLM will not have reached its full diffraction efficiency yet but only after the settling time, which is on the order of tens of milliseconds. Settling times can be reduced to about \(3\,\text {ms}\) by applying overdrive and phase change reduction [26]. Depending on the application, either the response time or the settling time can be chosen for \(\tau \) in Eq. 1.

A higher frame rate increases the efficiency especially for a low number of phase masks but still the efficiency is low if few pulses and a large number of masks is needed.

If the SLM does not have a fixed frame rate but switching can be performed on demand, the duty cycle is only influenced by the response time \(\tau \). A corresponding equation for the duty cycle can be derived by taking the limit of the frame rate towards infinity in Eq. 1:

$$\begin{aligned} \begin{aligned} \lim _{f_{\text {s}}\rightarrow \infty }\text {DutyCycle}&= \frac{N_{\text {t}}}{N_{\text {t}}+\tau \cdot N_{\text {PM}}\cdot f_{\text {rep}}} \\&= \frac{t_0}{t_0+\tau \cdot N_{\text {PM}}}, \end{aligned} \end{aligned}$$
(2)

with \(t_0 = N_{\text {t}}/f_{\text {rep}}\) being the optimal processing time. This equation can be either interpreted in terms of pulses, where the denominator corresponds to the sum of used and unused pulses, or in terms of time, where the denominator corresponds to the prolonged processing time due to switching. In this case, the duty cycle will be close to unity if \(N_{\text {t}} \gg \tau \cdot N_{\text {PM}}\cdot f_{\text {rep}}\). Therefore, for a large number of used pulses and a low laser repetition frequency, averaging could be a viable option from an efficiency point of view.

3.3 Feasibility

Apart from the required synchronization in the case of averaging, a setup for phase-only beam shaping can be built with little effort especially since not a lot of optical components are required and alignment is easy. For amplitude and wave front shaping, there has to be a near perfect mapping between the preshaped amplitude profile and the applied phase mask on the plane of the second SLM. Besides more optical components, this requires fine alignment and readjustment from time to time.

4 Conclusion

Both, averaging and amplitude and wave front shaping give convincing results. Depending on the chosen criteria, the one or the other way of achieving a uniform ablation profile seems to be more advantageous. Averaging is more reliable when the focus lies on the ablation depth, whereas amplitude and wave front shaping enables sharper and more precise contours in the lateral plane. The introduced roughness does not significantly differ between the methods. In both cases approximately the same amount of material is ablated, however, the system parameters have to be chosen appropriately that averaging can compete in efficiency. While averaging requires almost no expense in alignment, the \(0{\text {th}}\) order of non-diffracted light completely vanishes for amplitude and wave front shaping and only this method can be chosen if a single pulse already needs to exhibit a uniform profile.