Phenomenon of heat conduction in Si nanowires

Abstract

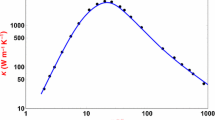
The lattice thermal conductivity of nanowires has been resolved into in-plane and cross-plane components using modified phenomenological Callaway model. Which is based on the versatile use of electron and phonon linewidths of various scattering events instead of relaxation times have been made. This has been achieved with the help of many body quantum dynamical formulation of double time temperature dependent electron and phonon Green’s functions via a comprehensive Hamiltonian, that includes the impact of defects, anharmonic phonon fields and electrons. These new results have been utilized to numerically estimate the thermal conductivity of silicon nanowires that shows a huge reduction as compare to bulk systems which is duly evidenced by experimental observations. This model purposed a fairly good agreement with experimental observation and this theoretical model is equally applicable for all nanowire structures.

Appendices

Point defect scattering

To illustrate the linewidth expresson for defect scattering in nanowire system, let us start with a model Hamiltonian $H=H_{p}+H_{D}+H_{A}+H_{e}+H_{ep}$ where the subscripts p, D, A, e and ep are defined the contributions of phonons, defects, anharmonic, electrons and electron-phonons, respectively. The articulable configuration of these Hamiltonian has been given in the references elsewhere [36,37,38,39, 53] and no need to introduce again. Now we consider the evaluation of double time temperature phonon Green’s function $G_{kk^{'}}(t-t^{'})=<<A_{k}(t);A_{k}^{*}(t^{'})>>$ with the help of given Hamiltonian. Considering the equation of motion techniques of many body quantum dynamics we get the appearance for Green’s functions in the form,

$$\begin{aligned}&G_{kk^{'}}(\omega )=\frac{1}{\pi }\omega _{k}\eta _{kk^{'}}[\omega ^{2}-{\tilde{\omega }}_{k}^{2}-2\omega _{k}P(kk^{'},\omega )]^{-1} \end{aligned}$$

(13)

$$\begin{aligned}&{\tilde{\omega }}_{k}^{2}=&\omega _{k}^{2}+\frac{\omega _{k}}{2\pi }<[F_{k}(t),B_{k}^{*}(t)]>\nonumber \\&+\frac{2}{\pi }\sum _{k_{1}}C(-k,k_{1})<[F_{k}(t);B_{k_{1}}^{*}(t^{'})]>\nonumber \\&+\frac{4}{\pi }(\omega ^{2}-\omega _{k}^{2})C(-k,k_{1})\omega _{k}^{-1} \end{aligned}$$

(14)

where,

$$\begin{aligned}&F_{k}(t)=&4\pi \sum _{k_{1}}[D(-k,k_{1})+\frac{\omega _{k_{1}}}{\omega _{k}}C(-k,k_{1})]A_{k_{1}}\nonumber \\&+16\pi \sum _{k_{1},k_{2}}C(-k,k_{1})\nonumber \\&D(-k,k_{1})\omega _{k}^{-1}A_{k_{1}} +2\pi \sum _{s\ge 3}\sum _{k_{1},k_{2}...k_{3}}sV^{s}(k_{1},k_{2},....-k)\nonumber \\&A_{k_{1}}A_{k_{2}}....A_{k_{s-1}} \end{aligned}$$

(15)

The above term is known as the renormalized mode frequency. The response function $P^{D}(kk^{'},\omega )$ to manifest the influence of defects and impurities is accomplished by the initiation of renormalized Hamiltonian [53]

$$\begin{aligned} H^{0}_{ren}=\frac{\hbar }{4}\sum _{k}{\tilde{\omega }}_{k}^{(1)}(A_{k}^{*}A_{k}+B_{k}^{*}B_{k}) \end{aligned}$$

(16)

as a consequence we get,

$$\begin{aligned} P^{D}(kk^{'},\omega )=8\sum _{k_{1}}R(-k,k_{1})R^{*}(-k,k_{1})\omega _{k_{1}}(\omega ^{2}-{\tilde{\omega }}_{k_{1}}^{2})^{-1} \end{aligned}$$

(17)

For a small quantity $\epsilon$, the response function $P^{D}(kk^{'},\omega )$ has been squeezed out in terms of real and imaginary parts as [38]

$$\begin{aligned} P^{D}(kk^{'},\omega +i\epsilon )=\Delta _{k}^{D}(\omega )-i\Gamma _{k}^{D}(\omega ) \end{aligned}$$

(18)

where $\Delta _{k}^{D}(\omega )$ is identified as the phonon frequency shift and imaginary part $\Gamma _{k}^{D}(\omega )$ is named the phonon line width at the half topmost. So that,using the equation (A.4),(A.5) and (A.6) we get the expression for defect scattering in the form of equation (7) with,

$$\begin{aligned}&|R(-k,k_{1})|\nonumber &=\left( \frac{\omega _{k_{1}}}{\omega _{-k}}\right) C(-k,k_{1})+D(-k,k_{1})+4\sum _{k_{1}^{'}}C(-k,k_{1}^{'})\nonumber \\&D(-k_{1}^{'},k_{1})\omega _{-k}^{-1} \end{aligned}$$

(19)

In the above expressed form, the coefficients $C(-k,k_{1})$ and $D(-k,k_{1})$ are associated to change in mass and force constant due to companionship of defects and adulterants. Which can be drafted in the form [37, 38, 54]

$$\begin{aligned}&C(-k,k_{1})\nonumber \\&=\left( \frac{M_{0}}{4N\mu }\right) (\omega _{-k}\omega _{k_{1}})^{1/2}[e(-k)e(-k_{1})]\left[\sum _{l}^{N}fe^{i(-k+k_{1})R_{l}}\right.\nonumber \\&\left.-\sum _{i}^{n}e^{i(-k+k_{1})R_{i}}\right] \end{aligned}$$

(20)

$$\begin{aligned}&D(-k,k_{1})=\left( \frac{1}{4N}\right) (\omega _{-k}\omega _{k_{1}})^{-1/2}\sum _{l,l^{'}}\frac{\phi _{l,l^{'}}}{M_{0}}\nonumber \\&[e(-k)e(k_{1})]e^{i(-kR_{l}+k_{1}R_{l^{'}})} \end{aligned}$$

(21)

Let us consider a crystal with N atoms in which n lattice sites are engrossed by irregularly distributed defects/impurities of comprise mass $M^{'}$ and $N-n$ sites are occupied by atom of mass M. Here,$C=\frac{n}{N}$ is the impurity consolidaion and $\mu =\frac{MM^{'}}{(M^{'}M)}$.The effective mass of the phonon of the crystal represented by $M_{0}^{-1}=\frac{C}{M^{'}}+\frac{(1-C)}{M}$. Where, $R_{l}$ label the equilibrium position of the $l^{th}$ atom in the crystal, the symbol i nominates the position of impurity atom. With the help of above expressions, $|R(-k,k_{1})|^{2}$ is obtained as,

$$\begin{aligned}&|R(-k,k_{1})|^{2}=\left( \frac{\omega _{k_{1}}}{\omega _{-k}}^{2}\right) C(-k,k_{1})C^{*}(-k,k_{1})\nonumber \\&\quad +\left( \frac{\omega _{k_{1}}}{\omega _{-k}}C(-k,k_{1})D^{*}(-k,k_{1})\right) \nonumber \\&\quad +\left( \frac{\omega _{k_{1}}}{\omega _{-k}}\right) 4C(-k,k_{1})\sum _{k_{1}^{'}}C^{*}(-k,k_{1}^{'})D^{*}(-k_{1}^{'},k_{1})\omega _{-k}^{-1}\nonumber \\&\quad +\left( \frac{\omega _{k_{1}}}{\omega _{-k}}\right) \nonumber \\&\quad D(-k,k_{1}) C^{*}(-k,k_{1})\nonumber \\&\quad +D(-k,k_{1})D^{*}(-k,k_{1})4D(-k,k_{1}) \sum _{k_{1}^{'}}C^{*}\nonumber \\&\quad (-k,k_{1}^{'}) D^{*}(-k_{1}^{'},k_{1})\omega _{-k}^{-1}\nonumber \\&\quad +4\left( \frac{\omega _{k_{1}}}{\omega _{-k}}\right) C^{*}(-k,k_{1}) \sum _{k_{1}^{'}}C(-k,k_{1}^{'}) D\nonumber \\&\quad (-k_{1}^{'},k_{1})\omega _{-k}^{-1} \nonumber \\&\quad +4D^{*}(-k,k_{1}) \sum _{k_{1}^{'}}C(-k,k_{1}^{'}) D(-k_{1}^{'},k_{1}) \omega _{-k}^{-1} +16\nonumber \\&\quad \sum _{k_{1}^{'}} C(-k,k_{1}^{'})D(-k_{1}^{'},k_{1})\omega _{k}^{-1}\nonumber \\&\quad \sum _{k_{1}^{'}}C^{*}(-k,k_{1}^{'})D^{*}(-k_{1}^{'})\omega _{-k}^{-1} \end{aligned}$$

(22)

Considering the dispersion relation for nanowire as [28] $k_{\parallel }^{2}=k_{x}^{2}$ and $k_{\perp }^{2}=k_{y}^{2}+k_{z}^{2}$ the physical expression for $|R(-k,k_{1})|^{2}$ in nanowire system is accomplished as,

$$\begin{aligned}&\quad |R(-k,k_{1})|^{2}=\left( \frac{M_{0}}{4N\mu }\right) ^{2}(\omega _{k_{\perp }}^{2}+\omega {k_{\parallel }}^{2})\alpha ^{2}\nonumber \\&\quad +\left( \frac{M_{k_{1}}}{16N^{2}\mu }\right) (\omega _{k_{\perp }}^{2}+\omega _{k_{\parallel }}^{2})\alpha \nonumber \\&\quad +\left( \frac{M_{0}}{16N^{3}\mu ^{2}}\right) (\omega _{k_{\perp }}^{2}+\omega _{k_{\parallel }}^{2})^{\frac{3}{2}}\alpha ^{2} +\left( \frac{M_{k_{1}}^{2}}{16N^{3}M_{0}\mu }\right) \nonumber \\&\quad (\sqrt{\omega _{k_{\perp }}^{2}+\omega _{k_{\parallel }}^{2}})^{\frac{1}{2}}\alpha \nonumber \\&\quad +\left( \frac{M_{0}M_{k_{1}}}{64N^{3}\mu ^{2}}\right) (\omega _{k_{\perp }}^{2}+\omega _{k_{\parallel }}^{2})\alpha +\left( \frac{M_{k_{1}}^{2}}{16N^{3}M_{0}\mu }\right) \nonumber \\&\quad (\sqrt{\omega _{k_{\perp }}^{2}+\omega _{k_{\parallel }}^{2}})^{\frac{1}{2}}\alpha +\left( \frac{M_{k_{1}}^{2}}{16N^{2}\mu ^{2}}\right) (\sqrt{\omega _{k_{\perp }}^{2}+\omega _{k_{\parallel }}^{2}})^{6}\alpha ^{2} \end{aligned}$$

(23)

In the above expression,$\alpha$ is disclosed as follows $\alpha =[CN^{2}-R_{avg}^{2}]$, which shows impurity concentration and average number of particle dependency. To retrieve simplified form, we reorganize summation in to integration for nanowire case and after some algebraic facilitate we get the term as,

$$\begin{aligned} \Gamma _{k_{i}}^{D}(\omega )=(A_{1_{i}}\omega _{i}^{5}+A_{2_{i}}\omega _{i}^{2}+A_{3_{i}}\omega )\sum _{k_{\perp }}\Theta (\omega ^{2}-\omega _{k_{\perp }}^{2}) \end{aligned}$$

(24)

In the expression (A.6) ,term $\Theta (\omega ^{2}-\omega _{k_{1}}^{2})$ is a heaviside unit step function. which is introduce as,

$$\begin{aligned} \Theta (t)= {\left\{ \begin{array}{ll} 0 &{} \text {if t<0}\\ 1 &{} \text {if t>0} \end{array}\right. } \end{aligned}$$

(25)

where $A_{1_{i}}=\frac{M_{k_{i}}^{2}q}{8N^{2}\mu ^{2}v_{i}}\alpha ^{2}$ ,$A_{2_{i}}=\frac{M_{k_{i}}q}{8N^{3}\mu ^{2}}\alpha ^{2}$ and $A_{3_{i}}=(\frac{M_{0}}{4N\mu })^{2}\alpha ^{2}+\frac{M_{k_{i}}}{8N^{2}\mu }\alpha +\frac{M_{0}M_{k_{i}}}{64N^{3}\mu ^{2}}\alpha$ Where q represents the length of specimen. As, we can observe from the given expression that the value of these parameters chiefly depends on the change of mass and force due to isotopic defects and impurity in to in-plane and cross-plane.

Phonon-phonon scattering

For the evaluation of lifetime for phonon-phonon scattering, anharmonic potential for bulk materials is given by [37, 38, 54]

$$\begin{aligned} |V_{3}(K_{1},k_{2},k_{3})|^{2}=\frac{1}{288N}\frac{|\Delta (k_{1}+k_{2}+k_{3})|^{2}|\phi (k_{1},k_{2},k_{3})|^{2}}{(\omega _{k_{1}}\omega _{k_{2}}\omega _{k_{3}})^{\frac{1}{2}}} \end{aligned}$$

(26)

Where $\phi _{3}(k_{1},k_{2},k_{3})$ is cubic anharmonic coefficient and this can be expressed in the form,

$$\begin{aligned}&\phi _{3}(k_{1},k_{2},k_{3})\nonumber \\&\quad =\sum _{\alpha \beta \gamma }\sum _{lmn}\frac{\phi _{lmn}}{\sqrt{M_{k_{1}}M_{k_{2}}M_{k_{3}}}}e_{\alpha }(k_{1})e_{\beta }(k_{2})e_{\gamma }(k_{3}) e^{2\pi ik_{1}R_{l}}\nonumber \\&\quad e^{2\pi ik_{2}R_{m}} e^{2\pi ik_{3}R_{n}} \end{aligned}$$

(27)

Where $\alpha$,$\beta$,$\gamma$=1,2,3 and there corresponds, respectively, to the components in the x, y and z direction. In this mathematical statement, $\phi _{lmn}$ represents the force coefficient. Which can be expressed as [55]

$$\begin{aligned} \phi _{lmn}=\frac{\partial ^{3}}{\partial x\partial y\partial z}[V(r)] \end{aligned}$$

(28)

To obtain the results in the nanowire structures, the above partial differentiation has been illustrated as,

$$\begin{aligned} \phi _{lmn}=\frac{\partial ^{3}}{\partial x\partial y\partial z}[V(xy)V(z)]=V^{''}(x)V^{'}(yz) \end{aligned}$$

(29)

After simplifying eq.(B.1) by considering appropriate dispersion relation (described in appendix A) and with the help of some algebraic tools the simplified version of above mention equation we get,

$$\begin{aligned}&|V_{3}(k_{1},k_{2},k_{3})|^{2}\nonumber \\&\quad =\frac{1}{288N}\frac{1}{M_{k_{1}}M_{k_{2}}M_{k_{3}}}[12M_{k_{1}}M_{k_{2}}\omega _{k_{1_{\perp }}}^{2}\omega _{k_{2_{\perp }}}^{2}2\cos (2\pi R_{n^{=}}k_{3_{\perp }})\nonumber \\&\quad +4M_{k_{1}} M_{k_{2}}\omega _{k_{3_{\perp }}}^{2} 2\cos (2\pi R_{m^{=}}k_{3_{\perp }})\nonumber +4M_{k_{2}}M_{k_{3}}\omega _{k_{2}}^{2}\omega _{k_{3}}^{2} 2\cos \nonumber \\&\quad (2\pi R_{l^{=}}k_{1_{\perp }}) \nonumber \\&\quad +2 M_{k_{3}} \omega _{k_{3_{\perp }}}^{2} 2\cos (2\pi R_{l^{=}}k_{1_{\perp }})2\cos (2\pi R_{m^{=}}k_{3_{\perp }})\nonumber +2M_{k_{2}} \omega _{k_{2_{\perp }}}^{2}2\cos (2\pi R_{l^{=}}k_{1_{\perp }}) 2\cos (2\pi R_{n^{=}}k_{3_{\perp }})\nonumber \\&\quad +2M_{k_{1}}\omega _{k_{1_{\perp }}}^{2}2\cos \nonumber \\&\quad (2\pi R_{m^{=}}k_{2_{\perp }}) 2\cos (2\pi R_{n^{=}}k_{3_{\perp }})\nonumber \\&\quad +2\cos (2\pi R_{l^{=}}k_{1_{\perp }})2\cos (2\pi R_{m^{=}}k_{2_{\perp }})\nonumber \\&\quad 2\cos (2\pi R_{n^{=}}k_{3_{\perp }})] \frac{\sin ^{2}\pi a_{3}(N+1)k_{1_{\parallel }}}{\sin ^{2}\pi a_{3}k_{1_{\parallel }}} \frac{\sin ^{2}\pi a_{3}(N+1)k_{2_{\parallel }}}{\sin ^{2}\pi a_{3}k_{2_{\parallel }}}\nonumber \\&\quad \frac{\sin ^{2}\pi a_{3}(N+1)k_{3_{\parallel }}}{\sin ^{2}\pi a_{3}k_{3_{\parallel }}} \sum V^{'}(y,z)V^{'\star }(y,z) \end{aligned}$$

(30)

Substituting this expression in eq.(12) and converting summation in to integration, we get the symbolically form of linewidth for phonon-phonon scattering of nanowire structures as follows,

$$\begin{aligned} \Gamma _{k}^{3A}(\omega )=\sum _{i}B_{i}\omega _{i}^{2}coth\left( \frac{\hbar \omega _{i}}{2k_{B}T}\right) \sum _{k_{\perp }}\Theta (\omega ^{2}-\omega _{k_{\perp }}^{2}) \end{aligned}$$

(31)

Where,

$$\begin{aligned}&B_{i}=\frac{q^{2}}{128N\pi ^{2}M_{k_{i}}^{3}v^{2}_{i}}\frac{\sin ^{2}\pi a_{1}(N+1)k_{i}}{\sin ^{2}\pi a_{1}k_{i}}\frac{\sin ^{2}\pi a_{2}(N+1)k_{i}}{\sin ^{2}\pi a_{2}k_{i}}\nonumber \\&\quad \frac{\sin ^{2}\pi a_{3}(N+1)k_{i}}{\sin ^{2}\pi a_{3}k_{i}}\nonumber \\&\quad (2\cos (2\pi R_{{\bar{l}}}k_{i})2\cos (2\pi R_{{\bar{m}}}k_{i})\nonumber \\&\quad +2M_{k_{i}}2\cos (2\pi R_{{\bar{l}}}k_{i})2\cos (2\pi R_{{\bar{m}}}k_{i})\nonumber \\&\quad +2M_{k_{i}}2\cos (2\pi R_{{\bar{l}}}k_{i})2\cos (2\pi R_{{\bar{n}}}k_{i})\nonumber \\&\quad +2M_{k_{i}}2\cos (2\pi R_{{\bar{m}}}k_{i})2\cos (2\pi R_{{\bar{n}}}k_{i})\nonumber \\&\quad +4M^{2}_{k_{i}}2\cos (2\pi R_{{\bar{l}}}k_{i})+4M^{2}_{k_{i}}2\cos (2\pi R_{{\bar{m}}}k_{i})\nonumber \\&\quad +4M^{2}_{k_{i}}2\cos (2\pi R_{{\bar{n}}}k_{i})+8M^{3}_{k_{i}})\nonumber \\&\quad \sum _{y,z}V^{'}(y,z)V^{*'}(y,z) \end{aligned}$$

(32)

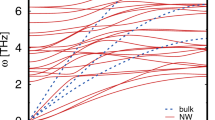
Where $R_{{\bar{l}}}$, $R_{{\bar{m}}}$ and $R_{{\bar{n}}}$ are indicates the equilibrium position of l,m and n atom in the crystal, respectively. If we restricted the motion of particles in y and z directions than, $V^{'}(y,z)$ is consider as the potential of nanowires. It means that there are two dimensional potential which limits the motion of phonons in these directions.

Interference scattering

On the basis of simplification has given in appendix A and appendix B, the symbolical form of interference scattering can be expressed as,

$$\begin{aligned} \Gamma _{k}^{3D}(\omega )=\sum _{i}D_{i}\omega _{i}^{4}coth\left( \frac{\hbar \omega _{i}}{2k_{B}T}\right) \end{aligned}$$

(33)

Where,

$$\begin{aligned}&D_{i}=\left( \frac{M_{0}}{4N\mu }\right) \frac{q^{2}}{128N\pi ^{2}M_{k_{i}}^{3}v^{2}_{i}}\frac{\sin ^{2}\pi a_{1}(N+1)k_{i}}{\sin ^{2}\pi a_{1}k_{i}}\nonumber \\&\quad \frac{\sin ^{2}\pi a_{2}(N+1)k_{i}}{\sin ^{2}\pi a_{2}k_{i}}\frac{\sin ^{2}\pi a_{3}(N+1)k_{i}}{\sin ^{2}\pi a_{3}k_{i}}\nonumber \\&\quad (2\cos (2\pi R_{{\bar{l}}}k_{i})2\cos (2\pi R_{{\bar{m}}}k_{i})\nonumber \\&\quad +2M_{k_{i}}2\cos (2\pi R_{{\bar{l}}}k_{i})2\cos (2\pi R_{{\bar{m}}}k_{i})\nonumber \\&\quad +2M_{k_{i}}2\cos (2\pi R_{{\bar{l}}}k_{i})2\cos (2\pi R_{{\bar{n}}}k_{i})\nonumber \\&\quad +2M_{k_{i}}2\cos (2\pi R_{{\bar{m}}}k_{i})2\cos (2\pi R_{{\bar{n}}}k_{i})\nonumber \\&\quad +4M^{2}_{k_{i}}2\cos (2\pi R_{{\bar{l}}}k_{i})+4M^{2}_{k_{i}}2\cos (2\pi R_{{\bar{m}}}k_{i})\nonumber \\&\quad +4M^{2}_{k_{i}}2\cos (2\pi R_{{\bar{n}}}k_{i})+8M^{3}_{k_{i}})\alpha ^{2}\nonumber \\&\quad \sum _{y,z}V^{'}(y,z)V^{*'}(y,z) \end{aligned}$$

(34)

and the various symbol used in the above expression have been expressed in Appendix A and Appendix B.