1 Introduction

As neutron scattering and analytics have become highly valuable tools to study the structure and dynamics of condensed matter and to perform chemical analyses of bulk samples in many areas of research over the last decades with a high output of publications from all over the world [1], the demand for neutron beam time remains consistently at high levels. Conventional neutron provision by nuclear reactors is serving this demand but the construction and maintenance of such large-scale research facilities are increasingly costly and time consuming. Therefore, neutron beam time is progressively secured by alternative routes, in particular accelerator-driven neutron sources (ADNS) as spallation neutron sources or compact accelerator-based neutron sources (CANS) [2,3,4].

Since large neutron facilities such as the ESS in Lund (Sweden), SNS in Oak Ridge (USA) or J-Parc in Tsukuba (Japan) cannot meet the demand for neutron beam time alone [5], increasing efforts are ongoing to provide neutrons via CANS.

In response to current developments and to push forward the possibilities for fundamental research with neutrons, the Jülich Centre for Neutron Science (JCNS) has developed a concept for a high power, high brilliance CANS optimized for neutron scattering on small samples in the framework of the Jülich High-Brilliance neutron Source (HBS) project [6,7,8,9].

Low energy reactions (10–100 MeV) yield much fewer neutrons per incident proton than spallation processes (\(\sim\) 20–30 neutrons for spallation [10]). However, this inefficiency of the individual reaction is compensated by two factors: (i) the much higher flux of incident protons for the same beam power on the target and (ii) more neutron beam extraction due to the compact target-moderator-reflector (TMR) unit [4]. Moreover, CANS benefit from fewer shielding requirements, less waste and reasonable construction costs for the building to house it in [11].

Like all particle accelerators, CANS are surrounded by strong, intense radiation fields of a diverse multitude of particles ranging from protons or neutrons to “exotic” particles such as muons, pions or neutrinos. Owing the direct exposure to the primary ion beam, the target potentially represents the most endangered entity. The continuous irradiation of the target material with these energetic particle showers alters the material’s properties on a microscopic scale, before macroscopic changes become visible as material degradation.

All detrimental alterations ultimately endanger the mechanical integrity and hence its safe operation. A target’s lifetime is predominantly limited by:

  1. (i)

      The activation of the material

  2. (ii)

      thermodynamical target degradation

  3. (iii)

      radiation-induced material damage

With regard to radiation protection principles, the (i) activation of the material can be studied and predicted quite precisely with simulative tools and experiments and hence is not a major difficulty [12, 13]. The process of (ii) thermodynamical target degradation, for example, through fatigue or oxygen deposits caused by repetitive cyclic and excessive heat loadings, can be counteracted and slowed down with an efficient heat removal system.

The (iii) radiation-induced material damage, however, can show very diverse patterns, and due to its non-trivial nature, it represents a challenge. In solids, the damage is mainly on account of lattice defects in the crystal, for example, dislocation loops [14], adatoms [15] or craters on surfaces [16], empty regions [17] or over- or undercoordinated atoms [18]. All these complex structural defects arise through the displacement of atoms in atomic collisions, representing simple point defects (PDs).

Although some useful literature on the consequences of radiation damage in tantalum exists [19,20,21,22,23,24,25,26,27], the derivation of threshold values is generally impeded as atomic displacements and associated damage patterns strongly depend on the exact irradiation conditions such as irradiation time, temperature, particle energy, particle flux and even the particle type itself [28,29,30]. In addition, the literature still lacks reliable reference values from highly precise molecular dynamics (MD) simulations or experiments [30], automatically implying that there is always a basic need for the analysis of the radiation-induced material damage.

The findings and conclusions obtained in this work contribute to the specific design and operation of the proposed HBS facility [6,7,8,9]. Independent of this, they are also expected to be of benefit to the nuclear physics and engineering community as there yet exist many uncertainties and various routes to obtain dpa values. This work offers a comprehensive recipe to obtain reliable values using SRIM and FLUKA for qualitative damage assessments.

In the present work, the simulation of the damage production and the discussion of its evolution over time are restricted to a primary proton beam energy of 70 MeV. Although the future HBS accelerator could in principle also be operated at variable energies even above 70 MeV, numerical calculations and simulations have identified 70 MeV to be the optimum energy with respect to tantalum as designated target material and other important technical specifications of the accelerator facility [9, 31]. A proton energy of 70 MeV results in a competitive neutron yield of 9.1 \(\cdot\) 10\(^{14}\) s\(^{-1}\) mA\(^{-1}\) for the \(^{181}\)Ta(p,xn)W reaction (\(\sim\) 0.10 n/p, estimated with MCNP and cross-sections for proton reactions taken from the TENDL 2017 database) [9] but also keeps essential risks concerning the target integrity, such as hydrogen embrittlement and mechanical stress due to temperature gradients, in a moderate frame that can be handled and counteracted well.

2 Methodology of the dpa concept

Energetic particles (i.e., \({E}_\mathrm{{kin}}\) > 1 eV) are capable of transferring an amount of kinetic energy to stationary crystal lattice atoms high enough to overcome binding energies. Displaced atoms are termed as primary-knock on atoms (PKAs) and can in turn further kick out atoms, resulting in a collision cascade with a huge diversity of particles.

As an accepted standard indicator for radiation damage in materials, displacement per atom (dpa) represents a physical unitless quantity that states how often an atom was displaced [32, 33]:

$$\begin{aligned} \mathrm{dpa}\, =\, \int _{0}^{t_i}\mathrm{d}t\, \int _{E_{\min }}^{E_{\max }}\sigma _d(E)\, \phi (E,t)\, \mathrm{d}E \end{aligned}$$
(1)

In Eq. (1) \(\phi (E,t)\) is the energy and time-dependent particle flux, \(\sigma _\mathrm{{d}}(E)\) the displacement cross-section as a function of energy E, \({t}_{\mathrm{i}}\) the irradiation time, \({E}_{\mathrm{min}}\) the minimum and \({E}_{\mathrm{max}}\) the maximum particle energy, respectively.

A first and useful formalism for the prediction of atomic displacements is given by the hard-sphere model of Kinchin and Pease (KP), originally proposed in 1955 [34]. Based on the conventional hard-sphere assumptions [28, 29], the amount of atomic displacements \(N_{\mathrm{d,KP}}\)(E) after the KP model can be computed as [29]:

$$\begin{aligned} N_\mathrm{d,KP}(E)={\left\{ \begin{array}{ll} 0 &{} {{\hbox {for}}\; E\,<\, E_\mathrm{d}}\\ 1 &{} {{\hbox {for}}\; E_\mathrm{d}\,<\, E\,<\, 2\, E_\mathrm{d}}\\ \frac{E}{2\, E_\mathrm{d}} &{} {{\hbox {for}}\; 2\, E_\mathrm{d}\,<\, E\, <\, E_\mathrm{c}}\\ \frac{E_\mathrm{c}}{2\, E_\mathrm{d}} &{} {{\hbox {for}} E\, >\, E_\mathrm{c}} \end{array}\right. } \end{aligned}$$
(2)

In Eq. (2), E represents the primary particle’s (i.e., PKA) kinetic energy, \({E}_\mathrm{{d}}\) is the threshold displacement energy and \({E}_{\mathrm{c}}\) is an energy cutoff that ensures elastic collisions as inelastic energy losses cannot induce displacements.

The threshold displacement energy \({E}_{\mathrm{d}}\) is defined as the minimum amount of energy (typically \(\sim\) 10–100 eV for most metals [35]) a projectile has to transfer to a material atom to leave its initial lattice site and create a stable defect (Frenkel pair).

For tantalum, the literature reports values between 32 and 130 eV [36], owing to a highly anisotropic behavior of \({E}_{\mathrm{d}}\). However, a thorough literature review also defines \({E}_{\mathrm{d}}\)= 90 eV as a reasonable, well accepted and quite frequently used average [37,38,39]. Since this value also corresponds to the recommendation of the American Society for Testing and Materials (ASTM) [30, 40], it has been used for all simulations.

The introduction of a comprehensive stopping theory by Lindhard et al. [41] and the associated recognition that only nuclear-deposited energy in elastic collisions results in atomic displacements lead to a modified version of the KP model [42]:

$$\begin{aligned} N_\mathrm{d,NRT}(T_\mathrm{d})={\left\{ \begin{array}{ll} 0 &{} {{\hbox {for}}\; T_\mathrm{d}\,<\, E_\mathrm{d}}\\ 1 &{} {{\hbox {for}}\; E_\mathrm{d}\,<\, T_\mathrm{d}\,<\, \frac{2\, E_\mathrm{d}}{\eta }}\\ \frac{\eta \, T_\mathrm{d}}{2\, E_\mathrm{d}} &{} {{\hbox {for}}\; \frac{2\, E_\mathrm{d}}{\eta }\,<\, T_\mathrm{d}\, <\, \infty } \end{array}\right. } \end{aligned}$$
(3)

Equation (3) is basically a refinement of Eq. (2) and termed as NRT model, named after Norget, Robinson and Torrens [42]. In this formalism, \({N}_\mathrm{{d,NRT}}({T}_\mathrm{{d}})\) is the number of atomic displacements, \({T}_{\mathrm{d}}\) is the nuclear-deposited energy and \(\eta\) is the displacement efficiency. The formalism for the available damage energy \({T}_{\mathrm{d}}\) can be taken from various publications, e.g., [43,44,45]. It is computed according to Robinson’s analytic fitting [46] of the Lindhard–Scharff–Schiøt (LSS) energy loss partitioning function [47]. The displacement efficiency \(\eta\) was found to be 0.8 [48] and takes defect recombination effects into account.

2.1 Damage calculation with SRIM

Fig. 1
figure 1

SRIM simulation of different collision events and phonon production in the tantalum target. a Calculations for the damage rates \({R}_{\mathrm{d}}\) are based on the number of target displacements, i.e., 101/Ion in the case of an average and \(\sim\) 8 \(\times\) 10\(^{-6}\) Å\(^{-1}\) Ion\(^{-1}\) for a peak value. Note that the numbers of events are related as: n(Target Displacements) = n(Target Vacancies) + n(Replacement Collisions). Furthermore: n(Target Displacements) > n(Target Vacancies) > n(Replacement Collisions). b Ta recoil atoms spend most of their energy for phonon production. Note, that the generated PHONON.txt file revealed the ordinate unit to be eV Å\(^{-1}\) Ion\(^{-1}\) instead of eV Å\(^{-1}\)

Full size image

Stopping and Range of Ions in Matter (SRIM) is a broad collection of MC software packages that enables one to calculate numerous features of ion transport problems in matter over a wide range of elements [49, 50]. Since it does not yield dpa values as a direct output, the user rather has to process the obtained data properly.

For damage calculation purposes, SRIM can be run in two different modes [35, 49]; (i) the Ion Distribution and Quick Calculation of Damage mode and (ii) the Detailed Calculation with Full Damage Cascades mode. Whereas the first one tracks only primary ions (i.e., protons) and hence is not a proper solution to depict the whole cascade damage, the latter one tracks every recoil atom from its creation until its kinetic energy falls below \({E}_{\mathrm{d}}\).

Assuming a continuous operation within a full power year (fpy), average (dpa per incident proton integrated over the entire target depth) and peak displacement doses (dpa/fpy) were calculated based on scaling a displacement rate \({R}_{\mathrm{d}}\) (dpa/s) with time (365 days). SRIM offers a wide range of routes to obtain dpa values. In this work, calculations are based on the formalism introduced in [35]. Therefore, data from the collision events output plot (see Fig. 1a) were processed with various equations.

In the case of an average damage rate, Eq. (4) was used:

$$\begin{aligned} R_\mathrm{d}\, =\, \frac{\frac{n({\hbox {Displacements}}/{\hbox {Ion}})_\mathrm{SRIM}}{d}\cdot \, \phi }{N {\hbox {(Ta)}}} \end{aligned}$$
(4)

For peak values, the equation above modifies to:

$$\begin{aligned} R_\mathrm{d}\, =\, \frac{n({\hbox {Displacements}}/{\hbox {Ion}}/{\AA })_\mathrm{SRIM}\cdot \, \phi }{N {\hbox {(Ta)}}} \end{aligned}$$
(5)

In Eqs. (4) and (5), n is the number extracted from the collision events plot and d is the target thickness (0.5 cm). Based on the specifications in the HBS project (see also Table 1) [9], a primary proton energy of 70 MeV, an average beam current of 1.43 mA and 100 cm\(^{2}\) surface area of the target, the proton flux \(\phi\) was determined to be 8.92606 \(\times\) 10\(^{-3}\) Å\(^{-2}\) s\(^{-1}\). The number density of tantalum N(Ta) was calculated to be 0.0554 atoms Å\(^{-3}\).

2.2 Damage calculation with FLUKA

FLUKA (FLUktuierende KAskade, Fluctuating Cascade) is a general purpose MC code qualified for calculations of particle transport and interactions in matter [51, 52]. Radiation damage studies are a very traditional application of FLUKA, since it was originally developed for that purpose. In contrast to SRIM, it is possible to obtain dpa values as a direct output of simulations in FLUKA, a feature enabled by use of the DPA-SCO option in the WHAT(2) field of the USRBIN scoring card.

FLUKA uses a sophisticated model for dpa calculations, based on a uniform implementation of the classical standard NRT formula [Eq. (3)] with a minimum input by the user [53]. The only parameter that has to be defined is \({E}_{\mathrm{d}}\) (90 eV), done with a MAT-PROP card and the SDUM as DPA-ENER.

The numerical output of FLUKA simulations is normalized per unit primary weight (i.e., source proton). However, care must be taken that region binned values (average) in contrast to axially binned values (peak) do not represent dpa values. Consultation with FLUKA experts in the official FLUKA mailing list revealed that region binned values are multiplied by the volume of the region. Hence, to obtain proper dpa values, the numerical output must be divided by that volume.

Owing a cylindrical volume source of the same radius as the target, unlike SRIM values FLUKA values were not multiplied with the HBS flux but rather with the number of incident protons per second, i.e., 8.92606 \(\times\) 10\(^{15}\) protons s\(^{-1}\).

3 Proton-induced damage

Fig. 2
figure 2

Proton electronic energy deposition along the target depth and recoil atom distribution in SRIM. a The protons deposit more and more energy with increasing target depth, and the maximum (Bragg peak) is not located in the target. Recoils are not depicted, as the corresponding IONIZ.txt file revealed their electronic energy losses to be \(\sim\) 4 orders of magnitude smaller. Indeed, they lose a significant amount of energy by phonon production (see Fig. 1b). b Distribution of Ta recoil atoms produced along the target depth. The highest recoil density at the rear implies that besides inelastic energy losses, also the nuclear-deposited energy peaks at the rear, and hence the number of atomic displacements

Full size image

The damage caused by protons was examined with SRIM and FLUKA. Though the preliminary overview simulation with SRIM kept track of recoils, it basically reflects the damage due to primary protons. This is the case, because it was evident that the nuclear stopping of the recoil atoms does not result in atomic displacements (see Fig. 1a) but in the creation of phonons (see Fig. 1b). Furthermore, the track visualization in the GUI of SRIM did not show a significant cascade creation of recoils. Nuclear reactions resulting in particle creation are not considered by default in SRIM [49].

3.1 SRIM investigations

The tantalum target was modeled as a single layer of 5 mm thickness, and the used ion and target data can be taken from Table 1.

Table 1 Set parameters for the SRIM simulation. Due to limitations in computing time using 70 MeV protons entering a tantalum layer, a total of 15.000 ions was taken to satisfy statistics. Lattice binding energy \({E}_{\mathrm{l}}\) and surface binding energy \({E}_{\mathrm{s}}\) are given for the sake of completeness
Full size table

Since the completion of the history of a single proton in tantalum was observed to take up much computing time, the total number of primary ions that were run was set to 15.000. Although small statistical fluctuations in the data remained, the result is considered to be satisfactory. Note that these fluctuations could also represent anomalous peaks and dips due to the concept used of a free flight path of ions. Although the damage between several interaction events is distributed over the flight path in between, damage cascades are only created at the end of each flight path.

The distribution of collision events in the target is depicted in Fig. 1a, they are related as: Target Displacements = Target Vacancies + Replacement Collisions. Since only a part of the defects recombines, the relation of the number n of these events is as follows: n(Target Displacements) > n(Target Vacancies) > n(Replacement Collisions).

The calculation of damage values after Eqs. 4 and 5 is based on the number of target displacements and not vacancies. Although defect recombination takes place, one has to assume that this phenomenon is not taken into account in a precise way in SRIM, whose prediction of recombination processes is anyway limited by the nature of the binary collision approximation (BCA). Therefore, the determination of dpa values based on atom displacements will lead to conservative results.

Undoubtedly, the rear of the target, i.e. the exit side of primary protons, is the most endangered area with the highest number of atomic displacements. As only nuclear energy losses result in displacements, this implies that the frequency of elastic collisions for all particles generated during the cascade peaks at the back of the target.

In principle, it is well known that nuclear energy losses tend to rise with decreasing kinetic energy of the corresponding particles and the electronic losses in turn peak at high ion energies. However, one should be aware that the actual behavior of these two competing quantities is a strong function of the mass ratio of all involved particles to each other. Therefore, at first sight, an increase in the electronic energy losses (see Fig. 2a) of the protons over the target depth might be surprising, but was also observed in [54].

Fig. 3
figure 3

FLUKA geometry taken from flair [56, 57], modified with coordinate axes. The proton beam impinges from the left perpendicular on the target (dark green), the emitted neutrons get thermalized in the spherical PE moderator (light green) beyond a beamstop (blue)

Full size image

Note that the recoils produced are not visible in Fig. 2a since the corresponding IONIZ.txt file revealed their electronic energy losses to be \(\sim\) 4 orders of magnitude smaller compared to protons. Therefore, they do not preferably lose energy in inelastic interactions such as ionization but rather spend most of their energy on phonon creation (see Fig. 1b). In addition to Fig. 1a, the Ta recoil distribution in the target (see Fig. 2b) also implies that the number of dpa peaks at the back of the target. In many projectile-absorber combinations, the PKAs unleash huge cascades. For pure tantalum and 70 MeV protons, however, the contribution of recoil atoms to displacements is negligible small. The recoils predominantly lose kinetic energy by phonon creation (see Fig. 1b), and SRIM lacks data for nuclear reactions resulting in the creation of new particles [49]. Therefore, it is reasonable to restrict the produced damage completely to the source protons.

Figure 1a also shows that the amount of replacement collisions increases towards the back of the target. This phenomenon plays a crucial role at lower proton energies, where nuclear stopping dominates. Indeed, the proton displacement cross-section for tantalum is observed to rise towards lower ion energies [55]. Hence, the average mean free path length between atomic collisions decreases, ultimately leading to an increased energy and defect density, favoring replacement collisions. Many-body collisions during thermal spikes will also increase the number of replacement collisions but the BCA is incapable of depicting that.

3.2 FLUKA investigations

With FLUKA simulations, a more realistic picture of the environment surrounding the target can be constructed than with SRIM simulations. In the frame of Combinational Geometry (CG), the whole geometrical setup is described by bodies and regions, the latter one built by combining bodies with different Boolean operations (union, subtraction, intersection).

In all simulations, the primary proton beam is defined as a cylindrical volume source, emitting protons homogenously. The cylinder radius is equal to the target radius, i.e., 5.64 cm.

The geometrical setup utilized for all FLUKA simulations is depicted in Fig. 3. The small water layer of 0.45 cm behind the target is denoted as “beamstop” and serves to ultimately stop the primary source protons.

Fig. 4
figure 4

FLUKA plots of dpa and energy deposition \({E}_\mathrm{{dep}}\) from protons. Both quantities are normalized per primary, i.e., source proton. For the spatial distributions, a radius of 0 corresponds to the target longitudinal symmetry axis (z-axis, beam direction). Vertically (x-axis), the radial binning did not distinguish between the top and bottom side of the target, i.e., each radial bin covers a volume of angle of 360\(^\circ\) around the z-axis (see Fig. 3 for the axes arrangement). a Proton atomic displacements as a function of the target depth. b Total energy deposition by protons over the target depth. c Spatial distribution of the proton atomic displacements. d Spatial distribution of the energy deposited by protons

Full size image

In the HBS project, both the target thickness and the proton energy are matched such that the Bragg peak does not occur inside the target itself but rather in the subsequent beamstop. This represents a technological design improvement, as the heat generation inside is reduced significantly without a considerable decrease in the neutron yield (\(\sim\) 0.10 n/p [9]).

To reduce the energy of the neutrons produced to values demanded by various neutron scattering methods, e.g., diffractometers, analytical spectrometers or imaging, the whole geometry is surrounded by a thermal moderator made of polyethylene (PE) with a radius of 10 cm (see Fig. 3).

Regarding the particle transport, a global threshold of 10\(^{-14}\) GeV was defined by a PART-THR card for all hadrons, muons and neutrons generated during the collisions cascade. For electrons, positrons and photons, the default values were taken (i.e., 513 keV for electrons and positrons and 0.1 keV for photons). In order to obtain satisfying statistics and to prevent artifacts due to statistical fluctuations, the number of primary source protons to be simulated was always set to be 10\(^{7}\).

The extent of atomic displacements and total energy deposition \({E}_\mathrm{{dep}}\) as a function of the target depth is given in Fig. 4. In agreement with the SRIM simulations, FLUKA also determines the back of the target to be the most vulnerable region (see Fig. 4a, b). For the binning, the target was divided axially into 100 pieces (bins) and the output of the USRBIN estimator was filtered for the contribution of the protons by means of a proper AUXSCORE card. Thus, the contribution of secondary protons produced via nuclear reactions was also taken into account. However, this approximation is reasonable since the contribution of secondary protons at 70 MeV energy was found to be only \(\sim\) 0.5%.

Fig. 5
figure 5

FLUKA plots of dpa and energy deposition \({E}_\mathrm{{dep}}\) from neutrons. Both quantities are normalized per primary, i.e., source proton. For the spatial distributions, a radius of 0 corresponds to the target longitudinal symmetry axis (z-axis, beam direction). Vertically (x-axis), the radial binning did not distinguish between the top and bottom side of the target, i.e., each radial bin covers a volume of angle of 360\(^\circ\) around the z-axis (see Fig. 3 for the axes arrangement). a Neutron atomic displacements as a function of the target depth. b Total energy deposition by neutrons over the target depth. c Spatial distribution of the neutron atomic displacements. d Spatial distribution of the energy deposited by neutrons

Full size image

In direct comparison to the energy deposition, atomic displacements rise much more steeply towards a narrower (Bragg) peak region. This is mainly attributed to the fact that the nuclear energy deposition becomes dominant near the Bragg peak where the ions are slowed down substantially. The Bragg peak of the energy deposition curve runs broader since also the electronic energy losses increase towards the back of the target (see Fig. 2a).

In order to obtain information on the spatial damage distribution inside the target, a 50 \(\times\) 50 binning in axial z-direction and radius was also performed (see Fig. 3c, d). Besides the great similarity between deposited energy and atomic displacements again, one can observe a radial homogenously distributed pattern at every depth. This is attributed to the homogenous source and the protons’ perpendicular hitting of the target.

The radial binning did not distinguish between the top and bottom side of the target. Each radial bin at a certain target depth covers an angle around the longitudinal symmetry axis of the target (i.e., z-axis) of 360\(^\circ\). However, as the proton source is defined homogenously this did not lead to any errors.

4 Neutron-induced damage

Fig. 6
figure 6

Neutron spectral data for a PE moderator and 70 MeV primary proton energy. a Energy differential neutron spectrum obtained with a USRTRACK card. The thermal peak results from the spherical moderator and might seem to be overemphasized, which is a consequence of the fixed bin width of the 260 FLUKA neutron energy groups below 20 MeV. b Neutron fluence \(\Phi\) over the target depth obtained with a USRBIN card. The neutron density peaks at the middle of the target and decreases toward the outer surfaces

Full size image
Table 2 Division of the neutron spectrum into different energy groups. As the transport of neutrons carrying a kinetic energy less than 20 MeV (referred to as “low-energy neutrons”) is performed in FLUKA by default by means of a multigroup algorithm, the energy boundaries of the 260 neutron groups are fixed. Unfortunately, these boundaries do not coincide with the generally accepted values. Therefore, based on the fixed boundaries of the 260 FLUKA neutron groups given in the FLUKA manual [52], the actual boundaries were adjusted to be as close as possible to the theoretical ones
Full size table

Similar to the proton-induced damage, the damage caused by the emitted neutrons was characterized based on the axial and two-dimensional spatial distribution of atomic displacements and energy deposition \({E}_\mathrm{{dep}}\) in the target (see Fig. 5a–d). Additionally, the spatial distribution (spectra) of neutrons inside the target is of importance, and hence, the fluence \(\Phi\) was also scored.

Obviously, in contrast to the protons, the amount of energy deposition and the dpa peaks near the middle of the target and decreases axially toward the outer surfaces. This is also the case for the radial variation of dpa and energy deposition. Therefore, the spatial damage pattern of neutrons looks like a cloud.

The damage pattern of the neutrons is as expected, based on the obtained spectral data, depicted in Fig. 6. In the middle of the target, the primary protons are actually slowed down to an energy corresponding to the neutron production peak (see Fig. 6b). Hence, most neutrons are emitted here and displace atoms most efficiently.

The representation of the neutron fluence as a differential energy spectrum (i.e., d\(\Phi\)/dE, fluence in each energy bin normalized to 1 MeV; see Fig. 6a) might lead to an overestimation of the thermal peak, as the binning width for neutrons below 20 MeV kinetic energy is automatically given in the frame of the 260 FLUKA neutron energy groups. Since the fluence is normalized per MeV and the bin width below 20 MeV is smaller than above, the fluence below 20 MeV seems bigger than it is. Note that neutrons carrying a kinetic energy of less than \({E}_\mathrm{{d}}\) are incapable to induce atomic displacements.

In order to obtain depth information on the neutrons’ density and information on their energy, two measures were taken: First, the target was divided into 50 equal regions (i.e., each of 0.01 cm thickness). A corresponding USRTRACK card was assigned to each of these regions to obtain energy spectral data. Secondly, the USRTRACK data for each bin were divided into five energy groups (see Table 2) and then post-processed with MS Excel.

As apparent in Table 2, it was not possible to divide the energy range exactly by the generally used boundaries. This is the case, since the transport of neutrons with energies lower than 20 MeV (termed as “low-energy neutrons” in FLUKA) is performed in FLUKA by default by a multigroup algorithm, for a total of 260 neutron groups. The energy boundaries of these groups can be taken from a table in the official manual [52]. The boundaries used to define the groups were adjusted from that table to be as close as possible to the theoretical ones.

The neutron fluence for all five neutron energy groups is plotted over the target depth in Fig. 7. Simulations without a moderator showed that cold, thermal and epithermal neutrons come from the moderator surrounding the target. Only fast and resonance neutrons have the capability to cause atomic displacements. In comparison to Fig. 6a, this plot also unmistakably shows that the number of low-energy neutrons (thermal peak) is much smaller that of fast neutrons.

Comparing the number of displacements from neutrons and protons, clearly, protons are much more harmful than neutrons. Indeed, the neutrons’ contribution to average and peak displacement doses was found to be comparably negligible with \(\sim\) 4% and \(\sim\) 1.5%, respectively. For tantalum, this damage pattern is also reported in the literature [58, 59].

Fig. 7
figure 7

Neutron fluence \(\Phi\) for five different neutron energy groups according to Table 2 obtained with a PE moderator. The number of neutrons decreases with decreasing neutron energy

Full size image
Table 3 Numerical results for the calculated damage rates \({R}_\mathrm{{d}}\) and annual doses
Full size table

In a simulation of the hadronic collision cascade, the contribution of different particles to the amount of dpa was examined. As can be seen in Fig. 8, protons dominate by far in contrast to neutrons.

Fig. 8
figure 8

Contribution from protons and neutrons to the total atomic displacements. Protons dominate by far, neutrons’ contribution is negligible

Full size image

To have only a minor contribution of neutrons to atomic displacements was surprising, as intense and frequent collisions between neutrons and target nuclei are unhindered by Coulomb repulsion due to the neutrons’ absence of a net electric charge. Therefore, various validation simulations were performed with the aim of finding an explanation of the observed damage pattern. In the frame of these simulations, the annual average and peak displacement doses of neutrons were scored for a varying moderator radius r (0 \(\le r \le\) 50 cm), varying target thickness d (0 \(\le d \le\) 10 cm) and substitution of the moderator by a natural uranium reflector (0.72% U-235 and 99.28% U-238) in order to scatter back fast neutrons. However, none of these approaches were able to explain the neutrons’ minor contribution to the displacements.

In the WHAT(4) field of a LOW-NEUT card a printing flag was set, which gives total cross-sections for all 260 low-energy neutron groups (10\(^{-11}\) to 20 MeV) for all defined media in the FLUKA output file. The macroscopic transport cross-section \(\Sigma _{tr}\) was calculated as the product of this total cross-section and the number density N(Ta) of tantalum. The mean free transport path length \(\lambda _{tr}\) was then in turn determined as the inverse of the macroscopic cross-section \(\Sigma _{tr}\) (see Fig. 9).

Fig. 9
figure 9

Mean free transport path length \(\lambda _{tr}\) of neutrons inside the tantalum target. At kinetic energies greater than the displacement threshold \({E}_\mathrm{{d}}\) the average path length mostly exceeds the target thickness, resulting in rare interaction events

Full size image

Clearly, the mean average distance traveled by the neutrons between each collision exceeds the target thickness of 0.5 cm by far above the required threshold \({E}_\mathrm{{d}}\). Only some resonance neutrons might be capable of causing displacements. Therefore, in the case of protons and tantalum as a projectile-absorber combination, neutron atomic displacements are negligible in relative terms.

5 Target lifetime estimation

A definitive and precise statement about the target’s expected maximum lifetime, exclusively based on simulative damage values, is neither possible nor recommended. For this purpose, challenging experiments with regard to radiation safety and protection issues are indispensable. In addition, the literature still lacks reliable reference values for most materials throughout the whole periodic table, beyond which one could surely assume the material to suffer critical damage.

Therefore, based on obtained damage values and the meticulous literature review given below, rather a qualitative and cautious estimation for the minimum lifetime \(\tau _{\min }\) that could be reasonably expected is made.

The dpa values obtained serving as a basis for the lifetime estimations are given in Table 3. The damage rates are obtained by scaling the simulation output with the number of protons per second corresponding to the HBS proton current of 1.43 mA. Annual displacement doses reflect the accumulated number of displacements under the assumption of a continuous operation, i.e. a full power year (fpy).

5.1 Literature review

The available literature concerning radiation damage investigations of tantalum based on the dpa quantity is quite sparse and limited. However, as it is frequently used as spallation material and also regarded as a plasma-facing material [60] and solid target for neutrino production [61], a few data do exist. In addition, tungsten (\(Z=74\)) behaves in a similar way to tantalum and is often alloyed or coated with tantalum (solid solution) to reduce corrosion-erosion effects [62,63,64]. Investigations of such Ta-clad W targets may at least partly reflect the radiation damage behavior of tantalum.

For most solids, a very general rule of thumb proposes that the lifetime dose against radiation damage by protons can be taken as \(\sim\) 10\(^{22}\) p\(^{+}\)/cm\(^{2}\) [65]. Related to the target surface area of 100 cm\(^{2}\) in the HBS project this would mean that the target can withstand a total of 10\(^{24}\) primary source protons, roughly 3.5 years at 1.43 mA average beam current. Nevertheless, this value should be reviewed carefully and taken as a coarse estimation only since specific irradiation conditions such as the proton energy, or the target thickness are neglected.

Ipatova et al. found out that radiation-induced voids in pure tantalum, irradiated with 3 MeV protons, order and grow at 0.25 dpa (fluence of 2.8 \(\times\) 10\(^{18}\) p\(^{+}\)/cm\(^{2}\)) [20]. As voids are favored places for the accumulation of reaction products (e.g., H, He), blistering and swelling can start to continuously degrade the mechanical integrity.

Yasunaga et al. observed that the swelling, however, is negligible below \(\sim\) 730 \(^\circ\)C and 20 dpa in the case of heavy ion irradiation [21]. Wiffen also determined the swelling of tantalum after neutron irradiation to be negligible below 425 \(^\circ\)C [22].

In another work, Ipatova et al. investigated the effect of alloying content on the defect structure formation and evolution in the Ta-W system [23]. Studies of pure tantalum, irradiated with 3 MeV protons and a 9.5 mA beam current for 36 h at \(\sim\) 350 \(^\circ\)C, showed that radiation-induced hardening starts to occur roughly after irradiation begins, i.e. at doses \(\le\) 0.3 dpa. Dislocation loops as the starting point for the evolution of complex damage patterns are reported to occur in the same dose region but only at elevated temperatures of 700 \(^\circ\)C.

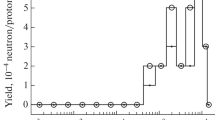
Villagrasa-Roussel et al. obtained simulative dpa values for a tantalum spallation target with conditions as proposed for the TRADE experiment [24]. The data for four different primary proton energies (140, 300, 500 and 1000 MeV) were fitted and extrapolated to the origin in order to derive a value corresponding to the HBS energy of 70 MeV (see Fig. 10). The beam current of 0.14 mA was scaled to 1.43 mA, resulting in a dpa value of 107. As expected, this value exceeds all obtained values due to occurrence of spallation reactions. Since the HBS will operate at an energy of 70 MeV below the spallation threshold and no proper experimental data on the TRADE project are reported in the literature yet, this also has no significance for the considerations within this paper. On the other hands, if such experiments existed and did not reveal a failure of tantalum, this would distinctly indicate that there should be no problems with the Ta target optimized for the HBS project.

Fig. 10
figure 10

Extrapolation of the dpa values in a Ta spallation target obtained by C. Villagrasa-Roussel et al. [24] The curve was fitted with a sigmoidal hill fitting (3 parameters)

Full size image

A very suitable way of estimating the lifetime is given by the pulsed spallation source ISIS (Spallation Neutron Source at Rutherford-Appleton Laboratory), as they have used tantalum for a long time and still use it nowadays as cladding for W targets. In an extensive test program for the lifetime of structural components of spallation targets, Chen et al. investigated spent target components from spallation facilities [25, 26]. Based on investigations of the irradiation-induced alterations of mechanical properties, the testing also included a spent tantalum target of ISIS.

In several irradiation campaigns over six years, this target was irradiated with 800 MeV protons up to a maximum fluence of 1.7 \(\times\) 10\(^{21}\) p\(^{+}\)/cm\(^{2}\) (\(\sim\) 1.7 Ah) below temperatures of 200 \(^\circ\)C. Microhardness measurements, three-point bending tests, tensile tests and optical micrography at RT and 250 \(^\circ\)C revealed radiation hardening accompanied with a drop in ductility already below doses of 0.6 dpa.

However, remarkably the tantalum target retained a very high ductility even after a displacement dose of 11 dpa. Scanning electron microscope (SEM) investigations revealed typical ductile fracture surfaces and between 0.6 dpa and 11 dpa the strain-to-necking ratio remained constant.

In the work above by Chen et al., the calculated displacement damage of 11 dpa refers solely to protons [26], hence neglecting neutrons. Therefore, in [27] Byun and Maloy report the irradiation of a tantalum target from ISIS exclusively by neutrons in the high flux isotope reactor (HFIR) at the Oak Ridge National Laboratory (ORNL) at an irradiation temperature of 100 \(^\circ\)C. Already at a dose of 0.14 dpa tensile tests at RT and 250 \(^\circ\)C showed that the tantalum target experienced embrittlement.

In the same measurements, also a Ta-10W (90% Ta and 10% W) specimen has been tested. The probe broke at a dose of 25.2 dpa with minor necking strain, indicating a substantial loss in ductility.

Also at ISIS, the 800 MeV synchrotron provides protons for two target stations (TS) with Ta-clad W targets [66,67,68]. In neither of them is the lifetime limited due to radiation damage. In TS1 (160 kW power), the expected lifetime was about 4–5 years but this value was not reached due to a thermocouple failure in the system, in TS2 (32 kW power) operation was stopped after about 1.5 years due to the release of activation products into the cooling water circuit, probably due to a welding failure [67, 68].

5.2 Proposed lifetime

For a lifetime estimation, the reference values of 11 dpa and 0.14 dpa obtained from Ta targets operated at ISIS should be reasonable, especially in the case of the 11 dpa value, as the extent of damage inside this target must be assumed to exceed the one in the HBS target due to spallation processes (800 MeV proton energy). Furthermore, it is reported that this target was not replaced due to radiation damage. Rather, ISIS performed a change to Ta-clad W targets for reasons of increased neutron output, reduced decay heat and enhanced thermal conductivity. Hence, the target probably would have been able to withstand even higher doses.

Although neutrons’ contribution to displacements is negligible in the HBS project compared to that of protons, it seems that even small doses might be sufficient to cause substantial changes in material properties. However, Byun and Maloy considered the embrittlement in [27] to have been premature. One should be aware that the target was annealed for 2 h at 1200 \(^\circ\)C in vacuum before irradiation, and hence, the accumulation of oxygen in the range of 400 wppm might have weakened the material and been the reason for the early embrittlement.

The minimum lifetimes are estimated based on known dpa values derived from tantalum irradiation tests with targets operated or manufactured for ISIS (i.e., 11 and 0.14 dpa) and the obtained average displacement rates \({R}_\mathrm{{d}}\) (see Table 3), as depicted in Table 4. The calculation of \(\tau _{\min }\) based on peak rates would surely lead to shorter lifetimes. However, in order to account for the whole bulk and strength of the material and to obtain a value reflecting the reaction of the complete target volume on the radiation damage, the lifetime estimation is based on average values of \({R}_\mathrm{{d}}\).

Table 4 Estimations of the expected average minimum target lifetime \(\tau _{\min }\)
Full size table

Values corresponding to 11 dpa were obtained based on proton damage rates, whereas those based on 0.14 dpa were calculated with the damage rates of neutrons. Values are given in units of years (a) and units of total accumulated primary proton beam charge (Ah) in the target (see Table 4).

As expected, SRIM proposes a shorter value for \(\tau _{\min }\) than FLUKA due to the differences in the physical dpa models. A further reduction in the FLUKA-obtained values is done as the displacement efficiency \(\eta\) is not constant but rather implemented into FLUKA as a function of the kinetic particle energy above \(\sim\) 1-2 keV [53]. Hence, \(\eta\) is not constant but variable, and the migration and recombination of FPs are taken into account in a more accurate way.

Since the NRT model reflects the current accepted standard in atom displacement models and is more accurate than the KP model, FLUKA values should be taken as more realistic in comparison to SRIM values. In addition, since protons dominate in dpa and the low lifetime based on neutron damage is most probably due to a pre-treatment, it should be reasonable to take the minimum lifetime \(\tau _{\min }\) of the target to be 2.6 years.

5.3 Reliability assessment

A meaningful lifetime estimation regarding radiation-induced material damage by atomic displacements should always consider actual irradiation conditions. With respect to these conditions, the temperature exhibits the most notable and dominating influence on atomic displacements.

Due to the strong temperature dependence of the diffusion of mobile defects, the extent of displacements remaining after recombination processes is a strong function of the temperature. Current simulations of the temperature determine the maximum temperature inside the HBS target to be \(\sim\) 120 \(^\circ\)C and the average temperature to be around \(\sim\) 65 \(^\circ\)C [9].

As a refractory metal and with regard to the melting temperature \(T_{m}\) (\(\sim\) 3000 \(^\circ\)C), the dominant effect of the radiation will be radiation hardening with an associated reduction in ductility (up to \(\sim\) 0.3 \(T_{m}\) [69]), starting already at roughly 0.1 dpa. Irradiation creep and void swelling are not expected to limit the lifetime substantially as they dominate between 0.3 and 0.6 \(T_{m}\). Given these low temperatures and a clever internal cooling design, a change in the crystal BCC structure of Ta (\(\alpha\)-phase) can probably be excluded, also excluding associated changes in the \({E}_\mathrm{{d}}\) [70] or other fundamental physical properties.

Although unclear at the moment how often, the target has to be replaced regularly with regard to activation limits. The activity of the HBS target is in the same order of magnitude of the Ta-clad W target of the ISIS facility [9, 71]. At a total exposure of 1.94 Ah with 800 MeV protons, it was replaced after approximately 540 days. In the HBS project, a total activity in the range of PBq is already reached within the first 30 days [9] of continuous operation (\(\sim\) 1.0 Ah). Due to radiation safety and disposal issues, the target will operate for a maximum period of one year. With regard to Table 4, it is clear that no critical radiation damage is expected during this period.

An ultimate reliability check of the obtained simulative values requires the benchmark with experimental data obtained under realistic conditions as prevailing in the frame of the parameters of the HBS project. The actual damage pattern on a microscopic level is a strong function of the frame irradiation conditions applied, and as the displacement process underlies a random nature coupled with a certain probability (cross-section) such as radioactive decay, a prediction of damage is generally impeded. The absolute number of atomic displacements does not inherently reflect the microscopic damage. Therefore, experimental investigations of activated material are indispensable. The actual damage pattern can only be assessed by means of advanced microscopic techniques such as transmission electron microscopy (TEM) or scanning electron microscopy (SEM) [72,73,74,75]. The application of such methods allows to identify doses (dpa) where critical defect structures start to emerge.

6 Conclusions

The proton and neutron radiation-induced material damage produced in a tantalum target as described within the HBS project was assessed by means of simulations. The SRIM and FLUKA MC codes have been used to extract information on atomic displacements, energy deposition and neutron spectral data. Based on damage rates \({R}_{\mathrm{d}}\) (dpa/s), average and peak annual displacement doses were calculated for a continuous operation mode in a full power year (fpy). Coupled with the meticulous literature review, the minimum lifetime \(\tau _{\min }\) of the target was estimated carefully.

SRIM simulations clearly mark the back of the target as the most vulnerable area, with the highest number of tantalum recoil atoms and hence atomic displacements. Recoil atoms lose most of their energy in phonon creation, instead of further displacing atoms and thereby initiating large cascades. Apart from that, the contribution of secondary protons was found to be negligible in FLUKA simulations. Consequently, it is reasonable to restrict the outcomes of the SRIM simulation to the primary source protons only.

Axially the proton damage increases toward the back, radially it remains constant due to the homogenous volume source applied. In contrast, the neutron damage peaks axially and radially in the middle of the target and decrease toward the outer surfaces.

Comparison of the proton and neutron-induced damage on an absolute scale determines the neutron-induced displacements to be totally negligible. This fact is a material-specific phenomenon, as the mean free path length \(\lambda _{tr}\) of neutrons capable of causing displacements usually exceeds the target thickness. Though the spherical PE moderator increases the total neutron population inside the target, these neutrons mainly belong to low-energy neutrons of kinetic energy less than the threshold displacement energy \({E}_{\mathrm{d}}\).

The meticulous literature review yielded a few useful hints for a target lifetime estimation. In particular, the irradiation of Ta targets from the ISIS facility allowed the derivation of reasonable lifetimes. Based on obtained average damage rates \({R}_{\mathrm{d}}\) in order to account for the whole bulk of the material and two reference values, one referring to protons (11 dpa) and one to neutrons (0.14 dpa), minimum lifetimes \(\tau _{\min }\) were estimated. Since the lower lifetime based on neutrons is most probably attributed to a material weakening as a consequence of oxygen uptake during a pre-irradiation treatment, the lifetimes based on protons should be taken as more accurate. From these in turn, the FLUKA value should be taken as more accurate in comparison to the one from SRIM as the latter inherently overestimates the damage due to the KP model.

Based on the damage induced by protons, indeed the main agents here, a minimum lifetime of 2.6 years (33 Ah) is proposed. This value also remains reasonable when considering frame irradiation conditions. Since the temperature achieved in the target keeps within a moderate frame and the target must be replaced at regular intervals anyway, a critical failure before the proposed time is very unlikely.

A final clarification of the maximum target lifetime with a small amount of uncertainty requires the irradiation of samples and subsequent investigations by microscopic techniques such as TEM or SEM. Despite the challenging character of such experiments with regard to the observance of radiation protection principles, special radiation damage test facilities already exist with proper handling options for the activated material (e.g., at PSI, ISIS and Forschungszentrum Jülich).